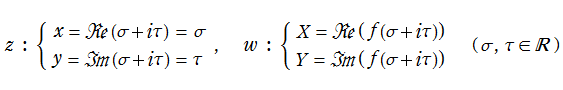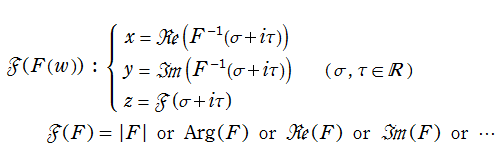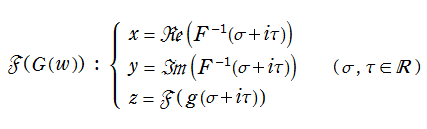特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
Home Menu
グラフの凡例
当サイトに掲載しているグラフは、それを作成した Mathematica の Version が 5.01 と 8.01 の二種類混在しています (Ver.5~6の間でプロット機能の変更点が多く、旧コード 「FunctionPlot.m」 の Ver.8対応化に時間を要したことが主な理由)。
両者は基本的に同じタイプのグラフであり、一般に通用している関数の描画方法に則っていますが、デザイン的に若干の違いもあるので、以下ではその詳細を説明します。
この他、複素関数を描画する別の方法として等角写像図と、これを応用した多価関数の描画方法についても、この頁で説明します。ただし、サイト内にはここで説明していないタイプのグラフも存在します (特に複素変数ではないグラフ)。
なお、当サイトではグラフの画像を、すべて PNG 形式で掲載しています。
MathematicalFunctionPlot.m
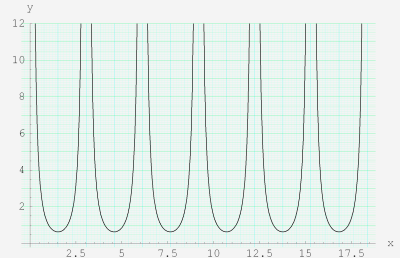
実変数関数プロット(方眼紙付き)
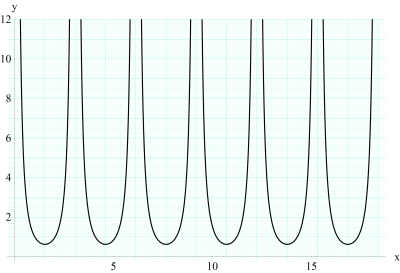
典型的な関数のグラフ。定義域が線分上にあり、値域が実数になる場合に使用する。背景に置かれる方眼紙は、太線の間を細線が2分割し、さらに太線と細線の間を極細線が5分割する。方眼紙の色は上記の水色とは限らず、曲線の色に応じて変えている。
なお、ひとつの方眼紙上に複数のグラフを重ね描きしているときの曲線のカラーリングは、助変数の値が大きくなるにしたがって、後述の 「色相環」 の反時計回りになるようにしている。
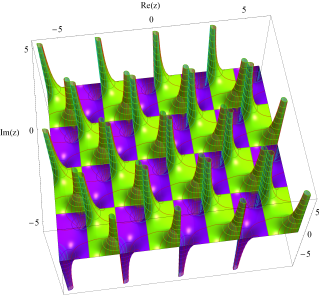
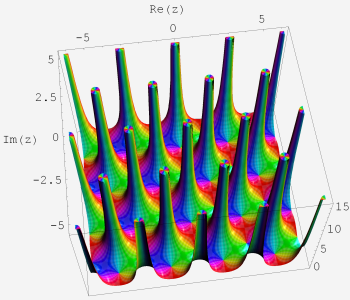
複素変数関数プロット:絶対値と偏角(3次元)
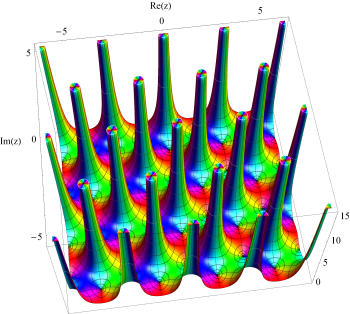
複素変数関数の値について、その絶対値を底面から曲面までの高さ、偏角を曲面のカラーリングで表わしたグラフ。カラーリングは 「色相環」に基づいている (詳細は次のグラフで説明)。視覚補助のため、曲面上に絶対値・偏角それぞれの等高線を引いている。絶対値の等高線は底面で黒、描画範囲の最大値で白になるようなグラデーションになる。偏角の等高線は黒のみ。
偏角の等高線は常に等間隔だが、絶対値の等高線は多くが指数関数的な間隔で引かれる。絶対値が急激に増大もしくは0に近づくような関数は指数関数と指数関数の合成関数的な間隔、逆に、絶対値の変化が緩慢な関数は等間隔で引かれる場合もある。
絶対値が描画範囲を超えた部分は平面で塞がれるが、偏角のカラーリングと等高線は延長される。
このグラフを真上から見た場合 (つまり曲面の高さを無視した場合) のグラフが、次の 「偏角のみ2次元グラフ」 と一致する (等高線は両者で一致するように統一したが、定義域の範囲は異なる場合がある → 多くは絶対値が急激に増大する関数のとき)。
座標軸のラベルは、「Re」 が実数方向、「Im」 が虚数方向を表わす (以下同様)。
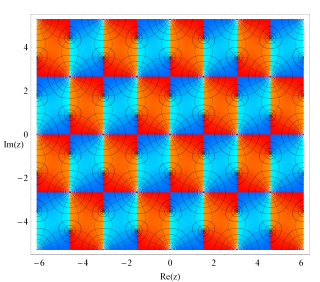
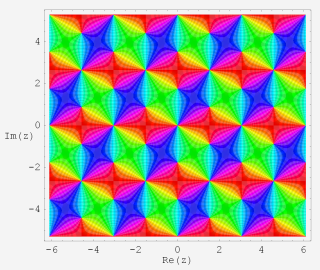
複素変数関数プロット:偏角のみ(2次元)
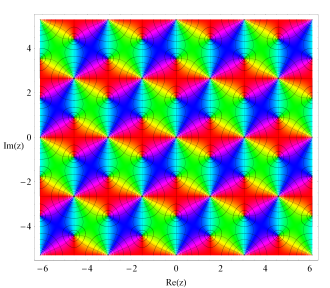
複素変数関数の値について、その絶対値を等高線のグラデーションのみ、偏角をカラーリングと等高線で表わしたグラフ。カラーリングは 「色相環」 に基づいている。偏角が0のときを赤にしている。絶対値の等高線は0のとき黒、前の 「絶対値・偏角3次元グラフ」 での最大値で白になるようなグラデーションになる。最大値を超えた絶対値の等高線もこのグラフでは延長して引かれ、白が継続する。偏角の等高線は黒のみ。等高線の間隔の取り方は、「絶対値・偏角3次元グラフ」 と同じ原則に従っている。(Böttcher 関数は、最小絶対値が1なので、これを描画の底面として絶対値等高線の色および間隔を決定している。)
(色相環について)
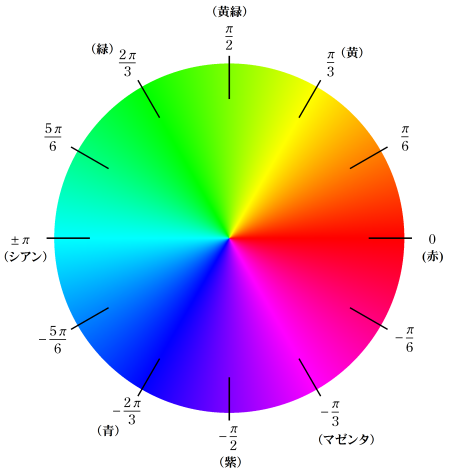
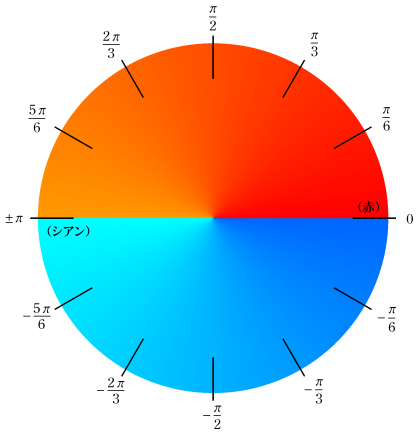
偏角を表わす色相環は、次の凡例図のとおり。図に表示した角度はラジアンとする。
このうち、赤・緑・青は 「光(加法混合)の三原色」、黄・シアン・マゼンタは 「色(減法混合)の三原色」 と呼ばれる。(→ Wikipedia 「色相」, 「原色」 を参照。)
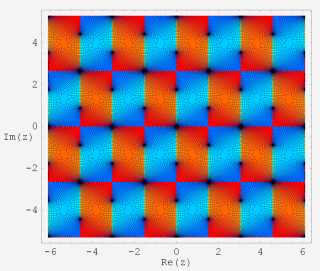
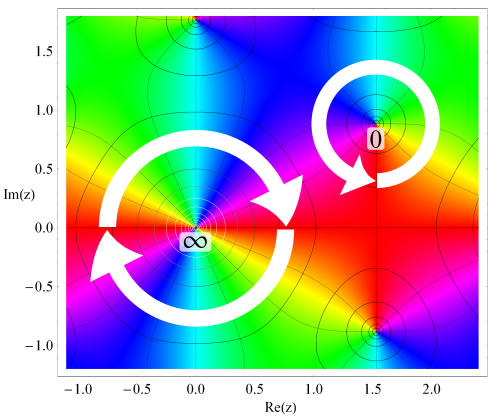
後述の 「FunctionPlot.m」 と異なり、絶対値の等高線がグラデーションになっているので、零点と極の違いは、より判別しやすくなっているが、基本的には、色相環が反時計回りならば零点、時計回りならば極となることでも判別できる。また、色相環のサイクルが現れる回数によって、その位数も読み取れる。
下の図は最初のグラフを拡大したもので、零点の位数は1、極の位数は2であることが分かる。
因みに、真性特異点の場合はサイクルが無限回現れ、分岐点の場合は実数回 (サイクルが断絶した偏角方向に分枝切断線を設ける) となる。
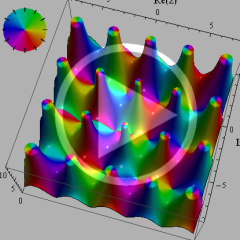
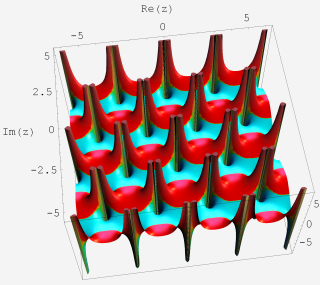
複素変数関数プロット:実部または虚部(3次元)
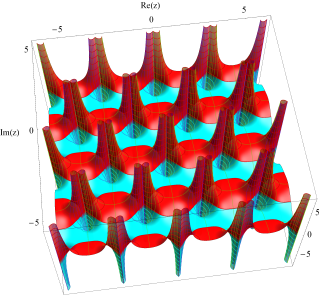
複素変数関数の値について、実部を垂直軸方向に0から曲面までの高さで表わしたグラフが左、虚部のグラフが右。つまり、複素変数関数の真の姿は、二つのグラフの和 (2成分のベクトル) となる。カラーリングは色相環における実数方向の2色を実部のグラフ、純虚数方向の2色を虚部のグラフで採用している (詳細は下記のとおり)。両者とも、値が0のときの曲面は不透過だが、値の絶対値が大きくなるにしたがって曲面の透過率が増えるようにしている。
視覚補助のため、曲面上に実部・虚部それぞれの等高線を引いている。等高線の色は曲面と同じ考え方で配色されている。
実部のグラフでは、実部の等高線は常に等間隔、虚部の等高線は関数的間隔となる。一方、虚部のグラフでは、虚部の等高線は常に等間隔、実部の等高線は関数的間隔となる。ここに、関数的間隔はほとんどが指数関数を使用している。
値が描画範囲を超えたときに曲面が切り取られる部分は、通常は平面で塞がれない。(オプション指定によって、平面で塞がれるようにしたグラフもある。)
(2色の選定方法の概念図)
因みに、後述の 「FunctionPlot.m」 もこれと同じ考え方に基づいている。
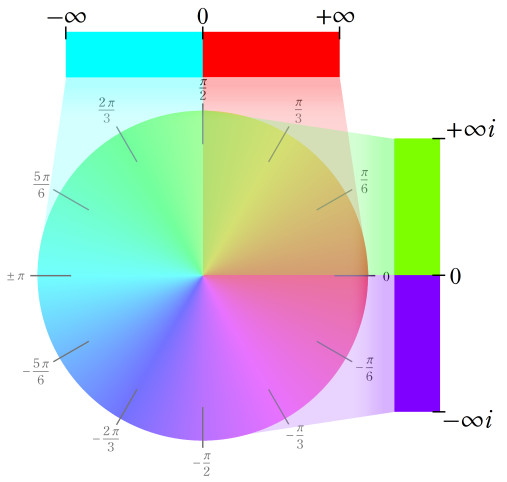
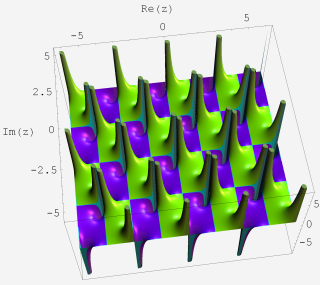
複素変数関数プロット:基本領域(2次元)※
複素変数関数の値について、その絶対値を等高線のグラデーションのみ、偏角をカラーリングと等高線で表わしたグラフ。本質的には、「偏角のみ2次元グラフ」 と同じだが、カラーリングに 「2値に偏向された色相環」 を使用している。このため、互いに曲線を介して隣接しあう2色1組の領域は、そこで複素関数がすべての複素数値を唯一度だけ取ることになる。絶対値の等高線は0のとき黒、「絶対値・偏角3次元グラフ」 での最大値で白になるようなグラデーションになる。最大値を超えた絶対値の等高線もこのグラフでは延長して引かれ、白が継続する。偏角の等高線は黒のみ。等高線の間隔の取り方は、「絶対値・偏角3次元グラフ」 と同じ原則に従っている。
※ 「基本領域」 とは、合同変換群の部分群の作用により、平面上でタイル張りが可能となる多角形領域のことを言うので、これに該当する一部の楕円関数や保型関数の場合を除き、このプロットに基本領域の名称を与え、そのコマンド名を 「FundamentalRegionPlot」 としたのは本来ならば相応しくなかった。(しかし、今更変更できない。)
下記で説明するとおり色相環の断続が実軸上にあるので、むしろこのプロットは、(その描画対象が解析関数であれば) 各領域の境界曲線に対する 「Schwarz の鏡映原理」 を表わす。
(2値に偏向された色相環について)
偏角を表わす2値偏向型の色相環は、次の凡例図のとおり。図に表示した角度はラジアン。
つまり、偏角の正負に応じて塗り分けられる。視覚補助のため、若干のグラデーションがある。
【 Petite Galerie 】
関数を変えず、色相環のみ回転させた場合の図
(零点は色相環の回転方向と同じになるが、極は逆回転になる。)
(零点は色相環の回転方向と同じになるが、極は逆回転になる。)
FunctionPlot.m
FunctionPlot.m (Ver.5)
FunctionPlot.m (Ver.8)
実変数関数プロット(方眼紙付き)
このグラフは、「MathematicalFunctionPlot.m」 と見た目の違いがほとんど無く、カラーリング原則も同じ。ただし、画質はこちらのほうが少々荒い。複素変数関数プロット:絶対値と偏角(3次元)
曲面上の等高線の代わりに、カラーリングの明暗エフェクトを用いて同等の効果を出している点のみが、「MathematicalFunctionPlot.m」 とは異なる。ただし、明暗エフェクトはグラデーションではなく周期的なので、絶対値の大小までは表わしていない。明暗エフェクトの周期間隔は、「MathematicalFunctionPlot.m」 と同じ考え方で等間隔、指数関数的間隔、指数関数と指数関数の合成関数的間隔が使い分けされている。カラーリングは、次の 「偏角のみ2次元グラフ」 と一致する。
複素変数関数プロット:偏角のみ(2次元)
直前の 「絶対値・偏角3次元グラフ」 と同じく、等高線の代わりに、カラーリングの明暗エフェクトを用いて同等の効果を出している点が、「MathematicalFunctionPlot.m」 とは異なる。カラーリングの色相環は、「MathematicalFunctionPlot.m」 と全く同じ。複素変数関数プロット:実部または虚部(3次元)
「MathematicalFunctionPlot.m」 と同じカラーリングを採用しているが、曲面の透過率は適用されない (透過率の代わりに明暗率を適用しているが、あまり判然としない)。等高線は引かれない。また、値が描画範囲を超えたときに曲面が切り取られる部分は、平面で塞がれる。
複素変数関数プロット:基本領域(2次元)
「MathematicalFunctionPlot.m」 とほぼ同じだが、絶対値の等高線に対するグラデーション機能のみが無い。このため、零点と極の判別が付きにくいという欠点がある。このグラフも、等高線の間隔の取り方を種々使い分けている。等角写像図と多価関数の描画方法
(等角写像図および多価関数描画用の Package ファイルは作成せず、個別に記述したコードを、各 Mathematica Notebook ファイルに収録することとする。なお、以下に掲載しているグラフのコードは、「Mathematica Code」 の頁にあります。)等角写像図 ― 複素関数を描画するもう一つの方法
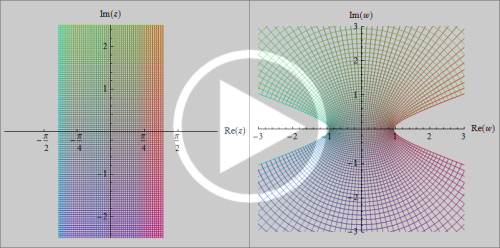
これまで例示してきた複素関数の描画方法は、すべて定義域 (独立変数=複素平面) を固定し、値域 (従属変数=複素関数値) を曲面の高低および色調で表示するものであった。これらは、実関数のグラフを曲線で表示する (馴染みのある) 描画方法を、自然な形で複素関数の場合に拡張しており、それゆえ同様の方法が他でも広く採用されている。これとは逆に、等角写像図は複素関数によって定義域がどのように変形されるかを表示する。解析的な一変数の複素関数は、(臨界点を除いて) 角度を変えない写像 (=等角写像) になるので、それが視覚的にも分かるよう、等角写像図では写像元の定義域を直交格子などの単純な図形にすることが多い。
ソフトウェア上で等角写像図を描画する方法は種々あるが、もし、媒介変数表示のグラフを描画できる環境ならば、関数
で描画できる。
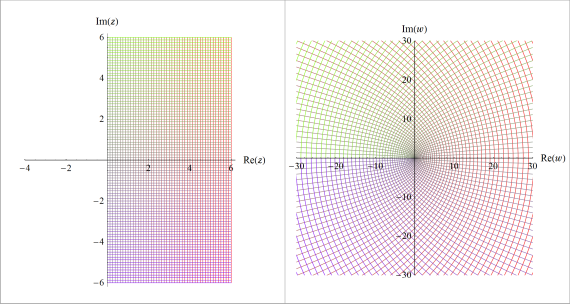
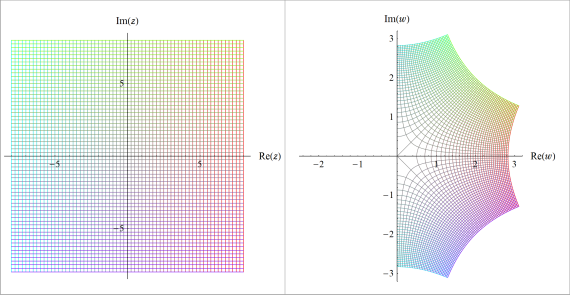
次の例は、二次関数
(以降、
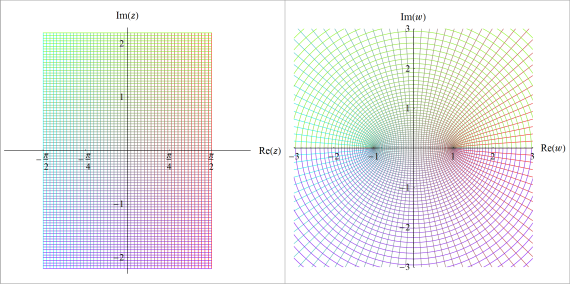
正弦関数
上記2例からも分かるように、写像先
当サイトでは、等角写像図による複素関数の描画を、今まで (2018年9月まで) 採用して来なかった。その理由は、いくつかの欠点があるからである。例えば、
① 写像元のグラフも描画が必要。少なくともプレゼンテーションの観点からは、省略しない方が望ましい (前掲の例でも明らかなように)。
② 等角写像図では、零点や特異点の位置および分布状況が分かりづらい。
③ 実質は逆関数を描画するので、何枚もの分枝が重なり合う複雑な図になることが多い。(例えば、ガンマ関数またはゼータ関数の等角写像図。)
④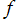 が分枝切断線を持つ場合、等角写像図は部分領域になる。その領域の拡張は、多価関数への解析接続と同程度の困難を有する。
が分枝切断線を持つ場合、等角写像図は部分領域になる。その領域の拡張は、多価関数への解析接続と同程度の困難を有する。
② 等角写像図では、零点や特異点の位置および分布状況が分かりづらい。
③ 実質は逆関数を描画するので、何枚もの分枝が重なり合う複雑な図になることが多い。(例えば、ガンマ関数またはゼータ関数の等角写像図。)
④
④の簡単な例として、
(この場合、解析接続は例外的に容易で、右半分を原点中心に180°回転したコピーを左半分にも補えばよい。)
しかしながら、今後は等角写像図も少しずつ追加して行こうと考えています。
多価関数の描画方法
複素変数の多価関数は、分枝切断線を設定して便宜上の一価関数 (主値) とし、これを描画する方法が一般に採用されており、当サイトもこれに従っている。ところが、等角写像図の描画方法を応用すれば、
によって多価のままで描画できる。もし、合成関数
とすれば良い。(第2種楕円積分とその逆関数は、この合成関数の事例である。)
ただし、この方法で描画できる多価関数の種類は、関数
次の例は、逆正弦関数
(順に、
多価関数のグラフも、(描画可能な関数ならば) 追加して行く予定です。