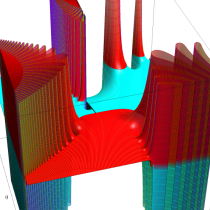
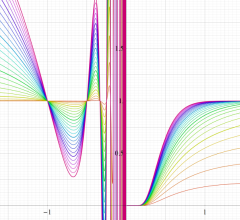
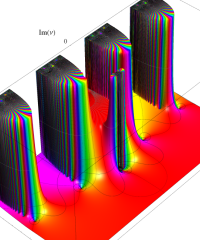
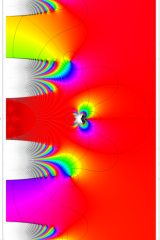
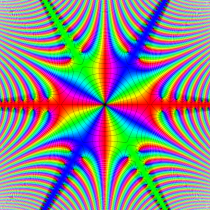
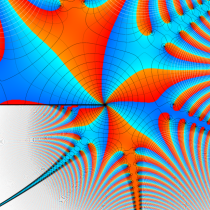
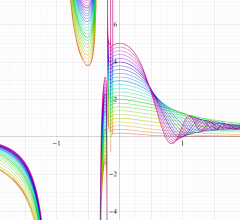
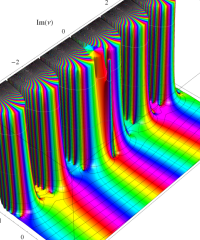
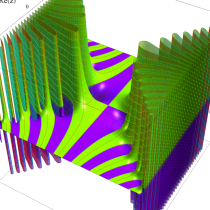
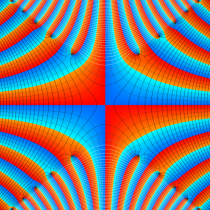
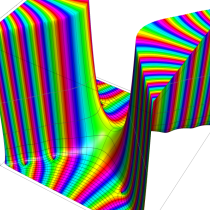
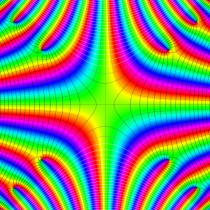
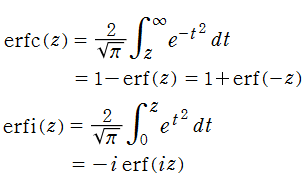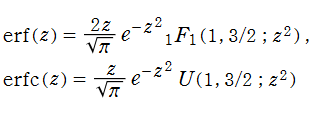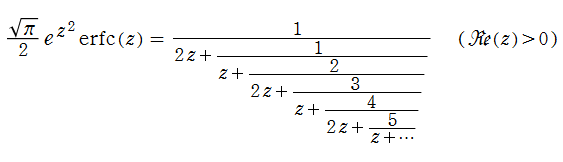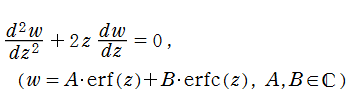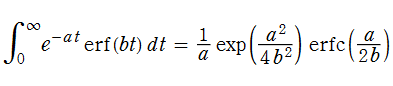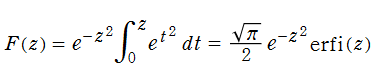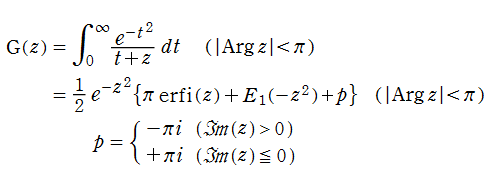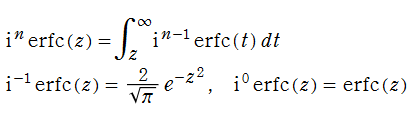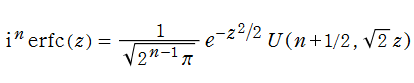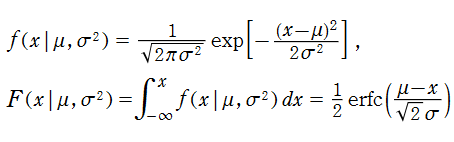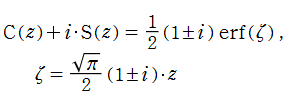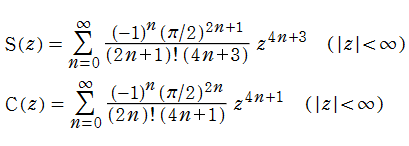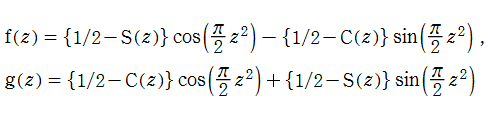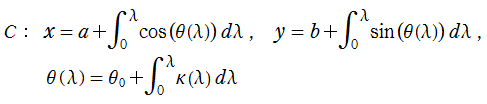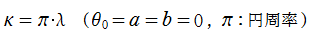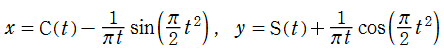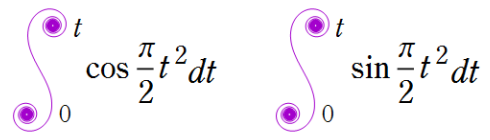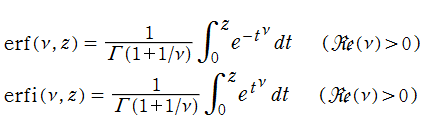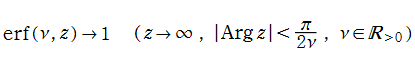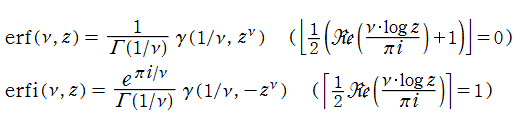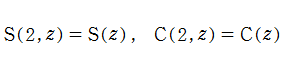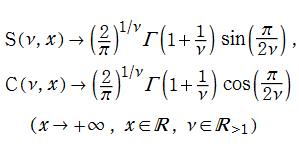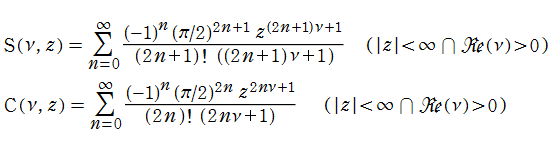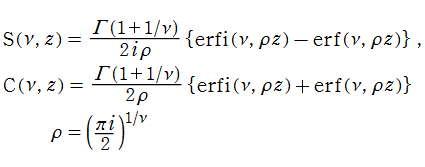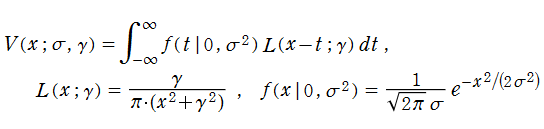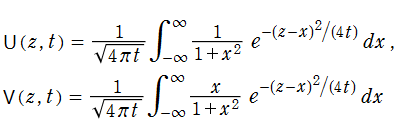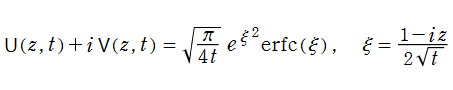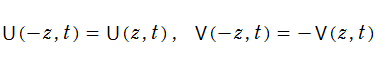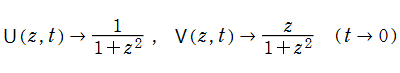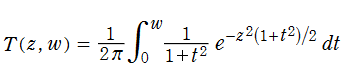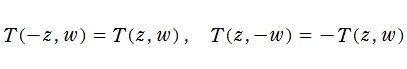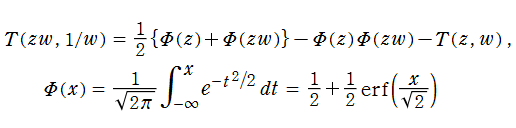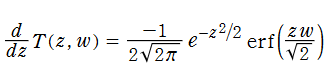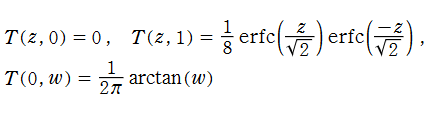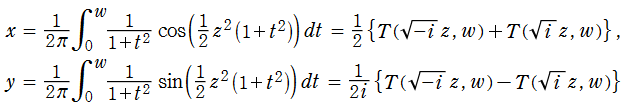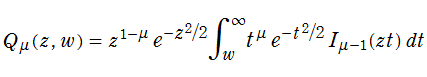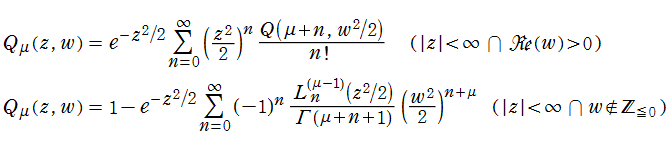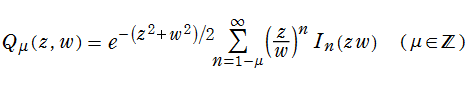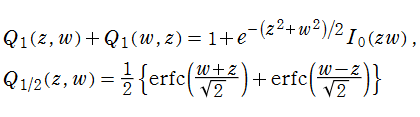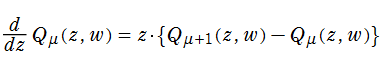特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
誤差関数
誤差関数
日:誤差関数,誤差積分英:Error function,仏:Fonction d'erreur,独:Fehlerfunktion
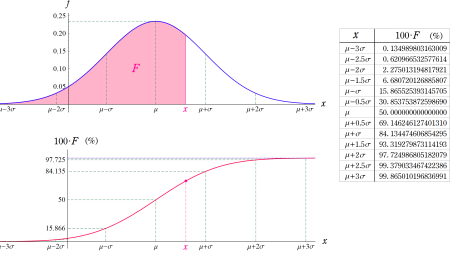
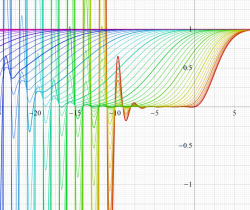
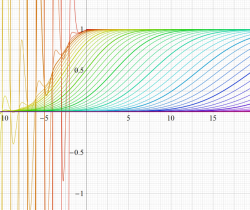
統計学における1次元絶対連続分布は、正規分布 (または Gauss 分布) と呼ばれる確率密度関数で表わされる。これは、調査標本や起こりうる確率事象が中央値で最も多く、それから離れるに従い少なくなるという自然現象を、連続化・理想化したモデルを意味しており、その中央値を最大値とする丘陵形の曲線を成す。正規分布の確率密度関数は初等関数であるが、事象の数え上げ (累積分布関数) はその積分になり、初等関数に還元できない。現在では、この積分の主要な部分
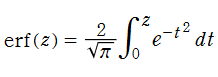
本質的には誤差関数と同じであるが、若干の変形を施した、
が併せて定義され、前者は相補誤差関数、後者は虚部誤差関数と呼ばれる。定積分の形から、誤差関数と虚部誤差関数は奇関数である。
誤差関数は、冪級数
に展開され、複素平面上で超越整関数となる (したがって、相補・虚部誤差関数も超越整関数である)。また、漸近的に

が挙げられる。
相補誤差関数は、正規分布の累積分布関数のように誤差関数を左右反転する必要がある場合に重宝する。また、漸近級数展開式や連分数展開式は、相補誤差関数の方が若干簡単な形になる。例えば後者は、
となる※1。さらに、誤差関数と相補誤差関数は、次の2階線形常微分方程式の2基本解となる。
この線形常微分方程式は、
次の特別な Laplace 変換式は、誤差関数に対して自己言及的である。
誤差関数の応用分野は、前述のような歴史もあって確率論や統計学が中心となる。そこで扱われる確率分布の種類は膨大であるが、そのいくつかは正規分布の変形から生じており、したがって誤差関数の類似も数多く存在する。後述の Voigt 関数、Owen のT関数、および Marcum のQ関数もそのような例であり、それらが満たす公式では誤差関数もよく出現することとなる。
他の応用分野としては、単位格子中の静電ポテンシャルを計算する Ewald 法、高温プラズマ中の線形波動の伝播理論などがある。
また、誤差関数は積分表示式が簡潔な形であるため、単なる演算の結果として現れることも多く、それゆえ純粋数学的な応用事例にも散見される (例えば、変形 Appell - Lerch 級数など)。
やや枝葉末節的であるが、利便性その他の理由から、誤差関数に関連する補助的な関数がいくつか定義されている。ここでは、次の二つの関数を取り挙げる。
虚部誤差関数と指数二次関数との積は公式等で度々出現する。そのため
なる関数が定義され、これを研究した H. G. Dawson に因み、Dawson 関数 (あるいは Dawson 積分) と呼ばれる。明らかに Dawson 関数は奇関数であり、複素平面上の超越整関数である。
Goodwin - Staton 関数は、積分あるいは積分指数関数との和
で定義され、その名称は1948年に E. T. Goodwin および J. Staton がこれを研究したことに由来する。Goodwin - Staton 関数は
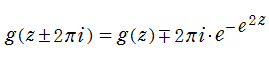
この他にも、相補誤差関数の逐次積分 (Repeated integrals of the complementary error function)
が定義されている。しかし、この関数は
のとおり放物柱関数と本質的に同じなので、ここでは取り扱わない※3。
【註記】
※1:この連分数展開式は P. S. Laplace による。ただし、相補誤差関数ではなく誤差関数の公式として求めたので、形は少々異なる。
※2:Wikipedia の記事 「Goodwin-Staton integral」 では、公式として奇関数の対称性を挙げているが、その根拠はよく分からなかった (単に、奇関数とする 「定義」 を採用しているだけかもしれない。2022年8月23日 調査日現在)。
※3:詳細は、「NIST Handbook of Mathematical Functions」 の §7. 18等を参照。なお、個人的感覚であるが、この関数記号には少々違和感を覚える (虚数の累乗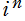 の因子に見えてしまう)。
の因子に見えてしまう)。
※1:この連分数展開式は P. S. Laplace による。ただし、相補誤差関数ではなく誤差関数の公式として求めたので、形は少々異なる。
※2:Wikipedia の記事 「Goodwin-Staton integral」 では、公式として奇関数の対称性を挙げているが、その根拠はよく分からなかった (単に、奇関数とする 「定義」 を採用しているだけかもしれない。2022年8月23日 調査日現在)。
※3:詳細は、「NIST Handbook of Mathematical Functions」 の §7. 18等を参照。なお、個人的感覚であるが、この関数記号には少々違和感を覚える (虚数の累乗
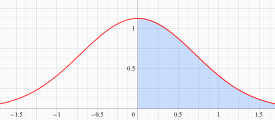
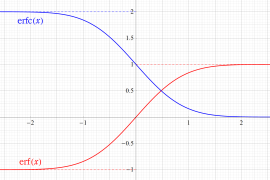
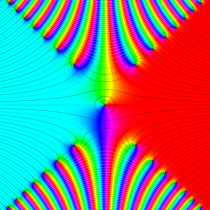
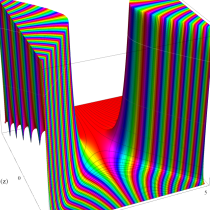
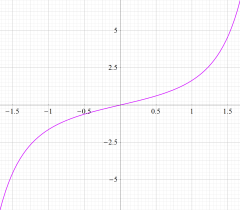
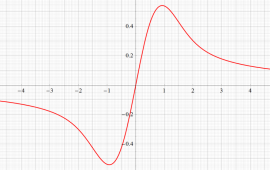
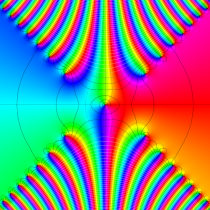
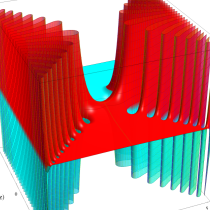
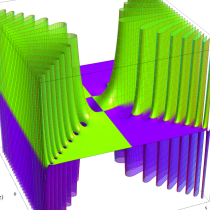
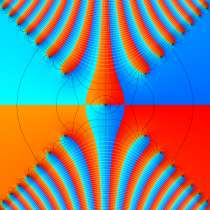
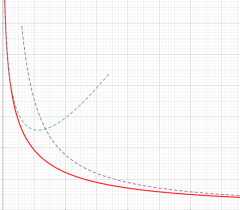
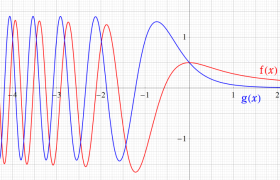
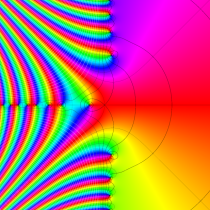
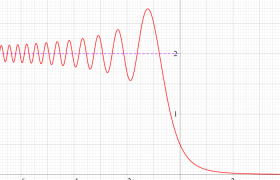
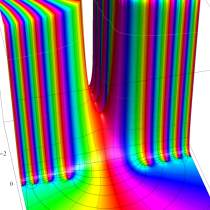
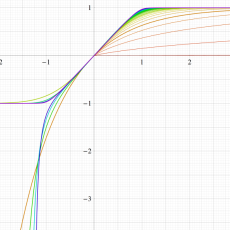
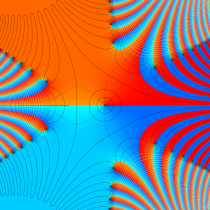
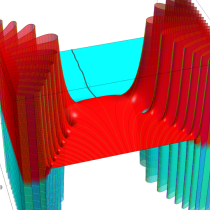
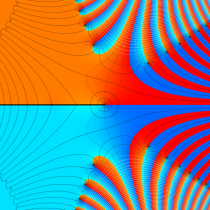
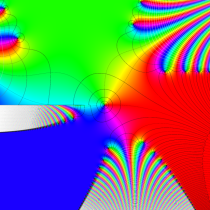
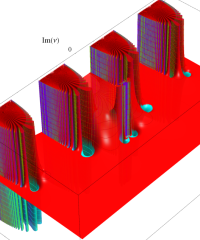
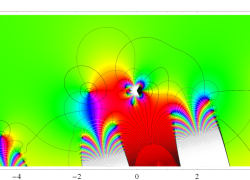
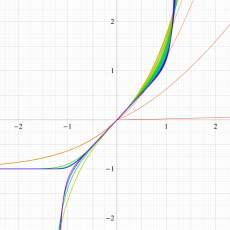
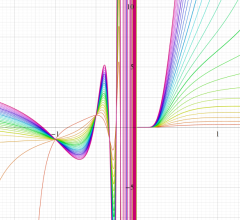
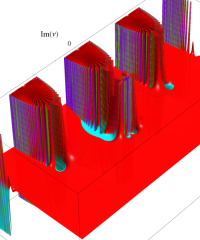
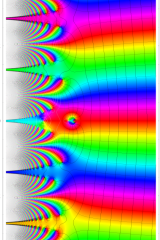
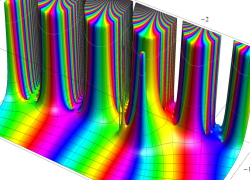
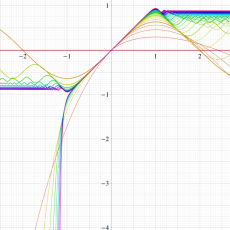
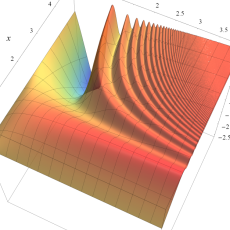
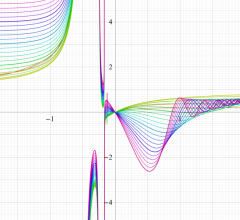
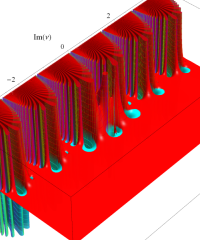
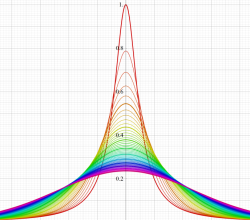
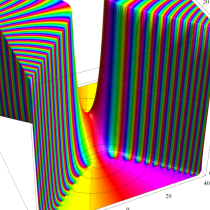
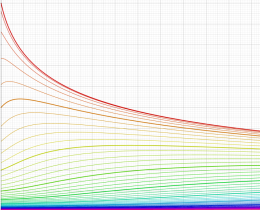
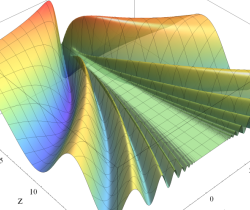
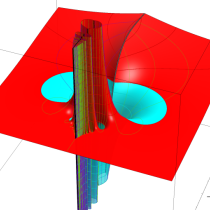
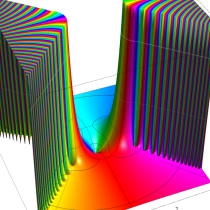
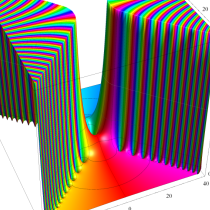
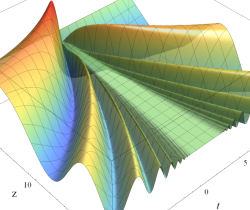
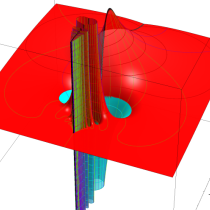
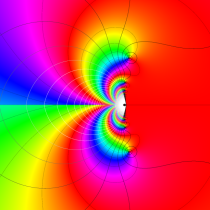
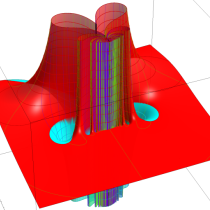
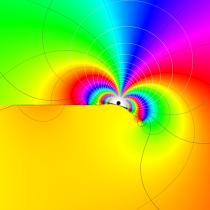
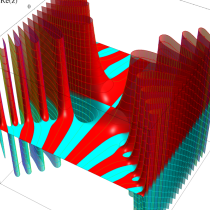
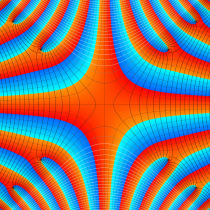
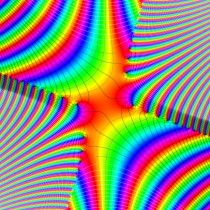
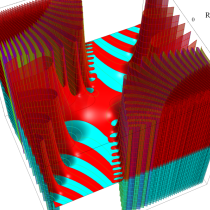
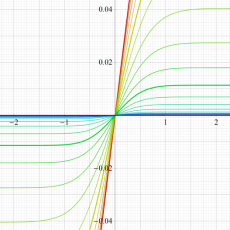
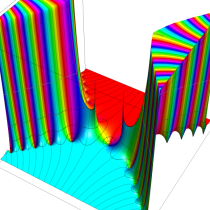
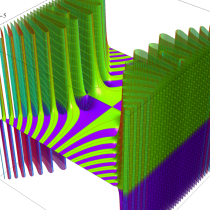
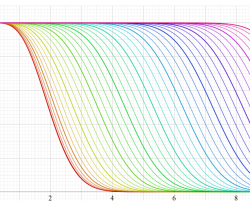
実変数の誤差関数
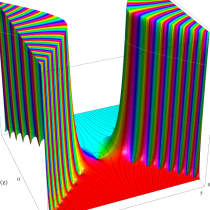
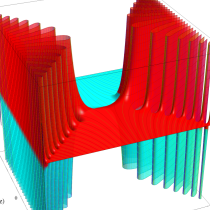
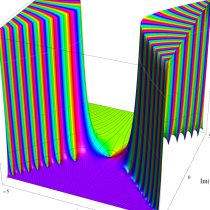
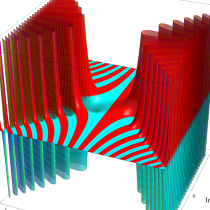
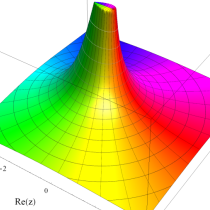
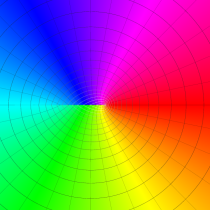
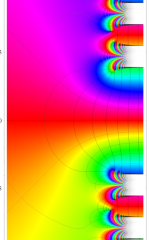
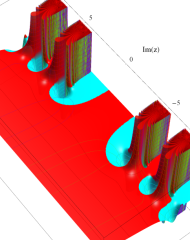
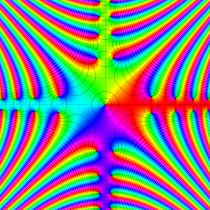
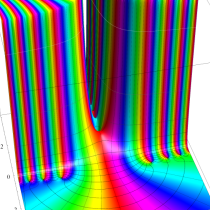
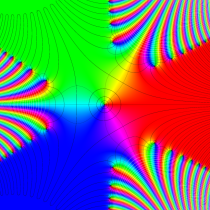
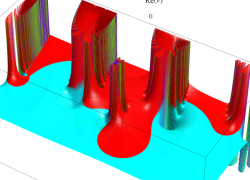
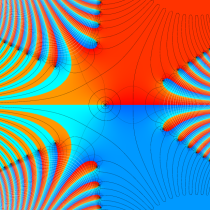
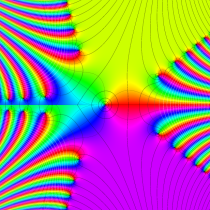
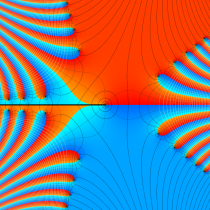
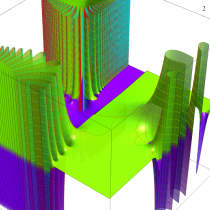
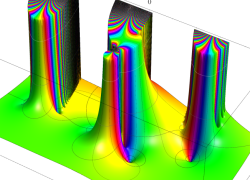
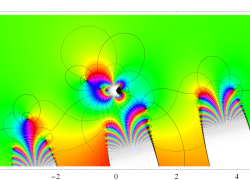
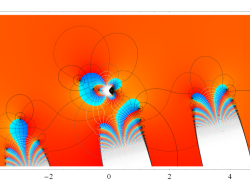
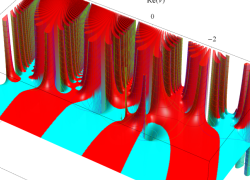
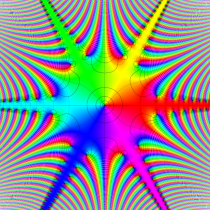
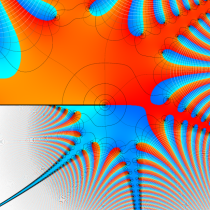
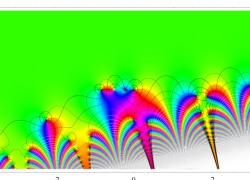
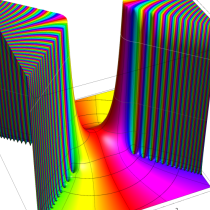
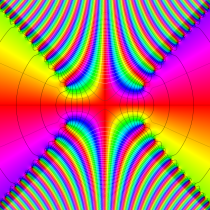
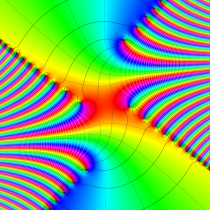
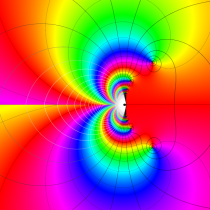
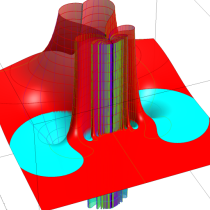
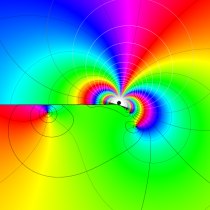
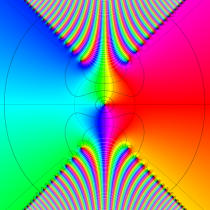
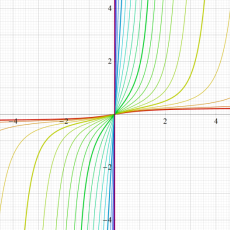
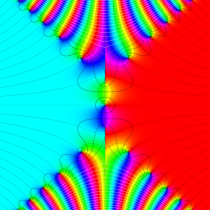
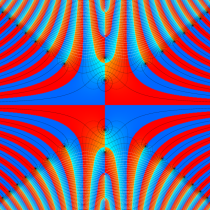
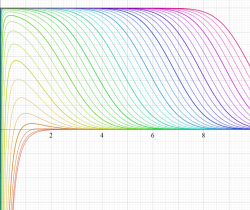
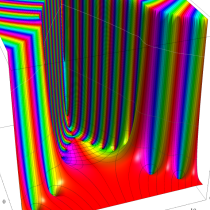
複素変数の誤差関数
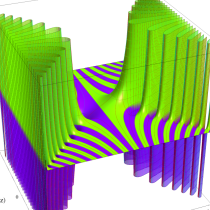
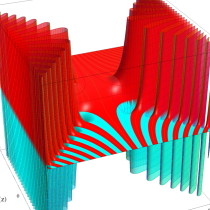
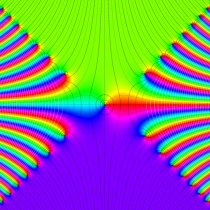
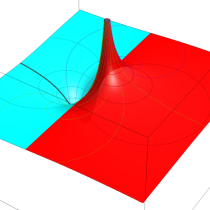
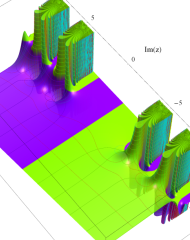
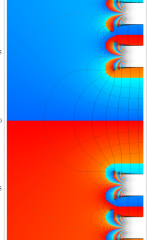
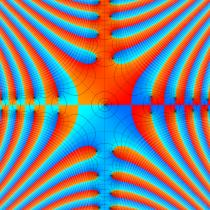
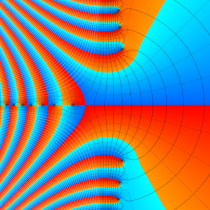
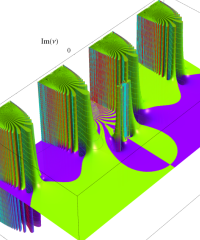
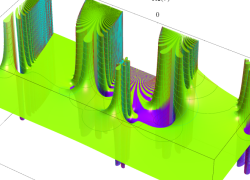
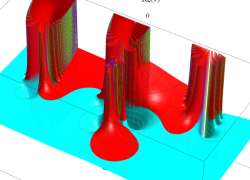
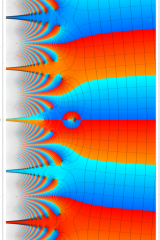
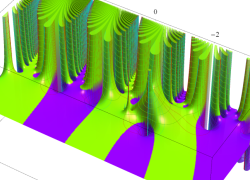
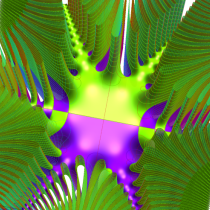
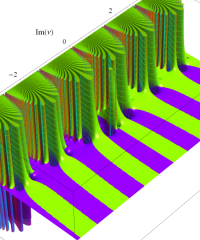
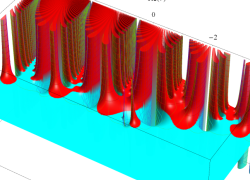
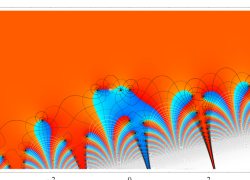
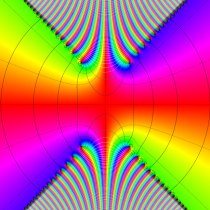
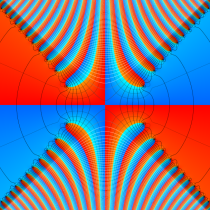
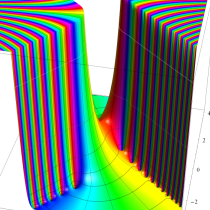
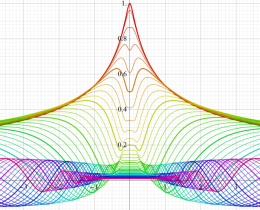
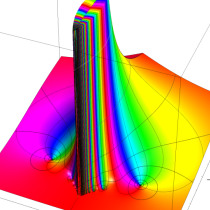
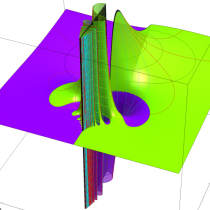
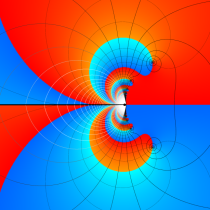
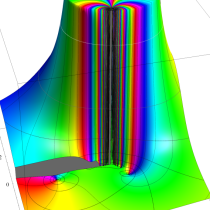
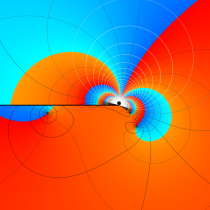
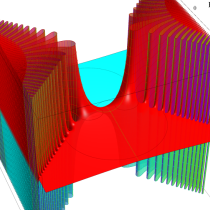
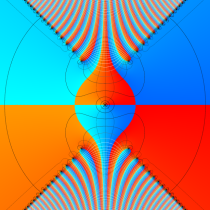
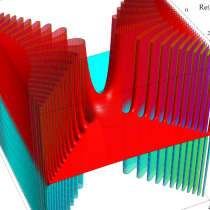
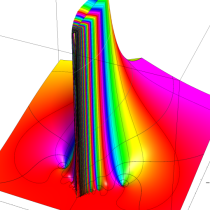
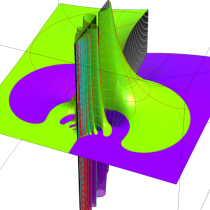
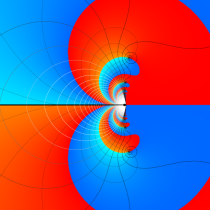
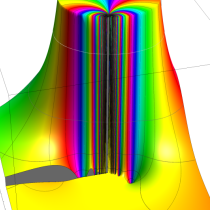
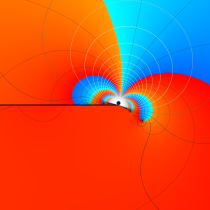
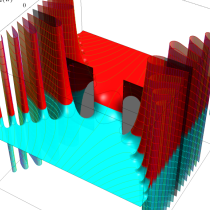
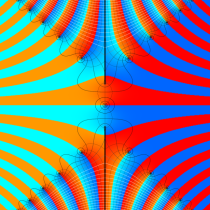
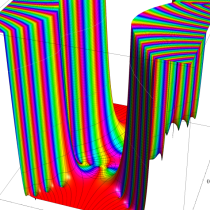
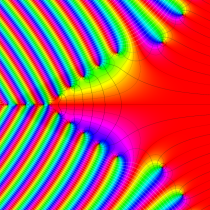
複素変数の相補誤差関数
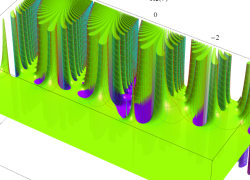
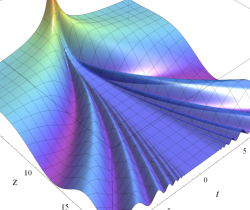
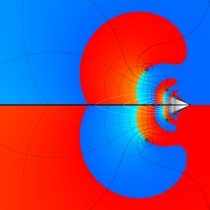
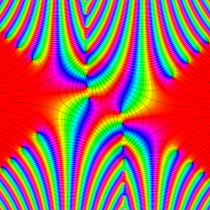
と表わされる。二つの関数の意味をグラフ等にすると、次のようになる。
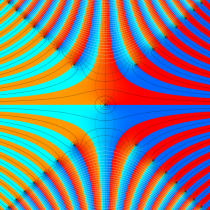
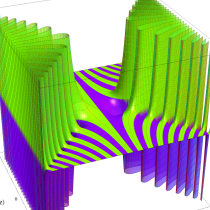
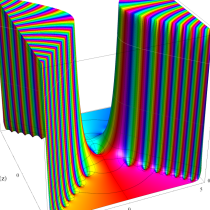
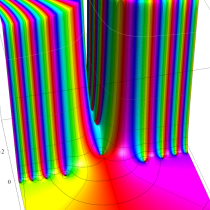
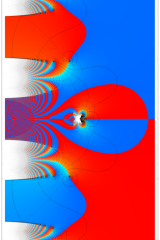
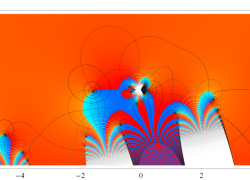
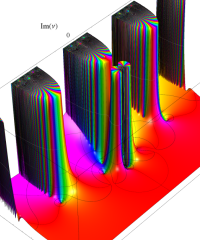
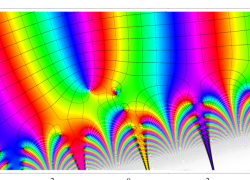
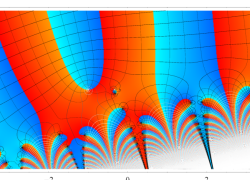
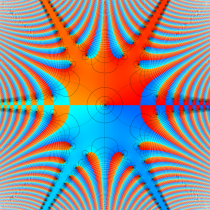
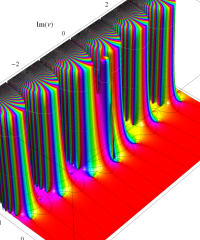
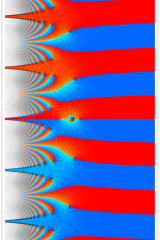
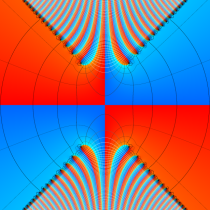
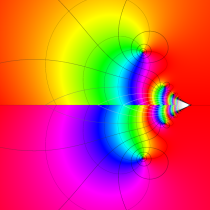
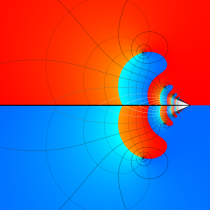
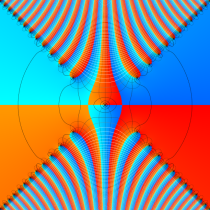
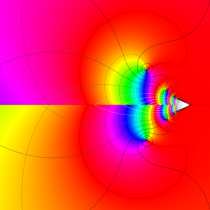
複素変数の虚部誤差関数
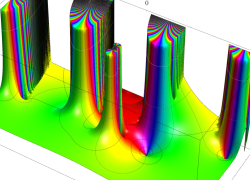
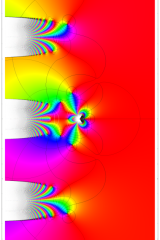
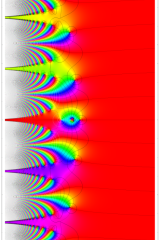
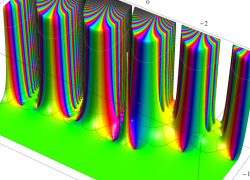
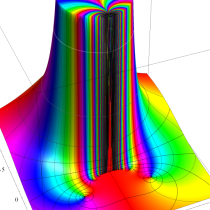
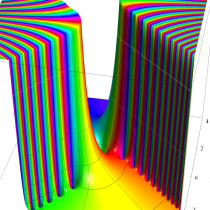
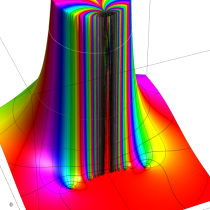
複素変数の Dawson 関数
複素変数の Goodwin - Staton 関数
複素変数の Goodwin - Staton 指数関数
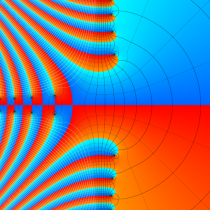
Fresnel 関数
日:Fresnel関数,フレネル積分英:Fresnel integral,仏:Intégrale de Fresnel,独:Fresnelsche Integrale
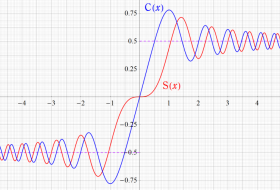
誤差関数と同様に、二次関数を代入した三角関数の積分も応用等で頻繁に現れ、比較的古くから研究されていた。現在では、
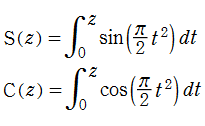
誤差関数を指数関数の類似と見た場合、Fresnel 関数は三角関数に相当するものであって、両者は
の関係にある。
Fresnel 関数は、冪級数
に展開され、ともに奇関数かつ複素平面上で超越整関数となる。また、漸近的に
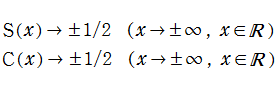
漸近級数展開式や相互関係式など幾つかの公式では、Fresnel 補助関数
を定義しておくと、何かと便利である。
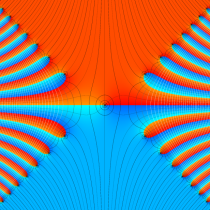
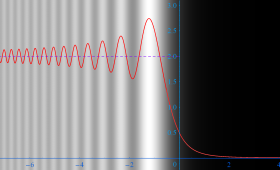
Fresnel 関数の著しい応用分野は光学とクロソイド曲線である。前者の例としては、「Fresnel interference pattern」 と呼ばれる現象がある。これは、点光源から発せられた (レーザー等の) 光が直線エッジを持つ薄い板で遮られてスクリーン上に影をつくるとき、その境界線近傍に生じる微細な干渉縞のことを言う。その干渉縞の明度を関数
Fresnel interference pattern:Edge of a shadow
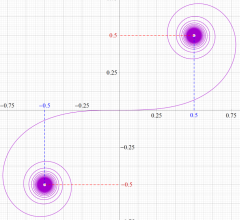
クロソイド曲線はもっと早い時期から現れている。1694年に Jak. Bernoulli は、曲率が曲線長に比例する曲線を求める問題を提出したが、1744年に L. Euler は、この解を現在の 「クロソイド曲線の媒介変数表示式」
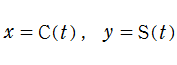
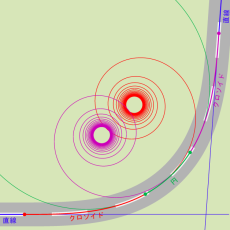
クロソイド曲線は、車両が一定速度で進行しながらハンドルを一定角速度で回したときに描く軌跡に相当するので、高速自動車道のカーブやインターチェンジの道路線形、ローラーコースターの垂直ループ部分等に適用されている。これらは、利用者に衝撃力が加わらないよう安全性を考慮した設計方法として広く知られており※2、1899年に A. N. Talbot が鉄道のカーブ設計に関して、初めて数学的に厳密な理論を展開した。
クロソイド曲線を道路線形に適用する場合の典型的な例
【註記】
※1:平面曲線の自然方程式とは、任意の平面曲線が座標と無関係に曲線長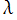 と曲率
と曲率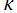 とで唯一に決定できるという 「平面曲線の基本定理」 に基づき、それを
とで唯一に決定できるという 「平面曲線の基本定理」 に基づき、それを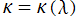 と表わした方程式のことで、その解となる曲線
と表わした方程式のことで、その解となる曲線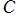 は、
は、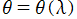 を
を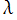 の端点の位置での接線と
の端点の位置での接線と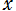 軸とが成す角度、
軸とが成す角度、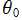 を
を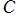 上の始点
上の始点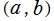 における初期値とするとき、
における初期値とするとき、
で表わされる (「座標と無関係」とは、曲線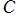 を平行移動した曲線もすべて解になるとの意味である)。
を平行移動した曲線もすべて解になるとの意味である)。
クロソイド曲線は、自然方程式
の解である。
※2:現在では、土木工学計算ソフトウェアの 「CAD」 等が普及しているので容易になったが、以前は 「クロソイド数値表」 や 「クロソイド定規」 を使用して設計しなければならなかった。
※1:平面曲線の自然方程式とは、任意の平面曲線が座標と無関係に曲線長
で表わされる (「座標と無関係」とは、曲線
クロソイド曲線は、自然方程式
の解である。
※2:現在では、土木工学計算ソフトウェアの 「CAD」 等が普及しているので容易になったが、以前は 「クロソイド数値表」 や 「クロソイド定規」 を使用して設計しなければならなかった。
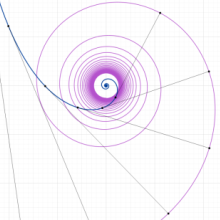
クロソイド曲線は螺線の一種である。
クロソイド曲線の曲率中心は螺線を描く。その媒介変数表示式は次のようになる。
つまり、逆に見るとこの螺線はクロソイド曲線の 「縮閉線」 であるから、これに巻き付けた糸を伸開するときに糸の先端がクロソイド曲線を描く。また、糸の接点 (無限遠にあるときを除く) から各螺線の巻き付き点までの曲線長は、クロソイド曲線が無限長であっても、その縮閉線は有限長であることが分かる。
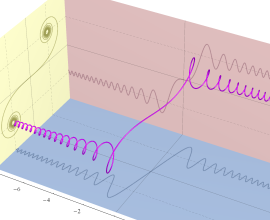
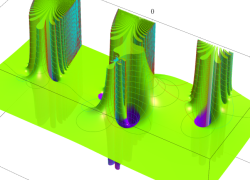
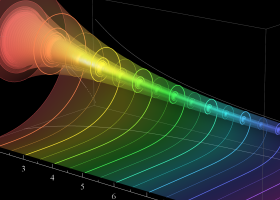
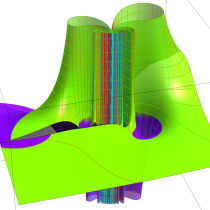
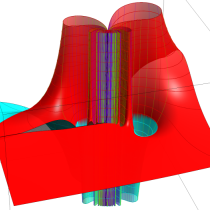
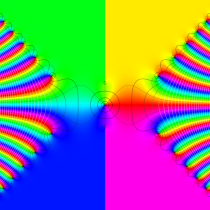
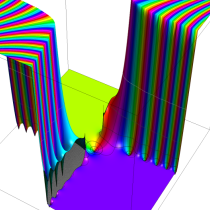
Fresnel 関数の曲線およびクロソイド曲線の射影元となる空間曲線。
複素変数の Fresnel 正弦関数
複素変数の Fresnel 余弦関数
複素変数の Fresnel 補助関数
複素変数の Fresnel 補助関数
複素変数の Fresnel interference pattern 関数
【 Petite Galerie?】
超誤差関数
比較的詳しい特殊関数の公式集では、誤差関数の積分表示式における指数関数の引数を、を独自に超誤差関数と総称し、狭義には前者を超誤差関数、後者を超虚部誤差関数と呼ぶこととする。この定数因子は、極限値が簡単な
になり、また、
となるように意図したものである。
超誤差関数は、冪級数
に展開され、
より一般の
と表わせる。ただし、付随する
今のところ、超誤差関数が扱われる応用分野はほとんどない。「共立 数学公式 附函数表 (1973年改訂増補版:共立出版)」 では、定数因子を除いた
複素変数の超誤差関数
複素変数の超誤差関数
複素変数の超誤差関数
複素変数の超誤差関数
複素変数の超誤差関数
複素変数の超虚部誤差関数
複素変数の超虚部誤差関数
複素変数の超虚部誤差関数
複素変数の超虚部誤差関数
複素変数の超虚部誤差関数
超 Fresnel 関数
誤差関数から超誤差関数への拡張を、同様に Fresnel 関数に対しても行い、超 Fresnel 関数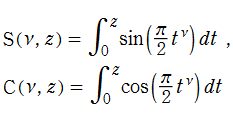
であり、極限値は
となる。
超 Fresnel 関数は、冪級数
に展開され、
より一般の
と表わされ、必要に応じてこれを解析接続したものとなる。
超 Fresnel 関数を媒介変数表示式に用いて、クロソイド曲線の拡張である 「(
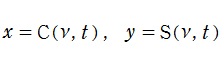
複素変数の超 Fresnel 正弦関数
複素変数の超 Fresnel 正弦関数
複素変数の超 Fresnel 正弦関数
複素変数の超 Fresnel 正弦関数
複素変数の超 Fresnel 正弦関数
複素変数の超 Fresnel 余弦関数
複素変数の超 Fresnel 余弦関数
複素変数の超 Fresnel 余弦関数
複素変数の超 Fresnel 余弦関数
複素変数の超 Fresnel 余弦関数
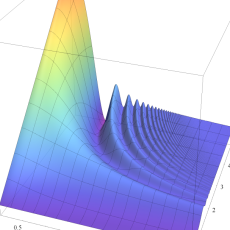
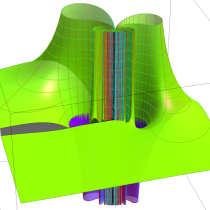
超 Fresnel 関数の曲線および3次の超クロソイド曲線の射影元となる空間曲線。
曲線上のある点での曲率が、原点からその点までの曲線の長さの3乗に比例する、4次の超クロソイド曲線。
超 Fresnel 関数の曲線および4次の超クロソイド曲線の射影元となる空間曲線。
次数
Voigt 関数
日:Voigt関数,フォークト関数英:Voigt function,仏:Fonction de Voigt,独:Voigt funktion
Voigt 関数は、分光学における Voigt 分布を論じる際に附随して現れる。X線光電子分光法 (XPS) では、スペクトルに含まれる各ピークを分離するとき、素粒子の熱運動からの影響を考慮する必要がある。元々の電磁波等のスペクトルは (中心化) Lorentz 分布
は、スペクトルのピーク形状を良く表わしており、この
一方、これの主要部分を整理したものが Voigt 関数
であり、前者を用いれば、Voigt 分布は
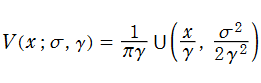
Voigt 関数は、特別な相補誤差関数の実部と虚部
に相当し、
を有する超越整関数である。一方、
によって定義される。
Voigt 関数の名称は、分光学における前述の研究をおこなった W. Voigt に因む。Voigt 関数の応用事例も、分光学に関連またはそれを援用する分野が中心となる。例えば、プラズマ診断技術、天体物理学、レーザー分光法などがある。
複素変数の Voigt 関数
複素変数の Voigt 関数
複素変数の Voigt 関数
虚軸上における Voigt 関数
虚軸上における Voigt 関数
複素変数の Voigt 関数
複素変数の Voigt 関数
複素変数の Voigt 関数
複素変数の Voigt 関数
複素変数の Voigt 関数
複素変数の Voigt 関数
虚軸上における Voigt 関数
虚軸上における Voigt 関数
複素変数の Voigt 関数
複素変数の Voigt 関数
複素変数の Voigt 関数
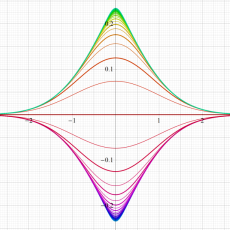
Owen のT関数
日:OwenのT関数,オーウェンT関数英:Owen's T function,仏:Fonction T d'Owen,独:Owen T-funktion
Owen のT関数は、積分表示式
で定義される関数で、
を有する。また、関数等式
を満たす。
Owen のT関数を
となり、(初等関数ではないが) 比較的簡潔である。
変数が特定の値をとるときの、Owen のT関数の還元式
が知られている。
Owen のT関数は、
Owen のT関数は主に統計学で応用事例があり、例えば、歪正規分布や非中心化t-分布の累積関数、ある種の多変数正規分布の累積関数を表わすときに現れる。1956年に統計学者 D. B. Owen が二変数正規分布を考察する際にこの関数を導入し、品質管理等に応用したので、後年その名が冠せられるようになった。
複素変数の Owen のT関数
複素変数の Owen のT関数
複素変数の Owen のT関数
複素変数の Owen のT関数
複素変数の Owen のT関数
複素変数の Owen のT関数
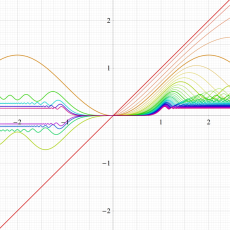
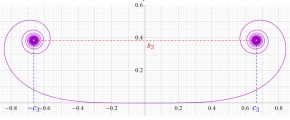
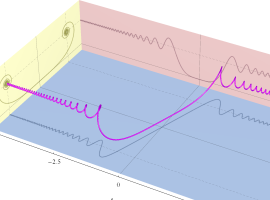
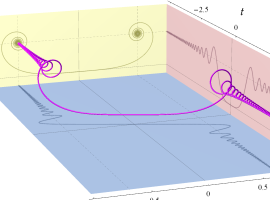
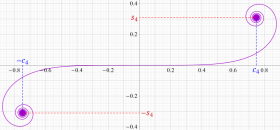
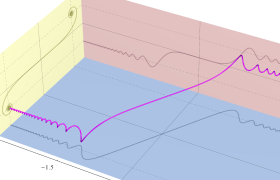
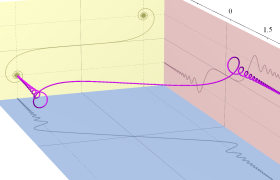
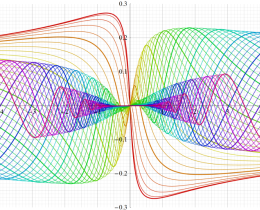
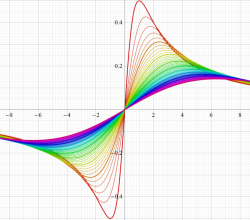
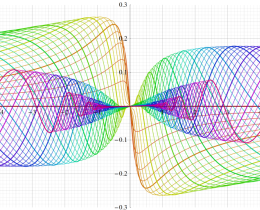
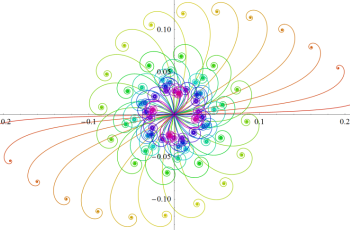
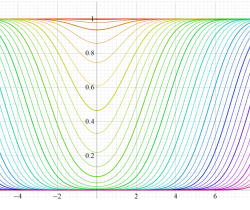
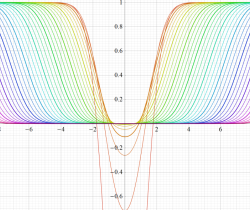
次のグラフは戯れとして描画した、Owen のT関数を用いるパラメトリック曲線群。
Marcum のQ関数
日:Marcum のQ関数,マーカムQ関数英:Marcum Q function,仏:Fonction Q de Marcum,独:Marcum Q-funktion
Marcum のQ関数は、次の積分表示式で定義される。
ここに、
この積分表示式から、数値計算に便利な種々の級数展開式が得られる。例えば、正則化不完全ガンマ関数、または Laguerre 陪多項式の項からなる級数
などがある。なお、前者は正則化不完全ガンマ関数を解析接続すれば、条件を超える領域でも収束する。
また、
などが知られている。
Marcum のQ関数の
となる。
Marcum のQ関数は、
Marcum のQ関数は主に統計学で使用され、非中心化カイ2乗分布、Rice 分布、および Skellam 分布の累積分布関数として現れる。関数名は、1950年から1960年にかけてこの関数を研究した J. I. Marcum に因む。
【註記】
※1:Mathematica 組込関数の Marcum のQ関数では、もっと複雑な形状の分枝切断線が (恐らく合理的な理由に基づいて) 置かれるが、当サイトでは採用しない。
※1:Mathematica 組込関数の Marcum のQ関数では、もっと複雑な形状の分枝切断線が (恐らく合理的な理由に基づいて) 置かれるが、当サイトでは採用しない。
複素変数の Marcum のQ関数
複素変数の Marcum のQ関数
複素変数の Marcum のQ関数
複素変数の Marcum のQ関数
複素変数の Marcum のQ関数
複素変数の Marcum のQ関数
複素変数の Marcum のQ関数
複素変数の Marcum のQ関数
【 Petite Galerie 】
「絡み合う空間クロソイド曲線」