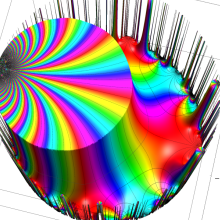
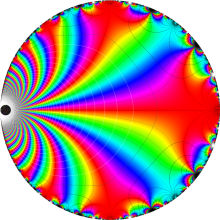
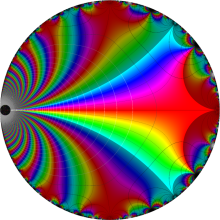
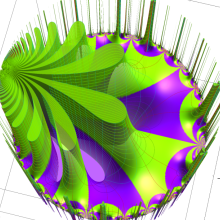
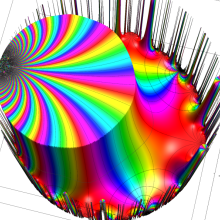
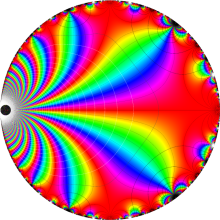
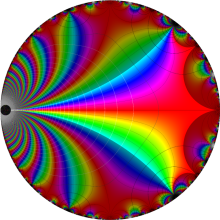
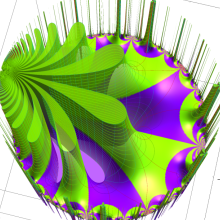
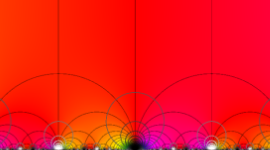
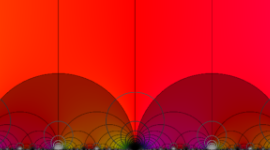
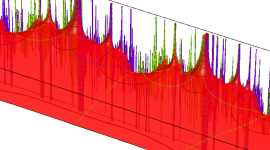
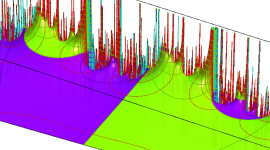
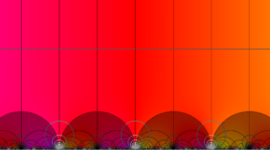
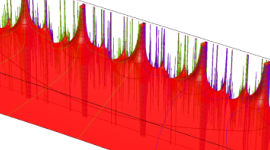
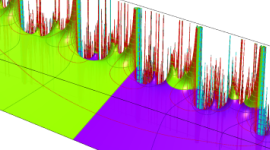
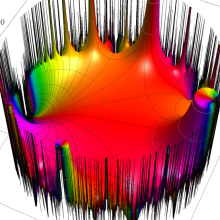
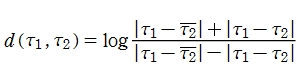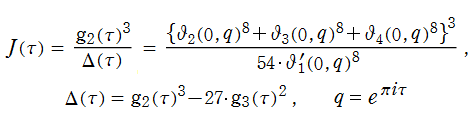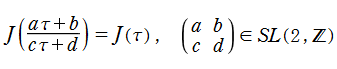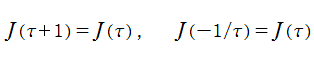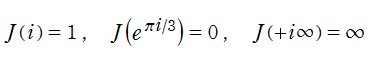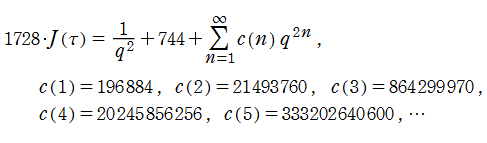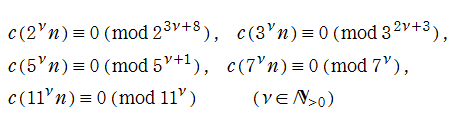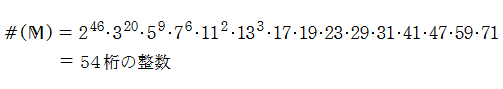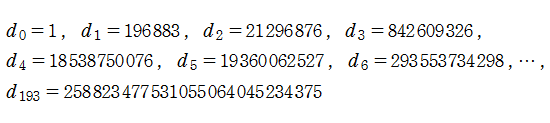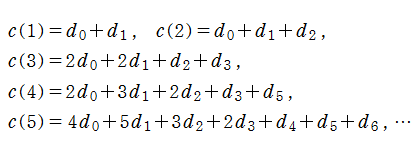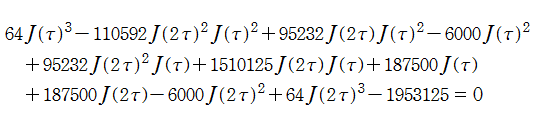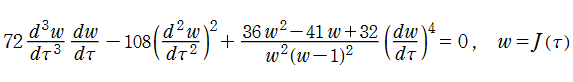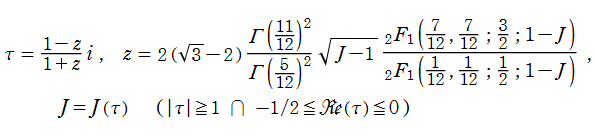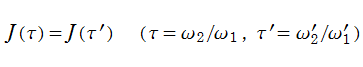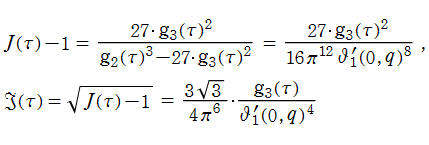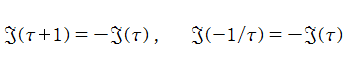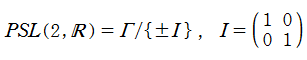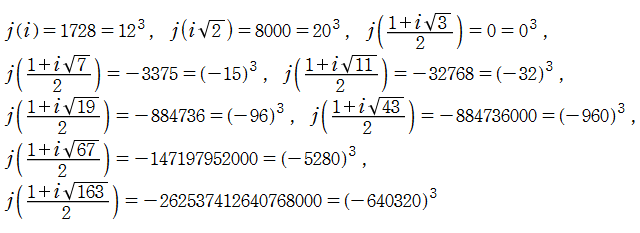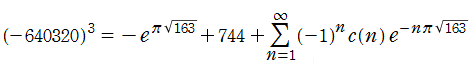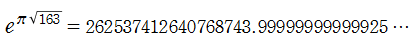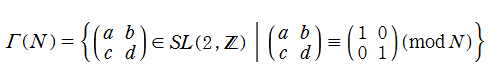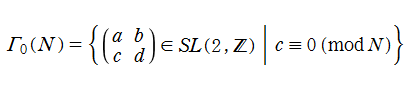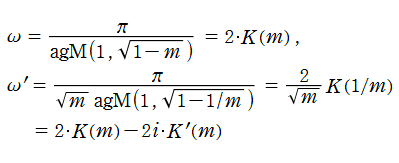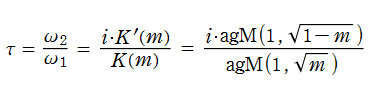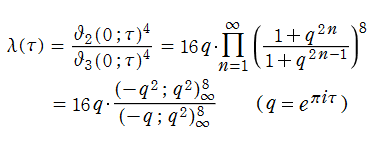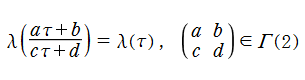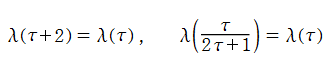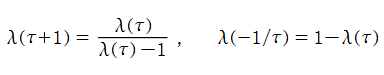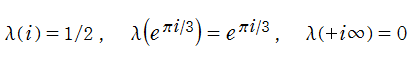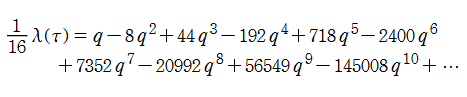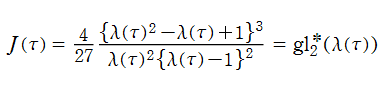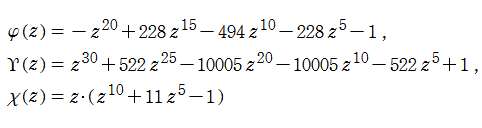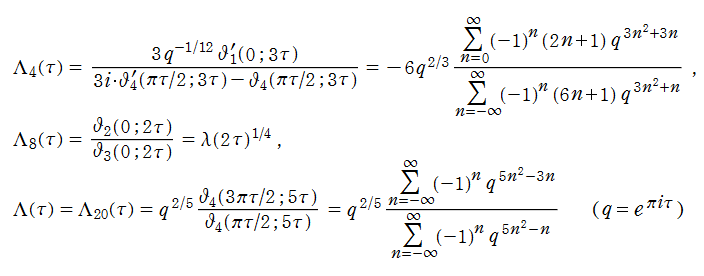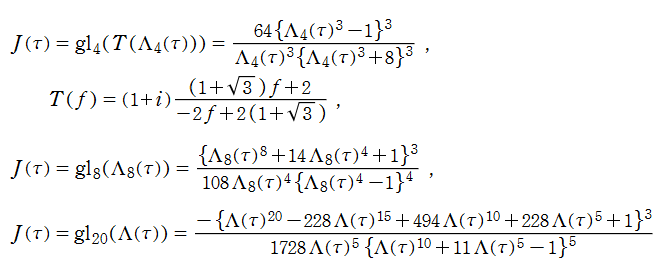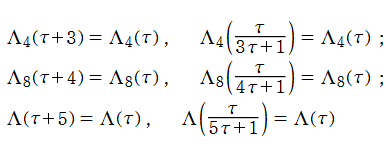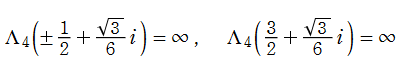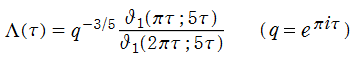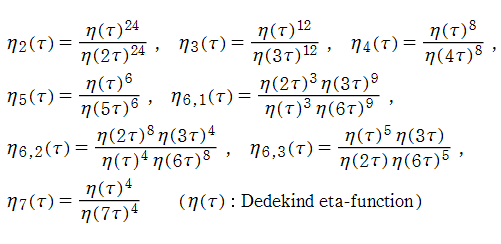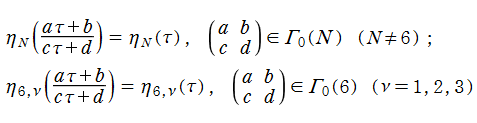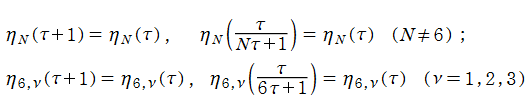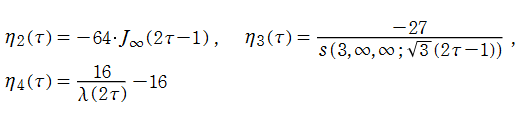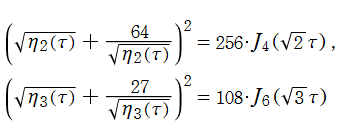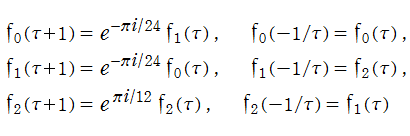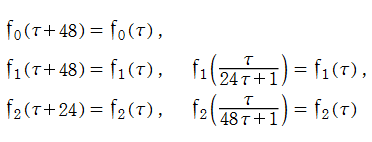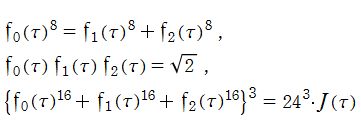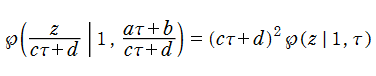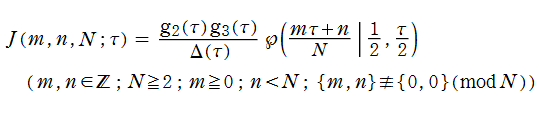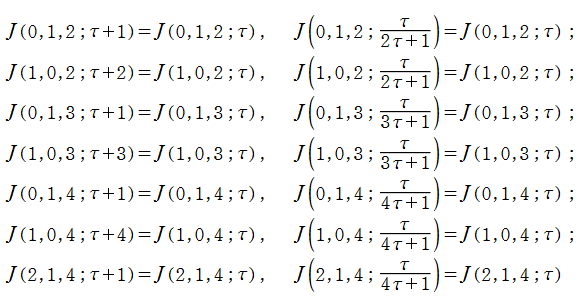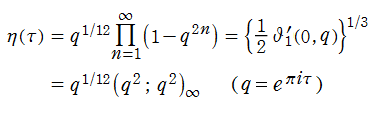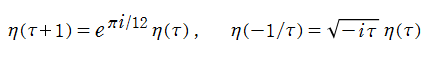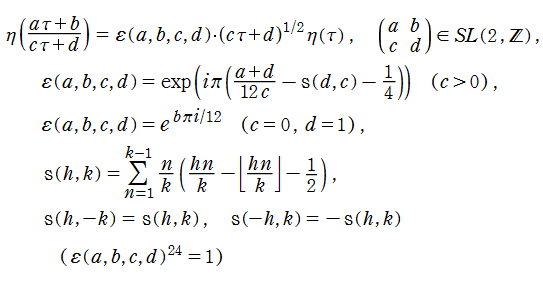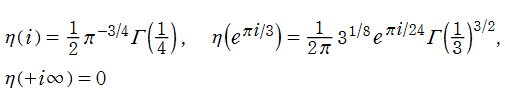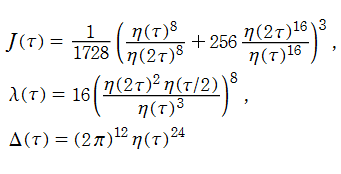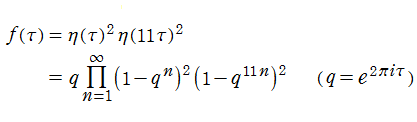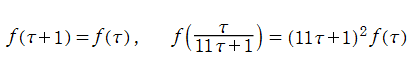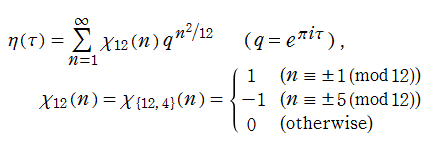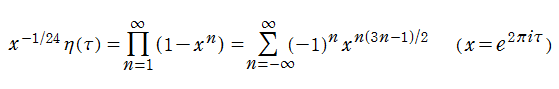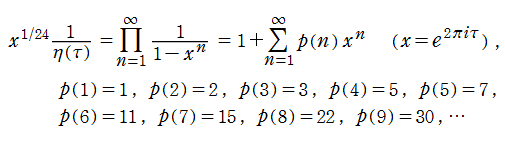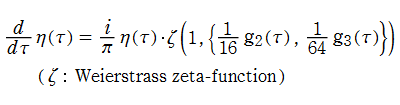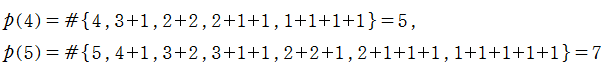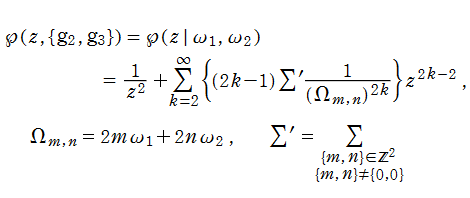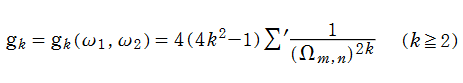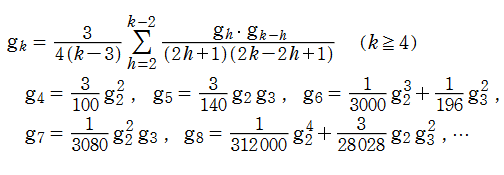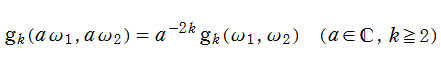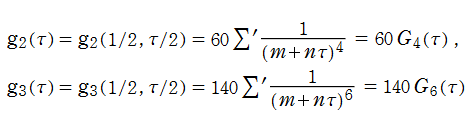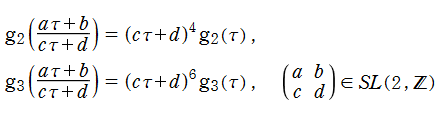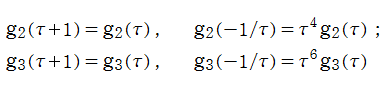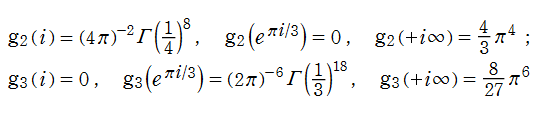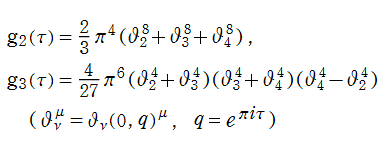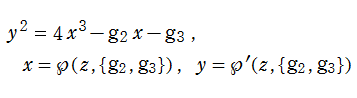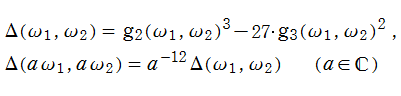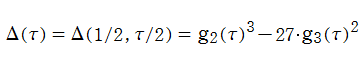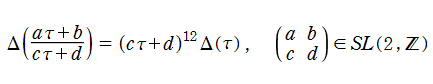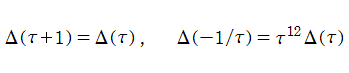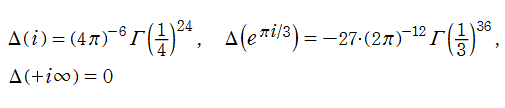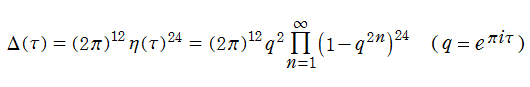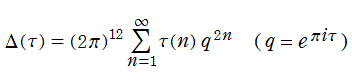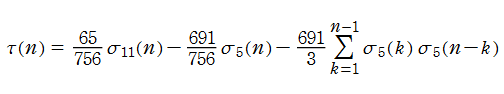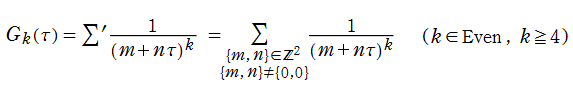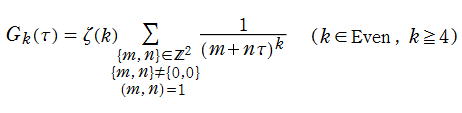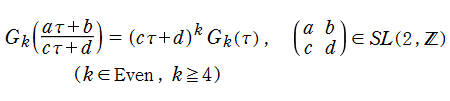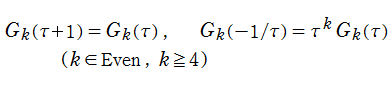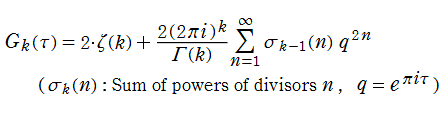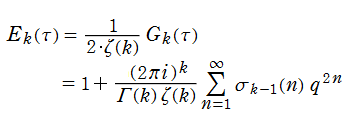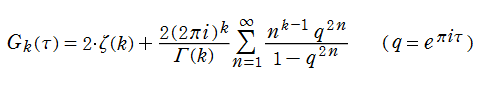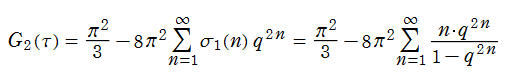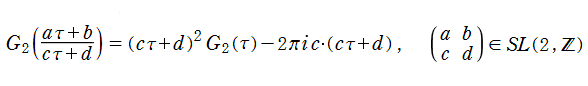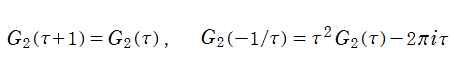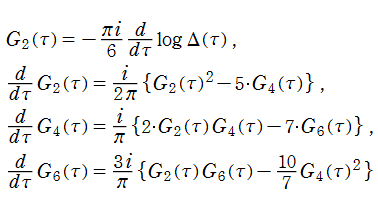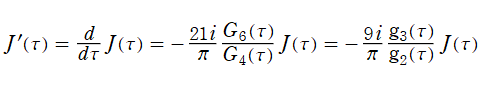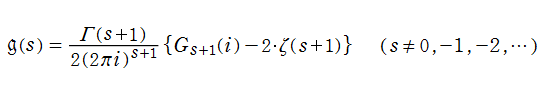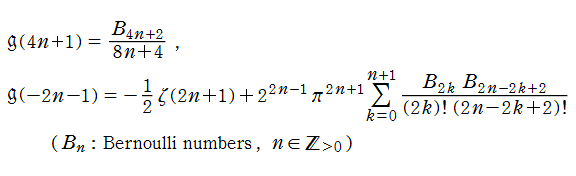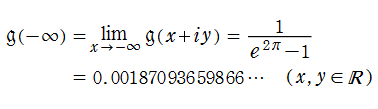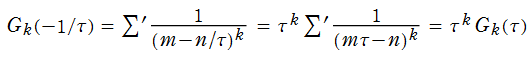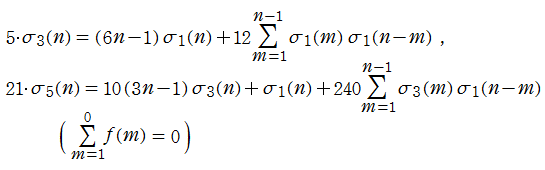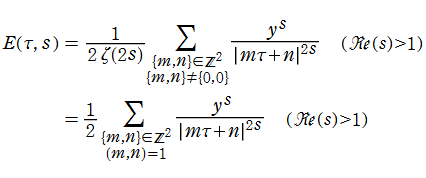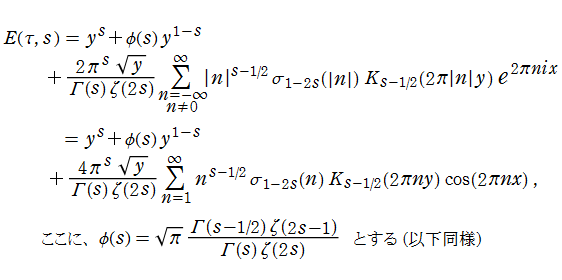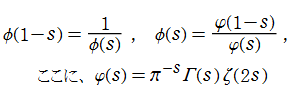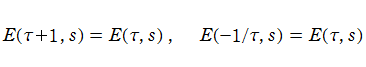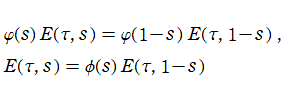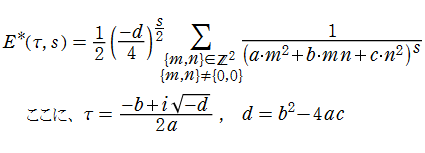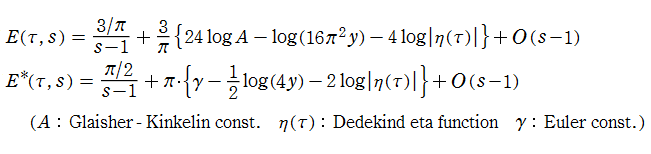特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
楕円モジュラー関数
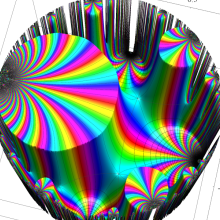
Klein の楕円モジュラー関数
日:楕円モジュラー関数,モジュラー関数英:Modular function,仏:Fonction modulaire,独:Modulfunktion
日:Kleinのj-不変量,クラインの絶対不変量
英:Klein's j-invariant,仏:j-invariant,独:j-funktion
楕円モジュラー関数は、保型関数の特別な場合であるが、分量の理由から、当サイトではこの頁で前者を扱い、後者のうち前者に含まれない例を次頁に後回しする。すなわち2頁で一体とする。
しかし、説明文はどちらか一方の頁に両者をまとめて記述することがある (次の概要文など)。
【始めに:保型関数および楕円モジュラー関数の概要】
保型関数は、いくつかの意味で楕円関数の拡張である。例えば、楕円関数は、二つの平行移動 (つまり離散的な特定の一次変換) の合成に対して不変な有理型関数で、その基本領域となる平行四辺形は、Euclid 幾何的な (通常の) 距離が定められた複素平面全体を一重に覆う。一方、保型関数は、特定の一次分数変換の合成に対して不変な有理型関数で、その基本領域となる円弧多角形は、非 Euclid 幾何的な距離が定められた複素平面の全体または部分領域を一重に覆う。
ところが歴史的には、楕円関数の第2変数 (母数=モジュラス) を、逆に二つの周期の比
保型関数は、群論,数論等で重要な関数である。代数多様体に関連した数論,類体論を始めとする代数的整数論等では、本質的な役割を担うとともに、ゼータ関数との神秘的な絡み合いも垣間見せる。一方、散在型有限単純群と保型関数との関係からは頂点作用素代数が派生し、これが1980年代中盤に、場の量子論,超弦理論,統計力学へ保型関数が応用されるという驚くべき邂逅をもたらすことになる。
特に楕円モジュラー関数は、それらの応用分野で出現する保型関数のほとんど (あるいは全て) を占めるので、とりわけ重要視されている。
【予備知識:上半平面・一次分数変換 etc.…】
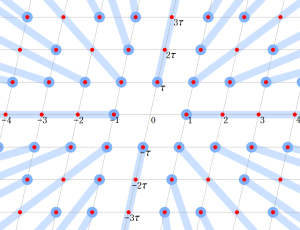
前にも触れたとおり、一般に保型関数の定義域は、複素平面全体になるか、様々な形状の (円または複数の円弧で囲まれた) 部分領域になるが、楕円モジュラー関数や応用上重要な保型関数の多くは、定義域として上半平面
加えて、
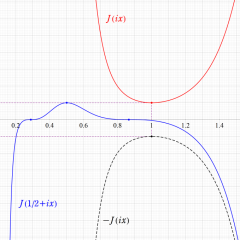
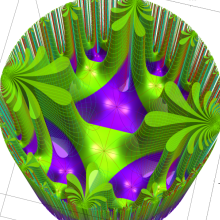
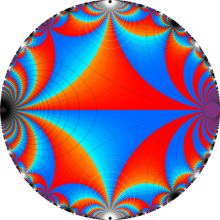
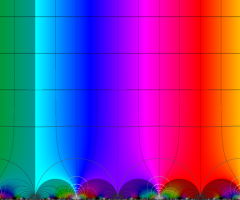
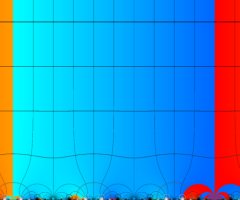
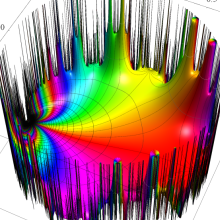
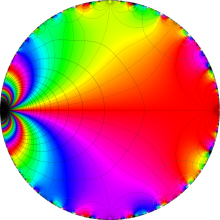
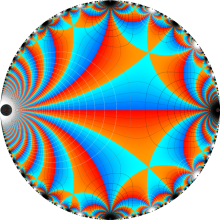
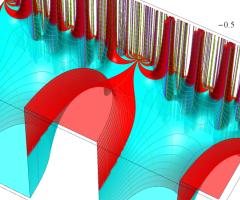
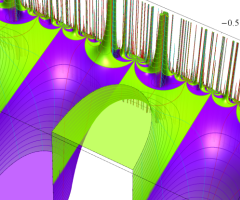
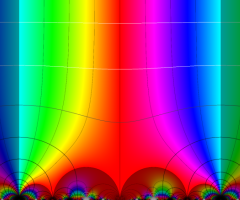
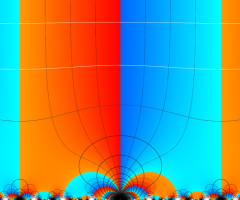
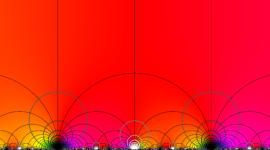
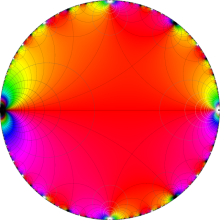
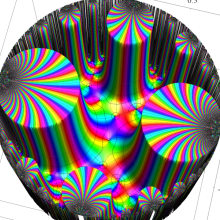
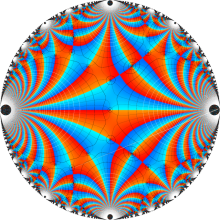
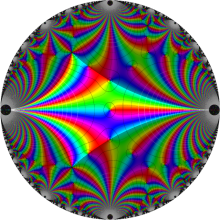
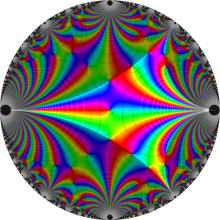
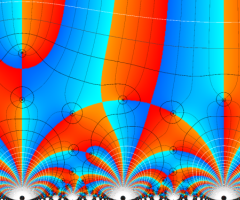
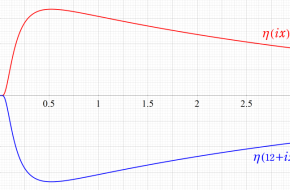
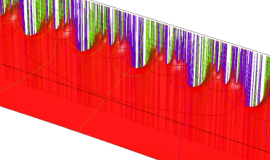
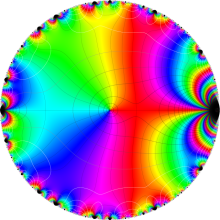
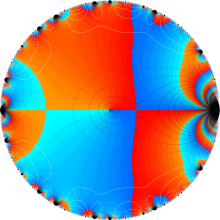
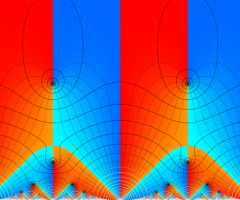
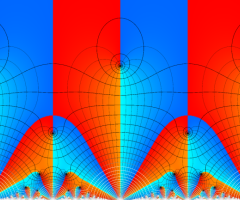
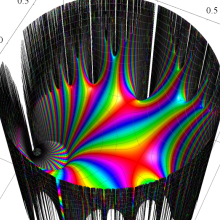
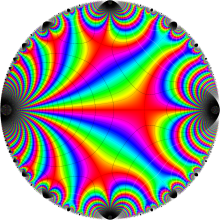
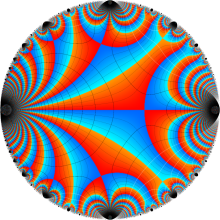
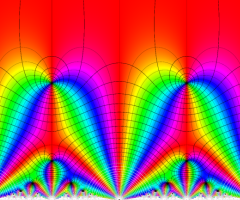
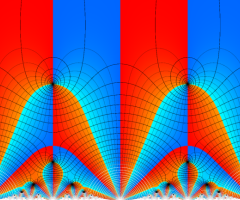
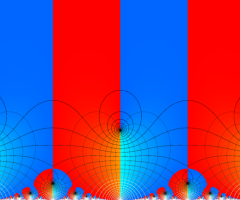
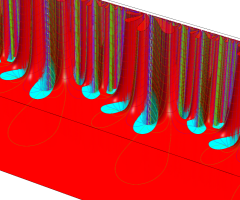
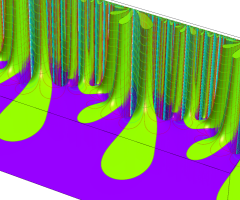
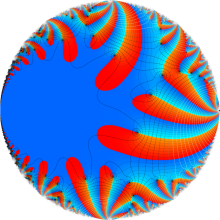
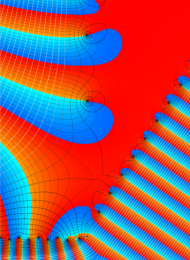
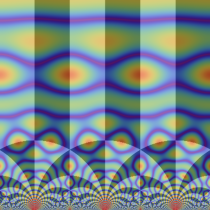
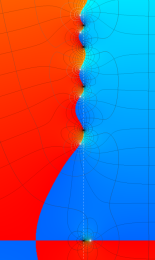
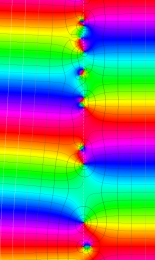
図: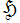 上の測地線。背景模様の円弧三角形の辺は、全て双曲的距離が等しい!。
上の測地線。背景模様の円弧三角形の辺は、全て双曲的距離が等しい!。
で与えられるとする。
が、
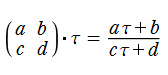
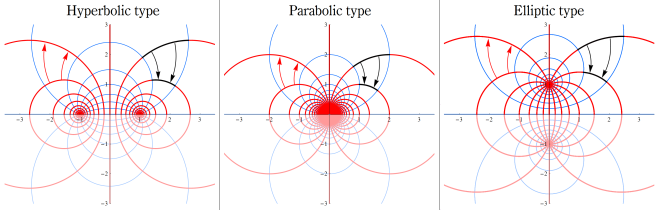
に対応する。(他に 「斜航型」 があるが、
変数
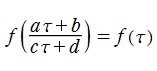
一方、保型因子を除いて不変、具体的には
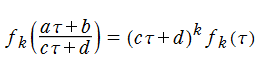
楕円モジュラー関数,楕円モジュラー形式とは、特殊線形群の離散部分群が 「モジュラー群」
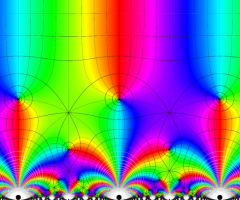
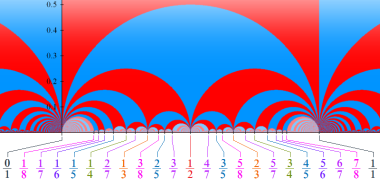
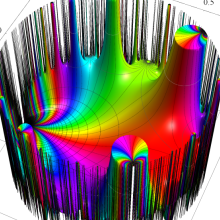
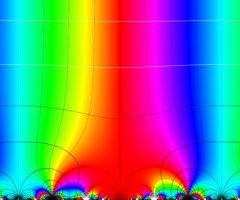
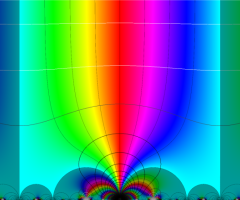
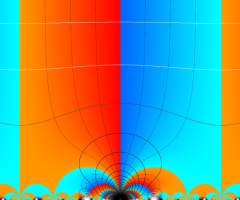
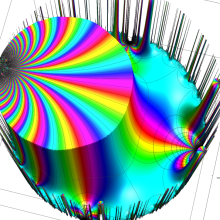
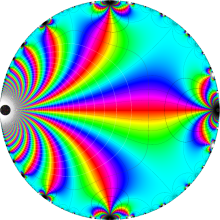
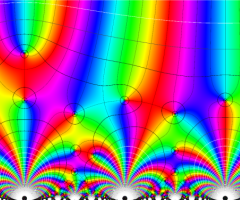
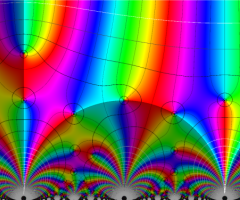
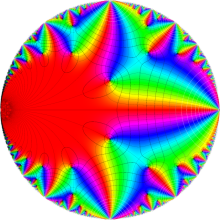
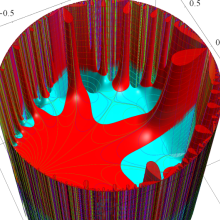
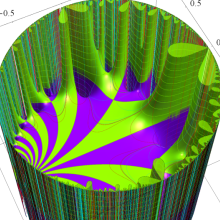
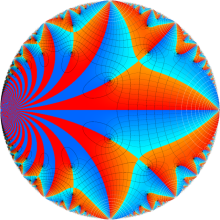
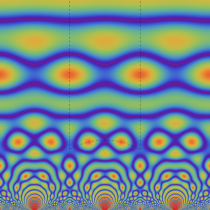
【Klein の楕円モジュラー関数】
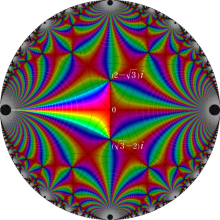
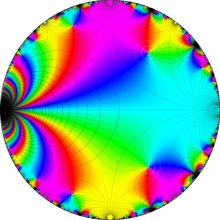
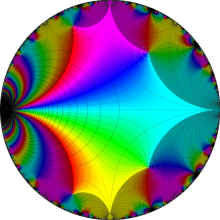
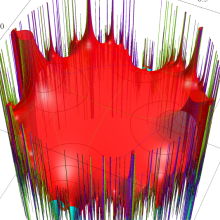
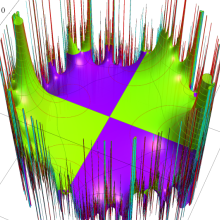
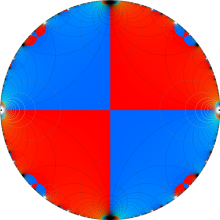
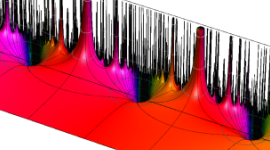
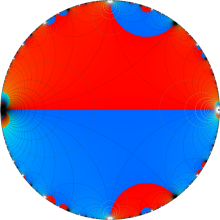
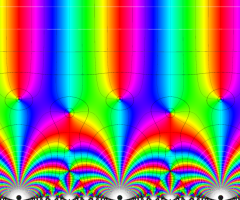
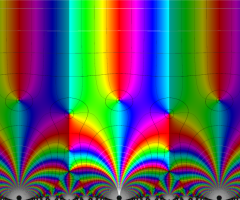
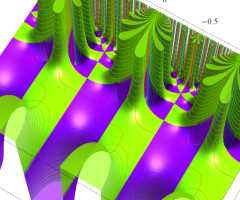
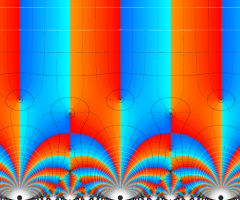
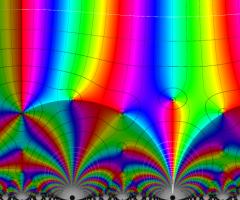
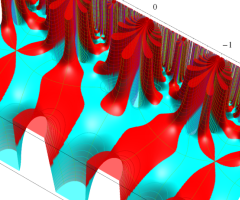
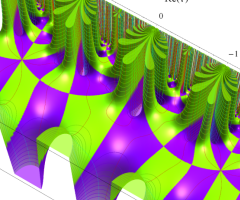
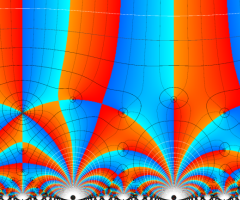
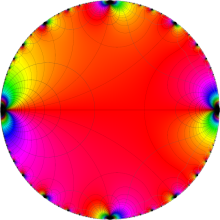
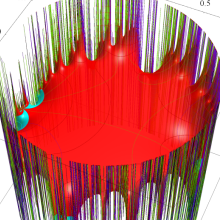
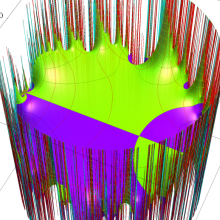
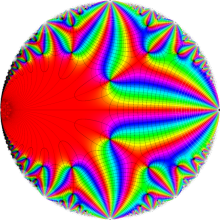
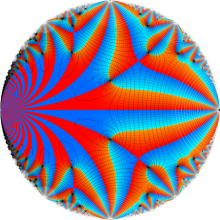
楕円モジュラー関数のうち、最も重要かつ基礎的な関数は、「Klein の楕円モジュラー関数」
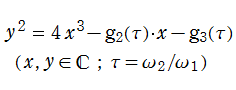
によって定義される。(注意:この頁では以降も、特に断らない場合は
Klein の楕円モジュラー関数は、モジュラー群が作用する一次分数変換に対して不変、つまり
を満たす。特に、その一次分数変換の生成元となる変換に対しては、
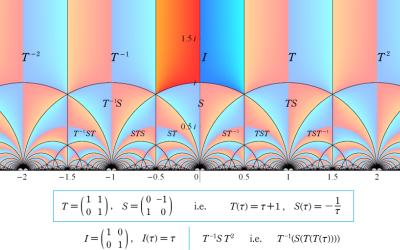
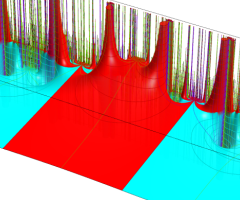
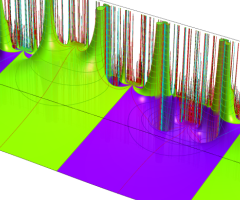
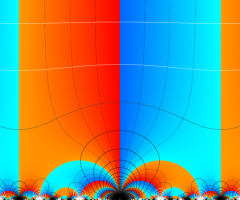
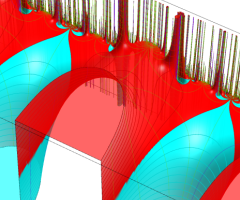
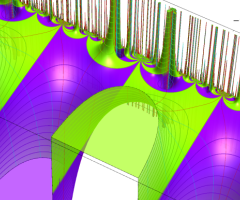
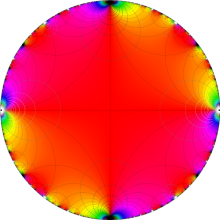
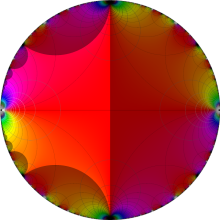
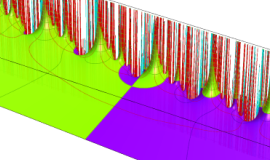
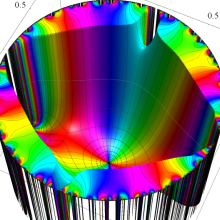
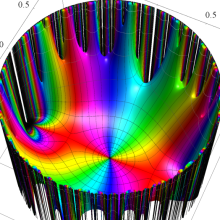
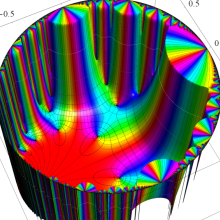
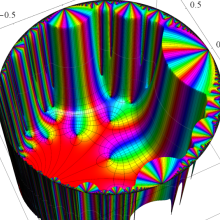
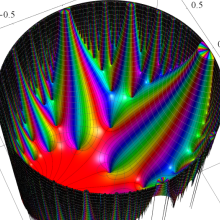
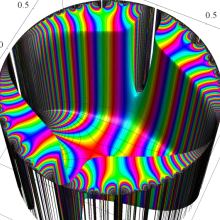
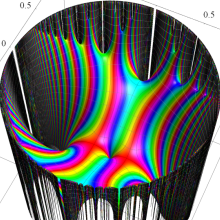
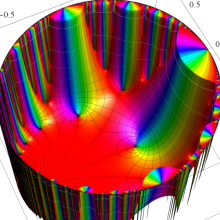
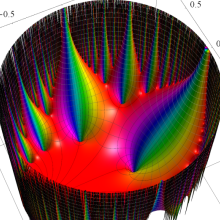
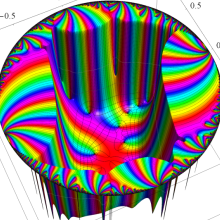
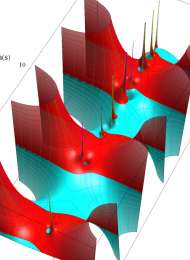
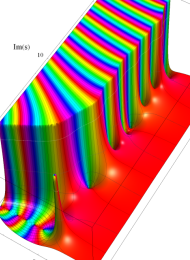
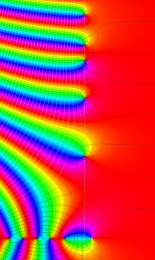
図:一次分数変換の合成と、 を覆う
を覆う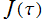 の基本領域との対応
の基本領域との対応
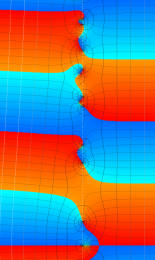
となる (周期性および保型性)。保型関数は一般に
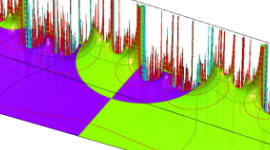
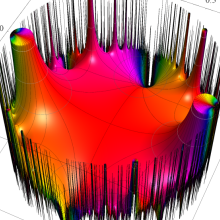
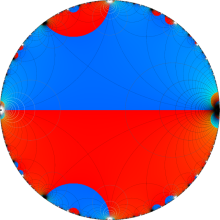
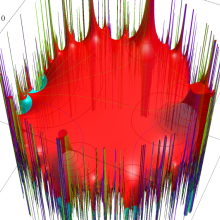
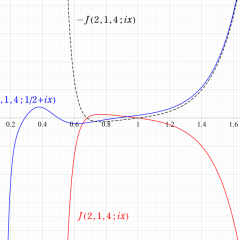
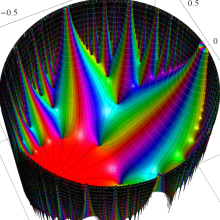
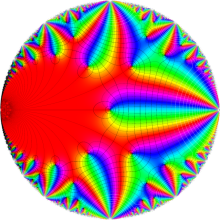
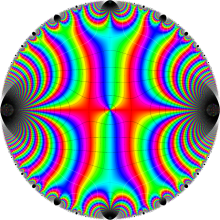
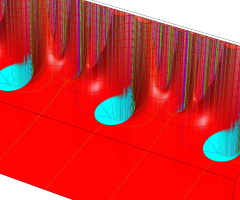
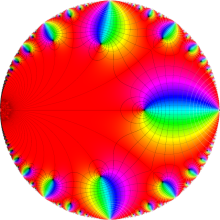
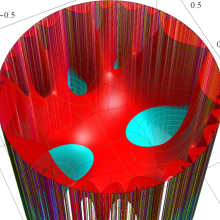
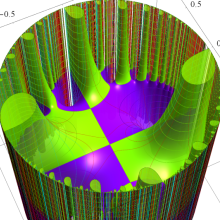
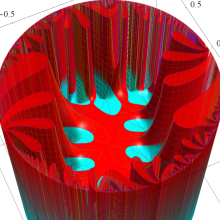
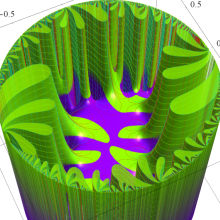
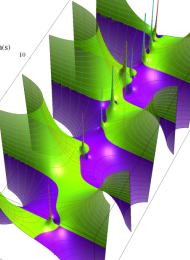
Klein の楕円モジュラー関数は、基本領域となる円弧四角形の半領域 (上図の濃い青色の領域) に附随する頂点と尖点での値が、
となる。変数
Klein の楕円モジュラー関数は周期関数であるので、Fourier 級数 (
に展開される※5。整係数
を満たす。さらに、26種類しかない散在型有限単純群のうち、位数 (群を構成する元の個数) が最大の
となる 「モンスター群」
を用いて、全ての
となる。この対応現象は 「モンストラス・ムーンシャイン (Monstrous Moonshine)」 と呼ばれている※6。
Klein の楕円モジュラー関数は、倍数公式
を満たす。一般に、
Klein の楕円モジュラー関数は、代数的な3階の非線形微分方程式
を満たす。
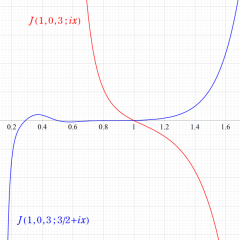
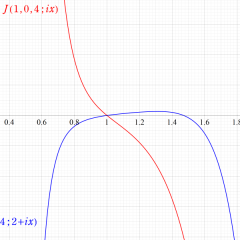
Klein の楕円モジュラー関数の逆関数は、具体的に超幾何関数を用いて、
と表わせる。
周期が
が成立することである。
ここでは併せて、
と解釈する。このとき、
を満たす。すなわち、周期は2となる。
【註記】
※1:上半平面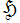 の点
の点 と単位円内部
と単位円内部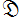 の点
の点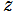 とは、狭義の 「Cayley 変換」 とその逆変換
とは、狭義の 「Cayley 変換」 とその逆変換
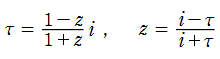
によって、一方から他方へ移り変われる。これらは、実軸上の4点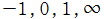 と単位円上の4点
と単位円上の4点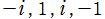 とが変換前後で対応する、特別な一次分数変換になっている。
とが変換前後で対応する、特別な一次分数変換になっている。
当サイトの保型関数に関連する頁では、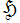 上の保型関数等を
上の保型関数等を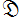 上に Cayley 変換したそれも、本質的に同じ関数と見做して扱う。「Gauss - Schwarz 理論」 における Schwarz の保型関数のように、まず
上に Cayley 変換したそれも、本質的に同じ関数と見做して扱う。「Gauss - Schwarz 理論」 における Schwarz の保型関数のように、まず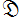 上の保型関数として与えられる例も存在するからである。
上の保型関数として与えられる例も存在するからである。
しかし、当然ながら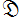 上の保型関数等が不変となる一次分数変換は、
上の保型関数等が不変となる一次分数変換は、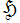 上のそれとは異なる。また、
上のそれとは異なる。また、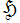 上の保型関数等
上の保型関数等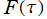 に対する
に対する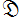 上のそれを、当サイトでは
上のそれを、当サイトでは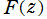 と略記するが、本来は
と略記するが、本来は
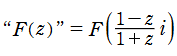
の意味であるとする。
※2:正確には、一次分数変換と準同型写像な群は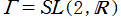 ではなく、射影特殊線形群
ではなく、射影特殊線形群
である。つまり、一次分数変換にすると符号が約されて同じになる複数の行列は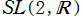 中の重複元と考えて、そこから全ての重複を取り除くと
中の重複元と考えて、そこから全ての重複を取り除くと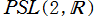 になる。
になる。
※3:当初、楕円曲線の不変式論では、絶対不変量を (一見して簡単な形の)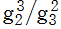 で定義することが多かったが、これを保型関数
で定義することが多かったが、これを保型関数
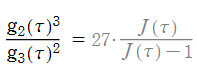
として見ると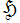 上の有理型関数になる。これと基本領域の形が同じであるが、零点・鞍点・極の位置が入れ替わる関数は下図のとおり6種類しかなく、そのうち
上の有理型関数になる。これと基本領域の形が同じであるが、零点・鞍点・極の位置が入れ替わる関数は下図のとおり6種類しかなく、そのうち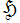 上の超越整関数となるのは2種類である。C. F. Klein は
上の超越整関数となるのは2種類である。C. F. Klein は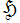 上で常に
上で常に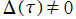 となる事実から、分母が
となる事実から、分母が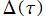 である絶対不変量、すなわち
である絶対不変量、すなわち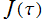 の方を採用した (1878年)。J. W. R. Dedekind も別の方法 (主にモジュラー群と Schwarz の鏡像原理) によって
の方を採用した (1878年)。J. W. R. Dedekind も別の方法 (主にモジュラー群と Schwarz の鏡像原理) によって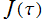 と全く同じ関数に辿り着いていた (1877年)。
と全く同じ関数に辿り着いていた (1877年)。
※4:特に、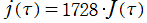 の値が有理整数 (通常の整数) になる虚二次体の数
の値が有理整数 (通常の整数) になる虚二次体の数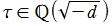 は、類数が1、すなわち
は、類数が1、すなわち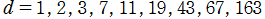 に限る。具体的な整数値は、
に限る。具体的な整数値は、
となっており、すべて立方数である。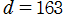 の場合を Fourier 級数にも代入すると、
の場合を Fourier 級数にも代入すると、
となるが、無限級数部分は絶対値が非常に小さい。よって、整数に非常に近くなる実数の有名な例
が得られる。
※5:数値計算可能な、係数 の漸近近似式と漸化式が、「Wolfram Functions Site」 の下記ページに掲載されている。
の漸近近似式と漸化式が、「Wolfram Functions Site」 の下記ページに掲載されている。
http://functions.wolfram.com/EllipticFunctions/KleinInvariantJ/06/02/
漸近近似式は第1種変形 Bessel 関数項の無限級数で表わされる。また、特に漸化式は数値計算に適している。
※6:散在型有限単純群,既約表現等の用語について、ここでは説明しない。詳細は、原田耕一郎 著 「モンスター:群のひろがり (岩波書店 1999年)」 等を参照して欲しい。次数の数表が同著の232頁に掲載されている。
※1:上半平面
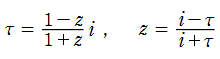
当サイトの保型関数に関連する頁では、
しかし、当然ながら
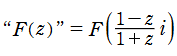
※2:正確には、一次分数変換と準同型写像な群は
である。つまり、一次分数変換にすると符号が約されて同じになる複数の行列は
※3:当初、楕円曲線の不変式論では、絶対不変量を (一見して簡単な形の)
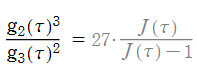
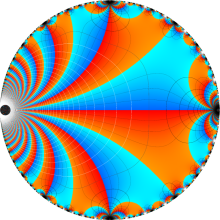
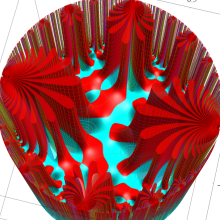
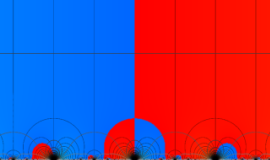
図:絶対不変量の候補となる6種類の楕円モジュラー関数 (ただし、 内部へ変換)
内部へ変換)
※4:特に、
となっており、すべて立方数である。
となるが、無限級数部分は絶対値が非常に小さい。よって、整数に非常に近くなる実数の有名な例
が得られる。
※5:数値計算可能な、係数
http://functions.wolfram.com/EllipticFunctions/KleinInvariantJ/06/02/
漸近近似式は第1種変形 Bessel 関数項の無限級数で表わされる。また、特に漸化式は数値計算に適している。
※6:散在型有限単純群,既約表現等の用語について、ここでは説明しない。詳細は、原田耕一郎 著 「モンスター:群のひろがり (岩波書店 1999年)」 等を参照して欲しい。次数の数表が同著の232頁に掲載されている。
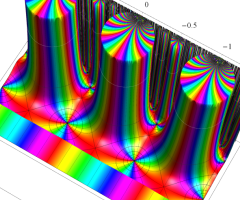
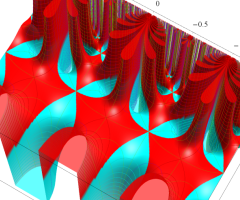
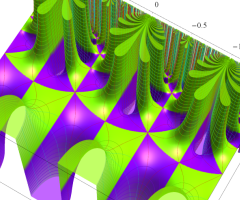
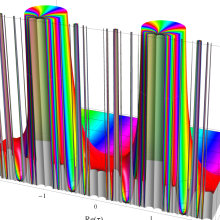
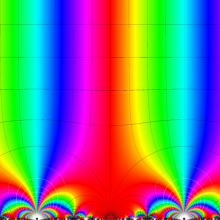
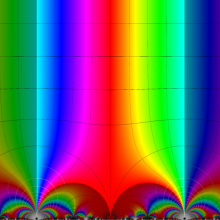
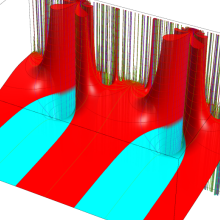
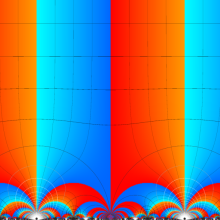
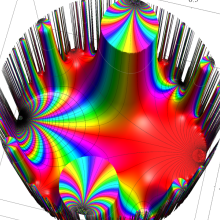
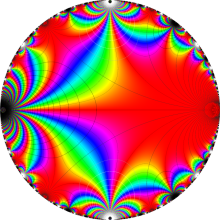
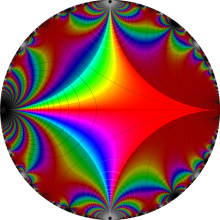
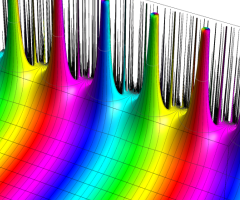
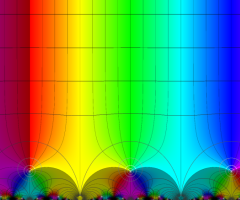
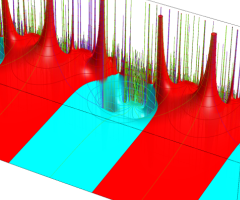
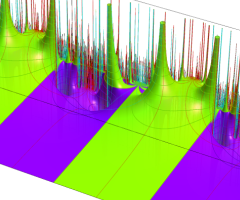
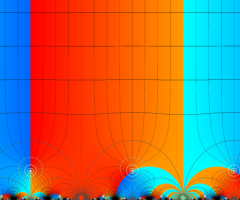
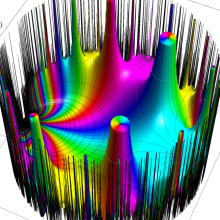
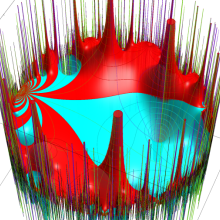
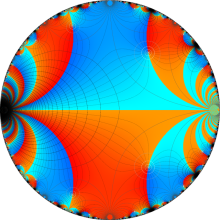
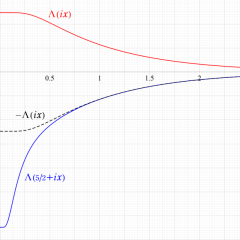
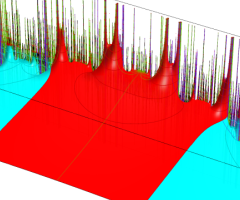
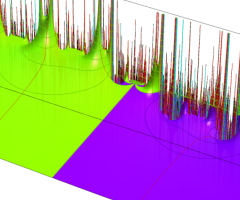
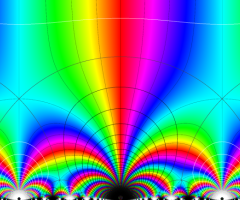
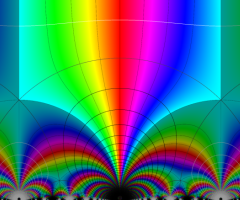
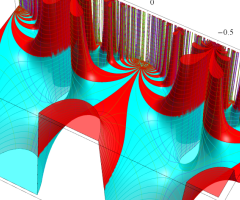
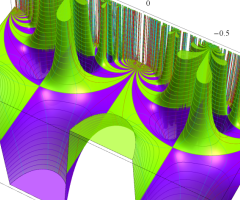
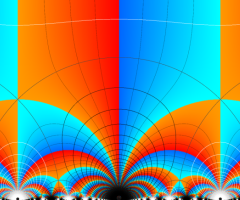
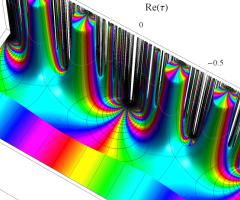
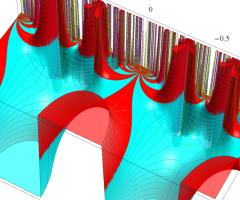
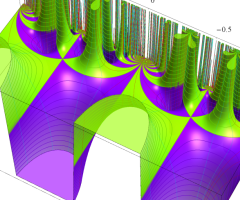
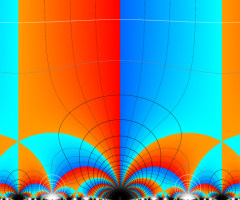
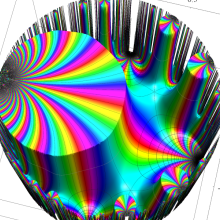
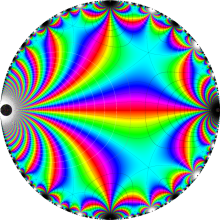
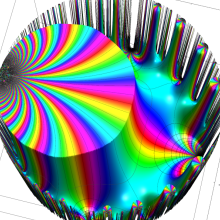
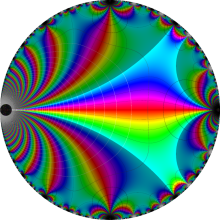
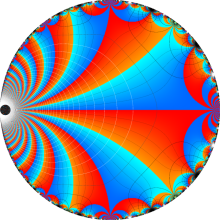
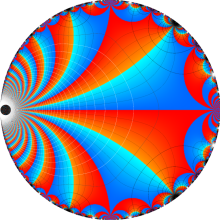
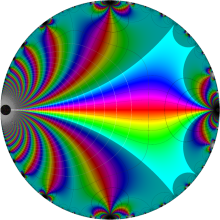
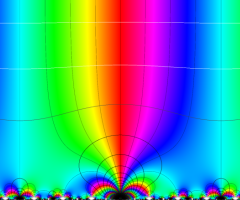
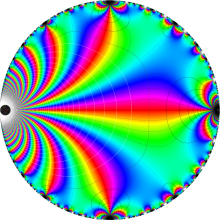
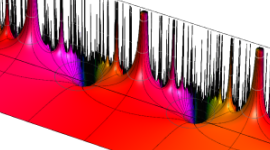
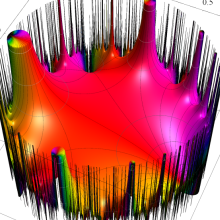
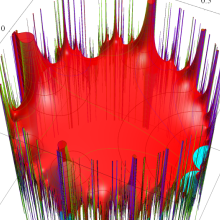
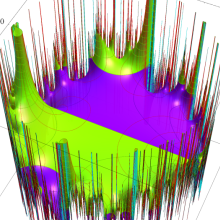
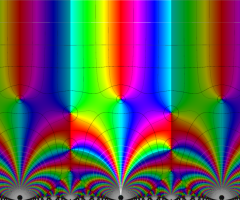
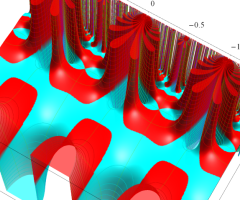
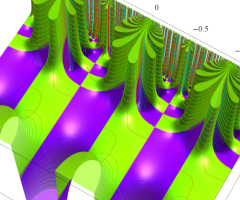
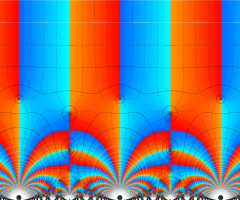
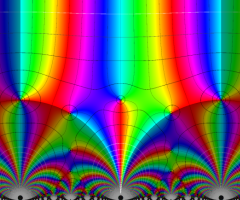
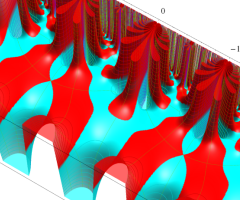
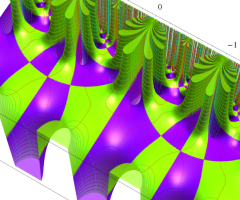
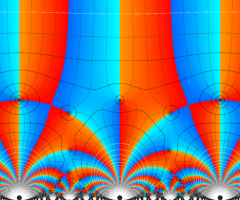
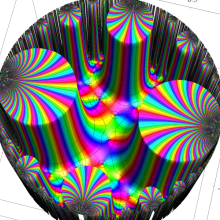
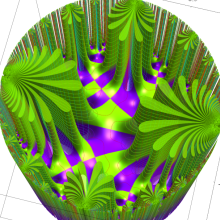
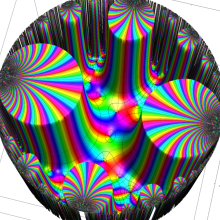
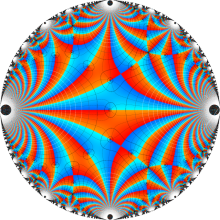
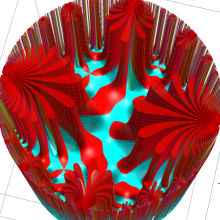
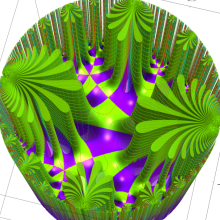
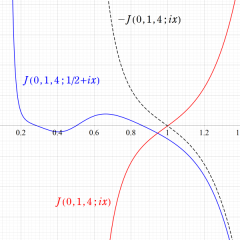
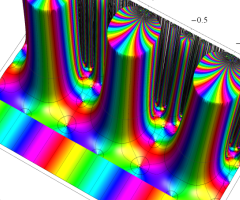
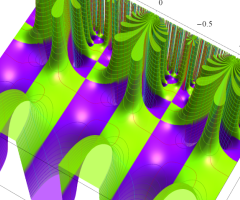
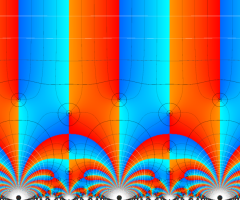
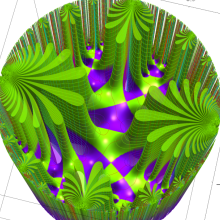
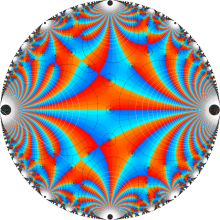
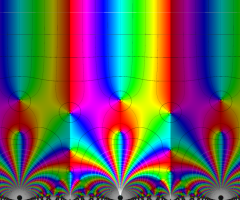
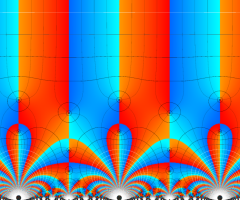
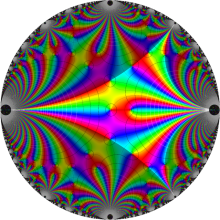
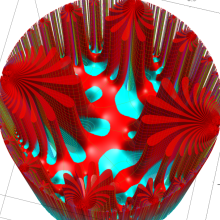
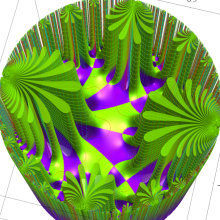
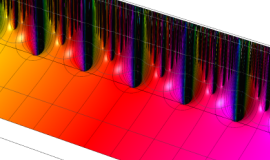
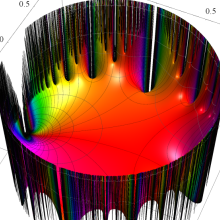
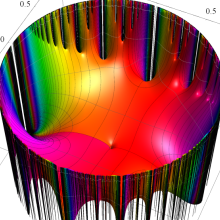
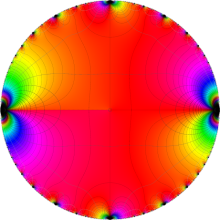
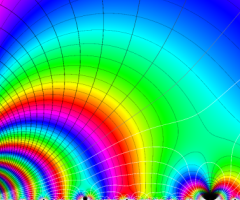
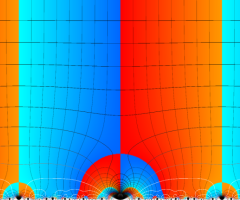
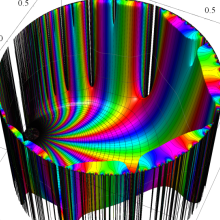
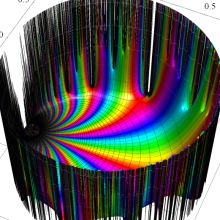
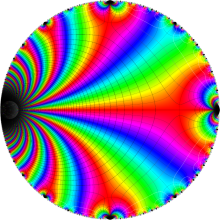
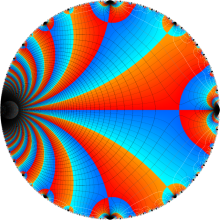
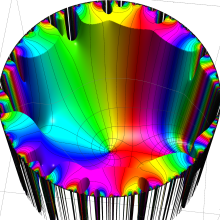
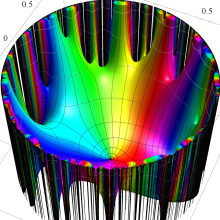
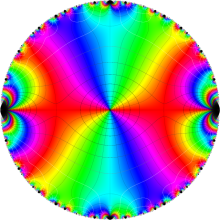
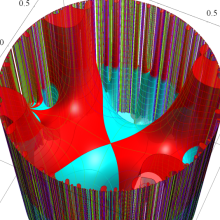
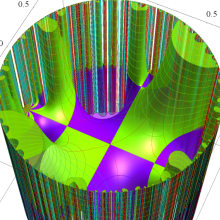
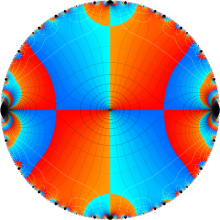
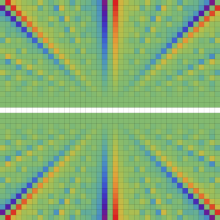
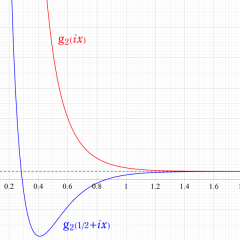
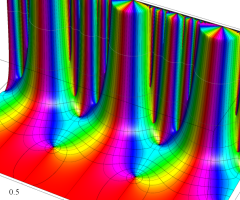
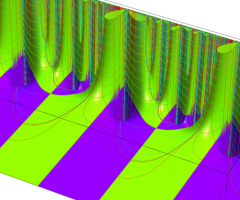
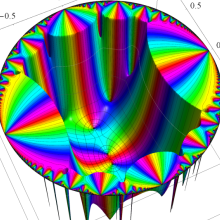
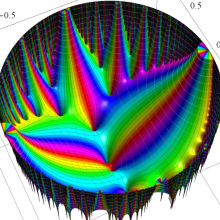
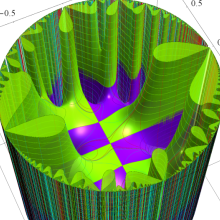
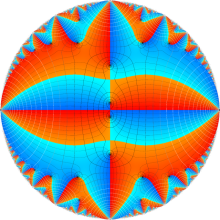
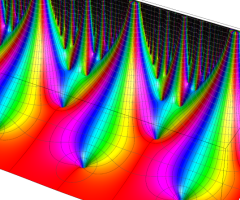
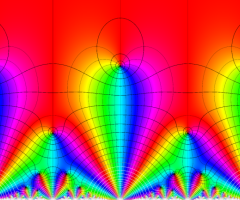
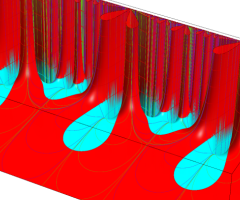
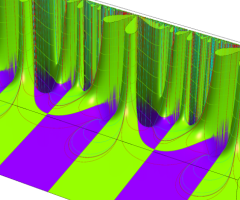
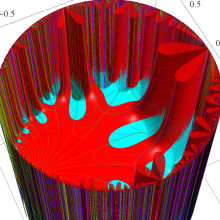
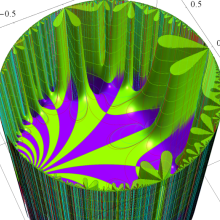
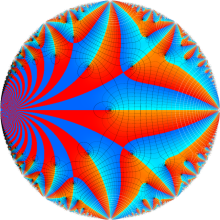
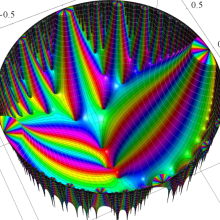
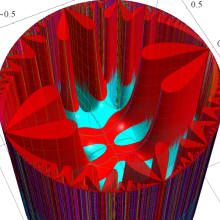
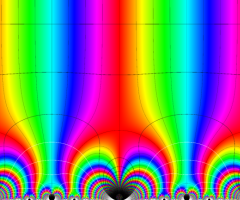
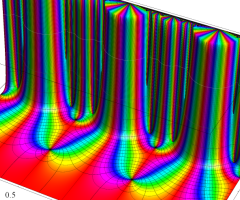
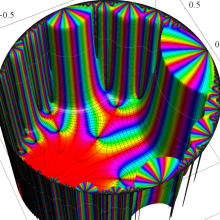
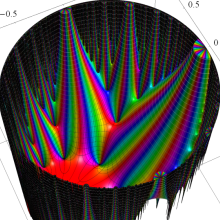
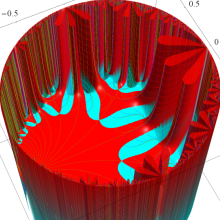
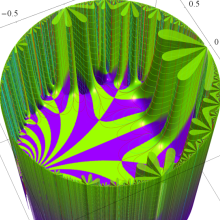
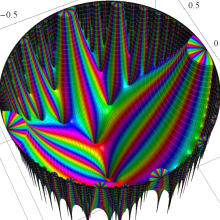
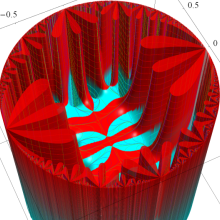
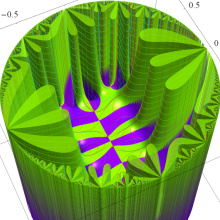
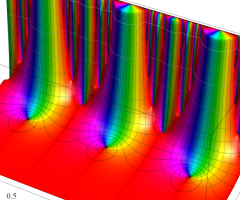
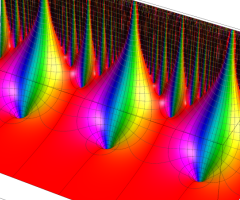
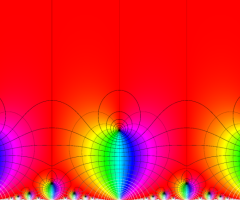
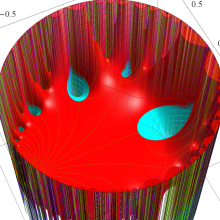
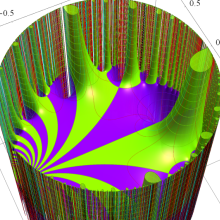
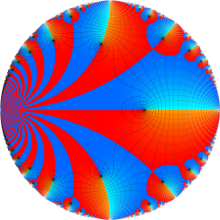
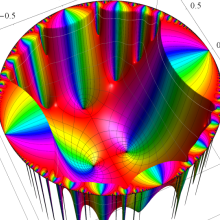
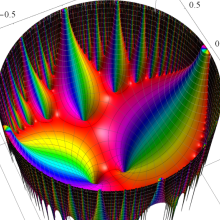
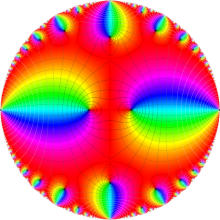
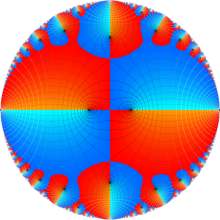
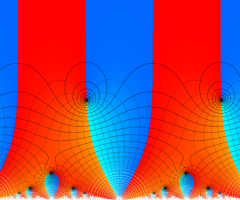
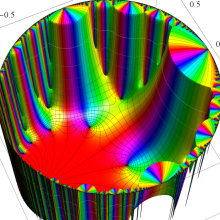
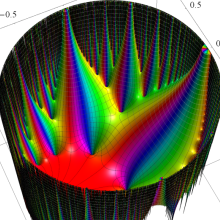
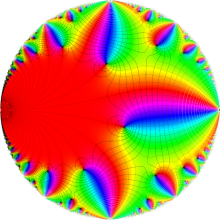
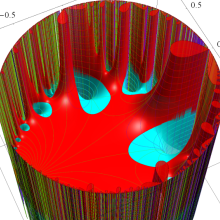
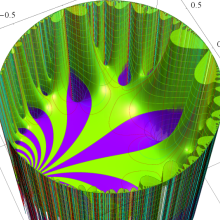
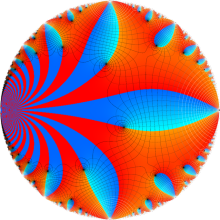
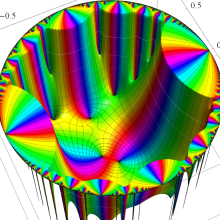
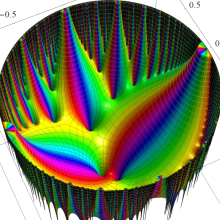
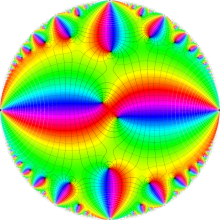
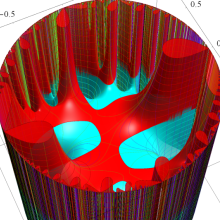
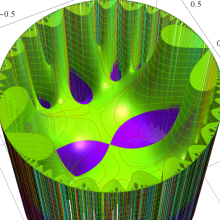
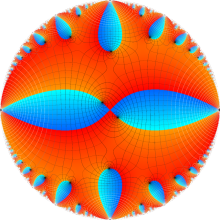
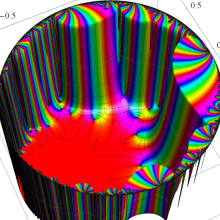
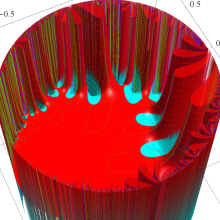
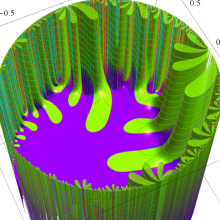
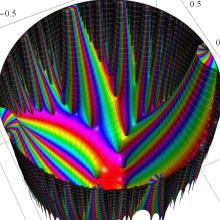
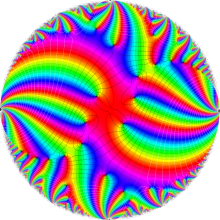
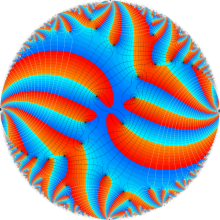
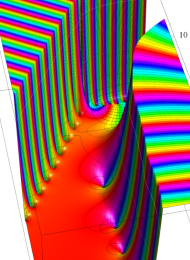
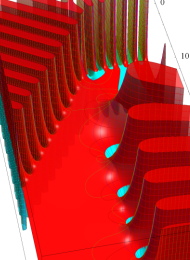
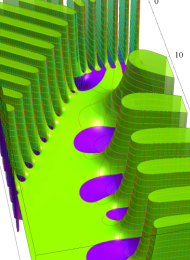
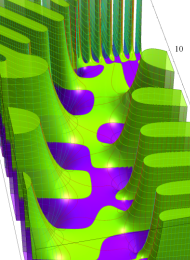
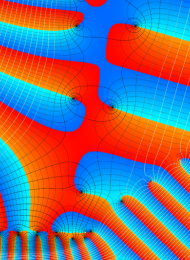
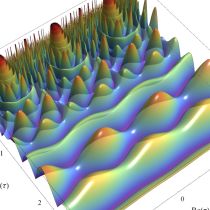
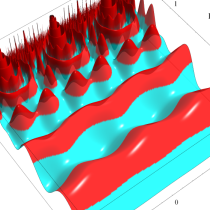
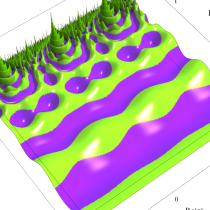
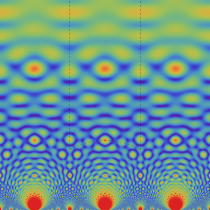
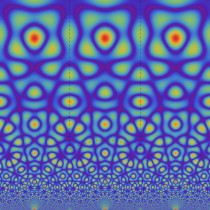
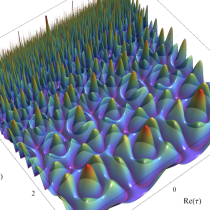
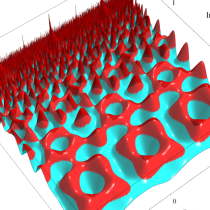
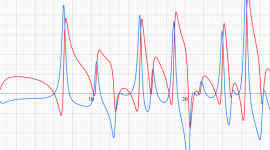
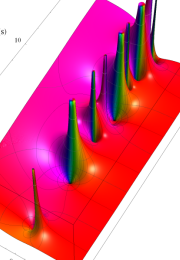
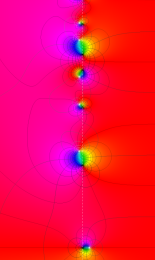
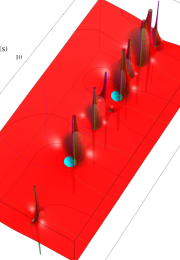
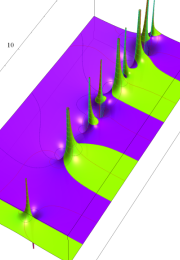
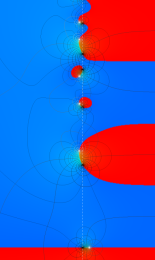
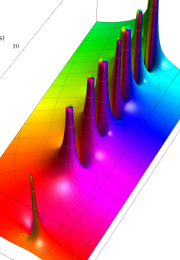
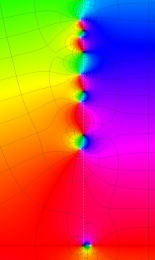
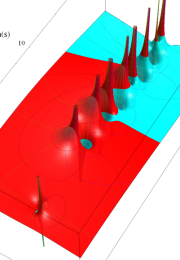
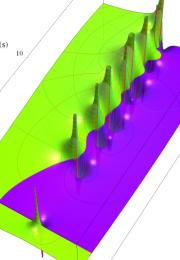
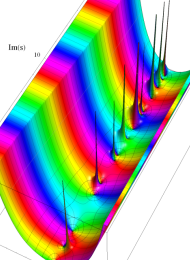
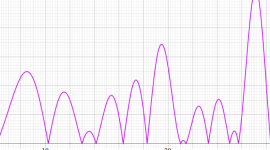
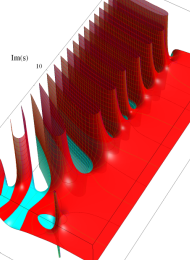
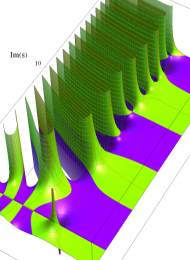
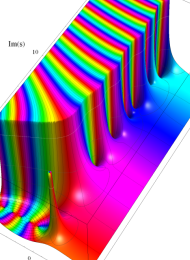
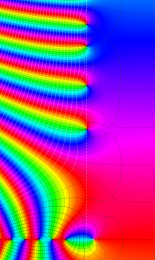
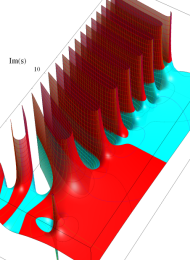
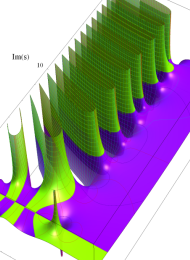
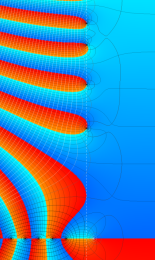
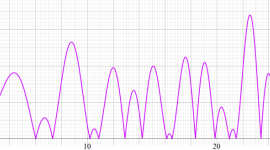
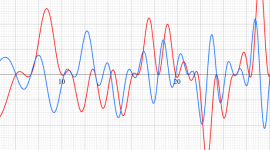
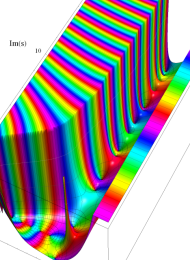
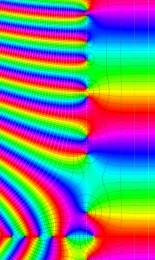
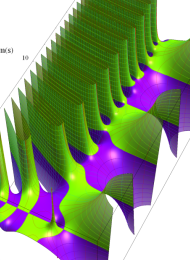
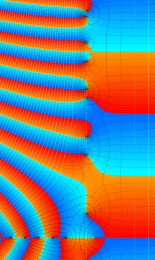
Klein の楕円モジュラー関数の基本領域が、円弧多角形であることを示したグラフ。
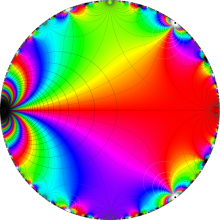
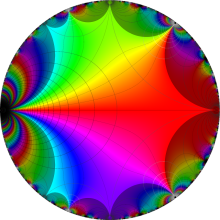
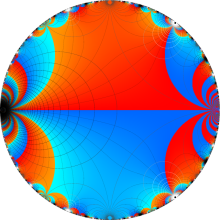
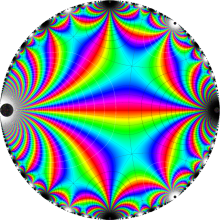
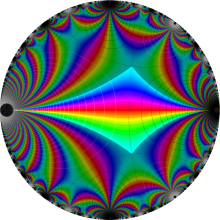
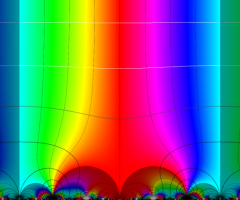
楕円モジュラー・ラムダ関数
日:楕円モジュラー・ラムダ関数英:elliptic modular lambda function,仏:Fonction modulaire lambda,独:Lambda-Funktion
【モジュラー群の主合同部分群・合同部分群】
を
また、それぞれの群を集合と見たときの部分集合関係が
は、それに該当する。
楕円モジュラー関数には、
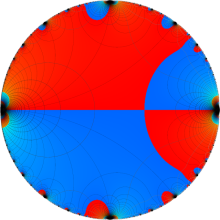
【楕円モジュラー・ラムダ関数】
Gauss は、算術幾何平均との関係が明示された、
を周期とする楕円関数 (一般レムニスケート関数) を研究した際、与えられた
を
で表わすことができる。
楕円モジュラー・ラムダ関数は、主合同部分群
を満たす。特に、その一次分数変換の生成元となる変換に対しては、
となる (周期性および保型性)。一方、モジュラー群が作用する一次分数変換の生成元に対しては、
を満たす。
保型関数は一般に
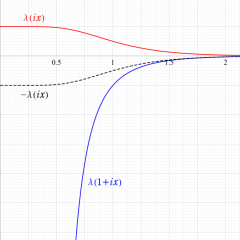
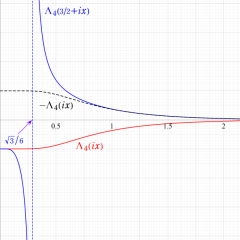
楕円モジュラー・ラムダ関数は、
なる値をとる。
楕円モジュラー・ラムダ関数は周期関数ゆえ、Fourier 級数 (
に展開される。
楕円モジュラー・ラムダ関数を Galois 的有理関数
になる。
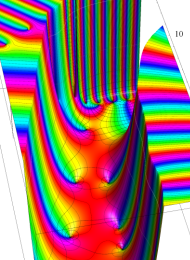
楕円モジュラー・ラムダ関数の尖点は、
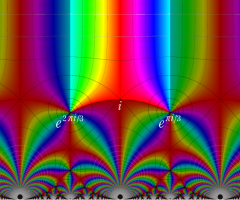
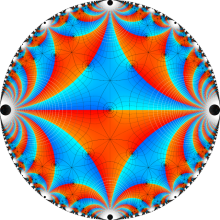
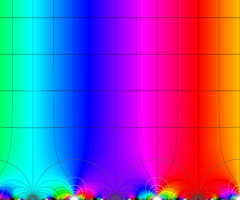
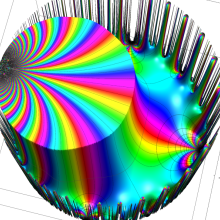
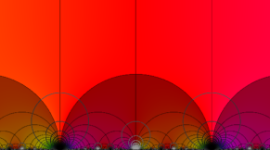
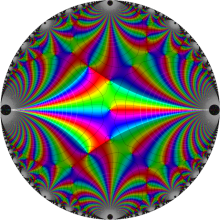
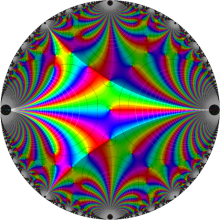
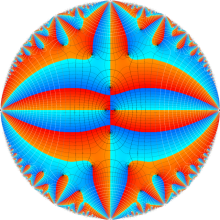
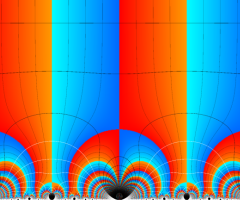
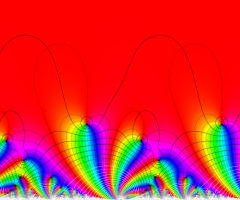
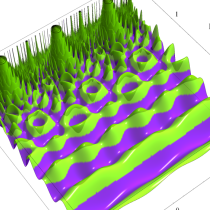
図:楕円モジュラー・ラムダ関数の尖点の位置と Farey 数列。
Gauss は、1810年代には楕円モジュラー・ラムダ関数について多くの結果を手中にしながら秘密のヴェールに包んだ。しかし、Klein の楕円モジュラー関数が現れるまでの間、楕円モジュラー・ラムダ関数は最も基礎的な保型関数として、19世紀中葉に名を残す数学者の多くが論文等で取り上げ、その神秘は次第に解明されていった。特に C. Hermite は、理論展開の中で主合同部分群
【註記】
※1:Farey 数列の名称は、地質学者 J. Farey が1816年におこなった数列と音階に関する研究に因むが、その内容は推測を含み不完全であった。より数学的に厳密な研究は、1802年に C. Haros がおこなっていたので、 本来ならば Haros 数列と呼ぶべきであろう。
※1:Farey 数列の名称は、地質学者 J. Farey が1816年におこなった数列と音階に関する研究に因むが、その内容は推測を含み不完全であった。より数学的に厳密な研究は、1802年に C. Haros がおこなっていたので、 本来ならば Haros 数列と呼ぶべきであろう。
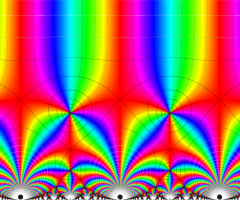
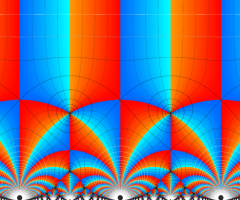
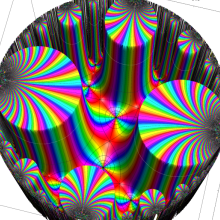
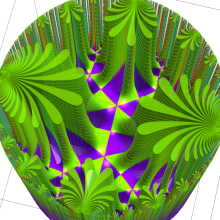
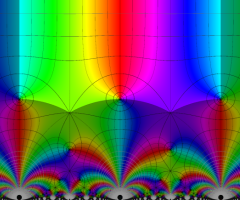
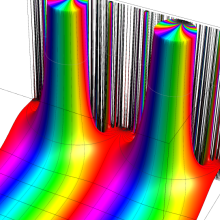
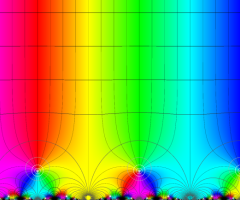
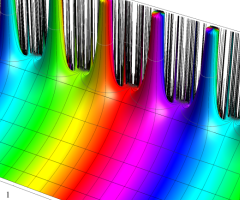
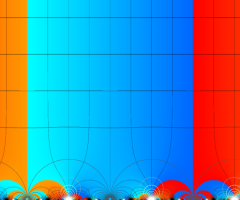
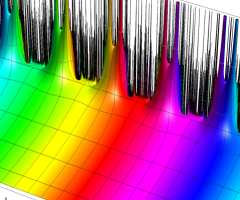
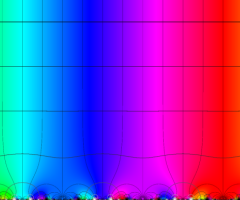
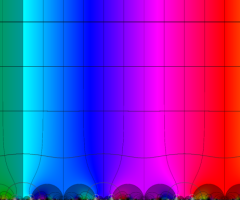
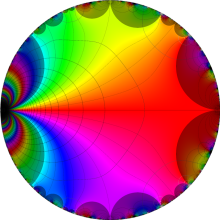
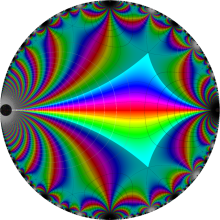
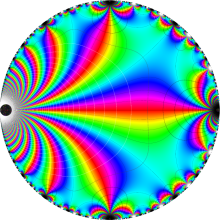
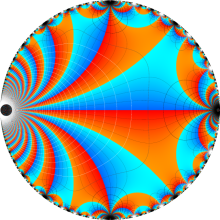
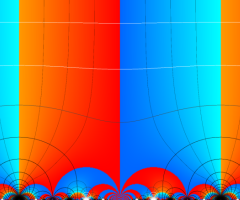
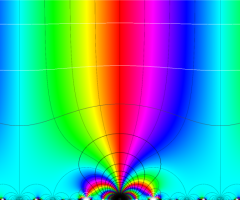
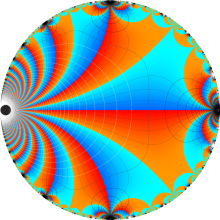
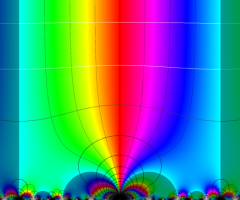
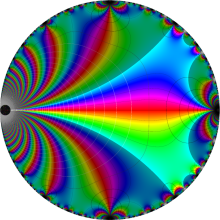
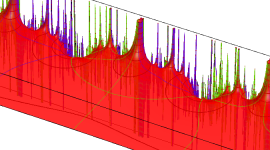
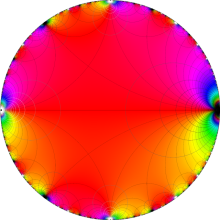
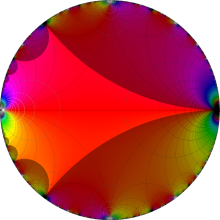
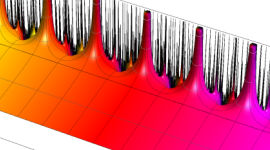
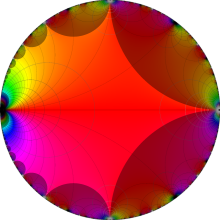
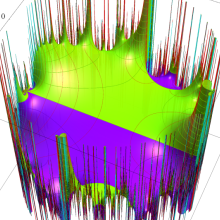
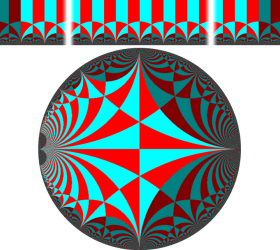
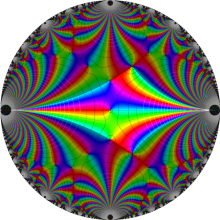
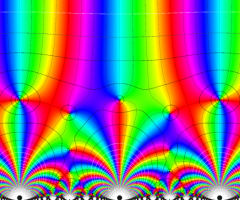
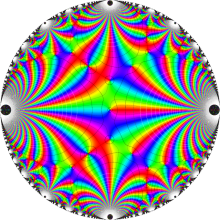
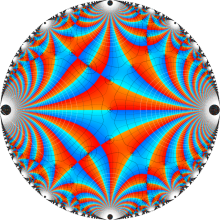
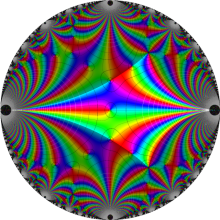
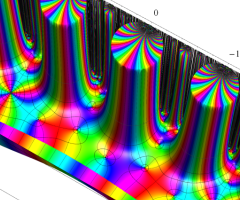
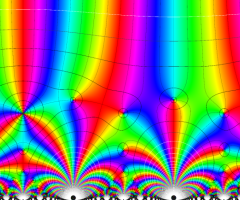
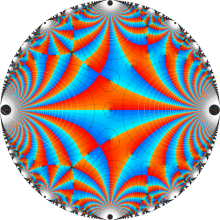
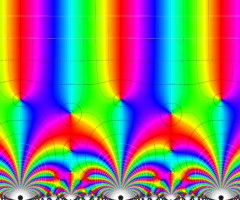
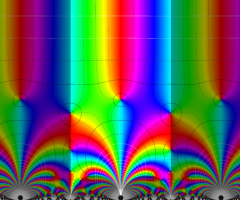
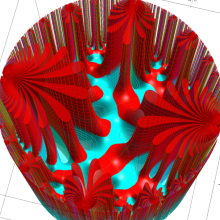
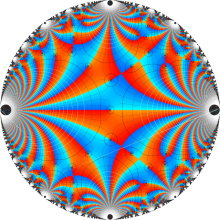
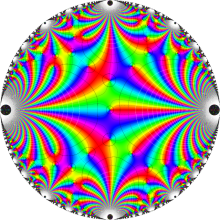
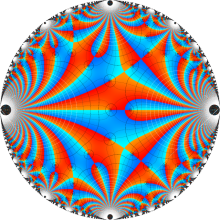
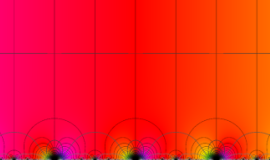
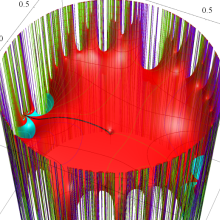
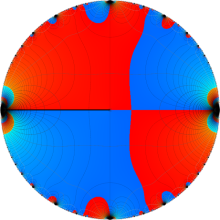
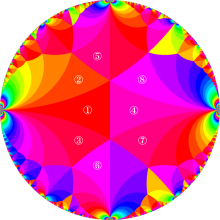
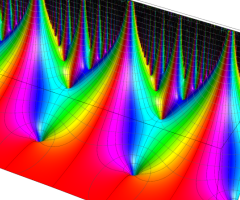
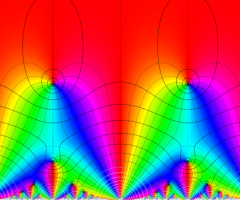
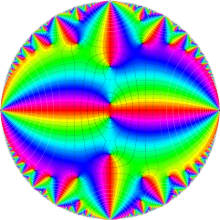
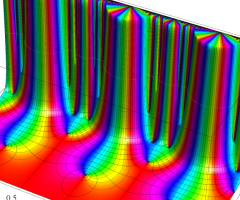
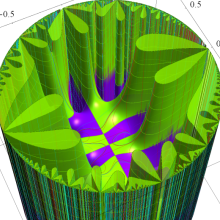
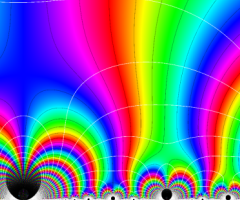
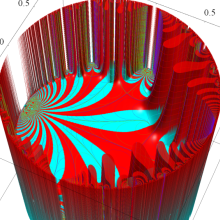
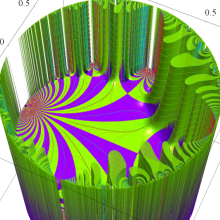
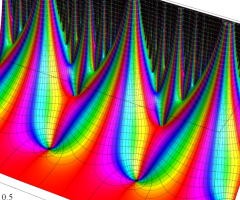
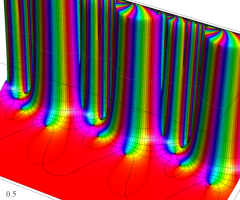
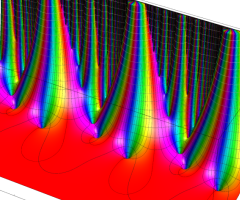
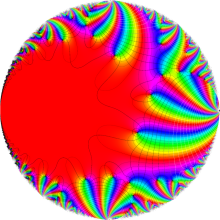
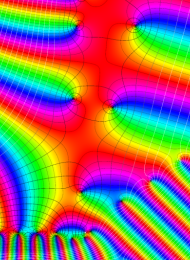
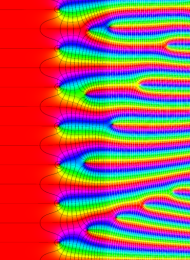
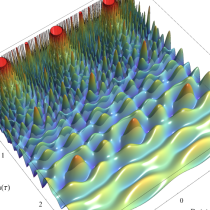
楕円モジュラー・ラムダ関数の基本領域が、円弧多角形であることを示したグラフ。
なお、このときの円弧三角形は、双曲型非 Euclid 平面上の 「理想三角形」 と呼ばれる (3個の内角がすべて0°で、3辺の双曲的距離がすべて
楕円モジュラー・ラムダ関数の基本領域は、Klein の楕円モジュラー関数のそれの6倍に一致する。
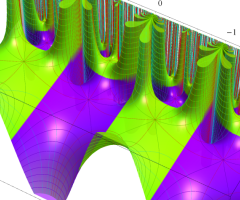
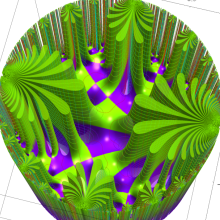
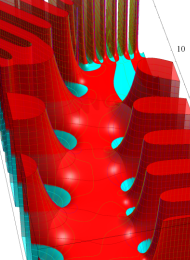
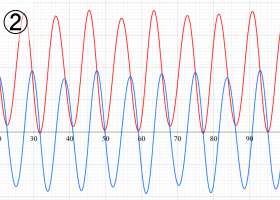
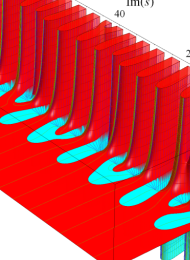
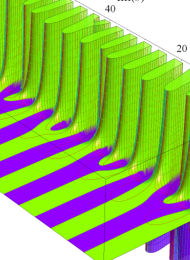
アニメーション(① 14.0MB, ② 15.4MB)
複素変数の楕円モジュラー・ラムダ関数のグラフ。連続的に基本領域間を移り変わる様子。①
【 Petite Galerie 】
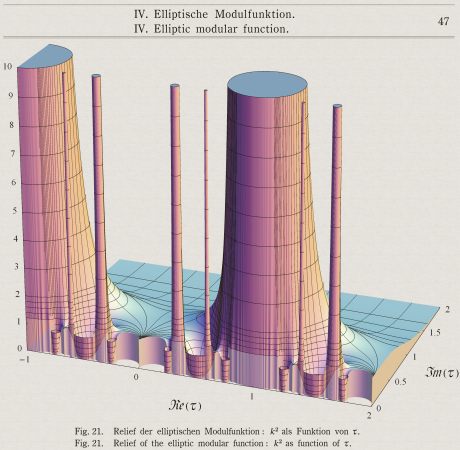
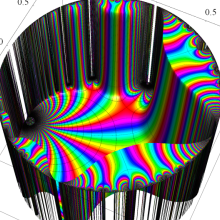
Jahnke & Emde 著 「Funktionentafeln…」 の47頁にある楕円モジュラー・ラムダ関数の図を再現。
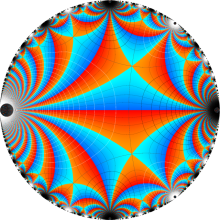
正多面体方程式に附随する楕円モジュラー関数
【正多面体方程式】Klein によって理論が構築された正20面体の場合を例に、正多面体方程式の概要を説明する。
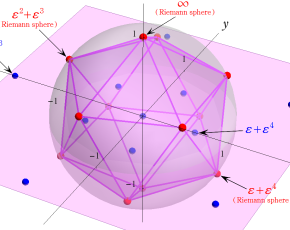
正20面体の中心を原点に置き、かつ頂点を下図のように置いて固定する。Riemann 球面上の無限遠点から複素平面上へ正20面体の像を射影し、20個の面の中点、30個の辺の中点、12個の頂点に対応する複素平面上の座標値を全て求める。
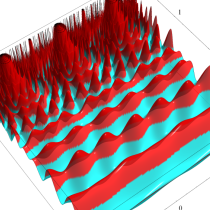
図:Riemann 球面に内接し、頂点の位置を固定した正20面体。
3本の多項式
は、前述の複素座標値を根に持つ (ただし、無限遠点にある根を
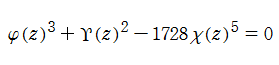
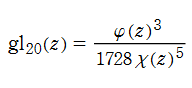
で互いに対応している。
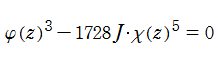
【正多面体方程式に附随する楕円モジュラー関数】
楕円モジュラー関数
を、「正多面体方程式に附随する楕円モジュラー関数」 と呼ぶ※1。これらの関数は、Galois 的有理関数と
の関係にある。例えば、前述の正20面体方程式で
正多面体方程式に附随する楕円モジュラー関数は、主合同部分群が作用する一次分数変換に対して不変で、それぞれ
を満たす。特に、一次分数変換の生成元となる変換に対しては、
となる (周期性および保型性)。
を持ち、これらの点を
【註記】
※1:この関数名称、並びに 以外の関数記号は、当サイトが独自に定めたものである。
以外の関数記号は、当サイトが独自に定めたものである。
これらの関数はあまり書籍等で見かけないが、例えば次の掲載事例がある。
① F. Klein 著, 関口次郎 訳 「正20面体と5次方程式:シュプリンガー数学クラシックス5 (旧版-1997年)」 p.146~147: と
と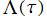
② A. Erdelyi,W. Magnus,F. Oberhettinger,F. G. Tricomi 著 「Higher Transcendental Functions (Vol.Ⅲ )」 p.24: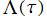 のみ
のみ
ただし、①に掲載されている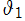 を用いた
を用いた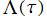 の表示式は誤っている可能性がある。手計算および (無限級数表示式, Galois 的有理関数との一致, 保型性を確認する) 数値検証によれば、次の表示式が得られる。
の表示式は誤っている可能性がある。手計算および (無限級数表示式, Galois 的有理関数との一致, 保型性を確認する) 数値検証によれば、次の表示式が得られる。
※1:この関数名称、並びに
これらの関数はあまり書籍等で見かけないが、例えば次の掲載事例がある。
① F. Klein 著, 関口次郎 訳 「正20面体と5次方程式:シュプリンガー数学クラシックス5 (旧版-1997年)」 p.146~147:
② A. Erdelyi,W. Magnus,F. Oberhettinger,F. G. Tricomi 著 「Higher Transcendental Functions (Vol.Ⅲ )」 p.24:
ただし、①に掲載されている
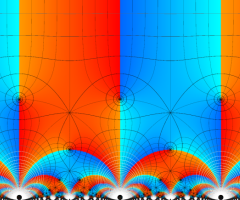
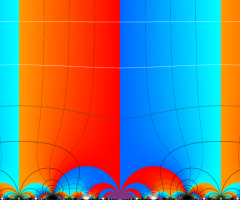
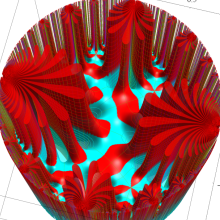
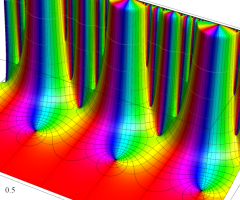
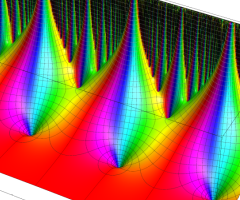
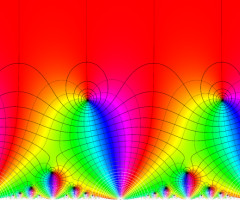
楕円モジュラー関数
楕円モジュラー関数
楕円モジュラー関数
エータ積による楕円モジュラー関数
ここでは、Dedekind のエータ関数の積 (「エータ積」と呼ばれる) の商として表わされる楕円モジュラー関数の例を取り上げる。【Conway - Norton の楕円モジュラー関数】
前に、モンスター群と Klein の楕円モジュラー関数とを結び付けるモンストラス・ムーンシャインに触れたが 、他の有限群に対しても、類似の現象 (単に 「ムーンシャイン」 と呼ばれ、これに有限群の名を冠することが多い) で結び付く保型関数の例が知られている。
J. H. Conway と S. P. Norton が例示したエータ積で表わされる171種類の保型関数も、モンスター群の部分群に対するムーンシャインを持つことが証明されている (1992年 R. E. Borcherds による)。
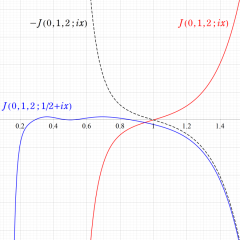
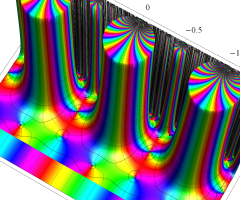
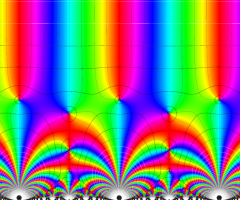
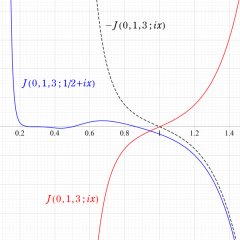
171種類の Conway - Norton の楕円モジュラー関数のうち、比較的簡単な例を列挙すれば、
となり、当サイトでは上記のみを取り上げる。ただし、これらの関数が持つ具体的なムーンシャインは複雑なので触れない。また、背景となる理論の説明も (大変難しいので) 行わない。詳細は、原田耕一郎 著 「モンスター:群のひろがり」 等を参照して欲しい。(関数記号
前掲の Conway - Norton の楕円モジュラー関数は、合同部分群
を満たす。特に、一次分数変換の生成元となる変換に対しては、
となる (周期性および保型性)。
Conway - Norton の楕円モジュラー関数のうち、いくつかは他の保型関数によって表わすことができる。例えば、数論的保型関数並びに Schwarz の保型関数 (の特殊な場合)、楕円モジュラー・ラムダ関数によって
となる (このうち
と表わせるが、
【Weber の楕円モジュラー関数】
H. M. Weber (1898年) によって導入された保型関数
を、Weber の楕円モジュラー関数という※1。モジュラー群が作用する一次分数変換の生成元に対して、
となるので、ここから周期性と保型性
も導かれる。
Weber の楕円モジュラー関数は、興味深い相互関係式
を満たす。
Weber の楕円モジュラー関数は、代数的整数論、間接的ではあるが特定のムーンシャイン現象に応用される。
【註記】
※1:当サイトでは、記号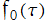 を使用したが、本来は付番なしの
を使用したが、本来は付番なしの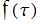 で表記される。
で表記される。
なお、この Weber は、Anger - Weber 関数, 放物柱関数を研究した H. F. Weber とは別人である。
※1:当サイトでは、記号
なお、この Weber は、Anger - Weber 関数, 放物柱関数を研究した H. F. Weber とは別人である。
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Conway - Norton の楕円モジュラー関数
Weber の楕円モジュラー関数
Weber の楕円モジュラー関数
Weber の楕円モジュラー関数
一般の楕円モジュラー関数
【保型形式としてのWeierstrass の楕円関数 (
となるのであった (当該頁からの再掲)。よって
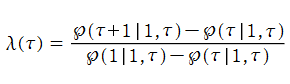
【一般の楕円モジュラー関数】
主合同部分群
とで生成される (この意味から、当サイトでは
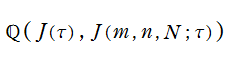
当サイトでは
となる。したがって、最左辺にある7種類の関数のみグラフを掲載する。
上記7種類の関数は、不変となる一次分数変換の生成元に対して、周期性および保型性
を満たす。
【註記】
※1:これは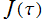 と
と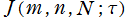 の代数関数になるが、それを具体的に導出するのは簡単ではない。例が、清水英男 著 「保型関数 (岩波書店 1992年)」 の149~151頁にある。また、代数関数で結ばれているがゆえ、単純に描画しただけのグラフでは分枝切断線が生じ、解析接続が必要になる。よって、そのような構成例を当サイトでは一切掲載していない。
の代数関数になるが、それを具体的に導出するのは簡単ではない。例が、清水英男 著 「保型関数 (岩波書店 1992年)」 の149~151頁にある。また、代数関数で結ばれているがゆえ、単純に描画しただけのグラフでは分枝切断線が生じ、解析接続が必要になる。よって、そのような構成例を当サイトでは一切掲載していない。
※2:体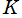 の 「拡大」 とは、
の 「拡大」 とは、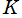 を部分体として含む大きな体 (拡大体)
を部分体として含む大きな体 (拡大体)  を作ることである。例えば、上記の虚二次体
を作ることである。例えば、上記の虚二次体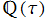 自体も、有理数体
自体も、有理数体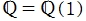 から見れば拡大体である。
から見れば拡大体である。
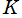 の元を係数とするある代数方程式 (多項式) を定め、そのすべての根を用いて
の元を係数とするある代数方程式 (多項式) を定め、そのすべての根を用いて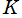 から
から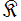 が作られる拡大を 「Galois 拡大」 と言い、そのうち、
が作られる拡大を 「Galois 拡大」 と言い、そのうち、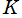 の元を動かさない
の元を動かさない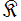 から
から への自己同型写像が成す群 (Galois 群) が可換群になっている場合を特に 「Abel 拡大」 と言う。
への自己同型写像が成す群 (Galois 群) が可換群になっている場合を特に 「Abel 拡大」 と言う。
※1:これは
※2:体
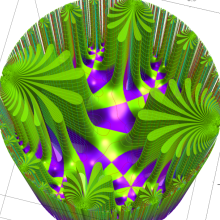
一般楕円モジュラー関数
一般楕円モジュラー関数
一般楕円モジュラー関数
一般楕円モジュラー関数
一般楕円モジュラー関数
一般楕円モジュラー関数
一般楕円モジュラー関数
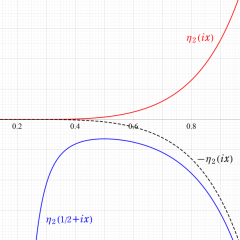
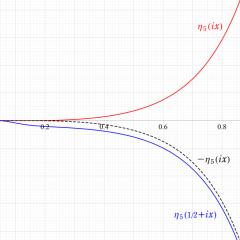
Dedekind のエータ関数
日:Dedekindのエータ関数,デーデキントのη関数英:Dedekind eta function,仏:Fonction êta de Dedekind,独:Dedekindsche η-funktion
保型関数を楕円関数の母数から構築する当時の定番となっていた方法を改め、モジュラー群の作用による不変性を持つ (今日で言うところの)
大抵の場合、Dedekind のエータ関数は無限乗積
で定義され、それは上記のとおりテータ零値や q-シフト因子によっても表現できる※2。
Dedekind のエータ関数は、モジュラー群が作用する一次分数変換の生成元となる変換に対して、
を満たす (擬周期性および擬保型性) ので、正確には楕円モジュラー形式ではないが、広義として重み 1/2 の楕円モジュラー形式に含めることが多い。実際、この重みの小さいことが他の楕円モジュラー形式を表わすときに好都合となる。
モジュラー群が作用する一次分数変換すべてに対しては、
となり、やや複雑である。しかし、ここに現れる24乗根因子
Dedekind のエータ関数は、
なる値をとる。また、Dedekind のエータ関数は
前述のとおり、種々の楕円モジュラー関数・楕円モジュラー形式は、Dedekind のエータ関数で表わすことができる。例えば、
等が知られている。この他、Eichler のL関数と関係する尖点形式
は、前々節で触れたエータ積の例になっており、合同部分群
を満たす。
この
と展開される。もっと有名な事例を挙げれば、等式
の第2辺と第3辺を結ぶ 「Euler の五角数定理」※3、および分割数を係数で与える母関数の
がある。分割数
Dedekind のエータ関数の導関数は、
となる。
また、Dedekind のエータ関数は Kronecker の極限公式にも現れる。詳細は実解析的 Eisenstein 級数を参照。
【註記】
※1:楕円モジュラー関数 (Elliptische Modulfunktion) なる名称は、このとき Dedekind が使い始め、以後定着した。
※2:当サイトでは、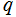 を変数とする場合を
を変数とする場合を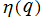 と略記するが、本来は
と略記するが、本来は
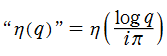
の意味であるとする。以降、Eisenstein 級数等の保型形式も同様である。
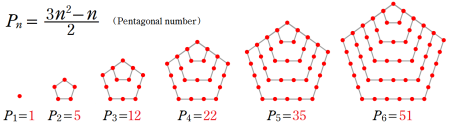
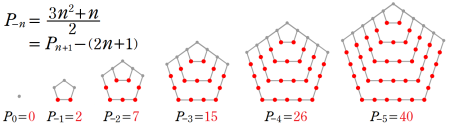
※3:五角数とは、次のように並べられた点の個数である。
五角数定理ではインデックスが負数になる項も含まれる。そのときの五角数は、次の図のように解釈される。
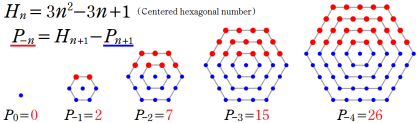
なお、五角数は 「中心付き六角数」 と関係がある。
このような点の並びで表わされる自然数は、「多角数」, 「図形数」 と称され、既に古代ギリシャ時代から研究されていた。
※4:例えば、
となっている。
※1:楕円モジュラー関数 (Elliptische Modulfunktion) なる名称は、このとき Dedekind が使い始め、以後定着した。
※2:当サイトでは、
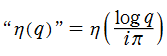
※3:五角数とは、次のように並べられた点の個数である。
五角数定理ではインデックスが負数になる項も含まれる。そのときの五角数は、次の図のように解釈される。
なお、五角数は 「中心付き六角数」 と関係がある。
このような点の並びで表わされる自然数は、「多角数」, 「図形数」 と称され、既に古代ギリシャ時代から研究されていた。
※4:例えば、
となっている。
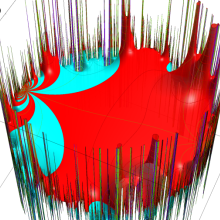
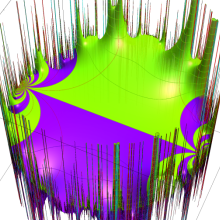
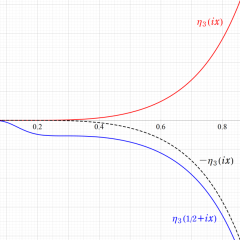
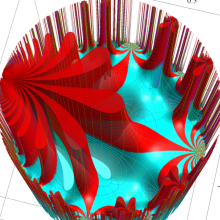
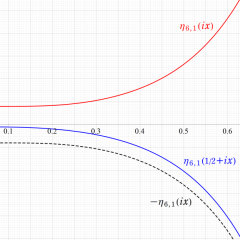
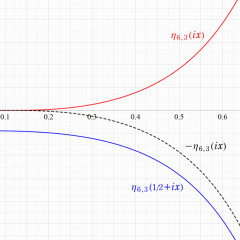
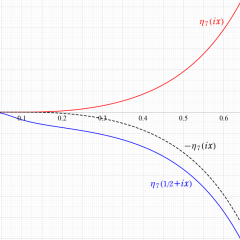
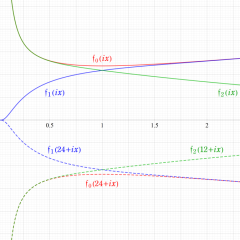
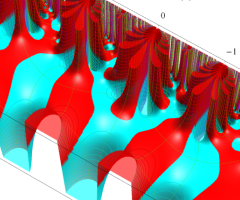
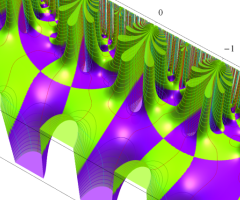
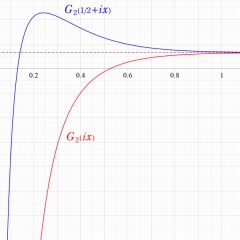
2番目は、値域を逆双曲線正弦目盛にした場合である。
2番目は、値域を逆双曲線正弦目盛にした場合である。
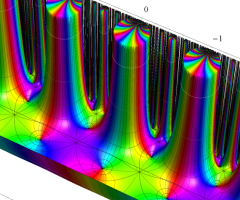
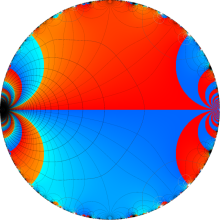
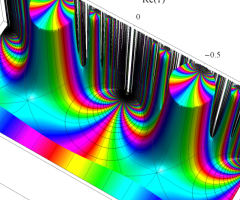
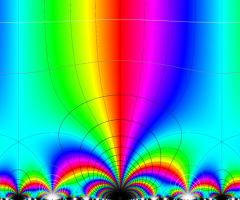
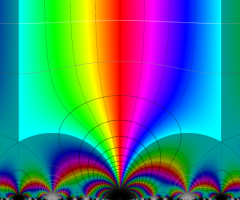
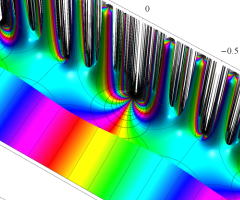
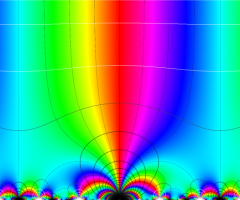
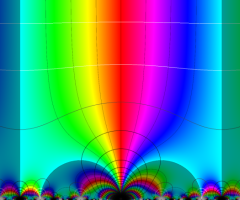
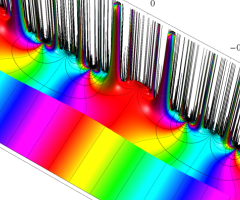
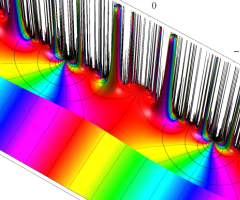
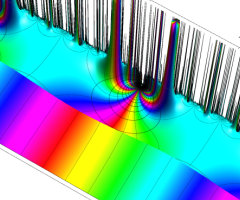
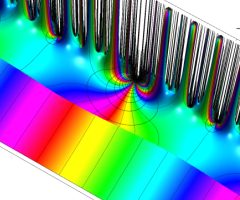
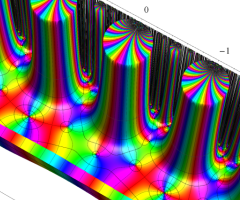
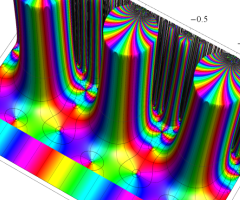
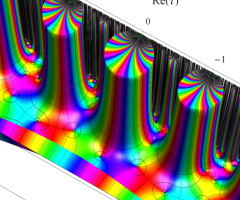
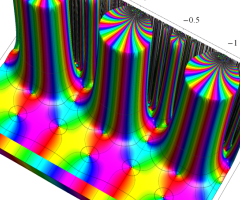
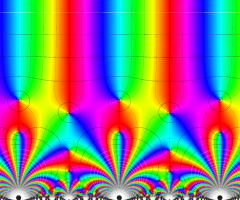
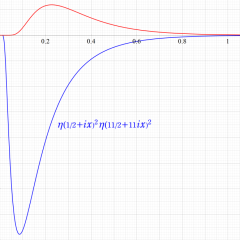
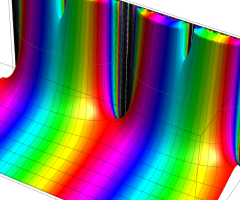
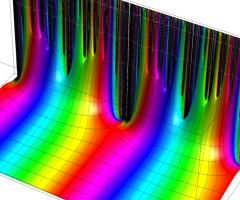
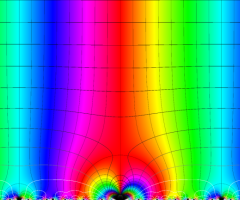
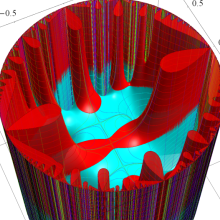
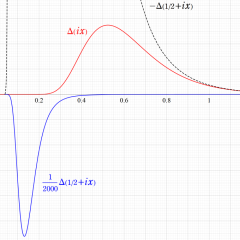
Dedekind のエータ関数がモジュラー変換を受けたときに生じる24乗根因子
(Klein の楕円モジュラー関数上で変換を表現し、彩色は
楕円モジュラー形式 (不変量・判別式)
日:楕円モジュラー形式,モジュラー形式英:Modular form,仏:Forme modulaire,独:Modulform
ここで扱う楕円モジュラー形式は、楕円関数論で定数として現れるが、
【不変量 ― 楕円モジュラー形式の基本例】
Weierstrass の楕円関数を、原点中心に Laurent 級数展開すると、
となる※1。このとき、すべての係数は
と置けば、
で表わされる。
を持つので、
が得られる。この導出過程と不変式論に由来して、
不変量は、モジュラー群が作用する一次分数変換に対して、
を満たす。特に、その一次分数変換の生成元となる変換に対しては、
となる (周期性および擬保型性)。
不変量は、
なる値をとる。一般に不変量の値は、テータ零値による表示式
等で求められる。
【判別式 ― 尖点形式の基本例】
Weierstrass の楕円関数とその導関数とでパラメータ表示される代数方程式 (楕円曲線)
の判別式、およびその斉次性
によって、同様に楕円モジュラー形式
が得られる。このことから、
判別式は、モジュラー群が作用する一次分数変換に対して、
を満たす。特に、その一次分数変換の生成元となる変換に対しては、
となる (周期性および擬保型性)。
判別式は、
なる値をとる。
Dedekind のエータ関数との関係から、判別式は無限乗積
に展開される。この式は、理論と数値計算の双方で扱い易く、都合が良い。
判別式は
に展開され、
Fourier 係数
は、比較的簡単な (しかし数値計算には向かない) 例である。また、合同関係式
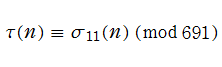
【註記】
※1:![Ω[m, n]](siki_spec110/modular26000.png) を
を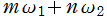 で表示する書籍等も多い。当然、その場合の関連する公式は、当サイトに掲示しているそれとは若干異なる形になる。
で表示する書籍等も多い。当然、その場合の関連する公式は、当サイトに掲示しているそれとは若干異なる形になる。
※2:したがって、 (k≠2, 3)](siki_spec110/modular26200.png) のグラフは掲載せず、これに相当する Eisenstein 級数のグラフで掲載する。
のグラフは掲載せず、これに相当する Eisenstein 級数のグラフで掲載する。
※1:
※2:したがって、
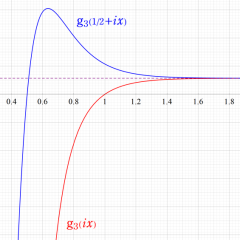
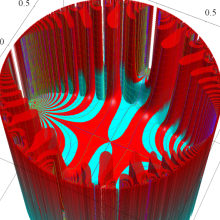
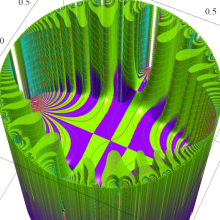
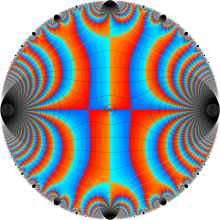
Eisenstein 級数
日:Eisenstein級数,アイゼンシュタイン級数英:Eisenstein series,仏:Série d'Eisenstein,独:Eisensteinreihe
現在では Weierstrass 流として知られる楕円関数論と同様の理論を、K. T. W. Weierstrass より約15年早く展開した F. G. M. Eisenstein の名に因み、既に前節で現れていた分数級数
は、「Eisenstein 級数」 と呼ばれる。時折、総和がわたる格子の二整係数を、互いに素であるものに限定した、
で定義されることもあるが、両者は全く同じ関数である※1。
Eisenstein 級数は、楕円モジュラー形式の典型的な例であって、モジュラー群が作用する一次分数変換に対して、
を満たす。特に、その一次分数変換の生成元となる変換に対しては、
となる (周期性および擬保型性)※2。
Eisenstein 級数は、Fourier 級数
に展開される (この Fourier 級数展開式を、Eisenstein 級数と呼ぶことも多い)。しばしば、その定数項が1になるよう全体を定数倍した 「正規化 Eisenstein 級数」
が代わりに定義される。
NISTにある公式:27.7.5を用いると、Fourier 級数展開式から直ちに Lambert 級数展開式
が得られる。Fourier 級数および Lambert 級数展開式は、理論展開および
重みが一般的な場合のうち、最も注目される例が、
であり、モジュラー群が作用する一次分数変換に対して、
を満たす。特に、その一次分数変換の生成元となる変換に対しては、
となる※3。この
また、
等が知られている※4。このうち1番目と3番目の式を援用すれば、Klein の楕円モジュラー関数の導関数は、
となることが導かれる。
ある種の Dirichlet 級数は、重み
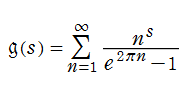
と表わされる。
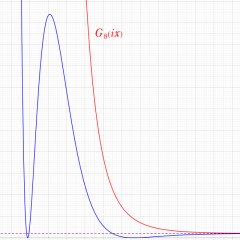
Glaisher - Ramanujan 関数は、特殊値
を持つ。後者は S. Ramanujan によって得られた。
Glaisher - Ramanujan 関数は、複素
となる。
【註記】
※1:下図を参照。青い半直線上にある格子点で部分和を取ったのち、それらを総和すれば第2の級数表示式が得られる。すなわち、Riemann ゼータ関数の共通因子が括り出せる。
※2:この関数等式は、分数級数から容易に導くことができる。例えば、擬保型性は (重み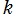 が4以上の偶数であるがゆえ)、
が4以上の偶数であるがゆえ)、
となる。
※3:重み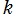 が正の偶数でない場合の
が正の偶数でない場合の](siki_spec110/modular24400.png) が満たす関数等式は、(恐らく何らかの研究結果があると思われるが) 当サイト管理人が調査した限りでは不明である。今後、判明すれば記事を追加する予定である。
が満たす関数等式は、(恐らく何らかの研究結果があると思われるが) 当サイト管理人が調査した限りでは不明である。今後、判明すれば記事を追加する予定である。
※4:導関数の公式のうち、2~3番目を Fourier 級数で表現して係数比較すれば、約数関数の恒等式
が得られる。
※1:下図を参照。青い半直線上にある格子点で部分和を取ったのち、それらを総和すれば第2の級数表示式が得られる。すなわち、Riemann ゼータ関数の共通因子が括り出せる。
※2:この関数等式は、分数級数から容易に導くことができる。例えば、擬保型性は (重み
となる。
※3:重み
※4:導関数の公式のうち、2~3番目を Fourier 級数で表現して係数比較すれば、約数関数の恒等式
が得られる。
アニメーション(9.88MB)
アニメーション(6.08MB)
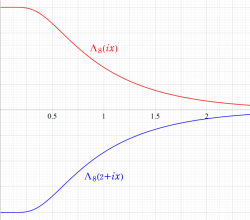
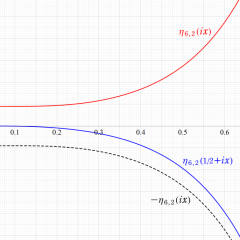
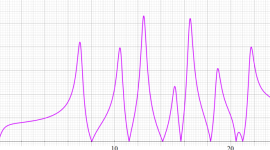
重み
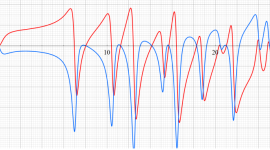
Glaisher - Ramanujan 関数
複素変数の Glaisher - Ramanujan 関数
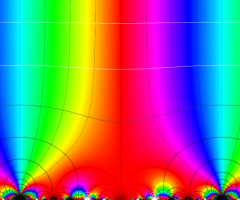
実解析的 Eisenstein 級数
日:実解析的Eisenstein級数,非正則アイゼンシュタイン級数英:Real analytic Eisenstein series,Non-holomorphic Eisenstein series,
仏:Série rélle analytique d'Eisenstein,独:Reel-analytisch Eisensteinreihe
上半平面
で定義される非正則な Eisenstein 級数である。これは、"
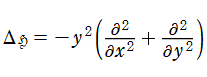
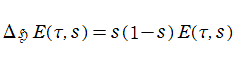
実解析的 Eisenstein 級数は、"
に展開される。これは、格子点をわたる無限級数よりも広い
を満たす。一方、
を満たし、ゼータ関数に類似している。ただし、
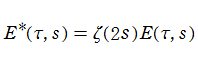
によっても表わされる。(Epstein のゼータ関数は、1903年に P. Epstein によって導入された。当サイトでは未掲載。)
「第1 Kronecker の極限公式」 とは※2、1位の極
のこと (通常は後者の方) を言う※3。
一般の特殊線形群
【註記】
※1:ただし、実解析的 Eisenstein 級数は、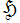 上の任意関数が正規固有関数展開されるときの級数項にではなく、積分変換項 (が必要となる特殊線形群の元のとき) の被積分関数に現れるという意味で、固有関数に相当する。固有値も連続変数
上の任意関数が正規固有関数展開されるときの級数項にではなく、積分変換項 (が必要となる特殊線形群の元のとき) の被積分関数に現れるという意味で、固有関数に相当する。固有値も連続変数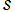 に対して定まる値なので、むしろ Fourier (積分) 変換の連続スペクトルに相当している。
に対して定まる値なので、むしろ Fourier (積分) 変換の連続スペクトルに相当している。
一方、級数項に現れる固有関数は Maass 波動形式と呼ばれ、その場合の固有値は離散的に分布する。
※2:当サイトでは、「第2 Kronecker の極限公式」 については説明しない。
※3:実は、前者の Kronecker 極限公式は当サイト管理人が求めた結果で見慣れない形になっている。そのため、導出過程 (特に、Glaisher - Kinkelin 定数が現れる理由) を独自研究の頁に掲載しています。
※1:ただし、実解析的 Eisenstein 級数は、
一方、級数項に現れる固有関数は Maass 波動形式と呼ばれ、その場合の固有値は離散的に分布する。
※2:当サイトでは、「第2 Kronecker の極限公式」 については説明しない。
※3:実は、前者の Kronecker 極限公式は当サイト管理人が求めた結果で見慣れない形になっている。そのため、導出過程 (特に、Glaisher - Kinkelin 定数が現れる理由) を独自研究の頁に掲載しています。
実解析的 Eisenstein 級数
アニメーション(12.80MB)