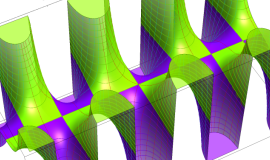
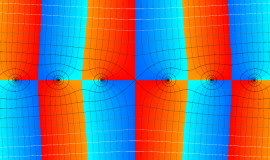
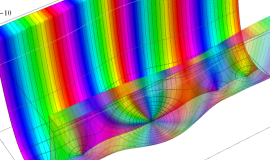
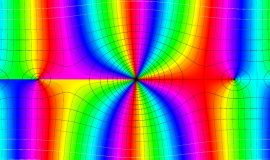
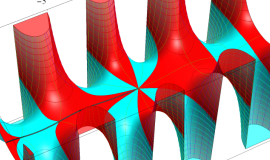
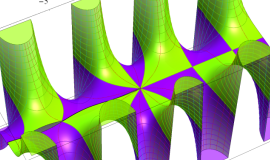
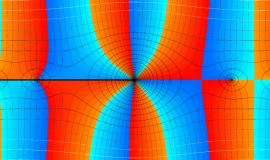
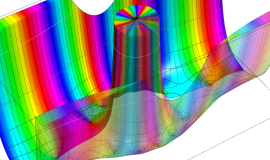
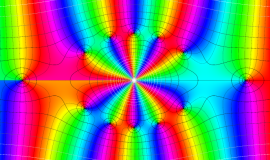
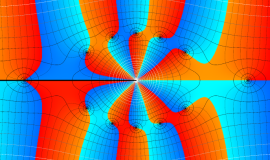
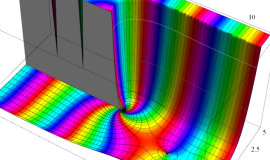
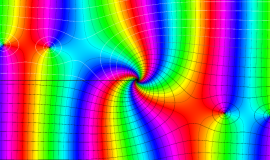
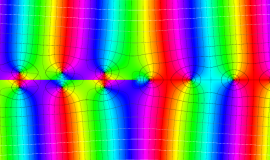
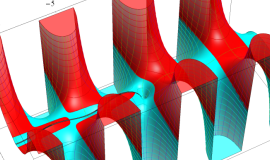
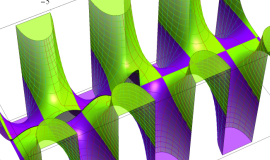
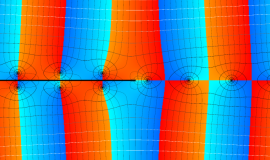
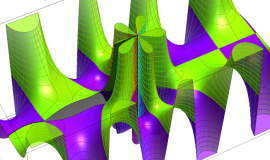
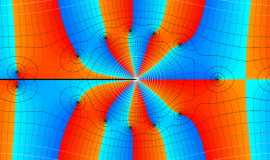
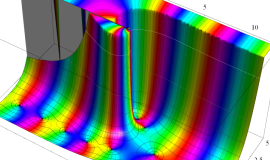
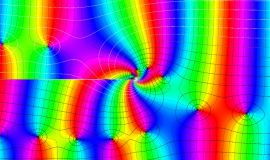
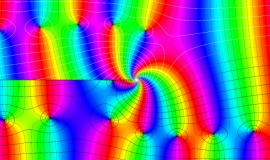
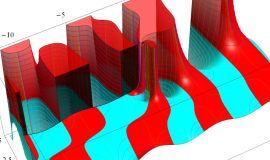
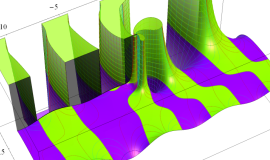
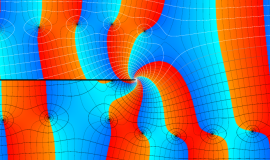
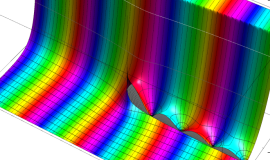
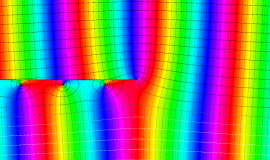
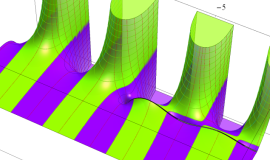
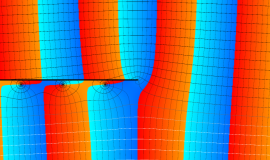
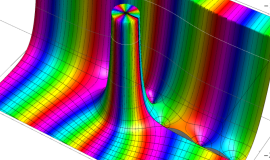
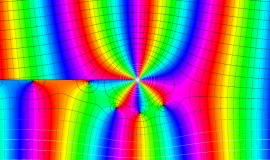
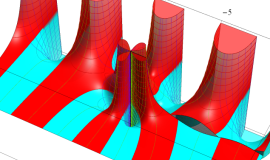
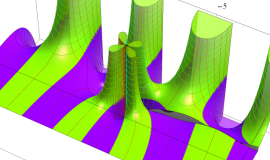
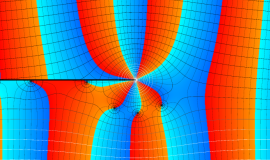
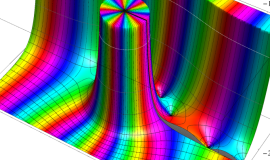
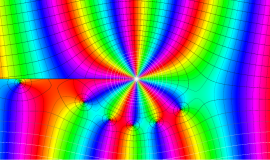
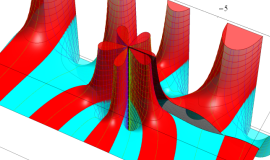
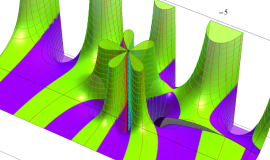
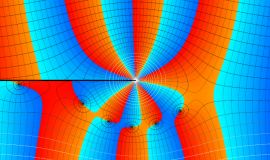
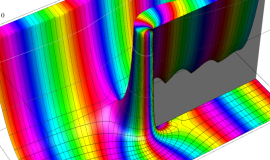
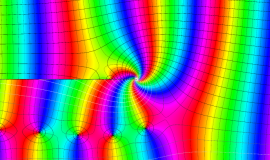
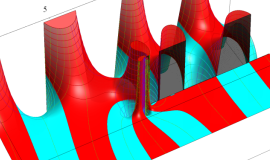
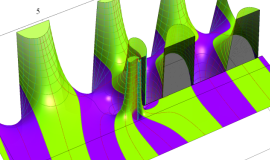
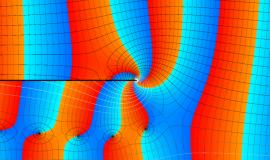
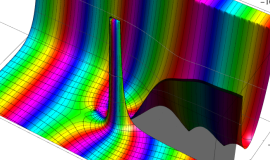
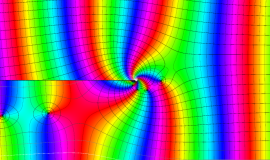
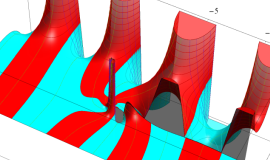
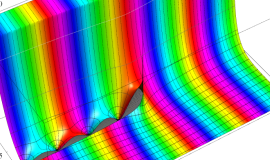
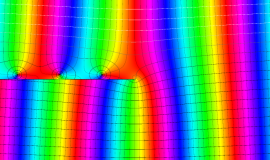
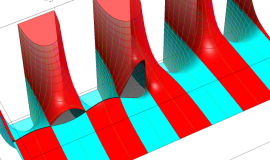
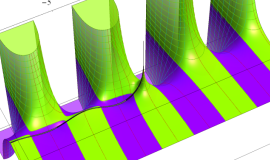
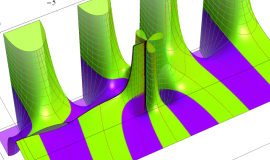
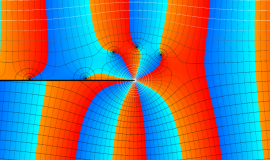
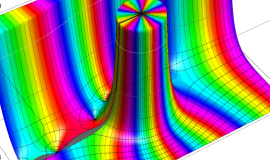
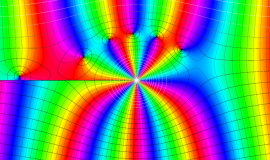
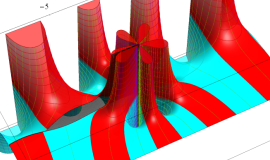
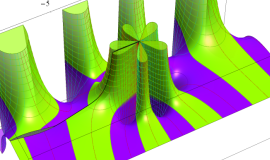
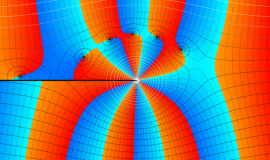
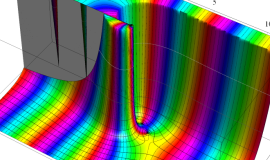
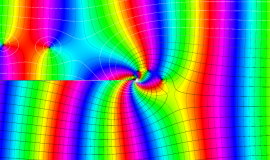
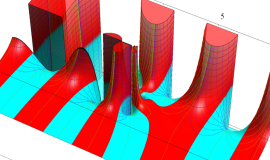
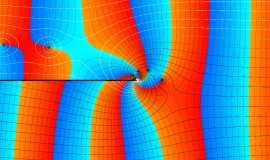
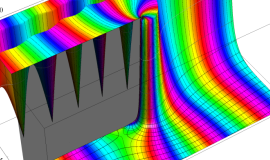
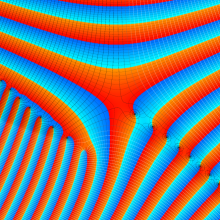
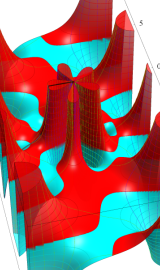
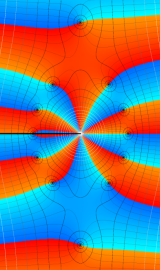
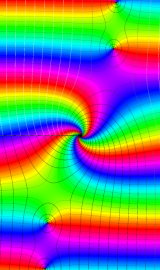
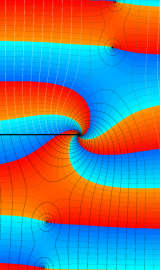
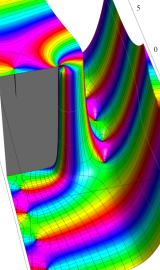
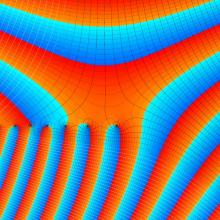
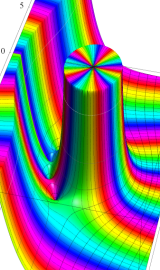
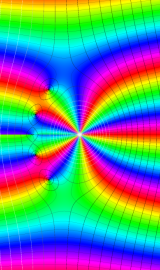
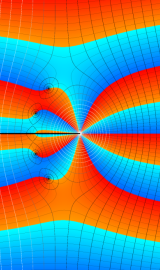
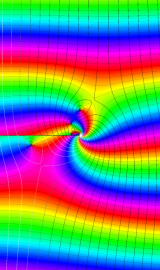
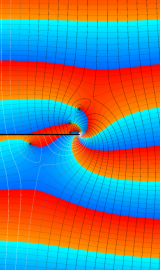
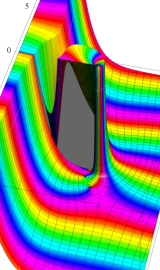
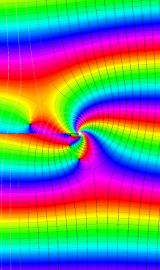
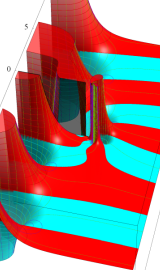
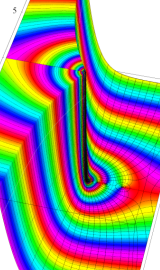
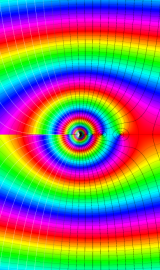
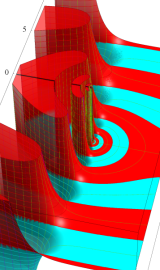
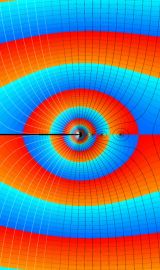
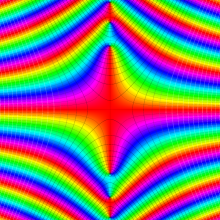
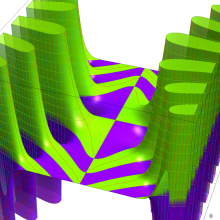
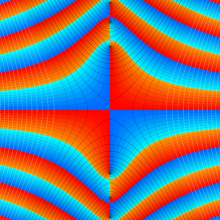
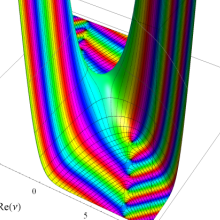
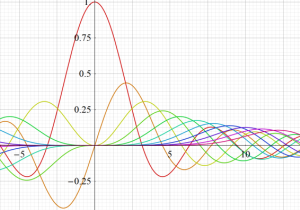
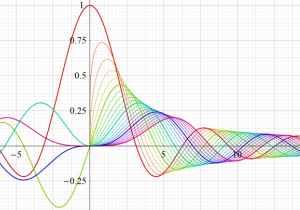
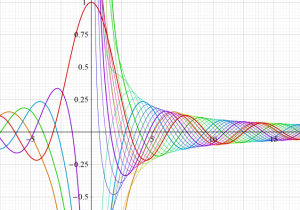
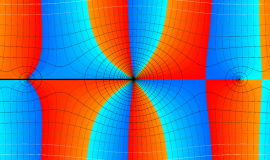
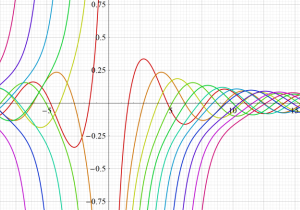
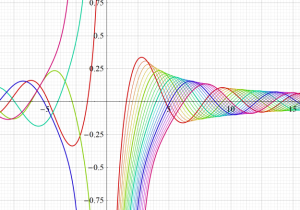
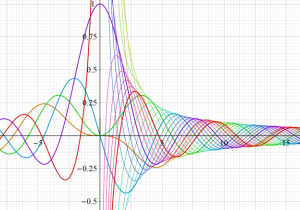
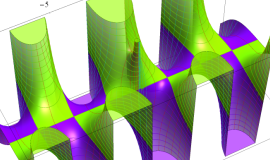
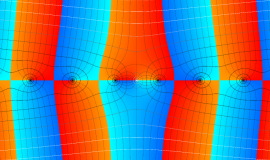
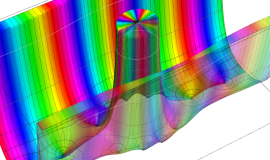
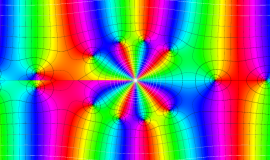
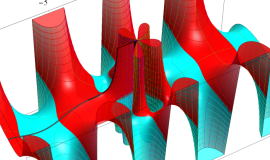
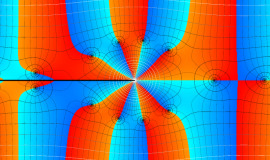
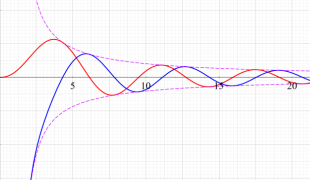
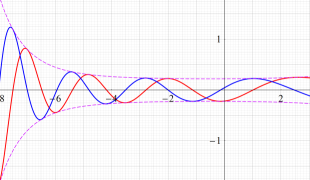
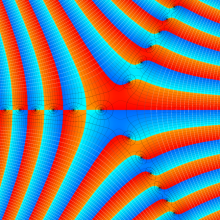
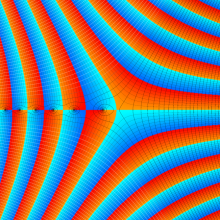
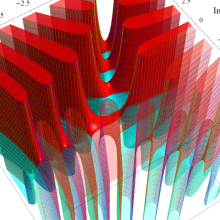
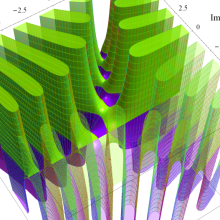
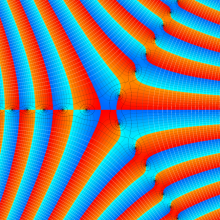
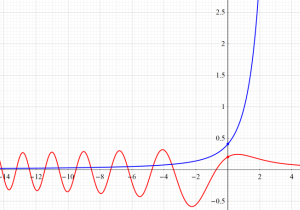
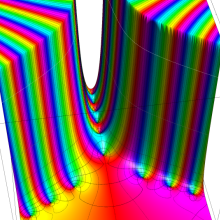
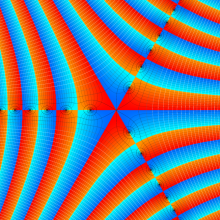
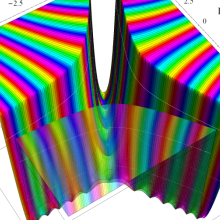
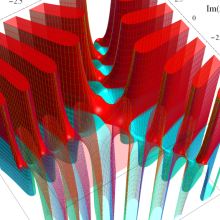
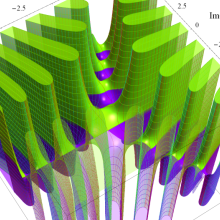
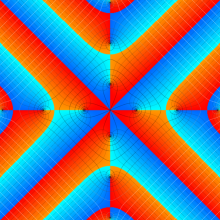
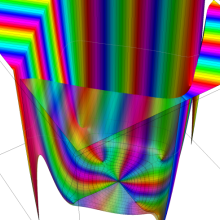
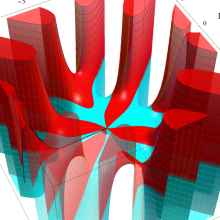
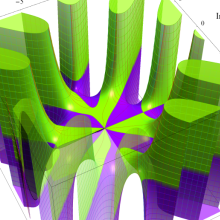
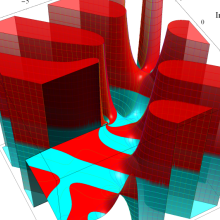
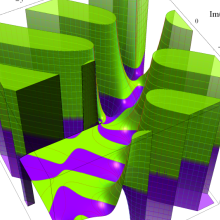
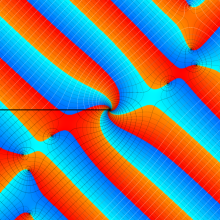
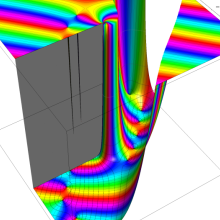
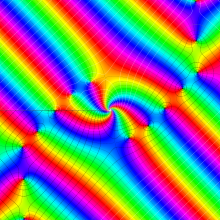
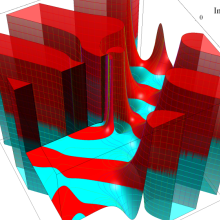
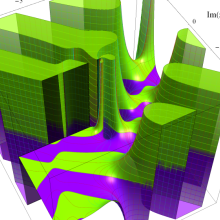
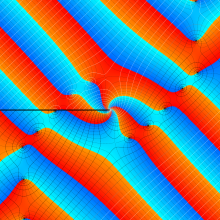
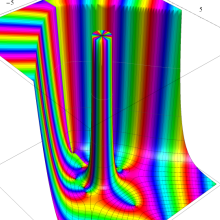
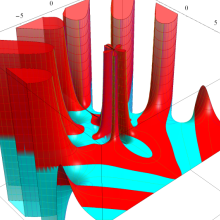
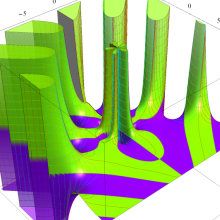
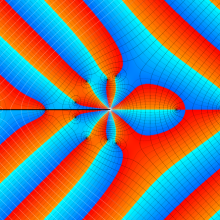
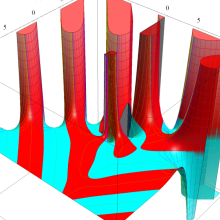
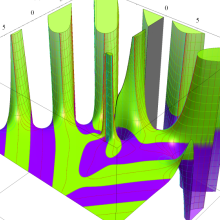
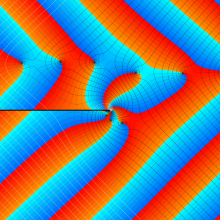
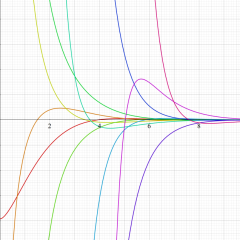
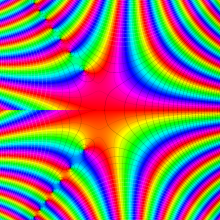
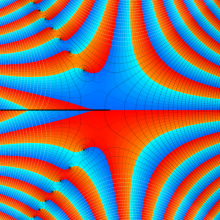
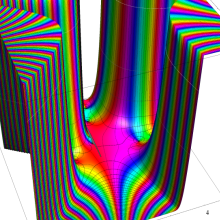
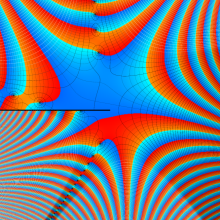
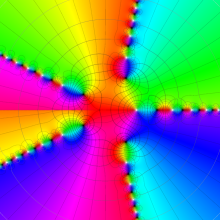
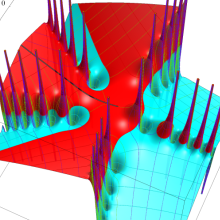
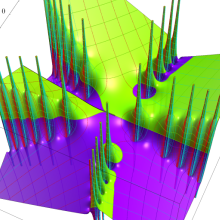
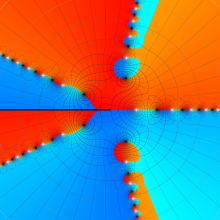
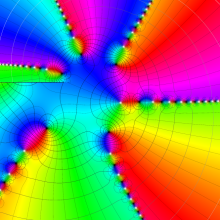
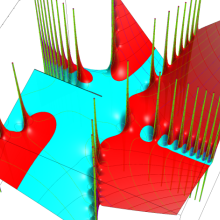
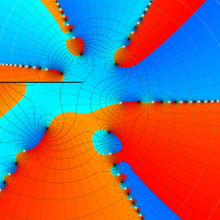
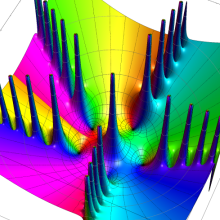
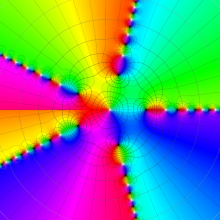
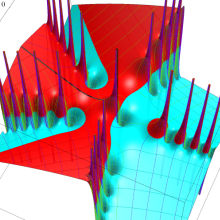
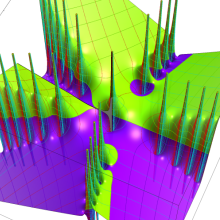
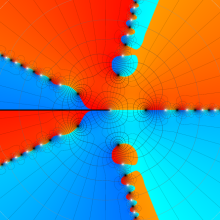
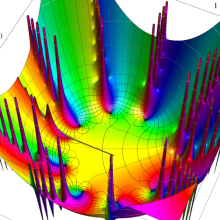
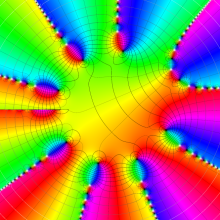
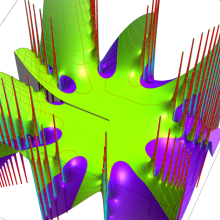
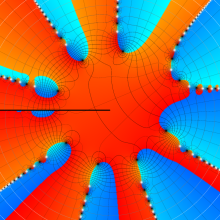
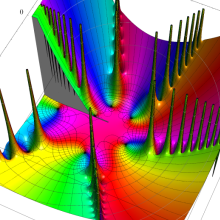
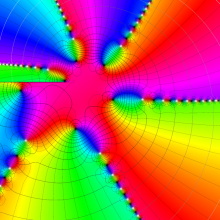
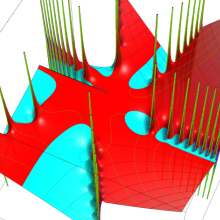
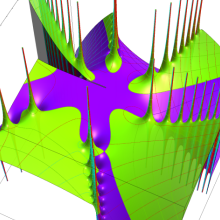
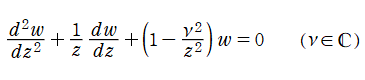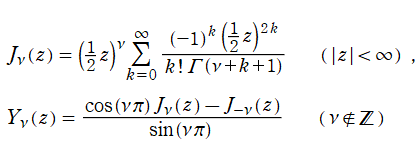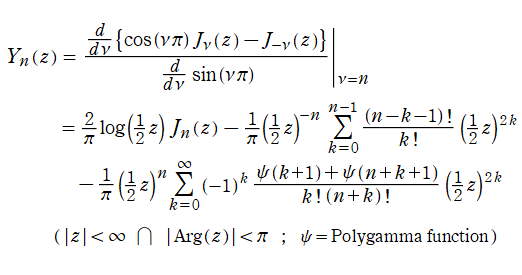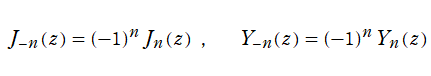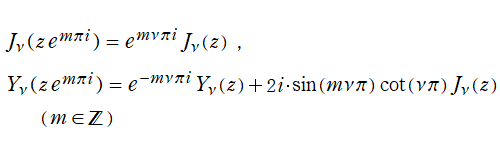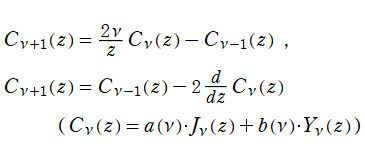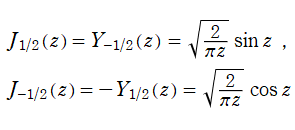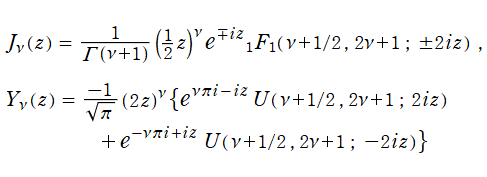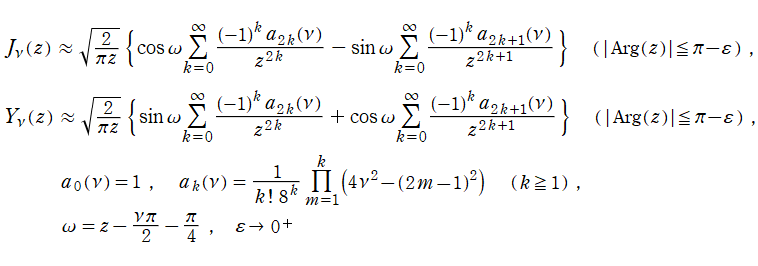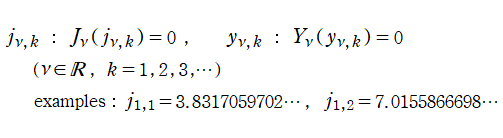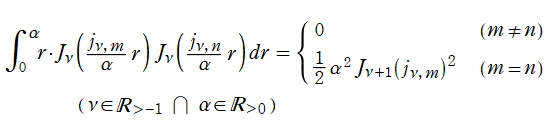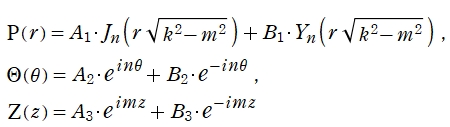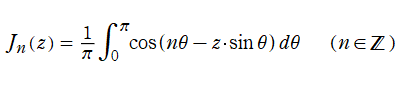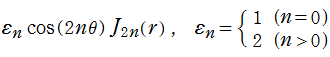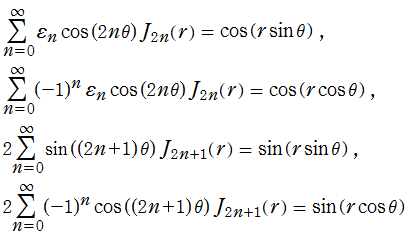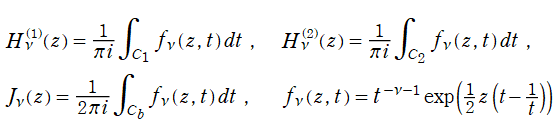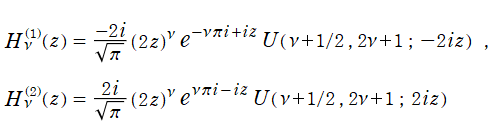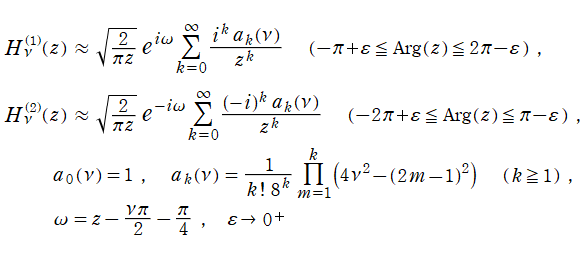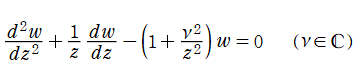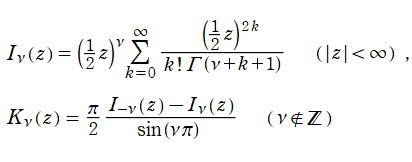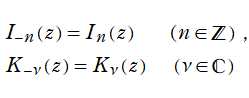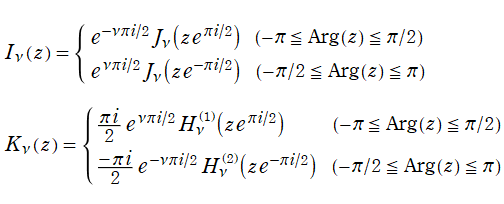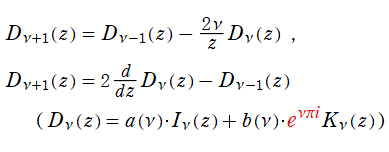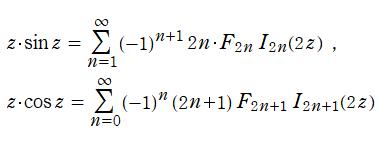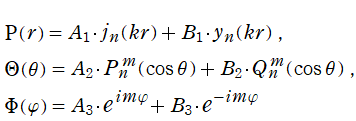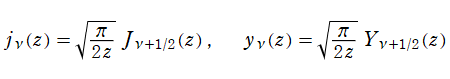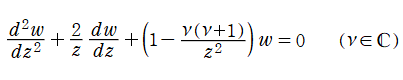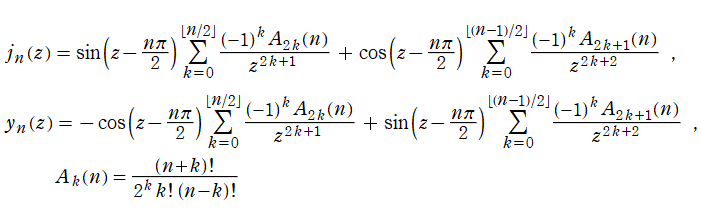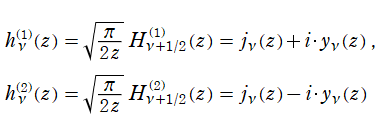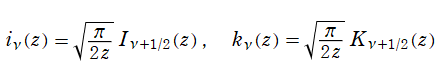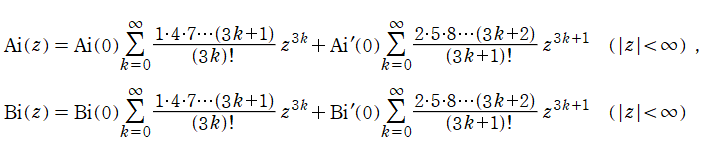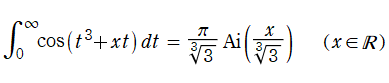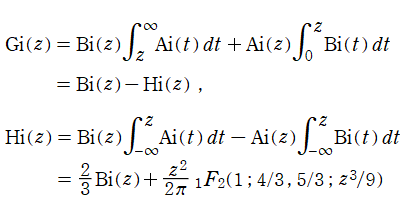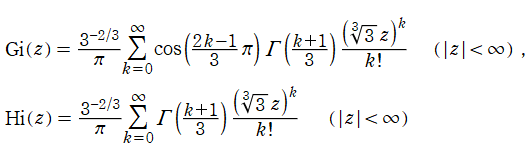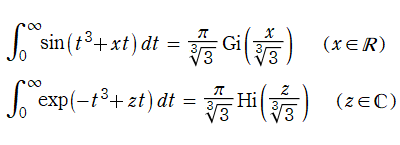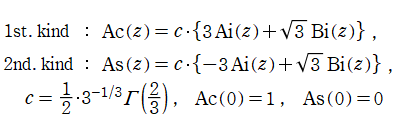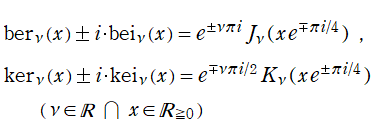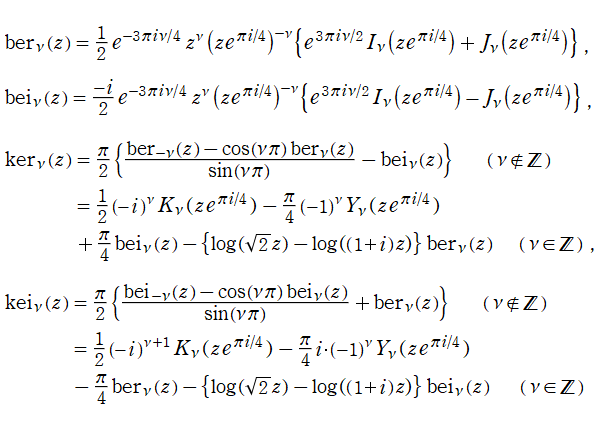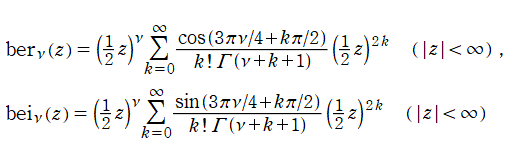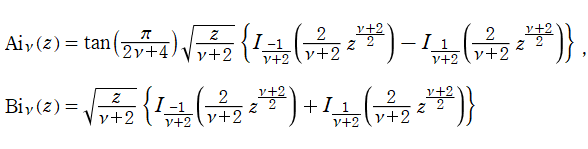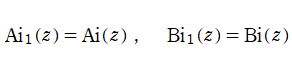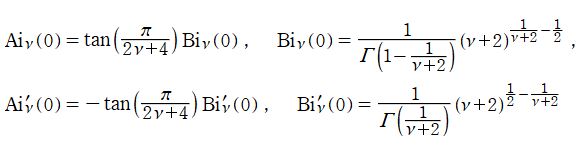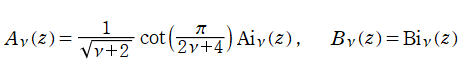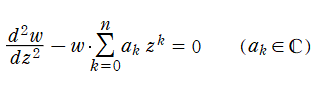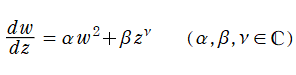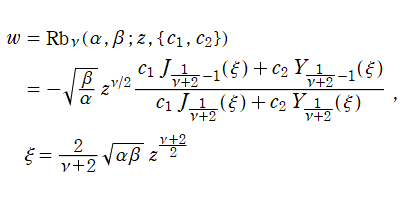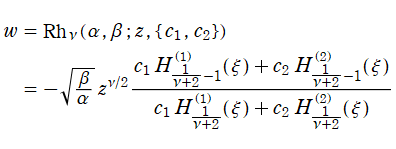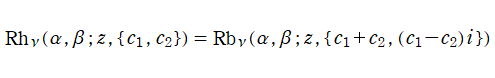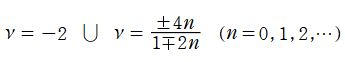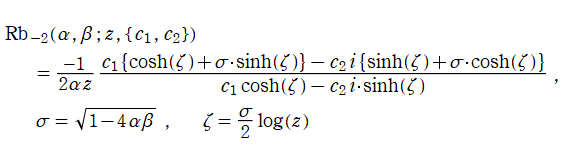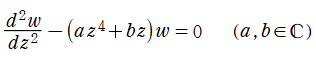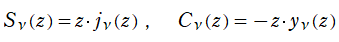特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
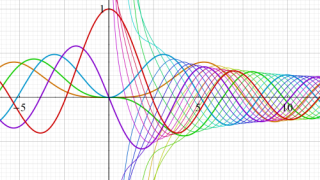
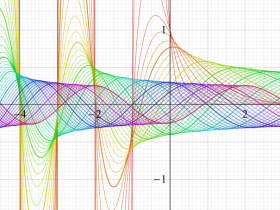
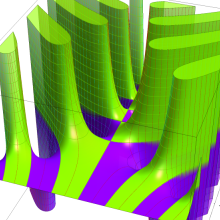
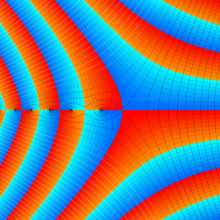
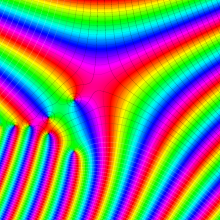
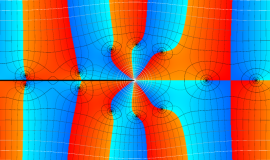
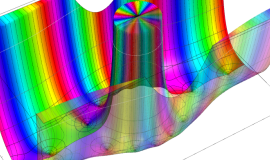
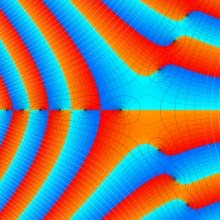
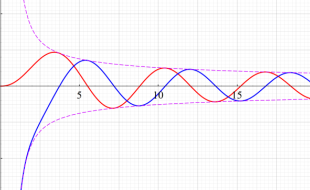
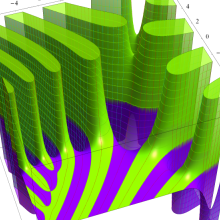
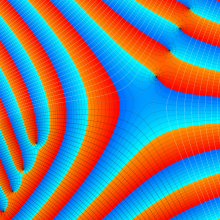
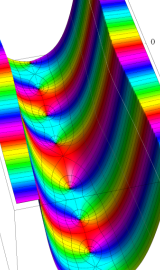
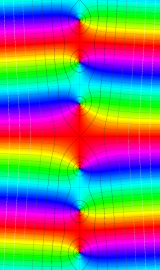
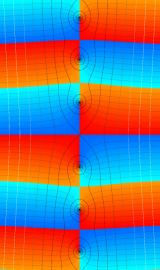
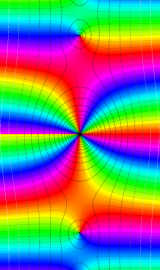
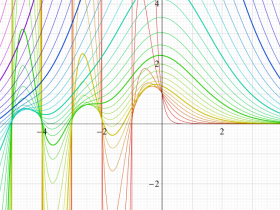
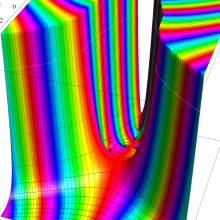
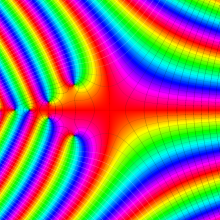
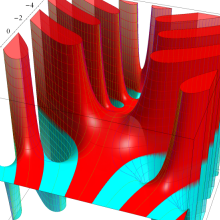
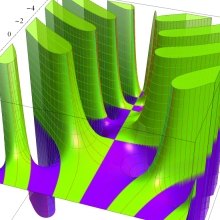
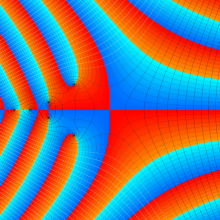
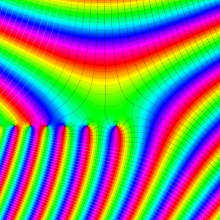
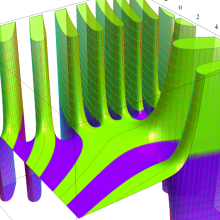
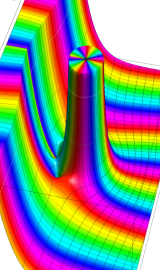
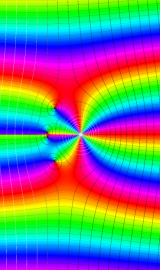
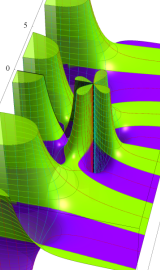
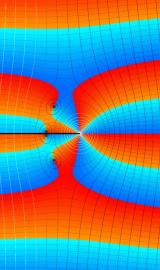
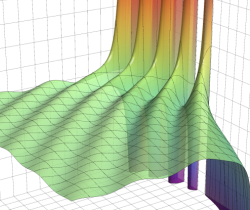
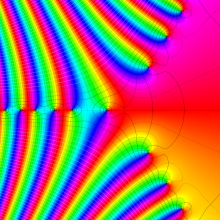
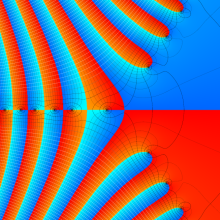
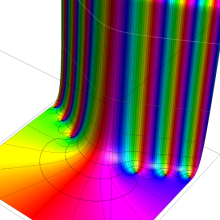
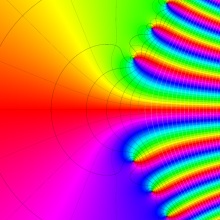
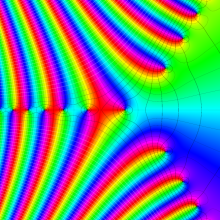
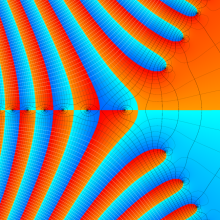
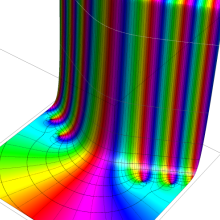
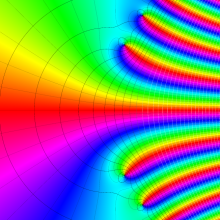
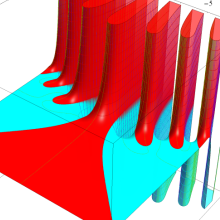
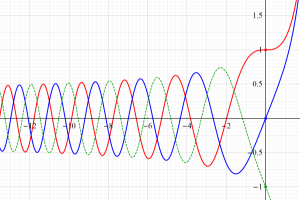
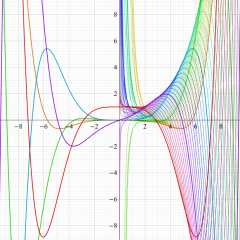
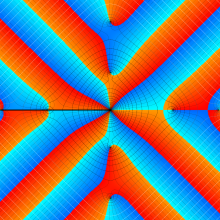
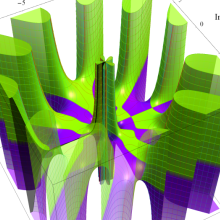
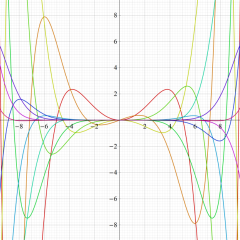
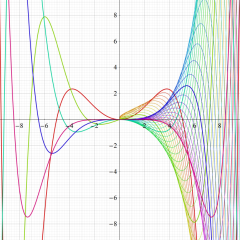
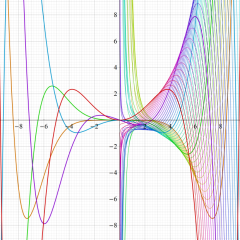
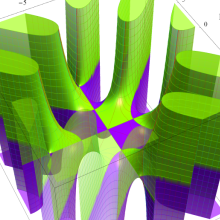
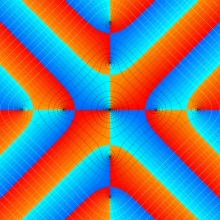
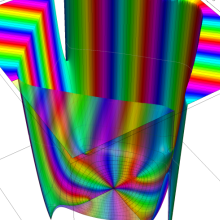
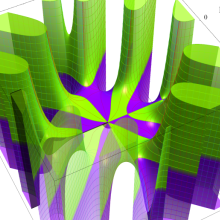
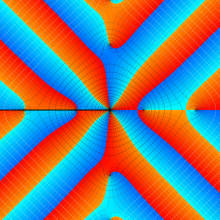
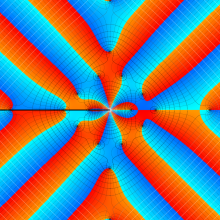
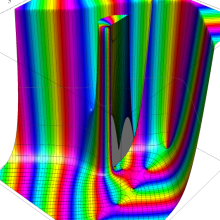
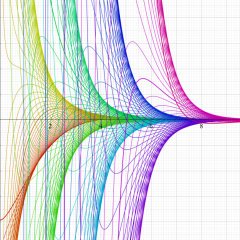
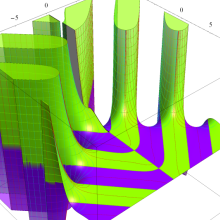
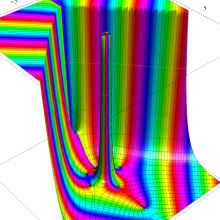
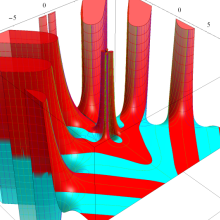
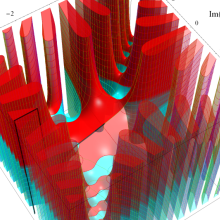
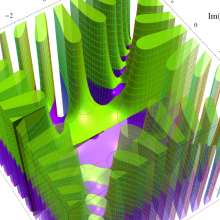
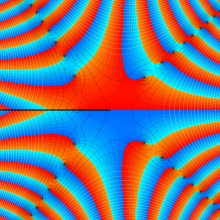
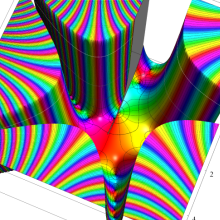
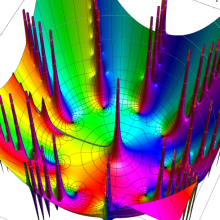
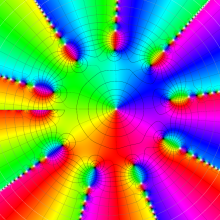
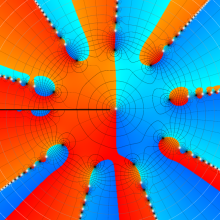
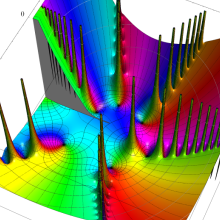
Bessel 関数
Bessel 関数
日:Bessel関数,ベッセル関数英:Bessel function,仏:Fonction de Bessel,独:Besselsche funktion
日:円柱関数
英:Cylinder function,仏:Fonction cylindrique,独:Zylinderfunktion
二階の線形常微分方程式
は、
を順に、第1種および第2種 Bessel 関数という※1。
で定義される。また、負の整数次に対しては、
によって求められる。
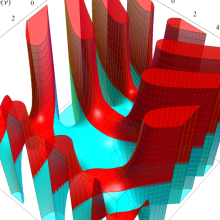
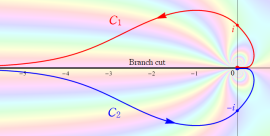
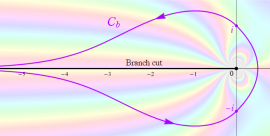
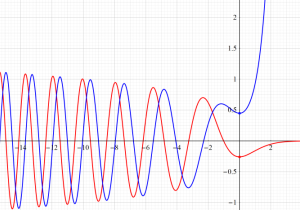
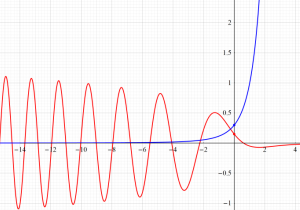
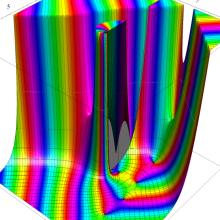
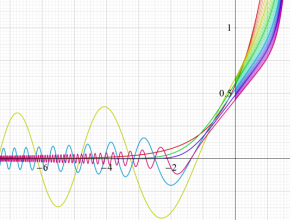
Bessel 関数は
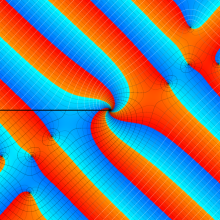
分枝切断線を越える解析接続は、
によって成される。例えば、
Bessel 関数は、
を満たす (これは 「隣接関係式」 と呼ばれる)。ここに
となるので、
Bessel の微分方程式は、合流型超幾何微分方程式の特別な場合であり、その解は互いに
の関係にある。先の隣接関係式など Bessel 関数の性質の多くは、合流型超幾何関数のそれに由来する。
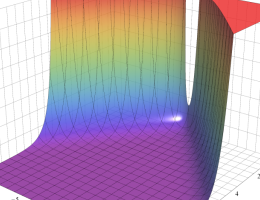
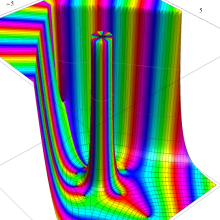
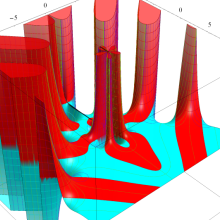
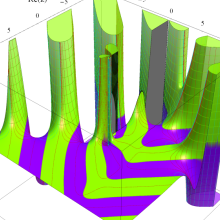
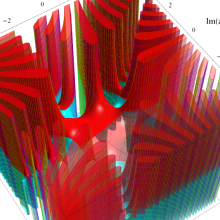
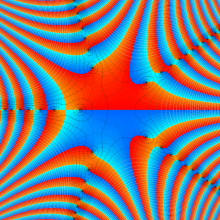
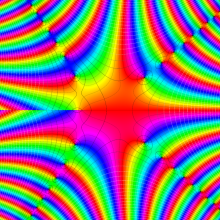
Bessel 関数は、
が得られている。
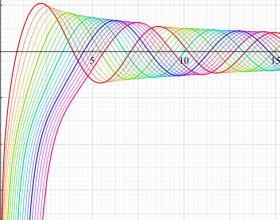
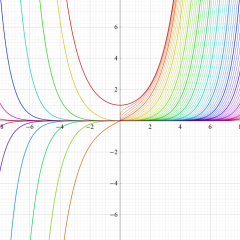
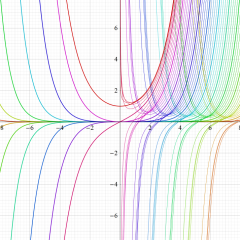
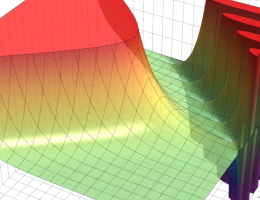
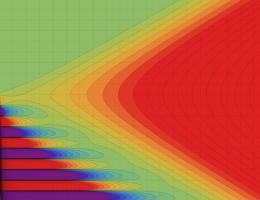
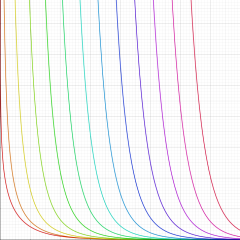
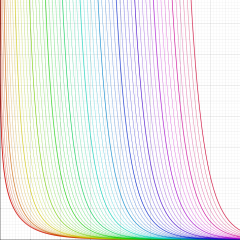
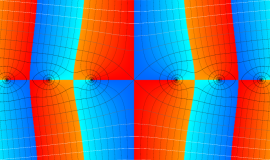
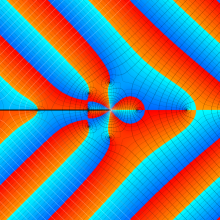
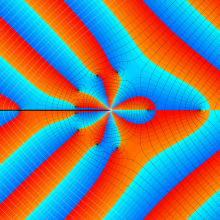
応用上、最も重要な Bessel 関数は
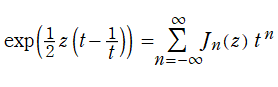
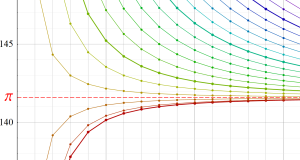
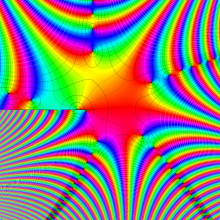
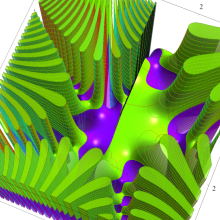
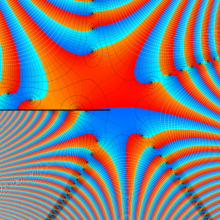
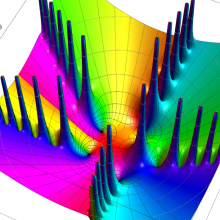
Bessel 関数は一般に複素零点を持つが、
で表記する習慣となっている。このとき、第1種 Bessel 関数が満たす直交性は、
で表わすことができる。
円柱座標
となり、Bessel 関数が動径
歴史的観点から見たときに重要な Bessel 関数の応用事例としては、1733年に D. Bernoulli が鉛直方向に均一な重さの鎖が微小振動するときの固有振動を級数解で求め、これが実質的に第1種 Bessel 関数の特別な場合であった事、1764年には L. Euler が円形膜の調和振動を研究し、漸近級数展開式や実零点の数値を求めた事などが挙げられる。特に、1824年には F. W. Bessel が天体力学における Kepler 方程式の解を第1種 Bessel 関数項の無限級数で表わすとともに、Bessel 関数を単体の研究対象として本格的に取り上げた事はよく知られている。積分表示式
は、このとき彼によって与えられ、記号
19世紀以降、Bessel 関数が特に重要視されていた特殊関数であった事は、書籍での扱われ方を見ても分かる。G. N. Watson が1922年に著した 「A Treatise on the Theory of Bessel Functions」 は、Bessel 関数の専門書でありながら約800頁を有する。特殊関数全般を扱う書籍 (例えば、M. Abramowitz & I. Stegun の 「Handbook of …」 等) でも Bessel 関数には多くの頁が割かれ、数表も充実していた。これは、現在でも多くの人が、Bessel 関数を特殊関数の例として最初に挙げる理由の一つにもなっている。
【註記】
※1:この頁に掲載している冪級数等で0次の項が現れる場合は、特に断らない限り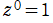 と規約する。(他の頁でも、概ねこの規約に従っている。)
と規約する。(他の頁でも、概ねこの規約に従っている。)
※2:例えば、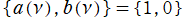 ならば
ならば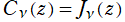 、
、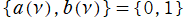 ならば
ならば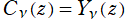 となる。またこの要領で、後述の Hankel 関数も全く同じ隣接関係式を満たすことが分かる。
となる。またこの要領で、後述の Hankel 関数も全く同じ隣接関係式を満たすことが分かる。
※3:例えば、次の結果が得られている。
・代数的数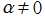 に対して、
に対して、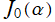 の値は超越数 (1929年 C. L. Siegel)
の値は超越数 (1929年 C. L. Siegel)
・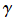 を Euler - Mascheroni 定数とするとき、
を Euler - Mascheroni 定数とするとき、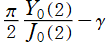 の値は超越数 (K. Mahler)
の値は超越数 (K. Mahler)
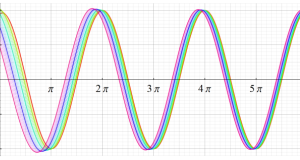
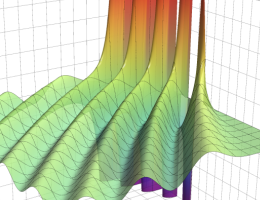
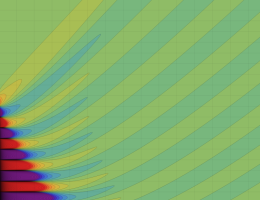
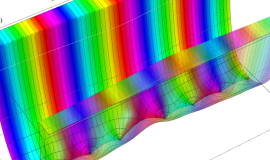
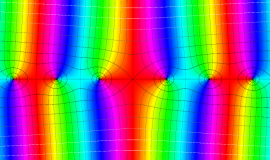
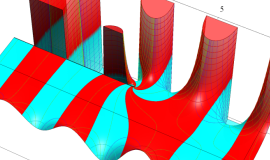
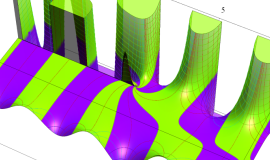
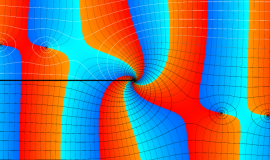
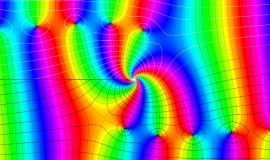
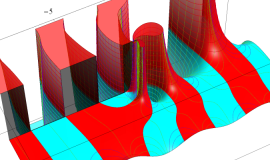
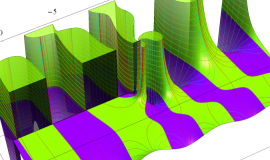
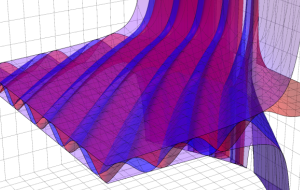
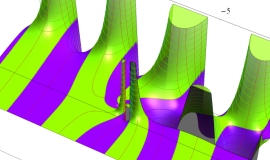
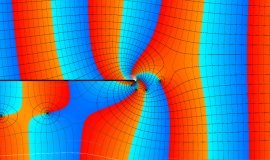
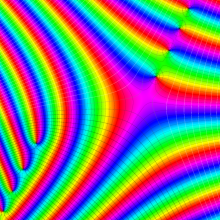
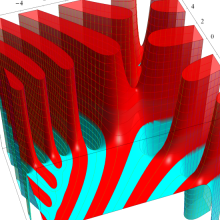
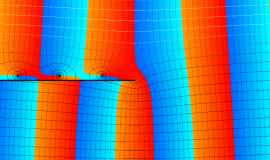
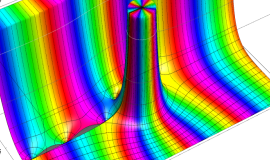
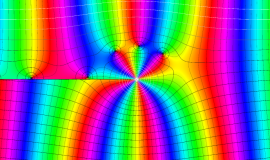
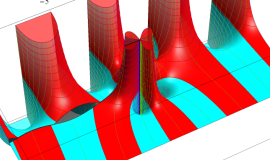
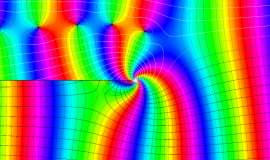
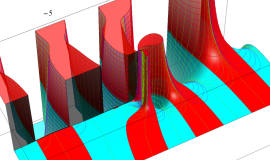
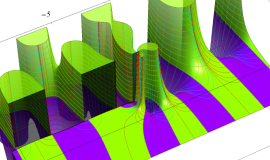
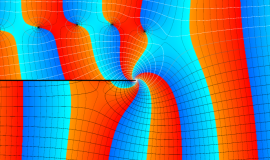
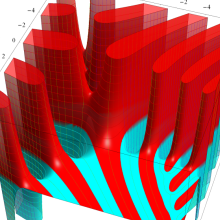
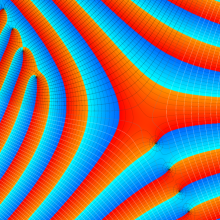
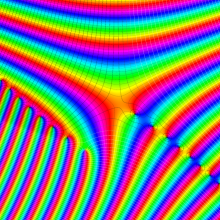
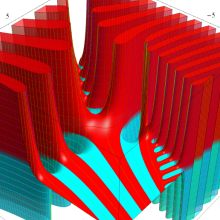
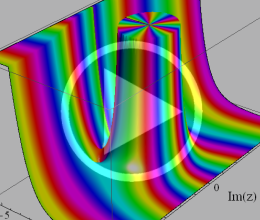
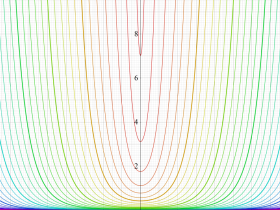
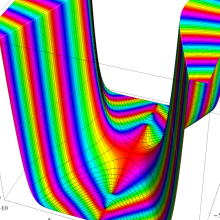
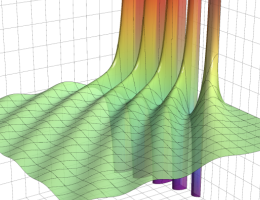
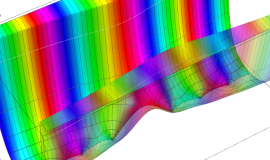
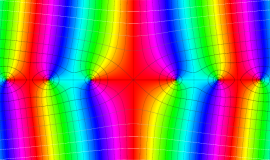
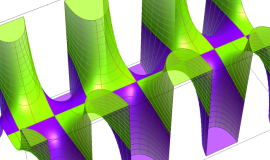
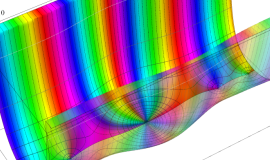
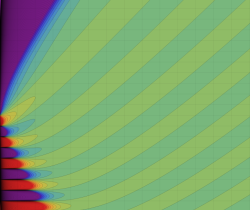
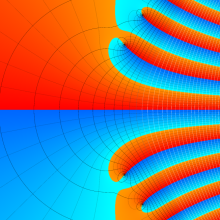
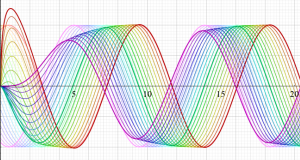
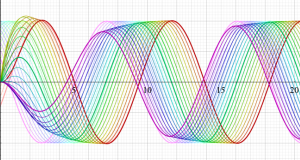
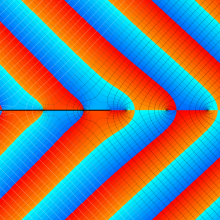
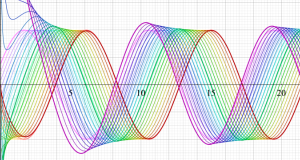
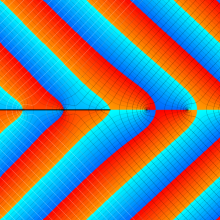
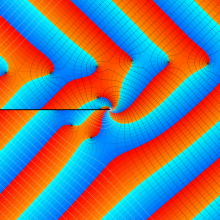
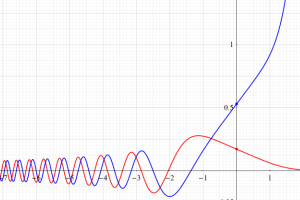
その他:Bessel 関数の典型的な応用事例について追加する。円柱座標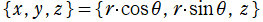 における関数
における関数
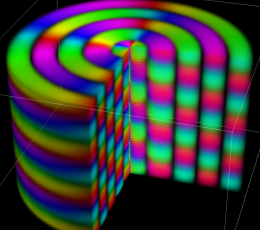
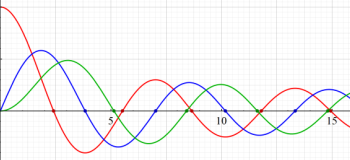
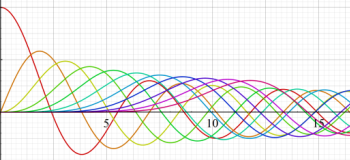
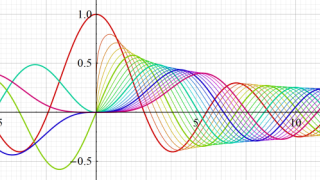
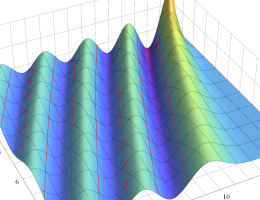
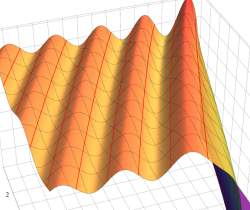
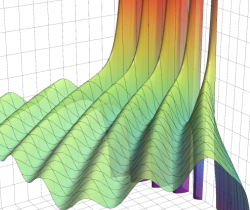
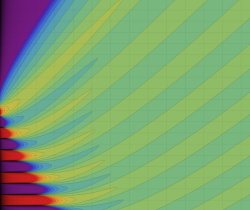
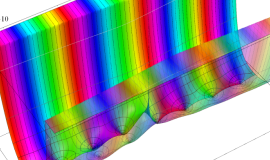
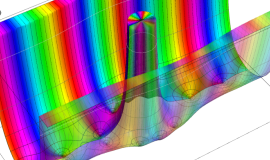
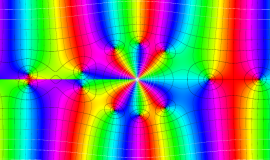
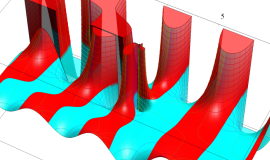
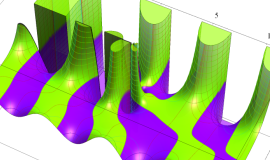
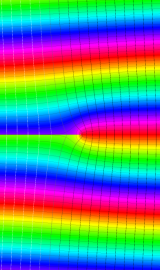
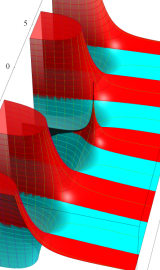
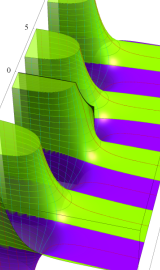
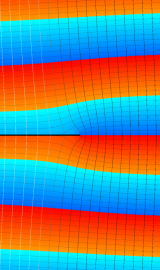
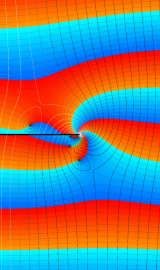
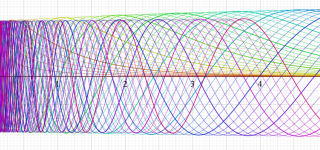
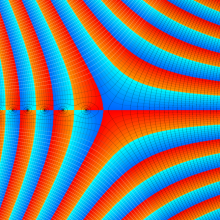
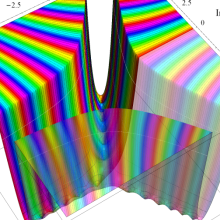
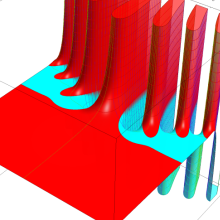
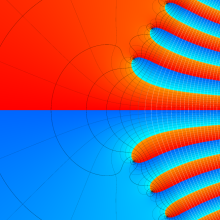
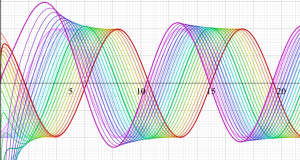
が表わす波形は 「円柱波」 と呼ばれ、次のグラフのようになる。つまり、角度方向が余弦関数、動径方向が第1種 Bessel 関数に由来した波形になる。
このとき、すべての円柱波を総和 (合成振動) すると、平面波 (平行波) に変換される!。
上記のアニメーションは、次の1番目の公式が意味するところを視覚化したものである。他の3個の公式も類似する意味を持っており、これらは第1種 Bessel 関数が持つ重要な性質の一つである (この公式は 「Jacobi - Anger expansion」 の特別な場合)。
※1:この頁に掲載している冪級数等で0次の項が現れる場合は、特に断らない限り
※2:例えば、
※3:例えば、次の結果が得られている。
・代数的数
・
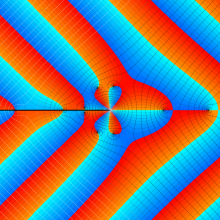
その他:Bessel 関数の典型的な応用事例について追加する。円柱座標
が表わす波形は 「円柱波」 と呼ばれ、次のグラフのようになる。つまり、角度方向が余弦関数、動径方向が第1種 Bessel 関数に由来した波形になる。
このとき、すべての円柱波を総和 (合成振動) すると、平面波 (平行波) に変換される!。
アニメーション(6.08MB)
上記のアニメーションは、次の1番目の公式が意味するところを視覚化したものである。他の3個の公式も類似する意味を持っており、これらは第1種 Bessel 関数が持つ重要な性質の一つである (この公式は 「Jacobi - Anger expansion」 の特別な場合)。
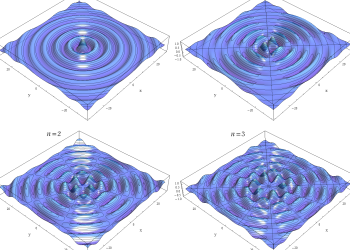
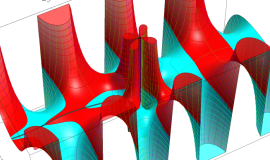
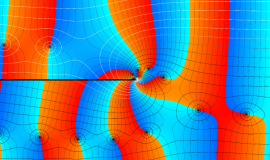
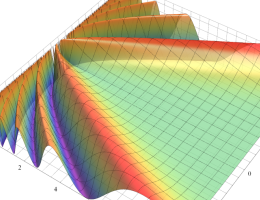
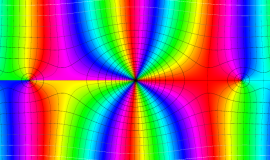
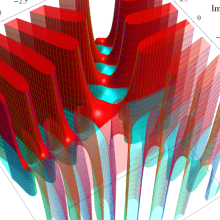
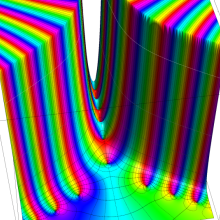
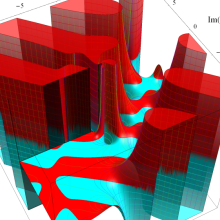
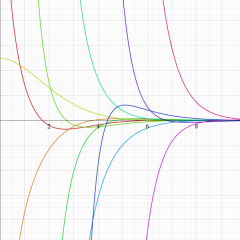
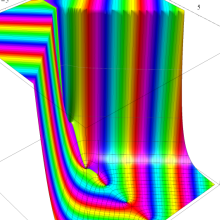
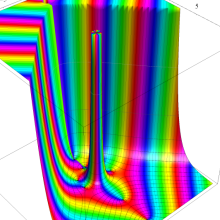
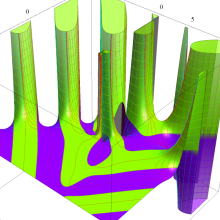
関数
よって、
アニメーション(11.4MB)
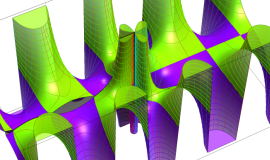
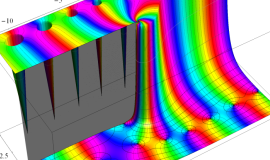
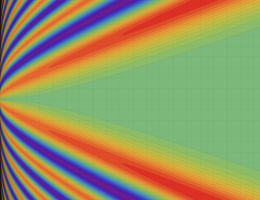
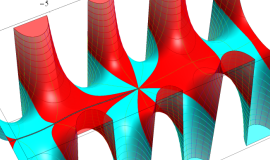
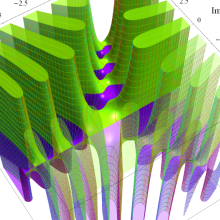
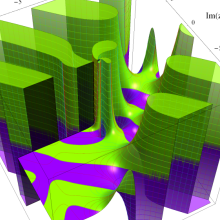
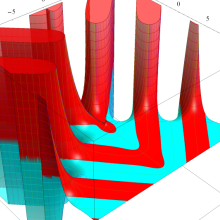
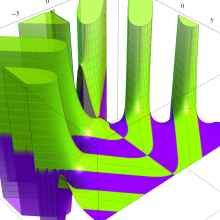
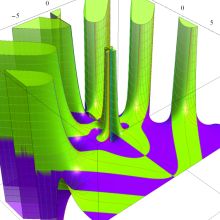
関数
よって、
アニメーション(11.5MB)
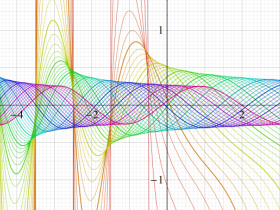
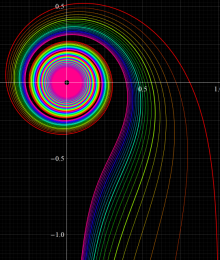
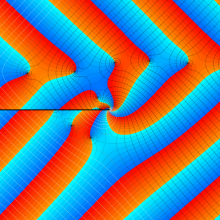
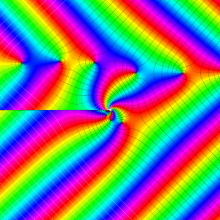
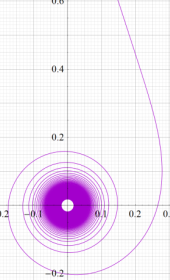
パラメトリック曲線
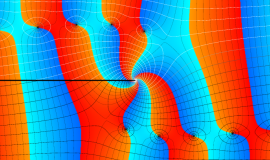
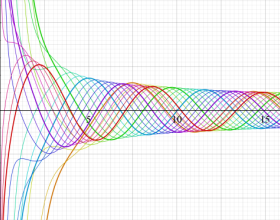
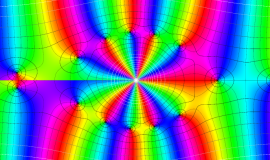
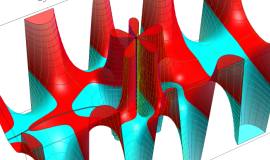
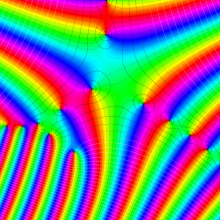
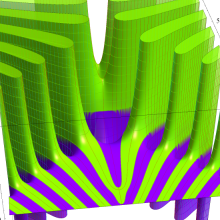
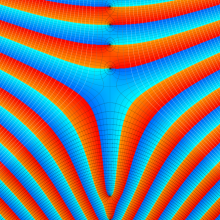
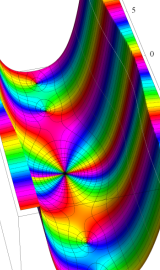
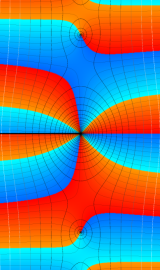
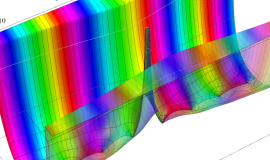
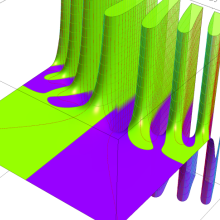
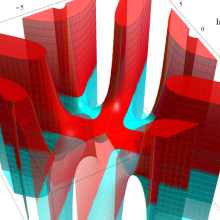
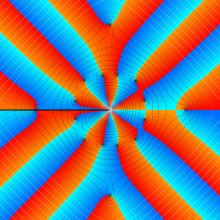
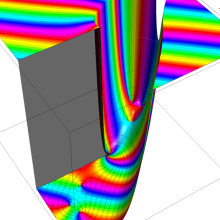
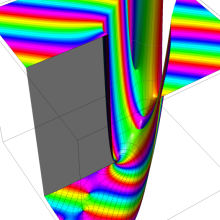
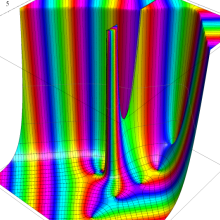
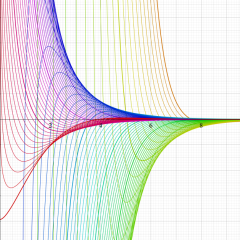
Hankel 関数
日:Hankel関数,ハンケル関数英:Hankel function,仏:Fonction de Hankel,独:Hankelsche funktion
19世紀の中葉に複素関数論が整備されると、早速これは Bessel 関数にも適用されるようになり、1868年には E. C. J. Lommel が
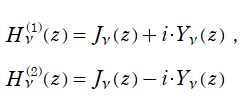
この積分表示式から、
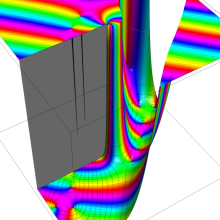
1880年には N. Y. Sonin によっても、共通の被積分関数に対する積分経路だけを変えて、Bessel の微分方程式の解を構成する同様の方法が独立に論じられた。これらの理論は、一般的な線形常微分方程式の解の接続係数を決定する問題の原型となった。
さて、Hankel 関数が満たす公式は、多くの場合 Bessel 関数のそれよりも簡潔な形となる。例えば、合流型超幾何関数との関係式は、
となる。また、
は、その表示が特に簡潔なため、応用上 Hankel 関数が重宝される最も大きな理由となっている。
以上を総合して、
Hankel 関数の応用事例は、Bessel 関数のそれと共通する問題において、境界条件が無限遠に移行した場合に多い。理由は、それらが前述の積分表示式や漸近級数展開式の利点を生かせるからである。例えば、円柱進行波 (原点を発生源とし無限遠に伝搬する、二次元の同心円波動) の解析がその最たる事例である。Hankel 関数に固有の応用事例も若干あり、非定常翼理論における揚力の問題が有名である。
アニメーション(10.1MB)
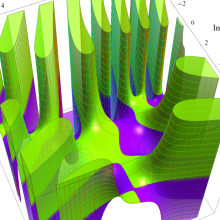
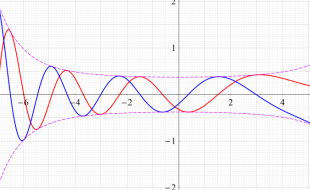
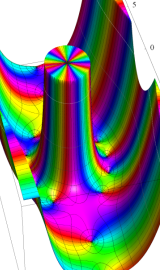
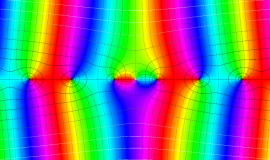
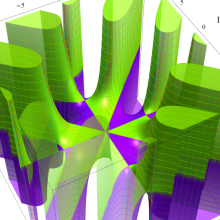
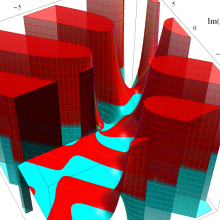
変形 Bessel 関数
日:変形Bessel関数,変形ベッセル関数,双曲線Bessel関数英:Modified Bessel function,仏:Fonction de Bessel modifiée,独:Modifizierte Besselsche funktion
数学および物理学等では、Bessel の微分方程式に対して変換
が頻繁に出現する。これは 「変形された Bessel の微分方程式」 と呼ばれ、その解の基本系
を順に、第1種および第2種変形 Bessel 関数という。
を用いる。
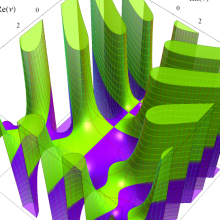
変形 Bessel 関数も、
の関係にあると定義される。
変形 Bessel 関数が満たす隣接関係式は、
となる (同様に、
以上を総合すれば、
変形 Bessel 関数の応用事例も、Bessel 関数のそれと共通する部分が多いが、固有の事例としては中性子の拡散問題などがある。また、確率論や統計学に現れることも他の Bessel 関数と趣を異にする。その一例として、当サイトでは既に Marcum のQ関数を取り上げた。
Bessel 関数自体、物理学との接点を多く持ちながら純粋数学でも応用事例が多い関数であるが、変形 Bessel 関数はその点で著しい。例えば、級数項に
が知られている。ここに、
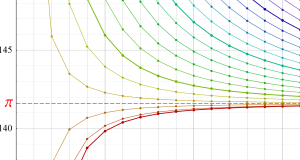
また、変形 Bessel 関数の漸近級数展開式を用いると、非常に高速・高精度で Euler - Mascheroni 定数が求められる。詳細は論文※3を参照。
【註記】
※1:例えば、NISTの公式10.31.1等を参照。
※2:D. Castellanos 「Rapidly Converging Expansions with Fibonacci Coefficients」 (The Fibonacci Quarterly No.24, (1986), p.70-82)
※3:R. P. Brent & F. Johansson 「A Bound for the Error Term in the Brent - McMillan Algorithm」 (Mathematics of Computation Vol.84, No.295, (2015), p.2351-2359)
※1:例えば、NISTの公式10.31.1等を参照。
※2:D. Castellanos 「Rapidly Converging Expansions with Fibonacci Coefficients」 (The Fibonacci Quarterly No.24, (1986), p.70-82)
※3:R. P. Brent & F. Johansson 「A Bound for the Error Term in the Brent - McMillan Algorithm」 (Mathematics of Computation Vol.84, No.295, (2015), p.2351-2359)
アニメーション(7.04MB)
因みに、
アニメーション(9.17MB)
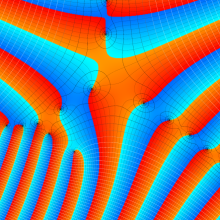
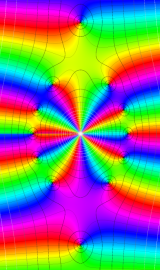
球 Bessel 関数
日:球 Bessel関数,球ベッセル関数英:Spherical Bessel function,仏:Fonction de Bessel sphérique,独:Sphärische Besselfunktion
球座標 (三次元の極座標)
となる。ここに、天頂角
で定義される (当サイトでは、次数を
の解の基本系を成す。
結局のところ、球 Bessel 関数は Bessel 関数に無理関数をかけたものに過ぎないが※1、前述の解
に還元される。
繰り返しになるが、球 Bessel 関数の応用事例は球座標に因るものが占める。すなわち、境界条件を球面に定めた電磁波・素粒子等の分布や伝搬を、動径方向で見る場合の問題に現れる。よって、物理学等での出現頻度は割合高い。問題の性質によっては、解の基本系として球 Hankel 関数
を採用した方が良いことも起こり得る。また、必要に応じて変形球 Bessel 関数 (Modified spherical Bessel function)
も定義される※2。
【註記】
※1:したがって、グラフの掲載数を若干減らす。
※2:当サイトでは (冗長と考えて)、球 Hankel 関数と変形球 Bessel 関数のグラフは掲載しない。因みに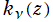 は
は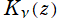 と異なり、
と異なり、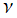 が純虚数のときに正の実軸上で実数値を取らない。
が純虚数のときに正の実軸上で実数値を取らない。
※1:したがって、グラフの掲載数を若干減らす。
※2:当サイトでは (冗長と考えて)、球 Hankel 関数と変形球 Bessel 関数のグラフは掲載しない。因みに
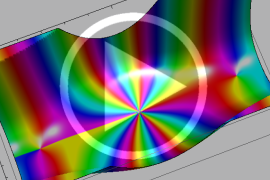
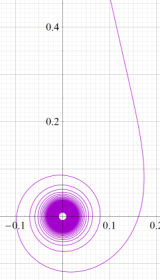
パラメトリック曲線
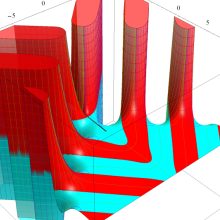
Airy 関数
日:Airy関数,エアリー関数英:Airy function,仏:Fonction d'Airy,独:Airysche funktion
日:Scorer関数,スコラー関数
英:Scorer function,仏:Fonction de Scorer,独:Scorersche funktion
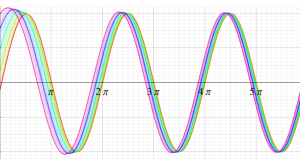
ここまで見てきた限り、Bessel 関数が特に重要とされるのは整数次または半奇数次の場合であったが、現在では±1/3次の場合にも有用性が認められ、Bessel 関数から独立した別の関数として定義されている。
単振動が満たすそれに次いで形が簡単な、二階の線形常微分方程式
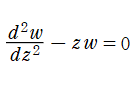
を順に、第1種および第2種 Airy 関数という。両者は超越整関数である。
Airy 関数の冪級数展開式は、
となる。なお、
1838年に G. B. Airy は、光学における虹の問題 (水滴による分光) を説明する際、積分
を用いたが、後年これが 「Airy 積分」 と呼ばれるようになり、関数名称の由来にもなった。また、1850年に G. G. Stokes は虹の問題を再び取り上げ、前述の漸近級数展開式を導いて計算数値を改良した。なお、記号
光学は Airy 関数の主要な応用分野であるが、他にも量子力学 (線形ポテンシャルを持つ均質電場内の粒子)、非線形波動 (ソリトン方程式、KdV方程式の解)、半導体工学などに現れる。最後に挙げた事例では、
均一に荷重された無限板の解析等では、Airy の微分方程式を非斉次に変形した、
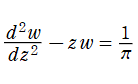
を順に、第1種および第2種 Scorer 関数という。同様に、両者は超越整関数である。
Scorer 関数の数値計算では、冪級数および漸近級数展開式を使い分けることになる。例えば前者は、
となる※2。
Airy 積分に相当する Scorer 関数の公式は、
である。
Scorer 関数なる名称は、1949~1950年に R. S. Scorer が大気圏内におけるパルス波動の分散を研究した際、併せてこの関数を導入したことに因む。
【註記】
※1:Airy 関数の漸近級数展開式については、NISTの9.7 Asymptotic Expansions 等を参照。
※2:Scorer 関数の漸近級数展開式については、NISTの9.12(viii) 等を参照。
※1:Airy 関数の漸近級数展開式については、NISTの9.7 Asymptotic Expansions 等を参照。
※2:Scorer 関数の漸近級数展開式については、NISTの9.12(viii) 等を参照。
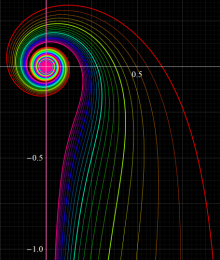
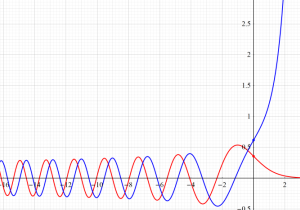
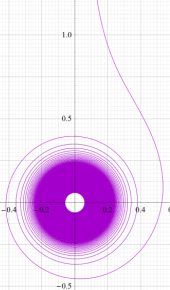
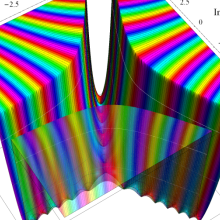
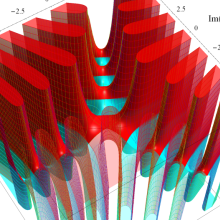
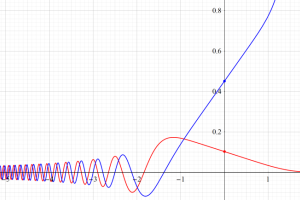
Airy 関数によるパラメトリック曲線
複素変数の第1種 Airy 関数
複素変数の第2種 Airy 関数
複素変数の第1種 Airy 導関数
複素変数の第2種 Airy 導関数
複素変数の第1種 Scorer 関数
複素変数の第2種 Scorer 関数
複素変数の第1種 Scorer 導関数
複素変数の第2種 Scorer 導関数
両者とも零点が原点対称な位置に並ぶが、特に
実変数の (原点対称型) Airy 関数
複素変数の (原点対称型) 第1種 Airy 関数
複素変数の (原点対称型) 第2種 Airy 関数
Kelvin 関数
日:Kelvin関数,ケルヴィン関数,Thomson関数英:Kelvin function,仏:Fonction de Kelvin,独:Kelvinsche funktion
変形 Bessel 関数は、言わば引数を
が用意されている。
で定義される。これは、対数分岐点
で計算した結果と一致する。次数
Kelvin 関数は、円柱形状の導電体の内部で電流が軸部よりも周辺部に多く流れる現象 (表皮効果) の説明等に現れるが、電気工学以外の応用事例は少ない。歴史的に見ても、Lord. Kelvin (本名は W. Thomson) が電気工学に関連してこの関数を導入したのが始まりで、これが Kelvin 関数なる名称の由来になっている (希に Thomson 関数と呼ぶこともある)。
なお、古い書籍等では、
を見かけることもある (3行目は実部・虚部関数の記号が入れ替わっているが、誤りではない) ※3。しかし、冗長であるため当サイトでは扱わない。
【註記】
※1:NISTの10.65(ii) 等を参照。
※2:漸近級数展開式については、NISTの10.67(i) 等を参照。
※3:A. Erdelyi 他 「Higher Transcendental Functions (Vol.Ⅱ)」 の p.6 を参照。
※1:NISTの10.65(ii) 等を参照。
※2:漸近級数展開式については、NISTの10.67(i) 等を参照。
※3:A. Erdelyi 他 「Higher Transcendental Functions (Vol.Ⅱ)」 の p.6 を参照。
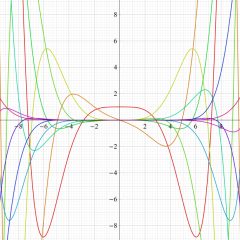
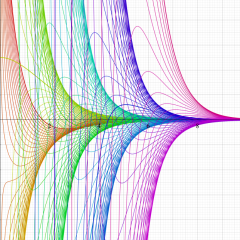
関数
アニメーション(11.4MB)
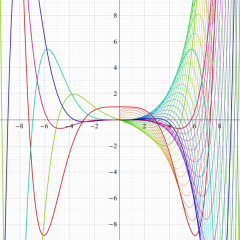
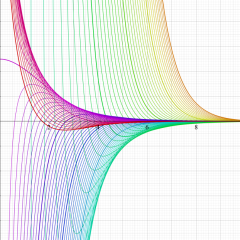
関数
関数
関数
アニメーション(10.1MB)
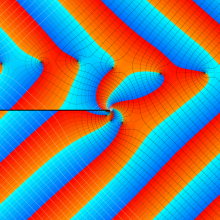
一般 Airy 関数
Airy の微分方程式を一般化した線形常微分方程式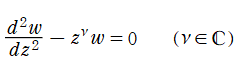
を順に、第1種および第2種一般 Airy 関数と呼ぶ。両者は
明らかにこの定義は、Airy 関数に還元される場合の
を含み、また、
で表わされる。
NISTの9.13(i)で定義されている一般 Airy 関数
の関係にある (ただし、NISTでは次数を
の型にまとめることができる。この方程式の解は、
(狭義の) Riccati の微分方程式
は、J. F. Riccati が1722年に発見した非線形常微分方程式で、当時は一般に求積不能な (変数分離法等で解けない) 方程式として注目されたが、現在では
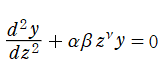
となる。当サイトではこれを独自に定義し、(Bessel 型の) Riccati 関数と呼ぶ※2。解の基本系を Hankel 関数に取ることも当然可能で、併せて (Hankel 型の) Riccati 関数
も独自に定義する。よって、両者は
の関係にある。
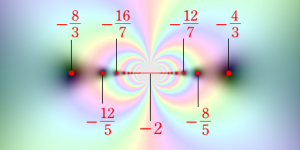
Riccati の微分方程式は、
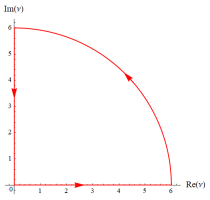
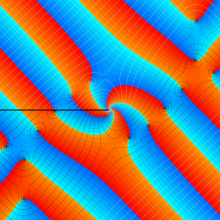
図:Riccatiの微分方程式が変数分離法等で解ける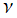 の位置図
の位置図
の場合のみ変数分離法等で解ける。後者は同時に、Riccati 関数に現れる Bessel 関数の次数が半奇数になる場合である。一方、前者の
で定義する (双曲線関数を解の基本系に採用した場合)。
【註記】
※1:サイト管理人が調べた限りでは、他にも例外として微分方程式
の解が合流型超幾何関数で表わせる。
逆に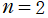 ならば、解はすべて放物柱関数で表わせる。
ならば、解はすべて放物柱関数で表わせる。
※2:これは、「Riccati - Bessel 関数」
とは異なる。
※1:サイト管理人が調べた限りでは、他にも例外として微分方程式
の解が合流型超幾何関数で表わせる。
逆に
※2:これは、「Riccati - Bessel 関数」
とは異なる。
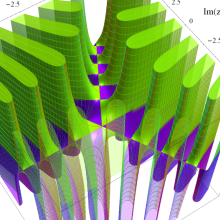
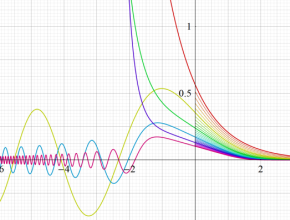
一般 Airy 関数によるパラメトリック曲線
一般 Airy 関数によるパラメトリック曲線
アニメーション(13.3MB)