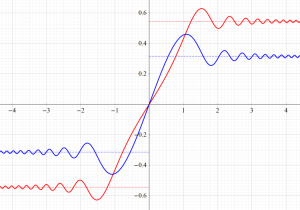
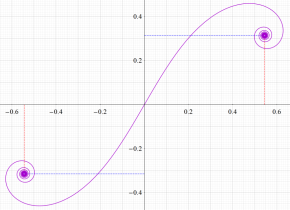
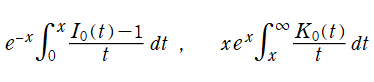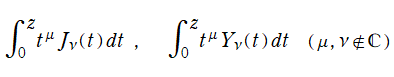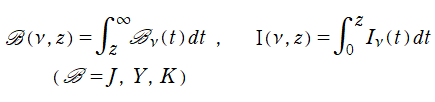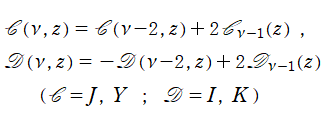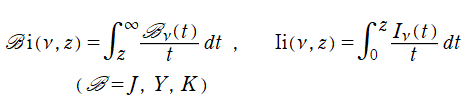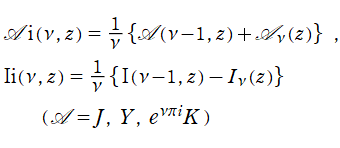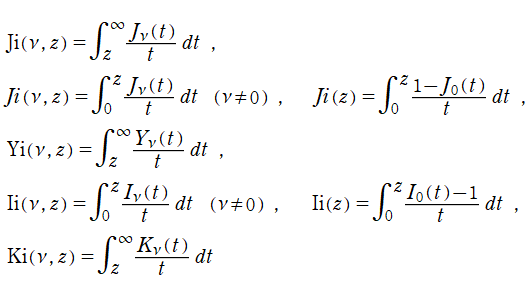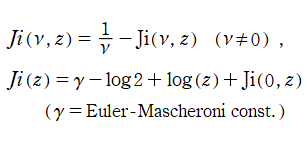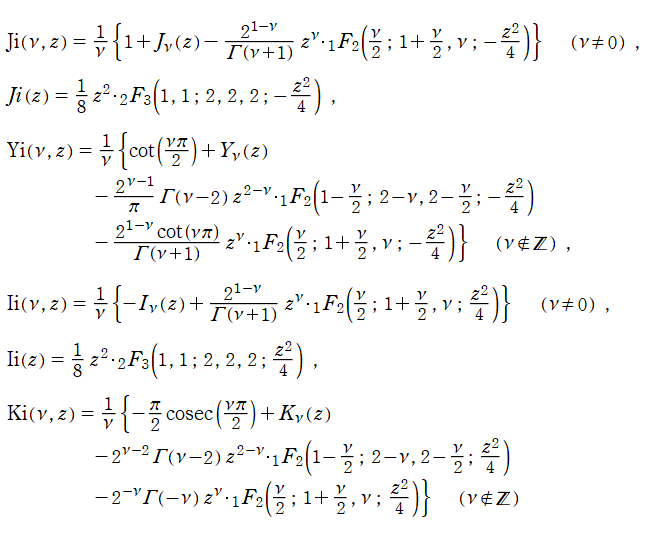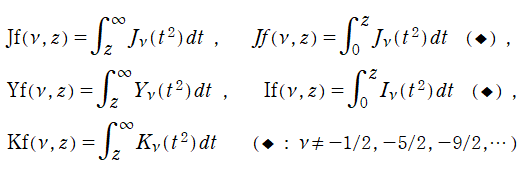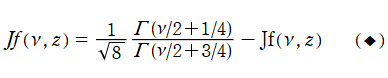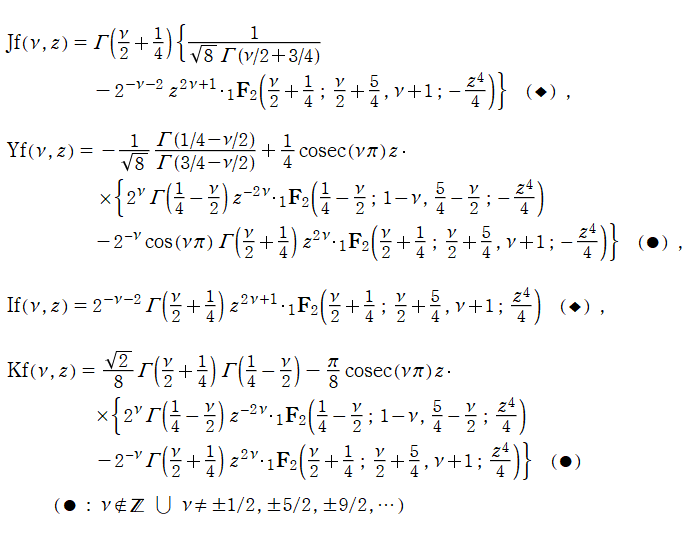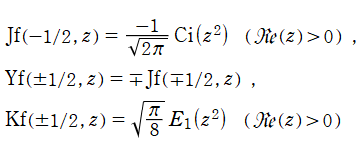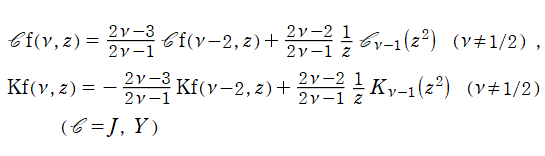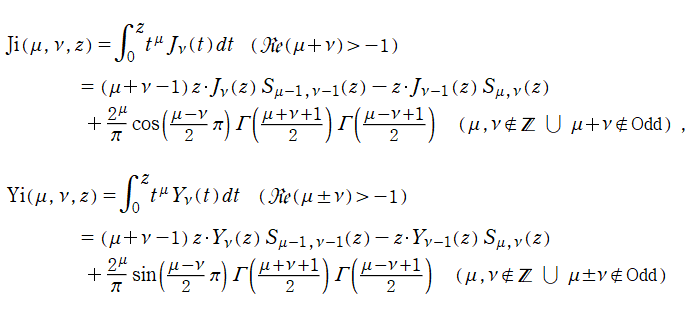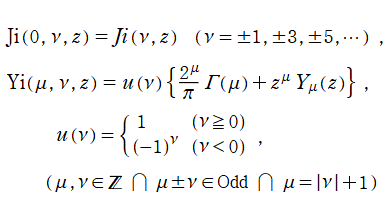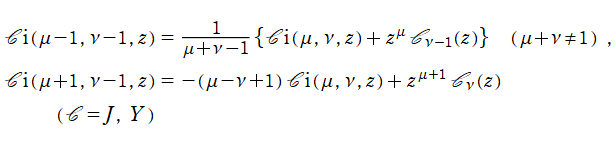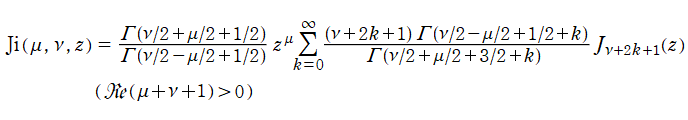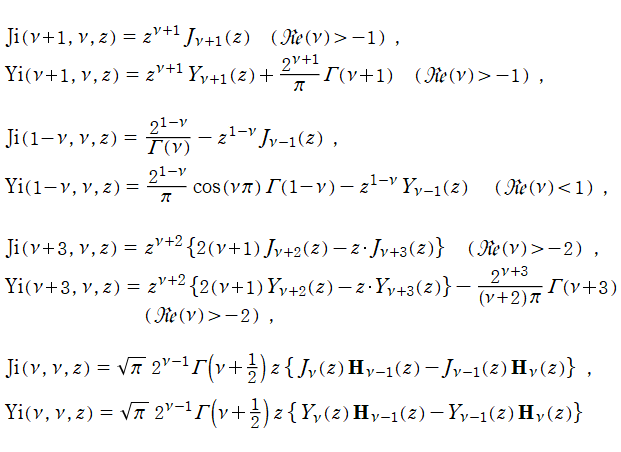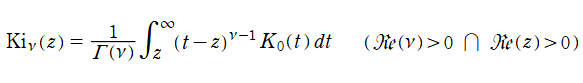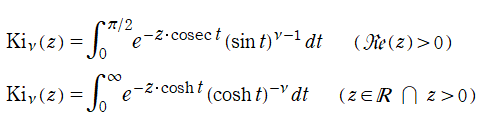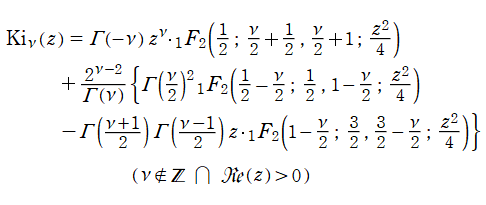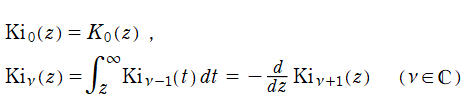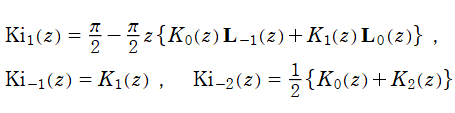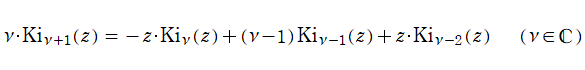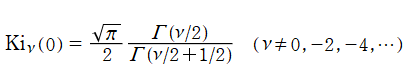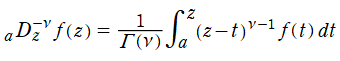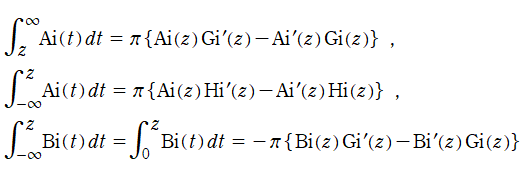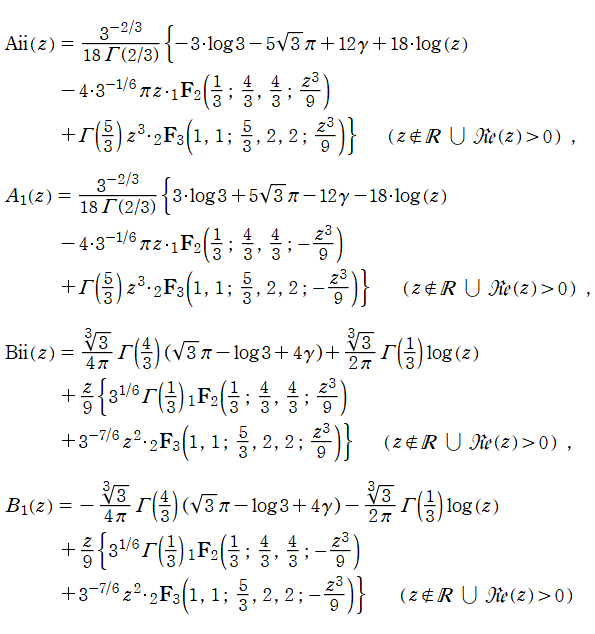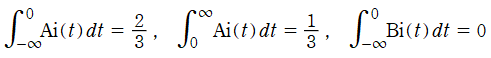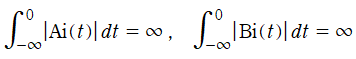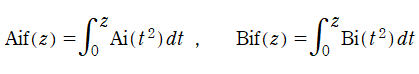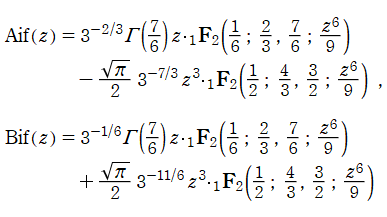特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
積分 Bessel 関数
積分 Bessel 関数
【始めに:頁全体の概要】特殊関数論では、既知の特殊関数をさらに積分すると得られる新しい関数の探索、またはその還元の可否について詳しい研究がなされ、その成果は公式集に収められている。殊に Bessel 関数のそれは充実しており、例えば M. Abramowitz & I. Stegun の 「Handbook of Mathematical Functions」 では、第11章の全体がこのテーマで占められている。また、数式処理システムの発達によって、このような積分が還元できる範囲は拡大されつつある。
当サイトではこれを踏まえ、また分量上の理由もあって、Bessel 関数およびその関連関数とは異なる頁で、この種の積分関数を掲載することとした。しかしながら、ここで主に取り上げるのは、被積分関数と同等または簡単なクラスに還元できない事例で、しかも Bessel 関数を三角関数の類似と見た場合の、積分三角関数や Fresnel 関数に相当する関数である (これを当サイトでは、積分 Bessel 関数, および Bessel - Fresnel 関数と呼ぶ)。両者は被積分関数の形が比較的シンプルであり、特に、前者は過去に
等の数表も作られていた事に鑑みて取り上げる (前述 A & S の第11章にも、それらの数表がある)。なお両者は、一般積分 Bessel 関数
を介して、前頁の Lommel 関数とも関係がある。
さらに、Airy 関数に対しても同様の類似を考え、独自定義関数として導入する。したがって、以上の積分関数に使用している関数記号は、すべて当サイト独自のものである。
一方、これらとは異なり、応用上の必要から導入された Bickley - Naylor 関数についても触れる。
【積分 Bessel 関数】
始めに、被積分関数の形が最も簡単な、
について説明する (一部の例を除いて、後述のとおり積分 Bessel 関数と関係がある)。両者は、次数
を満たすので、もし、簡単な関数に還元される事例が二つ存在し、しかも互いの次数差が1であれば次々と還元事例が得られる。実際に
積分三角関数または積分双曲線関数の類似
は、
となるので、
以上のことを踏まえ、当サイトでは
の関係にある。なお、
積分 Bessel 関数および積分変形 Bessel 関数の、一般超幾何関数による閉形式
は、実際の数値計算等に便利であるが※1、
または
を初期関数として、前述の漸化式から
最も厄介なのが
等で得られる。このとき漸近級数の併用が望まれるが、数式の掲載は省略する※2。
恐らく、積分 Bessel 関数の応用事例は存在しない。変形 Bessel 関数の積分 (Synchrotron function)
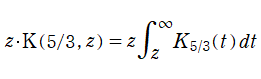
【註記】
※1:当然ながら、数式処理システムに一般超幾何関数が実装されていない場合は、それ自体の (冪級数、漸近級数等による) コードを別途記述しなければならない (以下同様)。
※2:Abramowitz & Stegun の482頁にある公式 11.1.24~11.1.27 を参照。
※1:当然ながら、数式処理システムに一般超幾何関数が実装されていない場合は、それ自体の (冪級数、漸近級数等による) コードを別途記述しなければならない (以下同様)。
※2:Abramowitz & Stegun の482頁にある公式 11.1.24~11.1.27 を参照。
前述のとおり、
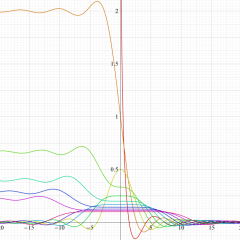
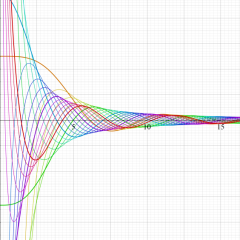
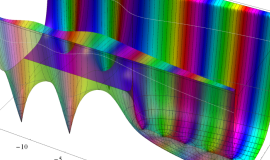
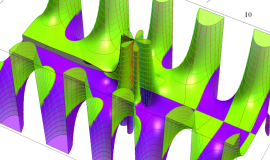
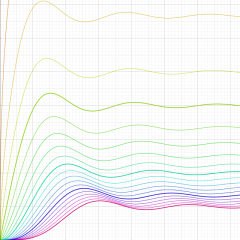
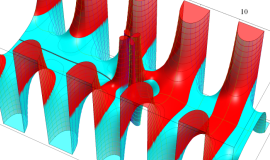
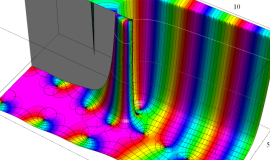
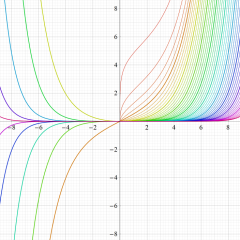
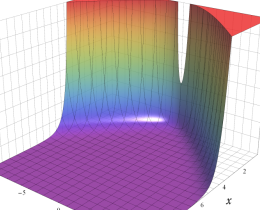
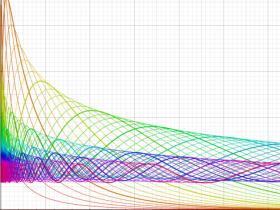
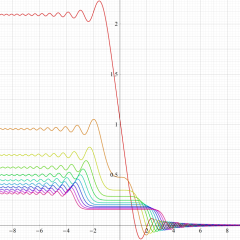
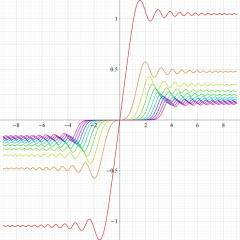
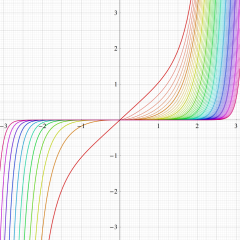
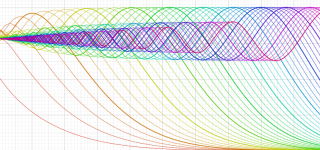
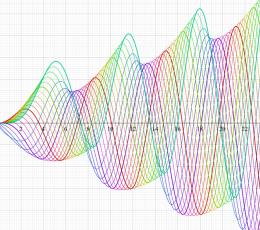
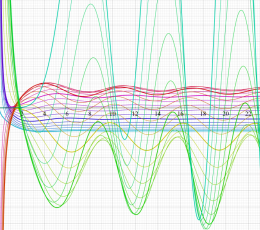
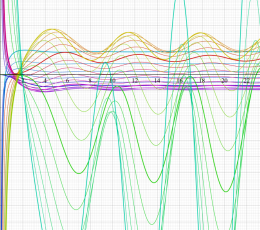
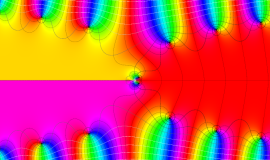
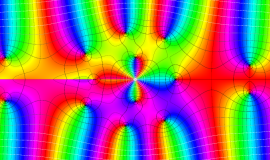
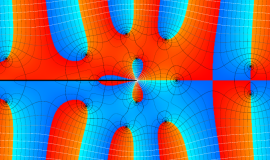
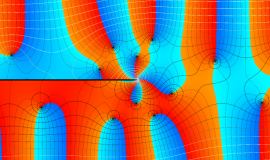
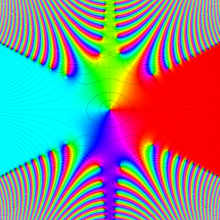
実変数の積分第1種 Bessel 関数
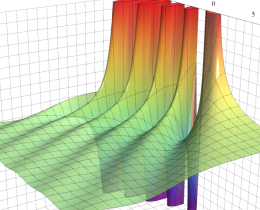
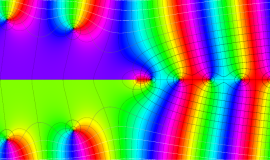
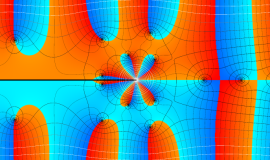
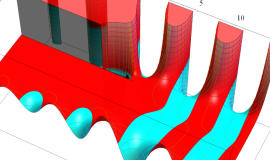
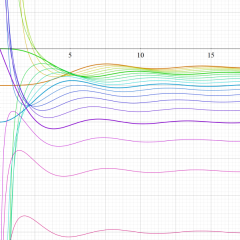
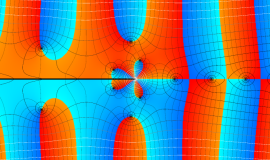
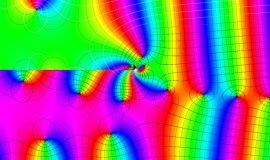
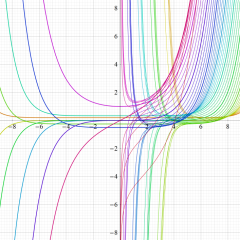
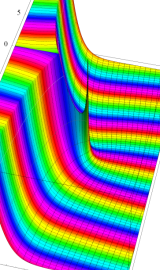
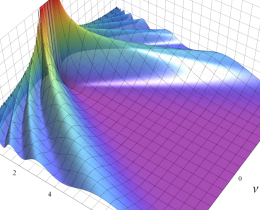
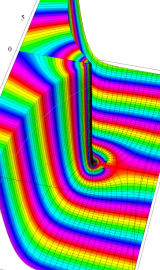
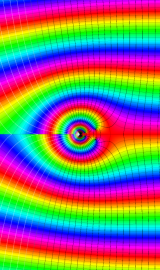
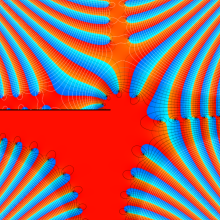
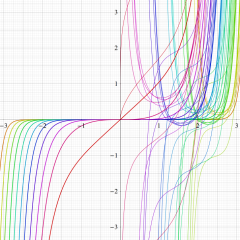
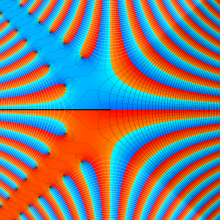
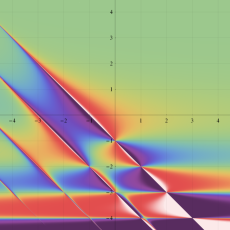
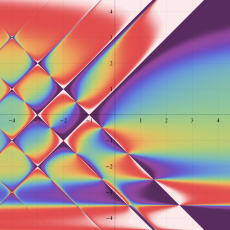
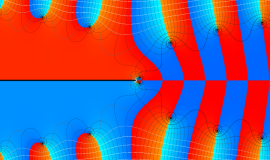
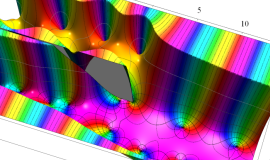
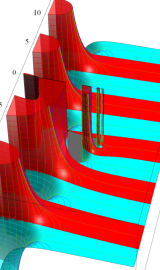
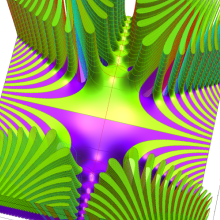
複素変数の積分第1種 Bessel 関数
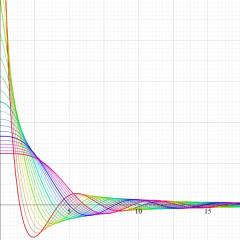
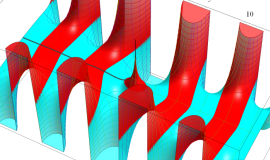
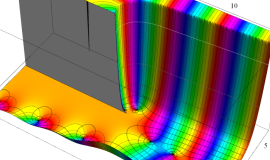
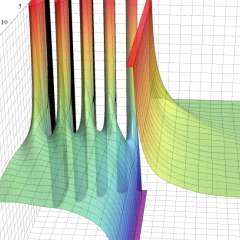
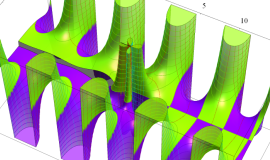
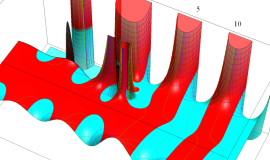
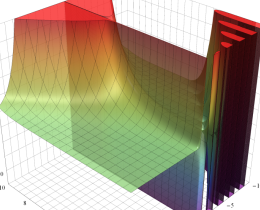
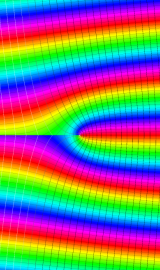
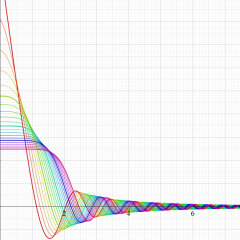
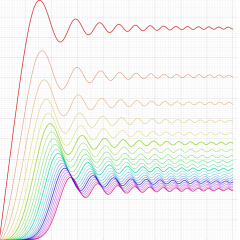
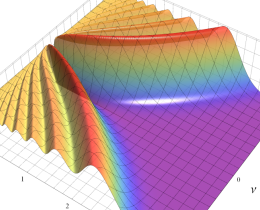
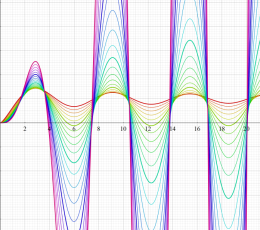
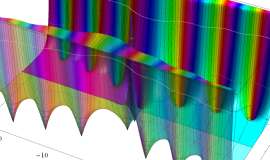
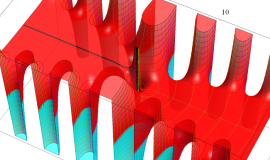
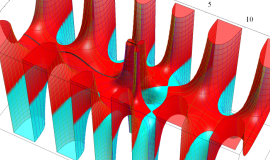
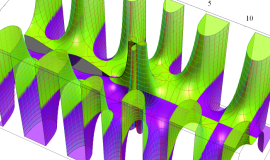
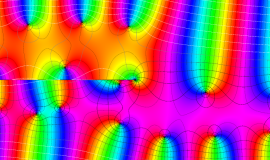
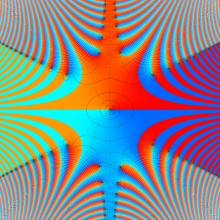
実変数の積分第1種変形 Bessel 関数
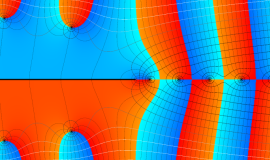
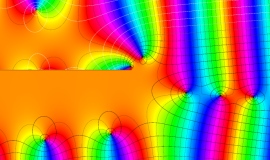
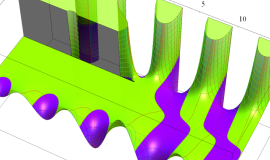
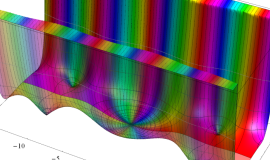
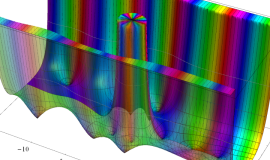
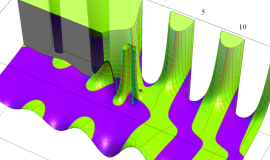
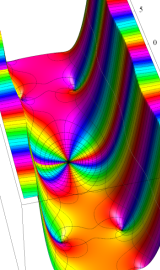
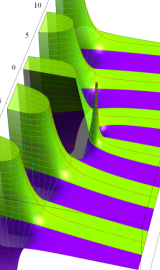
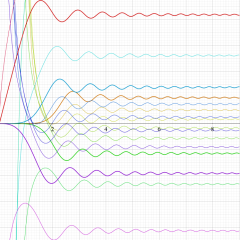
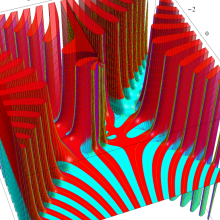
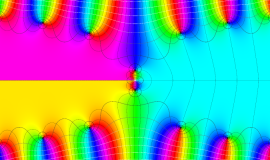
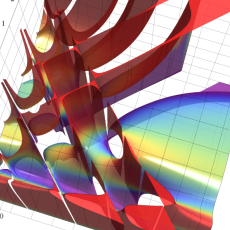
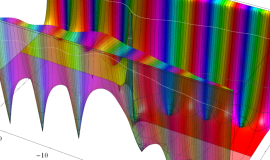
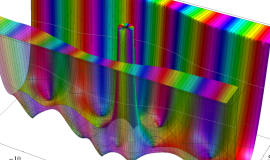
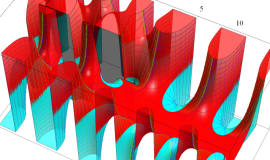
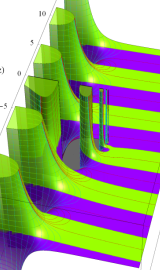
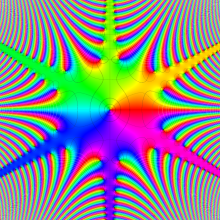
複素変数の積分第1種変形 Bessel 関数
Bessel - Fresnel 関数
後述する一般積分 Bessel 関数の特殊なケースとして表わせる、Fresnel 関数の類似、を独自に定義し、Bessel - Fresnel 関数および変形 Bessel - Fresnel 関数と呼ぶ。これらの関数は
の関係にある (
Bessel - Fresnel 関数および変形 Bessel - Fresnel 関数の、正規化された一般超幾何関数による閉形式
は、実際の数値計算等に便利であるが、条件式
または、
を初期関数とする漸化式
によって求める。
恐らく、Bessel - Fresnel 関数の応用事例は存在しない。
前述のとおり、
一般積分 Bessel 関数
積分 Bessel 関数と Bessel - Fresnel 関数は、より一般的な積分の特別な場合である。上記のうち、Lommel 関数によって表示可能な、
を独自に定義し、一般積分 Bessel 関数と呼ぶ。両者は
Lommel 関数の表示式が使用できない格子点
を初期関数とする漸化式
によって求める。
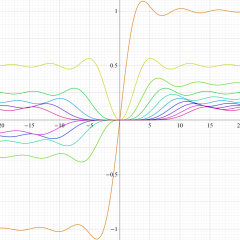
一般積分第1種 Bessel 関数は、Bessel 関数項の級数
に展開される。
などがある。
恐らく、一般積分 Bessel 関数の応用事例も存在しない。
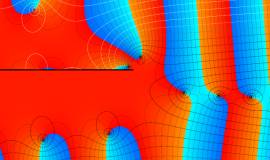
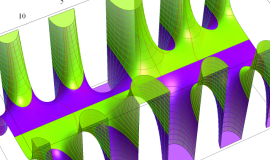
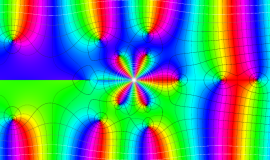
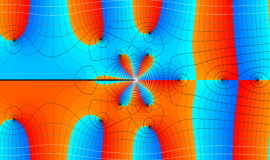
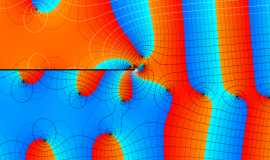
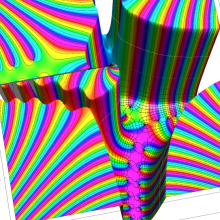
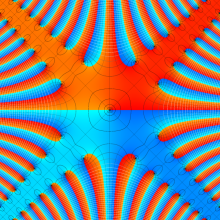
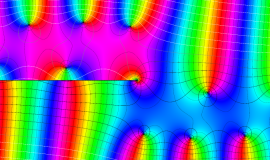
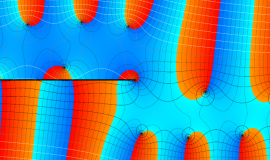
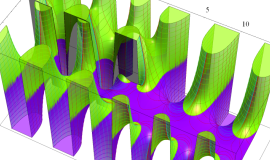
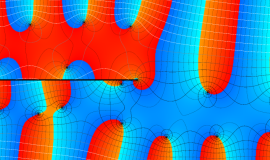
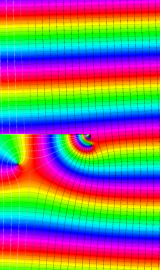
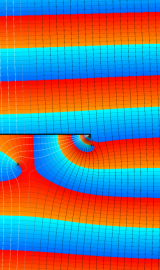
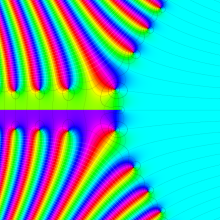
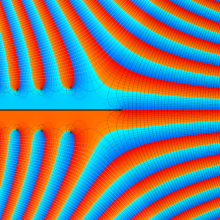
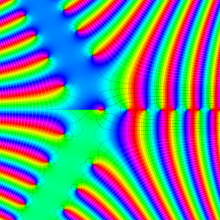
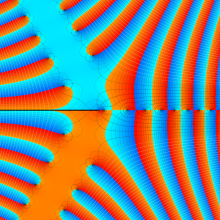
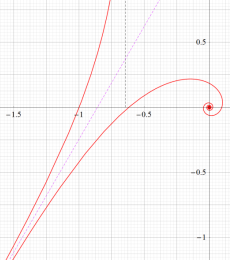
色が断絶している直線上、すなわち
3番目は、
色が断絶している直線上、すなわち
3番目は、
Bickley - Naylor 関数
日:Bickley-Naylor関数※1,ビックリー・ネイラー関数英:Bickley-Naylor function,仏:Fonction de Bickley-Naylor,独:Bickley-Naylor funktion
第2種変形 Bessel 関数の Riemann - Liouville 積分※2に相当する
を、Bickley - Naylor 関数という。積分表示式は上記以外にも、
等が知られている。
Bickley - Naylor 関数は、一般超幾何関数による閉形式
で表わせる。
で定義されるが、実際の数値計算では、上記の
を初期関数とする漸化式
を用いた方が便利である。
Bickley - Naylor 関数は
となる。
Bickley - Naylor 関数は、球または円柱の内部に封じ込められた熱放射 (輻射熱) の分布、円柱形状の原子炉内部における中性子束の計算等に現れ、それらの応用事例では、専ら
1935年に W. G. Bickley は強制対流を研究した際、併せてこの関数を導入し、同年には J. Nayler ※1と共同で
【註記】
※1:Naylor の綴りは誤りであって、本来は Nayler が正しい。しかし、ある原子核物理学の教科書で誤植 (e → o) が発生し、以降それが一般に定着してしまった (当サイトでも、誤りを承知のうえ関数名称に対しては Naylor を使用する)。なお、J. Nayler について知られている事は少ない。イギリスの王立大学 (Imperial College) で工学の学士資格を取得している事等は判明している。(以上の内容は、Serge Marguet 著 「The Physics of Nuclear Reactors」 (2018年 Springer) の518頁にある脚注による。)
※2:Riemann - Liouville 積分とは、関数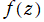 に対する演算子
に対する演算子
のことをいう。これは、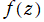 を
を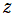 で
で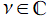 階積分したものに相当し、非整数階積分 (Fractional integral) とも呼ばれる。
階積分したものに相当し、非整数階積分 (Fractional integral) とも呼ばれる。
※1:Naylor の綴りは誤りであって、本来は Nayler が正しい。しかし、ある原子核物理学の教科書で誤植 (e → o) が発生し、以降それが一般に定着してしまった (当サイトでも、誤りを承知のうえ関数名称に対しては Naylor を使用する)。なお、J. Nayler について知られている事は少ない。イギリスの王立大学 (Imperial College) で工学の学士資格を取得している事等は判明している。(以上の内容は、Serge Marguet 著 「The Physics of Nuclear Reactors」 (2018年 Springer) の518頁にある脚注による。)
※2:Riemann - Liouville 積分とは、関数
のことをいう。これは、
積分 Airy 関数
比較的応用事例の多い Airy 関数は、その積分公式についても多数の結果が公式集に掲載されている。最も簡単な形の積分として、NISTの9.10(i)を例示すれば、となっている※1。以降では、これまでと同様に、Airy 関数に対しても積分三角関数および Fresnel 関数の類似を考える (後者については次節で扱う)。前者を具体的に、
で独自に定義し、積分 Airy 関数と呼ぶ。ここに、
積分 Airy 関数は、正規化された一般超幾何関数によって、
と表わすことができる。
【註記】
※1:これらの公式に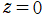 を代入し、
を代入し、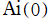 等を特殊値で表わすと、NISTの9.10(iv)にも掲載されている次の結果が得られる。
等を特殊値で表わすと、NISTの9.10(iv)にも掲載されている次の結果が得られる。
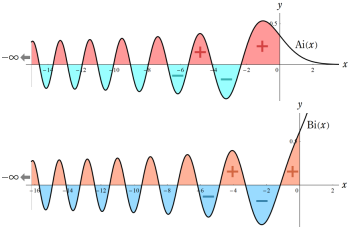
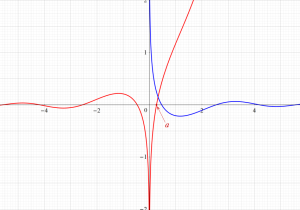
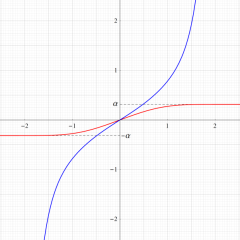
ただし、1番目, 3番目の定積分の値は、符号付き面積 (下図参照) で解釈し、
となるので、条件収束な広義積分としての値である。
※1:これらの公式に
ただし、1番目, 3番目の定積分の値は、符号付き面積 (下図参照) で解釈し、
となるので、条件収束な広義積分としての値である。
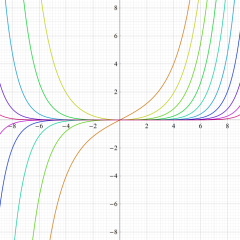
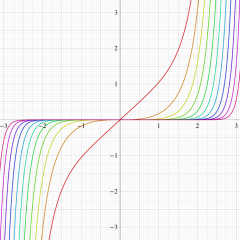
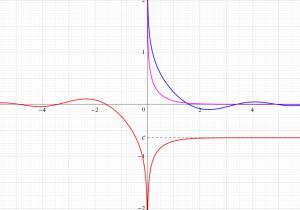
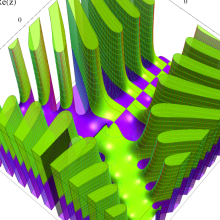
紫色の漸近線は、一次関数
Airy - Fresnel 関数
独自に定義した積分関数を、Airy - Fresnel 関数と呼ぶ。
同様に、正規化された一般超幾何関数で表わすと、
となる。両者はともに超越整関数である。
【 Petite Galerie 】
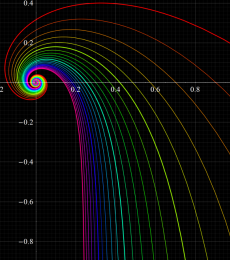
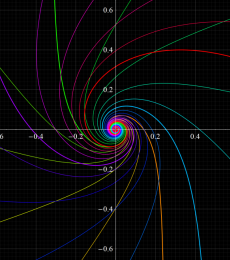
「蝶の飛翔」
(原点からの距離を変数とする第2種 Airy 関数で曲率が定まる曲線)
(原点からの距離を変数とする第2種 Airy 関数で曲率が定まる曲線)