Legendre 関数
日:
Legendre関数,
ルジャンドル関数
英:
Legendre function,仏:
Fonction de Legendre,独:
Legendre-funktion
二階の線形常微分方程式
は超幾何微分方程式の特別な場合であり、
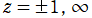
を確定特異点とする。これを Legendre の微分方程式といい、その解の基本系
+b・Q[ν](z)](siki_spec160/legendre00300.png)
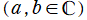
を成す二つの関数は、
超幾何関数で表わすと
となる。これを順に、第1種および第2種 Legendre 関数という。このうち、第1種は常に
=1](siki_spec160/legendre00600.png)
となるように選んだ特別な解であって、一般に
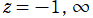
を対数分岐点とし、実軸上の区間
![(-∞, -1]](siki_spec160/legendre00800.png)
に分枝切断線が置かれる。第2種は一般に
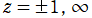
を対数分岐点とし、実軸上の区間
![(-∞, -1]](siki_spec160/legendre00800.png)
および
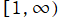
に分枝切断線が置かれる。分枝切断線
![(-∞, -1]](siki_spec160/legendre00800.png)
を越える解析接続は、
によって成される。
Legendre 関数はこの他にも、次数

に関する整数差の線形漸化式 (隣接関係式)、

の符号を変える公式等を満たすが、次節で扱う
Legendre 陪関数の特別な場合が Legendre 関数になるので、併せて次節も参照して欲しい。
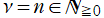
である第1種 Legendre 関数は、前述の分岐点まわりでの多価性が消えて、多項式
に還元される。しかし、これは応用面での出現頻度が高いため重要とされ、Legendre 多項式と呼ばれる。Legendre 多項式の上記以外の表現方法としては、母関数表示式および 「Rodrigues の公式」
が有名である。尤も、
=1](siki_spec160/legendre01600.png)
および
=z](siki_spec160/legendre01700.png)
を初期関数として漸化式を用いても容易に得られる※1。Legendre 多項式
](siki_spec160/legendre01800.png)
は、
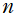
が偶数 (奇数) ならば偶関数 (奇関数) となる。直交多項式としての
](siki_spec160/legendre01800.png)
の性質は、同様に次節でまとめて触れる。
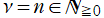
である第2種 Legendre 関数
](siki_spec160/legendre02100.png)
は
](siki_spec160/legendre01800.png)
で表わせるが、対数因子を持つ項も伴い
となる。第2種に対しても、母関数表示式
が知られている。また、
](siki_spec160/legendre02100.png)
は
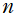
が偶数 (奇数) ならば奇関数 (偶関数) となる。

が半奇数のとき、Legendre 関数は
完全楕円積分で表わせる。特に、
となるので、漸化式からこの事が従う。
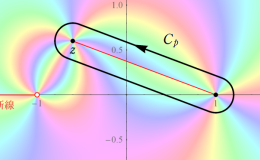
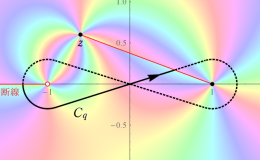
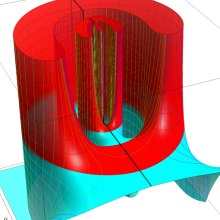
Legendre 関数の積分表示式も多数得られており、理論の審美的観点等から、これを Legendre 関数の導入定義とすることもある。そのような一例として、Schläfli 積分
がある※2。ここに、被積分関数は
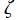
平面上の直線区間
![(-∞, -1]](siki_spec160/legendre00800.png)
および
![[1, z]](siki_spec160/legendre02400.png)
に分枝切断線を持ち、積分経路
![C[p]](siki_spec160/legendre02500.png)
または
![C[q]](siki_spec160/legendre02600.png)
の形と進路は下図のとおりとする。
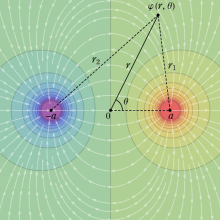
Legendre 関数 (特に Legendre 多項式) は、多くが Legendre 陪関数の応用事例に伴って現れる。Legendre 関数に顕著な応用事例としては、質点での重力ポテンシャル、点電荷によって生じる静電位分布を極座標で表わす問題等がある。例えば、極座標上の位置
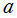
に点電荷
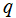
が1個あるとき、その周辺における静電位
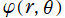
は、母関数表示式を示唆する形
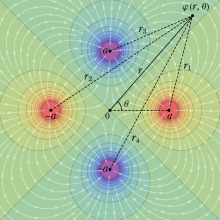
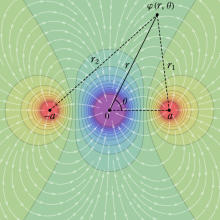
で与えられる。これは、電気双極子 (位置
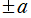
に正負の点電荷)、電気多重極子 (極座標または球座標の遠方で正負が打ち消されるよう点電荷を4個または8個配置する等) に拡張すると、上記級数で寄与が最も大きくなる初項のインデックスが、
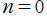
から
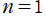
または
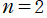
等に変わる。よって、原点から遠い位置での静電位
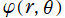
の分布状況は、無理関数で明示するよりも級数展開した方が把握しやすくなる※3。
図:電気双極子・電気4重極子・直線状電気4重極子による静電位分布
歴史的に Legendre 関数の萌芽は、1748年の D. Bernoulli による惑星などの回転楕円体における重力の研究に見出される。この問題は J. L. Lagrange, P. S. Laplace 等による研究を経て、1785年に A. M. Legendre が極座標に移行する前述の方法 (静電の場合と同じ方法) によって解を母関数で表示するアイデアに至り、そこに現れる係数自体の性質についても詳しく研究した。これが Legendre 関数の正式な導入時期とされ、関数名称の由来にもなっている。
](siki_spec160/legendre03400.png)
も含めて、その後も E. Heine (1842年), P. L. Chebyshev (1855年), L. Schläfli (1881年) 等による研究が続く。記号
](siki_spec160/legendre03300.png)
は、1875年に I. Todhunter が初めて導入した。
【註記】
※1:次数が小さい Legendre 多項式の具体的表示の羅列は、特殊関数の書籍では必ずと言って良いほど掲載されているので、冗長ながらここでもそれを掲載する。
※2:1881年に Schläfli は積分表示式を用いて、

を複素数とする Legendre 関数を初めて論じた。
※3:詳しくは、G. Arfken 著 「基礎物理数学3:特殊関数と積分方程式」 の83~88頁を参照。
なお、位置
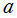
にある1個の点電荷
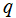
での正負が (静電ではなく) 周期
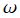
で単振動する場合の、時刻
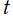
における電位
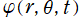
は、
となり、これは電波伝播を示す (ただし、Legendre 関数では表わせない)。例えば、電波発生源が直線状電気4重極子ならば、
となる。
図:電気双極子・電気4重極子・直線状電気4重極子による電波伝播の動画
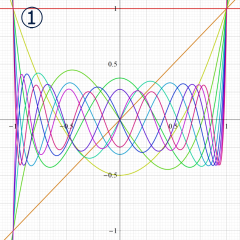
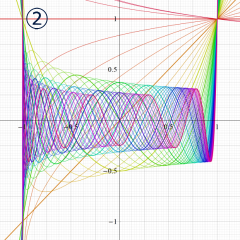
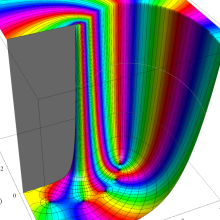
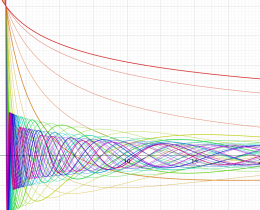
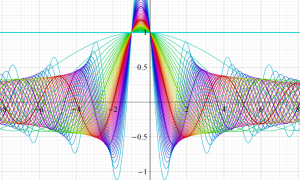
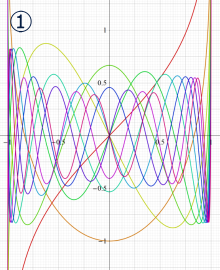
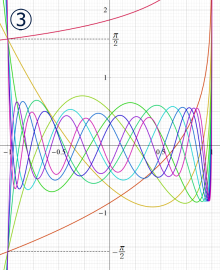
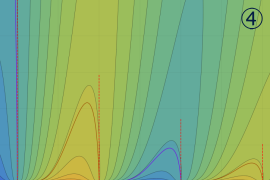
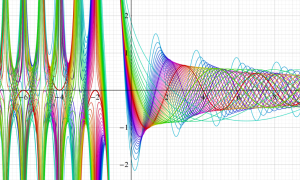
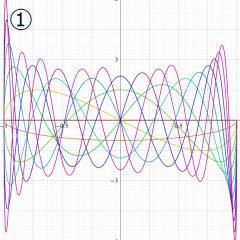
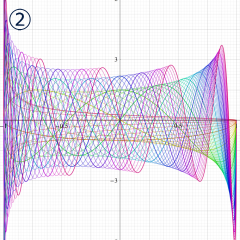
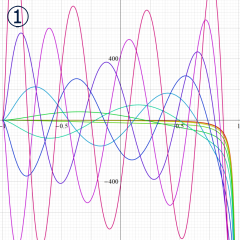
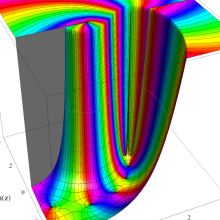
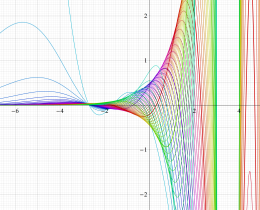
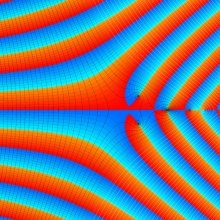
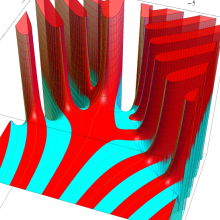
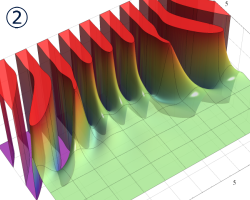
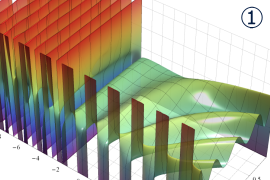
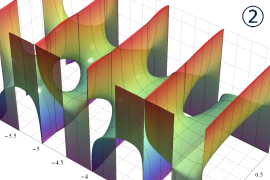
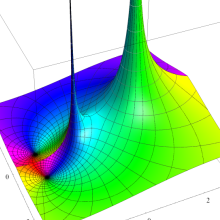
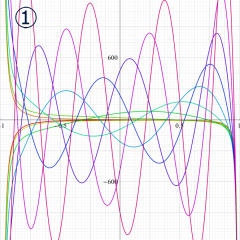
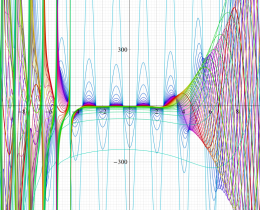
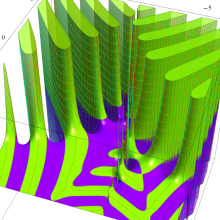
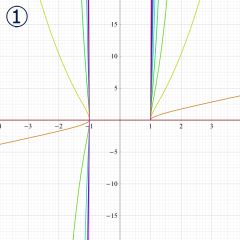
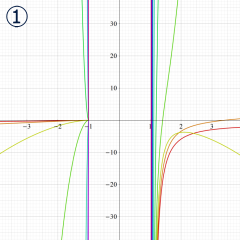
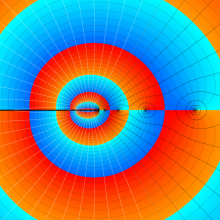
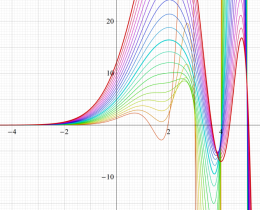
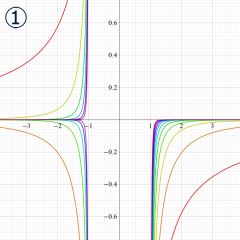
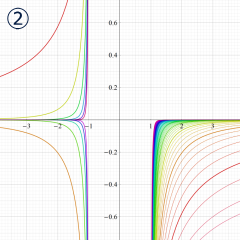
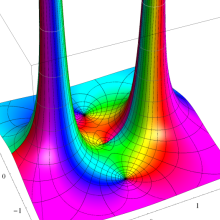
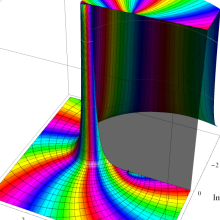
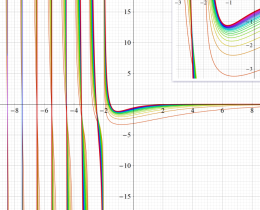
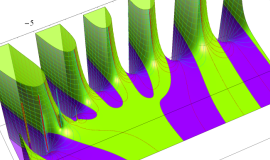
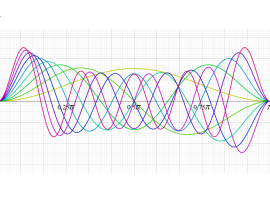
](siki_spec160/legendre05300.png)
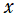
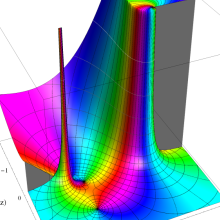
を実変数とする、第1種 Legendre 関数のグラフ。
①整数次 (Legendre 多項式)
](siki_spec160/legendre03900.png)
。
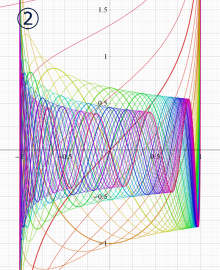
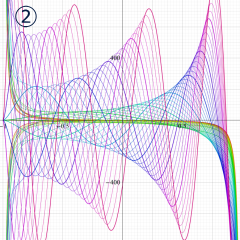
②実数次
](siki_spec160/legendre04000.png)
。
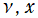
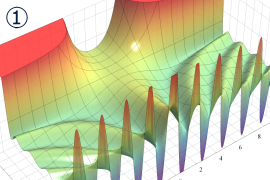
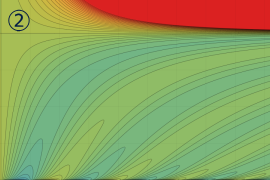
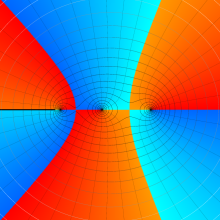
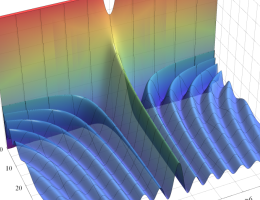
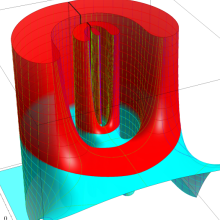
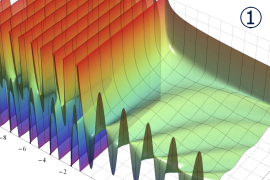
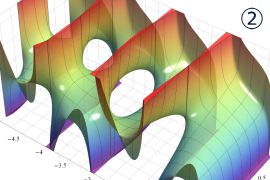
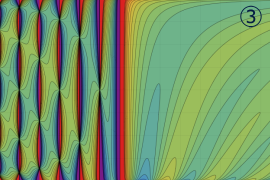
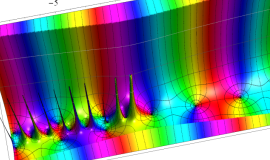
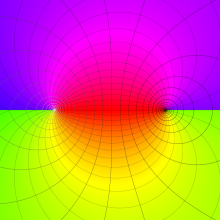
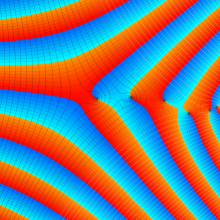
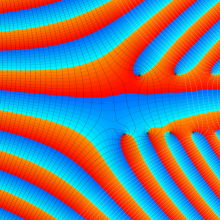
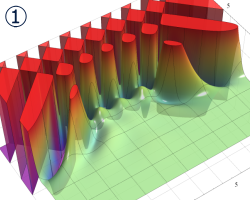
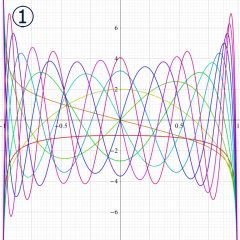
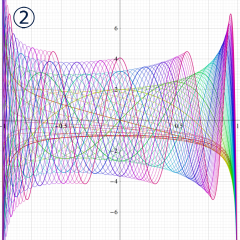
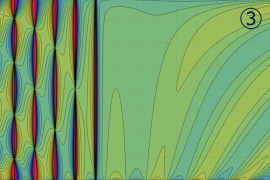
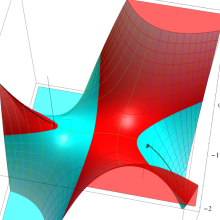
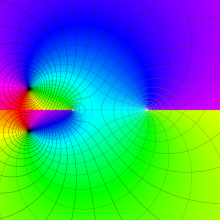
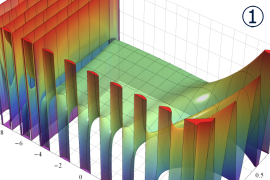
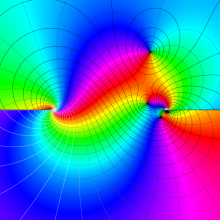
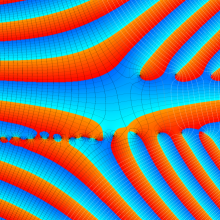
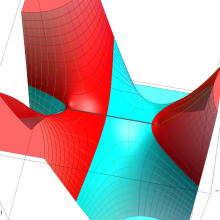
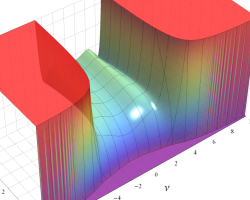
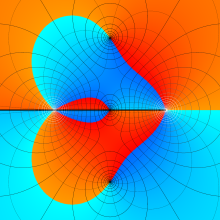
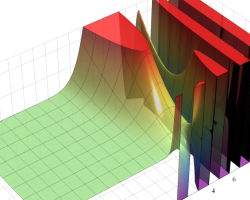
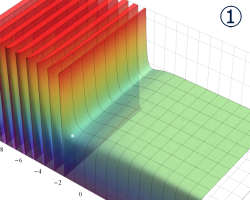
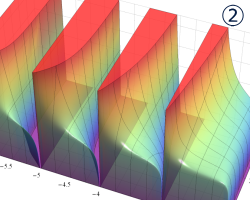
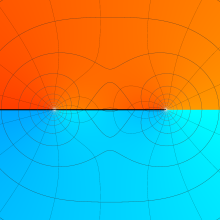
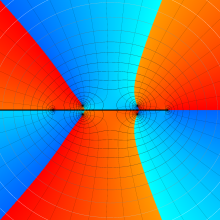
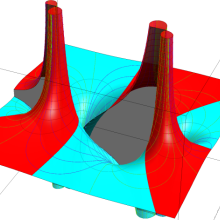
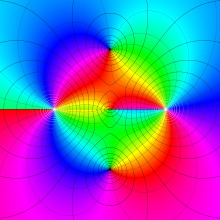
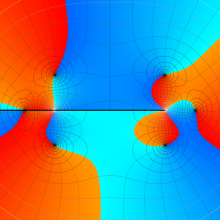
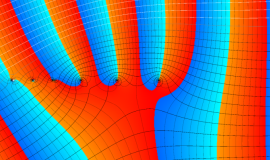
を実2変数とする、第1種 Legendre 関数
](siki_spec160/legendre04000.png)
のグラフ。
①公式
= P[-ν-1](z)](siki_spec160/legendre04200.png)
によって、このグラフは
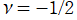
に対称となる。
②これに類似したグラフが、犬井鉄郎 著 「超幾何関数・球関数・円筒関数」 (1948年) の566頁にも掲載されている。
③等高線
=1](siki_spec160/legendre04400.png)
は直線
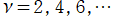
に接し、等高線
=-1](siki_spec160/legendre04600.png)
は直線
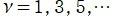
に接する。

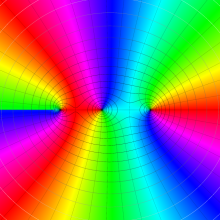
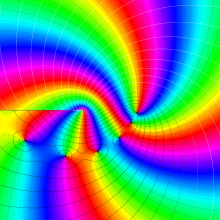
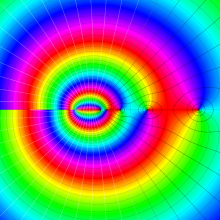
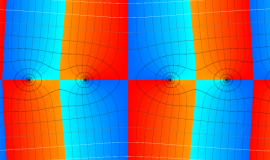
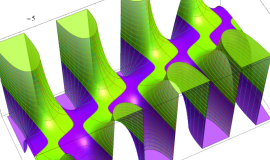
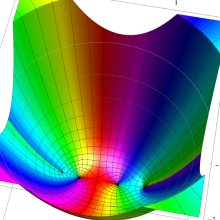
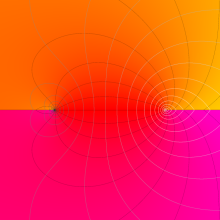
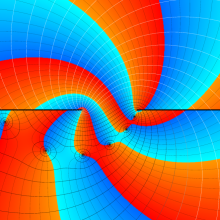
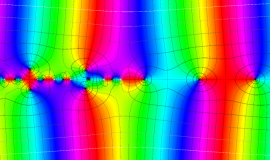
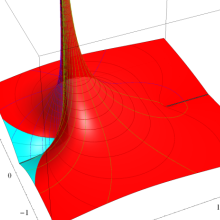
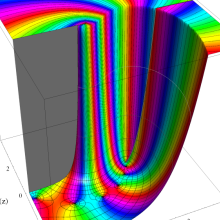
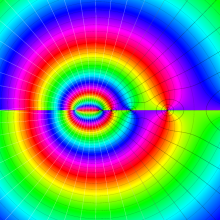
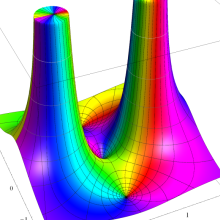
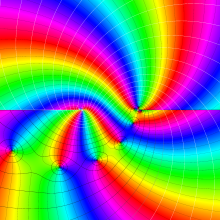
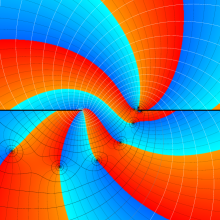
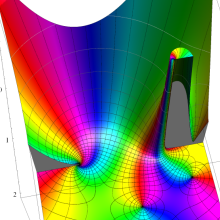
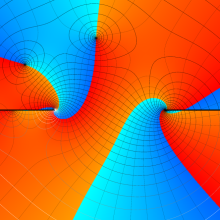
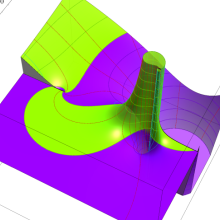
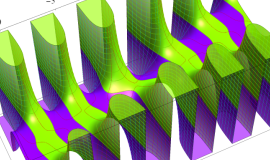
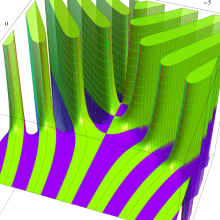
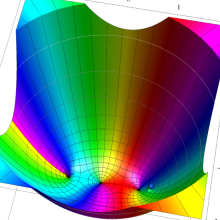
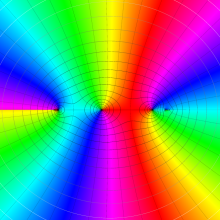
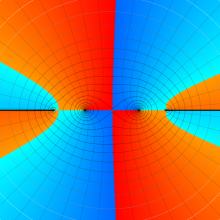
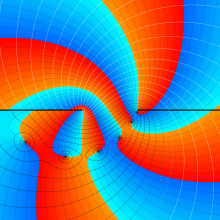
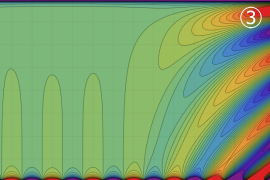
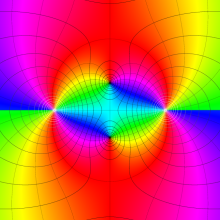
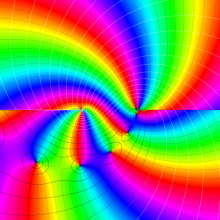
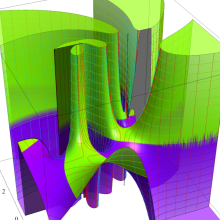
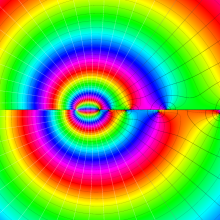
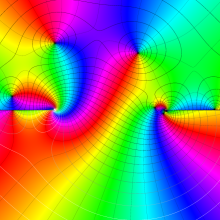
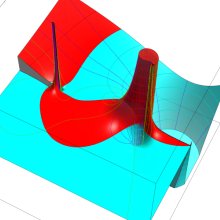
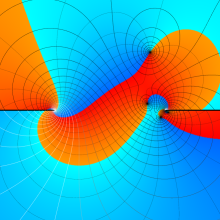
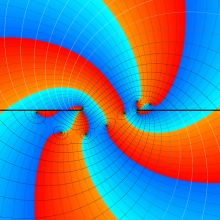
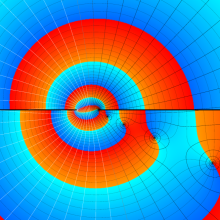
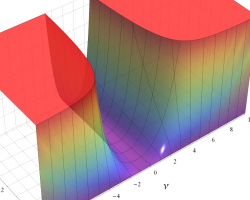
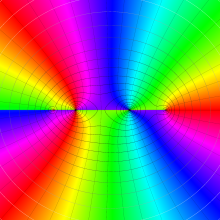
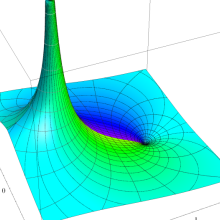
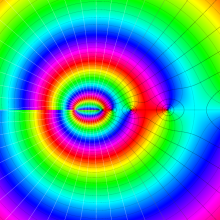
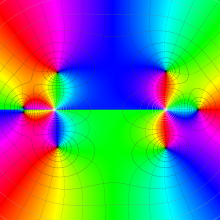
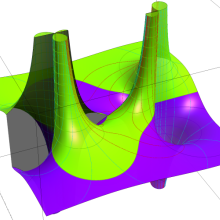
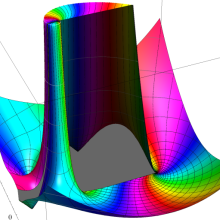
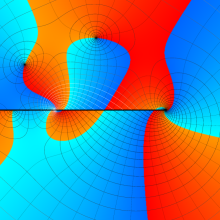
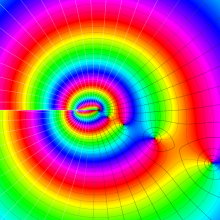
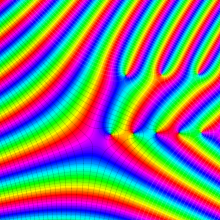
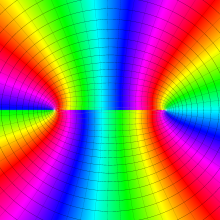
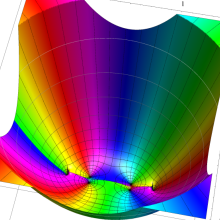
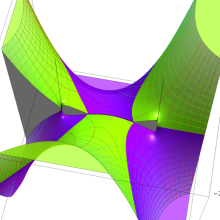
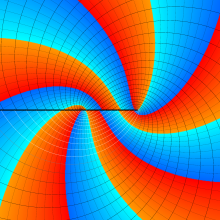
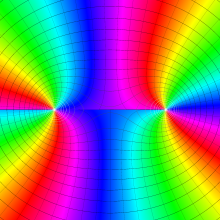
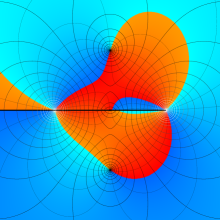
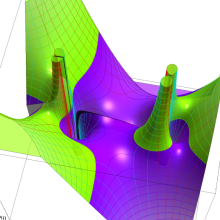
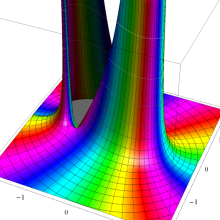
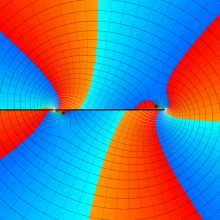
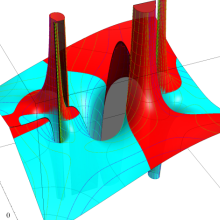
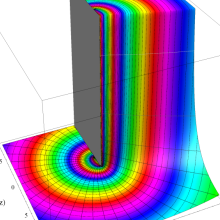
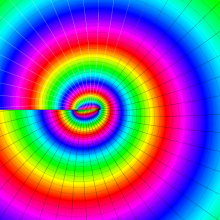
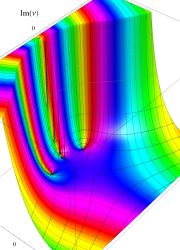
を複素変数とする、第1種 Legendre 関数
](siki_spec160/legendre04800.png)
のグラフ。

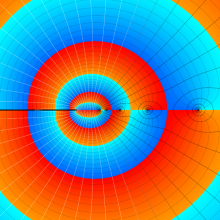
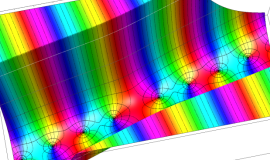
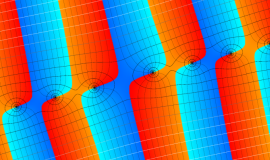
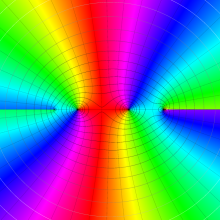
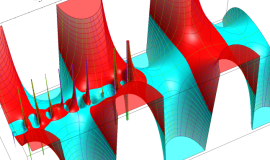
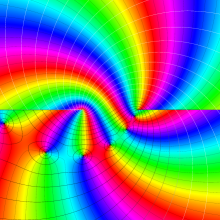
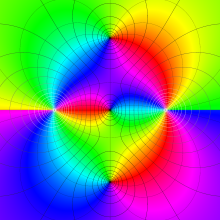
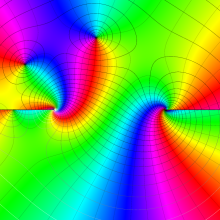
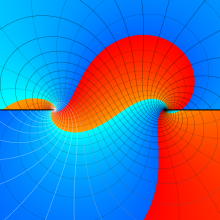
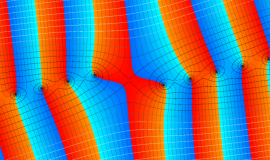
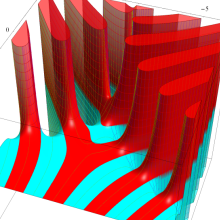
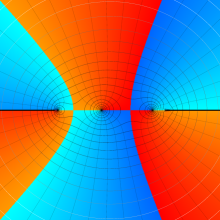
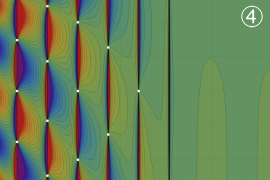
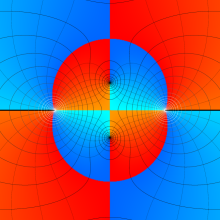
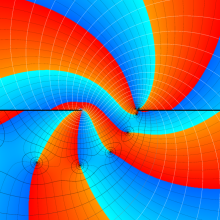
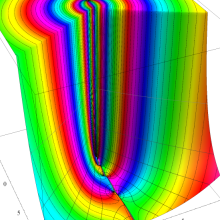
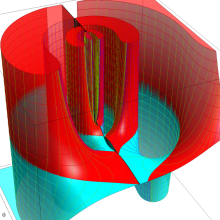
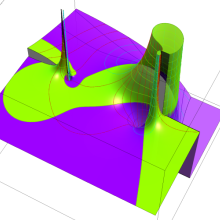
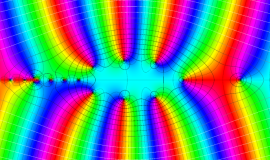
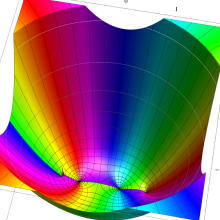
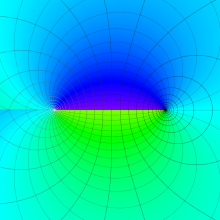
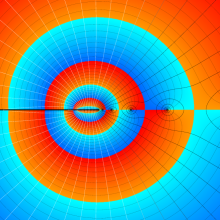
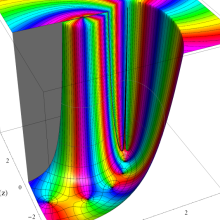
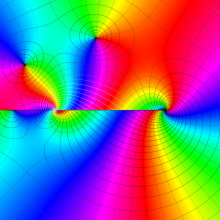
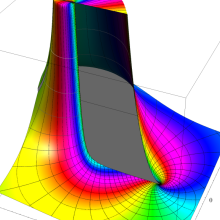
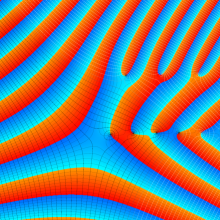
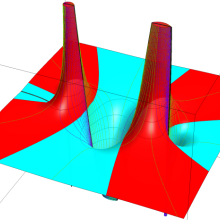
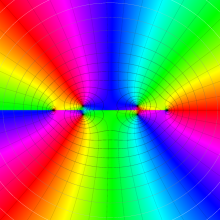
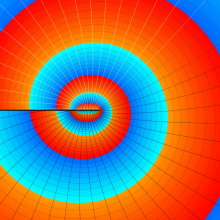
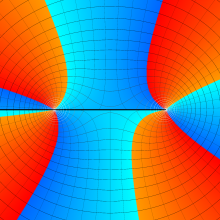
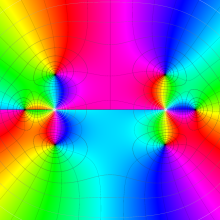
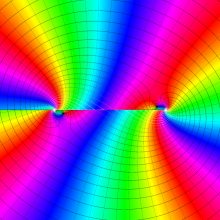
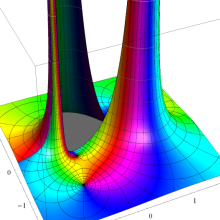
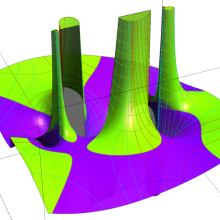
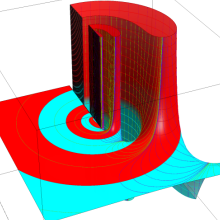
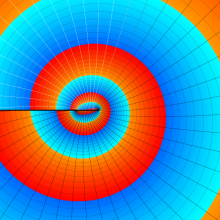
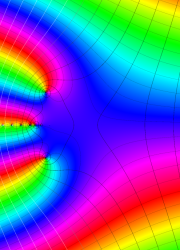
を複素変数とする、第1種 Legendre 関数
](siki_spec160/legendre04900.png)
のグラフ。

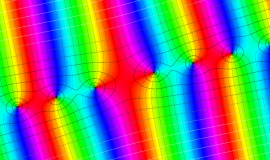
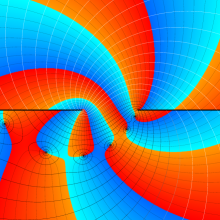
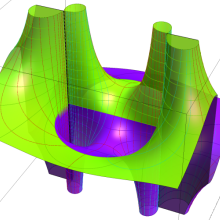
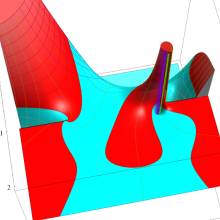
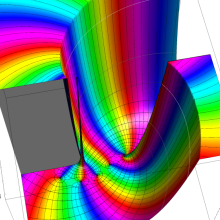
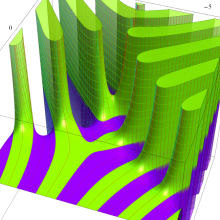
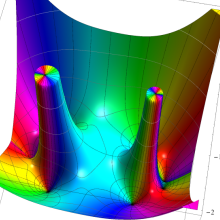
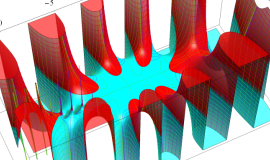
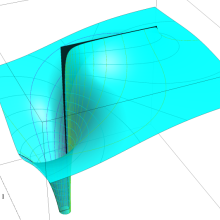
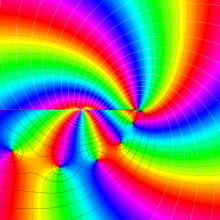
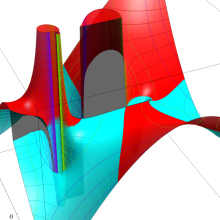
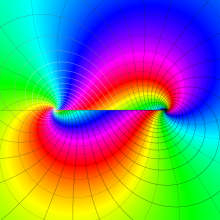
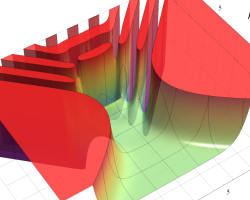
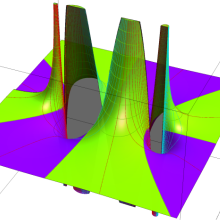
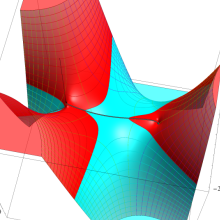
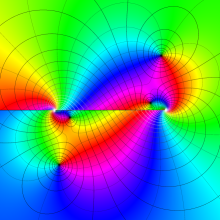
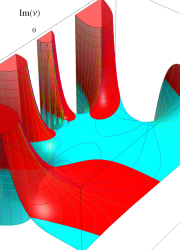
を複素変数とする、第1種 Legendre 関数
](siki_spec160/legendre05000.png)
のグラフ。
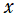
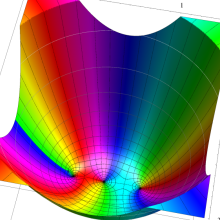
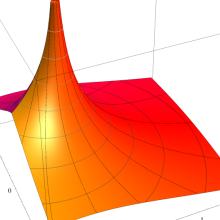
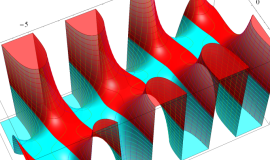
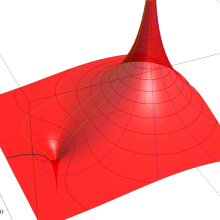
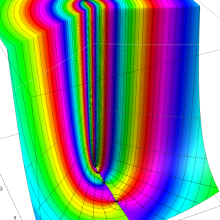
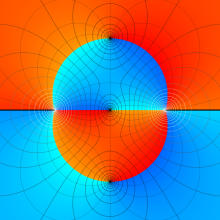
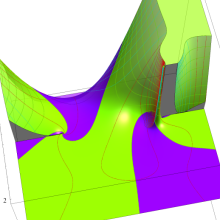
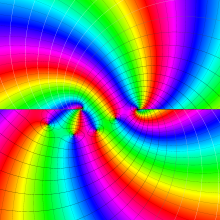
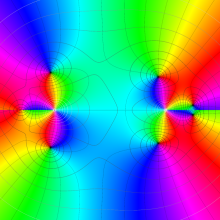
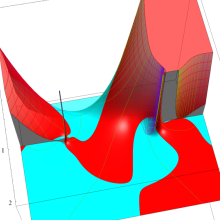
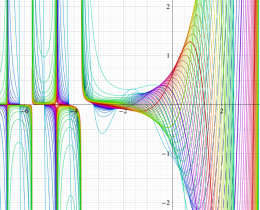
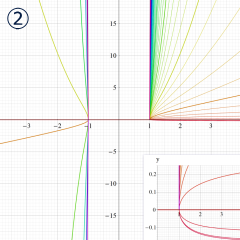
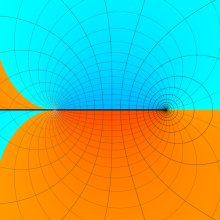
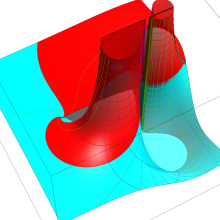
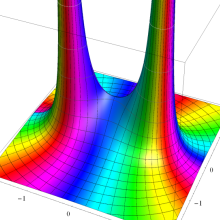
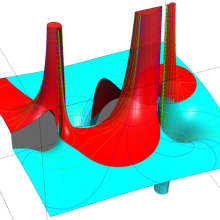
を実変数とする、第1種 Legendre 関数
](siki_spec160/legendre05100.png)
のグラフ。
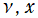
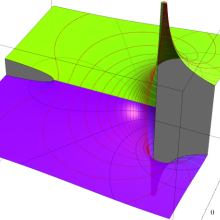
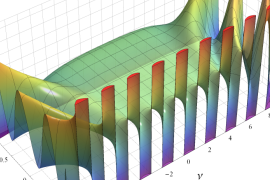
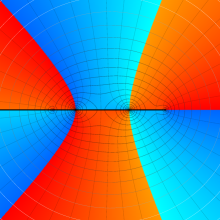
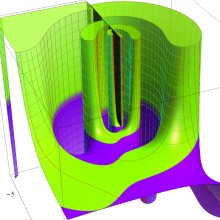
を実2変数とする、第1種 Legendre 関数
](siki_spec160/legendre05100.png)
のグラフ。

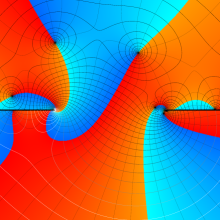
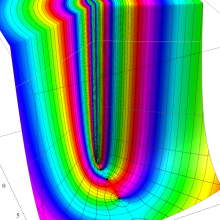
を複素変数とする、第1種 Legendre 関数
](siki_spec160/legendre05200.png)
のグラフ。
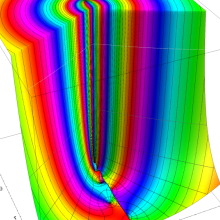
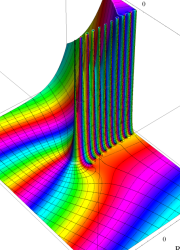
アニメーション
(10.4MB)

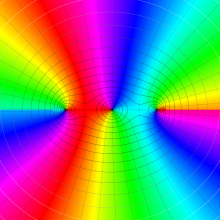
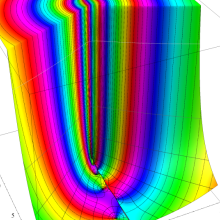
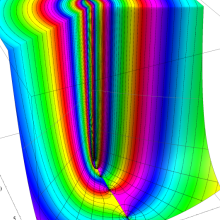
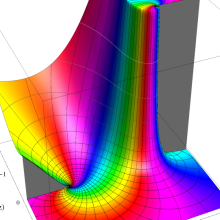
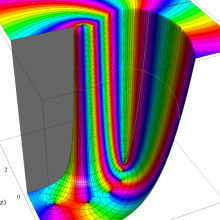
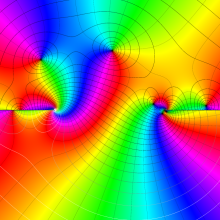
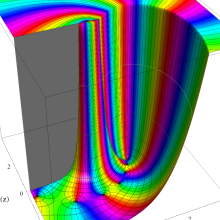
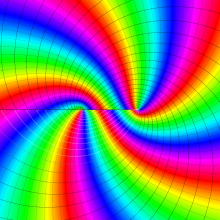
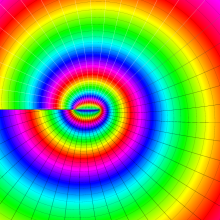
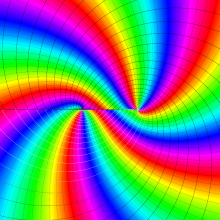
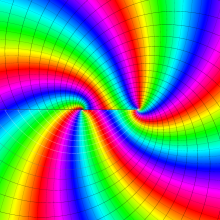
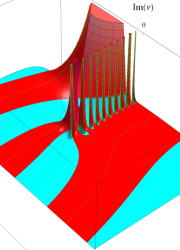
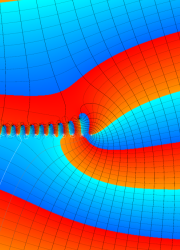
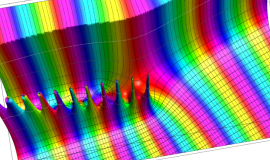
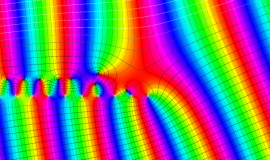
を複素変数とする、第1種 Legendre 関数
](siki_spec160/legendre03300.png)
のグラフ。

は実数を動く。
 (変数ν)](siki_spec160/legendre05600.png)

を実変数とする、第1種 Legendre 関数
](siki_spec160/legendre04000.png)
のグラフ。

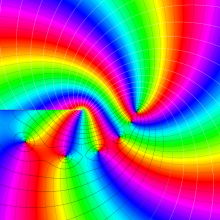
を複素変数とする、第1種 Legendre 関数
](siki_spec160/legendre05400.png)
のグラフ。

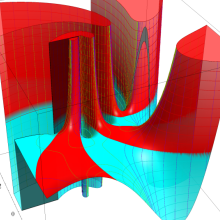
を複素変数とする、第1種 Legendre 関数
](siki_spec160/legendre05500.png)
のグラフ。
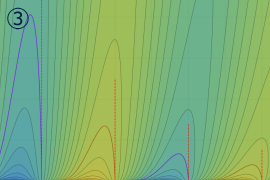
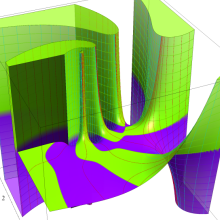
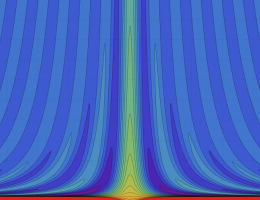
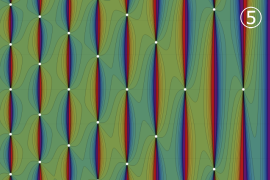
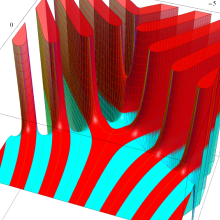
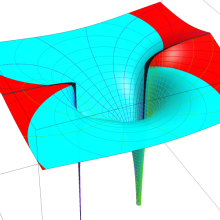
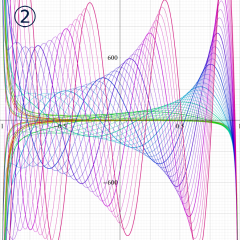
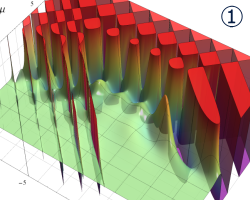
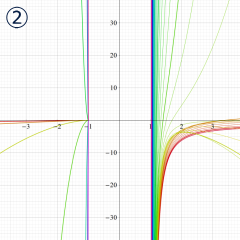
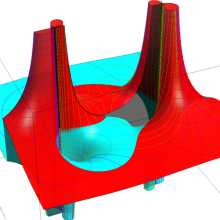
](siki_spec160/legendre07300.png)
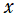
を実変数とする、第2種 Legendre 関数のグラフ。
①整数次
](siki_spec160/legendre05700.png)
。
②実数次
](siki_spec160/legendre05800.png)
。
③完全楕円積分で表わされる半奇数次の
](siki_spec160/legendre05800.png)
は、
=±π/2*(-1)^(ν+1/2)](siki_spec160/legendre05900.png)
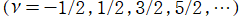
となる。
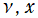
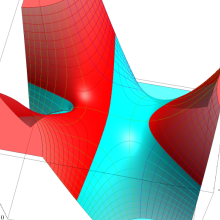
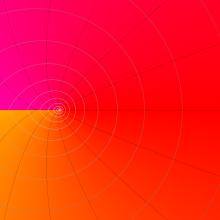
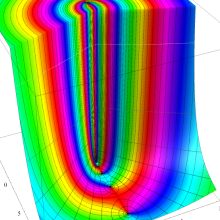
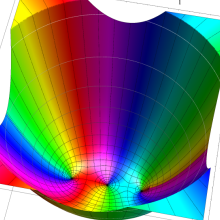
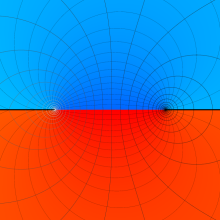
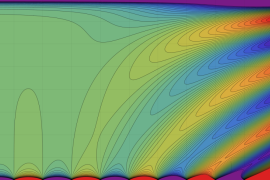
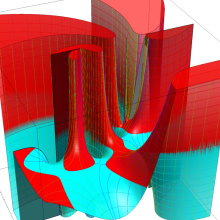
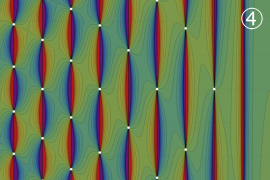
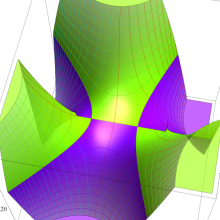
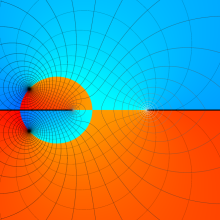
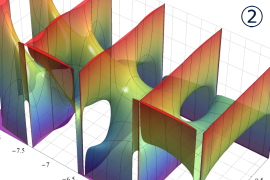
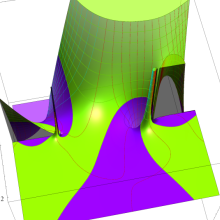
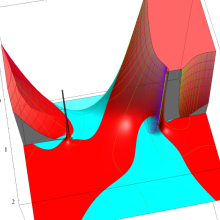
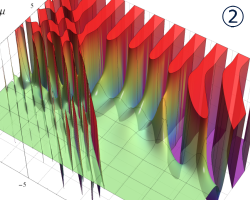
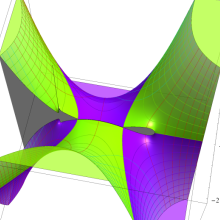
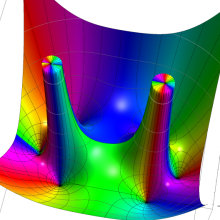
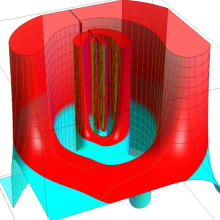
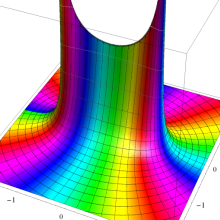
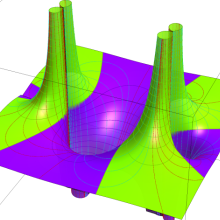
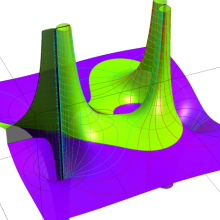
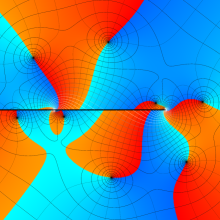
を実2変数とする、第2種 Legendre 関数
](siki_spec160/legendre05800.png)
のグラフ。
①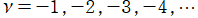
では関数が定義されない。
②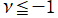
の範囲を拡大した場合。
③「超幾何関数・球関数・円筒関数」 にある図に準じたグラフ。
④等高線
=π/2](siki_spec160/legendre06200.png)
は直線
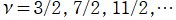
に接し、等高線
=-π/2](siki_spec160/legendre06400.png)
は直線
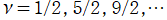
に接する。
⑤白点は等高線の共有点で、その
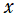
座標は
=0](siki_spec160/legendre06600.png)
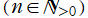
の実数根と一致する。

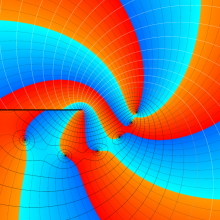
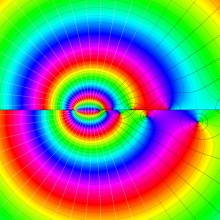
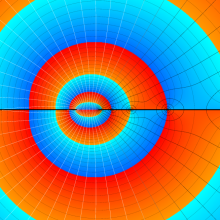
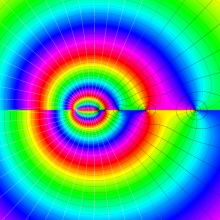
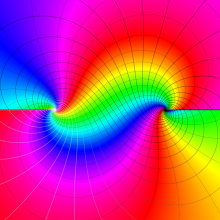
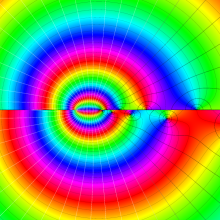
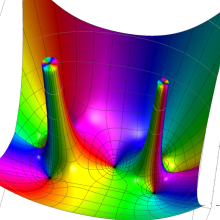
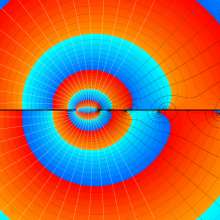
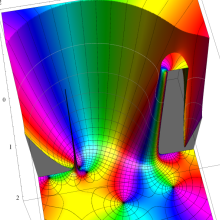
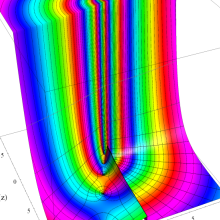
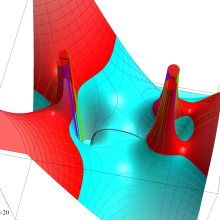
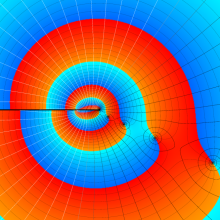
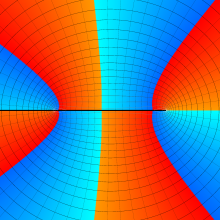
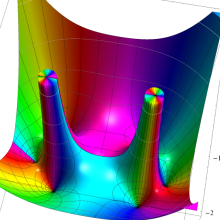
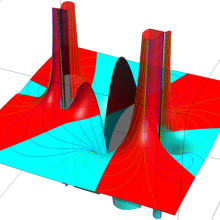
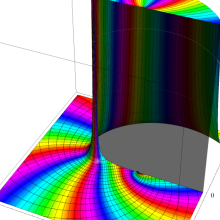
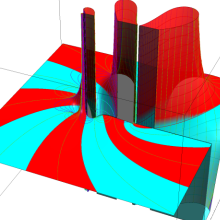
を複素変数とする、第2種 Legendre 関数
](siki_spec160/legendre06800.png)
のグラフ。

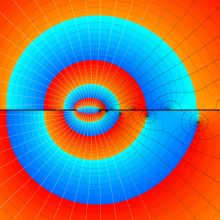
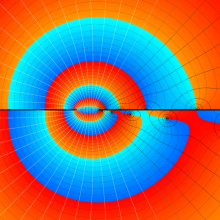
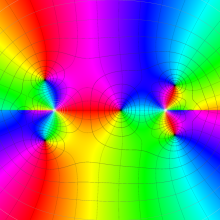
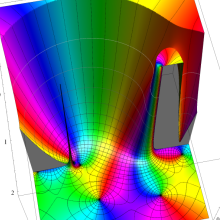
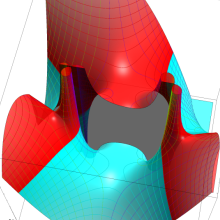
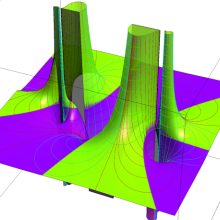
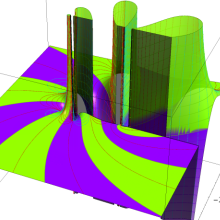
を複素変数とする、第2種 Legendre 関数
](siki_spec160/legendre06900.png)
のグラフ。

を複素変数とする、第2種 Legendre 関数
](siki_spec160/legendre07000.png)
のグラフ。

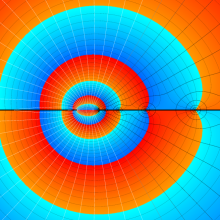
を複素変数とする、第2種 Legendre 関数
](siki_spec160/legendre07100.png)
のグラフ。

を複素変数とする、第2種 Legendre 関数
](siki_spec160/legendre07200.png)
のグラフ。
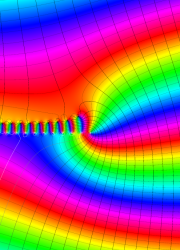
アニメーション
(10.1MB)

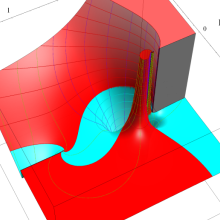
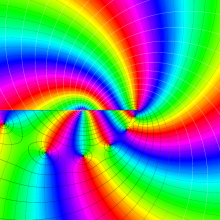
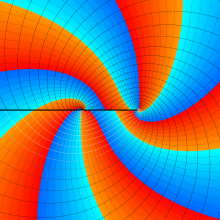
を複素変数とする、第2種 Legendre 関数
](siki_spec160/legendre03400.png)
のグラフ。

は実数を動く。
 (変数ν)](siki_spec160/legendre07600.png)

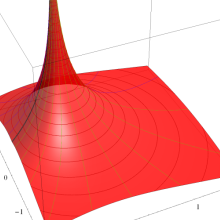
を実変数とする、第2種 Legendre 関数
](siki_spec160/legendre05800.png)
のグラフ。

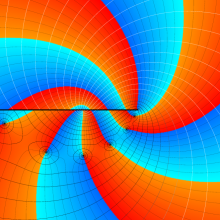
を複素変数とする、第2種 Legendre 関数
](siki_spec160/legendre07400.png)
のグラフ。

を複素変数とする、第2種 Legendre 関数
](siki_spec160/legendre07500.png)
のグラフ。
日:
Legendre陪関数,
ルジャンドル陪関数,
Legendre同伴関数
英:
Associated Legendre function,仏:
Fonction associée de Legendre,独:
Assoziierten Legendre-funktion
日:
球関数
独:
Kugelfunktion
Legendre 陪関数 (Ferrers 型) の定義は、Legendre 関数を逐次微分して無理関数因子を掛けた、
が元になっている※1。しかし、両者がともに満たす微分方程式とその解の表示によって、階数
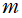
は複素数にまで拡張可能である。二階の線形常微分方程式
は Legendre の陪微分方程式と呼ばれ、
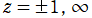
を確定特異点とする。その解の基本系
+b・Q[ν, μ](z)](siki_spec160/legendre07900.png)
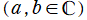
を成す二つの関数は、超幾何関数で表わすと
となる。これを順に、第1種および第2種 Legendre 陪関数 (Ferrers 型) という※2。両者は

が非負整数ならば、前述の逐次微分による定義と一致する。なお、
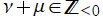
ならば
](siki_spec160/legendre08300.png)
は関数自体が存在しない。
第1種は一般に
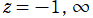
が対数分岐点および
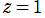
が代数 (

が非有理数ならば対数) 分岐点となり、第2種は一般に
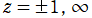
が対数分岐点となる。よって、両者ともに実軸上の区間
![(-∞, -1]](siki_spec160/legendre00800.png)
および
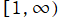
に分枝切断線が置かれる。このうち、分枝切断線
![(-∞, -1]](siki_spec160/legendre00800.png)
を越える解析接続は、
によって成される。
Legendre 陪関数は、次数

に関する整数差の線形漸化式 (隣接関係式)
を満たす。ここに
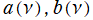
は、

に関して1を周期とする任意の周期関数である。また、

の符号を変える公式
が成り立つ。

に対して極限を取った Legendre 陪関数は、
Bessel 関数と
の関係にある。
特に重要なのが
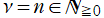
かつ
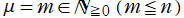
である第1種 Legendre 陪関数
](siki_spec160/legendre09100.png)
であり、Legendre 陪多項式と呼ばれる。正確には
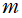
が偶数ならば多項式となるが、
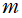
が奇数ならば多項式に
![Sqrt[1-z^2]](siki_spec160/legendre09200.png)
を掛けたものになる。このとき、
(x ∈ R)](siki_spec160/legendre09300.png)
は直交性
を満たす※3。
球座標 (三次元の極座標)
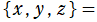
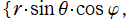
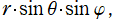
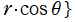
を用いて、Helmholtz 方程式の解を変数分離すると、天頂角
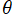
の方向に Legendre 陪関数が現れることは、既に
球 Bessel 関数の頁で触れた。同様に、球座標で Laplace 方程式
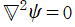
の解を
![ψ=Σ[m]Σ[n]{Ρ(r)Θ(θ)Φ(φ)}](siki_spec160/legendre09700.png)
の形に変数分離すれば、各座標方向は、
図:球座標における Laplace 方程式の解 (固有関数) →
Mathematica Code 
となる。それゆえ、Legendre 陪関数は 「球関数」 なる別名を持つ。Legendre 陪関数の物理学等への応用事例は、多くがこれらの方程式の解に由来する。例えば、帯電し回転している球面の周辺に生じる電磁界、球体まわりでの電磁波の回折、非圧縮な理想状態にある渦なし流体の速度分布、原子核の液滴モデルなどがある。後述の
球面調和関数も上記 Laplace 方程式の解に由来し、これは量子力学等で多用される。
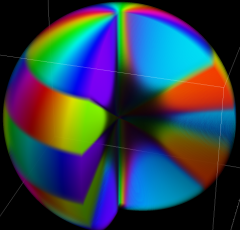
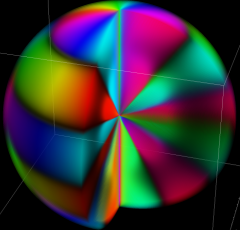
さらに、
扁長回転楕円体座標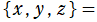
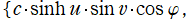
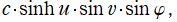
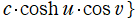
を用いて、Laplace 方程式の解を
![ψ=Σ[m]Σ[n]{Υ(u)Ξ(v)Φ(φ)}](siki_spec160/legendre10000.png)
の形に変数分離した場合にも Legendre 陪関数が現れ、
となる。扁平回転楕円体座標
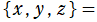
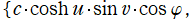
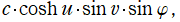
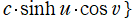
ならば、Laplace 方程式の解は
図:扁平回転楕円体座標における Laplace 方程式の解 (固有関数) →
Mathematica Code 
となる※4。これは、境界条件が回転楕円体である諸問題に現れ、一部は球座標のそれに類似する。よって、(Legendre 関数を含めた) Legendre 陪関数の応用事例数は、恐らく Bessel 関数に比肩するほど多いと思われる。
Legendre 関数の節で挙げた数学者の他にも、F. E. Neumann (1848年)※5, R. Olbricht (1888年), E. Hobson (1896年) 等が Legendre 陪関数の研究を手掛けている。"Ferrers 型" なる名称は、球面調和関数を研究した N. M. Ferrers (1877年) に由来する。
【註記】
※1:因子
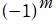
は 「Condon - Shortley の位相」 と呼ばれ、量子力学で必要になるため、球面調和関数はこの因子を含むように定義される。しかし書籍等によっては、この因子を省いた Legendre 陪関数の定義 (その場合、球面調和関数では因子を明示する定義) を採用していることもある。
※2:以降の説明では、Ferrers 型である旨を断っていない箇所があるが、当サイトでは Legendre 陪関数の記号を、Ferrers 型は
![P[ν, μ], Q[ν, μ]](siki_spec160/legendre10500.png)
、次節の
Hobson 型は
![Ph[ν, μ], Qh[ν, μ]](siki_spec160/legendre10600.png)
で記述しているので、恐らく判読できると思う。
※3:
](siki_spec160/legendre09100.png)
を
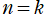
で現れる定数の平方根で割れば、その関数の直交積分は
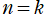
のとき常に1 (正規直交性) となる。このような調節を (直交関数の) 正規化という。
※4:Helmholtz 方程式の解を回転楕円体座標で変数分離したときは、Legendre 陪関数の代わりに
回転楕円体波動関数が現れる。
※5:F. E. Neumann は、第2種 Bessel 関数の別名で知られる C. G. Neumann の父。
](siki_spec160/legendre12400.png)
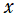
を実変数とする、第1種 Legendre 陪関数のグラフ。
①整数次
](siki_spec160/legendre10800.png)
。
②実数次
](siki_spec160/legendre10900.png)
。
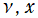
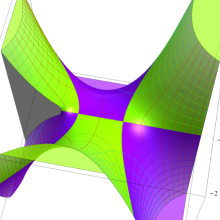
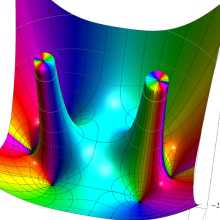
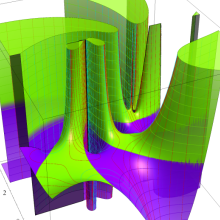
を実2変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre10900.png)
のグラフ。

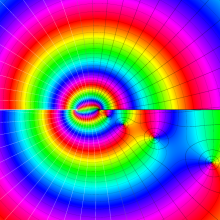
を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11000.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11100.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11200.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11300.png)
のグラフ。
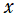
を実変数とする、第1種 Legendre 陪関数のグラフ。
①整数次
](siki_spec160/legendre11400.png)
。
②実数次
](siki_spec160/legendre11500.png)
。
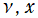
を実2変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11500.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11600.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11700.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11800.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11900.png)
のグラフ。
アニメーション
(11.2MB)

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11950.png)
のグラフ。

は実数を動く。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre12000.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre12100.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre12200.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre12300.png)
のグラフ。
 (変数ν)](siki_spec160/legendre12900.png)

を実変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre11500.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre12500.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre12600.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre12700.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre12800.png)
のグラフ。
 (変数μ)](siki_spec160/legendre13600.png)

を実変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre13000.png)
のグラフ。
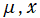
を実2変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre13000.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre13200.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre13300.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre13400.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre13500.png)
のグラフ。
 (実2変数ν, μ)](siki_spec160/legendre14000.png)
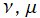
を実2変数とする、第1種 Legendre 陪関数のグラフ。
①](siki_spec160/legendre13800.png)
。
②](siki_spec160/legendre13900.png)
。
](siki_spec160/legendre16400.png)
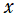
を実変数とする、第2種 Legendre 陪関数のグラフ。
①整数次
](siki_spec160/legendre14100.png)
。
②実数次
](siki_spec160/legendre14200.png)
。
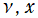
を実2変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre14200.png)
のグラフ。
①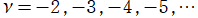
では関数が定義されない。
②負数の

方向を拡大した場合。
③「超幾何関数・球関数・円筒関数」 にある図に準じたグラフ。
④白点は等高線の共有点で、その
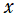
座標は
=0](siki_spec160/legendre14400.png)
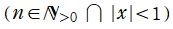
の実数根と一致する。

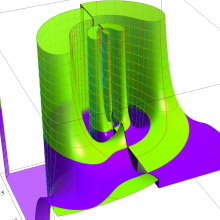
を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre14500.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre14600.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre14700.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre14800.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre14900.png)
のグラフ。
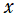
を実変数とする、第2種 Legendre 陪関数のグラフ。
①整数次
](siki_spec160/legendre15000.png)
。
②実数次
](siki_spec160/legendre15100.png)
。
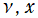
を実2変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15100.png)
のグラフ。
①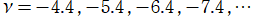
では関数が定義されない。
②負数の

方向を拡大した場合。
③「超幾何関数・球関数・円筒関数」 にある図に準じたグラフ。
④白点は等高線の共有点で、その
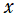
座標は
=0](siki_spec160/legendre15300.png)
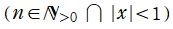
の実数根と一致する。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15400.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15500.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15600.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15700.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15800.png)
のグラフ。
アニメーション
(10.8MB)

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15850.png)
のグラフ。

は実数を動く。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15900.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre16000.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre16100.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre16200.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre16300.png)
のグラフ。
 (変数ν)](siki_spec160/legendre16900.png)

を実変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre15100.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre16500.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre16600.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre16700.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre16800.png)
のグラフ。
 (変数μ)](siki_spec160/legendre17500.png)

を実変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre17000.png)
のグラフ。
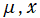
を実2変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre17000.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre17100.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre17200.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre17300.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre17400.png)
のグラフ。
 (実2変数ν, μ)](siki_spec160/legendre17800.png)
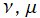
を実2変数とする、第2種 Legendre 陪関数のグラフ。
①](siki_spec160/legendre17600.png)
。
②](siki_spec160/legendre17700.png)
。
Legendre の陪微分方程式を満たすが、実軸上の区間
![(-∞, 1]](siki_spec160/legendre17900.png)
に分枝切断線が置かれるように選んだ、新しい解の基本系
+b・Qh[ν, μ](z)](siki_spec160/legendre18000.png)
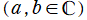
を成す二つの関数
を順に、第1種および第2種 Legendre 陪関数 (Hobson 型) という。これも、
](siki_spec160/legendre18300.png)
は
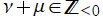
ならば関数自体が存在しない。分枝切断線
![(-∞, 1]](siki_spec160/legendre17900.png)
を越える解析接続は、
によって成される。
Hobson 型は、Ferrers 型の分枝と
の関係にある。特に、第1種の公式で条件区分が不要となるのは、
のみであって、しかもこの場合に限り
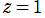
の分岐点が消えるので、分枝切断線は
![(-∞, -1]](siki_spec160/legendre00800.png)
に変わる。
Legendre 陪関数は、次数

に関する整数差の線形漸化式 (隣接関係式)
を満たす※1。ここに
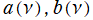
は、

に関して1を周期とする任意の周期関数である。また、

の符号を変える公式
が成り立つ。

に対して極限を取った Legendre 陪関数は、
変形 Bessel 関数と
の関係にある。
](siki_spec160/legendre18800.png)
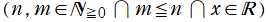
も直交性
を満たすが※2、
](siki_spec160/legendre18800.png)
自体は直交区間
![[-1, 1]](siki_spec160/legendre19100.png)
で実関数にならない。
Hobson 型が物理学等で応用される事例は少なく、むしろ複素関数論的な場面で現れることが多い。実際、変数
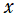
を区間
![[-1, 1]](siki_spec160/legendre19100.png)
の実数に限定した Ferrers 型では、複素変数の Hobson 型に対して実軸に上下から近付く極限を取った
が、しばしば定義として採用される。
"Hobson 型" なる名称は、Legendre 陪関数を研究した E. Hobson (1896年) に由来する。
【註記】
※1:Hobson 型が満たす二つの漸化式は、Ferrers 型が満たすそれと全く同じ形になっている。
※2:実は、
Ph[k, m](x)=(-1)^m*P[n, m](x)P[k, m](x)](siki_spec160/legendre19300.png)
となるからに過ぎない。
](siki_spec160/legendre21000.png)
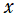
を実変数とする、第1種 Legendre 陪関数のグラフ。
①整数次
](siki_spec160/legendre19400.png)
。
②実数次
](siki_spec160/legendre19500.png)
。
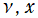
を実2変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre19500.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre19600.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre19700.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre19800.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre19900.png)
のグラフ。
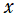
を実変数とする、第1種 Legendre 陪関数のグラフ。
①整数次
](siki_spec160/legendre20000.png)
。
②実数次
](siki_spec160/legendre20100.png)
。
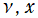
を実2変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20100.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20200.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20300.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20400.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20500.png)
のグラフ。
アニメーション
(11.1MB)

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20550.png)
のグラフ。

は実数を動く。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20600.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20700.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20800.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre20900.png)
のグラフ。
 (変数ν)](siki_spec160/legendre21200.png)

を複素変数とし、

と

を固定する場合の第1種 Legendre 陪関数
](siki_spec160/legendre18200.png)
は、
](siki_spec160/legendre08200.png)
を
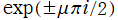
倍したものに過ぎないので、グラフの描画は省略する。
 (変数μ)](siki_spec160/legendre21800.png)

を実変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre21300.png)
のグラフ。
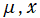
を実2変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre21300.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre21400.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre21500.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre21600.png)
のグラフ。

を複素変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre21700.png)
のグラフ。
 (実2変数ν, μ)](siki_spec160/legendre22300.png)
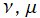
を実2変数とする、第1種 Legendre 陪関数
](siki_spec160/legendre21900.png)
のグラフ。
(因みに
](siki_spec160/legendre22000.png)
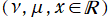
は、
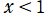
で実数値を取らないことに注意する。)
](siki_spec160/legendre24300.png)
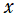
を実変数とする、第2種 Legendre 陪関数のグラフ。
①整数次
](siki_spec160/legendre22400.png)
。
②実数次
](siki_spec160/legendre22500.png)
。
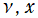
を実2変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre22500.png)
のグラフ。
①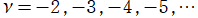
では関数が定義されない。
②負数の

方向を拡大した場合。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre22600.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre22700.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre22800.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre22900.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23000.png)
のグラフ。
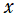
を実変数、および
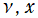
を実2変数とする第2種 Legendre 陪関数
](siki_spec160/legendre23100.png)
は、
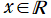
で実数値を取らない。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23300.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23400.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23500.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23600.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23700.png)
のグラフ。
アニメーション
(11.0MB)

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23750.png)
のグラフ。

は実数を動く。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23800.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre23900.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre24000.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre24100.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre24200.png)
のグラフ。
 (変数ν)](siki_spec160/legendre24900.png)

を実変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre22500.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre24500.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre24600.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre24700.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre24800.png)
のグラフ。
 (変数μ)](siki_spec160/legendre25500.png)

を実変数、および
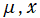
を実2変数とする第2種 Legendre 陪関数
](siki_spec160/legendre25000.png)
は、
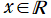
で実数値を取らない。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre25100.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre25200.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre25300.png)
のグラフ。

を複素変数とする、第2種 Legendre 陪関数
](siki_spec160/legendre25400.png)
のグラフ。
 (実2変数ν, μ)](siki_spec160/legendre25800.png)
](siki_spec160/legendre25600.png)
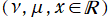
は、
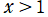
であっても一般に実数値を取らない。よって
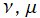
の実2変数グラフは省略する。
日:
球面調和関数
英:
Spherical harmonics,仏:
Harmonique sphérique,独:
Kugelflächenfunktion
球座標によって変数分離された Laplace 方程式の解のうち、応用面で特に重要となるのは
](siki_spec160/legendre25900.png)
を含まない (
![B[2]=0](siki_spec160/legendre26000.png)
となる) 場合である※1。また、
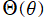
(ただし
](siki_spec160/legendre26200.png)
のみ) と
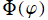
の基底関数は、正規直交性
を持つよう、予め正規化因子も含めた定義にしておくと、その分が煩雑にならなくて済む。一方、
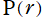
の基底関数は直交性を持たないので取り除くと、結局、二変数
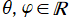
の関数
を導入するのが良いことになる。これを、球面調和関数という。併せて、
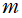
の符号を変える公式
がしばしば必要になる。
かくして球面調和関数は、単位球面全体で三次元の正規直交性
を満たす。したがって、球面上で定義された任意の連続関数
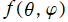
は、
に展開できる。これは Laplace 級数と呼ばれる。
なお量子力学では、3個の球面調和関数の積に対する、単位球面全体での積分
も現れる。ここに
は、「Wigner の 3-j 記号」 と呼ばれる※2。
実 Fourier 級数に準じて、
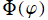
の基底関数が余弦, 正弦関数となるように選んだ球面調和関数
が、特に古典的な (量子力学でない) 物理問題等で必要となることがある。さらに、これら
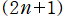
種類の球面調和関数を細分して、
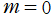
の場合を帯球調和関数 (Zonal spherical harmonics)、
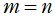
の場合を扇球調和関数 (Sectorial sph. har.)、その他
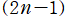
種類の場合を縞球調和関数 (Tesseral sph. har.) と呼ぶことがある※3。
球面調和関数は、これまでに述べた電磁気学・重力に関する問題の他、多重極モーメントの各テンソル成分への分離、周辺光による間接照明の輝度測定等に現れるが、20世紀になると量子力学での応用事例が多数得られ、その重要性が一段と増した。そのうち特に有名なのが、水素原子核の周囲における電子の存在確率であり、
Laguerre 陪関数とともに現れる (詳細は、別頁 「
特殊関数応用編」 を参照)。
球面調和関数なる名称は、1867年に W. Thomson (Lord. Kelvin) と P. G. Tait が初めて使用した。
【註記】
※1:なぜならば、
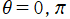
のとき
=±∞](siki_spec160/legendre28000.png)
となり、大抵の問題では不要または不適となるからである。
※2:付随する条件式から、Wigner の 3-j 記号は
![j[k]](siki_spec160/legendre28100.png)
が非負整数 (または正の半奇数) に限定され、これに伴い
![m[k]](siki_spec160/legendre28200.png)
が整数 (または半奇数) に限定された多変数関数であって、(虚数) 指数関数、
ガンマ関数 (階乗関数)、多項式で表わされることが分かる。
Wigner の 3-j 記号は、直交関数系の理論で普遍的に現れる。NISTの第34章は、この Wigner の 3-j 記号に関して詳細な情報を載せている。
※3:この名称の意味は、後に掲載しているグラフによって明らかになるであろう。
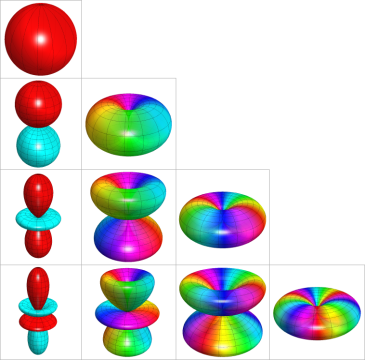
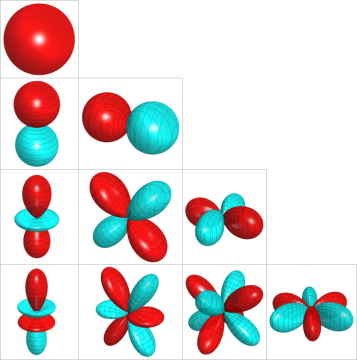
](siki_spec160/legendre30400.png)
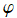
に由来する複素数因子が消えるため常に実数値をとる、実変数
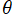
の球面調和関数
](siki_spec160/legendre28300.png)
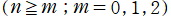
のグラフ。
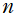
が小さい場合の球面調和関数
)](siki_spec160/legendre28500.png)
のグラフ。
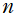
が小さい場合の球面調和関数
))](siki_spec160/legendre28600.png)
のグラフ。
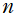
が小さい場合の球面調和関数
))](siki_spec160/legendre28700.png)
のグラフ。
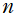
が比較的大きい球面調和関数
),](siki_spec160/legendre28800.png)
),](siki_spec160/legendre28900.png)
)](siki_spec160/legendre29000.png)
のグラフ。
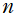
が比較的大きい球面調和関数
)),](siki_spec160/legendre29100.png)
)),](siki_spec160/legendre29200.png)
))](siki_spec160/legendre29300.png)
のグラフ。
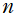
が比較的大きい球面調和関数
)),](siki_spec160/legendre29400.png)
)),](siki_spec160/legendre29500.png)
))](siki_spec160/legendre29600.png)
のグラフ。
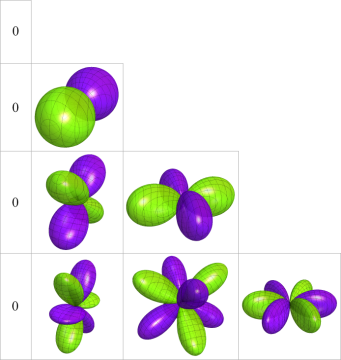
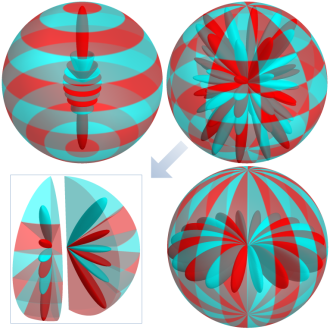
球面調和関数を原点から (原点中心の) 球面へ射影すると、帯球調和関数, 縞球調和関数, 扇球調和関数なる名称の意味が明らかになる。それを
)),](siki_spec160/legendre29100.png)
)),](siki_spec160/legendre29200.png)
))](siki_spec160/legendre29300.png)
で例示する。
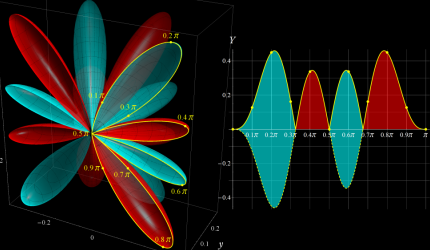
かつ変数
が実数を動くときの曲線を、
))](siki_spec160/legendre29800.png)
上で確認する。
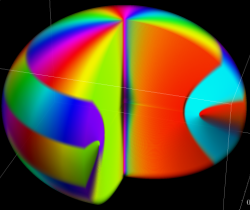
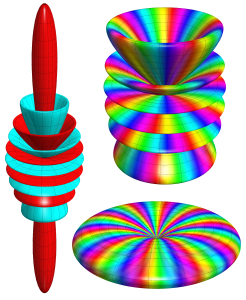
球面調和関数の合成 (有限級数)
に対する、
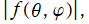
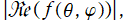
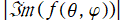
のグラフ。
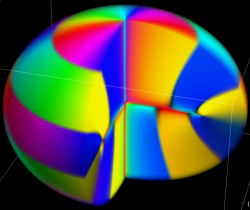
球面調和関数の合成 (有限級数)
に対する、
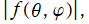
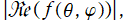
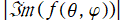
のグラフ。ここに、
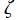
は
Riemann のゼータ関数である。
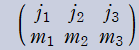
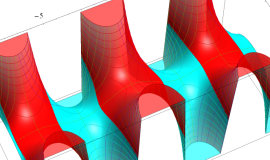
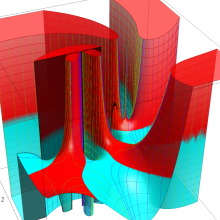
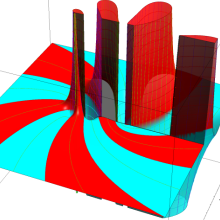
![m[1], m[2]](siki_spec160/legendre30500.png)
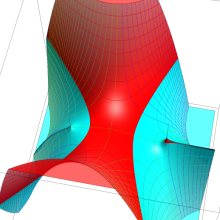
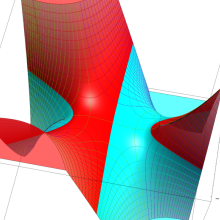
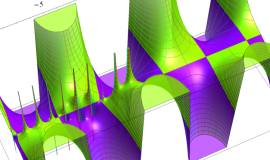
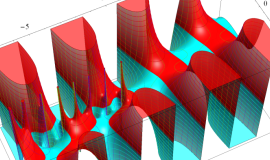
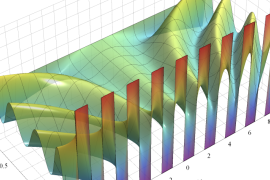
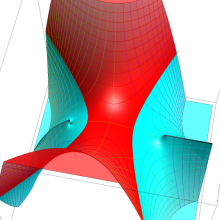
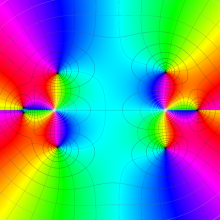
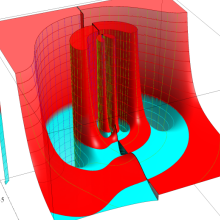
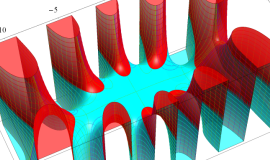
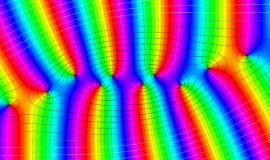
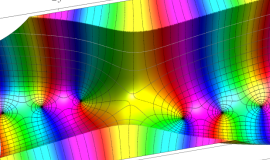
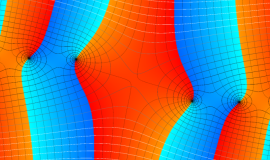
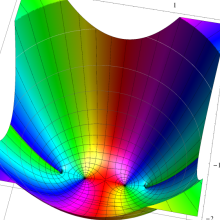
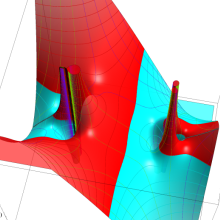
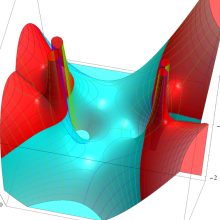
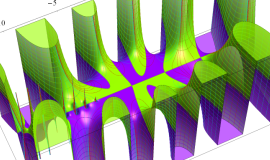
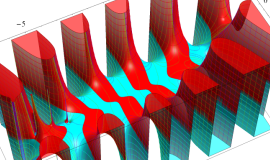
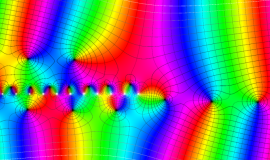
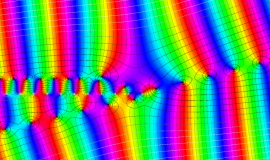
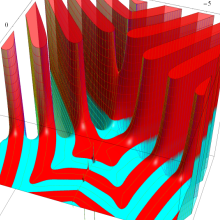
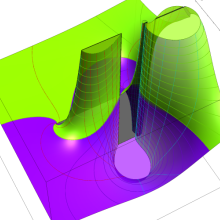
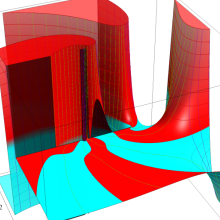
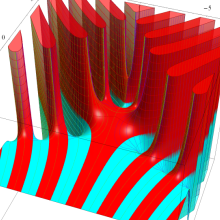
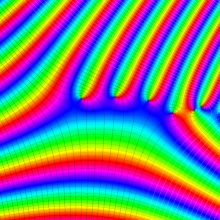
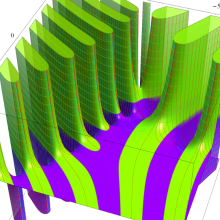
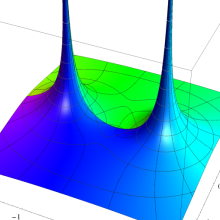
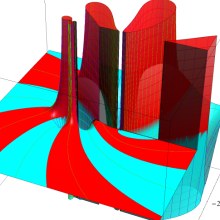
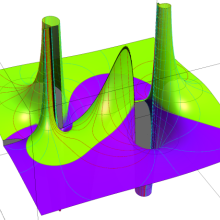
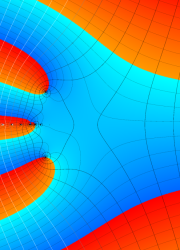
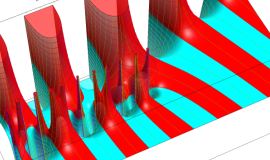
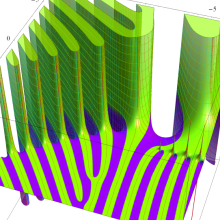
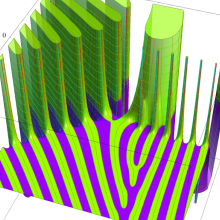
を整2変数とする、Wigner の 3-j 記号
![({40, 40, 60}, {m[1], m[2], -m[1]-m[2]})](siki_spec160/legendre30600.png)
のグラフ。
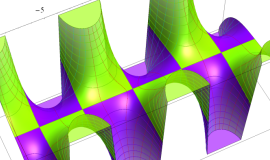
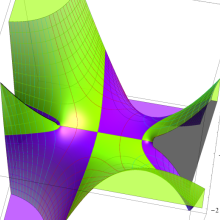
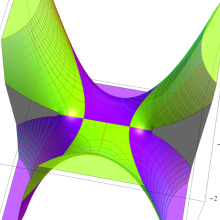
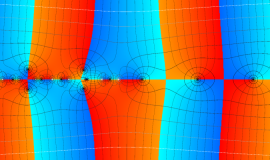
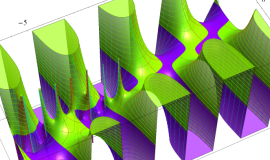
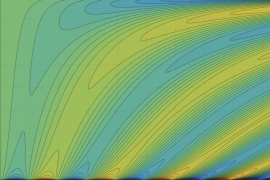
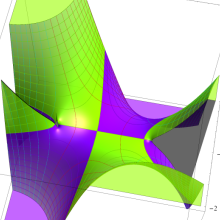
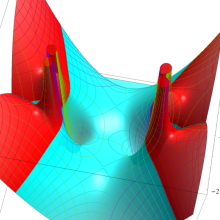
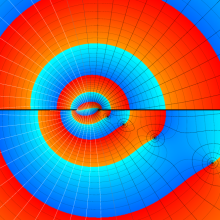
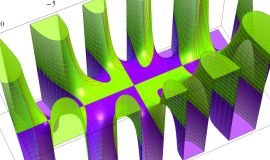
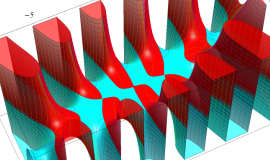
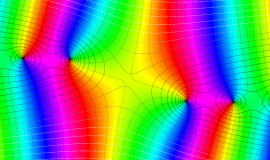
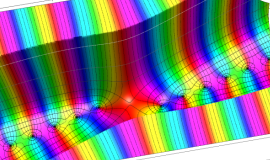
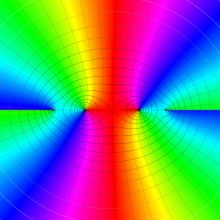
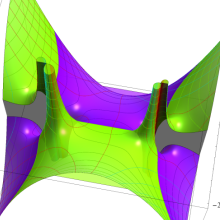
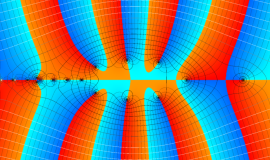
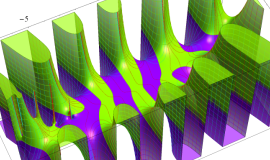
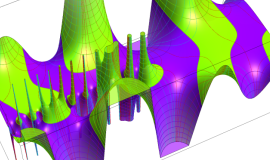
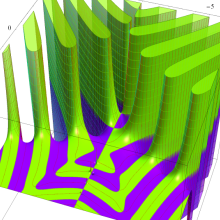
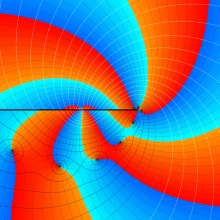
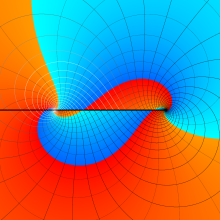
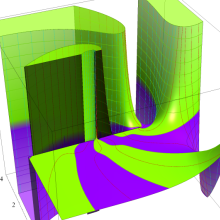
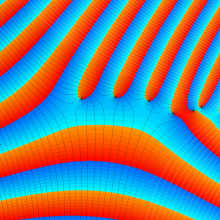
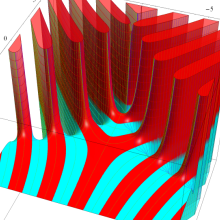
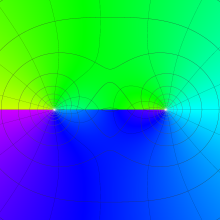
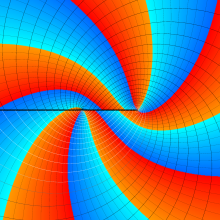
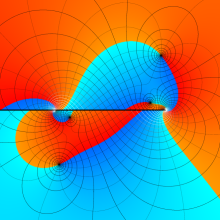
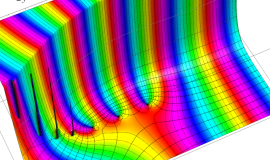
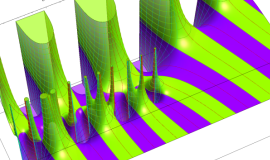
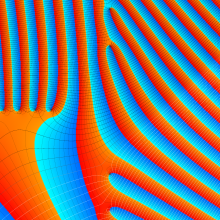
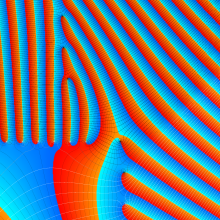
![m[1], m[2]](siki_spec160/legendre30500.png)
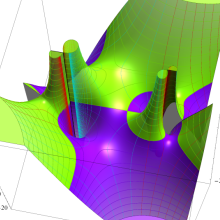
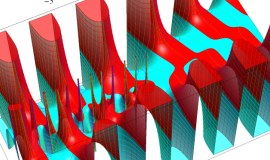
を半奇数の2変数とする、Wigner の 3-j 記号
![({75/2, 75/2, 35}, {m[1], m[2], -m[1]-m[2]})](siki_spec160/legendre30700.png)
のグラフ。
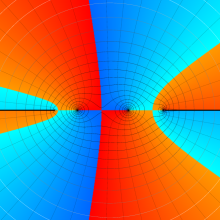
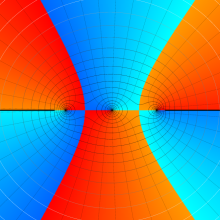
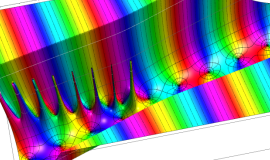
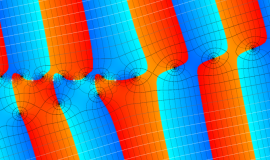
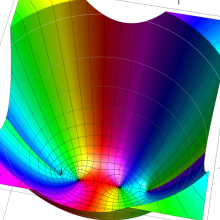
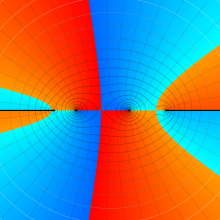
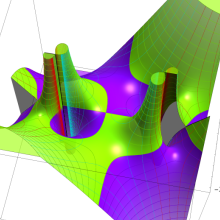
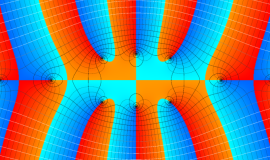
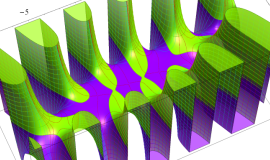
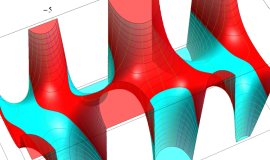
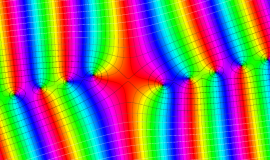
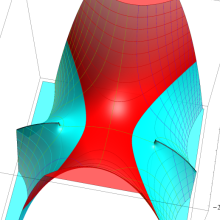
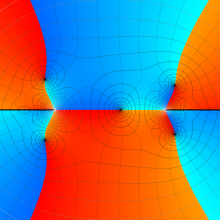
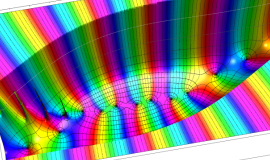
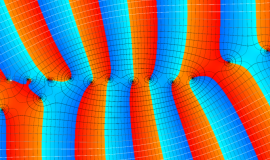
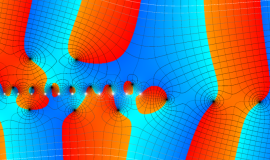
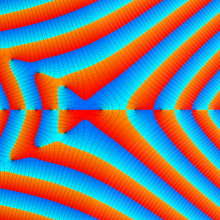
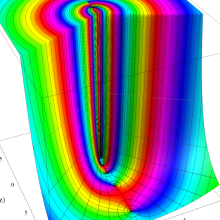
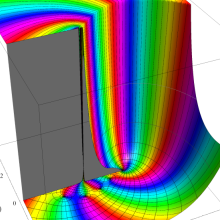
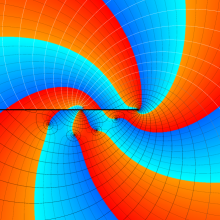
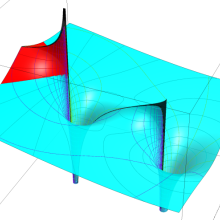
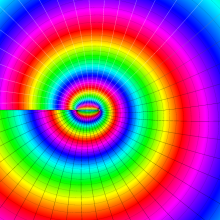
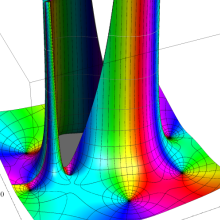
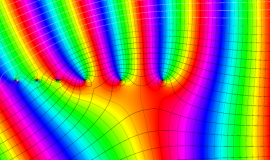
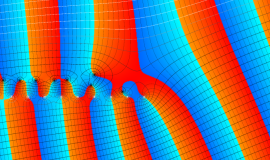
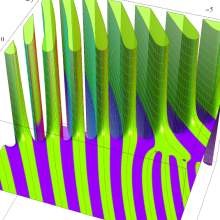
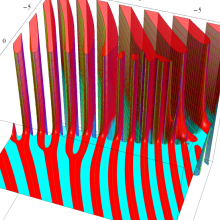
![m[1], m[2]](siki_spec160/legendre30500.png)
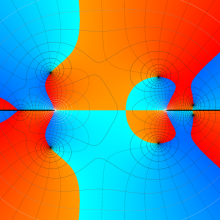
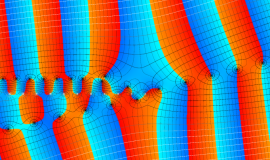
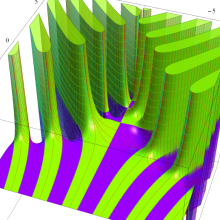
を整2変数とする、Wigner の 3-j 記号
![({40, 40, 80}, {m[1], m[2], -m[1]-m[2]})](siki_spec160/legendre30800.png)
のグラフ。これは、
![j[3]=j[1]+j[2]](siki_spec160/legendre30900.png)
となっている場合である。
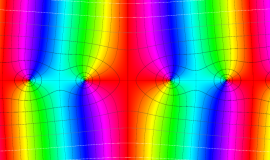
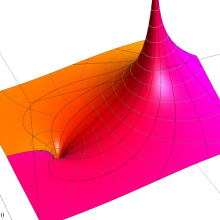
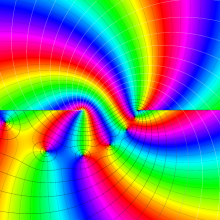
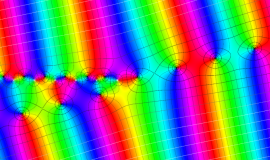
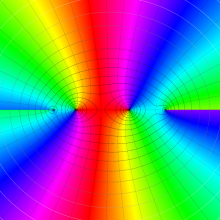
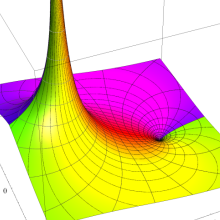
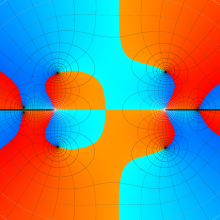
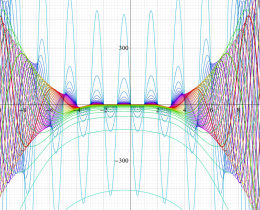
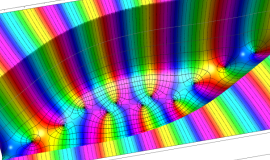
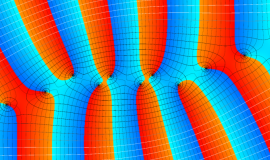
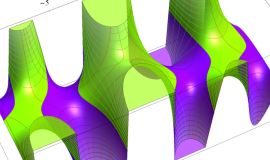
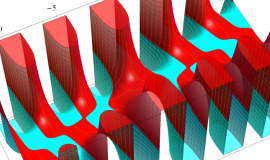
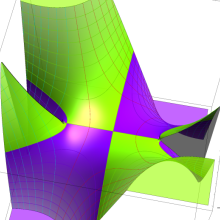
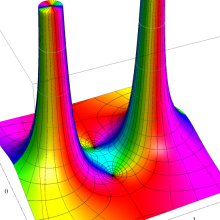
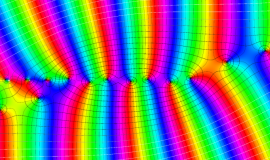
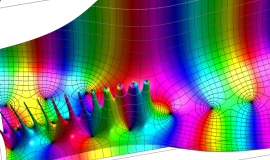
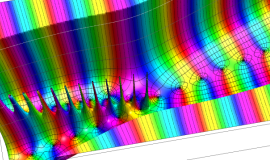
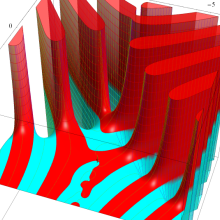
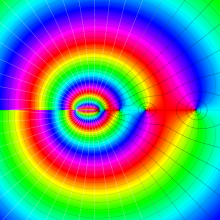
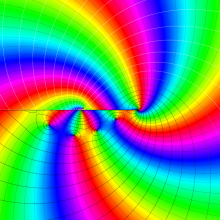
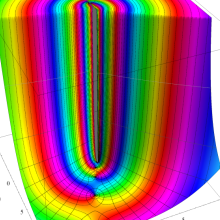
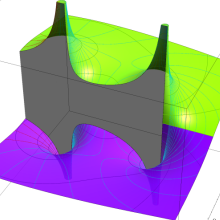
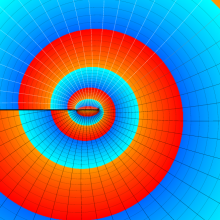
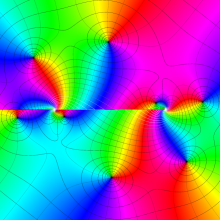
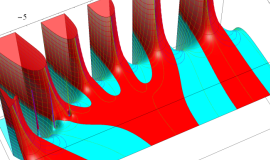
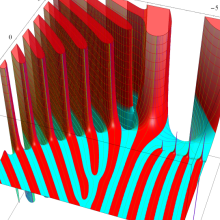
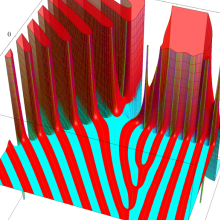
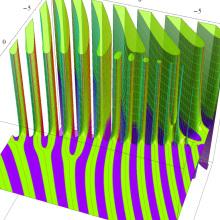
![j[1], j[2]](siki_spec160/legendre31000.png)
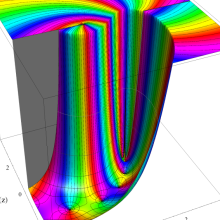
を整2変数とする、Wigner の 3-j 記号
![({j[1], j[2], j[1]+j[2]}, {5, 10, -15})](siki_spec160/legendre31100.png)
のグラフ。これも、
![j[3]=j[1]+j[2]](siki_spec160/legendre30900.png)
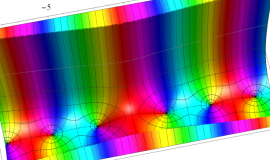
となっている場合である。
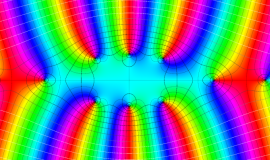
![j[1], j[2]](siki_spec160/legendre31000.png)
を整2変数とする、Wigner の 3-j 記号
![({j[1], j[2], j[1]+j[2]-10}, {10, 10, -20})](siki_spec160/legendre31200.png)
のグラフ。
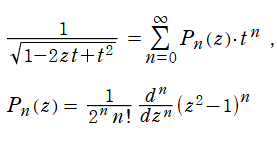
 を複素数とする Legendre 関数を初めて論じた。
を複素数とする Legendre 関数を初めて論じた。 にある1個の点電荷
にある1個の点電荷 での正負が (静電ではなく) 周期
での正負が (静電ではなく) 周期 で単振動する場合の、時刻
で単振動する場合の、時刻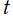 における電位
における電位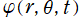 は、
は、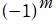 は 「Condon - Shortley の位相」 と呼ばれ、量子力学で必要になるため、球面調和関数はこの因子を含むように定義される。しかし書籍等によっては、この因子を省いた Legendre 陪関数の定義 (その場合、球面調和関数では因子を明示する定義) を採用していることもある。
は 「Condon - Shortley の位相」 と呼ばれ、量子力学で必要になるため、球面調和関数はこの因子を含むように定義される。しかし書籍等によっては、この因子を省いた Legendre 陪関数の定義 (その場合、球面調和関数では因子を明示する定義) を採用していることもある。![P[ν, μ], Q[ν, μ]](siki_spec160/legendre10500.png) 、次節の Hobson 型は
、次節の Hobson 型は![Ph[ν, μ], Qh[ν, μ]](siki_spec160/legendre10600.png) で記述しているので、恐らく判読できると思う。
で記述しているので、恐らく判読できると思う。](siki_spec160/legendre09100.png) を
を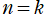 で現れる定数の平方根で割れば、その関数の直交積分は
で現れる定数の平方根で割れば、その関数の直交積分は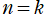 のとき常に1 (正規直交性) となる。このような調節を (直交関数の) 正規化という。
のとき常に1 (正規直交性) となる。このような調節を (直交関数の) 正規化という。Ph[k, m](x)=(-1)^m*P[n, m](x)P[k, m](x)](siki_spec160/legendre19300.png) となるからに過ぎない。
となるからに過ぎない。 のとき
のとき=±∞](siki_spec160/legendre28000.png) となり、大抵の問題では不要または不適となるからである。
となり、大抵の問題では不要または不適となるからである。![j[k]](siki_spec160/legendre28100.png) が非負整数 (または正の半奇数) に限定され、これに伴い
が非負整数 (または正の半奇数) に限定され、これに伴い![m[k]](siki_spec160/legendre28200.png) が整数 (または半奇数) に限定された多変数関数であって、(虚数) 指数関数、ガンマ関数 (階乗関数)、多項式で表わされることが分かる。
が整数 (または半奇数) に限定された多変数関数であって、(虚数) 指数関数、ガンマ関数 (階乗関数)、多項式で表わされることが分かる。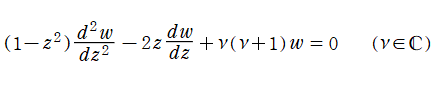
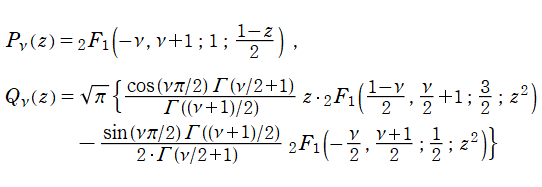
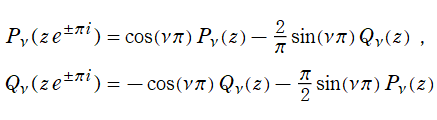
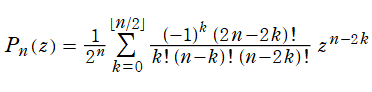
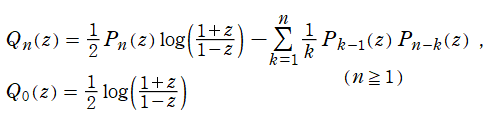
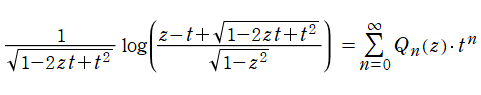
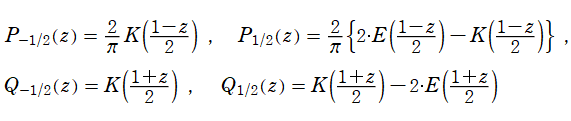
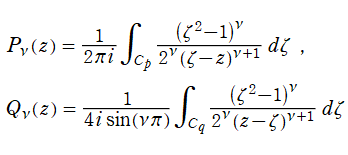
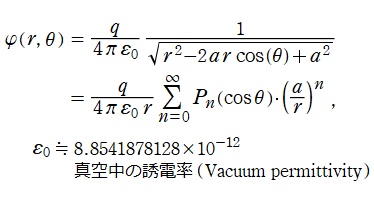
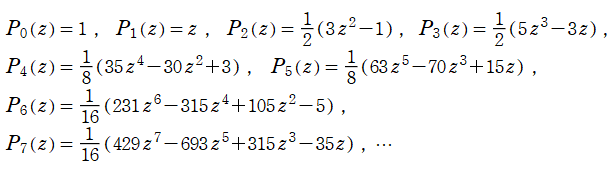
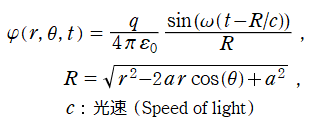
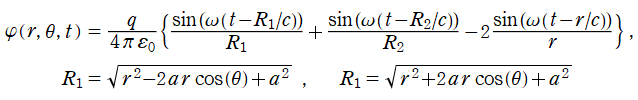
















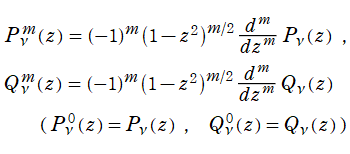
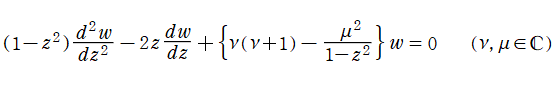
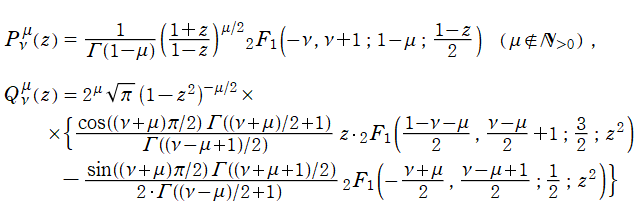
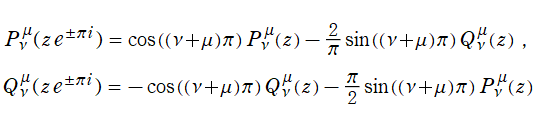
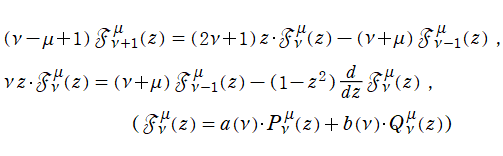
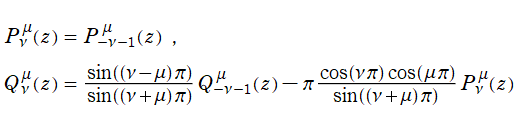
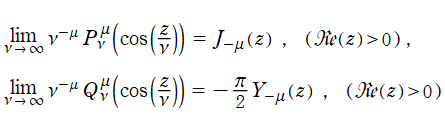


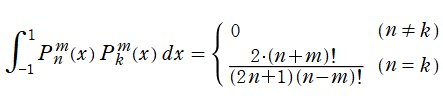
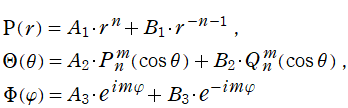
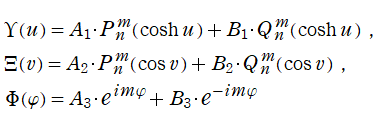
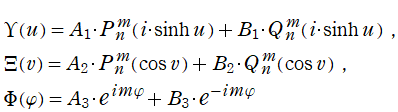







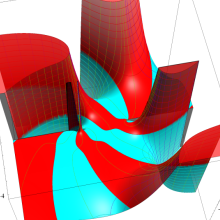

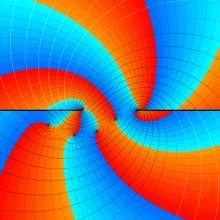
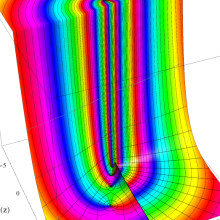
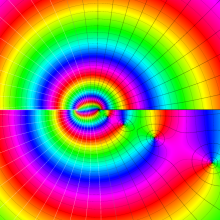
























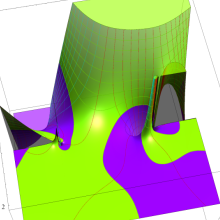
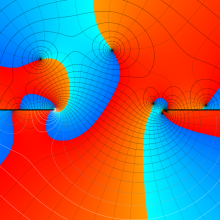

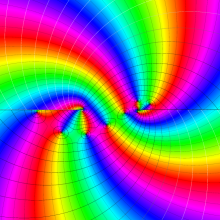

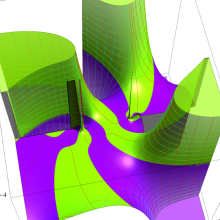



















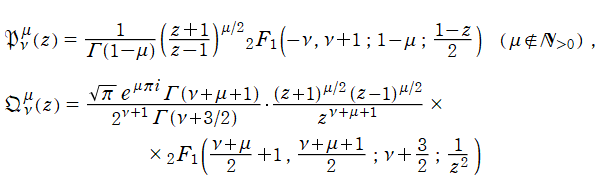

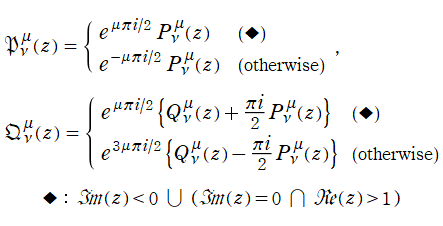
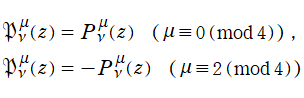
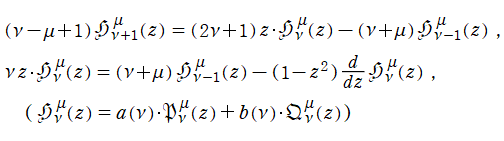
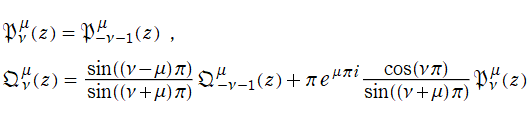
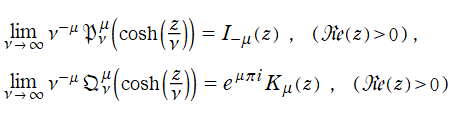
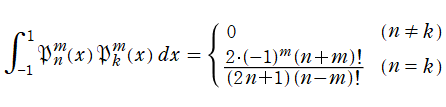
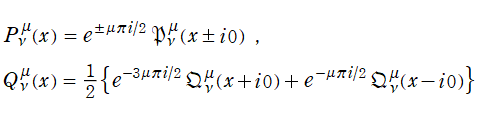





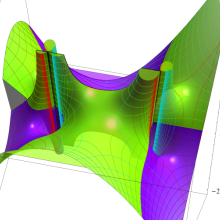
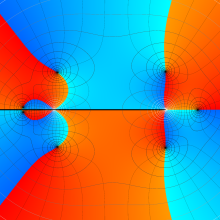
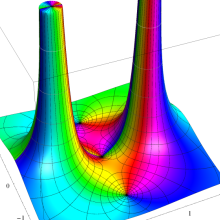
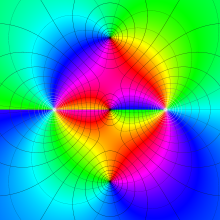










































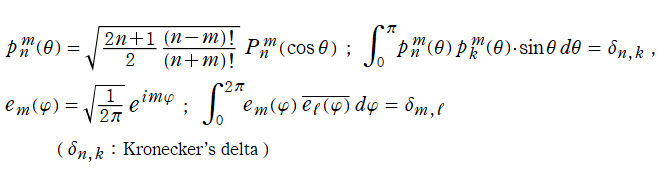
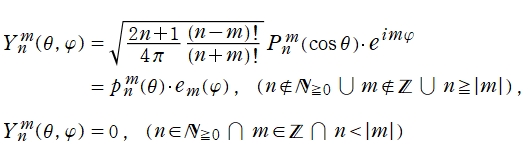
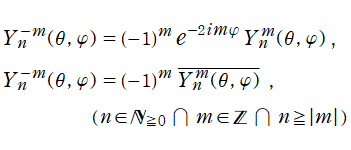

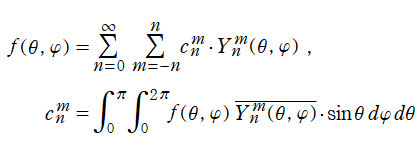
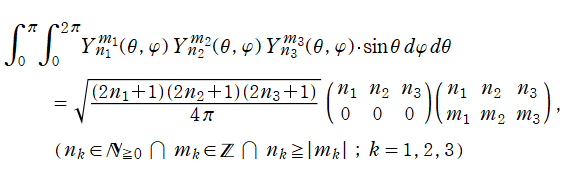

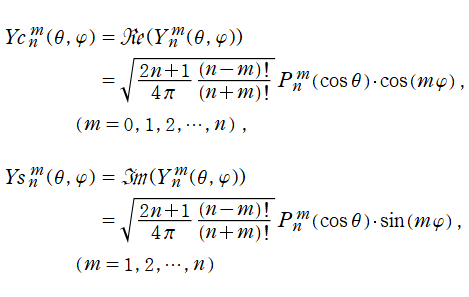


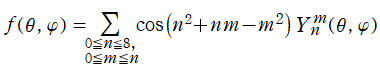



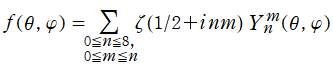



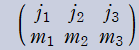
![Wignerの3-j記号のグラフ(変数 m[k])](gazou_spec160/160_5550_thumb.png)
![Wignerの3-j記号のグラフ(変数 m[k])](gazou_spec160/160_5560_thumb.png)
![Wignerの3-j記号のグラフ(変数 m[k])](gazou_spec160/160_5570_thumb.png)
![Wignerの3-j記号のグラフ(変数 m[k])](gazou_spec160/160_5580_thumb.png)
![Wignerの3-j記号のグラフ(変数 m[k])](gazou_spec160/160_5590_thumb.png)
![Wignerの3-j記号のグラフ(変数 m[k])](gazou_spec160/160_5600_thumb.png)
![Wignerの3-j記号のグラフ(変数 j[k])](gazou_spec160/160_5610_thumb.png)
![Wignerの3-j記号のグラフ(変数 j[k])](gazou_spec160/160_5620_thumb.png)
![Wignerの3-j記号のグラフ(変数 j[k])](gazou_spec160/160_5630_thumb.png)
![Wignerの3-j記号のグラフ(変数 j[k])](gazou_spec160/160_5640_thumb.png)