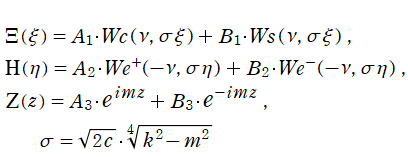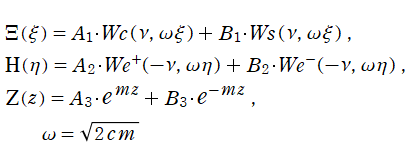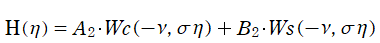特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
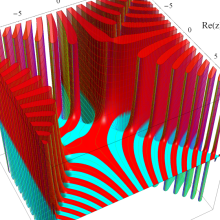
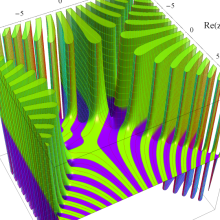
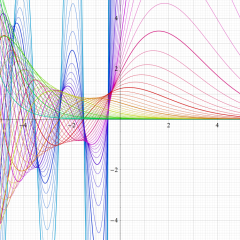
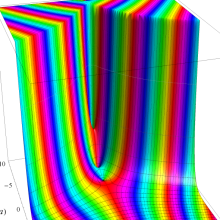
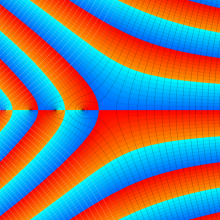
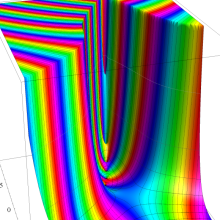
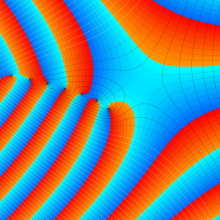
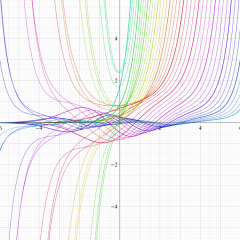
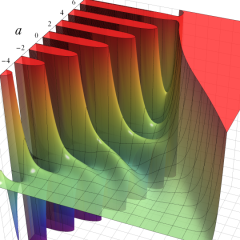
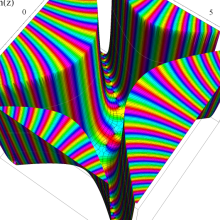
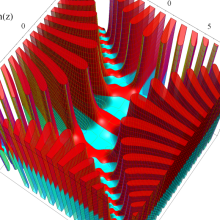
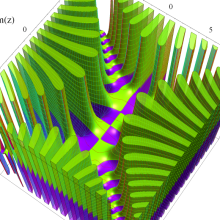
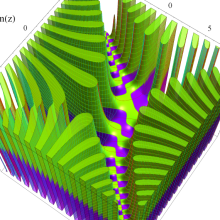
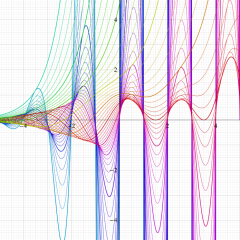
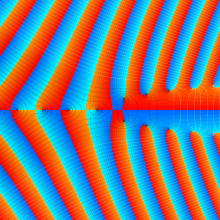
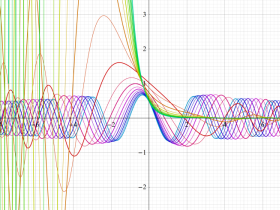
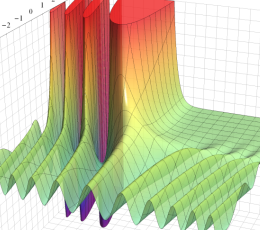
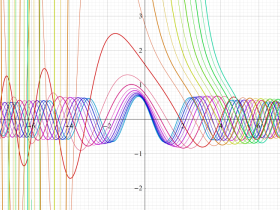
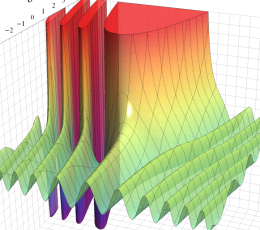
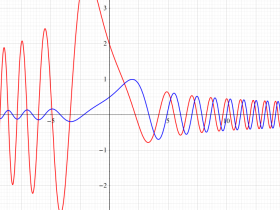
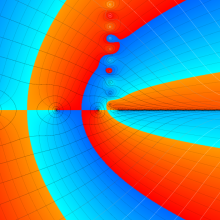
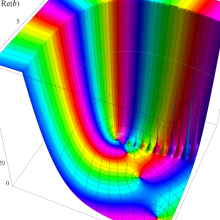
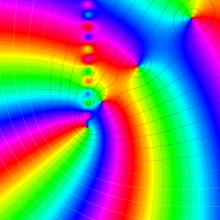
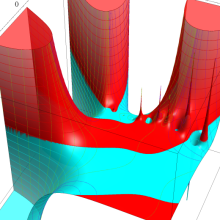
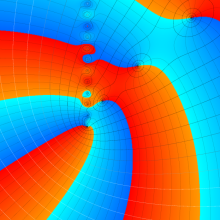
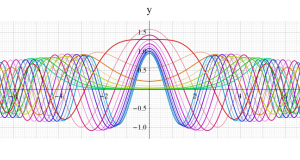
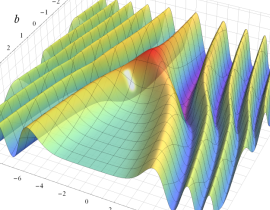
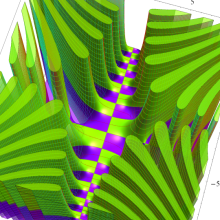
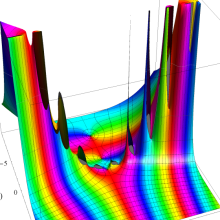
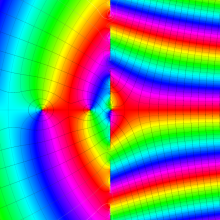
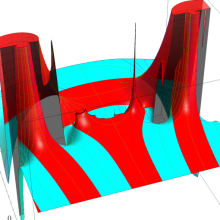
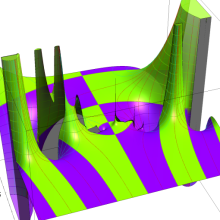
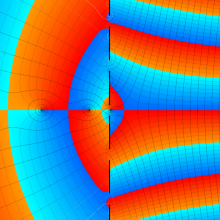
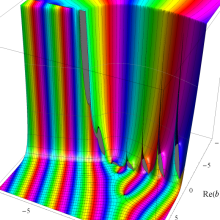
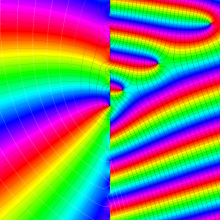
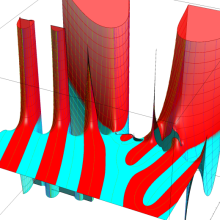
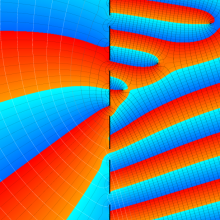
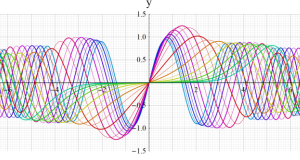
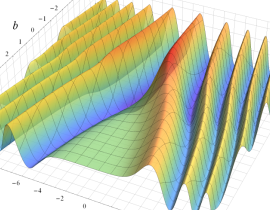
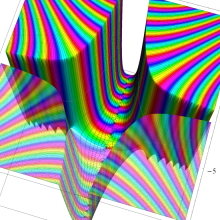
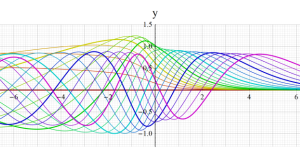
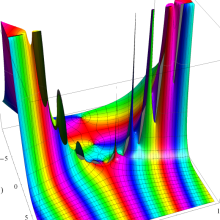
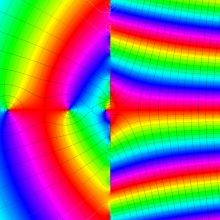
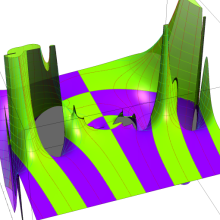
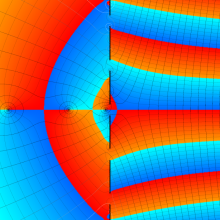
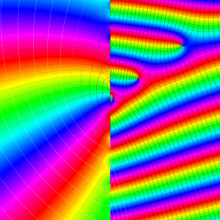
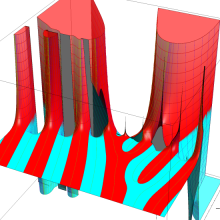
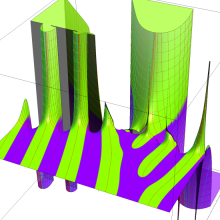
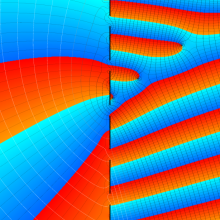
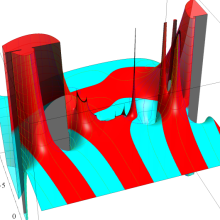
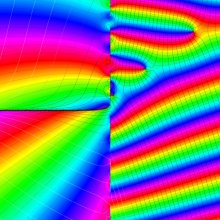
Hermite 関数
Hermite 関数
日:Hermite関数,エルミート関数英:Hermite function,仏:Fonction d'Hermite,独:Hermitesche funktion
二階の線形常微分方程式
は Hermite の微分方程式と呼ばれ、
を採用する※1。両者は常に
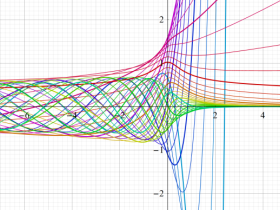
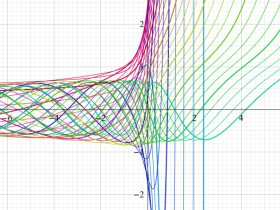
Hermite の微分方程式は、二つの線形独立な解として
で表わされる。
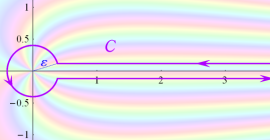
第1種 Hermite 関数は、複素線積分の表示式
によっても定義できる。ここに、被積分関数は
Hermite 関数は、次数
を満たす。ここに
で結ばれる。
に還元される。しかし、これは応用面での出現頻度が高いため重要とされ、Hermite 多項式と呼ばれる。Hermite 多項式の上記以外の表現方法としては、母関数表示式および 「Rodrigues の公式」
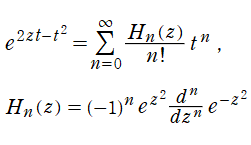
歴史的に、Hermite 関数の萌芽は P. S. Laplace (1810年) の研究に見出されるが、明確に Hermite 関数自体を取り上げて、その詳細な結果を導いた最初の研究は P. L. Chebyshev (1859年) による。少し遅れて独立に C. Hermite (1864年) も同様の研究を行い、後者の方が広く知られたため、以後その名を冠して呼ばれるようになった。
Hermite 関数 (特に Hermite 多項式) の応用事例として最も有名なものは、恐らく量子力学的調和振動子の波動関数であるが、この他にも確率論および統計学、(正規分布に従う複素乱数の) ランダム行列理論、数値積分計算法 (Gauss 求積法)、可積分系 (戸田方程式の解※3、Painlevé 方程式の古典関数解) 等が知られている。それらの多くが、Rodrigues の公式や逐次微分を介した誤差関数との関係式、線形漸化式、直交性に由来する。Hermite 関数は、後述の放物柱関数で記述することができるので、その応用事例とも被っている。
【註記】
※1:第2種 Hermite 関数の標準的な定義および関数記号は存在しない。上記](siki_spec180/hermite00600.png) は当サイトが独自に定めたものであるが、
は当サイトが独自に定めたものであるが、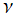 を非負整数に限れば、これに近い定義が 「岩波 数学公式Ⅲ 特殊関数」 p.94 にもある。ただし、同著が言う Hermite 関数とは、
を非負整数に限れば、これに近い定義が 「岩波 数学公式Ⅲ 特殊関数」 p.94 にもある。ただし、同著が言う Hermite 関数とは、
である。(超幾何関数系の第2種関数の定義方法に対する当サイトでの方針は、別頁 Questions を参照。)
※2:重要性と簡潔な形に鑑みて、Hermite 多項式も具体的な表示をここに羅列する。
※3:NISTの18.38(ii) によれば、
の例がある。(この式自体は、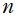 を複素数に変えても成立する。)
を複素数に変えても成立する。)
※1:第2種 Hermite 関数の標準的な定義および関数記号は存在しない。上記
である。(超幾何関数系の第2種関数の定義方法に対する当サイトでの方針は、別頁 Questions を参照。)
※2:重要性と簡潔な形に鑑みて、Hermite 多項式も具体的な表示をここに羅列する。
※3:NISTの18.38(ii) によれば、
の例がある。(この式自体は、
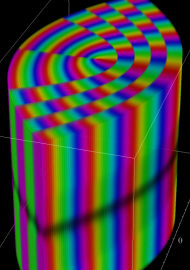
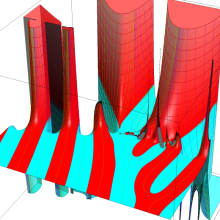
アニメーション(12.0MB)
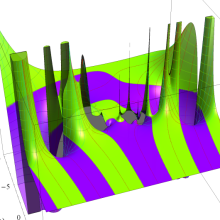
2番目は、
2番目は、
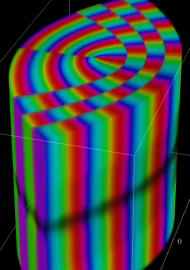
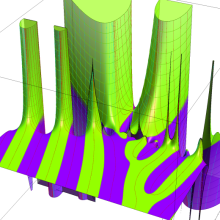
アニメーション(12.4MB)
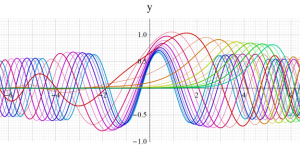
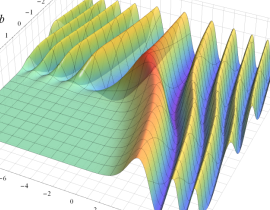
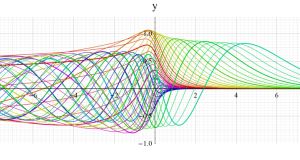
Hermite 関数(正規化)
【関数の直交性とは?】で定義する※1。もし、常に
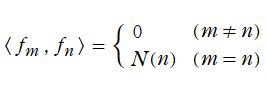
新たに、定数倍された
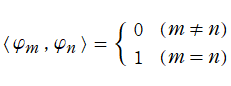
区間
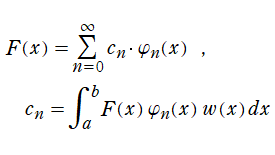
となった場合が Fourier 級数であるが、むしろ歴史的には、Fourier 級数を雛形として直交関数系の理論が発展した。また、最小二乗法から生じる高次連立方程式を解く過程で、元々は線形代数に現れる 「内積」 や 「直交」 の概念が (ベクトルの成分を関数、列全体に渡る和を積分に) 拡張され、ここでも直交関数系の理論が展開された※2。
さて、(重み関数を除いた)
になる直交関数系は、Fourier 級数の場合に並んで重要とされ、このとき
Legendre 多項式は重み関数を伴わない (
古典的直交多項式
の形に一括された線形漸化式を満たす。また、一般的な表記の Rodrigues の公式
で表わせる。さらに、
の解となる※3。一方、古典的でない直交多項式は、これらに相当する性質を持たないか、表示式の形が異なる。
【Hermite多項式の直交性と正規化】
Hermite 多項式
なる直交性を持っている。
そこで、当サイトでは独自に関数
を導入する※4。よって、
を満たす。関数
の違いしかないが、量子力学的調和振動子の問題で本質的な微分方程式
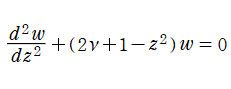
【註記】
※1:因みに、}](siki_spec180/hermite05400.png) が複素数値関数列のときの内積は、一方の関数の複素共役を取った
が複素数値関数列のときの内積は、一方の関数の複素共役を取った
で定義される。(この具体的事例が、既に球面調和関数の頁で現れた。)
なお、当サイトでは積分の種類を Riemann 積分 (通常の積分) として説明したが、本来は Lebesgue 積分まで含める必要がある。
※2:詳細は、伏見康治・赤井 逸 「直交関数系 (増補版)」 (1987年 共立出版) を参照。
※3:公式中の![κ[n, n]](siki_spec180/hermite08800.png) や
や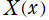 等の具体的な表示は、NIST の Table18.3.1 および Table18.5.1 にある (ただし、記号は当サイトと異なる)。
等の具体的な表示は、NIST の Table18.3.1 および Table18.5.1 にある (ただし、記号は当サイトと異なる)。
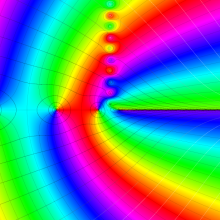
※4:関数記号は正規化 (Normalization) に基づく。また、応用上は意味を成さないが、当サイトでは](siki_spec180/hermite08300.png) のグラフの多くを、
のグラフの多くを、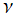 を非整数、
を非整数、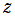 を複素変数として描画する。
を複素変数として描画する。
※1:因みに、
で定義される。(この具体的事例が、既に球面調和関数の頁で現れた。)
なお、当サイトでは積分の種類を Riemann 積分 (通常の積分) として説明したが、本来は Lebesgue 積分まで含める必要がある。
※2:詳細は、伏見康治・赤井 逸 「直交関数系 (増補版)」 (1987年 共立出版) を参照。
※3:公式中の
※4:関数記号は正規化 (Normalization) に基づく。また、応用上は意味を成さないが、当サイトでは
放物柱関数
日:放物柱関数英:Parabolic cylinder function,仏:Fonction cylindre parabolique,独:Parabolischezylinderfunktion
やや一般的な形の二階線形常微分方程式
は、より簡単な形の微分方程式
のいずれかに帰着できる。ただし、①は②に変換
①に対する放物柱関数は、Hermite 関数を用いて
とHermite関数の関係](siki_spec180/hermite10500.png)
一方、②に対して解の基本系を成し、いかなる
が定義されており、第1種および第2種の放物柱関数と呼ばれる。両者は合流型超幾何関数を用いて、
とも表わせる。したがって
を始め、多数の表示式が知られており、特殊関数の漸近展開等に応用される。また、後者は具体的に
となり、導関数も得られる。これらを援用すれば、放物柱関数は
となるので、放物柱関数は
ところで、③に対して解の基本系を成し、いかなる
も定義されている (ただし
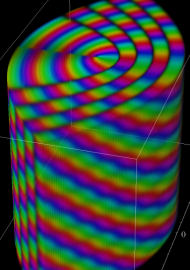
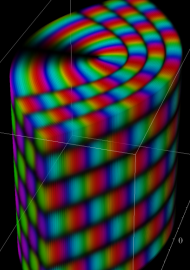
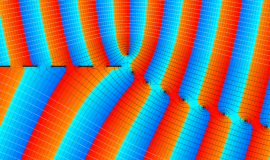
のごとく振る舞う点で著しい。当サイトでは、さらに (常に偶関数・奇関数となり) 余弦・正弦関数に相当する、互いに線形独立な二つの放物柱関数 (第1種, 第2種)
並びに、純虚指数関数に相当する、互いに線形独立な二つの放物柱関数 (第3種, 第4種)
を独自に導入する。次のとおり、これらの関数は Helmholtz 方程式等の解を記述する際に大変都合が良い。
放物柱座標
となり※2、放物柱関数が現れる。Laplace 方程式
となる※3。これらの方程式の解は、放物線または放物柱を境界とする領域内における、多数の物理問題に応用される。例えば、物体の振動、電磁波の散乱、極低温状態にある素粒子の分布等がある。
また、Hermite 関数の応用事例として知られる直交関数系の固有値問題、量子力学における調和振動子等を、若干異なったアプローチで論じる場合にも放物柱関数は使用される。
超幾何関数および Whittaker 関数の助変数、並びに Legendre 関数等の次数が大きい場合の漸近展開式では、それらの関数の大域的振る舞いを決める主要因子として、放物柱関数が現れる※4。
【註記】
※1:放物柱関数](siki_spec180/hermite10600.png) のグラフは掲載しない。(放物柱関数
のグラフは掲載しない。(放物柱関数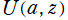 または正規化 Hermite 関数
または正規化 Hermite 関数](siki_spec180/hermite08300.png) のグラフとほとんど同じ、または非常に似ているので。)
のグラフとほとんど同じ、または非常に似ているので。)
※2: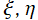 方向は、(各々の微分方程式を常に満たすという要件のもとで) 上記と異なる放物柱関数に変更することが可能である。例えば、古典的な物理問題等では
方向は、(各々の微分方程式を常に満たすという要件のもとで) 上記と異なる放物柱関数に変更することが可能である。例えば、古典的な物理問題等では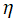 方向も実数値を取るよう、
方向も実数値を取るよう、
に変更した方が、恐らく便利である。(このような任意性は、他の座標系の場合にも当てはまる。)
※3:同様に Laplace 方程式の場合も、上記の変換等を施さない、表現の異なる解が有り得る。
※4:NISTの13.20(iii), 13.20(iv), 14.15(v), 15.12.7 を参照。
※1:放物柱関数
※2:
に変更した方が、恐らく便利である。(このような任意性は、他の座標系の場合にも当てはまる。)
※3:同様に Laplace 方程式の場合も、上記の変換等を施さない、表現の異なる解が有り得る。
※4:NISTの13.20(iii), 13.20(iv), 14.15(v), 15.12.7 を参照。
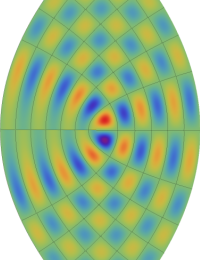
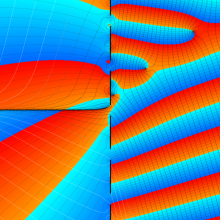
アニメーション(14.8MB)
アニメーション(9.28MB)
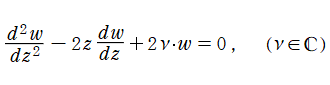
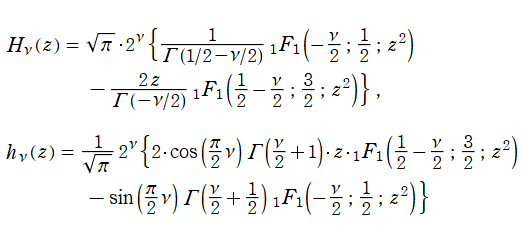
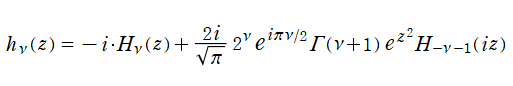
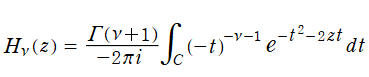
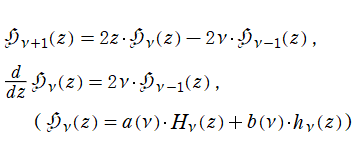
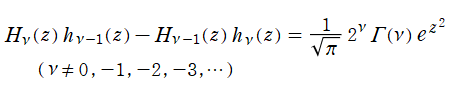
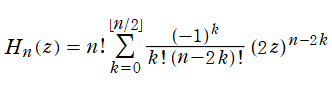
, he[ν](z)](siki_spec180/hermite02200.png)
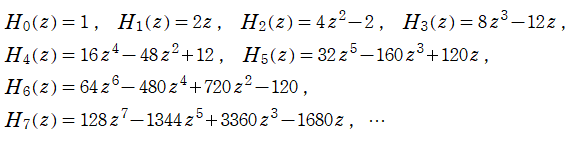































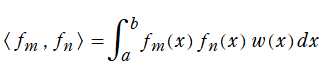
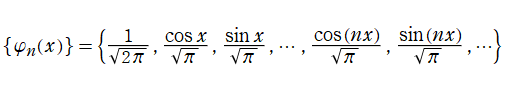
](siki_spec180/hermite06900.png)
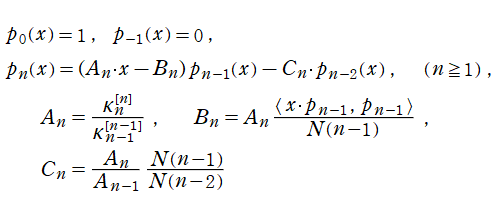
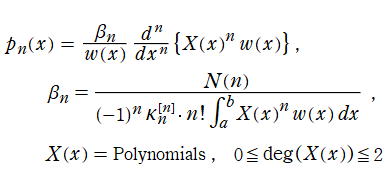
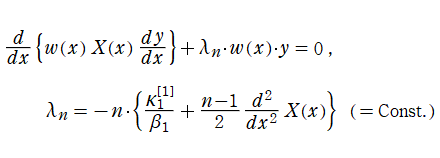
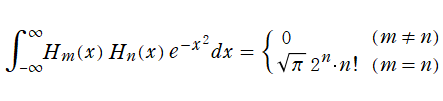
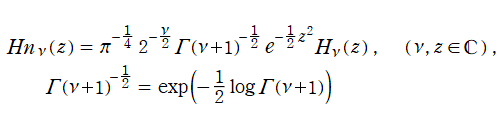

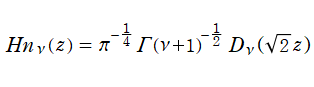
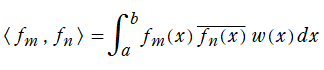










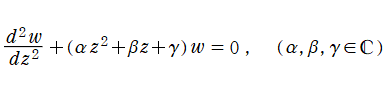
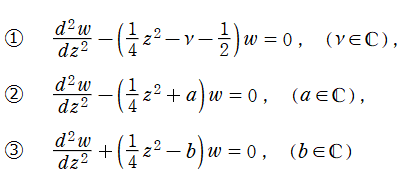
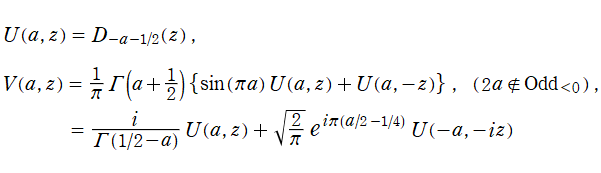
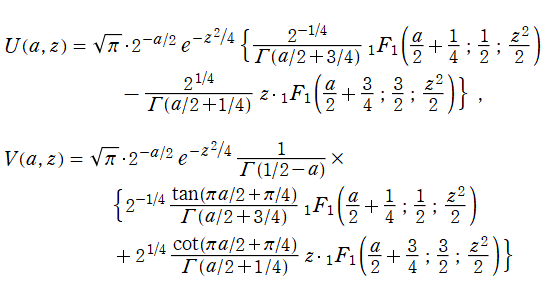

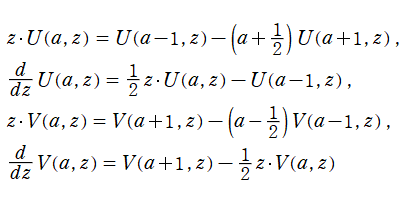
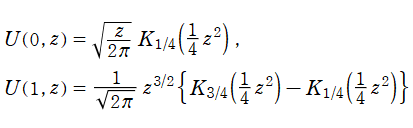
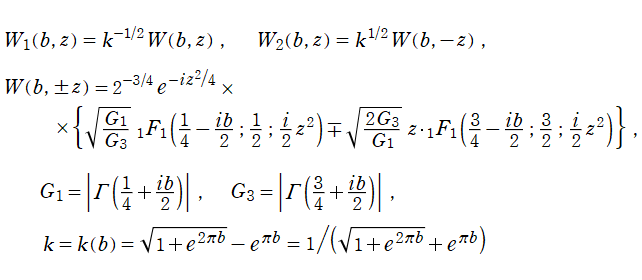
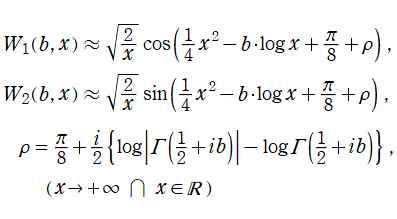
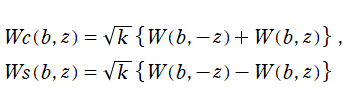
, We[-](b, z)の定義](siki_spec180/hermite12100.png)