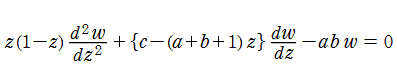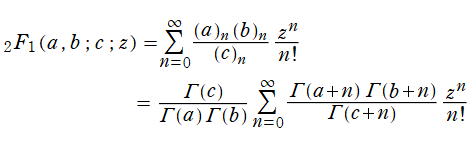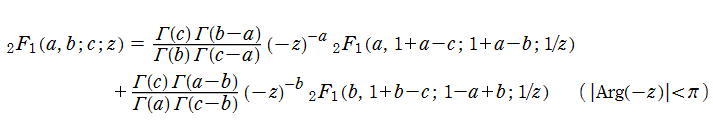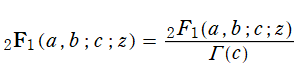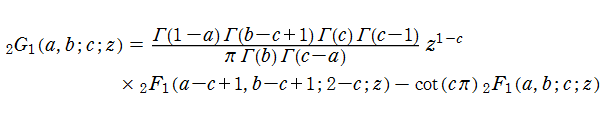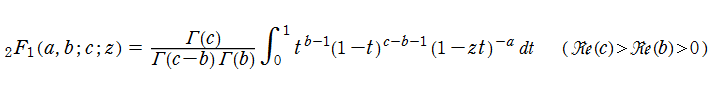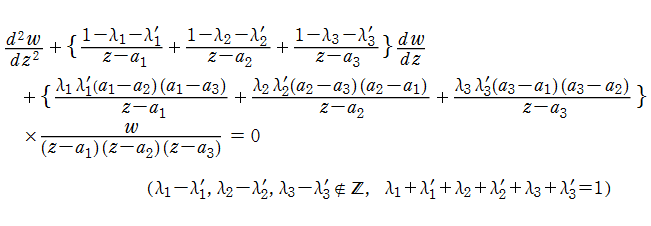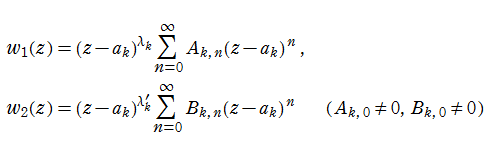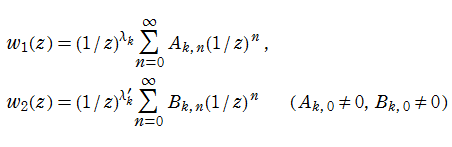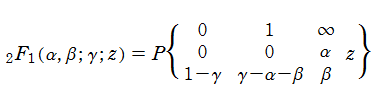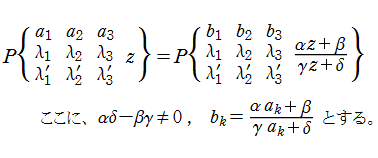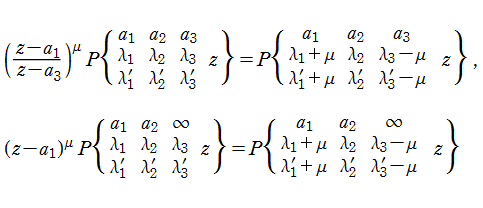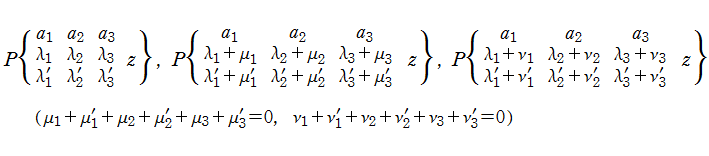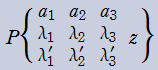特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
超幾何関数
超幾何関数
日:超幾何関数英:Hypergeometric function,仏:Fonction hypergéométrique,独:Hypergeometrische funktion
二階線形常微分方程式
は、3個の確定特異点
そのうち、原点で有限となる基本解
を、第1種超幾何関数という。特に、この級数は超幾何級数と呼ばれその収束半径は1であるため、実際には、これに線形接続公式
等による解析接続を施して定義域を拡張したものが、本来の第1種超幾何関数である。「超幾何級数」という名称は、幾何級数(等比級数)を含む形で一般化した級数という意味を持つ (Hyper geometric series の意訳)。記号
第1種超幾何関数に対して、ガンマ関数因子に由来する不定性を取り除いた 「正規化された超幾何関数」
は、数値計算等で好都合なため多用される。
一方、原点で無限大となる、
を、第2種超幾何関数と呼ぶ。ただし、
一般に超幾何関数は、複素平面上
超幾何微分方程式の一般解は、このような基本解の2個の線形結合式となるが、その係数(関数)は
のような、特殊値の一群を求めることができる。
超幾何関数の特別な場合として表わされる関数は非常に多く、Jacobi 関数、Gegenbauer 関数、Legendre 陪関数、完全楕円積分などがある。また、(
超幾何微分方程式の確定特異点のうち1を
なお、超幾何関数と直接関係は無いが、超幾何微分方程式の極限として表わされる微分方程式から生じる関数として、Lamé 関数、Mathieu 関数、回転楕円体波動関数などがある。これらは超幾何関数よりも高いクラスの関数であるが、比較的整った諸性質(隣接関係式など)を持っていない。言いかえれば、超幾何関数はそれら「美しい」性質を持つ関数としては、最も高度なものの例である。
超幾何関数は、1748年に L. Euler によって得られた積分表示式
で表わされ、逆にこれをもって超幾何関数の定義とする場合もある。この積分は
超幾何関数は、単独で物理学等に用いられることは少なく、むしろ応用上重要な種々の特殊関数どうしの関係、特殊関数の一般論的な側面が問題となる場合に用いられることが多い。
歴史的には、18世紀に Euler が初めて超幾何微分方程式とその解の研究を手掛けた。19世紀初頭になると、J. C. F. Gauss や N. H. Abel 等によって級数の収束性についての厳密な理論が展開され、特に 「Gauss の収束判定法」 は超幾何級数のために開発された。19世紀中葉では複素解析学が整備され、G. F. B. Riemann などの著名な数学者によって、複素領域で定義された線形常微分方程式の解となる関数の大域的理論や多価関数としての構造が深く研究された。ここでも超幾何微分方程式および超幾何関数が理論の具体的な雛形であり、発展の原動力となっている。その後、超幾何関数自体も一般化や多変数化など様々な拡張が考えられ、今なお盛んに研究されている特殊関数の一つになっている。
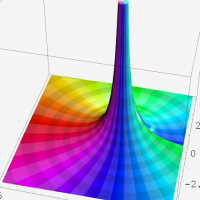
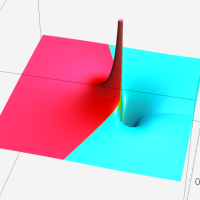
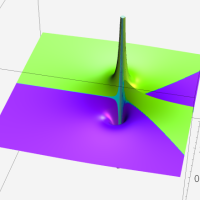
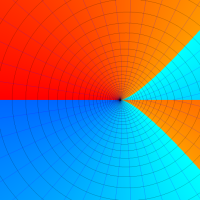
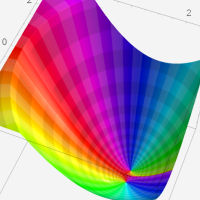
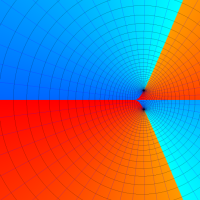
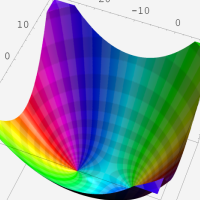
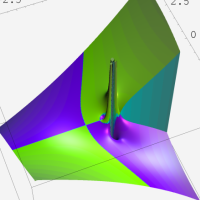
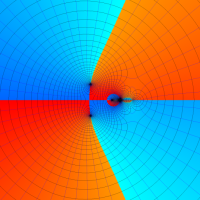
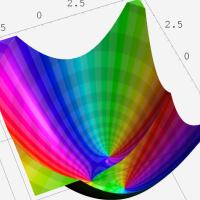
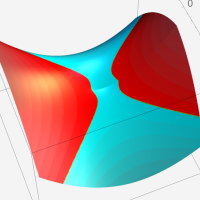
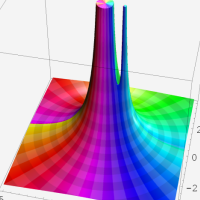
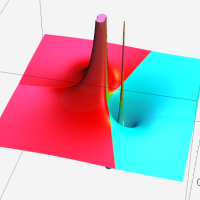
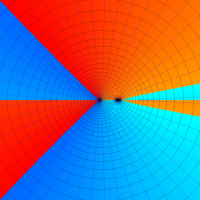
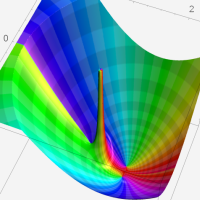
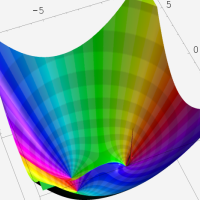
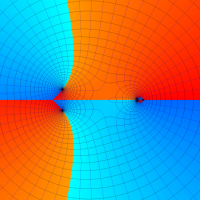
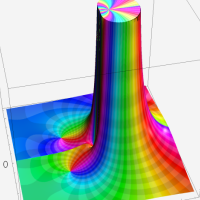
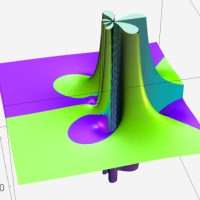
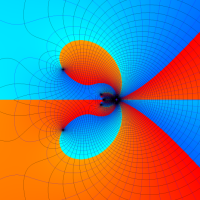
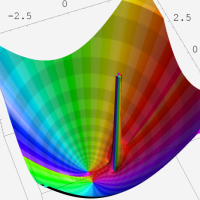
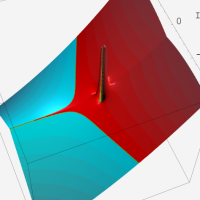
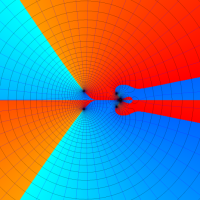
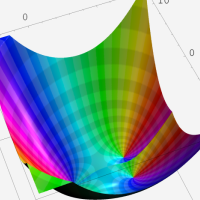
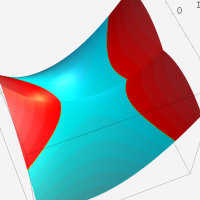
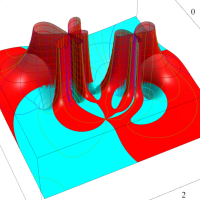
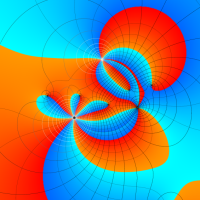
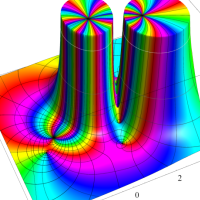
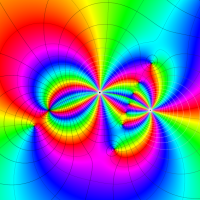
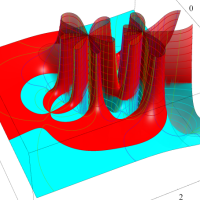
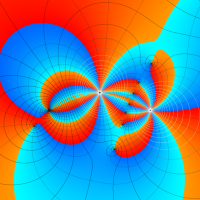
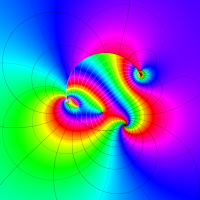
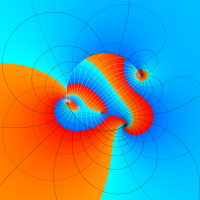
複素変数の第1種超幾何関数
複素変数の第1種超幾何関数
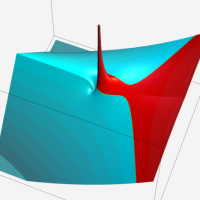
複素変数の第1種超幾何関数
複素変数の第1種超幾何関数
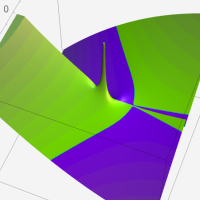
複素変数の第1種超幾何関数
複素変数の第1種超幾何関数
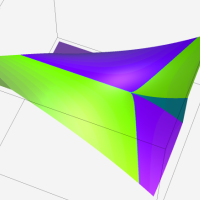
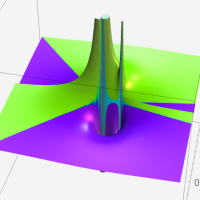
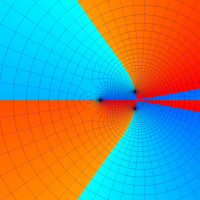
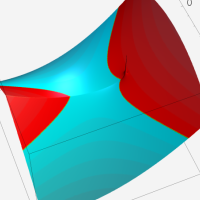
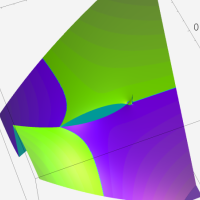
複素変数の第2種超幾何関数
複素変数の第2種超幾何関数
複素変数の第2種超幾何関数
複素変数の第2種超幾何関数
複素変数の第2種超幾何関数
複素変数の第2種超幾何関数
Riemann のP関数
日:RiemannのP関数,リーマンのP関数英:Riemann P-function,仏:Fonction P de Riemann,独:Riemannsche P-funktion
2階の線形常微分方程式
を、Riemann の微分方程式という。またその基本解(の代表)
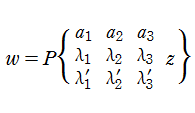
のように振る舞う関数に選定することができる。なお、確定特異点が無限遠点になる場合は、
と解釈する。
Riemann のP関数は、超幾何関数を用いて
と表わされる。逆に、超幾何関数は Riemann のP関数の特別な場合
である。Riemann の微分方程式の形によって、Riemann のP関数は、パラメータの列を入れ替えても、また
Riemann のP関数は、変数に一次分数変換を施した
なる関係を満たす。この他にも、
を満たす。より一般的に、
の3個の関数は、
Riemann のP関数は、超幾何関数の多価性を解明するために、G. F. B. Riemann が導入した※1。3個の確定特異点、およびこれらのいくつかを合流して得られる不確定特異点を持つ線形常微分方程式の解は、すべて Riemann のP関数によって表わすことができる。
なお、Riemann のP関数ではないが、確定特異点が3個よりも多い場合の解を、Riemann のP関数の記法に倣って記述することがある。例えば4個ならば、
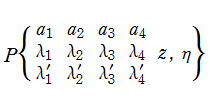
以下の描画における Riemann のP関数は、分枝切断線が3個の特異点
【註記】
※1:Pの発音は、Riemann がドイツ人であることからドイツ語読みの「ペー」と発音することがある。
他方、Riemann はPをギリシャ語の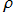 (ロー)の大文字の意味で用いたという説もある。
(ロー)の大文字の意味で用いたという説もある。
※1:Pの発音は、Riemann がドイツ人であることからドイツ語読みの「ペー」と発音することがある。
他方、Riemann はPをギリシャ語の
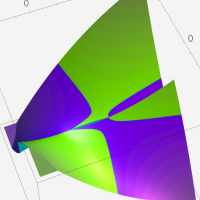
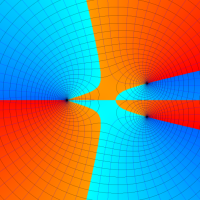
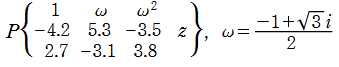 のグラフ。
のグラフ。複素変数の Riemann のP関数
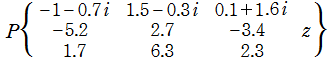 のグラフ。
のグラフ。複素変数の Riemann のP関数
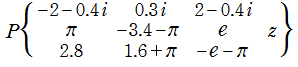 のグラフ。
のグラフ。複素変数の Riemann のP関数
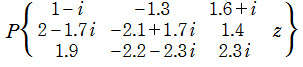 のグラフ。
のグラフ。