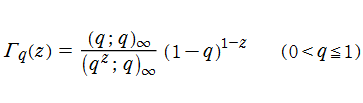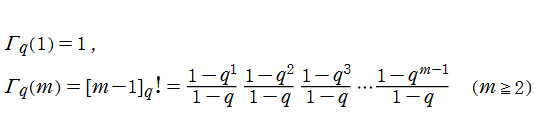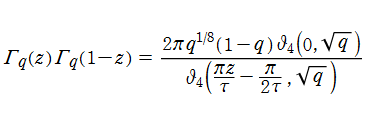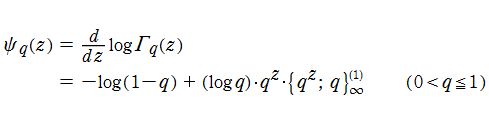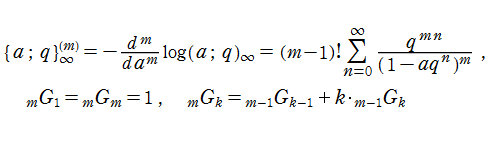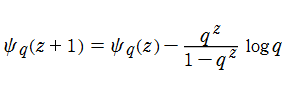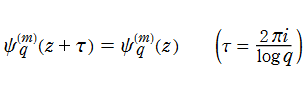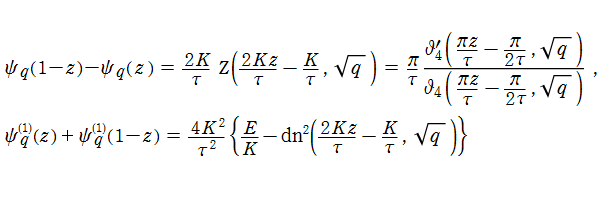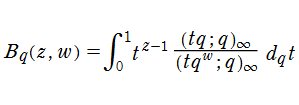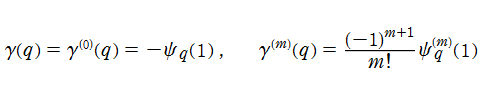特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
q-特殊関数 Menu
q-ガンマ関数(q-階乗関数)
q-ガンマ関数
日:q-ガンマ関数,q-Γ関数英:q-gamma function,仏:q-fonction gamma,独:q-gammafunktion
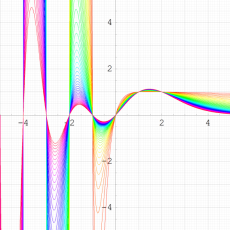
F. H. Jackson が定義した q-ガンマ関数
は、ガンマ関数の q-類似に相当する。つまり極限操作
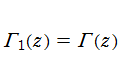
のように q-階乗となる。この値は、実数方向の擬周期性とも言うべき関数等式
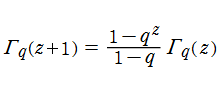
さらにガンマ関数には無い q-ガンマ関数の公式として、虚数方向の擬周期性とも言うべき
を満たす。したがってガンマ関数の相補公式で三角関数となる部分は、q-ガンマ関数の場合では
のように楕円テータ関数が現れる。
なお、q-ガンマ関数は、このほかにも倍数公式など多くの公式を満たす。
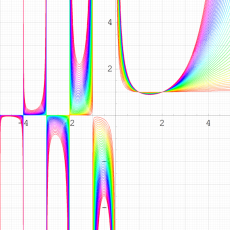
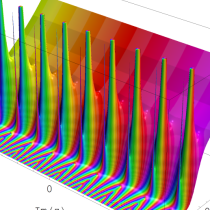
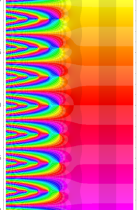
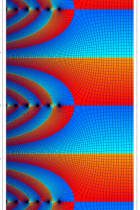
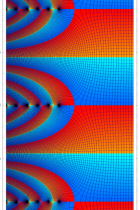
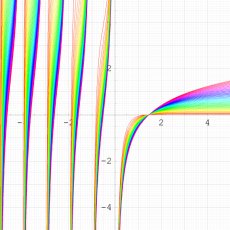
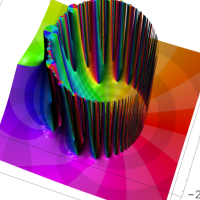
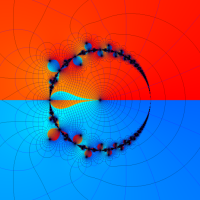
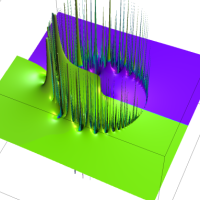
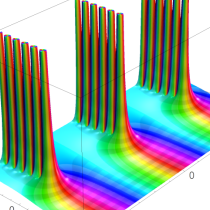
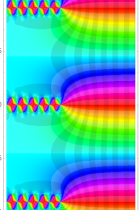
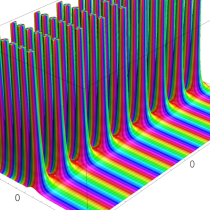
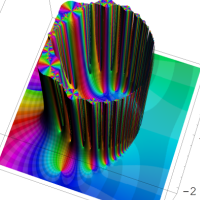
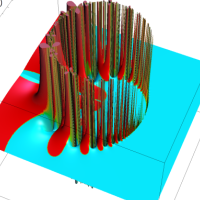
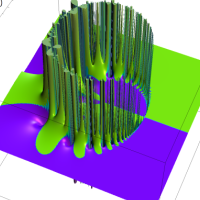
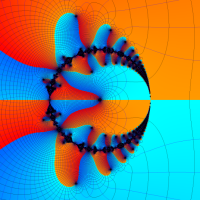
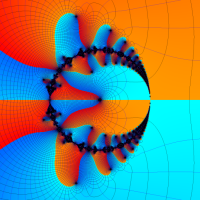
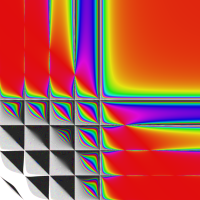
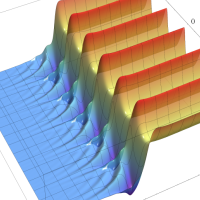
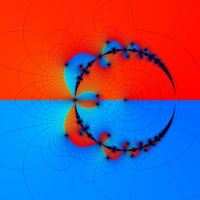
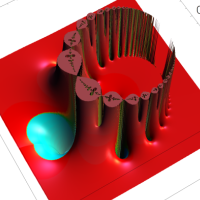
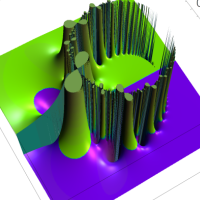
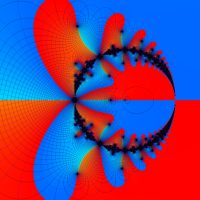
複素解析関数としての q-ガンマ関数は、
q-ガンマ関数は、q-超幾何関数を冪級数展開したときの係数を表わすために用いる等、他の q-特殊関数とともに現れることが多い。
アニメーション(6.10MB)
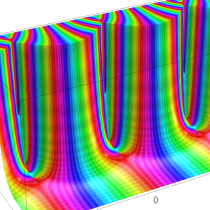
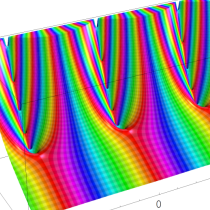
q-ポリガンマ関数
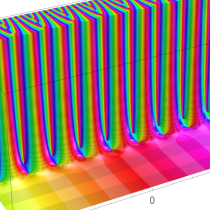
q-ガンマ関数を、変数を、q-ディガンマ関数という。および、これを逐次微分した
なる一群の関数 (q-トリガンマ関数, q-テトラガンマ関数, q-ペンタガンマ関数, …) を総称して、q-ポリガンマ関数という。ここに
である※1。(以下同様。)
q-ポリガンマ関数は極限操作
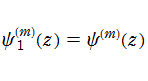
また、q-ディガンマ関数については実数方向の擬周期性とも言うべき関数等式
および特殊値の公式
を満たす。ここに
さらにポリガンマ関数には無い q-ポリガンマ関数の公式として、虚数方向では周期性
を持っている。したがって相補公式は、例えば q-ディガンマ関数および q-トリガンマ関数の場合
のように、楕円ゼータ関数および楕円関数が現れる。ここに、
なお、q-ポリガンマ関数は、このほかにも倍数公式など多くの公式を満たす。
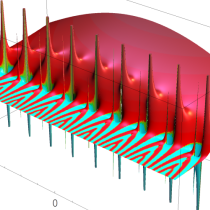
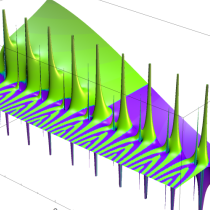
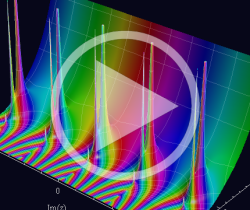
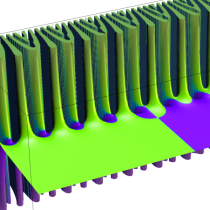
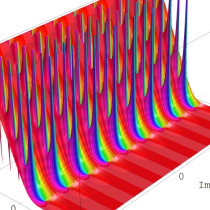
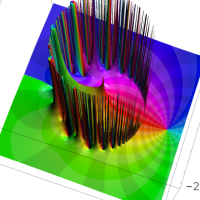
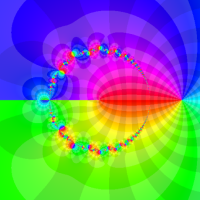
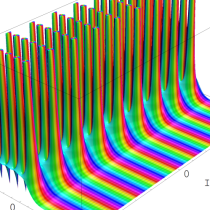
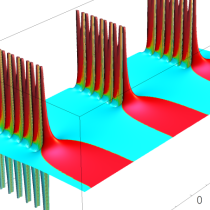
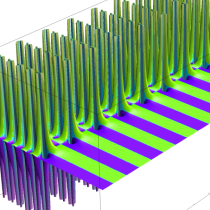
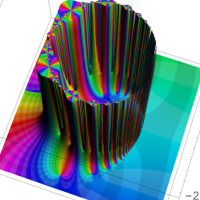
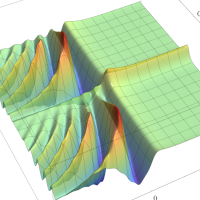
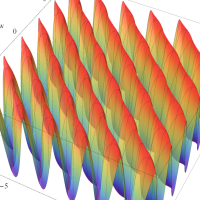
複素解析関数としての q-ポリガンマ関数は、
q-ポリガンマ関数は、Lambert 級数などの級数総和の値として現れるほか、q-ガンマ関数と同様に他の q-特殊関数に付随して現れることが多い。
【註記】
※1:この見慣れない記号は、独自に導入したものである。しかし、この記号は計算可能な数式で表現するための便宜的なもので、q-ポリガンマ関数が q-ガンマ関数の対数の逐次微分から得られるという定義そのものは変わらない。したがって、一般に定着している q-ポリガンマ関数と全く同じ値を与える。
※1:この見慣れない記号は、独自に導入したものである。しかし、この記号は計算可能な数式で表現するための便宜的なもので、q-ポリガンマ関数が q-ガンマ関数の対数の逐次微分から得られるという定義そのものは変わらない。したがって、一般に定着している q-ポリガンマ関数と全く同じ値を与える。
q-ベータ関数
q-ベータ関数は、q-ガンマ関数との間で次の関係がある。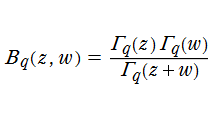
と解釈される。ここに
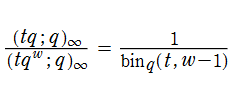
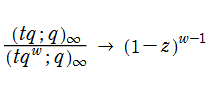
q-ベータ関数も、q-ガンマ関数と同様に他の q-特殊関数に付随して現れることが多い。
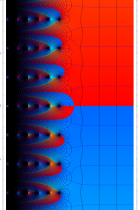
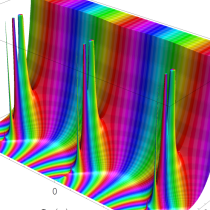
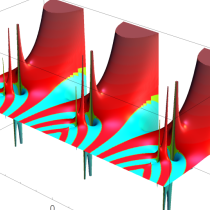
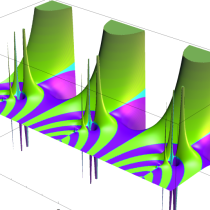
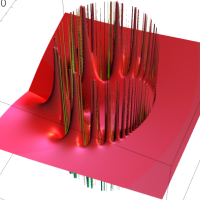
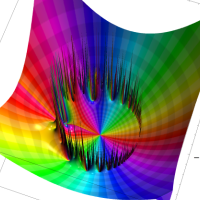
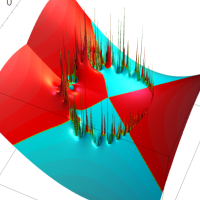
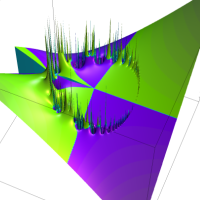
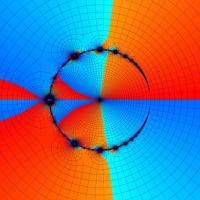
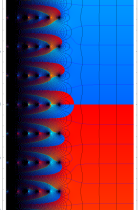
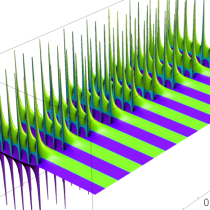
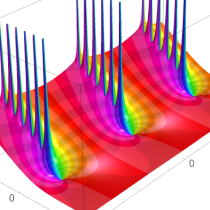
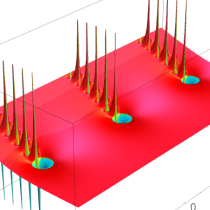
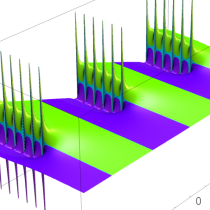
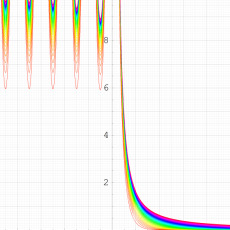
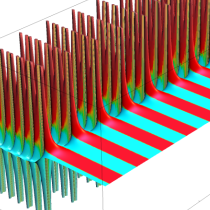
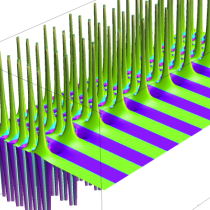
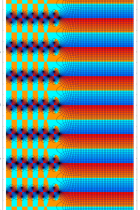
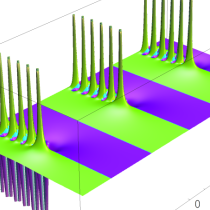
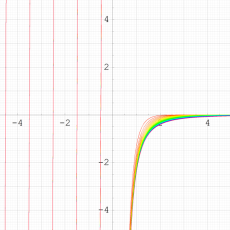
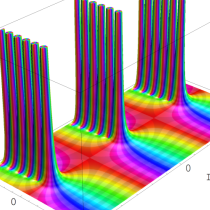
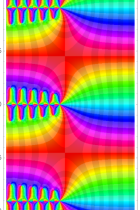
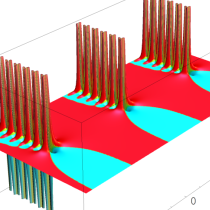
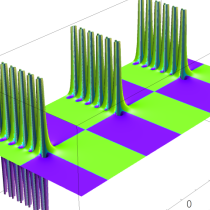
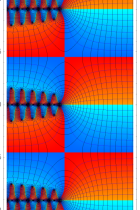
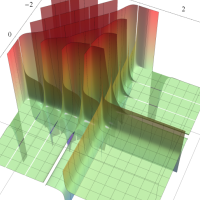
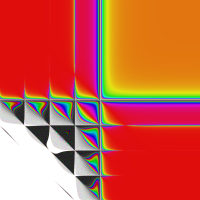
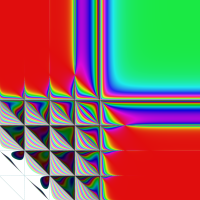
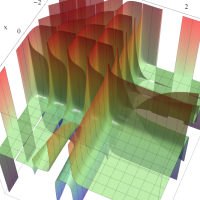
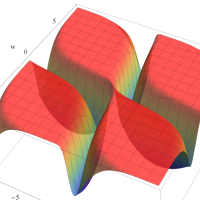
実2変数の q-ベータ関数
実2変数の q-ベータ関数のグラフ。 順に、①
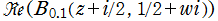 , ②
, ②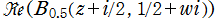 , ③
, ③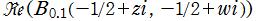 , ④
, ④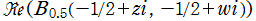 。
。q-Euler 定数
q-Euler 定数とは、q-ポリガンマ関数におけるをもとに定義される、Euler 定数
極限操作
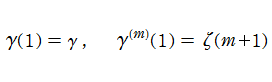
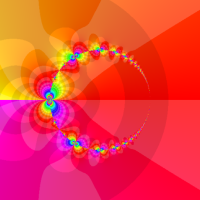
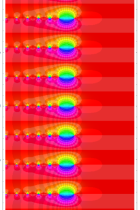
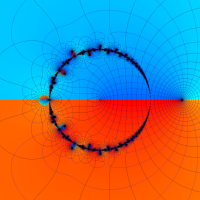
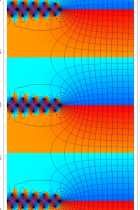
複素関数としての q-Euler 定数は、
複素変数の q-Euler 定数
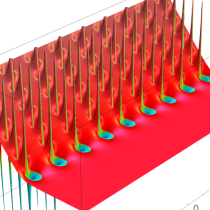
複素変数の q-Euler 定数
複素変数の q-Euler 定数
複素変数の q-Euler 定数