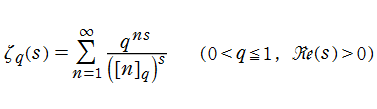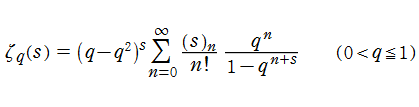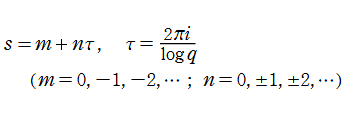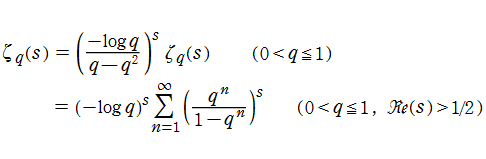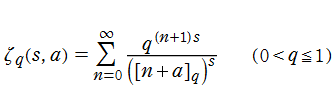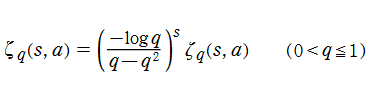特殊関数 グラフィックスライブラリー
Graphics Library of Special functions

q-ゼータ関数

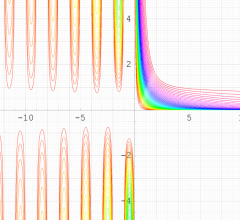
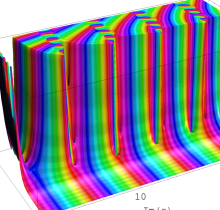
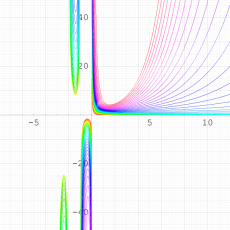
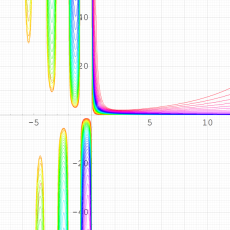
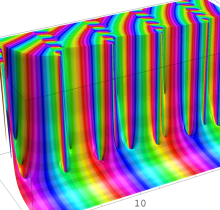
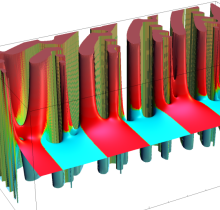
q-Riemann ゼータ関数

　Riemann ゼータ関数の q-類似に相当する

• 

を、q-Riemann ゼータ関数という (これと異なる定義も多く存在する)。極限操作によって
のとおり Riemann ゼータ関数に還元される。
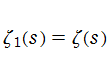
　さらに q-Riemann ゼータ関数は、のみならず、極を除く複素平面全体でも収束する級数

• 

で表わすことができる。
　複素解析関数としての q-Riemann ゼータ関数は、

• 

において１位の極を持つ有理型関数である。
　なお、q-Euler 定数の定義に基づくよう補正因子を掛けた

• 

を q-Riemann ゼータ関数とすることができる。
　一般に q-Riemann ゼータ関数は、Euler 素数積表示式や Riemann 予想に類似の性質・現象を持っていない。

　実変数の q-Riemann ゼータ関数のグラフ。＝0.02～0.98 (+0.02)。

• 

　を複素変数とする q-Riemann ゼータ関数のグラフ。

• 
• 
• 
• 
• 

　を複素変数とする q-Riemann ゼータ関数のグラフ。

• 
• 
• 
• 
• 

　を複素変数とする q-Riemann ゼータ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

　を複素変数とする q-Riemann ゼータ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

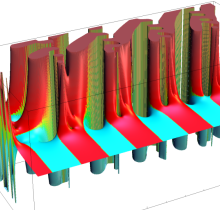
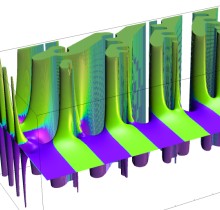
q-Hurwitz ゼータ関数

　Hurwitz ゼータ関数の q-類似に相当する

• 

を、q-Hurwitz ゼータ関数という (これと異なる定義も多く存在する)。極限操作によって
のように Hurwitz ゼータ関数に還元される。またのとき、q-Riemann ゼータ関数になる。
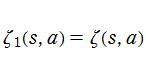
　さらに q-Hurwitz ゼータ関数は、のみならず、極を除く複素平面全体でも収束する級数

• 

で表わすことができる。
　複素解析関数としての q-Hurwitz ゼータ関数は、

• 

に1位の極を持つ有理型関数である。
　なお、q-Hurwitz ゼータ関数についても補正因子を掛けた

• 

を q-Hurwitz ゼータ関数の別定義とすることができる。

　実変数の q-Hurwitz ゼータ関数のグラフ。順に、①, ②。 いずれも ＝0.02～0.98 (+0.02)。

• 　①
  
• 　②
  

　を複素変数とする q-Hurwitz ゼータ関数のグラフ。

• 
• 
• 
• 
• 

　を複素変数とする q-Hurwitz ゼータ関数のグラフ。

• 
• 
• 
• 
• 

　を複素変数とする q-Hurwitz ゼータ関数のグラフ。

• 
• 
• 
• 
• 

　を複素変数とする q-Hurwitz ゼータ関数のグラフ。

• 
• 
• 
• 
• 

　を複素変数とする q-Hurwitz ゼータ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

　を複素変数とする q-Hurwitz ゼータ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

　を複素変数とする q-Hurwitz ゼータ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

　を複素変数とする q-Hurwitz ゼータ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
•