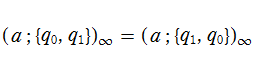特殊関数 グラフィックスライブラリー
Graphics Library of Special functions

楕円初等関数

楕円シフト因子

　楕円シフト因子は、q-シフト因子 (q-Pochhammer 記号) を楕円関数化したものに相当し、無限乗積

• 

で定義される。この形から、明らかに対称性
を持つことが分かる。

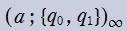
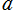
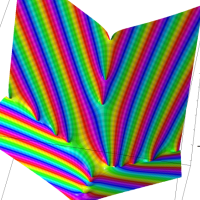
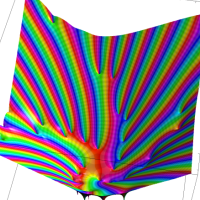
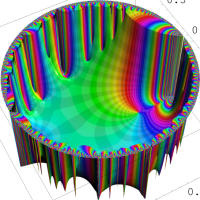
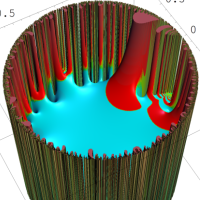
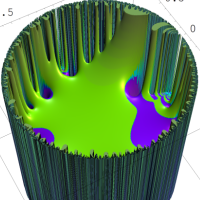
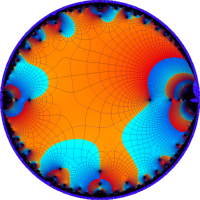
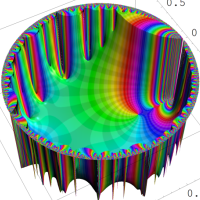
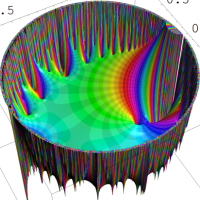
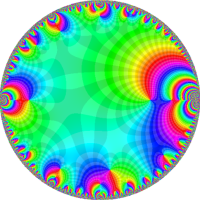
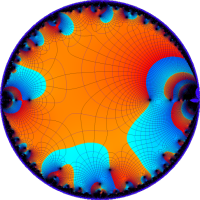
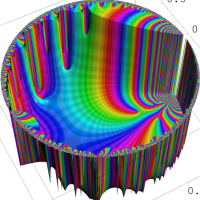
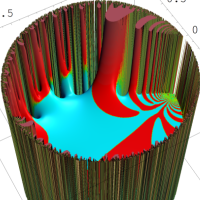
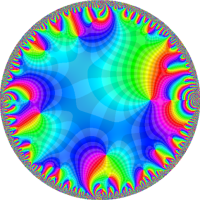
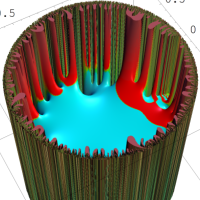
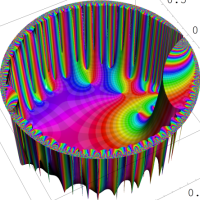
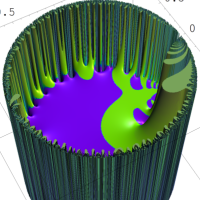
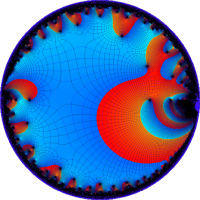
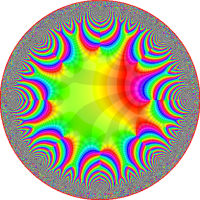
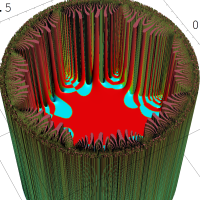
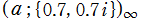
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

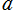
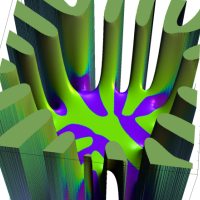
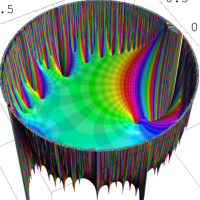
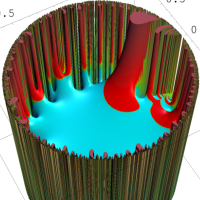
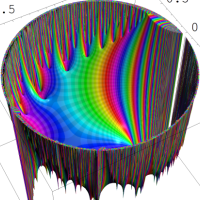
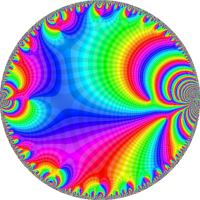
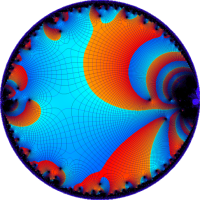
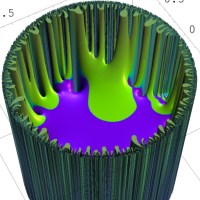
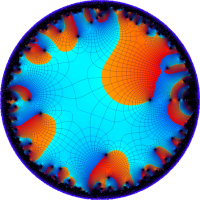
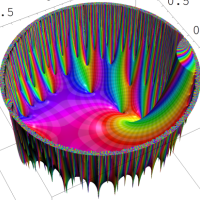
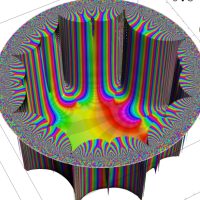
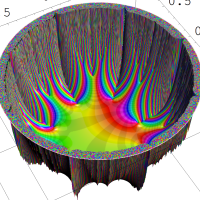
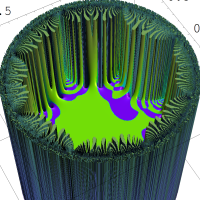
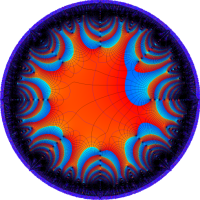
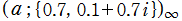
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

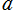
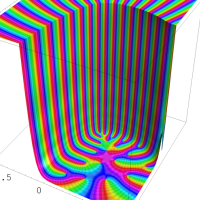
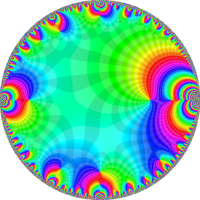
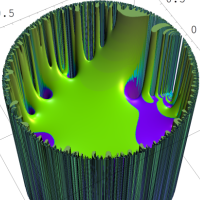
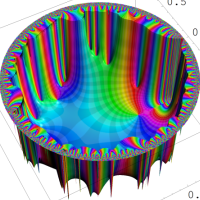
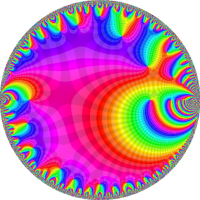
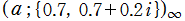
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

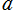
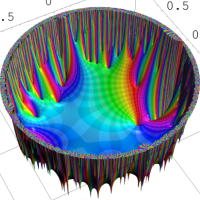
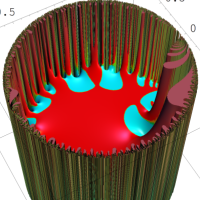
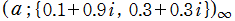
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

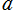
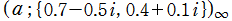
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

　アニメーション（15.40MB）
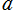
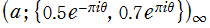
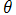
　を複素変数とする 楕円シフト因子のグラフ。＝1/50～2 (+1/50) 。

• 

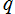
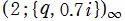
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

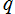
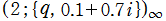
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

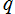
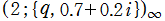
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

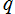
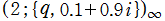
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

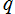
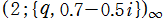
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

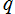
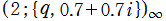
　を複素変数とする楕円シフト因子のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
•