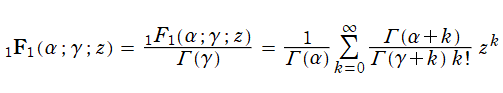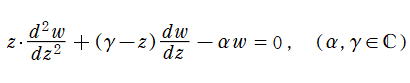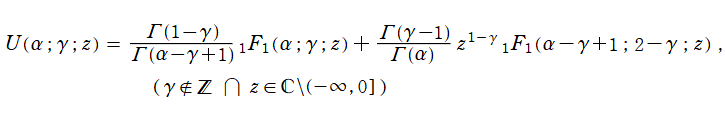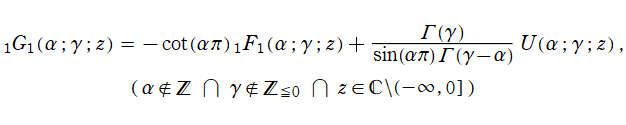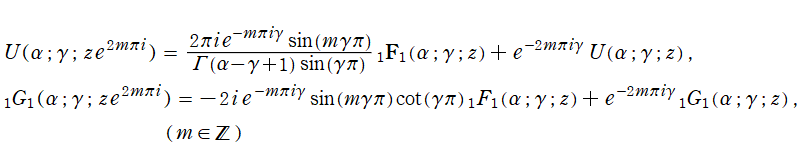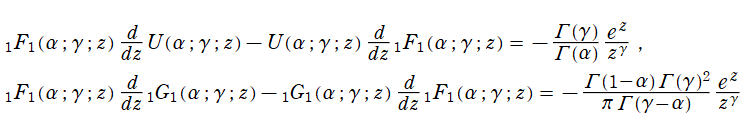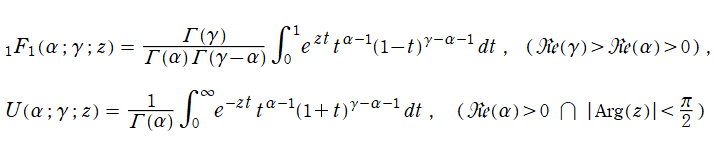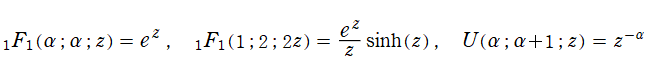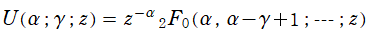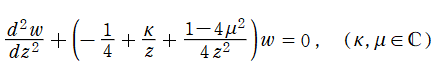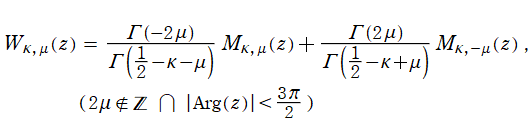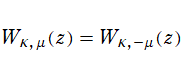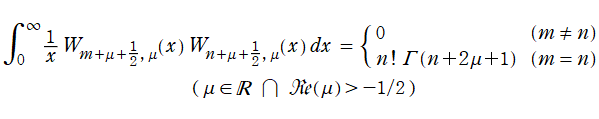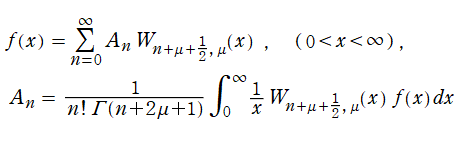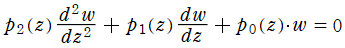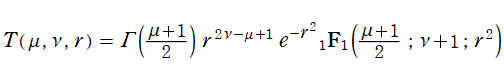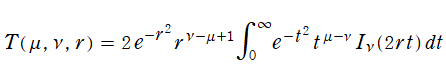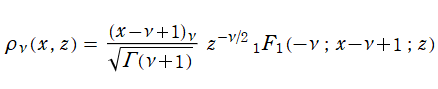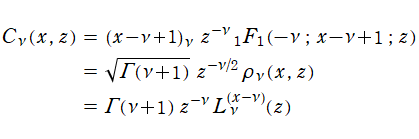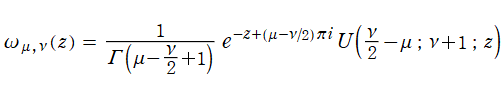特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
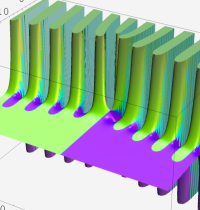
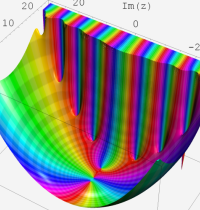
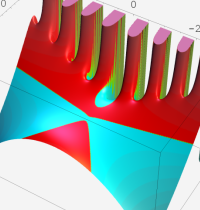
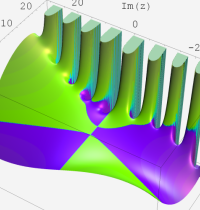
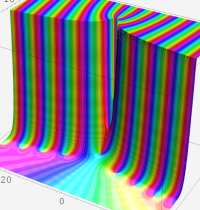
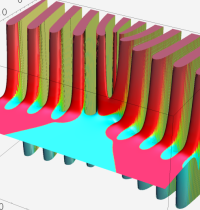
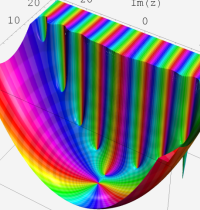
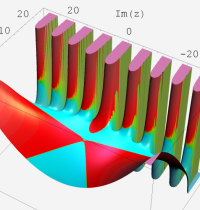
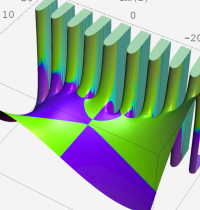
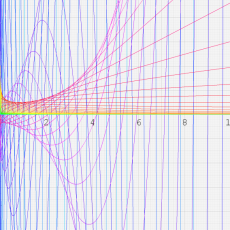
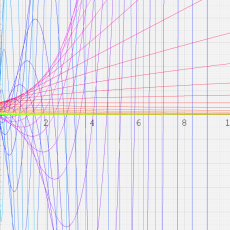
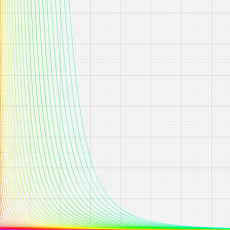
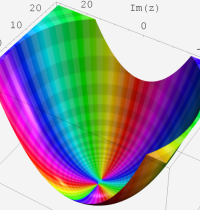
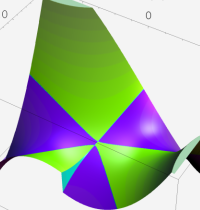
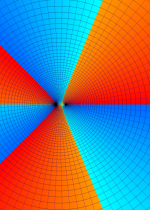
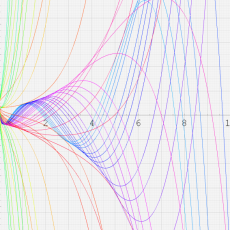
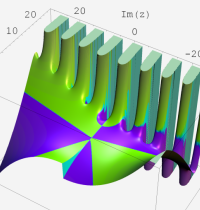
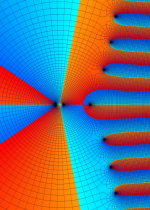
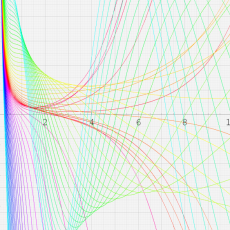
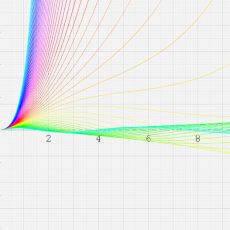
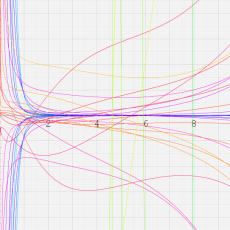
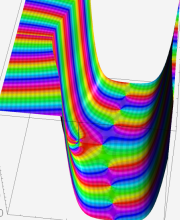
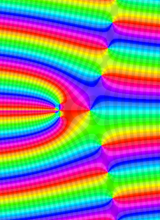
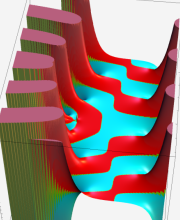
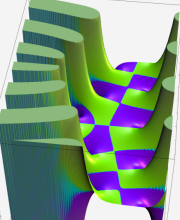
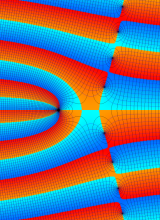
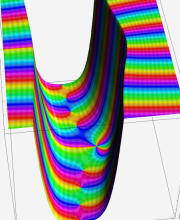
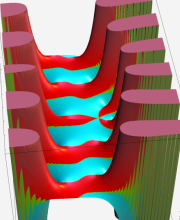
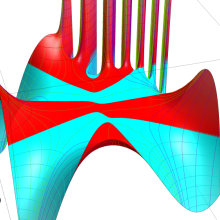
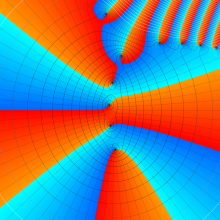
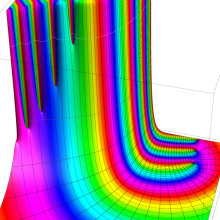
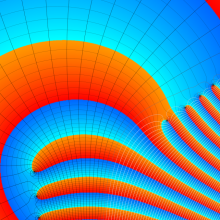
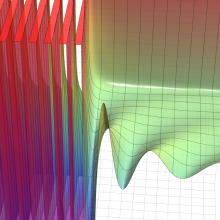
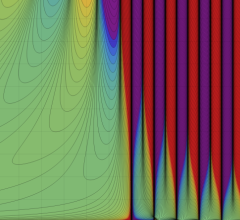
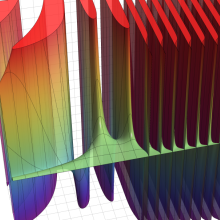
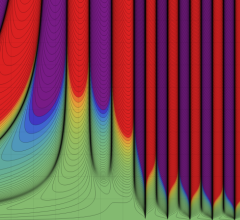
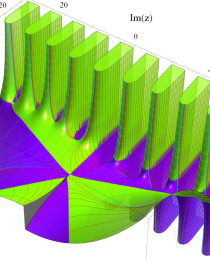
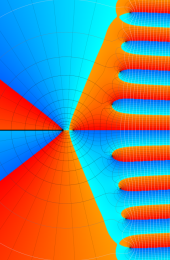
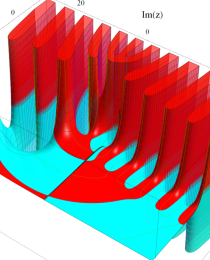
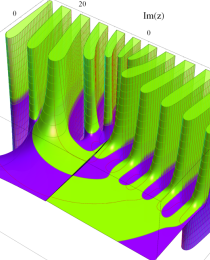
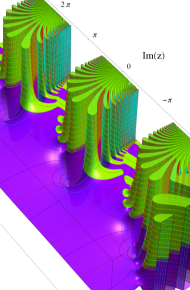
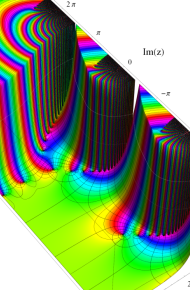
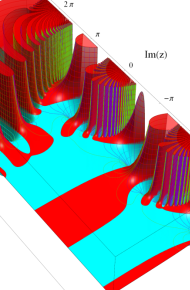
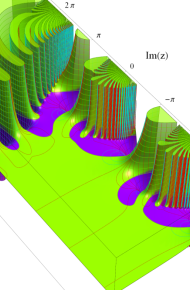
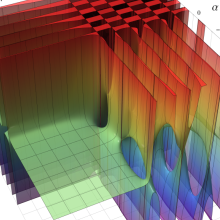
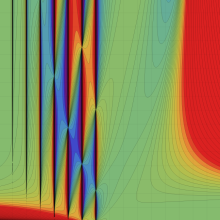
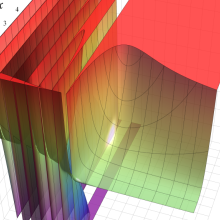
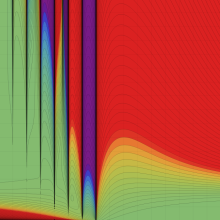
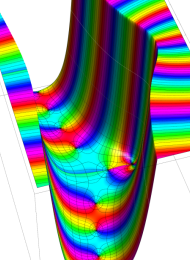
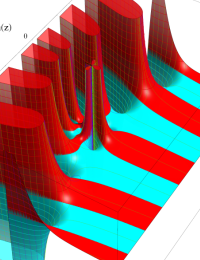
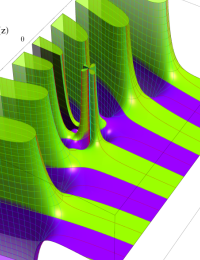
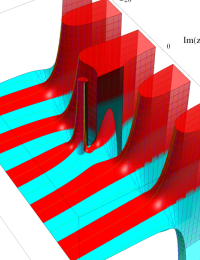
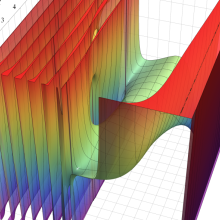
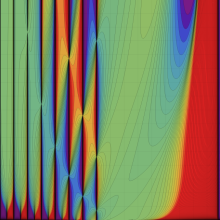
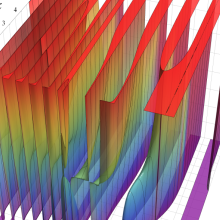
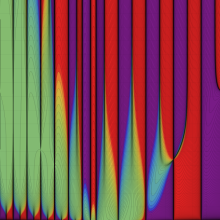
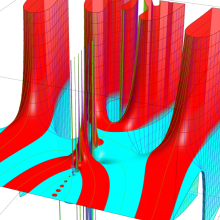
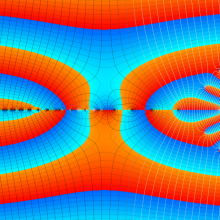
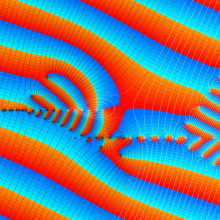
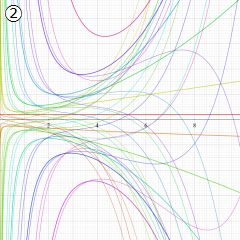
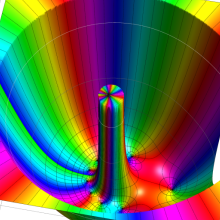
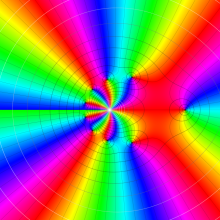
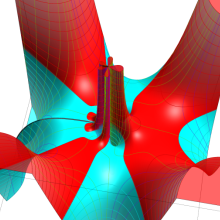
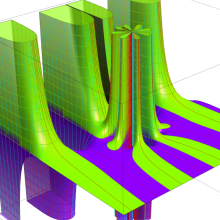
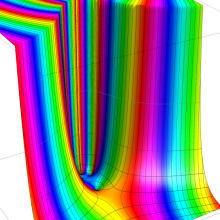
合流型超幾何関数
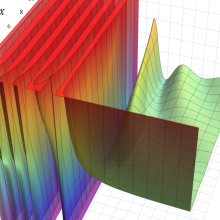
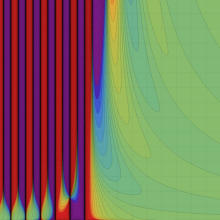
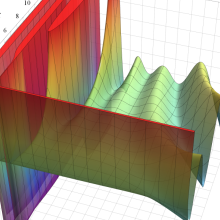
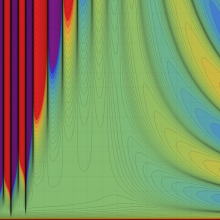
合流型超幾何関数
日:合流型超幾何関数英:Confluent hypergeometric function,仏:Fonction hypergéométrique confluente,
独:Konfluente hypergeometrische funktion
変数
で定義される関数
は、全ての
2階の線形常微分方程式
は、
で定義するのが標準となっている。この関数は
当サイトでは、合流型超幾何微分方程式を満たすが
を、併せて定義する。この関数は
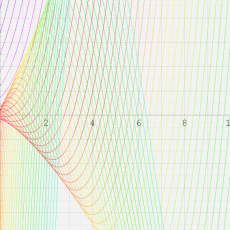
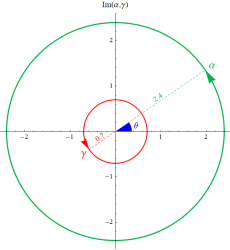
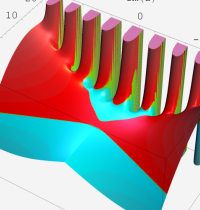
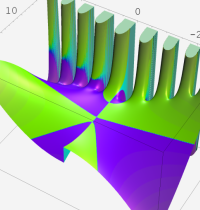
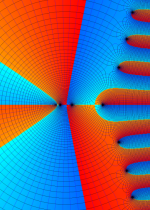
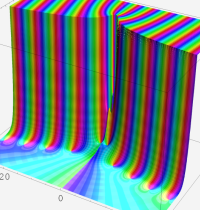
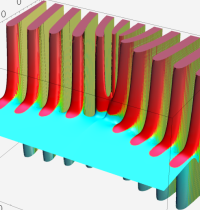
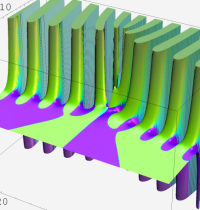
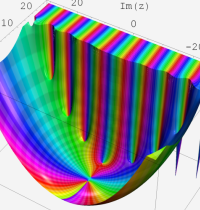
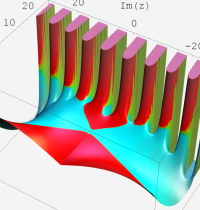
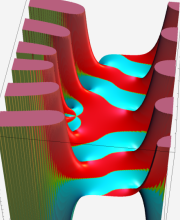
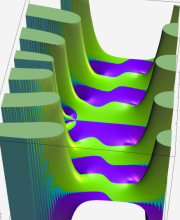
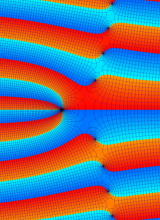
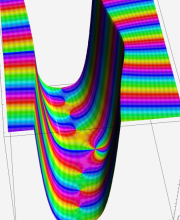
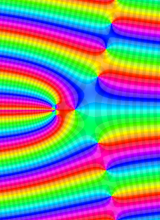
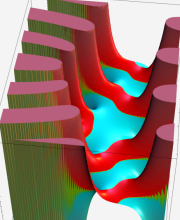
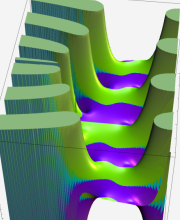
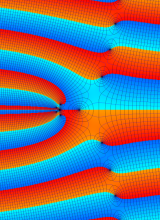
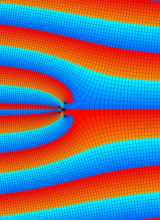
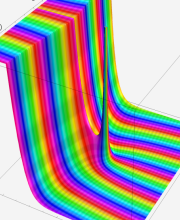
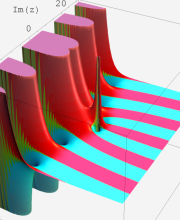
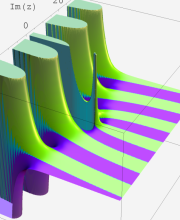
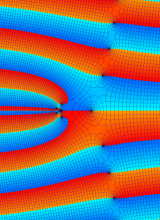
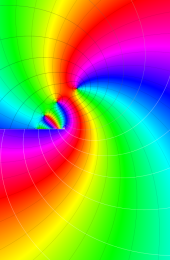
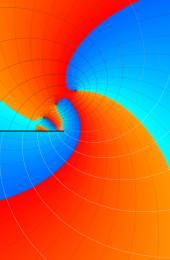
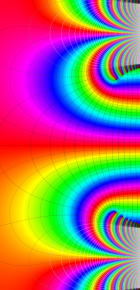
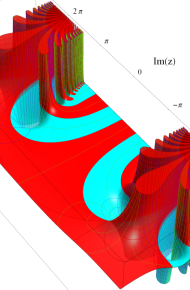
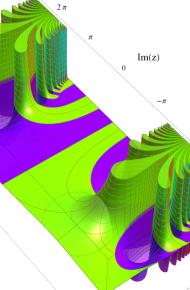
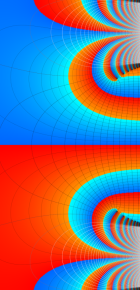
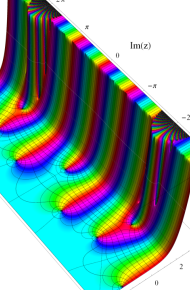
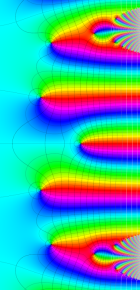
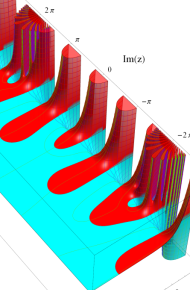
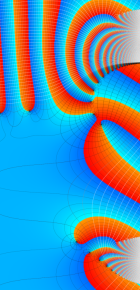
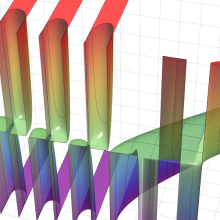
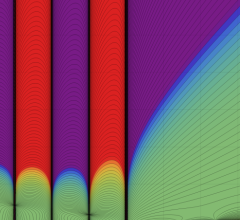
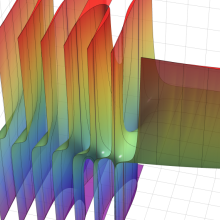
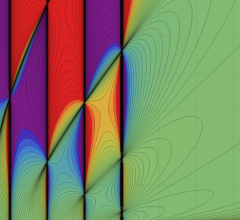
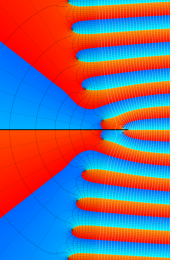
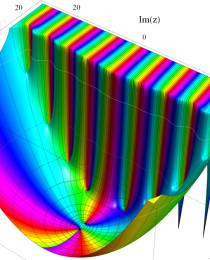
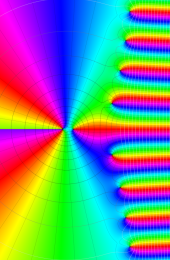
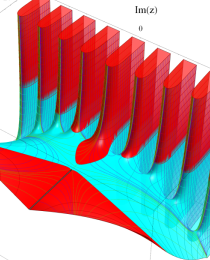
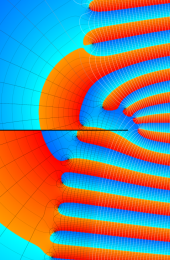
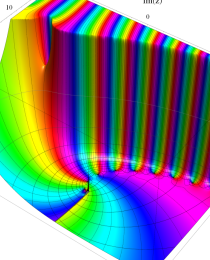
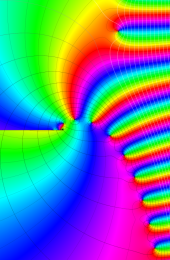
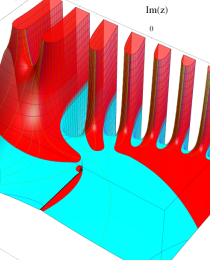
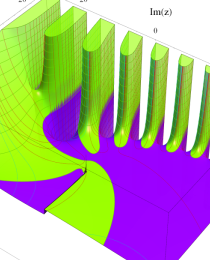
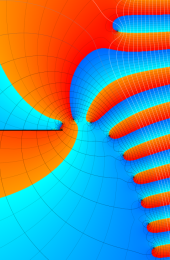
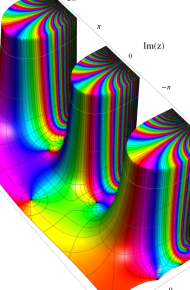
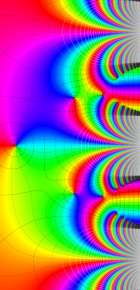
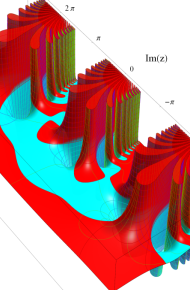
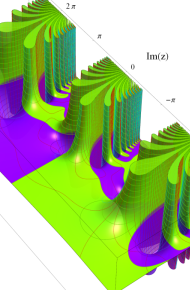
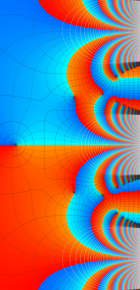
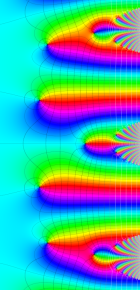
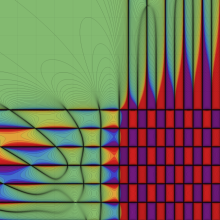
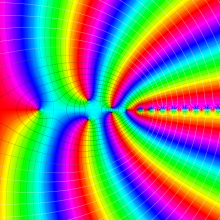
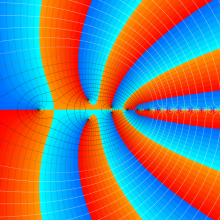
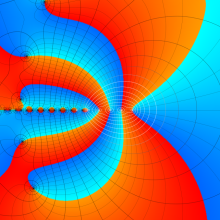
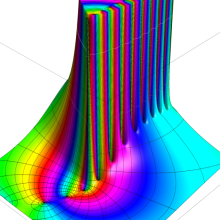
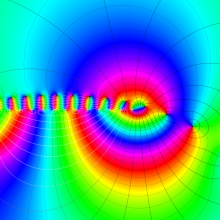
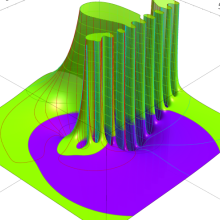
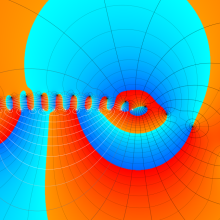
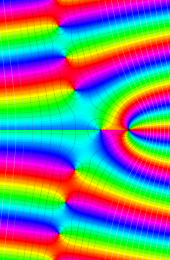
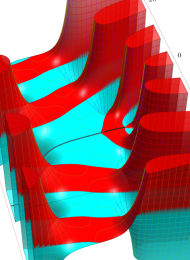
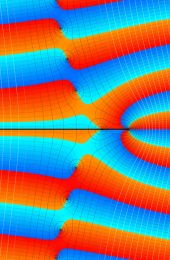
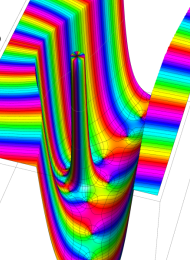
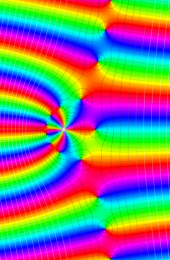
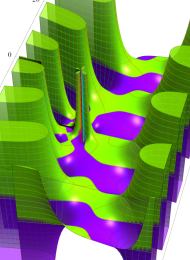
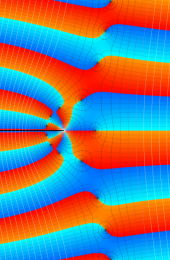
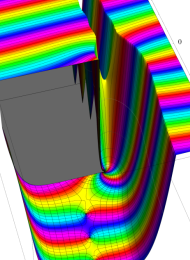
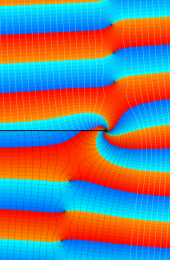
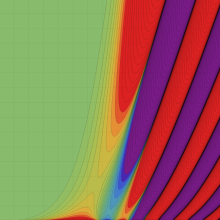
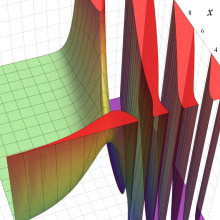
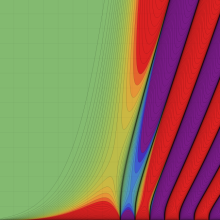
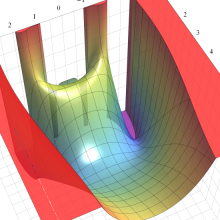
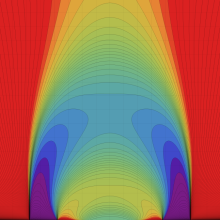
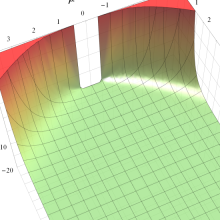
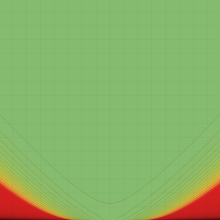
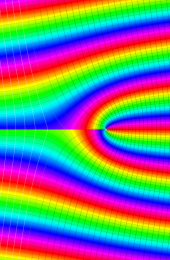
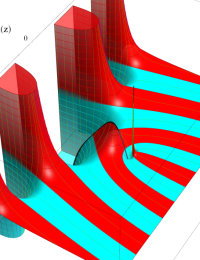
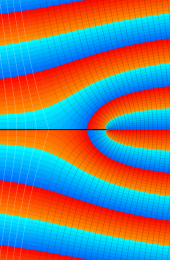
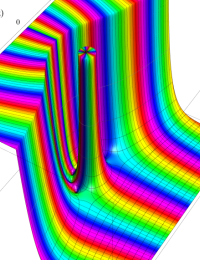
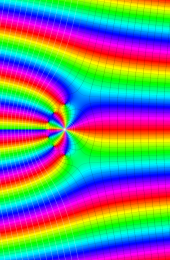
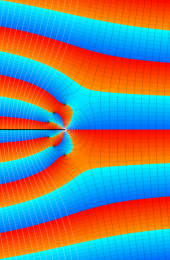
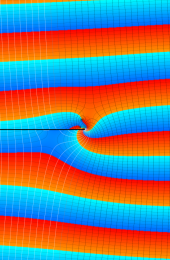
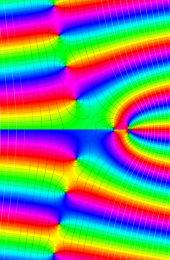
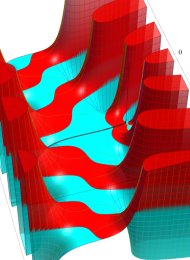
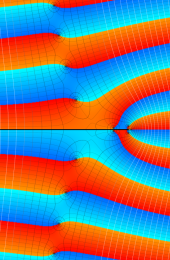
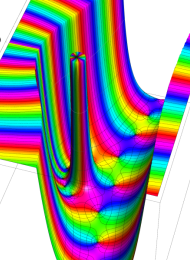
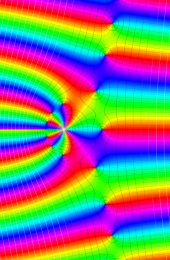
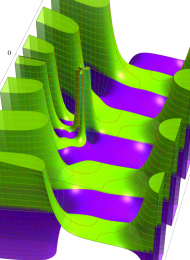
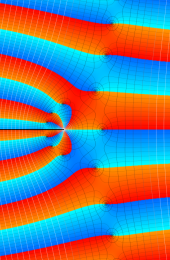
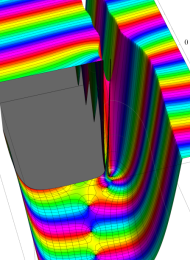
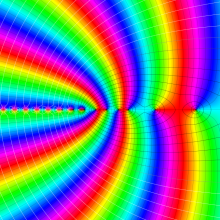
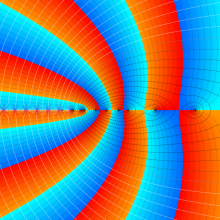
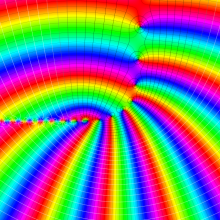
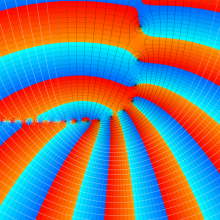
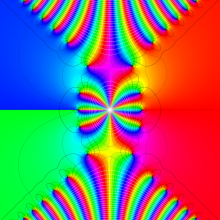
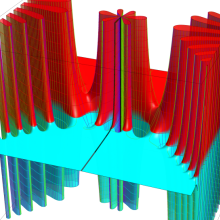
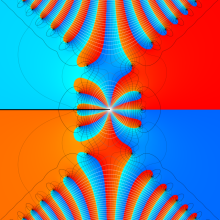
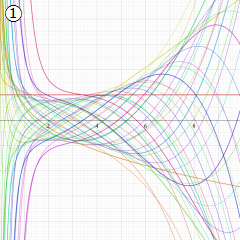
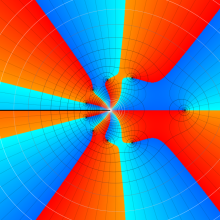
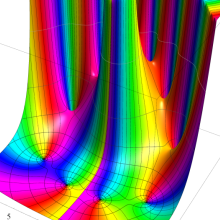
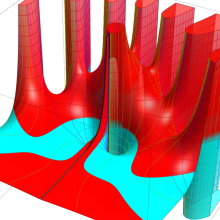
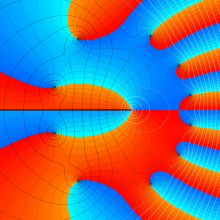
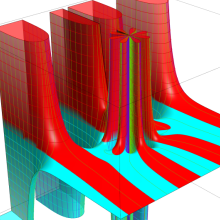
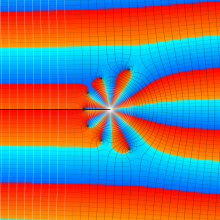
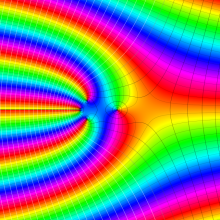
第2種合流型超幾何関数の分枝切断線
によって成される。この式を用いて
"合流型" とは、超幾何微分方程式の3個の確定特異点
によって、合流型超幾何関数が得られることと同じである※2。
合流型超幾何関数の
と、線形漸化式 (超幾何関数系では、これを 「隣接関係式」 とも言う。)
が有名である。ここに
となる。
合流型超幾何関数の
となる。これを先の線形漸化式に適用すれば、種々の微分漸化式が得られる。
さらに、合流型超幾何関数の導関数については、第1種と第2種の間でロンスキアン型の関係式
を満たす。
合流型超幾何関数の数値計算では、漸近級数展開式
が重要となる。特に
合流型超幾何関数は多くの積分表示式を持っているが、そのうち
は、最も基本的な式として知られる。また、Mellin - Barnes 型の積分表示式
は留数定理に基づいており、同様の考え方が Meijer のG関数に拡張される。
合流型超幾何関数の Laplace 変換のうち、
は、結果がより高い (超幾何関数の) クラスに上がる例である。
さらに特筆すべき合流型超幾何関数の性質は、連分数展開式
を持つことである。
多くの特殊関数は、合流型超幾何関数によって表わすことができる。具体的な表示式は、既に不完全ガンマ関数、積分指数関数、誤差関数、Bessel 関数、Hermite 関数、放物柱関数、Laguerre 陪関数、および Coulomb 波動関数の頁に掲載した※4。さらに、この頁の後半では Whittaker 関数、二三の関連関数についても触れる。
また、合流型超幾何関数はこれらの還元された特殊関数どうしの関係も明らかにする。例えば、整数次の Hermite 関数と (パラメータが
合流型超幾何関数が初等関数に還元される事例として、
が知られている。また、
合流型超幾何関数は、上記で列挙した特殊関数の総括・一般論で扱われる事が多く、これらの特殊関数の性質は合流型超幾何関数のそれに由来する。数式処理システムでは、それらの関係式を網羅的に実装して、できるだけ多くの積分計算、級数総和の結果が還元できるよう、年々改良が施されている。応用事例も多くがこれらの特殊関数と共通するが、統計学、極限ブラックホールへの摂動、断層撮影法など、合流型超幾何関数を直接用いる研究も増えつつある。また、現在では合流型超幾何関数の様々な類似も考案されている。例えば q-類似、有限体上での定義、行列変数などがある。
第1種合流型超幾何関数は、1836年に E. Kummer が初めて導入した※5。ただし、関数記号は
第2種合流型超幾何関数
【註記】
※1:よって、全ての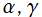 に対して基本解が存在する
に対して基本解が存在する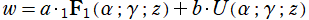 が、本来ならば一般解の表示として最も好ましい。
が、本来ならば一般解の表示として最も好ましい。
※2:一般に、Fuchs 型の常微分方程式の確定特異点が合流して生じる微分方程式を 「合流型微分方程式」、その解を 「合流型関数」 と総称することがある。超幾何関数よりも高いクラスの例では、Heun 関数とその合流型関数がある。
※3: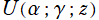 の漸近級数展開式を形式的に解釈し、
の漸近級数展開式を形式的に解釈し、
と表現することもある。ただし、関数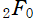 は本来ならば存在しない。
は本来ならば存在しない。
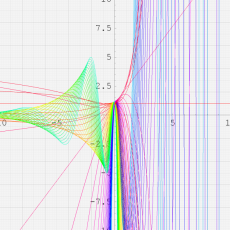
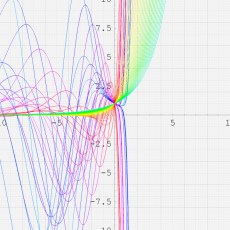
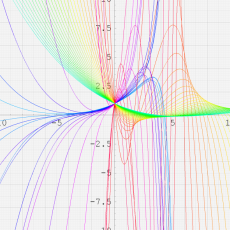
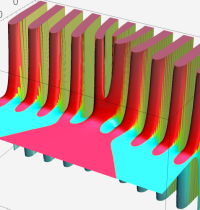
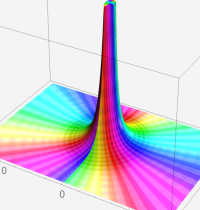
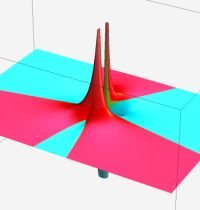
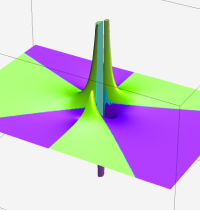
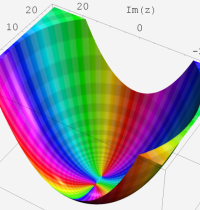
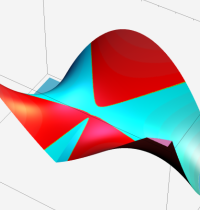
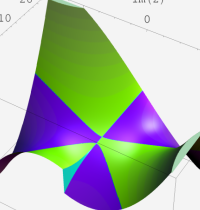
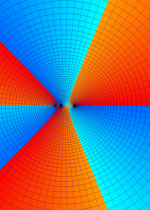
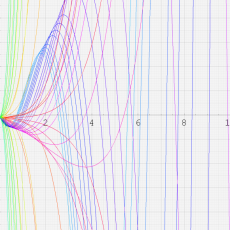
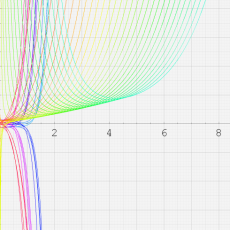
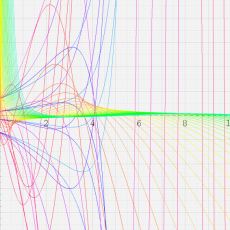
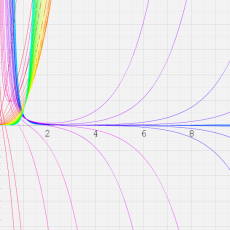
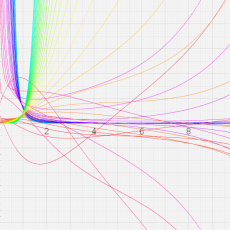
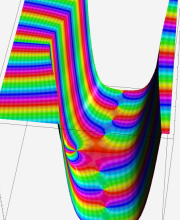
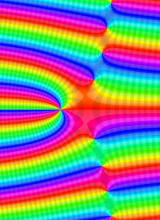
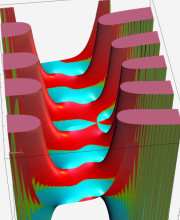
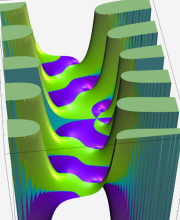
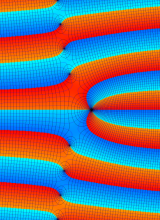
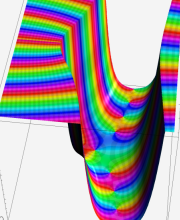
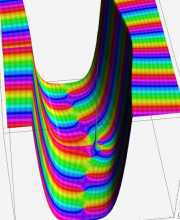
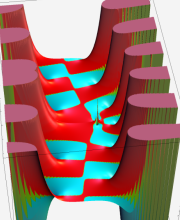
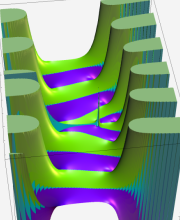
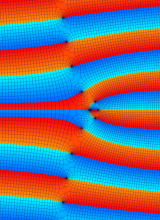
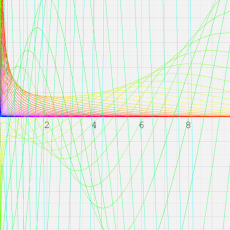
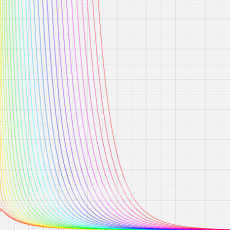
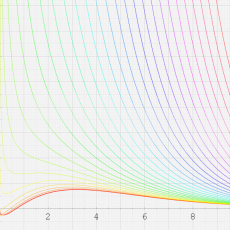
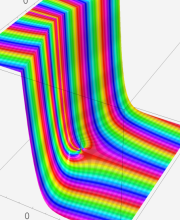
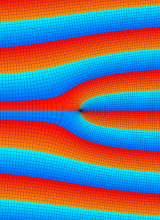
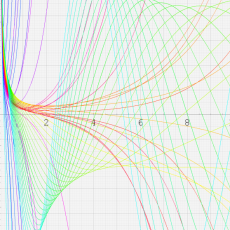
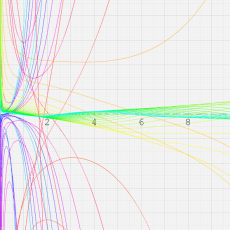
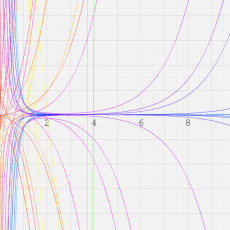
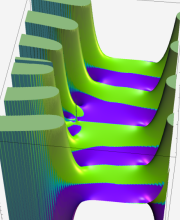
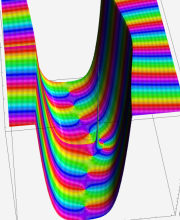
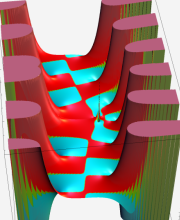
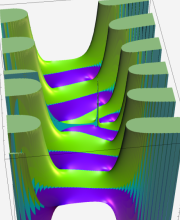
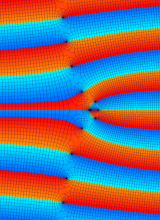
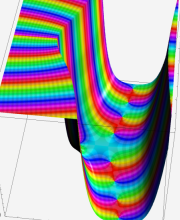
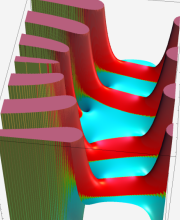
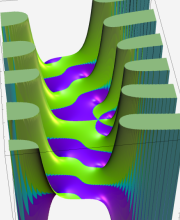
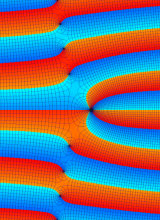
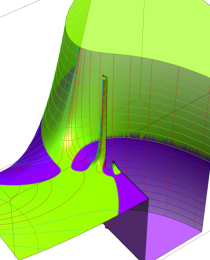
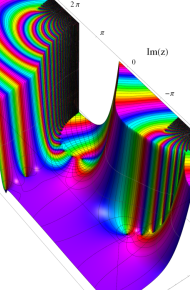
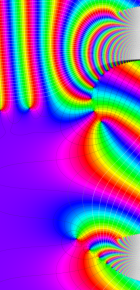
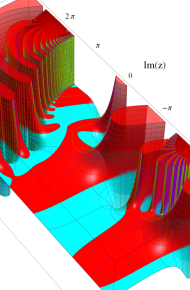
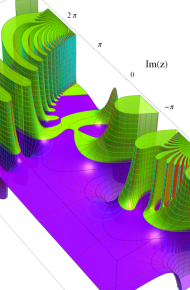
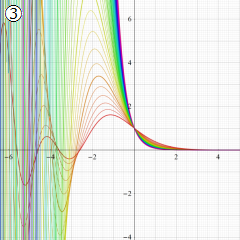
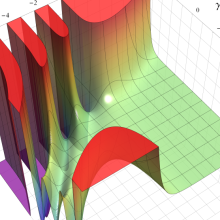
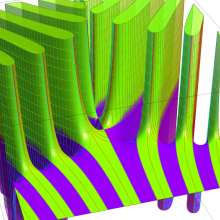
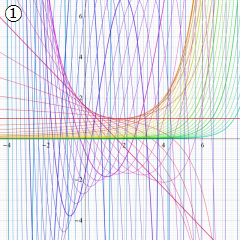
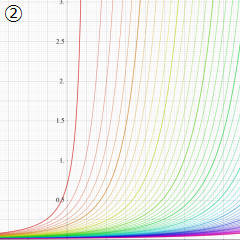
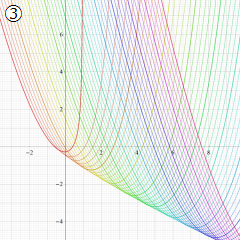
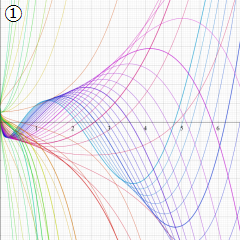
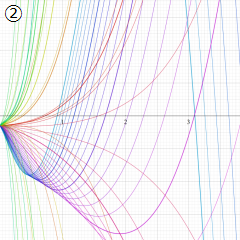
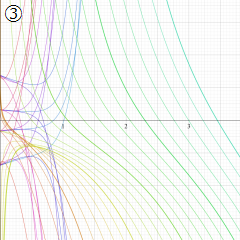
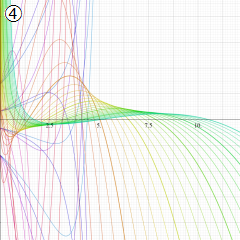
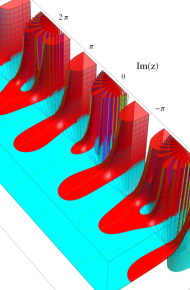
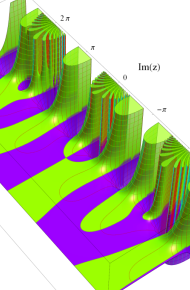
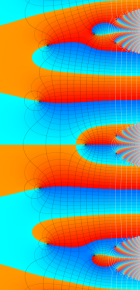
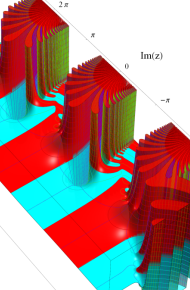
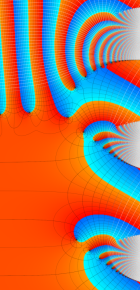
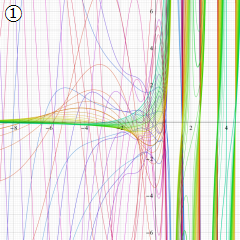
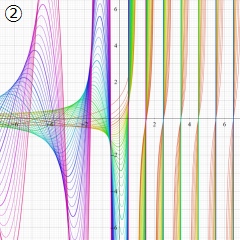
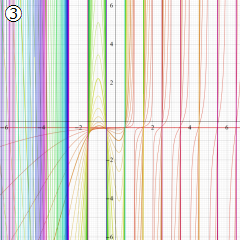
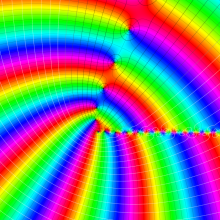
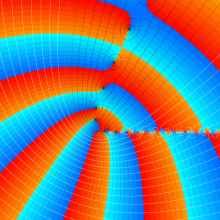
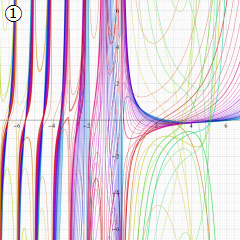
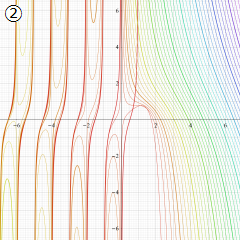
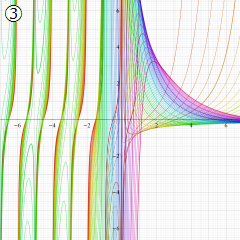
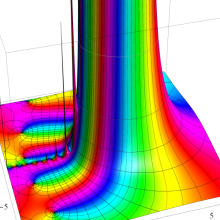
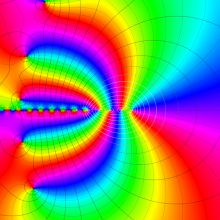
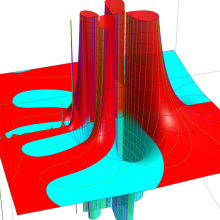
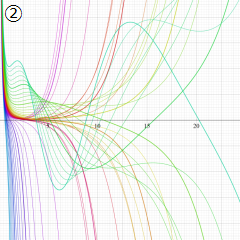
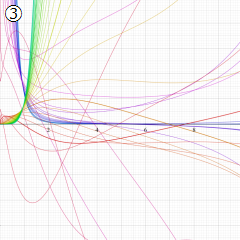
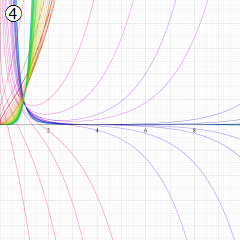
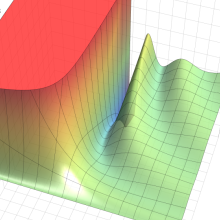
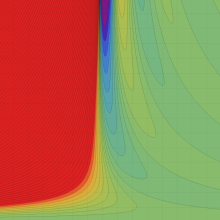
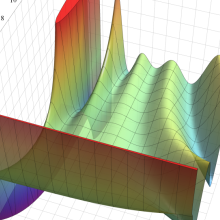
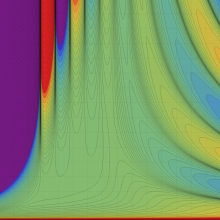
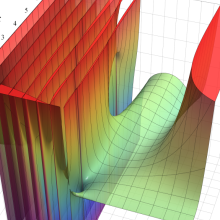
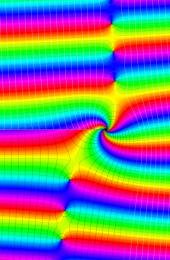
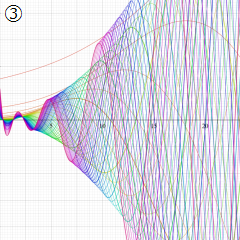
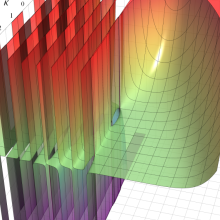
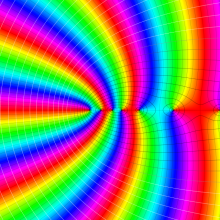
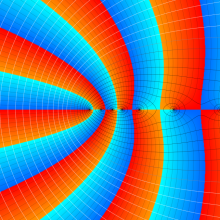
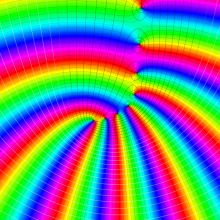
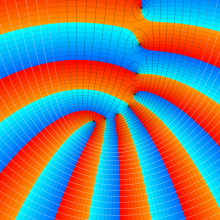
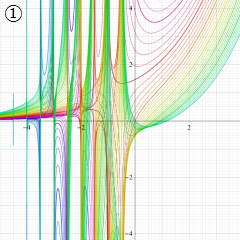
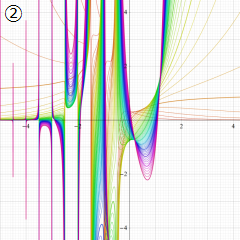
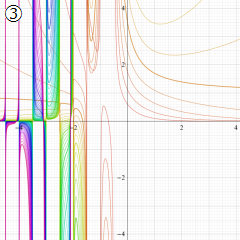
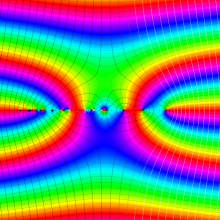
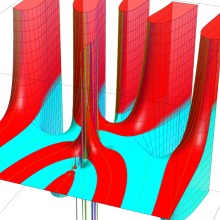
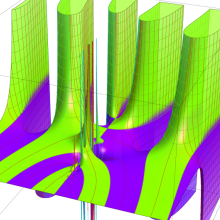
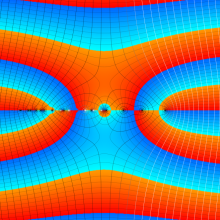
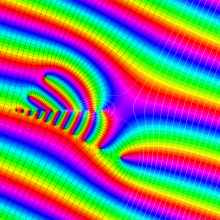
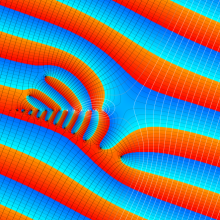
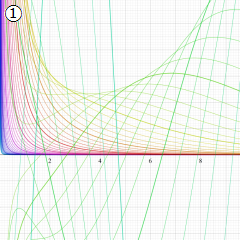
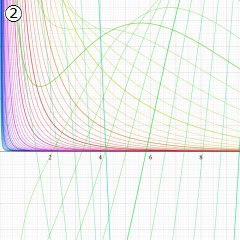
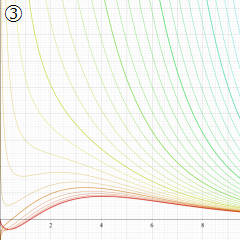
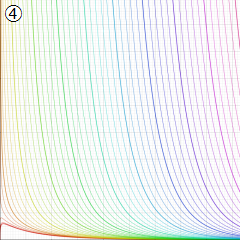
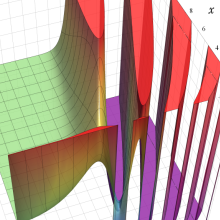
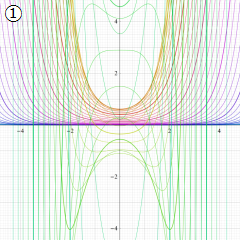
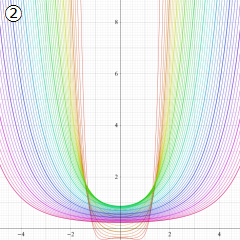
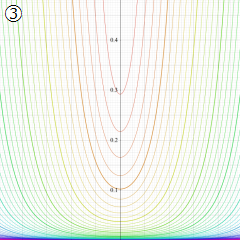
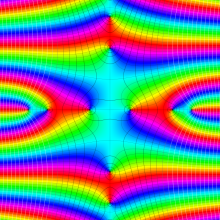
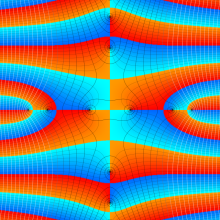
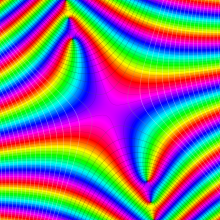
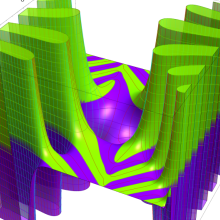
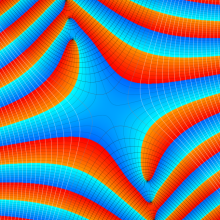
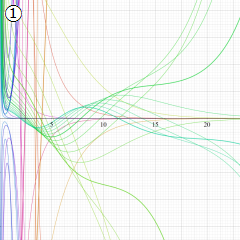
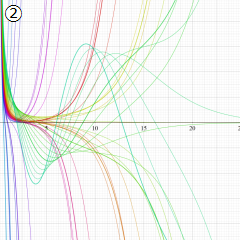
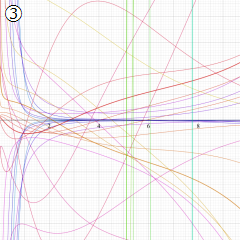
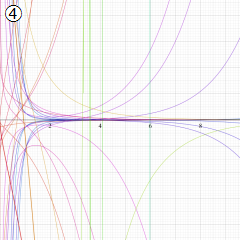
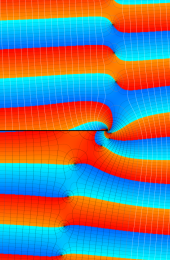
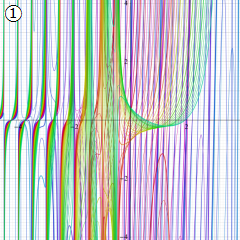
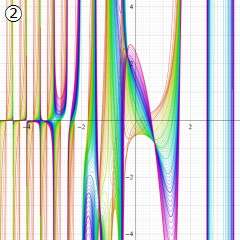
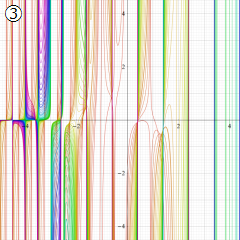
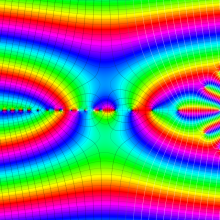
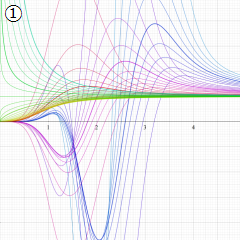
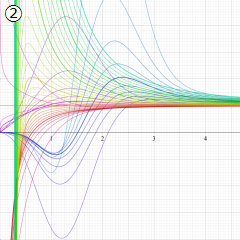
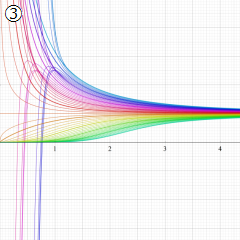
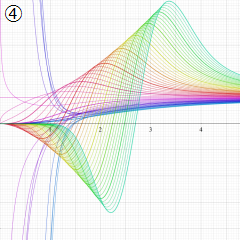
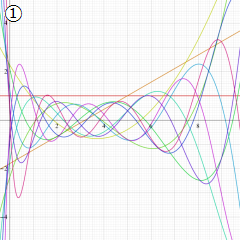
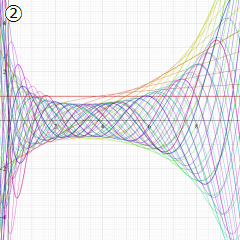
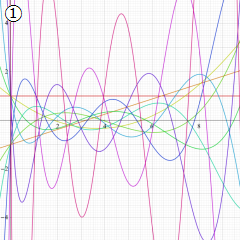
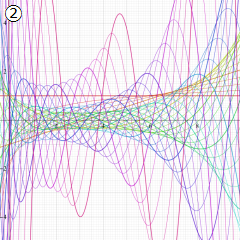
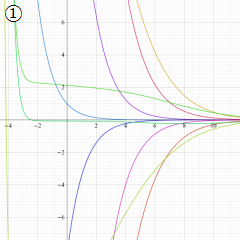
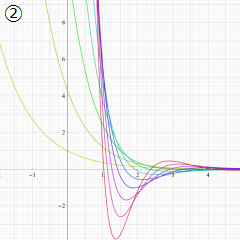
※4:したがって、これらの頁で既に合流型超幾何関数のグラフを掲載したとも言える。実際、合流型超幾何関数のグラフは Laguerre 陪関数のそれに大変似ている。
※5: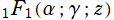 を Kummer 関数 (Kummer の合流型超幾何関数)、
を Kummer 関数 (Kummer の合流型超幾何関数)、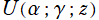 を Tricomi 関数と呼ぶこともある。
を Tricomi 関数と呼ぶこともある。
※1:よって、全ての
※2:一般に、Fuchs 型の常微分方程式の確定特異点が合流して生じる微分方程式を 「合流型微分方程式」、その解を 「合流型関数」 と総称することがある。超幾何関数よりも高いクラスの例では、Heun 関数とその合流型関数がある。
※3:
と表現することもある。ただし、関数
※4:したがって、これらの頁で既に合流型超幾何関数のグラフを掲載したとも言える。実際、合流型超幾何関数のグラフは Laguerre 陪関数のそれに大変似ている。
※5:
①
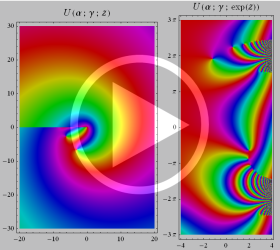
アニメーション(18.2MB)
①
①
①
①
アニメーション(18.2MB)
①
Whittaker 関数
日:Whittaker関数,ホイッタカー関数英:Whittaker function,仏:Fonction de Whittaker,独:Whittakersche funktion
「Whittaker の微分方程式」 と呼ばれる、2階の線形常微分方程式
も、
となる。これを順に、第1種および第2種 Whittaker 関数という。因みに Whittaker の微分方程式は、
は、
を満たす。このように Whittaker 関数は
1903年に E. T. Whittaker が、超幾何関数系の合流型関数から導かれる特殊関数の全貌を調べた論文で、
と、この帰結としての任意実関数
がある。ただし、現在ではほとんどの場合 Laguerre 陪関数で記述されている※3。
当サイトでは、独自の第2種 Whittaker 関数
を併せて定義する。
【註記】
※1:自己随伴形とは、2階の線形常微分方程式
の係数関数が = p[1](z)](siki_spec240/conhypgeo17300.png) を満たすものを言う。合流型超幾何微分方程式は自己随伴形ではない。
を満たすものを言う。合流型超幾何微分方程式は自己随伴形ではない。
※2:E. T. Whittaker 「An expression of certain known functions asgeneralized hypergeometric functions」 (Bulletin of the American Mathematical Society, Vol.10, No.3, (1903), p.125-134)
※3:その他の Whittaker 関数の性質、例えば![(-∞, 0]](siki_spec240/conhypgeo01400.png) を越える解析接続、線形漸化式、漸近級数展開式、積分表示式、および連分数展開式等は、合流型超幾何関数のそれから導くことができ、しかもその結果はNISTの13.14~13.23に詳しく載っているので省略する。
を越える解析接続、線形漸化式、漸近級数展開式、積分表示式、および連分数展開式等は、合流型超幾何関数のそれから導くことができ、しかもその結果はNISTの13.14~13.23に詳しく載っているので省略する。
また、第1種 Whittaker 関数は正規化 Laguerre 陪関数と
の関係にあり、変数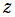 で見ると無理関数の違いしかない。よって、グラフの掲載数を控えめにする。
で見ると無理関数の違いしかない。よって、グラフの掲載数を控えめにする。
※1:自己随伴形とは、2階の線形常微分方程式
の係数関数が
※2:E. T. Whittaker 「An expression of certain known functions asgeneralized hypergeometric functions」 (Bulletin of the American Mathematical Society, Vol.10, No.3, (1903), p.125-134)
※3:その他の Whittaker 関数の性質、例えば
また、第1種 Whittaker 関数は正規化 Laguerre 陪関数と
の関係にあり、変数
合流型超幾何関数に関連する関数
歴史的に見ると、合流型超幾何関数はそれ自体よりも、研究目的に合わせて変形を施した関数の方が好まれる傾向にあり、それゆえ派生した関数の種類は多い。そのうちの幾つかは現在でも命脈を保っており、前述の Whittaker 関数や Coulomb 波動関数が代表的な例であるが、ここでは更に Toronto 関数, Cunningham 関数 および Poisson - Charlier 関数を取りあげる。ただし、現在の書籍等が Toronto 関数 および Cunningham 関数に言及する事は少なく、また、Poisson - Charlier 関数は多項式に還元される場合のみが注目されている。したがって当サイトでも、説明文や数式およびグラフの掲示は大幅に削減する。
【Toronto 関数】
本質的に第1種合流型超幾何関数であって、
なる関数を Toronto 関数という※1。元々は、1929年に A. Wagner が突風における風力と風向の分布および乱流の理論を研究した際に現れたもので、1943年以降 A. H. Heatley がこの関数の数表作成と改良を手掛けた。さらに Toronto 関数は、荷電された楕円体の電位分布に関する研究にも用いられる。
Toronto 関数は、積分表示式
で定義されることもある。ここに、
【Poisson - Charlier 関数】
本質的に第1種合流型超幾何関数であって、
なる関数を Poisson - Charlier 関数という。これは
を、Poisson - Charlier 多項式という※2。ここに、
【Cunningham 関数】
本質的に第2種合流型超幾何関数であって、
なる関数を Cunningham 関数 (Pearson - Cunningham 関数) という※4。1906年に K. Pearson がランダム移動の分布を研究した際、
【註記】
※1:" Toronto " が何に由来するかは不明。(Heatley がカナダ人なので、都市名の Toronto?)
※2:さらに因子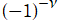 をかけたもので定義することもある。
をかけたもので定義することもある。
※3:Hahn クラスは、さらに大きな 「Askey クラス」 に包含される。NISTの18.19を参照。
※4:指数関数因子の引数部分が異なる二三の定義が存在する。当サイトが採用する上記の定義式は、E. Cunningham 「The ω-functions, a class of normal functions occurring in statistics」 (Proceedings of the Royal society of London. Series A : Mathematical and Physical character, Vol.81, Iss.548, (1908), p.310-331) および 「Course of Modern Analysis」 の353頁にある定義と一致する。(ただし、両者ではパラメーター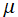 を
を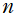 、
、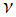 を
を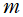 で表示している。)
で表示している。)
※1:" Toronto " が何に由来するかは不明。(Heatley がカナダ人なので、都市名の Toronto?)
※2:さらに因子
※3:Hahn クラスは、さらに大きな 「Askey クラス」 に包含される。NISTの18.19を参照。
※4:指数関数因子の引数部分が異なる二三の定義が存在する。当サイトが採用する上記の定義式は、E. Cunningham 「The ω-functions, a class of normal functions occurring in statistics」 (Proceedings of the Royal society of London. Series A : Mathematical and Physical character, Vol.81, Iss.548, (1908), p.310-331) および 「Course of Modern Analysis」 の353頁にある定義と一致する。(ただし、両者ではパラメーター
①