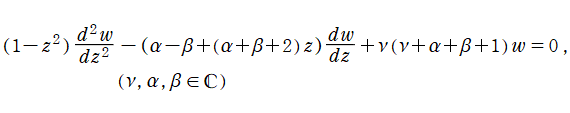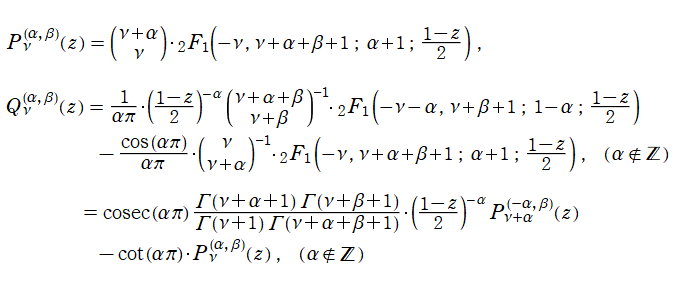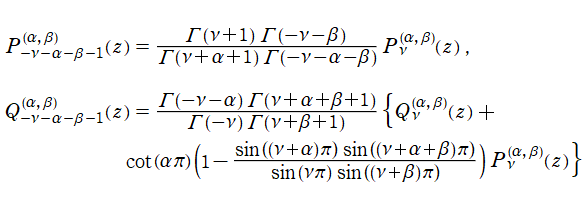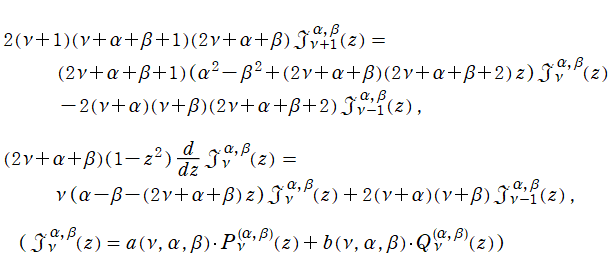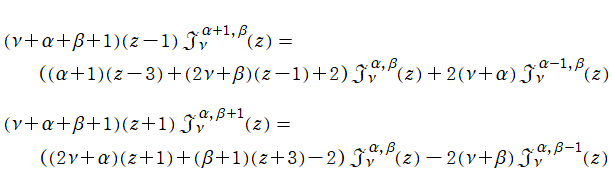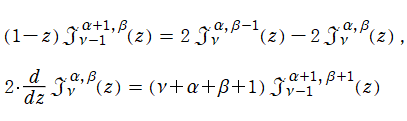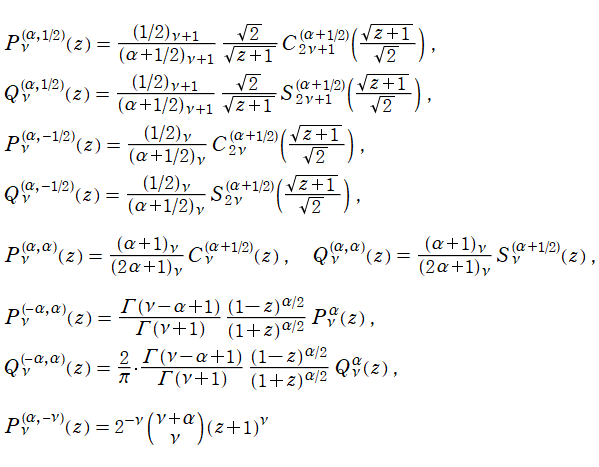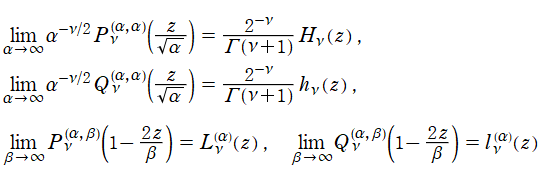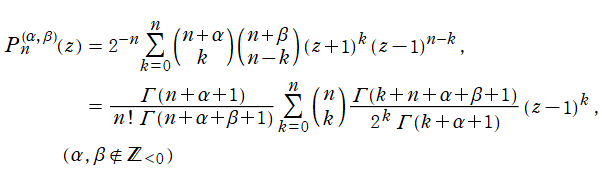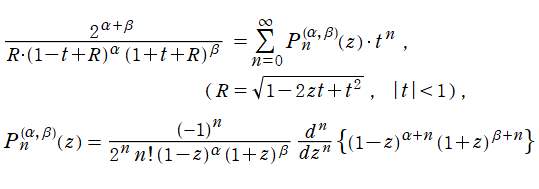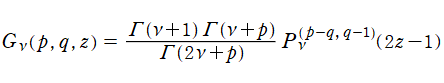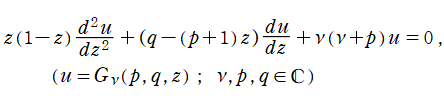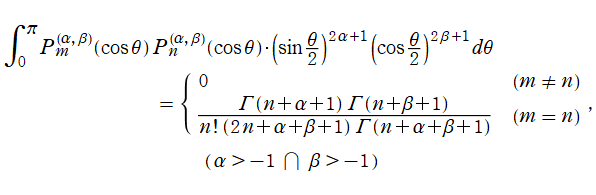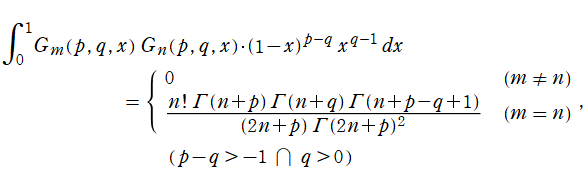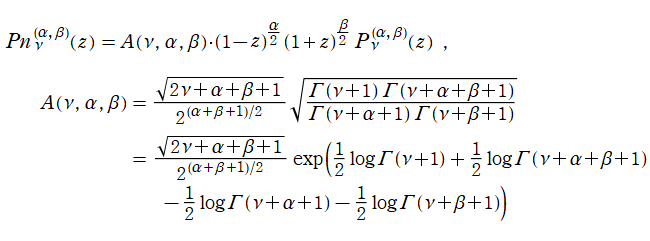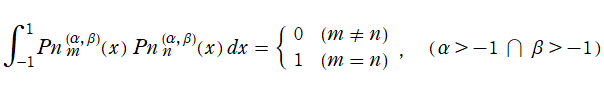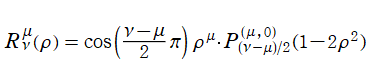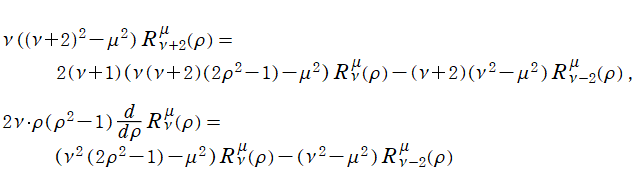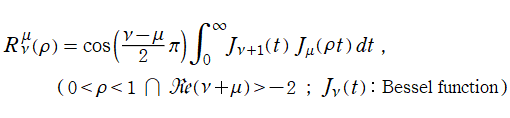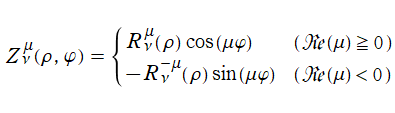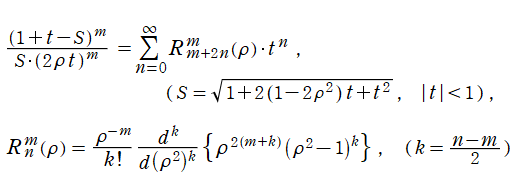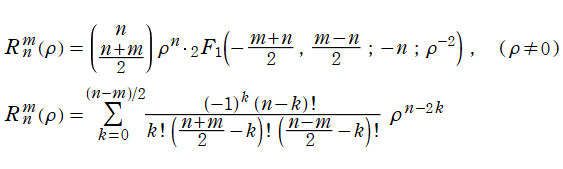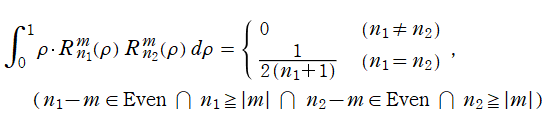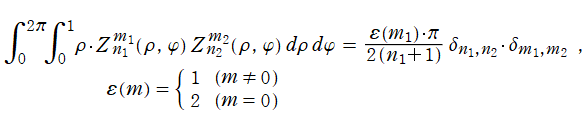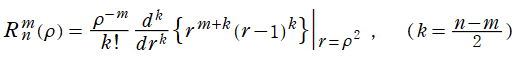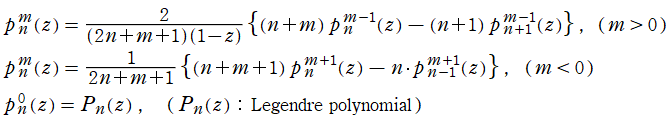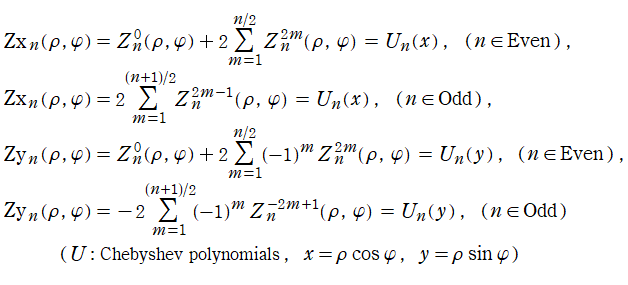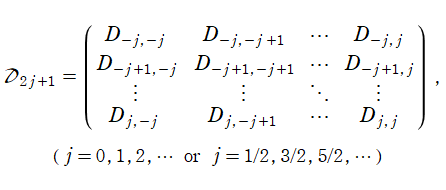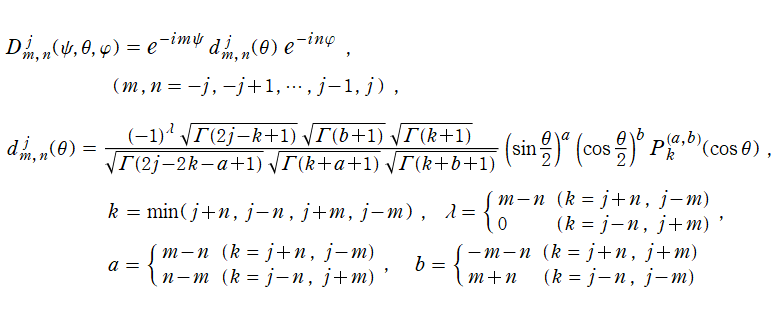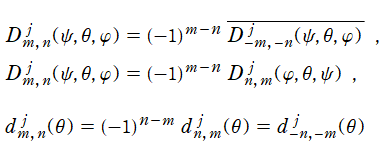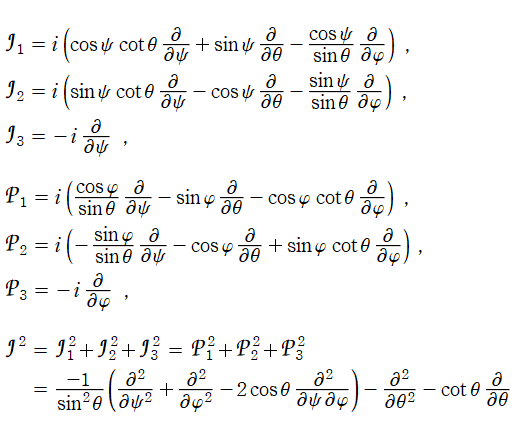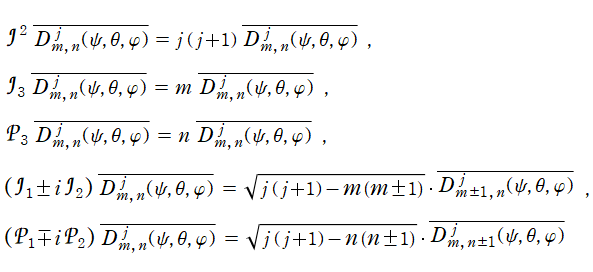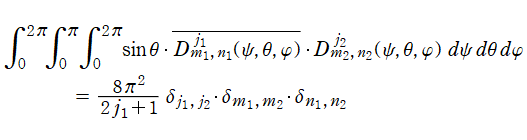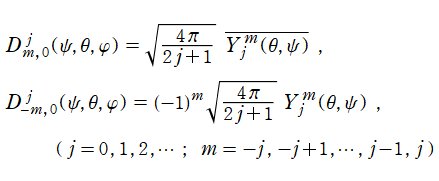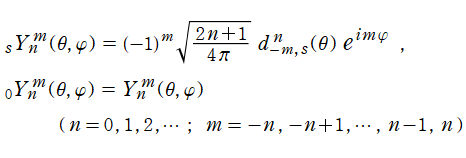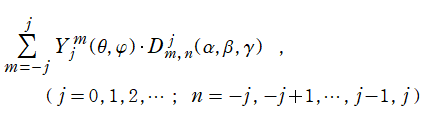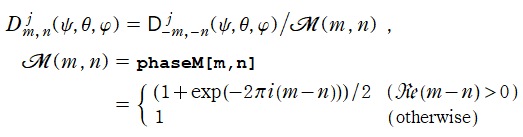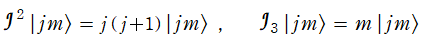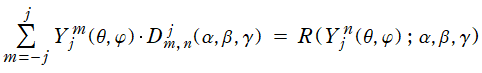Jacobi 関数
日:
Jacobi関数,
ヤコビ関数
英:
Jacobi function,仏:
Fonction de Jacobi,独:
Jacobische funktion
2階の線形常微分方程式
は超幾何微分方程式の別表現であって、
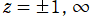
を確定特異点とする。これを Jacobi の微分方程式といい、その解の基本系
+b*Q[ν, (α, β)](z)](siki_spec220/jacobi00300.png)
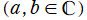
を成す二つの関数を
超幾何関数で表わせば、
となる。これを順に、第1種および第2種 Jacobi 関数という※1。第2種で
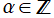
の場合は、上記の式に l'Hôpital の定理を適用する等、別の定義式が必要になる。
このうち第1種は、常に
となる特別な解であって、
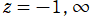
を一般に対数分岐点とし、実軸上の区間
![(-∞, -1]](siki_spec220/jacobi00900.png)
に分枝切断線が置かれる。次数が
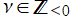
のときは
 = 0](siki_spec220/jacobi01100.png)
となる。
第2種は
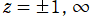
を一般に対数分岐点とし、実軸上の区間
![(-∞, -1]](siki_spec220/jacobi00900.png)
および
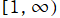
に分枝切断線が置かれる。ただし
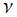
が半奇数ならば、
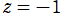
の分岐点は消える。また、
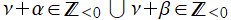
のときは
 = ∞](siki_spec220/jacobi01500.png)
となる。
Jacobi 関数は、
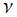
に関して準反転性
を持っている。
Jacobi 関数は、
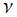
に関する線形漸化式および微分漸化式
を満たす。ここに
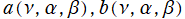
は、
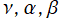
の三変数について1を周期とする任意の周期関数である。同様に、
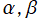
に関しても漸化式
を満たし、さらに、
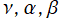
に関する簡易な形の漸化式
も満たす。
Jacobi 関数は
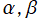
が特別な値の組合せのとき、
Gegenbauer 関数,
Legendre 陪関数, および冪関数
に還元され、それらの式でさらに
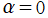
または
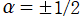
とすると、
Legendre 関数や
Chebyshev 関数が現れる。一方、
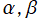
に対して極限を取ると、
Laguerre 陪関数または
Hermite 関数
に近付く。
第1種 Jacobi 関数は次数が
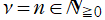
ならば、多項式
に還元される。これは Jacobi 多項式 (希に、超幾何多項式) と呼ばれ、応用で Jacobi 関数が使用されるのは、ほとんどこの場合に限られる。Jacobi 多項式は、母関数表示式および Rodrigues の公式
でも表わすことができ、種々の性質を導くのに便利である。Jacobi 多項式は古典的直交多項式の系統上で頂点に位置するが、その直交性についての詳細は
次節で触れる。なお、Jacobi 多項式は特別な
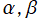
を除いて一般に偶関数または奇関数にならない。
しばしば
](siki_spec220/jacobi03000.png)
に代わる第1種 Jacobi 関数として、
を定義していることがある※2。ただし、Jacobi のそれとは異なる (若干簡単な) 形の微分方程式
を満たす。
第2種 Jacobi 関数についても、当サイトと違う様々な定義が存在する。例えば 「Higher Transcendental Functions vol.2」 の171頁では、
が掲載されている。この関数は Jacobi の微分方程式を満たし、実軸上の区間
![(-∞, -1]](siki_spec220/jacobi00900.png)
および
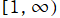
に分枝切断線が置かれる※3。
また、同著の170頁または Wolfram MathWorld の記事 「
Jacobi Function of the Second Kind」 では、第2種 Jacobi 関数版の
Hobson 型とも言うべく、実軸上の区間
![(-∞, 1]](siki_spec220/jacobi03400.png)
に分枝切断線が置かれた、
が掲載されている。この関数も Jacobi の微分方程式を満たす。
Jacobi 関数 (多項式) は、主に回転群が関係する剛体力学や量子力学で応用される。例えば、独楽などの回転運動、正の曲率を持つ空間内での Schrödinger 方程式の解、各種の拡張された球面調和関数および
Wigner のD行列に現れる。この他にも、可積分系の特殊解など応用範囲は他の古典的直交多項式と共通する部分もあるが、Jacobi 多項式で扱う内容はより高度になることが多い。さらに
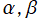
が複素数、

が純虚数となる Jacobi 多項式のうち、特別な場合
も応用事例があり、これは Romanovski 多項式と呼ばれる※4。粒子ポテンシャルが余接関数となった Schrödinger 方程式の解、ランダム行列理論が事例として知られている。
Jacobi 多項式は、1859年に C. G. J. Jacobi が導入したことから、その名で呼ばれるようになった。また、1870年には P. L. Chebyshev が一般の多項式論を展開した際に、併せて Jacobi 多項式を論じた。Romanovski 多項式は、1929年に V. I. Romanovsky (Romanovski) がある種の確率分布を研究した際に導入した。
【註記】
※1:第2種 Jacobi 関数
](siki_spec220/jacobi03700.png)
は当サイトが独自に定義したものであって、
](siki_spec220/jacobi03000.png)
が余弦関数に相当すると見たとき、
](siki_spec220/jacobi03700.png)
は正弦関数に相当する。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針は、別頁
Questions に掲示している。)
なお、第2種 Jacobi 関数の定義として広く採用されているのは
](siki_spec220/jacobi03800.png)
である。
※2:
](siki_spec220/jacobi03900.png)
のグラフは全て省略する。(実変数も、概形の関心領域が決定しづらいので省略する。)
※3:
](siki_spec220/jacobi04000.png)
のグラフは
](siki_spec220/jacobi03700.png)
と似ているので、

を変数とする場合のみ掲載し、個数も削減する。
※4:
](siki_spec220/jacobi04100.png)
のグラフも全て省略する。(同じく、概形の制御が難しいことに因る。)
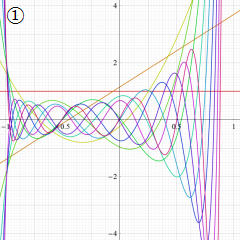
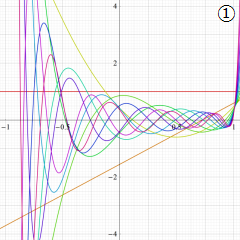
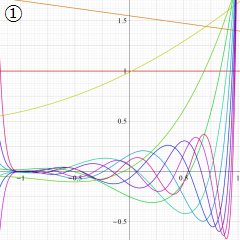
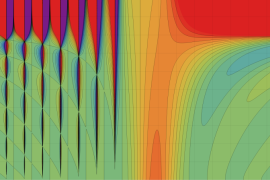
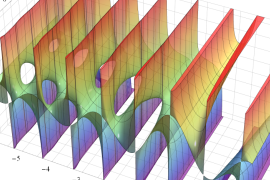
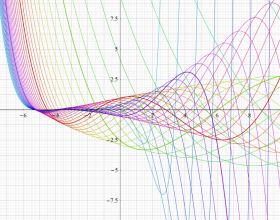
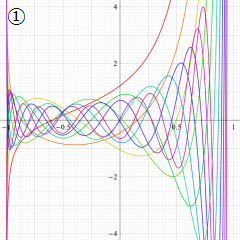
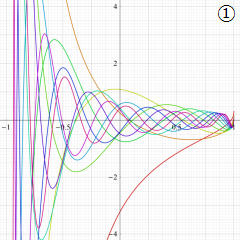
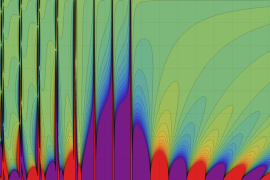
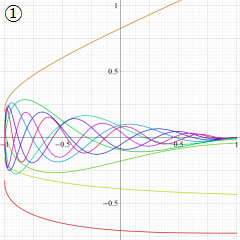
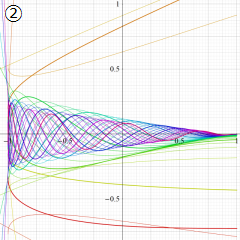
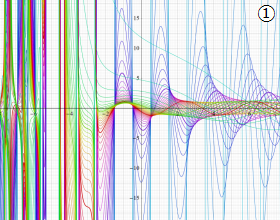
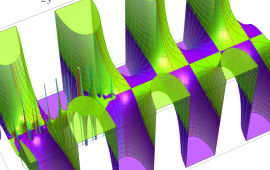
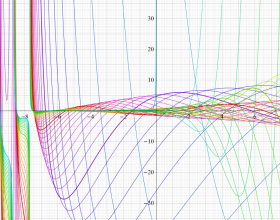
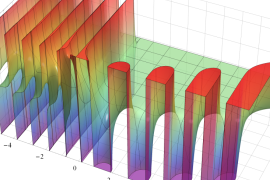
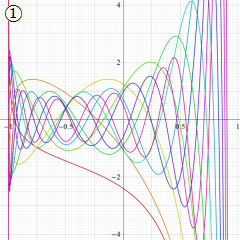
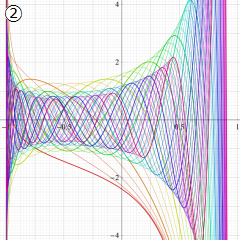
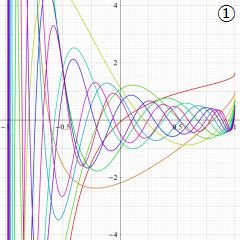
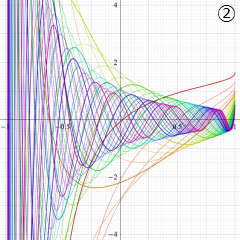
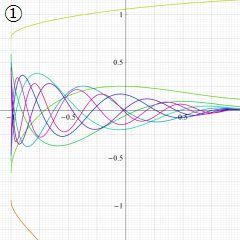
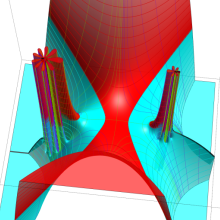
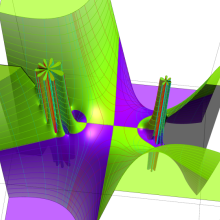
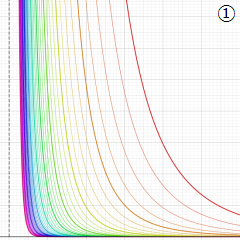
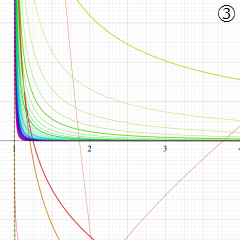
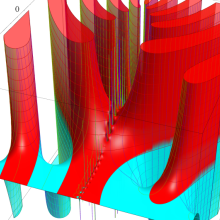
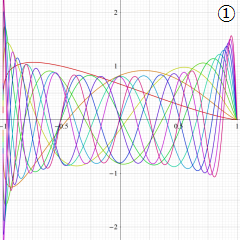
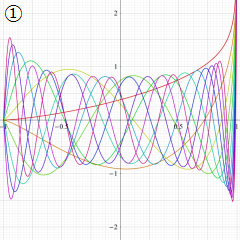
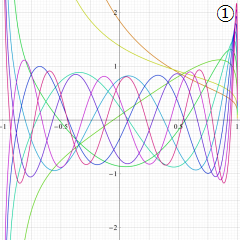
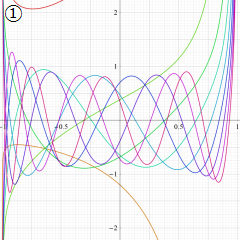
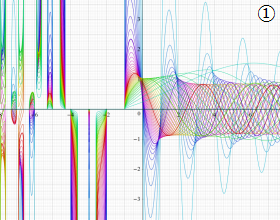
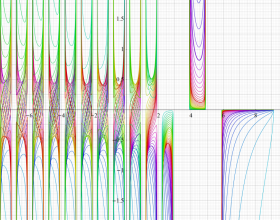
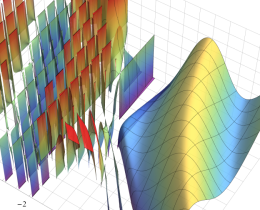
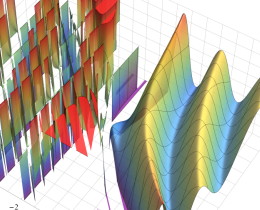
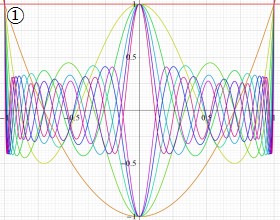
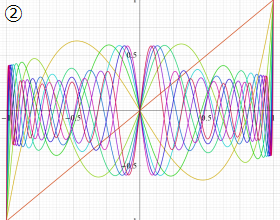
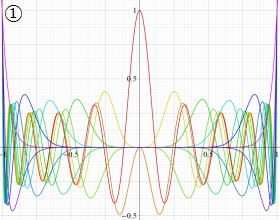
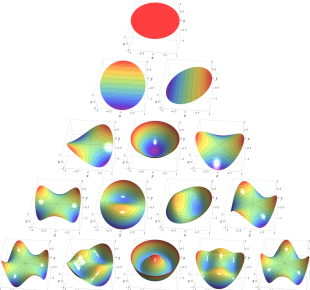
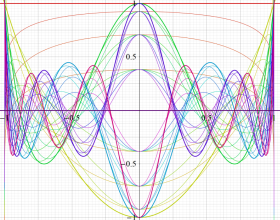
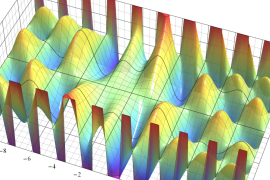
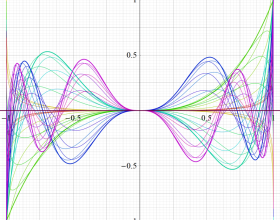
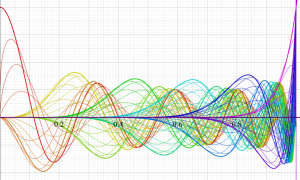
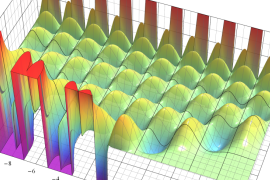
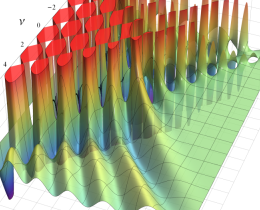
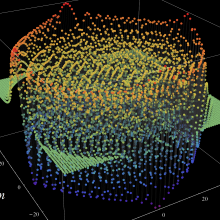
](siki_spec220/jacobi06600.png)
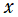
を実変数とする、第1種 Jacobi 関数のグラフ。
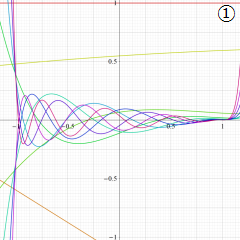
①整数次
](siki_spec220/jacobi04200.png)
(Jacobi 多項式)。
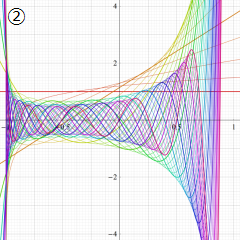
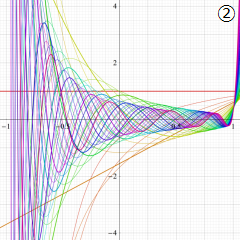
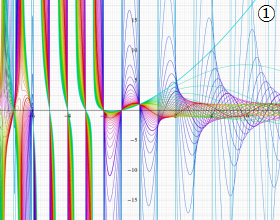
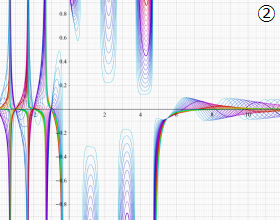
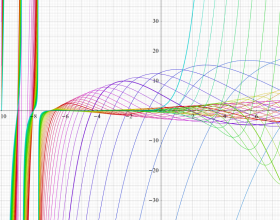
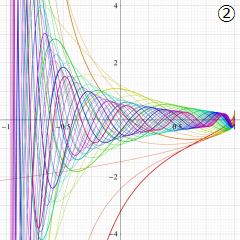
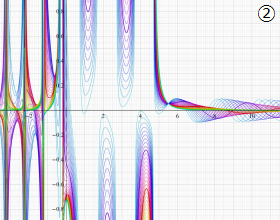
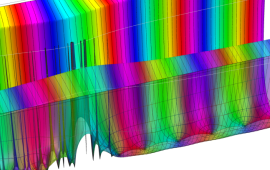
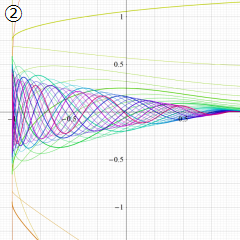
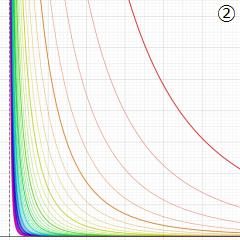
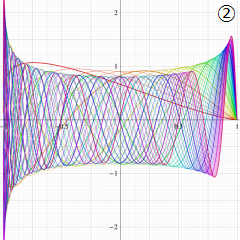
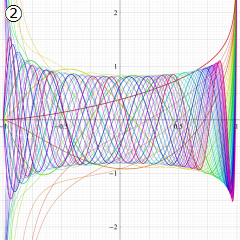
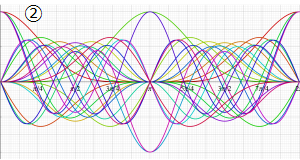
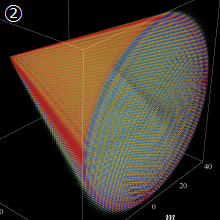
②実数次
](siki_spec220/jacobi04300.png)
。
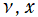
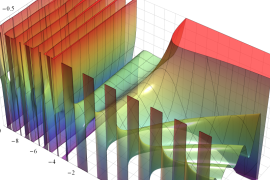
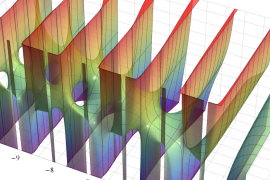
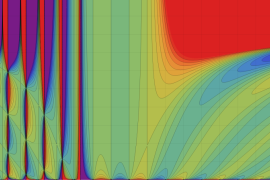
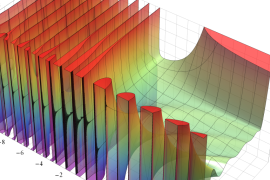
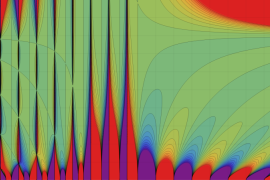
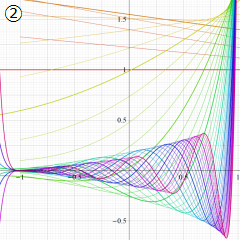
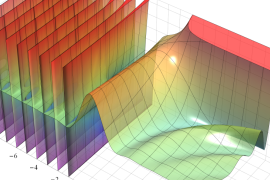
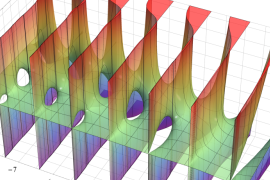
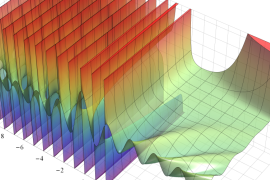
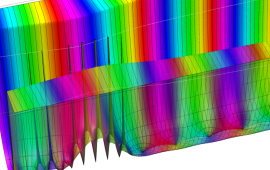
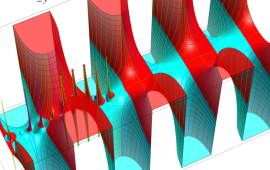
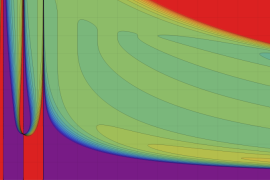
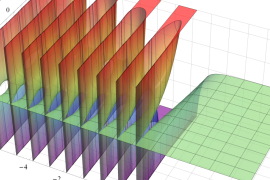
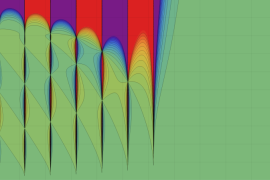
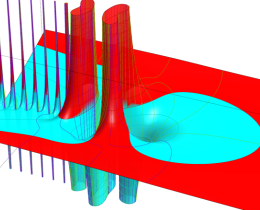
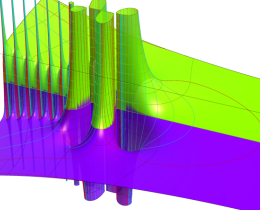
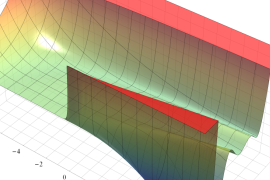
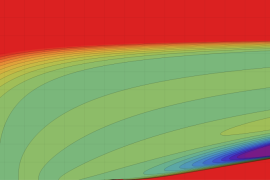
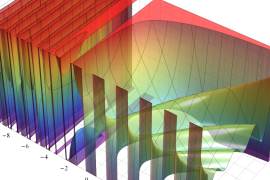
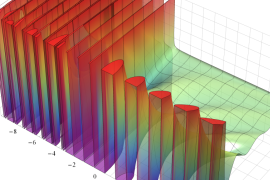
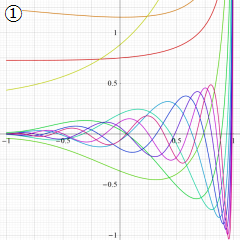
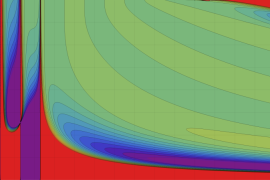
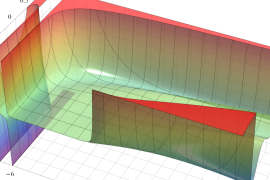
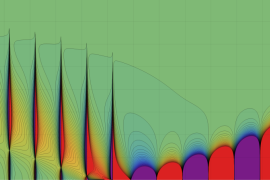
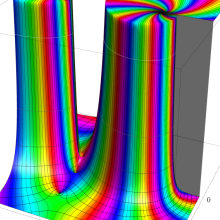
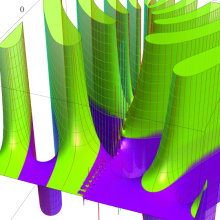
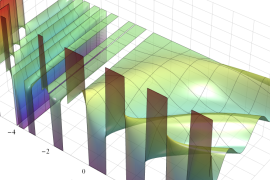
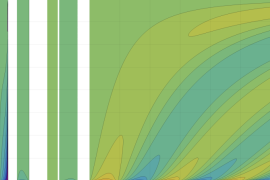
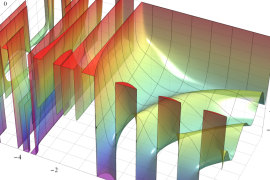
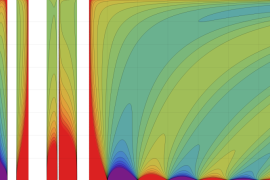
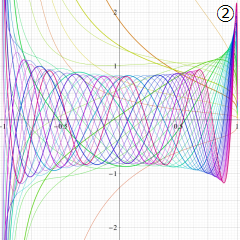
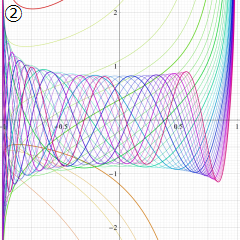
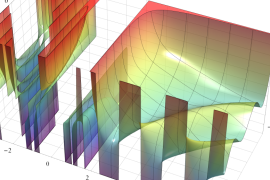
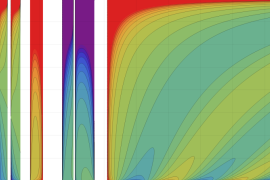
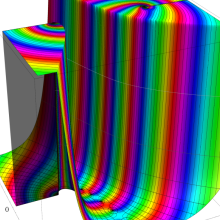
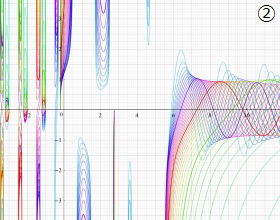
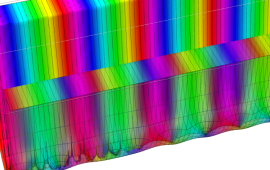
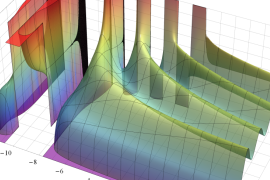
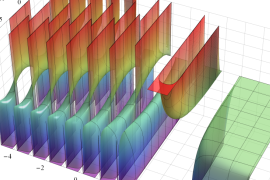
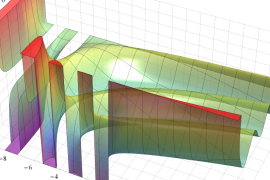
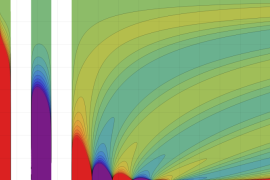
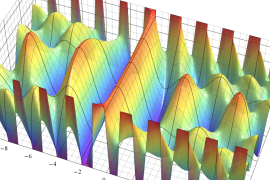
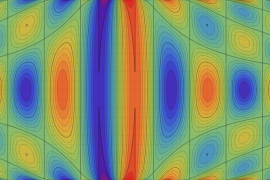
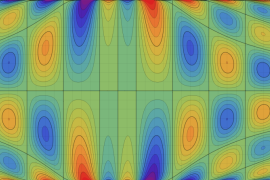
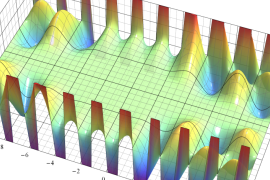
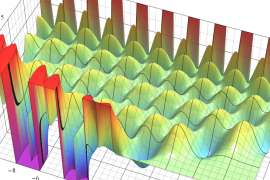
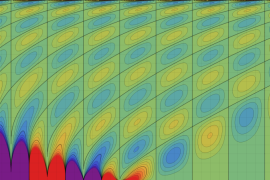
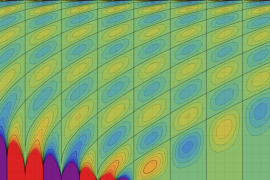
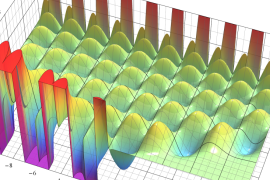
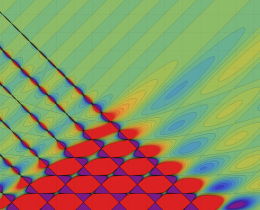
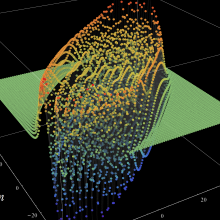
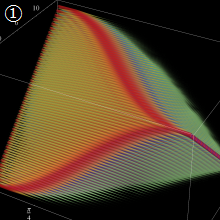
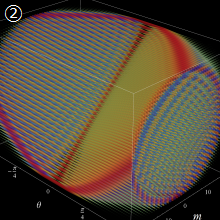
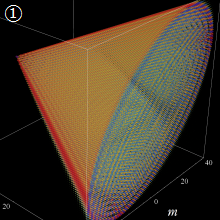
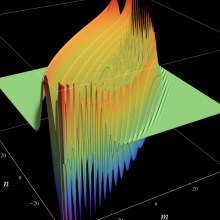
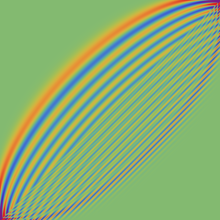
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi04300.png)
のグラフ。
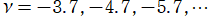
では関数が定義されない。
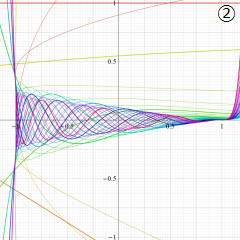
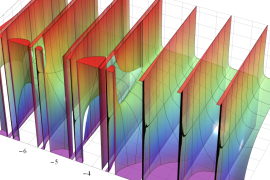
2番目は、
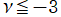
の範囲を拡大した場合。
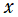
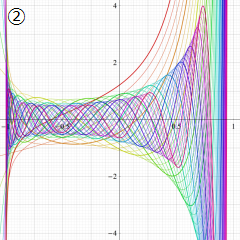
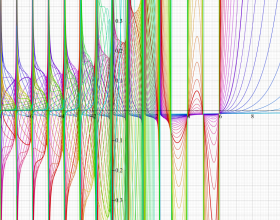
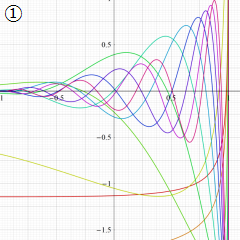
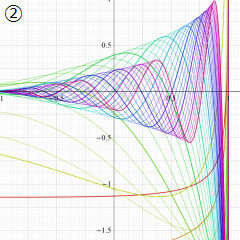
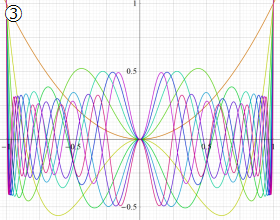
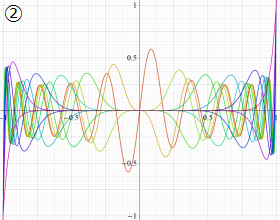
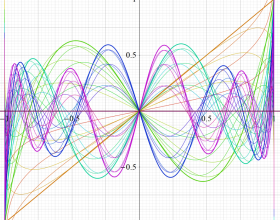
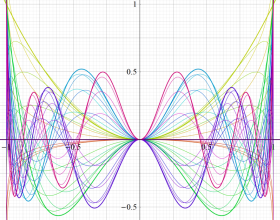
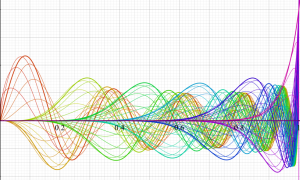
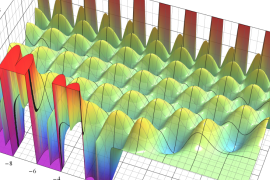
を実変数とする、第1種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi04700.png)
(Jacobi 多項式)。
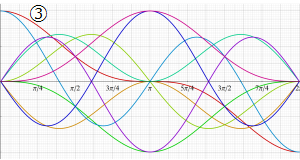
②実数次
](siki_spec220/jacobi04800.png)
。
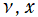
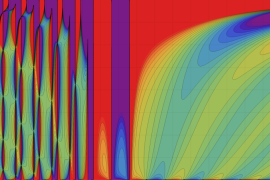
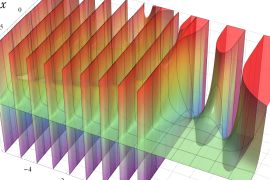
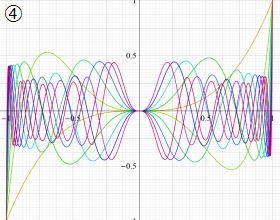
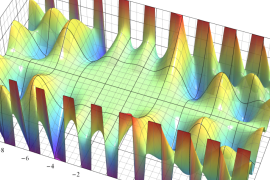
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi04800.png)
のグラフ。
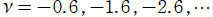
では関数が定義されない。
2番目は、
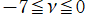
の範囲を拡大した場合。
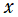
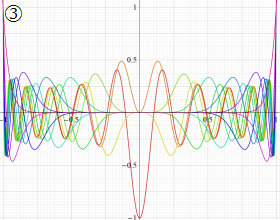
を実変数とする、第1種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi05100.png)
(Jacobi 多項式)。
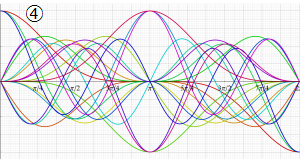
②実数次
](siki_spec220/jacobi05200.png)
。
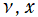
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi05200.png)
のグラフ。
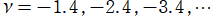
では関数が定義されない。
2番目は、
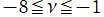
の範囲を拡大した場合。
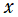
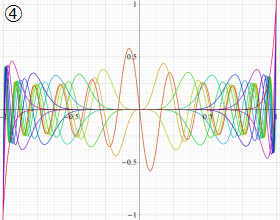
を実変数とする、第1種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi05500.png)
(Jacobi 多項式)。
②実数次
](siki_spec220/jacobi05600.png)
。
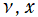
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi05600.png)
のグラフ。
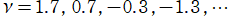
では関数が定義されない。
2番目は、
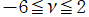
の範囲を拡大した場合。
アニメーション
(27.0MB)
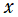
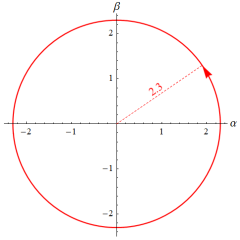
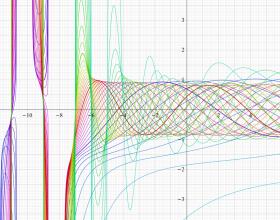
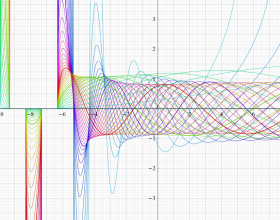
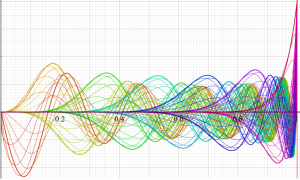
を実変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi05900.png)
のグラフ。ただし実数
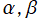
の組は、2番目の図の経路に沿って動く。

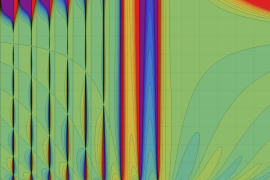
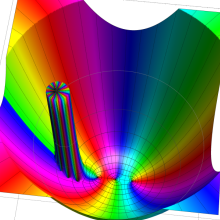
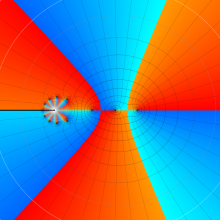
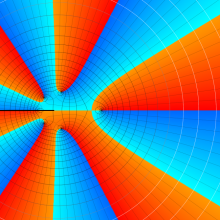
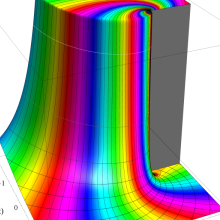
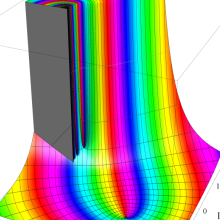
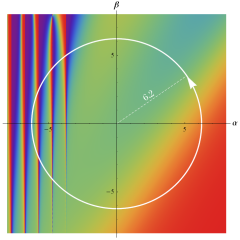
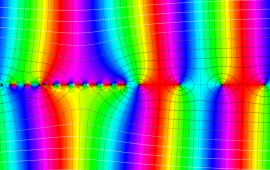
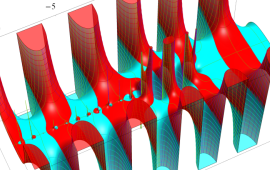
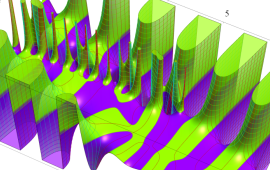
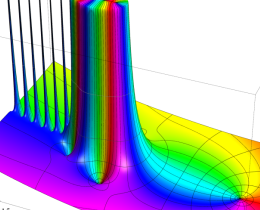
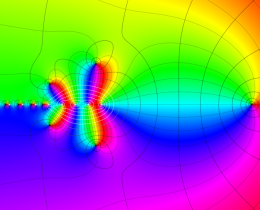
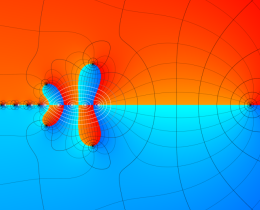
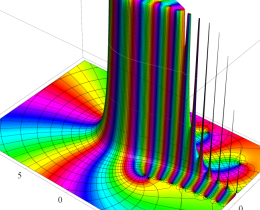
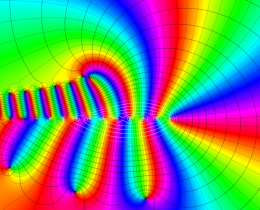
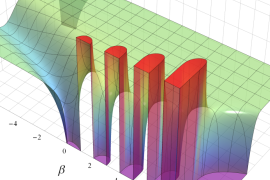
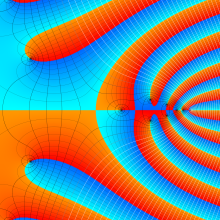
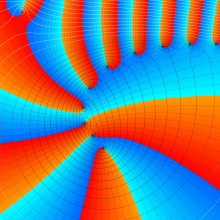
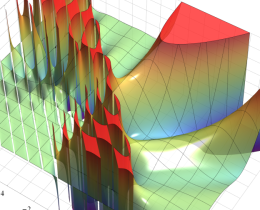
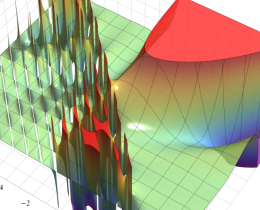
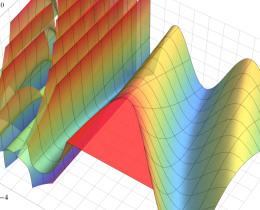
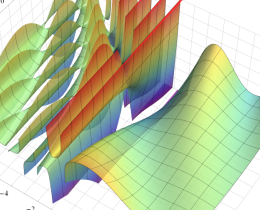
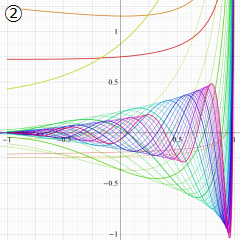
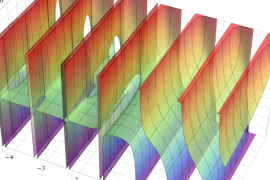
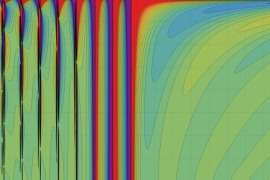
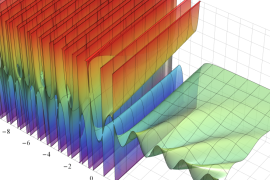
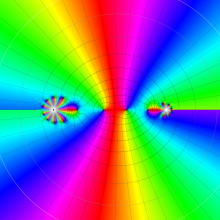
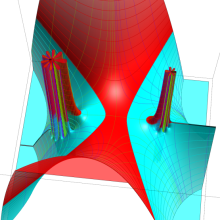
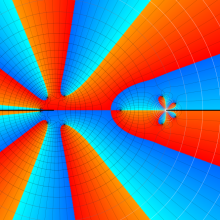
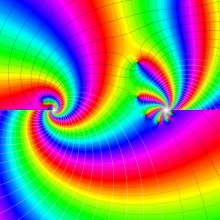
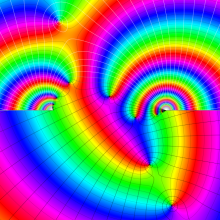
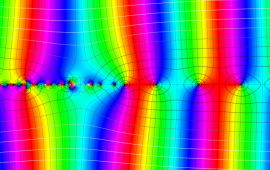
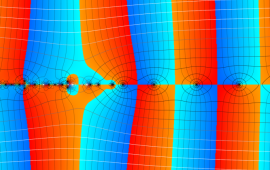
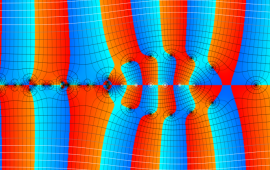
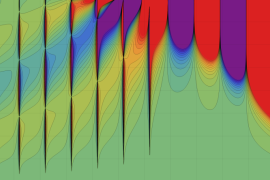
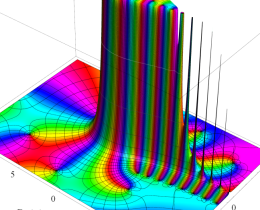
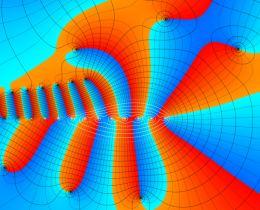
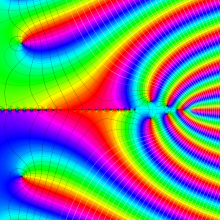
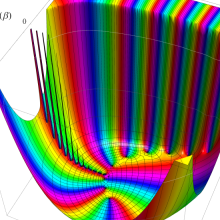
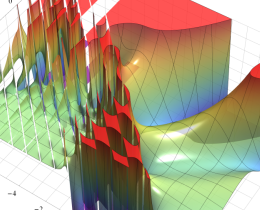
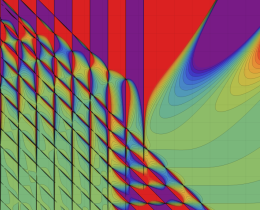
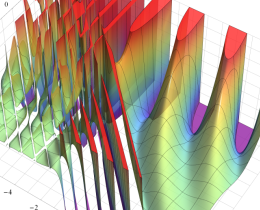
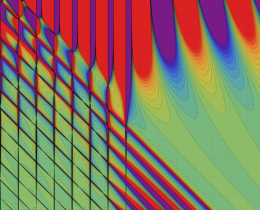
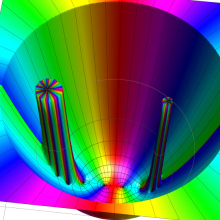
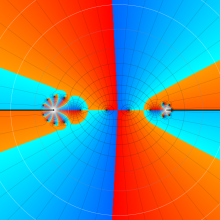
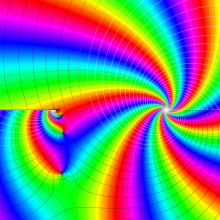
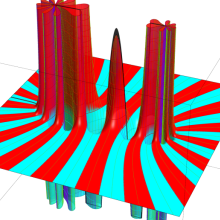
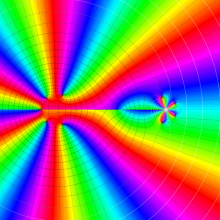
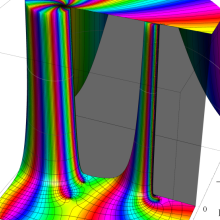
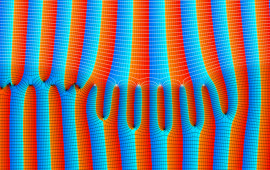
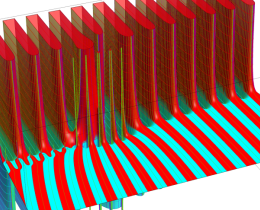
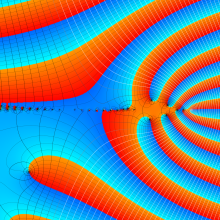
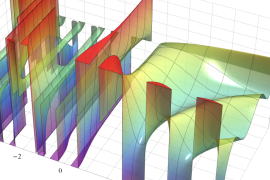
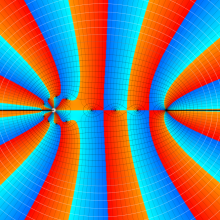
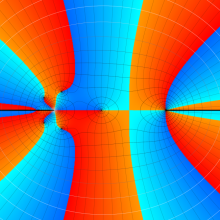
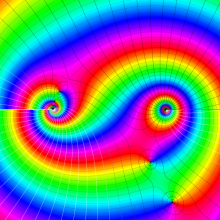
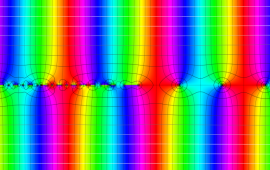
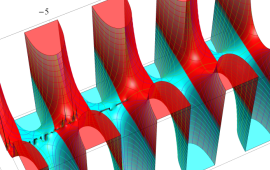
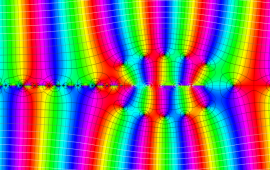
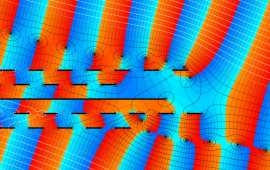
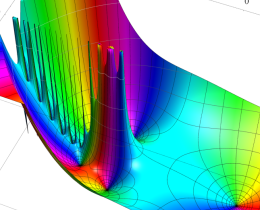
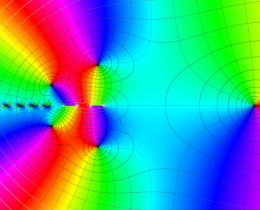
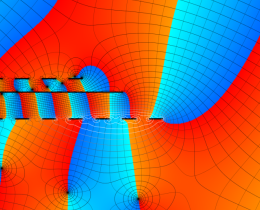
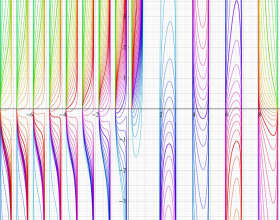
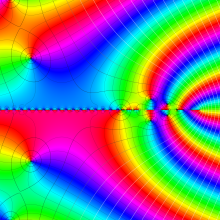
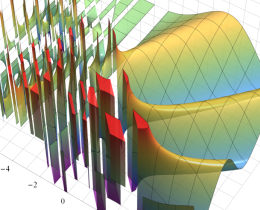
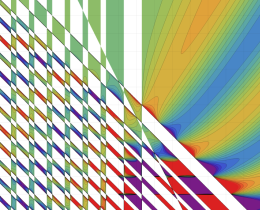
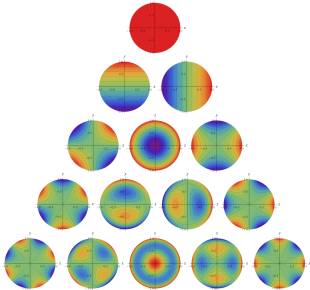
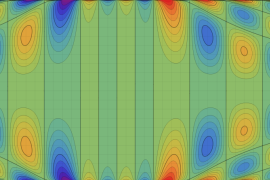
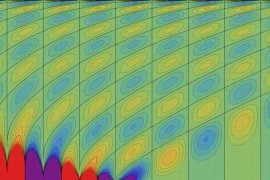
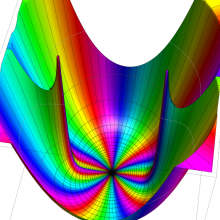
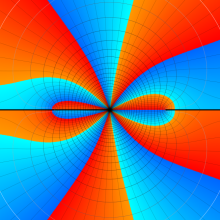
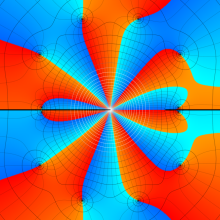
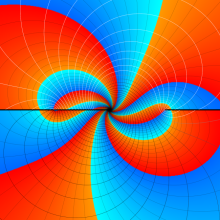
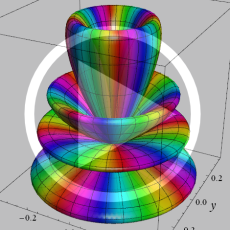
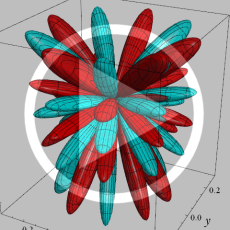
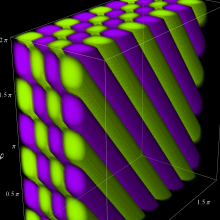
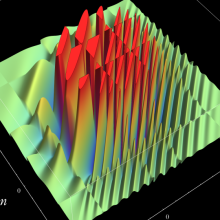
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi06000.png)
のグラフ。

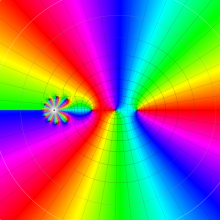
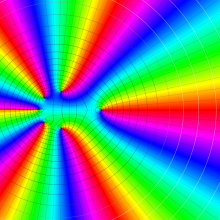
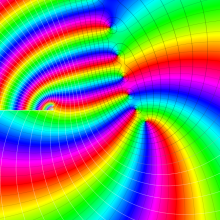
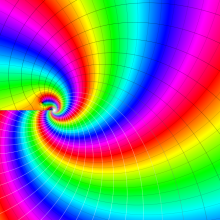
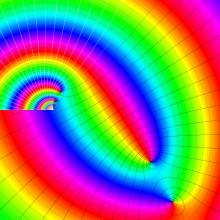
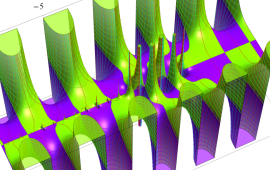
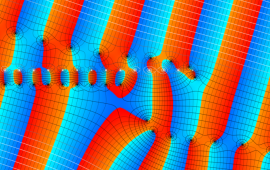
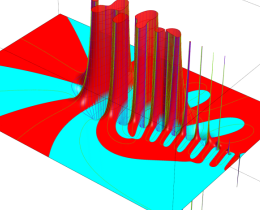
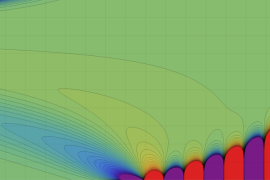
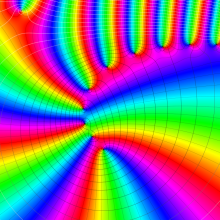
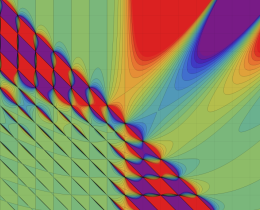
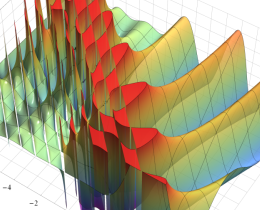
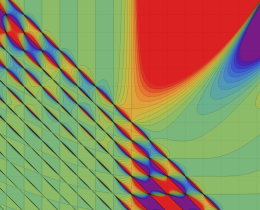
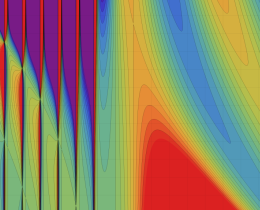
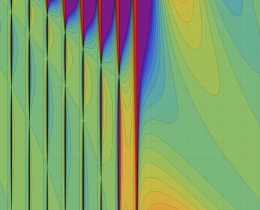
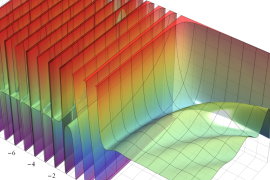
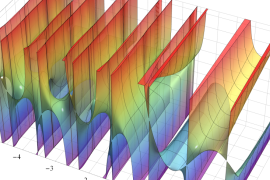
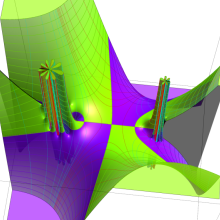
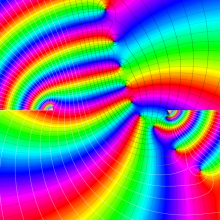
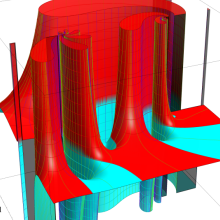
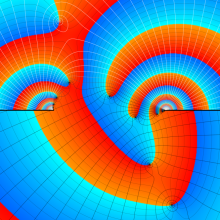
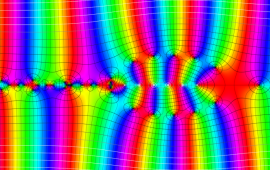
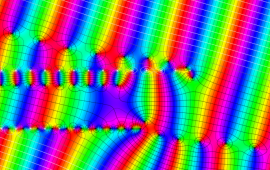
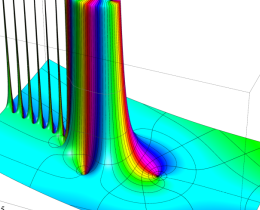
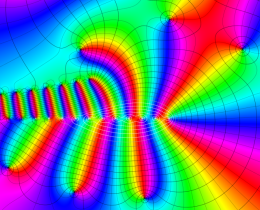
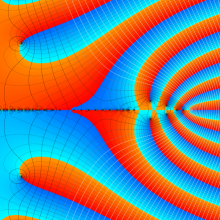
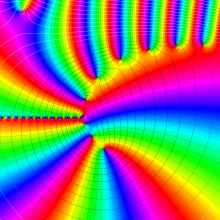
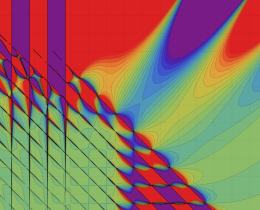
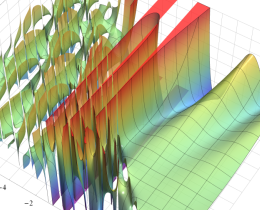
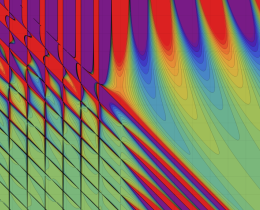
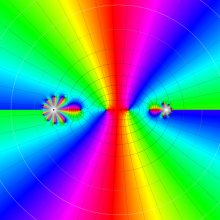
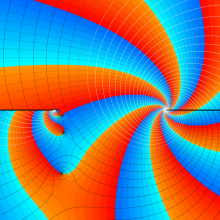
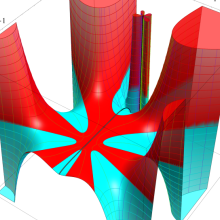
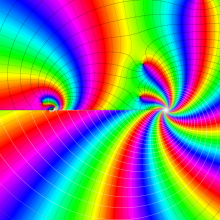
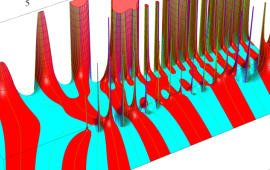
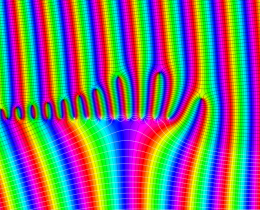
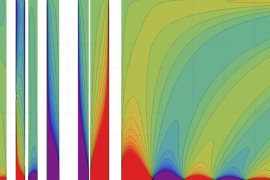
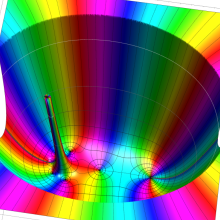
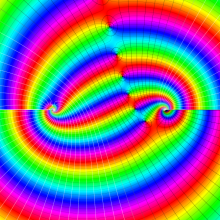
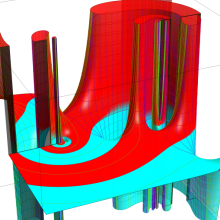
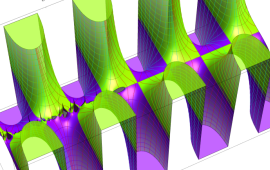
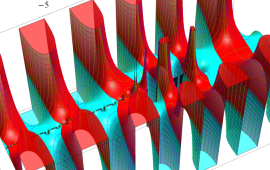
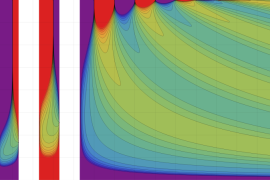
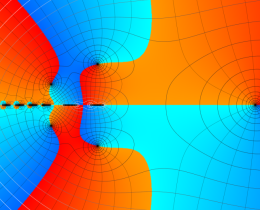
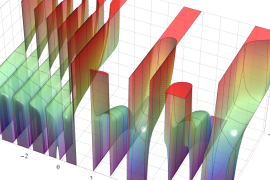
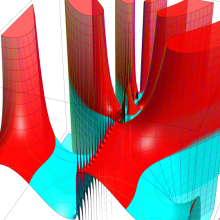
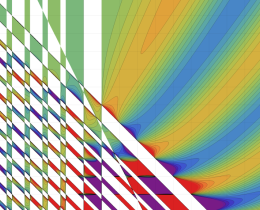
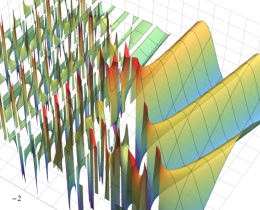
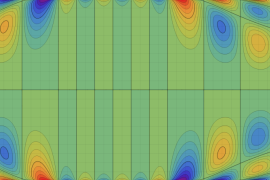
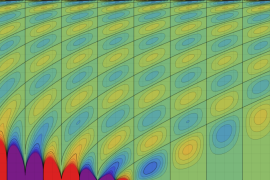
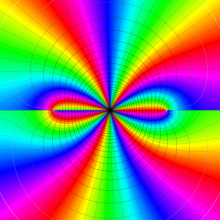
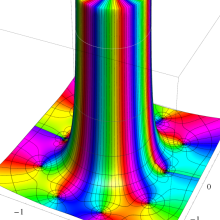
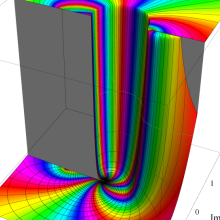
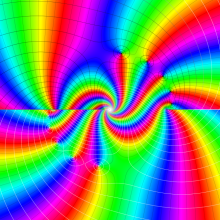
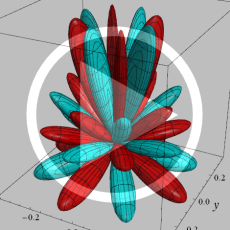
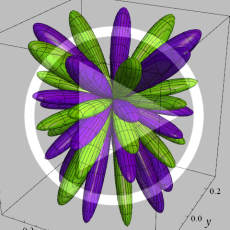
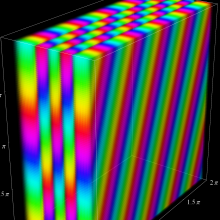
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi06100.png)
のグラフ。

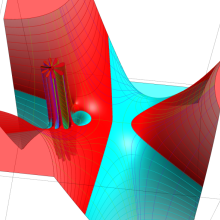
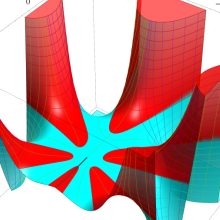
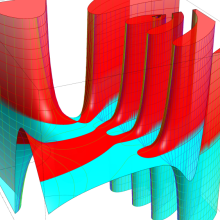
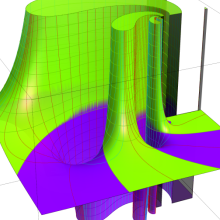
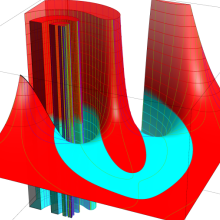
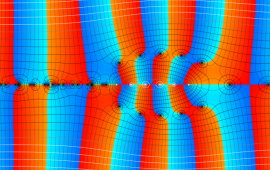
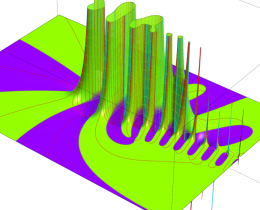
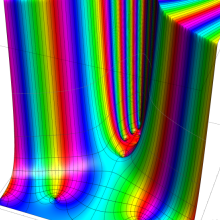
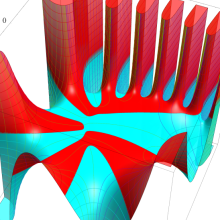
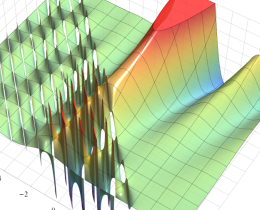
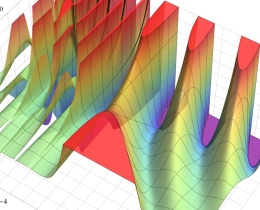
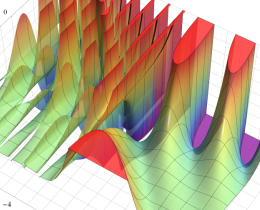
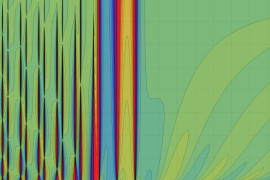
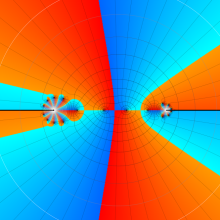
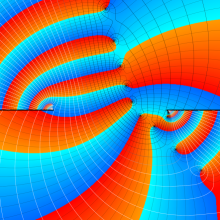
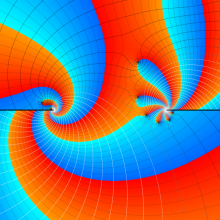
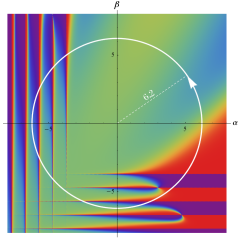
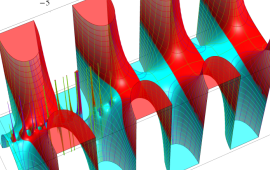
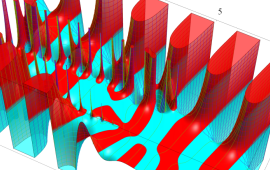
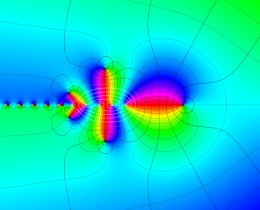
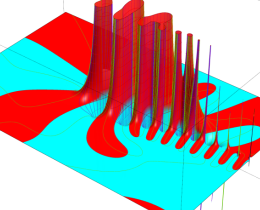
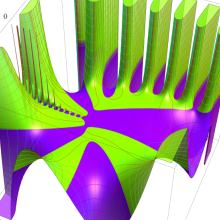
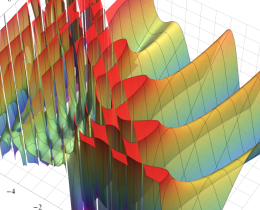
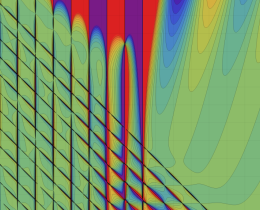
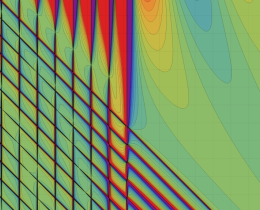
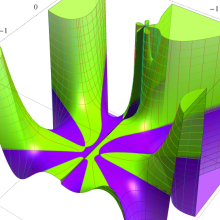
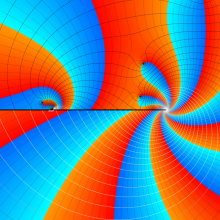
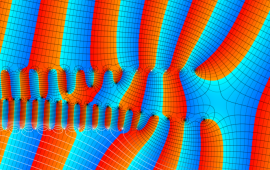
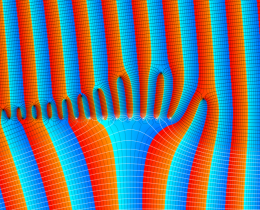
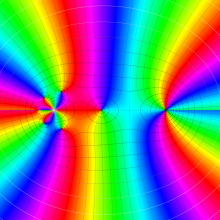
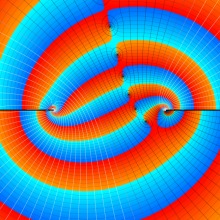
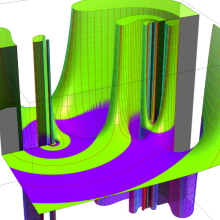
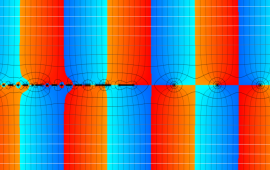
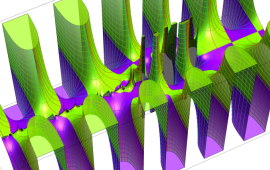
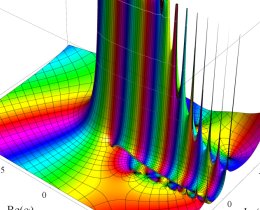
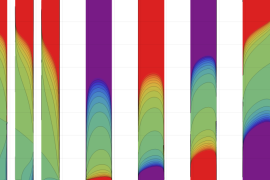
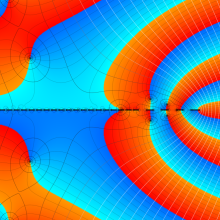
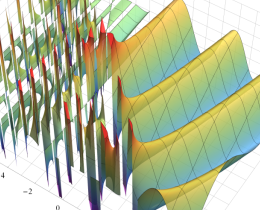
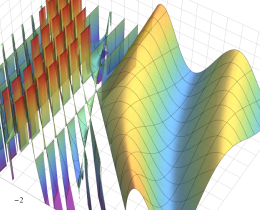
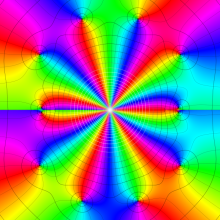
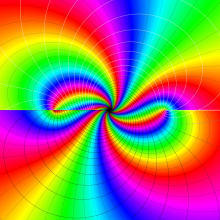
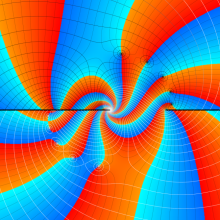
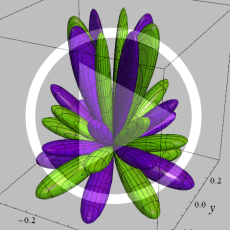
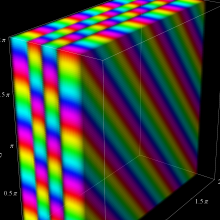
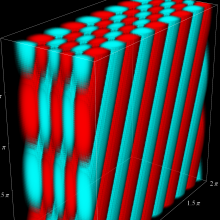
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi06200.png)
のグラフ。

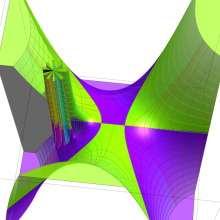
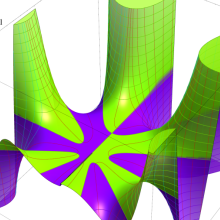
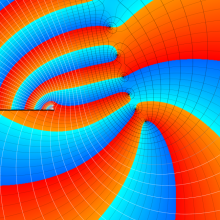
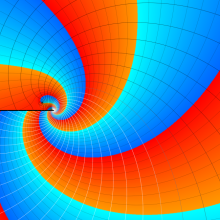
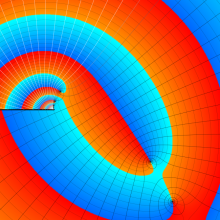
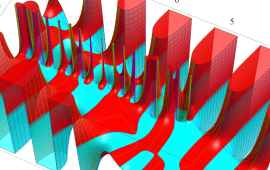
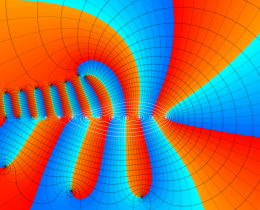
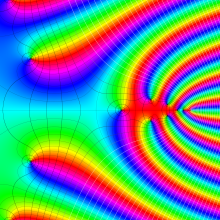
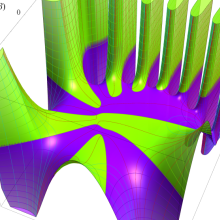
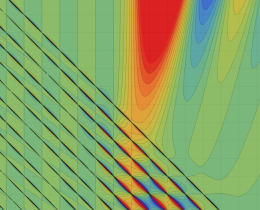
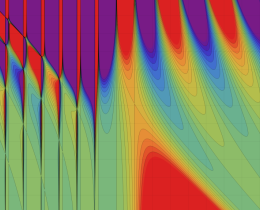
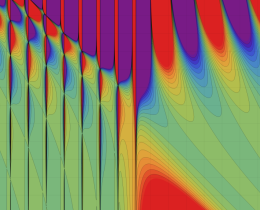
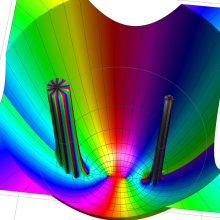
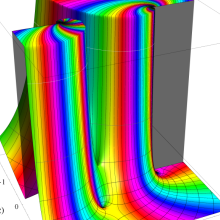
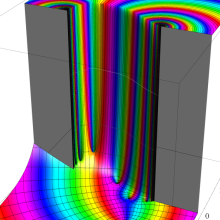
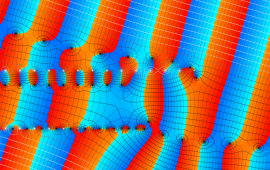
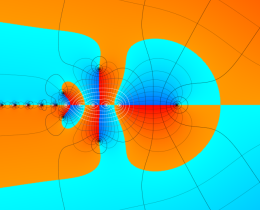
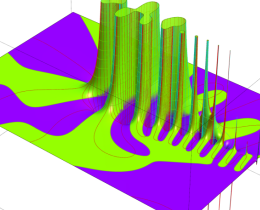
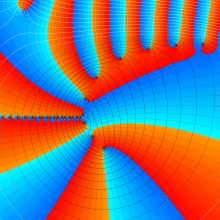
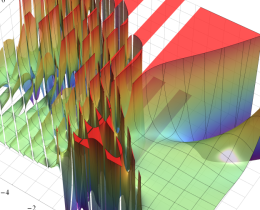
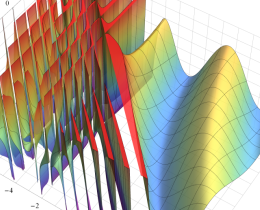
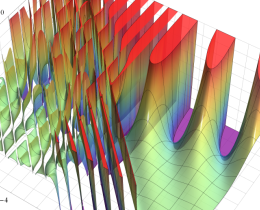
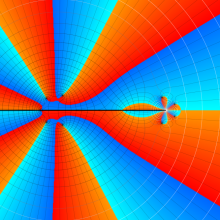
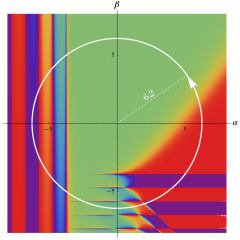
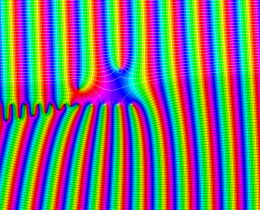
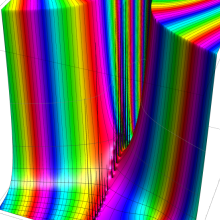
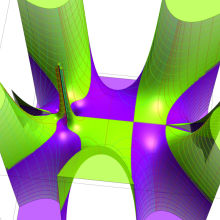
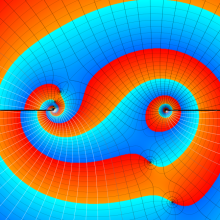
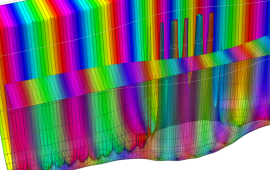
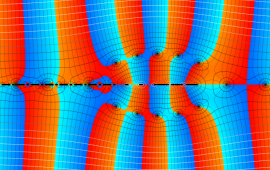
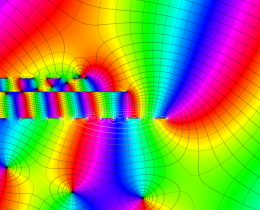
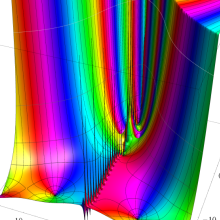
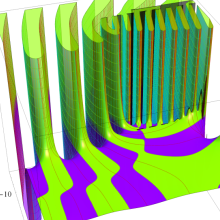
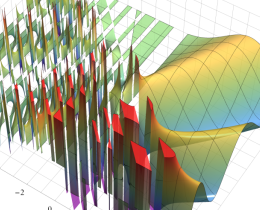
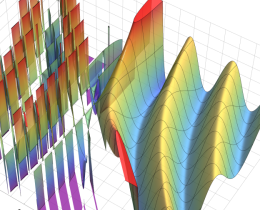
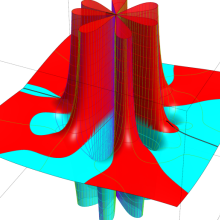
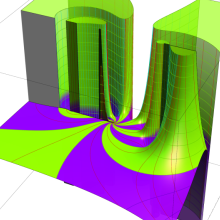
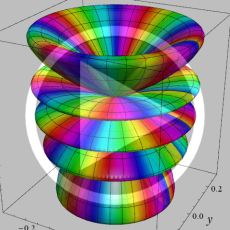
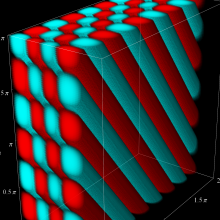
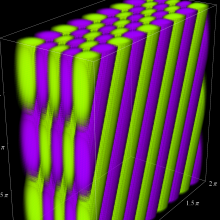
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi06300.png)
のグラフ。

を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi06400.png)
のグラフ。
アニメーション
(17.8MB)

を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi06500.png)
のグラフ。ただし実数
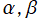
の組は、2番目の図の経路に沿って動く。
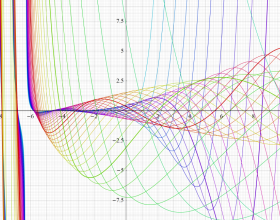
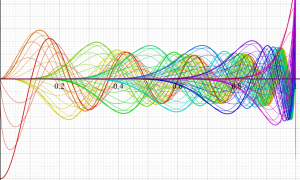
 (変数ν)](siki_spec220/jacobi07200.png)
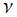
を実変数とする、第1種 Jacobi 関数のグラフ。
①](siki_spec220/jacobi06700.png)
。
②](siki_spec220/jacobi06800.png)
。
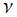
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi06900.png)
のグラフ。
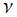
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi07000.png)
のグラフ。
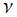
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi07100.png)
のグラフ。
 (変数α)](siki_spec220/jacobi08000.png)
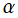
を実変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi07300.png)
のグラフ。
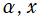
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi07300.png)
のグラフ。
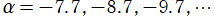
では関数が定義されない。
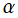
を実変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi07600.png)
のグラフ。
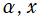
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi07600.png)
のグラフ。
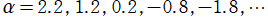
では関数が定義されない。
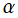
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi07800.png)
のグラフ。
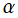
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi07900.png)
のグラフ。
 (変数β)](siki_spec220/jacobi08600.png)
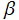
を実変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi08100.png)
のグラフ。
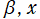
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi08100.png)
のグラフ。
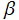
を実変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi08300.png)
のグラフ。
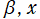
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi08300.png)
のグラフ。
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi08400.png)
のグラフ。
を複素変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi08500.png)
のグラフ。
 (変数ν,α)](siki_spec220/jacobi09200.png)
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi08800.png)
のグラフ。
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi08900.png)
のグラフ。
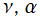
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi09000.png)
のグラフ。
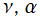
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi09100.png)
のグラフ。
 (変数ν,β)](siki_spec220/jacobi09800.png)
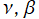
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi09400.png)
のグラフ。
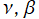
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi09500.png)
のグラフ。
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi09600.png)
のグラフ。
を実2変数とする、第1種 Jacobi 関数
](siki_spec220/jacobi09700.png)
のグラフ。
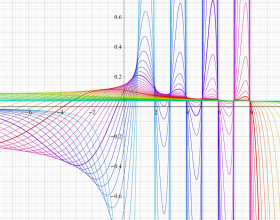
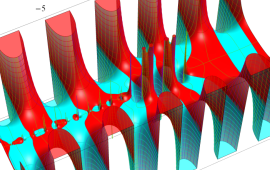
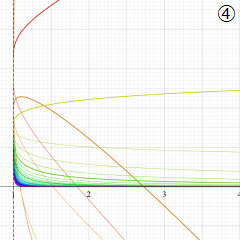
](siki_spec220/jacobi11400.png)
を実変数とする、第2種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi09900.png)
。
②実数次
](siki_spec220/jacobi10000.png)
。
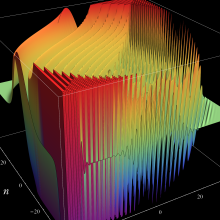
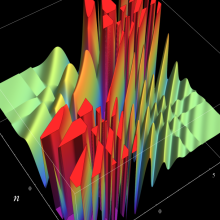
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi10000.png)
のグラフ。
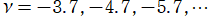
および
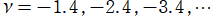
では関数が定義されない。
2番目は、
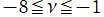
の範囲を拡大した場合。
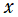
を実変数とする、第2種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi10100.png)
。
②実数次
](siki_spec220/jacobi10200.png)
。
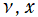
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi10200.png)
のグラフ。
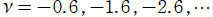
および
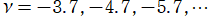
では関数が定義されない。
2番目は、
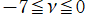
の範囲を拡大した場合。
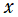
を実変数とする、第2種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi10300.png)
。
②実数次
](siki_spec220/jacobi10400.png)
。
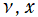
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi10400.png)
のグラフ。
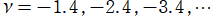
および
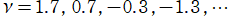
では関数が定義されない。
2番目は、
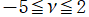
の範囲を拡大した場合。
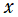
を実変数とする、第2種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi10600.png)
。
②実数次
](siki_spec220/jacobi10700.png)
。
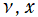
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi10700.png)
のグラフ。
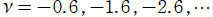
および
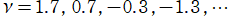
では関数が定義されない。
2番目は、
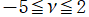
の範囲を拡大した場合。

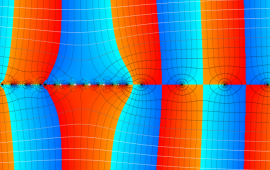
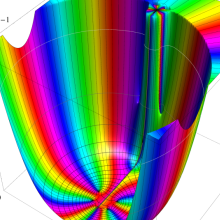
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi10800.png)
のグラフ。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi10900.png)
のグラフ。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi11000.png)
のグラフ。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi11100.png)
のグラフ。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi11200.png)
のグラフ。
アニメーション
(18.5MB)

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi11300.png)
のグラフ。ただし実数
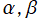
の組は、2番目の図の経路に沿って動く。
 (変数ν)](siki_spec220/jacobi12000.png)
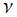
を実変数とする、第2種 Jacobi 関数のグラフ。
①](siki_spec220/jacobi11500.png)
。
②](siki_spec220/jacobi11600.png)
。
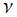
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi11700.png)
のグラフ。
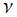
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi11800.png)
のグラフ。
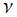
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi11900.png)
のグラフ。
 (変数α)](siki_spec220/jacobi12500.png)
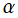
を実変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12100.png)
のグラフ。
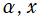
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12100.png)
のグラフ。
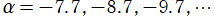
では関数が定義されない。
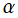
を実変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12200.png)
のグラフ。
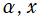
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12200.png)
のグラフ。
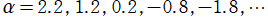
では関数が定義されない。
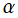
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12300.png)
のグラフ。
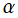
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12400.png)
のグラフ。
 (変数β)](siki_spec220/jacobi13200.png)
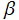
を実変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12600.png)
のグラフ。
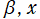
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12600.png)
のグラフ。
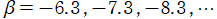
では関数が定義されない。
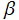
を実変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12800.png)
のグラフ。
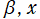
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi12800.png)
のグラフ。
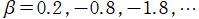
では関数が定義されない。
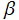
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi13000.png)
のグラフ。
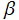
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi13100.png)
のグラフ。
 (変数ν,α)](siki_spec220/jacobi13700.png)
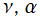
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi13300.png)
のグラフ。
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi13400.png)
のグラフ。
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi13500.png)
のグラフ。
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi13600.png)
のグラフ。
 (変数ν,β)](siki_spec220/jacobi14200.png)
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi13800.png)
のグラフ。
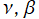
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi13900.png)
のグラフ。
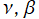
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi14000.png)
のグラフ。
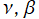
を実2変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi14100.png)
のグラフ。
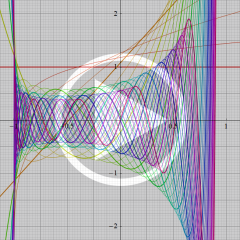
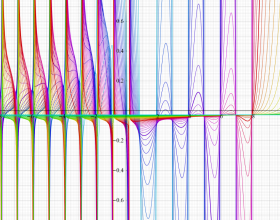
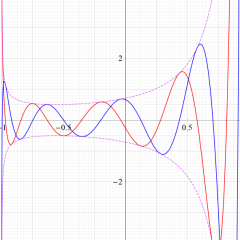
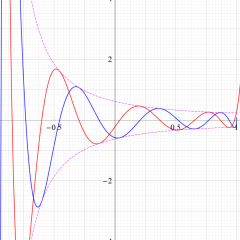
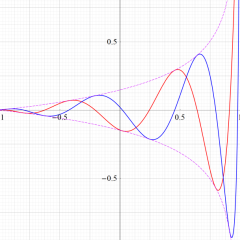
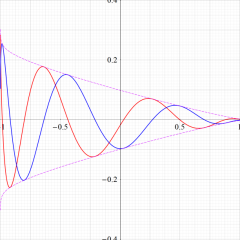
とQ[ν, (α, β)](z)の関係](siki_spec220/jacobi14500.png)
余弦・正弦関数に類似した
](siki_spec220/jacobi05900.png)
と
](siki_spec220/jacobi14300.png)
の関係。このとき、両者の包絡線は
^2+Q[ν, (α, β)](x)^2]](siki_spec220/jacobi14400.png)
となる。
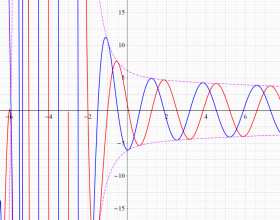
](siki_spec220/jacobi15600.png)
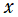
を実変数とする、第2種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi14600.png)
。
②実数次
](siki_spec220/jacobi14700.png)
。
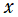
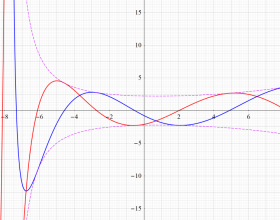
を実変数とする、第2種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi14800.png)
。
②実数次
](siki_spec220/jacobi14900.png)
。
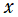
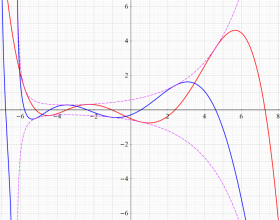
を実変数とする、第2種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi15000.png)
。
②実数次
](siki_spec220/jacobi15100.png)
。
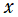
を実変数とする、第2種 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi15200.png)
。
②実数次
](siki_spec220/jacobi15300.png)
。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi15400.png)
のグラフ。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi15500.png)
のグラフ。
](siki_spec220/jacobi16500.png)
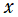
を実変数とする、第2種 Jacobi 関数のグラフ。いずれも実数次であって、
①](siki_spec220/jacobi15700.png)
。
②](siki_spec220/jacobi15800.png)
。
③](siki_spec220/jacobi15900.png)
。
④](siki_spec220/jacobi16000.png)
。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi16100.png)
のグラフ。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi16200.png)
のグラフ。

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi16300.png)
のグラフ。
アニメーション
(20.4MB)

を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi16400.png)
のグラフ。ただし実数
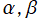
の組は、2番目の図の経路に沿って動く。
 (変数ν)](siki_spec220/jacobi16800.png)
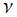
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi16600.png)
のグラフ。
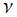
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi16700.png)
のグラフ。
 (変数α)](siki_spec220/jacobi17100.png)
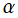
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi16900.png)
のグラフ。
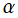
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi17000.png)
のグラフ。
 (変数β)](siki_spec220/jacobi17400.png)
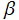
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi17200.png)
のグラフ。
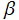
を複素変数とする、第2種 Jacobi 関数
](siki_spec220/jacobi17300.png)
のグラフ。
Jacobi 多項式
](siki_spec220/jacobi17500.png)
は、直交区間を
![[-1, 1]](siki_spec220/jacobi17600.png)
とする直交多項式であり、重み関数を伴う直交性
を持っている。拡張された球面調和関数などの応用事例では、上記に
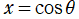
の置換積分を施した
がしばしば必要になる。
もし、前節で触れた
](siki_spec220/jacobi18000.png)
を Jacobi 多項式とするならば、その直交区間は
![[0, 1]](siki_spec220/jacobi18100.png)
となり、
なる直交性を持つ直交多項式となる。
Jacobi 多項式は、超幾何関数系で最も複雑な直交性を持つ古典的直交多項式であり、添字定数 (次数
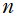
以外のパラメーター) が2個ある唯一のものである。
当サイトでは Jacobi 関数に対しても、独自に
を導入し、正規化 Jacobi 関数と呼ぶ※1。よって、
} (n ∈ N≧0)](siki_spec220/jacobi18400.png)
は
正規直交関数系を成すとともに、重み関数が現れない直交性
を満たす。
【註記】
※1:関数記号は正規化 (Normalization) に基づく。また、当サイトでは
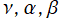
および

を複素数まで許容する。他の直交多項式と同様に、
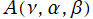
を対数ガンマ関数で表示しているのは、
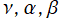
を複素変数とする場合に解析接続が考慮されるようにするためである。
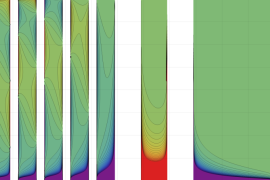
](siki_spec220/jacobi20300.png)
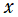
を実変数とする、正規化 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi18700.png)
。
②実数次
](siki_spec220/jacobi18800.png)
。
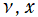
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi18800.png)
のグラフ。
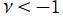
では関数が実数値を取らない帯状領域がある。
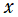
を実変数とする、正規化 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi19000.png)
。
②実数次
](siki_spec220/jacobi19100.png)
。
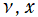
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi19100.png)
のグラフ。
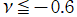
では関数が実数値を取らない帯状領域がある。
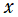
を実変数とする、正規化 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi19300.png)
。
②実数次
](siki_spec220/jacobi19400.png)
。
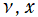
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi19400.png)
のグラフ。
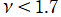
では関数が実数値を取らない帯状領域がある。
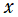
を実変数とする、正規化 Jacobi 関数のグラフ。
①整数次
](siki_spec220/jacobi19600.png)
。
②実数次
](siki_spec220/jacobi19700.png)
。
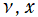
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi19700.png)
のグラフ。
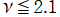
では関数が実数値を取らない帯状領域がある。

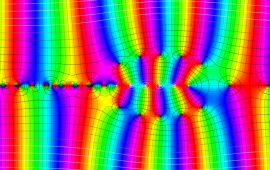
を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi19900.png)
のグラフ。

を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi20000.png)
のグラフ。

を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi20100.png)
のグラフ。

を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi20200.png)
のグラフ。
 (変数ν)](siki_spec220/jacobi20900.png)
を実変数とする、正規化 Jacobi 関数のグラフ。
①](siki_spec220/jacobi20400.png)
。
②](siki_spec220/jacobi20500.png)
。
を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi20600.png)
のグラフ。
を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi20700.png)
のグラフ。
を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi20800.png)
のグラフ。
 (変数α)](siki_spec220/jacobi21700.png)
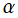
を実変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi21000.png)
のグラフ。
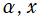
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi21000.png)
のグラフ。
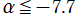
では関数が実数値を取らない帯状領域がある。
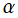
を実変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi21200.png)
のグラフ。
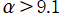
では関数が実数値を取らない。
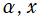
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi21200.png)
のグラフ。
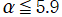
では関数が実数値を取らない帯状領域がある。
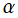
を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi21500.png)
のグラフ。
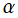
を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi21600.png)
のグラフ。
 (変数β)](siki_spec220/jacobi22500.png)
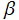
を実変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi21800.png)
のグラフ。
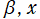
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi21800.png)
のグラフ。
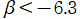
では関数が実数値を取らない帯状領域がある。
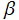
を実変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi22000.png)
のグラフ。
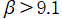
では関数が実数値を取らない。
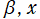
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi22000.png)
のグラフ。
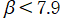
では関数が実数値を取らない帯状領域がある。
を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi22300.png)
のグラフ。
を複素変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi22400.png)
のグラフ。
 (変数ν,α)](siki_spec220/jacobi23000.png)
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi22600.png)
のグラフ。
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi22700.png)
のグラフ。
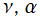
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi22800.png)
のグラフ。
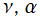
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi22900.png)
のグラフ。
 (変数ν,β)](siki_spec220/jacobi23500.png)
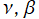
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi23100.png)
のグラフ。
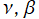
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi23200.png)
のグラフ。
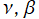
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi23300.png)
のグラフ。
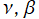
を実2変数とする、正規化 Jacobi 関数
](siki_spec220/jacobi23400.png)
のグラフ。
日:
Zernike関数,
ゼルニケ関数
英:
Zernike function,仏:
Fonction de Zernike,独:
Zernikesche funktion
Zernike 関数は、第1種 Jacobi 関数を用いた表示式
で定義される※1。一般に Zernike 関数は、
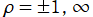
を第1種 Jacobi 関数に由来する対数分岐点、
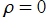
を
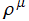
に由来する分岐点とし、実軸上の区間
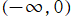
および
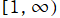
に分枝切断線が置かれる (特に
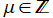
のときは、実軸上の区間
![(-∞, -1]](siki_spec220/jacobi00900.png)
および
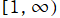
に分枝切断線が置かれる)。
Zernike 関数は、
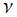
に関する線形漸化式および微分漸化式
を満たす。また、
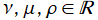
とするとき、積分表示式
で表わせる。
後述のとおり、応用では
](siki_spec220/jacobi24500.png)
を動径方向の関数と考え、方位角
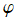
方向の因子を三角関数とした、
が定義される。当サイトでは、これを 「円板上の Zernike 関数」 と呼ぶことにする。
](siki_spec220/jacobi24500.png)
および
](siki_spec220/jacobi24700.png)
のうち、実際に応用面で重要となるのは、専ら
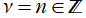
,
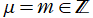
で、しかも
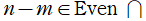
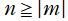
となる場合に限られる。このとき、
](siki_spec220/jacobi25100.png)
は前述の分枝切断線が消失して多項式となるので、Zernike 多項式と呼ばれる。また、
](siki_spec220/jacobi25200.png)
を 「円板上の Zernike 多項式」 と呼ぶことにする。
Zernike 多項式は、母関数表示式および Rodrigues の公式※2
で表わせる他、超幾何関数表示式および明示的な多項式
によっても表わせる。(実は、冒頭に掲げた定義式に現れる第1種 Jacobi 関数の部分は、Zernike 多項式のときに第1種 Legendre 関数の多項式で表わすことができる※3。)
Zernike 多項式の特に重要な性質は、重み関数
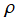
を伴う直交性
を持つことである。しかし、各種公式の形が枠組みから外れる等の理由で、Zernike 多項式は古典的直交多項式に含めない慣例となっている。
Zernike 多項式は光学の分野で重要であり、特に、天文学および眼科領域で使用されるレンズや精密光学機器の性能を向上する (歪みや干渉を抑える) ために応用される。また、画像処理における特徴検出にも Zernike 多項式が現れ、その技術は医療機器等に応用されている。これらの事例では、円板上の Zernike 多項式が持つ単位円板内部での直交性
が基礎となっている。
1932年に位相差顕微鏡を発明した F. Zernike は、これに必要となる円形凹面鏡の設計とその回折現象の解明にあたって、新たに Zernike 多項式を導入した事を1934年の論文で明らかにしたので、後年その名を冠して呼ばれるようになった。
【註記】
※1:因子
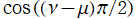
は Mathematica が採用する定義 (2023年1月現在) であって、通常この部分は
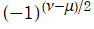
で定義される。ところが前者は、
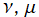
が整数でない実数のときでも、
](siki_spec220/jacobi24500.png)
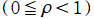
が実数値を取るという利点を持つ。Mathematica が今後この定義を変更する可能性もあるが、当サイトはこれを採用する。よって、Zernike 多項式を超える
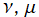
および
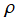
の場合についてもグラフを掲載するが、物理的な意味を全く持たないので、その個数を若干削減する (例えば、
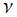
または
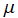
を複素変数とするグラフは省略する)。
※2:微分形式
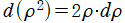
による表現を用いず、この公式を次のように解釈しても良い。
※3:この事は、
 = P[n, m](z)](siki_spec220/jacobi26300.png)
が満たす漸化式
から分かる。
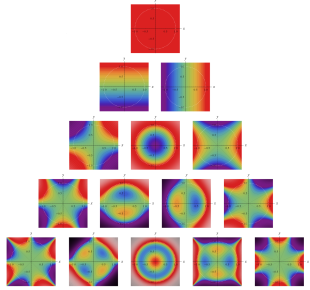
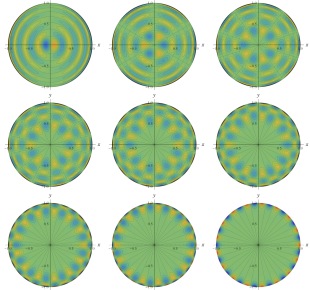
](siki_spec220/jacobi27300.png)
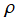
を実変数とする、Zernike 多項式のグラフ。
①](siki_spec220/jacobi26500.png)
。
②](siki_spec220/jacobi26600.png)
。
③](siki_spec220/jacobi26700.png)
。
④](siki_spec220/jacobi26800.png)
。
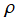
を実変数とする、Zernike 多項式のグラフ。
①](siki_spec220/jacobi26900.png)
。
②](siki_spec220/jacobi27000.png)
。
③](siki_spec220/jacobi27100.png)
。
④](siki_spec220/jacobi27200.png)
。
](siki_spec220/jacobi28100.png)
円板上の Zernike 多項式
](siki_spec220/jacobi25200.png)
のグラフ。
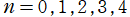
の場合。
(通常はこの表示形式のグラフを、「Zernike 多項式のグラフ」 として紹介している事が多い。)
前述の直交性により、
](siki_spec220/jacobi25200.png)
のグラフは単位円内部に限定することが多いが、関数自体は外部にも存在する。
円板上の Zernike 多項式
](siki_spec220/jacobi25200.png)
のグラフ。
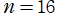
の場合。
円板上の Zernike 多項式
](siki_spec220/jacobi25200.png)
のグラフ。
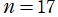
の場合。
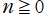
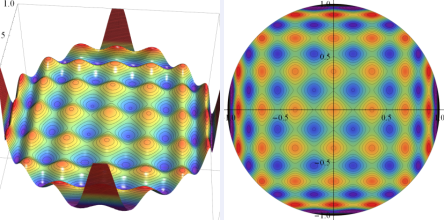
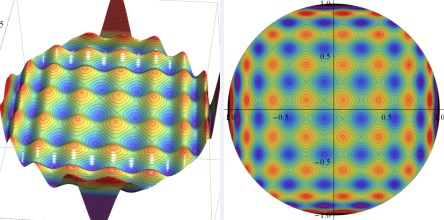
を共通とする、円板上の Zernike 多項式
](siki_spec220/jacobi25200.png)
の有限和
が成立する。これは、Bessel 関数の公式 「
Jacobi - Anger expansion」 に似ている。
+Zy[16](ρ, φ)](siki_spec220/jacobi27900.png)
のグラフ。
+Zy[17](ρ, φ)](siki_spec220/jacobi28000.png)
のグラフ。
](siki_spec220/jacobi29700.png)
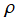
を実変数とする、Zernike 関数
](siki_spec220/jacobi28300.png)
のグラフ。
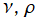
を実2変数とする、Zernike 関数
](siki_spec220/jacobi28300.png)
のグラフ。
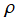
を実変数とする、Zernike 関数
](siki_spec220/jacobi28400.png)
のグラフ。
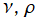
を実2変数とする、Zernike 関数
](siki_spec220/jacobi28400.png)
のグラフ。
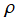
を実変数とする、Zernike 関数
](siki_spec220/jacobi28500.png)
のグラフ。
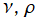
を実2変数とする、Zernike 関数
](siki_spec220/jacobi28500.png)
のグラフ。
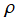
を実変数とする、Zernike 関数
](siki_spec220/jacobi28600.png)
のグラフ。
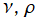
を実2変数とする、Zernike 関数
](siki_spec220/jacobi28600.png)
のグラフ。
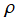
を実変数とする、Zernike 関数
](siki_spec220/jacobi28800.png)
のグラフ。
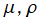
を実2変数とする、Zernike 関数
](siki_spec220/jacobi28800.png)
のグラフ。
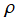
を実変数とする、Zernike 関数
](siki_spec220/jacobi28900.png)
のグラフ。
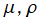
を実2変数とする、Zernike 関数
](siki_spec220/jacobi28900.png)
のグラフ。
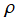
を実変数とする、Zernike 関数
](siki_spec220/jacobi29000.png)
のグラフ。
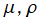
を実2変数とする、Zernike 関数
](siki_spec220/jacobi29000.png)
のグラフ。
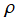
を実変数とする、Zernike 関数
](siki_spec220/jacobi29100.png)
のグラフ。
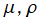
を実2変数とする、Zernike 関数
](siki_spec220/jacobi29100.png)
のグラフ。
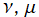
を実2変数とする、Zernike 関数
](siki_spec220/jacobi29200.png)
のグラフ。
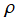
を複素変数とする、Zernike 関数
](siki_spec220/jacobi29300.png)
のグラフ。
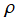
を複素変数とする、Zernike 関数
](siki_spec220/jacobi29400.png)
のグラフ。
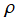
を複素変数とする、Zernike 関数
](siki_spec220/jacobi29500.png)
のグラフ。
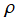
を複素変数とする、Zernike 関数
](siki_spec220/jacobi29600.png)
のグラフ。
](siki_spec220/jacobi29900.png)
円板上の Zernike 関数
](siki_spec220/jacobi24700.png)
のグラフ。
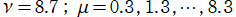
の場合。
日:
WignerのD関数,
ウィグナーD関数
英:
Wigner's D function,仏:
Fonction D de Wigner,独:
Wignersche D-funktion
角度
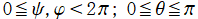
(ただし、この制限はしばしば不要になる) は、3次元直交直線座標
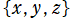
における原点中心の回転変換を指定する、(
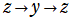
回転系の) Euler 角
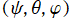
であるとする※1。
このとき Wigner のD行列
![D[2j+1]](siki_spec220/jacobi30400.png)
とは、
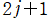
次のユニタリー行列 (ユニタリー性
![conj(T(D[2j+1]))・D[2j+1] = I[2j+1]](siki_spec220/jacobi30600.png)
を持つ
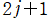
次の複素正方行列。ここに、
![I[2j+1]](siki_spec220/jacobi30700.png)
は
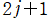
次の単位行列。)
であって、具体的にその要素
![D[m, n]](siki_spec220/jacobi30900.png)
が、Wigner のD関数
により
![D[m, n] = D[m, n, j](ψ, θ, φ)](siki_spec220/jacobi31100.png)
と表わされる行列を言う※2。特に
 = D[m, n, j](0, θ, 0)](siki_spec220/jacobi31200.png)
の部分は Wigner のd関数と呼ばれ、これの Jacobi 関数部分は、超幾何関数による閉形式または有限和で表示されることもある。
Wigner のD関数およびd関数は、
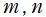
について反転性
を持つ。また、偏微分演算子を
と定めるとき、Wigner のD関数の共役複素数は
なる偏微分方程式を満たす※3。すなわち
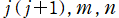
等は、この偏微分方程式の固有値である。
さらに、Wigner のD関数は Euler 角
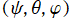
の全体をわたる直交性
を持っている。
Wigner のD関数は、
球面調和関数およびその拡張と関係がある。例えば
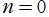
のとき、球面調和関数
に還元される。一方、量子力学における "スピン" を考慮した 「スピン加重球面調和関数 (Spin weighted spherical harmonics)」 は、Wigner のd関数を用いて、
と表わされる。
また重要な事実として、有限和
は、球面調和関数
](siki_spec220/jacobi32300.png)
を (
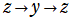
回転系の) Euler 角
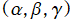
で回転変換したものと一致する。
Wigner のD行列は、回転群 (特殊直交群)
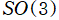
または特殊ユニタリー群
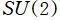
の既約行列表現 (各群の元全体から行列が成す群への写像) として、E. P. Wigner が1927年に導出した。主に、スピン角運動量が伴う量子力学、並びにその有限次元 Lie 群による表現論に応用される。
【註記】
※1:(
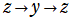
回転系の) Euler 角
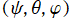
は、具体的に次の手順で回転が定まる。
① 
軸周りに
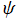
度回転
② 前記
①で移動後の
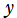
軸周りに
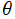
度回転
③ 前記
②で移動後の

軸周りに
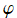
度回転
これをアニメーション
(3.72MB) で示すと、次のようになる。
同様に、他の回転系を採用することも可能であり、全部で12種類の回転系がある。
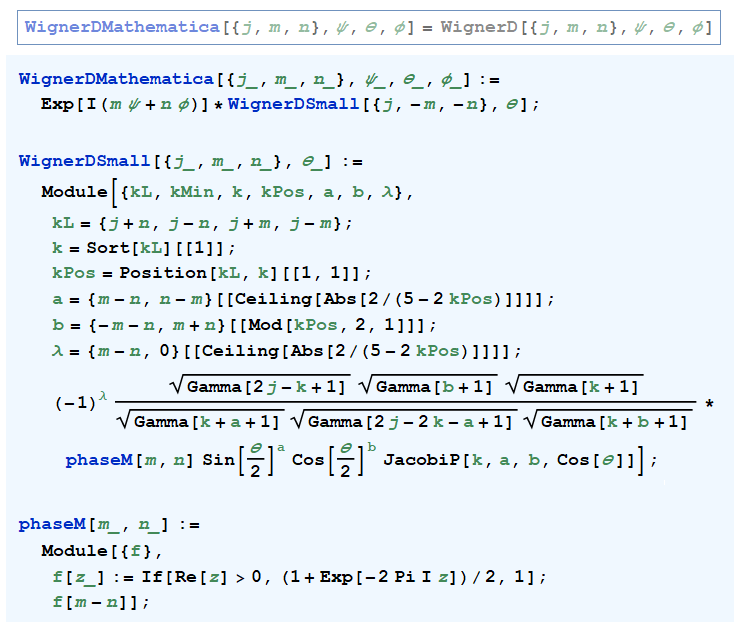
※2:
Mathematica の組込関数![WignerD[{j,m,n},ψ,θ,φ] =](siki_spec220/jacobi32700.png)
](siki_spec220/jacobi32800.png)
は、添字
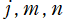
が整数でもなく半奇数でもない場合にも定義されており、しかも
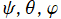
が複素数の場合でも計算可能である。それは次のコードと全く同じ動作になる (2023年3月現在)。
このとき、
](siki_spec220/jacobi32800.png)
と通常の定義
](siki_spec220/jacobi33200.png)
の関係は (添字と変数の拡張も含めて)、
となる。なお、コード
GaussHypergeometric.m では、Mathematica の組込関数よりも更に解析接続を施した Wigner のD関数も実装した。
※3:Wikipedia の記事にあるとおり、偏微分演算子
![J[k] (k = 1, 2, 3)](siki_spec220/jacobi33400.png)
等を Lie 代数の生成子と考え、更に量子力学で多用されるケット記号
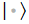
を用いて、しばしばこの偏微分方程式は
の形に略記される。
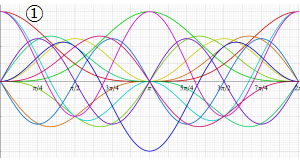
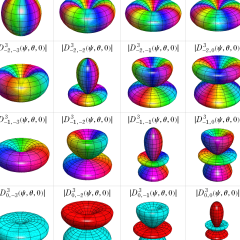
](siki_spec220/jacobi35300.png)
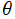
を実変数とする、Wigner のd関数のグラフ。
①](siki_spec220/jacobi33700.png)
(
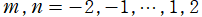
のうち、重複を除いた関数は12種類。)
②](siki_spec220/jacobi33900.png)
(
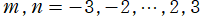
のうち、重複を除いた関数は22種類。)
③](siki_spec220/jacobi34100.png)
(
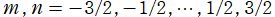
のうち、重複を除いた関数は9種類。)
④](siki_spec220/jacobi34300.png)
(
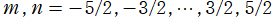
のうち、重複を除いた関数は18種類。)
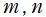
を整2変数とする、Wigner のd関数
](siki_spec220/jacobi34500.png)
のグラフ。
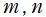
を整2変数とする、Wigner のd関数
](siki_spec220/jacobi34600.png)
のグラフ。
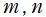
を整2変数、
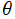
を実変数とする、Wigner のd関数
](siki_spec220/jacobi34700.png)
のグラフ。
①描画範囲が
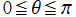
の場合。
②描画範囲が
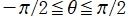
の場合。
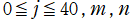
を整3変数とする、Wigner のd関数のグラフ。
①](siki_spec220/jacobi35100.png)
。
②](siki_spec220/jacobi35200.png)
。
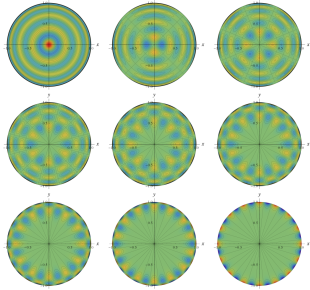
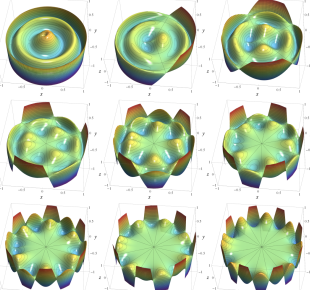
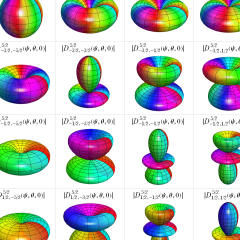
](siki_spec220/jacobi37200.png)
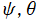
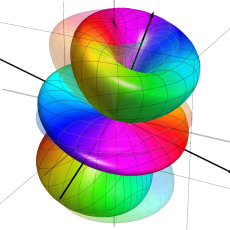
を変数とする、Wigner のD関数
),](siki_spec220/jacobi35500.png)
)),](siki_spec220/jacobi35600.png)
))](siki_spec220/jacobi35700.png)
のグラフ。(ただし、
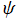
を極座標の方位角、
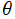
を極座標の天頂角として描画する:以下同様。)
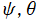
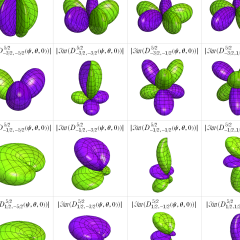
を変数とする、Wigner のD関数
),](siki_spec220/jacobi35800.png)
)),](siki_spec220/jacobi35900.png)
))](siki_spec220/jacobi36000.png)
のグラフ。
アニメーション
(3.66MB, 3.62MB, 3.61MB)
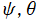
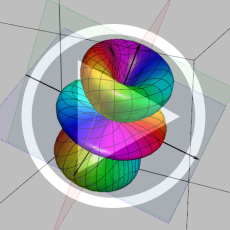
を変数とする、Wigner のD関数
),](siki_spec220/jacobi36100.png)
)),](siki_spec220/jacobi36200.png)
))](siki_spec220/jacobi36300.png)
のグラフについて、
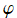
を動かしたときの動画。
アニメーション
(4.18MB, 4.35MB, 4.28MB)
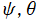
を変数とする、Wigner のD関数
),](siki_spec220/jacobi36400.png)
)),](siki_spec220/jacobi36500.png)
))](siki_spec220/jacobi36600.png)
のグラフについて、
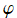
を動かしたときの動画。
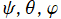
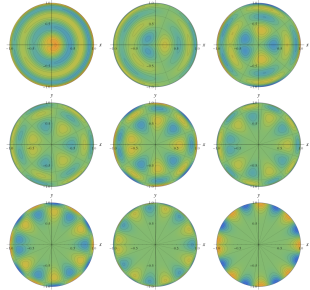
を変数とする、Wigner のD関数
),](siki_spec220/jacobi36100.png)
)),](siki_spec220/jacobi36200.png)
))](siki_spec220/jacobi36300.png)
のグラフを、直交直線座標
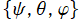
で描画する。
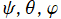
を変数とする、Wigner のD関数
),](siki_spec220/jacobi36400.png)
)),](siki_spec220/jacobi36500.png)
))](siki_spec220/jacobi36600.png)
のグラフを、直交直線座標
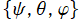
で描画する。
前述の有限和
が、球面調和関数
](siki_spec220/jacobi32300.png)
を Euler 角
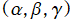
で回転変換したものと一致することを確認する。
 ; π/6, π/5, -π/4)](siki_spec220/jacobi36900.png)
の場合。グラフとアニメーション
(3.38MB)。
 ; -π/10, π/8, π/7)](siki_spec220/jacobi37000.png)
の場合。グラフとアニメーション
(3.58MB)。
 ; -2π/3, 2π/5, -3π/2)](siki_spec220/jacobi37100.png)
の場合。グラフとアニメーション
(3.64MB)。
 (m, n ∈ R)](siki_spec220/jacobi37700.png)
前述のとおり、Wigner のd関数は
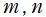
が実数のときにも定義できるが、物理的な意味は持たない。以下そのような事例を掲載する。
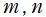
を実2変数とする、Wigner のd関数
)](siki_spec220/jacobi37300.png)
のグラフ。
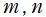
を実2変数とする、Wigner のd関数
)](siki_spec220/jacobi37400.png)
のグラフ。
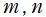
を実2変数とする、Wigner のd関数
)](siki_spec220/jacobi37500.png)
のグラフ。
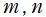
を実2変数とする、Wigner のd関数
)](siki_spec220/jacobi37600.png)
のグラフ。
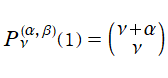
](siki_spec220/jacobi03700.png) は当サイトが独自に定義したものであって、
は当サイトが独自に定義したものであって、](siki_spec220/jacobi03000.png) が余弦関数に相当すると見たとき、
が余弦関数に相当すると見たとき、](siki_spec220/jacobi03700.png) は正弦関数に相当する。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針は、別頁 Questions に掲示している。)
は正弦関数に相当する。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針は、別頁 Questions に掲示している。)](siki_spec220/jacobi03800.png) である。
である。](siki_spec220/jacobi03900.png) のグラフは全て省略する。(実変数も、概形の関心領域が決定しづらいので省略する。)
のグラフは全て省略する。(実変数も、概形の関心領域が決定しづらいので省略する。)](siki_spec220/jacobi04000.png) のグラフは
のグラフは](siki_spec220/jacobi03700.png) と似ているので、
と似ているので、 を変数とする場合のみ掲載し、個数も削減する。
を変数とする場合のみ掲載し、個数も削減する。](siki_spec220/jacobi04100.png) のグラフも全て省略する。(同じく、概形の制御が難しいことに因る。)
のグラフも全て省略する。(同じく、概形の制御が難しいことに因る。)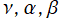 および
および を複素数まで許容する。他の直交多項式と同様に、
を複素数まで許容する。他の直交多項式と同様に、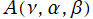 を対数ガンマ関数で表示しているのは、
を対数ガンマ関数で表示しているのは、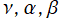 を複素変数とする場合に解析接続が考慮されるようにするためである。
を複素変数とする場合に解析接続が考慮されるようにするためである。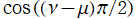 は Mathematica が採用する定義 (2023年1月現在) であって、通常この部分は
は Mathematica が採用する定義 (2023年1月現在) であって、通常この部分は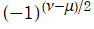 で定義される。ところが前者は、
で定義される。ところが前者は、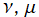 が整数でない実数のときでも、
が整数でない実数のときでも、](siki_spec220/jacobi24500.png)
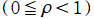 が実数値を取るという利点を持つ。Mathematica が今後この定義を変更する可能性もあるが、当サイトはこれを採用する。よって、Zernike 多項式を超える
が実数値を取るという利点を持つ。Mathematica が今後この定義を変更する可能性もあるが、当サイトはこれを採用する。よって、Zernike 多項式を超える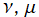 および
および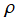 の場合についてもグラフを掲載するが、物理的な意味を全く持たないので、その個数を若干削減する (例えば、
の場合についてもグラフを掲載するが、物理的な意味を全く持たないので、その個数を若干削減する (例えば、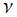 または
または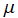 を複素変数とするグラフは省略する)。
を複素変数とするグラフは省略する)。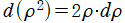 による表現を用いず、この公式を次のように解釈しても良い。
による表現を用いず、この公式を次のように解釈しても良い。 = P[n, m](z)](siki_spec220/jacobi26300.png) が満たす漸化式
が満たす漸化式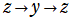 回転系の) Euler 角
回転系の) Euler 角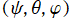 は、具体的に次の手順で回転が定まる。
は、具体的に次の手順で回転が定まる。![WignerD[{j,m,n},ψ,θ,φ] =](siki_spec220/jacobi32700.png)
](siki_spec220/jacobi32800.png) は、添字
は、添字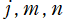 が整数でもなく半奇数でもない場合にも定義されており、しかも
が整数でもなく半奇数でもない場合にも定義されており、しかも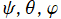 が複素数の場合でも計算可能である。それは次のコードと全く同じ動作になる (2023年3月現在)。
が複素数の場合でも計算可能である。それは次のコードと全く同じ動作になる (2023年3月現在)。](siki_spec220/jacobi32800.png) と通常の定義
と通常の定義](siki_spec220/jacobi33200.png) の関係は (添字と変数の拡張も含めて)、
の関係は (添字と変数の拡張も含めて)、![J[k] (k = 1, 2, 3)](siki_spec220/jacobi33400.png) 等を Lie 代数の生成子と考え、更に量子力学で多用されるケット記号
等を Lie 代数の生成子と考え、更に量子力学で多用されるケット記号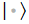 を用いて、しばしばこの偏微分方程式は
を用いて、しばしばこの偏微分方程式は 軸周りに
軸周りに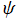 度回転
度回転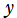 軸周りに
軸周りに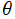 度回転
度回転 軸周りに
軸周りに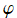 度回転
度回転