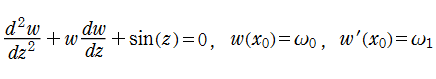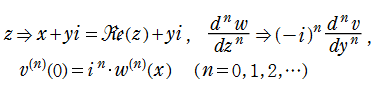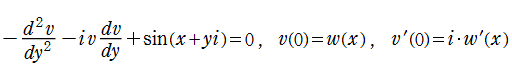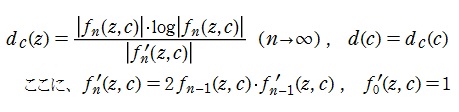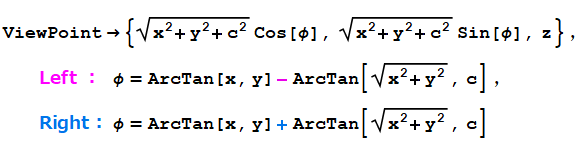特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
Mathematica関連 Menu
Mathematicaの(微妙な)Tips
Mathematica の一風変わった (しかし強引で微妙な) 使用例を紹介します。
なお、Böttcher 関数の計算法もここに掲載しています。
なお、Böttcher 関数の計算法もここに掲載しています。
NDSolveを複素領域で使う方法
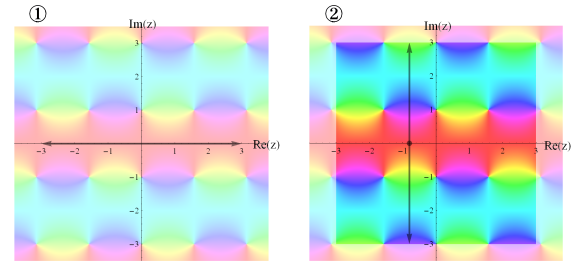
微分方程式の数値解を求める Mathematica の組み込み関数 「NDSolve」 は、解を求める区間が複素平面上の有限直線でなければならない。しかし、以下に示す方法を用いれば、複素平面上の有限2次元領域で解を求めることができる。
なお、この方法はいくつかの Mathematica-Packageファイルにおいて既に使用している。
実軸上に特異点が存在しない場合
【この方法の考え方】NDSolve は、解を求める区間が直線であることを踏まえて、次の手順を考える。
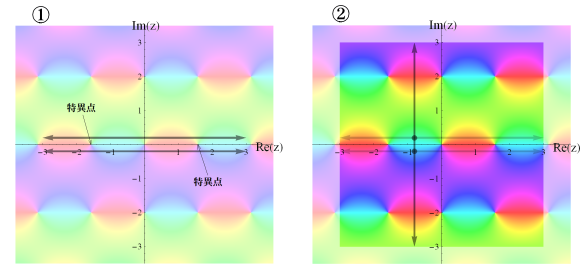
① まず普通どおり実軸上で数値解を求める。解である関数の引数が実数であれば、その数値解が即座に関数値となる。引数が (実数でない) 複素数であれば、(引数と同じ実部の) 数値解が手順②の初期値として使用される。したがって、数値解を求める実軸上の区間では、特異点が存在しないことが望まれる。
② 虚軸に平行な直線上で数値解を求める。このとき、初期値は①で求めた数値解、微分方程式は虚軸方向に変形したものを使用する。これによって、複素平面上の任意の矩形領域を定義域とする解を求めることができる。
以上、①②の手順を図示すれば次のようになる。② 虚軸に平行な直線上で数値解を求める。このとき、初期値は①で求めた数値解、微分方程式は虚軸方向に変形したものを使用する。これによって、複素平面上の任意の矩形領域を定義域とする解を求めることができる。
また、微分方程式の虚軸方向への変形方法、NDSolve の大まかな用法を、例えば常微分方程式
の解となる関数
①実部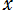 での関数値を、次のように普通の用法の NDSolve で求める。
での関数値を、次のように普通の用法の NDSolve で求める。
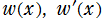 が得られる。この値を②の初期値に使用する。
が得られる。この値を②の初期値に使用する。
②微分方程式の独立変数や従属変数に対する形式的な変換規則
によって、前述の常微分方程式を虚数方向での式
に変形し、次のような用法で再び NDSolve を使用する。
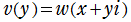 の値が得られる。
の値が得られる。
realFunctionW[x_, {ω0_, ω1_}]:=
Module[{sol, w, z},
sol=NDSolve[{w''[z]+w[z]*w'[z]+Sin[z]==0,
w[0]==ω0, w'[0]==ω1}, w, {z, x}];
{w[x], w'[x]}/.sol[[1]]
];
これによって、Module[{sol, w, z},
sol=NDSolve[{w''[z]+w[z]*w'[z]+Sin[z]==0,
w[0]==ω0, w'[0]==ω1}, w, {z, x}];
{w[x], w'[x]}/.sol[[1]]
];
②微分方程式の独立変数や従属変数に対する形式的な変換規則
によって、前述の常微分方程式を虚数方向での式
に変形し、次のような用法で再び NDSolve を使用する。
functionW[z_, {ω0_, ω1_}]:=
Module[{init, sol, v, y},
init = realFunctionW[Re[z], {ω0, ω1}];
sol = NDSolve[{-v''[y]-I*v[y]*v'[y]+Sin[Re[z]+y*I]==0,
v[0] == init[[1]], v'[0] == I*init[[2]]}, v, {y, Im[z]}];
v[Im[z]] /. sol[[1]]
]
これによって最終的に、Module[{init, sol, v, y},
init = realFunctionW[Re[z], {ω0, ω1}];
sol = NDSolve[{-v''[y]-I*v[y]*v'[y]+Sin[Re[z]+y*I]==0,
v[0] == init[[1]], v'[0] == I*init[[2]]}, v, {y, Im[z]}];
v[Im[z]] /. sol[[1]]
]
実際に、上記二つのコードのコピーを Mathematica に貼り付けてロードし、グラフを描画した結果は次のようになる。
【具体的コード・開発経過について】
さらに詳しい内容は、次の Mathematica-Notebookファイルをダウンロードしてご確認ください。
Van der Pol 方程式に適用した例
(File Size:zip形式で圧縮時 5,505KB,展開後 9,682KB)
Lame 関数に適用した例
(File Size:zip形式で圧縮時 428KB,展開後 1,073KB)
実軸上に特異点が存在する場合
【この方法の考え方】実軸上に特異点がある場合の回避策として、前の方法とは異なる2つの方法を考える。
方法1:実軸からわずかに平行移動した直線から始める方法。この手順を図示すれば次のようになる。
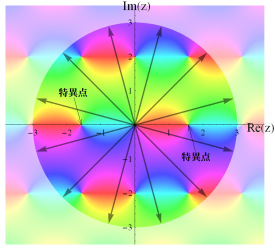
方法2:実軸上の1点から放射状に延びる直線群で求める方法。この方法を図示すれば次のようになる。
【具体的コード・開発経過について】
微分方程式の変換、NDSolve のコードは前述 「実軸上に特異点が存在しない場合」 よりも複雑になるので、詳しい内容は次の Mathematica-Notebookファイルをダウンロードしてご確認ください。
準 Painlevé 方程式に適用した例
(File Size:zip形式で圧縮時 4,059KB,展開後 9,941KB)
ColorFunctionの合成的な指示方法
(注意) これは、Mathematica Ver.6以降で可能な方法です。カラースキームにLighterやDarkerを適用する方法
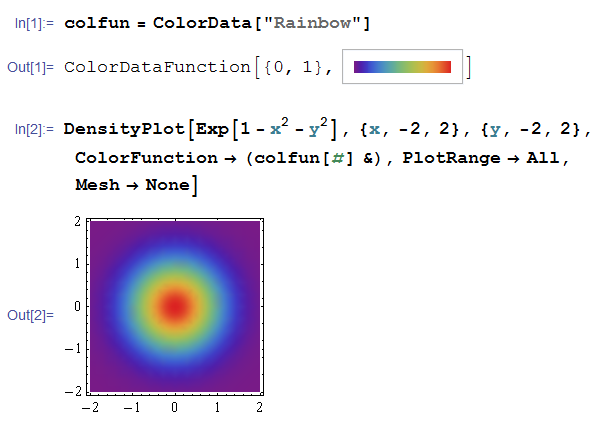
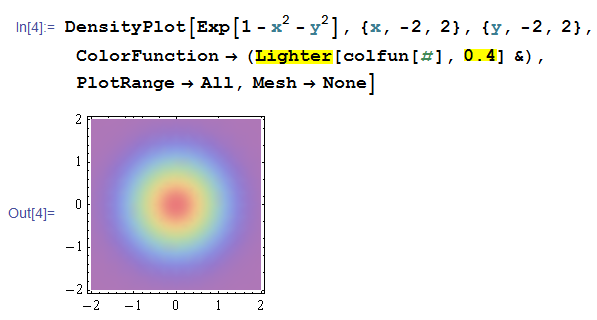
組込みのカラースキームを色関数として定義し、ColorFunctionで使用する普通の方法。今度は、カラースキーム自体を淡色にしたいが、次のように定義してもうまくいかない。
ColorDataFunction は、ColorFunction 等でスケール指示した時点で RGBColor に変換される。よって、次のようにすればよい。
なお、暗色にする場合は、単に Lighter を Darker に変えればよい。
Plot3DのColorFunctionに光沢や透過性を付加する方法
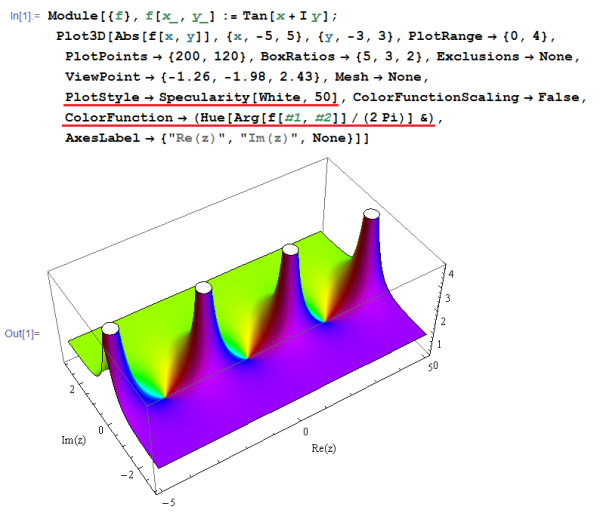
曲面のカラーリングは、オプション 「PlotStyle」 または 「ColorFunction」 で指定できる。しかし、PlotStyle と ColorFunction の両方で指定があるときは、ColorFunction の指定内容が優先され、PlotStyle の指定内容は (隠れてしまうため) 発現しない。ColorFunction で独自定義したカラーリングを指定し、かつ曲面が光沢や透過性も持つようにしたい場合、次のように PlotStyle で光沢等を指定しても無効になり、カラーリングのみになってしまう。
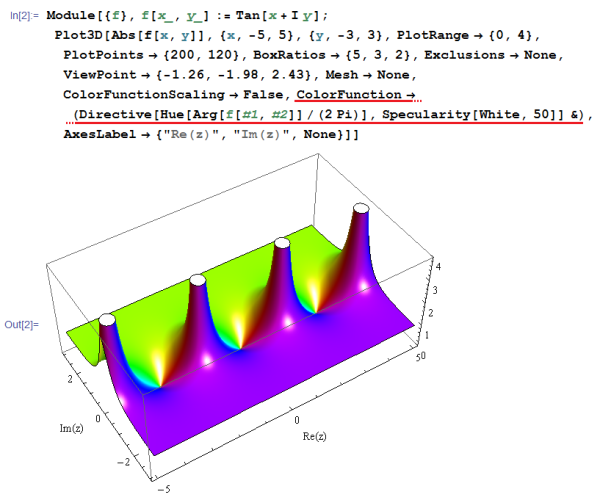
よって PlotStyle を使用せず、ColorFunction のみでカラーリングと光沢等を同時に指定する。具体的には、ColorFunction の純関数において 「Directive」 を併用すれば、次のように意図した結果になる。
(なお、ColorFunction で Directive を使用する方法は、「Wolfram言語&システム ドキュメントセンター」 の説明文 「詳細」 では言及があるが、「例題」 の使用例は掲載されていない。)
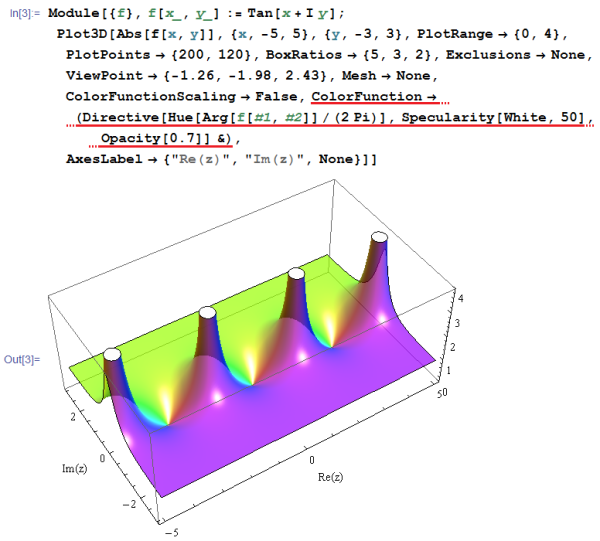
透過性を持たせたい場合は、単に Specularity[Color, number] を Opacity[number] に変えればよい。なお、次のようにすれば、光沢と透過性の両方を持つようにすることができる。
因みに、PlotStyle のみで独自カラーリングと光沢等を同時指定するのは、恐らく不可能と思われる。
逆に、Ver.8以降で可能なテクスチャー効果と光沢等の同時指定は、PlotStyle を用いて、
PlotStyle → Directive[Specularity[Color, number] ,
Texture[ExampleData[{"ColorTexture", "Texture名"}]]],
TextureCoordinateFunction → ({#1,#2}&)
とすればよい (この場合は、併せて 「TextureCoordinateFunction」 を指定しないと正常に動作しない)。Texture[ExampleData[{"ColorTexture", "Texture名"}]]],
TextureCoordinateFunction → ({#1,#2}&)
「Home」 にある Riemann のゼータ関数は、この方法によって描画した。また、「参考資料」 の頁の Header 画像もこのテクスチャー効果を応用したもので、「Mathematica Code」 の頁に Notebookファイルを掲載している。
Böttcher 関数の分枝切断線の処理方法
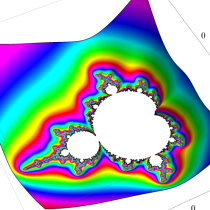
Böttcher 関数を級数で計算するときに生じる不自然な分枝切断線を除去する方法。ここでは、Mandelbrot 集合の Böttcher 関数を用いて説明しますが、Julia 集合の場合も同様の方法で取り扱うことができます。なお、この方法でも、一部の不自然な分枝切断線は除去できません。特に、細部を拡大するとこの事が分かります。また、単純に級数計算する場合に比べて、非常に多くの計算時間がかかります。
この方法で実際にプログラミングしたコードについては、「Version8で作成したファイル」 の 「特殊関数のグラフのコード」 中の Mathematica-Packageファイル FractalRelated.m にあります※1。
因みに、当サイトのように複素関数そのものを先に計算する方法は一般的ではなく、大抵は、エクスターナル・レイの曲線を辿るように計算する方法が採用されているようです。
(実のところ、以下に掲載する方法は技法的に見て"微妙"な点が多々あり、あまりお勧めできません。)
現象の再現・原因の確認
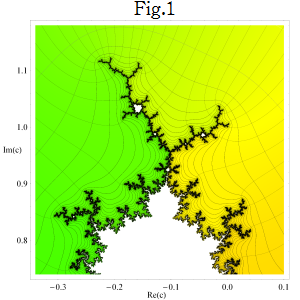
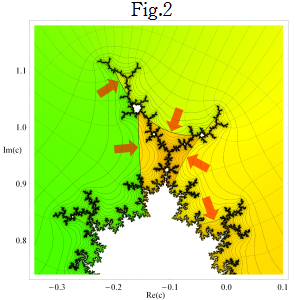
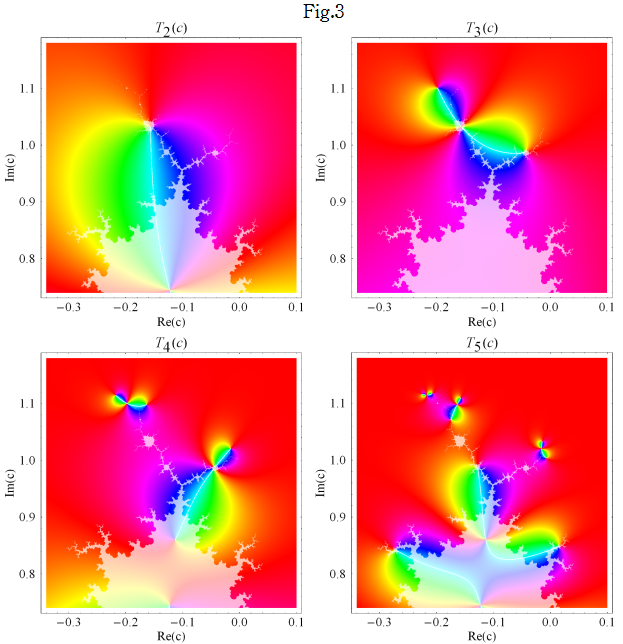
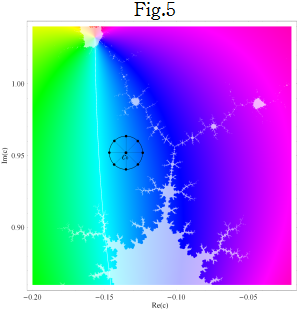
不自然な分枝切断線を除去するための処理を施した場合 (Fig.1) と、処理を施さずに級数展開式 (Böttcher 関数を参照) をそのまま数値計算に用いた場合 (Fig.2) を比較すると、次のようになる。(Fig.2) の原因を確認するため、偏角
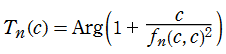
したがって、この分枝切断線と Mandelbrot 集合の境界線によって囲まれた領域内に
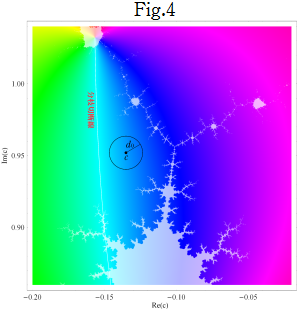
不自然な分枝切断線の除去方法
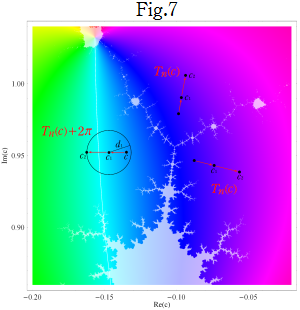
①引数②中心を
③円周上の等分点のうち、「連続的な Mandelbrot 集合反復回数関数※3」
④
以降は②から同様に繰り返すと、ある回数
【註記】
※1:Packageファイル 「FractalRelated.m」 では、少しでも計算速度をアップするため、Mathematica のコマンド 「Compile」 を併用しました。しかし、(プログラミングの技量不足もあって) Compile エラーのメッセージが出力されます。試験的に Compile を除去すると明らかに計算時間が長くなるので、一応 Compile の効果は出ていると思われます。
なお、2014年7月にリリースされた Mathematica Ver.10 では、新たに Böttcher 関数が実装されました。ここで扱った問題も恐らく解決されていると思います (ただし、確認はしていない)。
※2:Mandelbrot 集合までの最短距離関数は次の式で与えられます。ここに、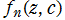 は Böttcher 関数の頁を参照。このとき
は Böttcher 関数の頁を参照。このとき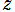 は Julia 集合の場合であって、Mandelbrot 集合の場合は
は Julia 集合の場合であって、Mandelbrot 集合の場合は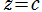 とします (以下同様)。
とします (以下同様)。
この式は、吉田怜史,藤村雅代,後藤泰宏「Böttcher 関数の構成による Julia 集合の可視化」(防衛大学校数理解析研究所講究録 No.1759(2011年)p.85~98) に記述があります。
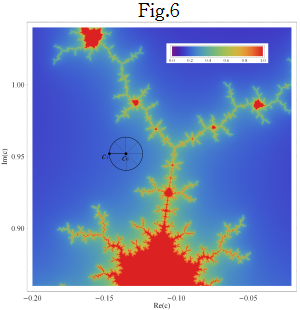
参考までに、最短距離関数を視覚化すると、次のようになります。
なお、ここで言う距離とは「曲線距離」ですので、②で半径を考えるのは本来問題があります。
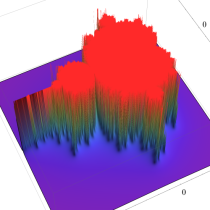
※3:「連続的な Mandelbrot 集合反復回数関数 (仮称)」とは、Mandelbrot 集合の複素力学系を反復した回数を表わす整数値関数「Mandelbrot 集合反復回数関数」の階段を、連続化してスロープ状にした次の関数です (さらに最大値が1になるよう、値域全体を規格化している)。
これの元々の式は、Paul Nylander のサイト http://www.bugman123.com/index.html に記述があります。
参考までに、連続的な Mandelbrot 集合反復回数関数を視覚化すると、次のようになります。
なお、この関数の代わりに前述の最短距離関数を用いて (関数値が最大になる点を選択して) も良いですが、計算がやや遅くなります。
※4:繰り返す上限回数は、級数項関数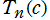 の値域を任意で指定することになりますが、あまり広範囲を指定すると膨大な計算時間がかかり、逆に範囲が狭いと除去できない不自然な分枝切断線が増えます。
の値域を任意で指定することになりますが、あまり広範囲を指定すると膨大な計算時間がかかり、逆に範囲が狭いと除去できない不自然な分枝切断線が増えます。
実は、かなり広い値域を指定しても除去できない部分が生じることを、既に試験的な計算で確認しています (この処理法が不完全である理由の一つ)。
※1:Packageファイル 「FractalRelated.m」 では、少しでも計算速度をアップするため、Mathematica のコマンド 「Compile」 を併用しました。しかし、(プログラミングの技量不足もあって) Compile エラーのメッセージが出力されます。試験的に Compile を除去すると明らかに計算時間が長くなるので、一応 Compile の効果は出ていると思われます。
なお、2014年7月にリリースされた Mathematica Ver.10 では、新たに Böttcher 関数が実装されました。ここで扱った問題も恐らく解決されていると思います (ただし、確認はしていない)。
※2:Mandelbrot 集合までの最短距離関数は次の式で与えられます。ここに、
この式は、吉田怜史,藤村雅代,後藤泰宏「Böttcher 関数の構成による Julia 集合の可視化」(防衛大学校数理解析研究所講究録 No.1759(2011年)p.85~98) に記述があります。
参考までに、最短距離関数を視覚化すると、次のようになります。
なお、ここで言う距離とは「曲線距離」ですので、②で半径を考えるのは本来問題があります。
※3:「連続的な Mandelbrot 集合反復回数関数 (仮称)」とは、Mandelbrot 集合の複素力学系を反復した回数を表わす整数値関数「Mandelbrot 集合反復回数関数」の階段を、連続化してスロープ状にした次の関数です (さらに最大値が1になるよう、値域全体を規格化している)。
これの元々の式は、Paul Nylander のサイト http://www.bugman123.com/index.html に記述があります。
参考までに、連続的な Mandelbrot 集合反復回数関数を視覚化すると、次のようになります。
なお、この関数の代わりに前述の最短距離関数を用いて (関数値が最大になる点を選択して) も良いですが、計算がやや遅くなります。
※4:繰り返す上限回数は、級数項関数
実は、かなり広い値域を指定しても除去できない部分が生じることを、既に試験的な計算で確認しています (この処理法が不完全である理由の一つ)。
三次元グラフを立体視の画像にする
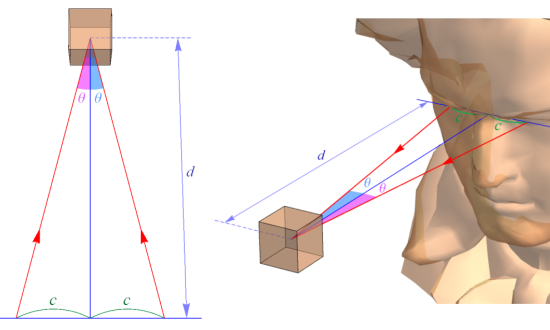
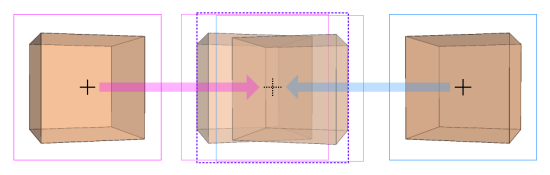
(VR および 3Dプリンターの時代に逆行するような技法が、ここでの話題となります。)人が三次元空間の奥行きや物体の立体感を認識できる理由は、次図のように左右の目で視点が異なること (両眼視差) にあります。次の図では、左右の瞳孔間の距離の半分を
もし、視点が異なる左右の画像を別々に作成し、左画像 (右画像) は左目 (右目) のみで見て、しかも焦点が中央で結ばれるようにできれば、人工的に立体感を再現できることになります。これが (裸眼で再現する) 立体視の原理です。その具体的な方法は、次図のように画像を左右に並べ、それよりも遠い (画面を突き抜けた) 位置で焦点を結ぶように見ると、左右の画像が次第に中央に寄り、ついには重なって一つの焦点を結んだかのようになるというものです。そのとき、描かれた物体に奥行きがあるように見えます。
注意!!
この立体視を長時間または頻繁に行うと、強い眼疲労・眼精疲労を起こす可能性があります。
【コード記述方法の要点】
コードは若干長く複雑なので、ここに全てを掲載することは省略しますが、要点のみを挙げれば次のようになります。
① 通常の (立体視でない) 画像を生成するときの視点が、オプション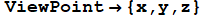 で指定されるならば、左右の画像における視点は
で指定されるならば、左右の画像における視点は
と指定すれば良い。(先に導入した定数のうち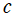 は使用するが、
は使用するが、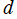 ,
,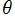 は他の定数で表わせるので不要。また、逆正接関数は
は他の定数で表わせるので不要。また、逆正接関数は![ArcTan[y/x]](siki_math020/stereo00600.png) ではなく、
ではなく、![ArcTan[x,y]](siki_math020/stereo00700.png) で記述する。後者の詳細は ArcTan を参照。)
で記述する。後者の詳細は ArcTan を参照。)
② DensityPlot 等で作成する模様を背景に置きたい場合は、 DensityPlot 等のオプション Epilog で Inset を指定値とし、その Inset の第1引数に Plot3D 等を記述する。その際、左画像 (右画像) では背景模様を左側 (右側) に若干ずらすと、物体が背景模様からも浮いているように見える。(ただし、Inset は Ver.6 以降の Mathematica で使用可能。)
③ 二つの画像を左右に (垂直位置を揃えて) 並べるため GraphicsRow を使用する。ただし、Ver.5 以前では GraphicsRow が使えないので、その場合は PNG 画像等に出力後、ペイントソフト等を用いて加工する。
なお、下記にある立体視画像のコードは、次の Mathematica-Notebookファイルに収録しています。と指定すれば良い。(先に導入した定数のうち
② DensityPlot 等で作成する模様を背景に置きたい場合は、 DensityPlot 等のオプション Epilog で Inset を指定値とし、その Inset の第1引数に Plot3D 等を記述する。その際、左画像 (右画像) では背景模様を左側 (右側) に若干ずらすと、物体が背景模様からも浮いているように見える。(ただし、Inset は Ver.6 以降の Mathematica で使用可能。)
③ 二つの画像を左右に (垂直位置を揃えて) 並べるため GraphicsRow を使用する。ただし、Ver.5 以前では GraphicsRow が使えないので、その場合は PNG 画像等に出力後、ペイントソフト等を用いて加工する。
(File Size:zip形式で圧縮時 22KB,展開後 154KB)
【立体視画像の作成例】
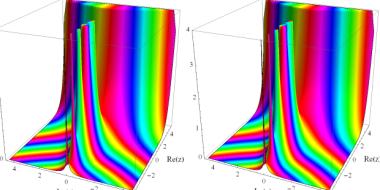
人によって視力等が異なるので一概には言えませんが、クリック後に開く画像は、画面から約60~80cm離れて見ると立体視しやすいように、大きさを加工・調節しています。
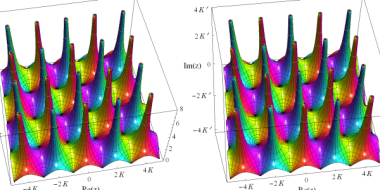
ガンマ関数 (等高線なし)
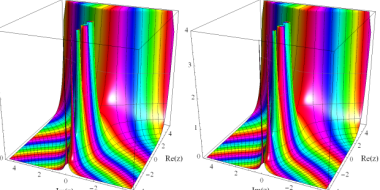
ガンマ関数 (等高線あり)
Jacobi の楕円関数
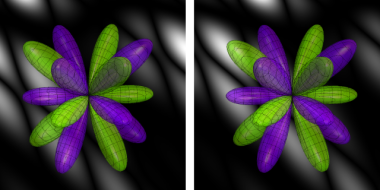
球面調和関数の虚部
球面調和関数の虚部 (アニメーション:1.95MB)
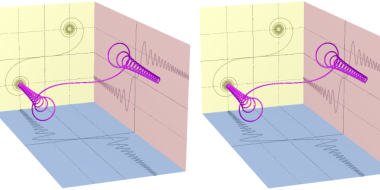
空間クロソイド曲線の射影
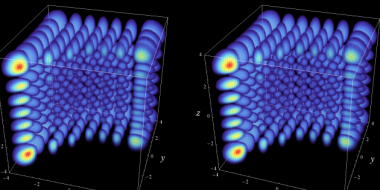
三次元の量子力学的調和振動子
Riemann ゼータ関数とその非自明零点
【 Petite Galerie 】
Mathematicaのグラフィックス要素でネオンサインを作る
(以前、福岡県宗像市に実在したネオンサインの再現。)
(以前、福岡県宗像市に実在したネオンサインの再現。)