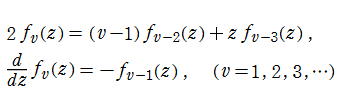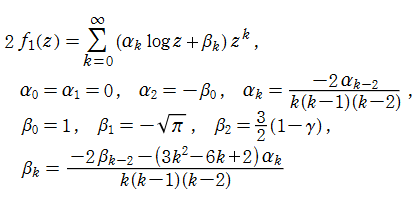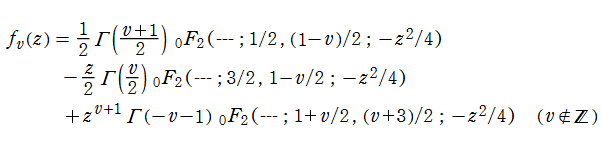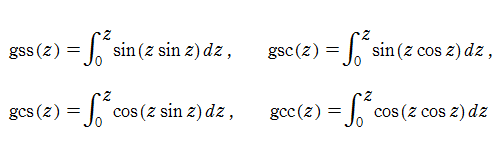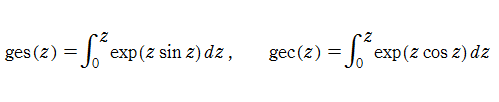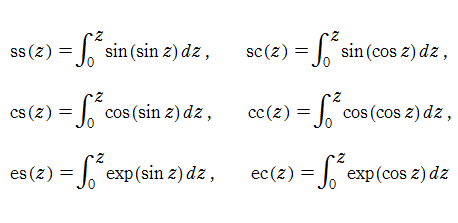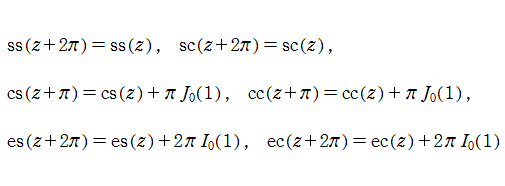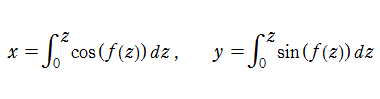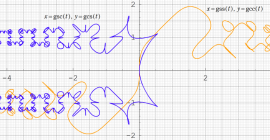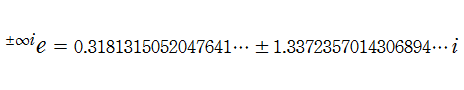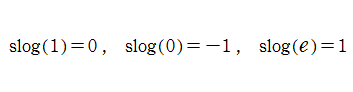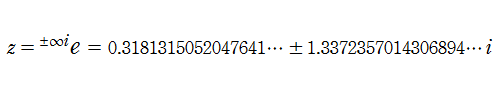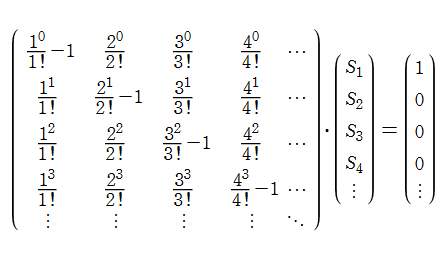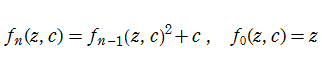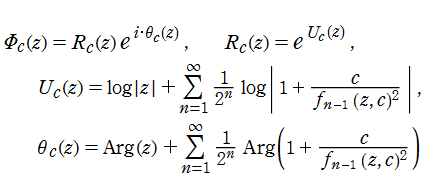特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
その他の特殊関数
Sievert 積分関数
Sievert 積分関数は、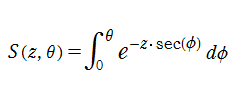
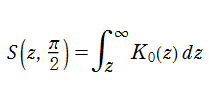
のように級数展開される。しかし、Sievert 積分関数は知られている公式が少なく、特に複素変数での計算が難しい。
この関数は、M. Abramowitz & I. A. Stegun 著 「Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables」 の p.1000に記述がある。関数名は、放射線物理学者の R. M. Sievert に由来するが、応用的にも、均一な媒質を通る放射線の減衰に関する問題で現れる。例えば、最大放射角度を
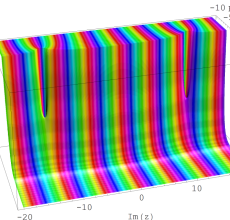
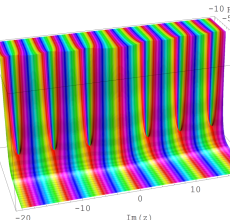
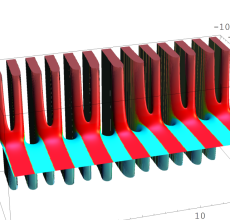
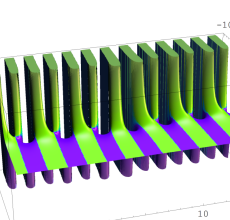
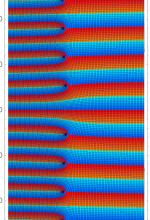
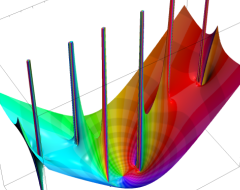
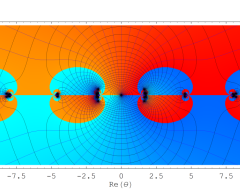
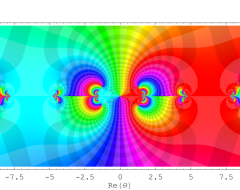
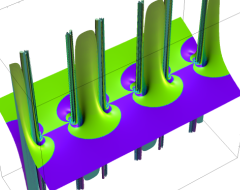
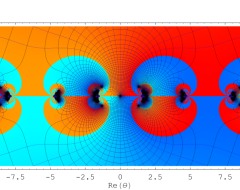
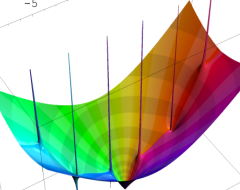
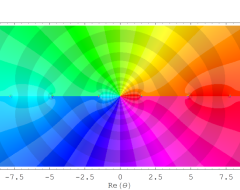
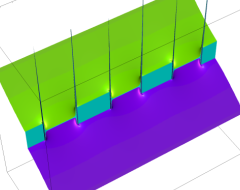
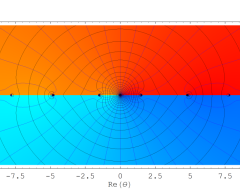
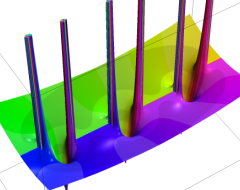
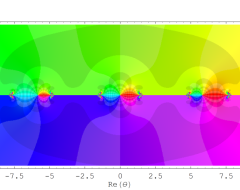
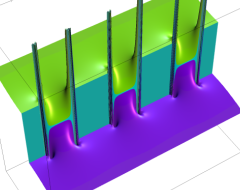
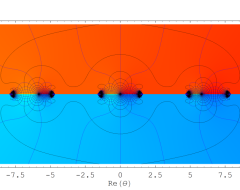
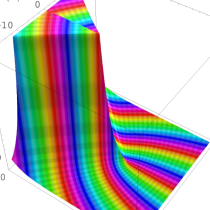
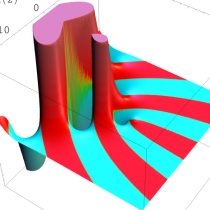
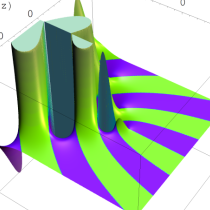
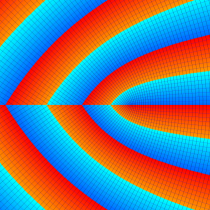
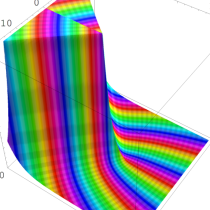
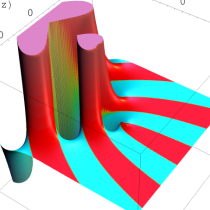
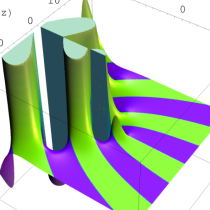
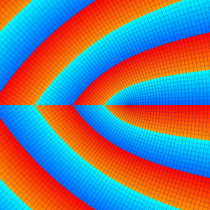
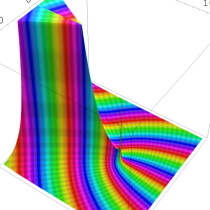
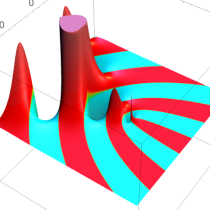
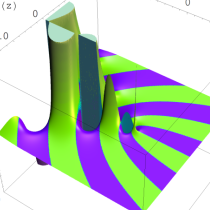
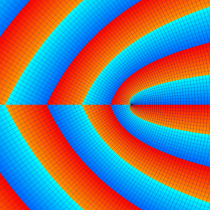
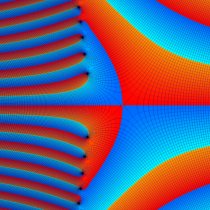
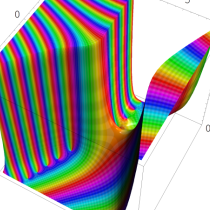
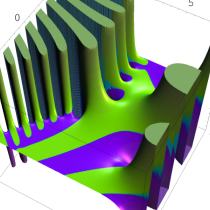
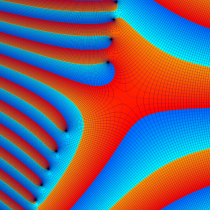
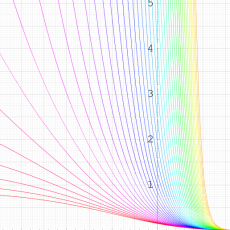
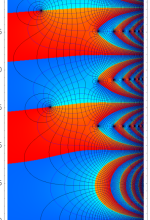
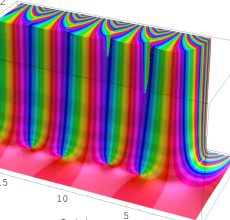
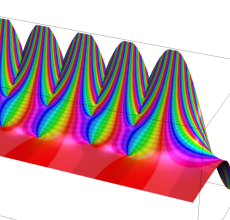
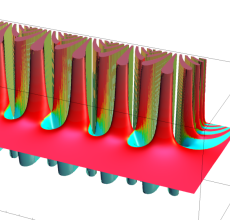
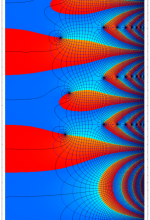
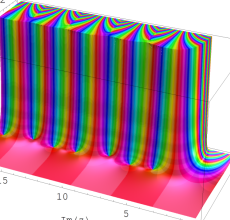
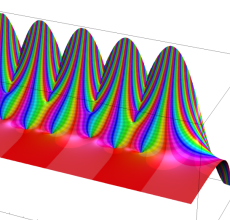
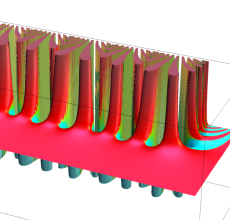
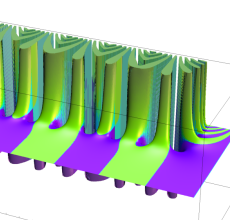
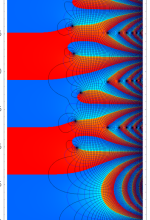
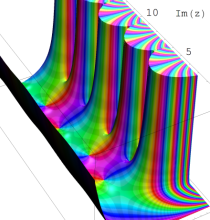
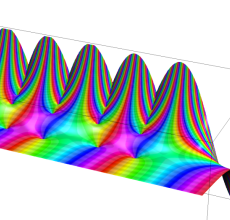
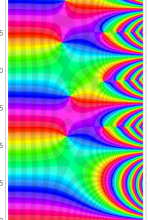
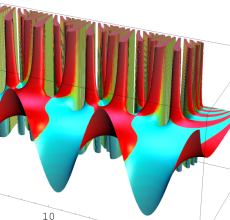
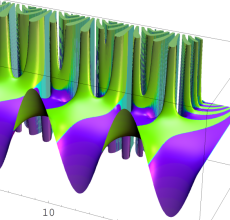
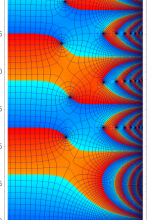
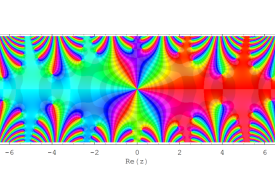
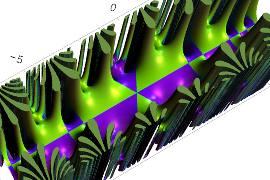
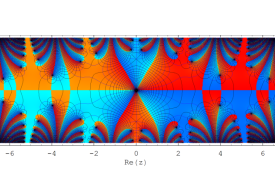
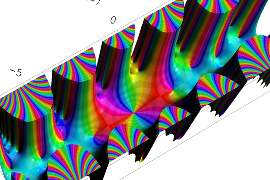
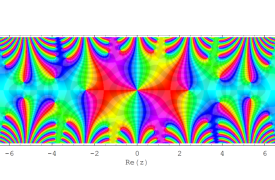
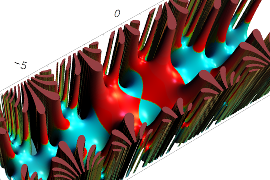
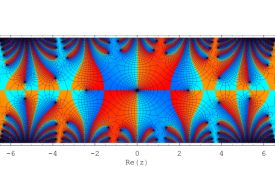
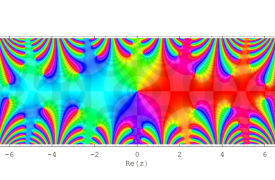
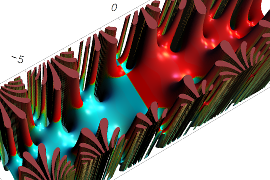
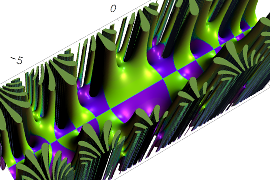
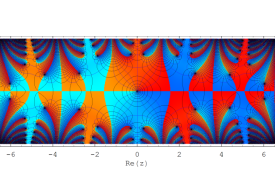
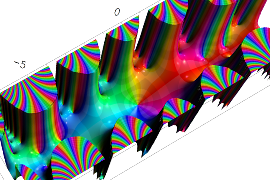
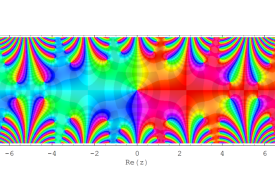
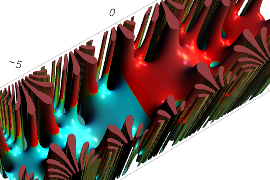
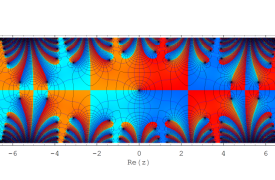
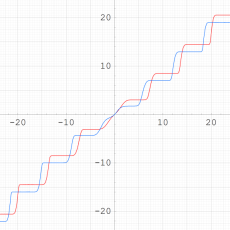
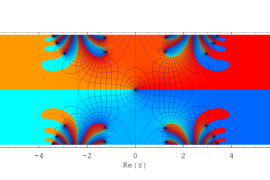
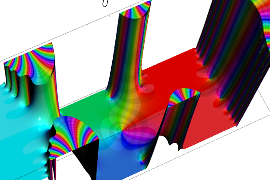
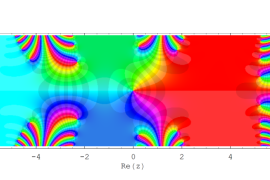
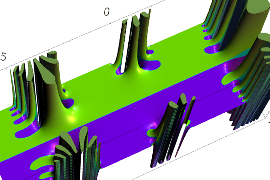
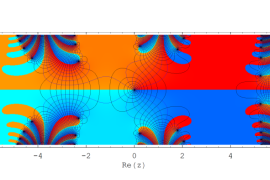
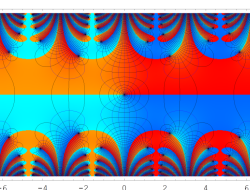
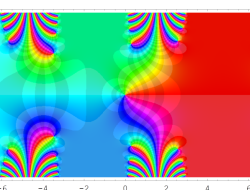
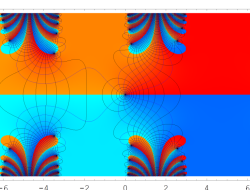
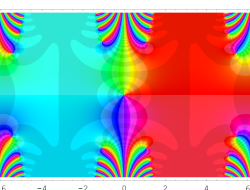
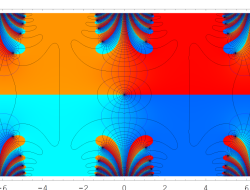
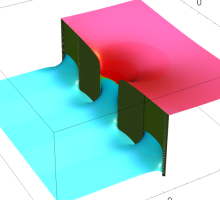
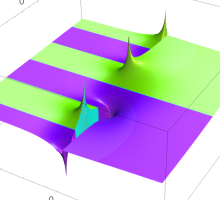
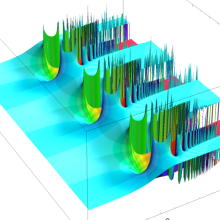
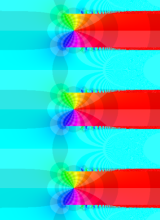
複素変数の Sievert 積分関数
複素変数の Sievert 積分関数
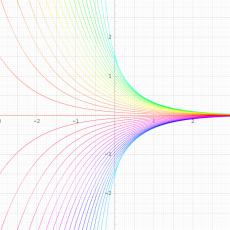
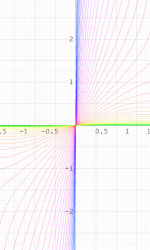
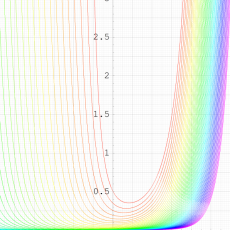
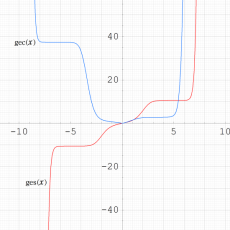
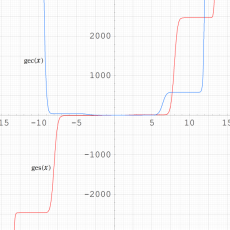
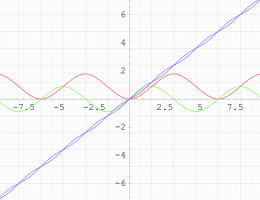
実変数
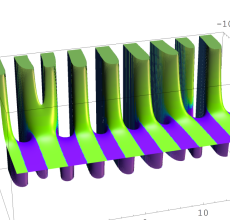
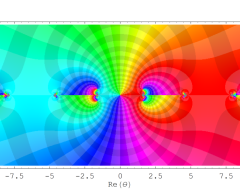
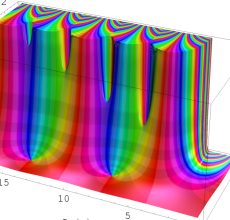
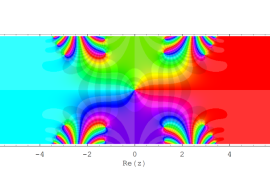
複素変数の Sievert 積分関数
複素変数の Sievert 積分関数
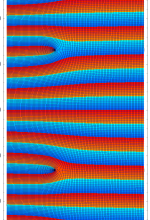
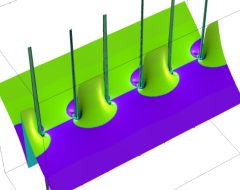
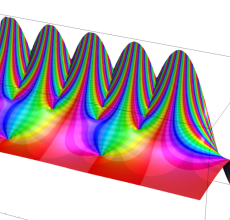
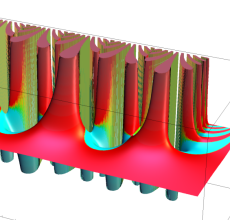
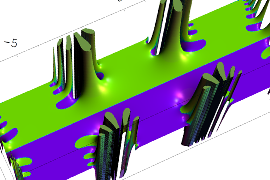
複素変数の Sievert 積分関数
複素変数の Sievert 積分関数
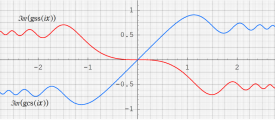
Abramowitz 積分関数
Abramowitz 積分関数は、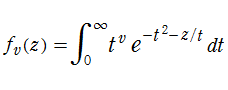
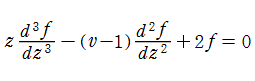
も満たす。(
によって定義される。ここに、
複素変数の Abramowitz 積分関数は、複素平面上
この関数は、1953年に M. Abramowitz が詳細な研究を行い、その結果が Abramowitz & Stegun 著 「Handbook of Mathematical Functions with Formulas, …」 の p.1001に掲載されている。ただし、具体的な関数名は示していない (W. J. Thompson 著 「Atlas for Computing Mathematical Functions (John Wiley & Sons, Inc. 1997)」 では " Abramowitz function " と称している)。
Abramowitz 積分関数は、原子核物理学における熱中性子の吸収、放射電磁波のスペクトルに関する問題等で現れる。
Abramowitz 積分関数は、変数に指数関数を代入した「Abramowitz 積分指数関数」
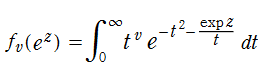
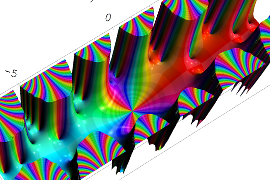
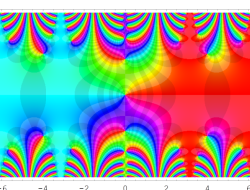
複素変数の Abramowitz 積分関数
複素変数の Abramowitz 積分関数
複素変数の Abramowitz 積分関数
複素変数の Abramowitz 積分関数
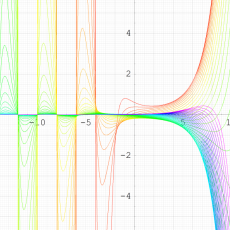
実変数
複素変数の Abramowitz 積分関数
複素変数の Abramowitz 積分関数
複素変数の Abramowitz 積分関数
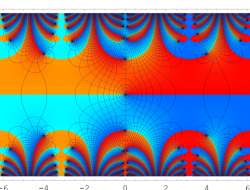
複素変数の Abramowitz 積分指数関数
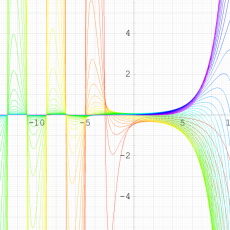
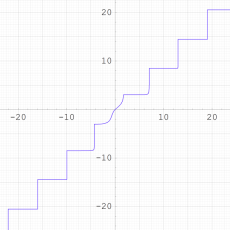
2番目は、1番目のグラフの垂直軸を常用対数目盛化した場合(以下同様)。
複素変数の Abramowitz 積分指数関数
複素変数の Abramowitz 積分指数関数
複素変数の Abramowitz 積分指数関数
Glasser 積分関数
ここでの Glasser 積分関数とは、一群の積分のことであるが、本来の Glasser 積分関数は、このうちの
また、これらの関数の派生として
さらに Glasser 積分関数に類似の、より簡単な積分
も定義する。
明らかに、周期性と擬周期性
を持っている。ここに
以上すべての Glasser 積分関数は超越整関数のため、無限遠点のほかには特異点を持たない。
なお、いくつかの Glasser 積分関数の組として、
の形になっているものを選べる。これは「平面曲線に関する自然方程式」の一例であって、この媒介変数表示で表わされる曲線は、
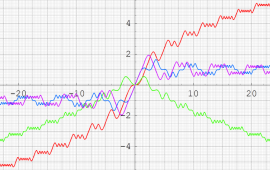
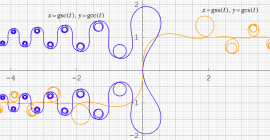
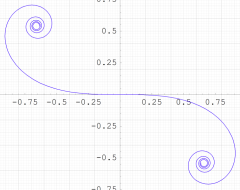
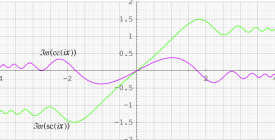
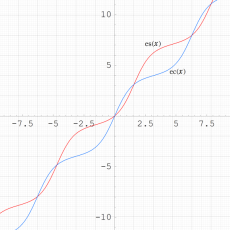
実変数の Glasser 積分関数による媒介変数表示のグラフ(自然方程式による曲線の例)。
①:
②:
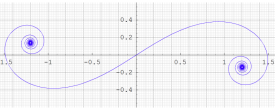
虚変数において、Fresnel 関数のような曲線となる
前の虚変数関数の組からなる媒介変数表示
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
次は、前のグラフの値が急増するため、逆双曲線正弦関数で縮めた関数
前の関数の組からなる媒介変数表示
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
虚変数の Glasser 積分関数
前の虚変数関数の組からなる媒介変数表示
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
複素変数の Glasser 積分関数
超指数関数
日:超指数関数,スーパー指数関数英:Super exponential function,仏:Fonction super exponentielle
日:テトレーション,英:Tetration,仏:Tétration,独:Potenzturm
「第1の演算」である「和」を繰り返した演算として「第2の演算」である「積」、積を繰り返した演算として「第3の演算」である「累乗」が生じる。累乗を繰り返して入れ子構造にしたものは、「第4の演算」という意味で「テトレーション」と呼ばれる。例えば
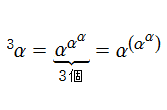
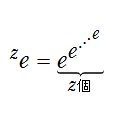
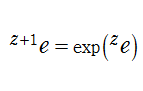
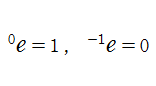
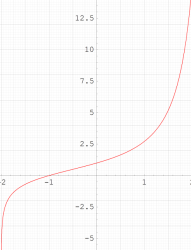
超指数関数は、複素平面上の区間
に近づく。この値は超越方程式
【註記】
※1:その方法はいくつか知られており、今後の研究によって新しい計算法が追加される可能性もある。当サイトの Mathematica コードでは、単に Newton 法を用いて後述の超対数関数の逆関数を直接求め、さらに、漸近近似式や上記の関数等式を用いて定義域を拡張している。
※1:その方法はいくつか知られており、今後の研究によって新しい計算法が追加される可能性もある。当サイトの Mathematica コードでは、単に Newton 法を用いて後述の超対数関数の逆関数を直接求め、さらに、漸近近似式や上記の関数等式を用いて定義域を拡張している。
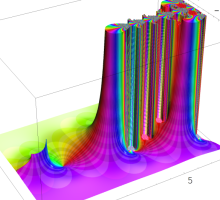
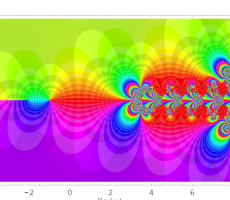
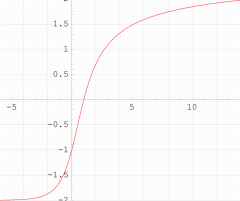
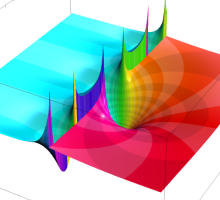
複素変数の超指数関数のグラフ。ただし
超対数関数
日:超対数関数,スーパー対数関数英:Super logarithm,仏:Super logarithme
超指数関数の逆関数
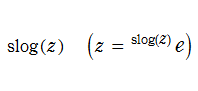
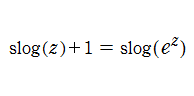
が分かる。このほか、
超対数関数は通常、複素平面上の2点
を特異点とし、
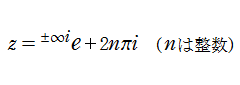
超対数関数の計算法はいくつか知られているが、現在も研究が進められており、未だ整理されていない感がある。当サイトがプログラミングで採用した一つの方法は Andrew Robbins によるもので※1、冪級数展開式
を用いる。ここに、係数
なる線形代数方程式を解いて得られる。
【註記】
※1 : Andrew Robbins「Solving for the analytic piecewise extension of Tetration and the Super-logarithm」(2005年)。なお、この論文はインターネット上のみで公開されている。論文中にも Mathematica のコードがあり、当サイトのコードは複素変数でも計算できるようにこれを書き換えたものである。
※1 : Andrew Robbins「Solving for the analytic piecewise extension of Tetration and the Super-logarithm」(2005年)。なお、この論文はインターネット上のみで公開されている。論文中にも Mathematica のコードがあり、当サイトのコードは複素変数でも計算できるようにこれを書き換えたものである。
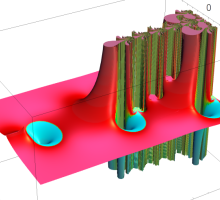
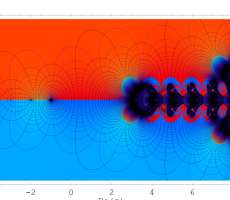
複素変数の超対数関数のグラフ。
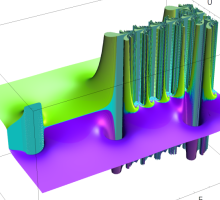
複素変数の超対数関数(周期関数型)のグラフ。
Böttcher 関数
日:Böttcher関数,ベトヒャー関数英:Böttcher function,仏:Fonction de Böttcher,独:Böttcher-funktion
の極限
もし、Julia 集合が単連結集合(孤立した部分を持たない集合)である場合、すなわち
が存在する。これを、Julia 集合の Böttcher 関数という。1905年に L. E. Böttcher が得た定理に基づいて、Böttcher 方程式と呼ばれる関数等式を満たす一般の Böttcher 関数(写像)の存在が保証されるが、Julia 集合の Böttcher 関数は、これの特別な例にあたる。
先の等角写像から、Julia 集合の Böttcher 関数は
具体的に、Julia 集合の Böttcher 関数は、
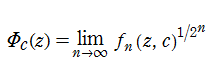
は収束が速いので、Julia 集合の Böttcher 関数の数値計算に使用できる。それでも、
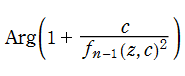
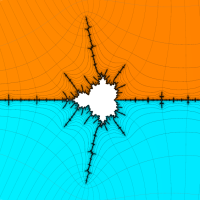
Mandelbrot 集合の Böttcher 関数
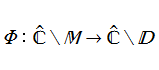
Mandelbrot 集合は、集合全体の縮小複製(しかし、それらは微妙に形が歪んでいて相似ではない)を境界の周辺に無数に持っており、あたかも「島」があるような非連結集合に見える。しかし実際は、樹状に延びる細い領域を介して「島」はすべて本体と繋がっており、単連結集合の一部分を成す。1982年に A. Douady と J. H. Hubbard は、
また、Mandelbrot 集合の面積は、Mandelbrot 集合の Böttcher 関数の逆関数を Laurent 級数展開したときの係数を用いた無限級数で表わすことができる(詳しくは、http://mathworld.wolfram.com/MandelbrotSet.html 等を参照。ただし、この級数は収束が非常に遅い)。
Böttcher 関数は等角写像の特殊な例であり、解析的に定義された関数であるものの、複素反復力学系やフラクタル幾何学を起源とし、前述のように専らこれらの分野で応用されることから、通常は特殊関数の一種として扱うことは少ない。
Julia 集合自体は、P. J. L. Fatou, G. M. Julia 等による複素数の反復軌道に関する研究が発端となっているが、これをパラメータ
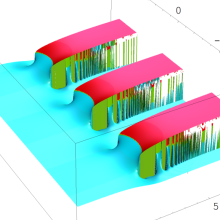
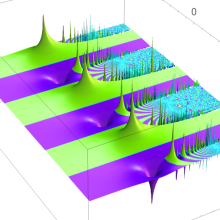
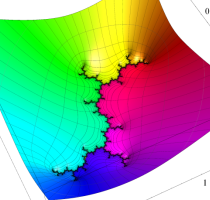
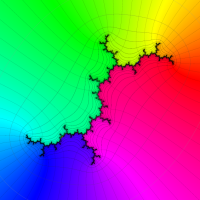
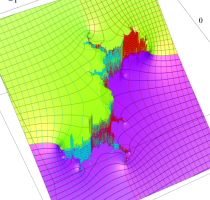
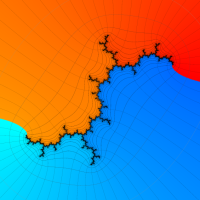
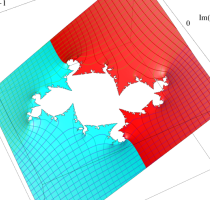
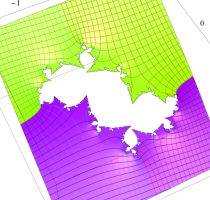
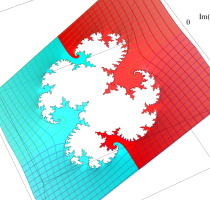
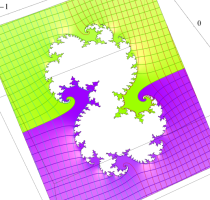
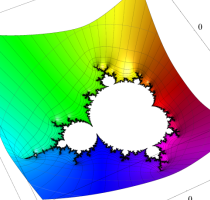
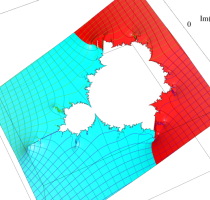
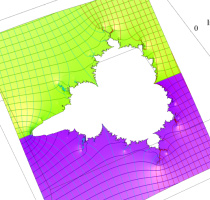
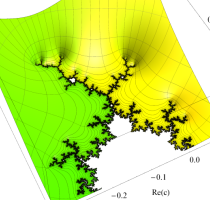
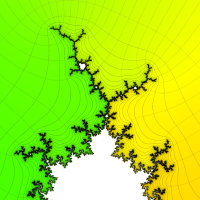
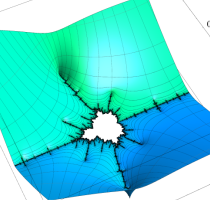
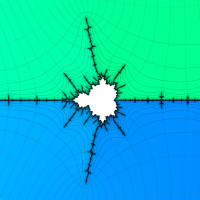
複素変数の(Julia 集合) Böttcher 関数
複素変数の(Julia 集合) Böttcher 関数
複素変数の(Julia 集合) Böttcher 関数
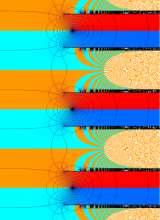
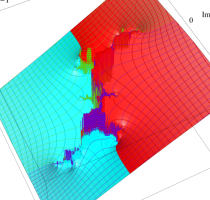
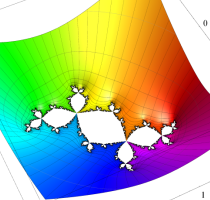
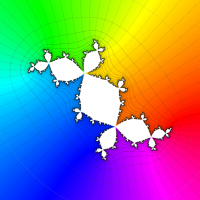
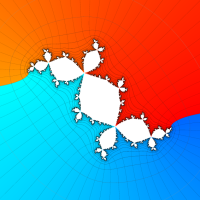
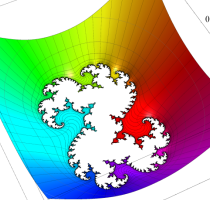
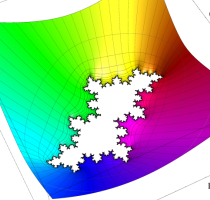
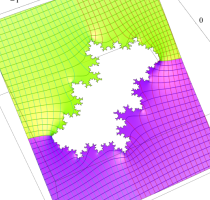
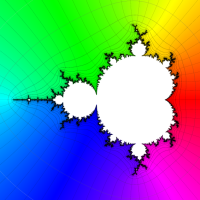
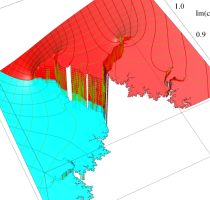
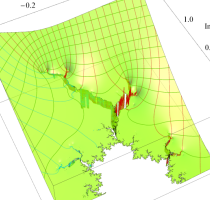
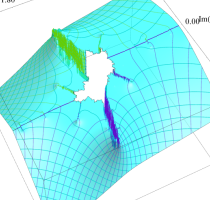
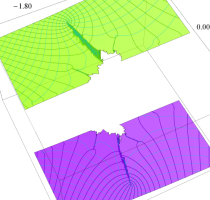
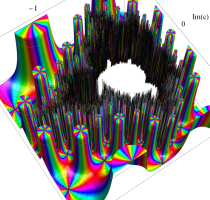
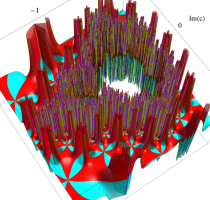
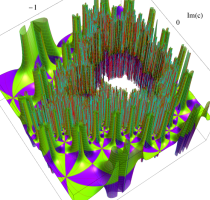
複素変数の(Mandelbrot 集合) Böttcher 関数
複素変数の(Mandelbrot 集合) Böttcher 関数