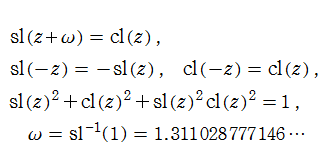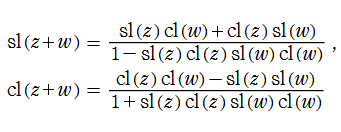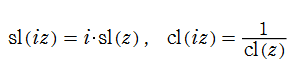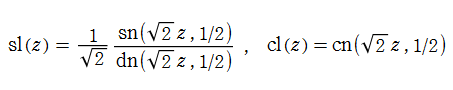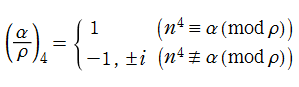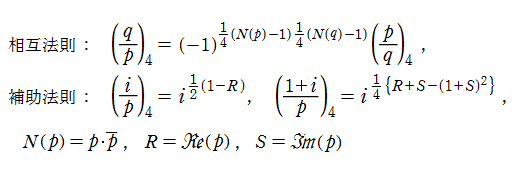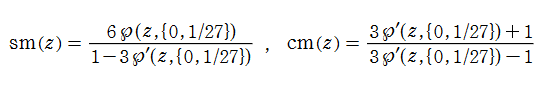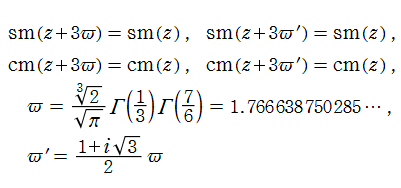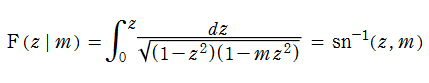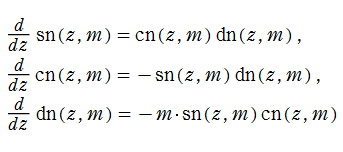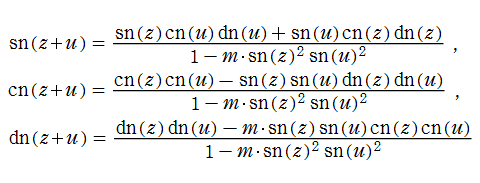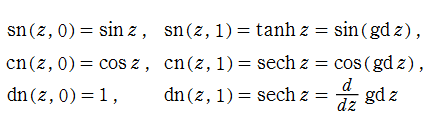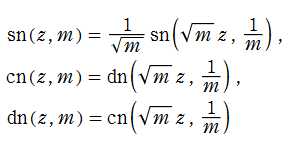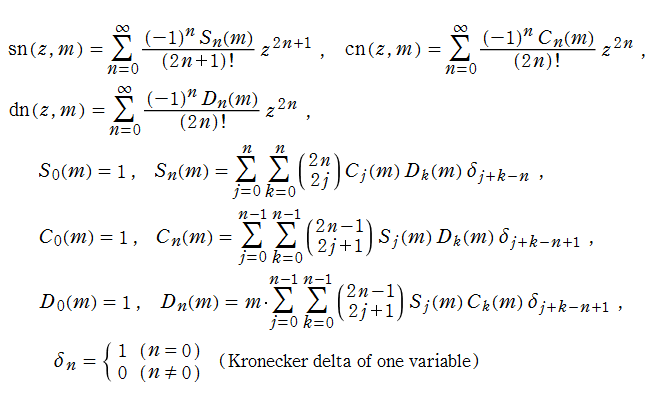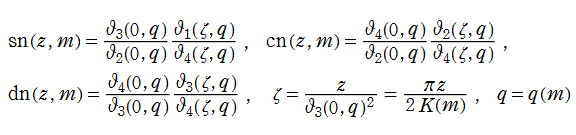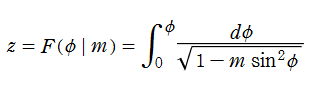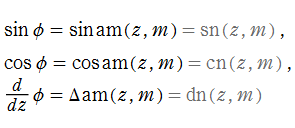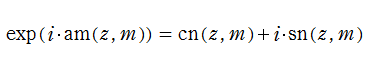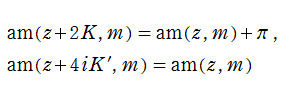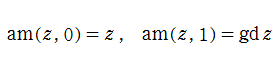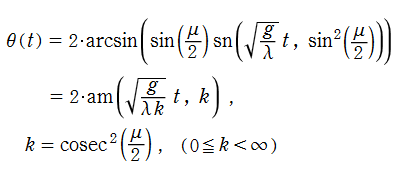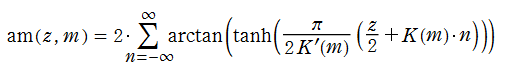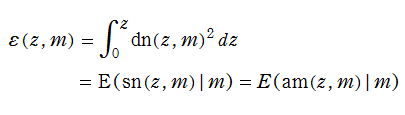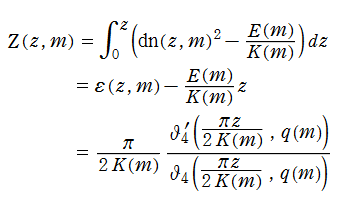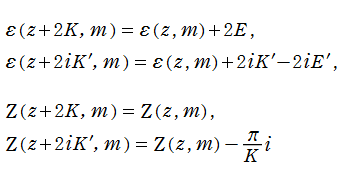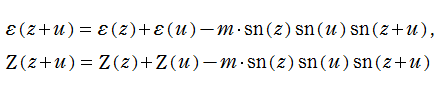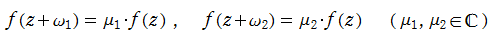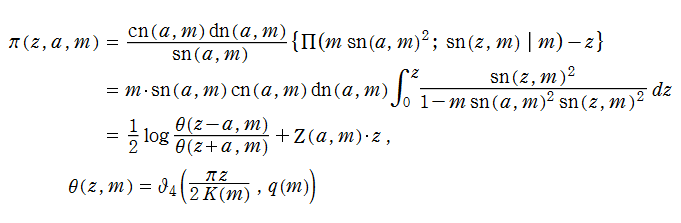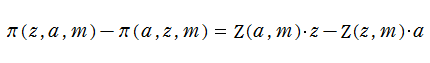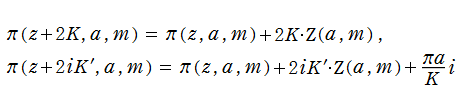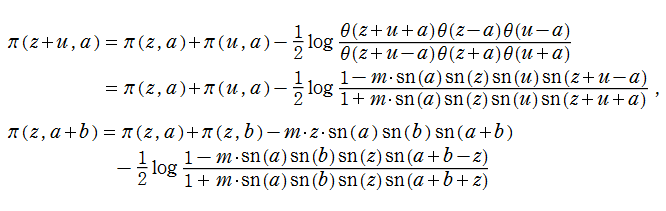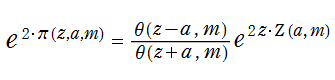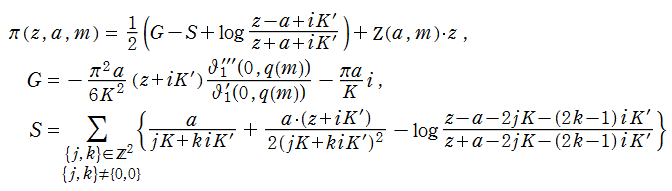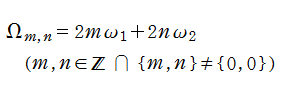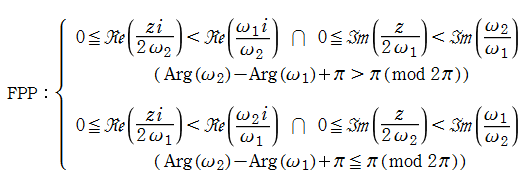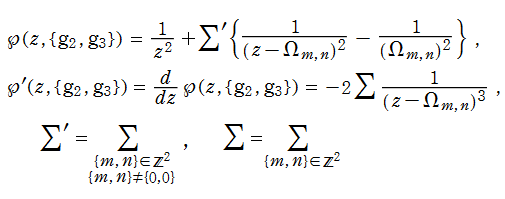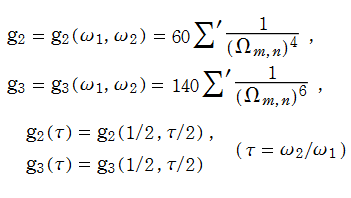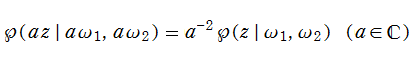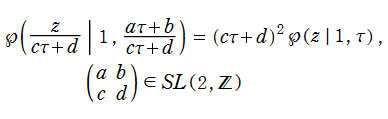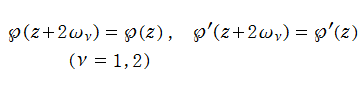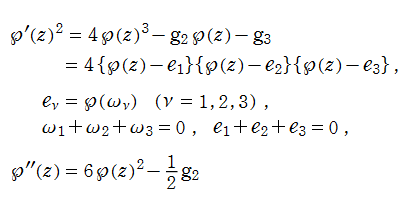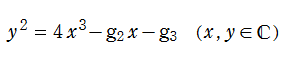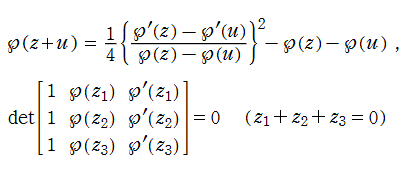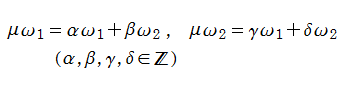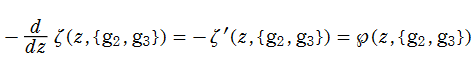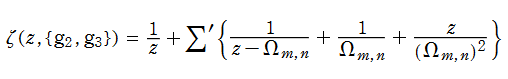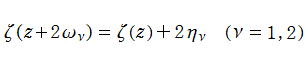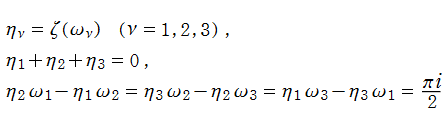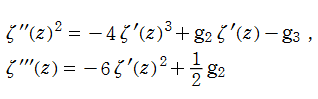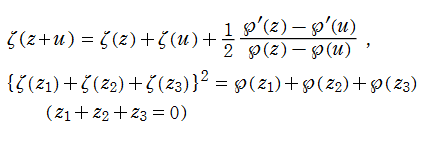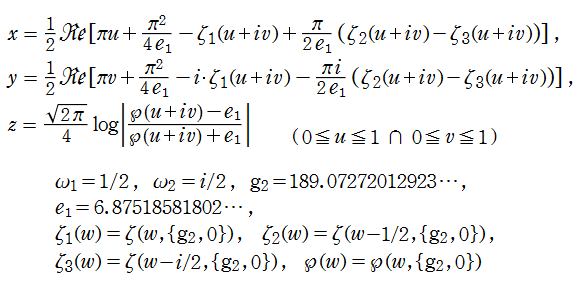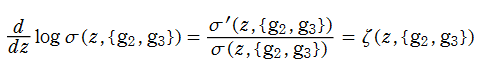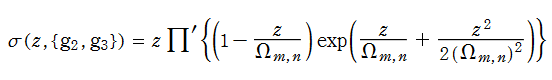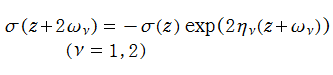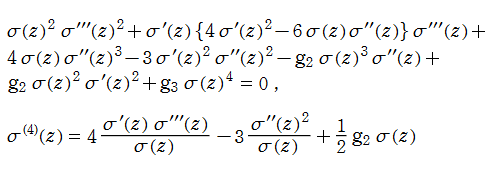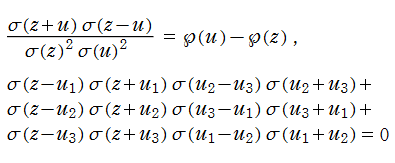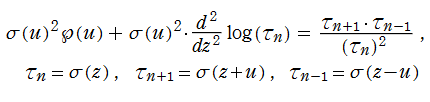特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
楕円関数
Gauss の楕円関数
日:Gaussの楕円関数,レムニスケート関数英:Gauss's elliptic function,仏:Fonction elliptique de Gauss,独:Lemniskatische funktion
【始めに:楕円関数の概要】
現在では、楕円関数の定義が 「複素平面上の二重周期有理型関数」 という簡潔な言葉で与えられる。ここに二重周期とは、二つの線形独立な基本周期を持ち、その比が実数にならない (つまり、周期が作る平行四辺形が潰れていない) ことを言う。また、その平行四辺形に含まれる極の位数の和は、2位を最小とする。これらの特徴にしたがって、楕円関数の具体的な表示式も直接与えられる。後述する Weierstrass の楕円関数がそのような例である。以上の理論は、専ら19世紀に整備された。
しかしながら、歴史的には別の方向 ― 第1種楕円積分の逆関数 ― から (2位の) 楕円関数が発見された。先行する楕円積分の発展史をも含めれば、楕円関数の萌芽自体は17世紀末から存在したと言える。実際、楕円関数が満たす代数的加法公式は、まず楕円積分の超越的加法公式として (逆楕円関数の形で) 求められていた。ただし、楕円積分の多価性から楕円関数の二重周期性を説明する Riemann 面や楕円曲線等の理論は、19世紀以降に属する。
楕円積分が元々は物理学等に起源を持ち、その応用範囲が広いことから、楕円関数も同様に有用である。しかし、楕円関数が一層重要な理由は、その高い対称性 ― それは単周期関数である三角関数よりも高い ― にある。それら整った形状の基本領域を持つ関数は、必然的に群論と結び付く。楕円関数の対称性は周期平行四辺形に留まらない。何というべき幸運 「楕円関数の基本周期の比も、逆関数にするとモジュラー関数になる事実」 に、我々は恵まれている。複素解析学が19世紀から急速に進展した理由には、楕円関数が人々に神秘的な印象を抱かせる、魅力ある研究題材であった事も原因の一つとして挙げられる。
更なる幸運:楕円関数は比較的階数の低い非線形微分方程式を満たし※1、その解は常に分岐点を持たない。しかも二重周期性を用いて容易に複素平面全体に (極を除いて) 解析接続できる。非線形微分方程式の解としては申し分の無い性質を有する、まさに "特殊な" 関数と言えよう。
19世紀に発祥した数学理論のほとんどがそうであったが、特に楕円関数論は現代数学の源流と呼ぶに相応しく、代数幾何学、代数的整数論などの純粋数学のみならず、格子模型や共形場理論などの数理物理学にも影響を及ぼしている。保型関数論と Abel 関数論を広義の楕円関数論と考えれば、その流域は更に大きくなる。
(以降、この頁では、歴史的経過にある程度沿った順で説明する。すなわち、Gauss → Jacobi → Weierstrass の名を冠した楕円関数の順に進む。)
【Gauss の楕円関数】
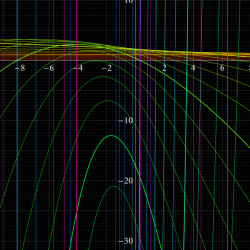
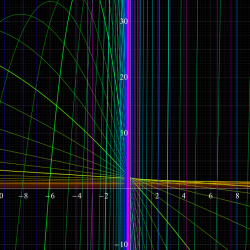
1796年頃に C. F. Gauss が、楕円積分
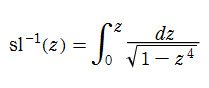
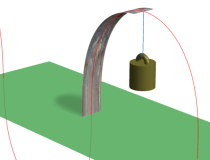
上記の楕円積分自体は、積分計算が伴う種々の具体的な問題中に、17世紀末から現れていた。まず、弾性を持つ物体の一端に偶力が加えられた時に生じる、エラスティカ (Elastica) なる曲線を求める問題があり、これをもっと簡単な代数曲線に関連付けたいという動機から、この楕円積分が現れた※2。一方で、種々の代数曲線の長さを求める問題 (求長問題と呼ばれる) では、楕円や双曲線およびレムニスケート (連珠形) の曲線長が楕円積分で表わされ、それらの相互関係が研究された。後者の結果は、主に G. C. Fagnano によって得られた。
当時から初等関数で表わせないと推測された楕円積分は、これに興味を抱いた L. Euler, Bernoulli 一家, J. L. Lagrange および A. M. Legendre 等によって盛んに研究され、(虚数乗法に繋がる) 変換理論、加法公式、標準形への分類など、やがて楕円関数論でも重要となる事柄に肉薄したが、なぜか "楕円積分の逆関数" には思い至らなかった※3。Gauss は、逆正弦関数の積分表示式
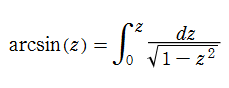
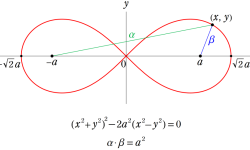
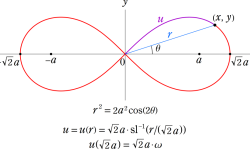
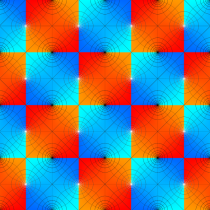
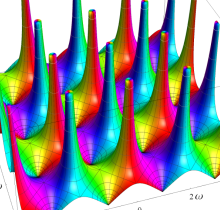
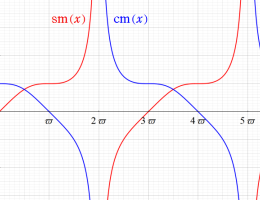
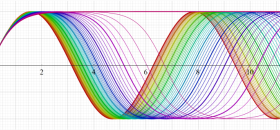
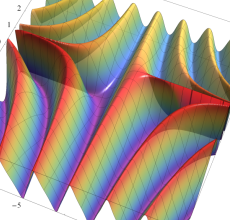
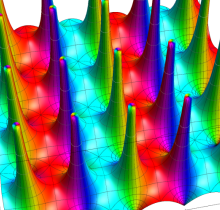
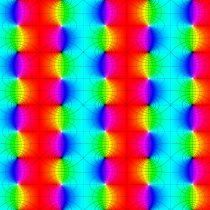
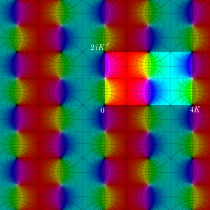
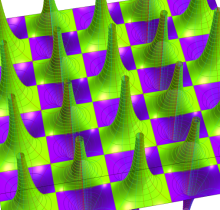
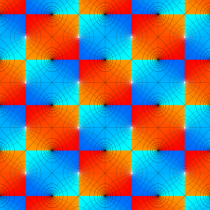
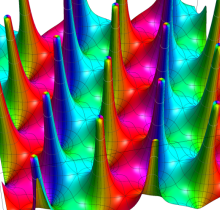
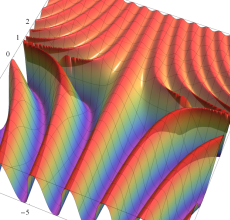
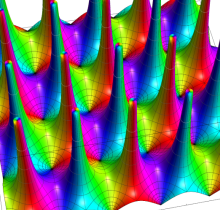
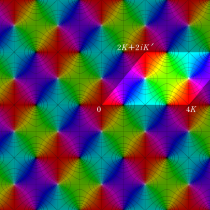
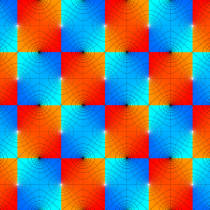
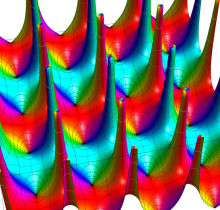
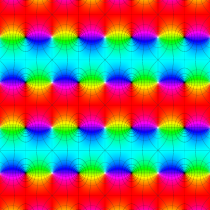
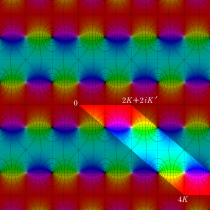
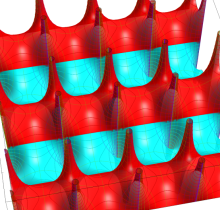
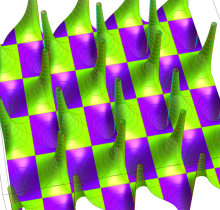
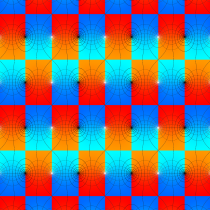
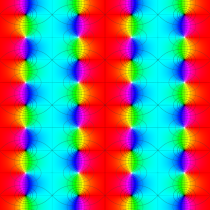
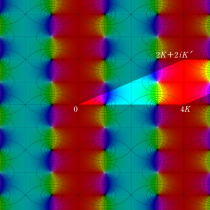
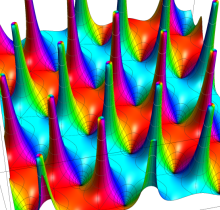
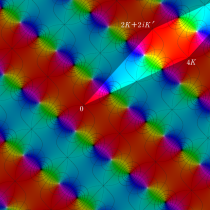
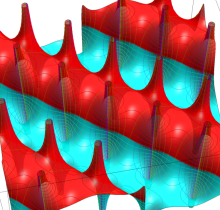
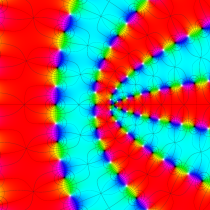
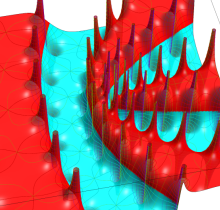
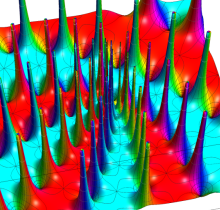
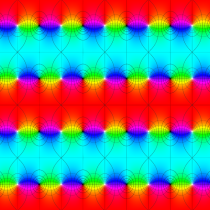
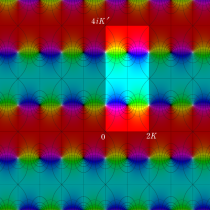
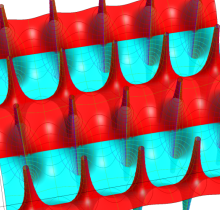
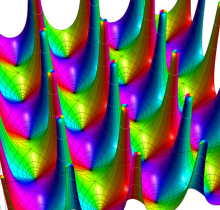
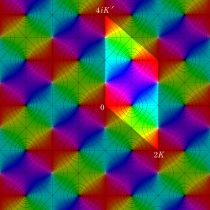
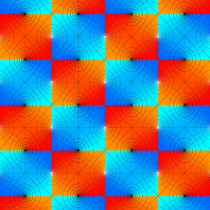
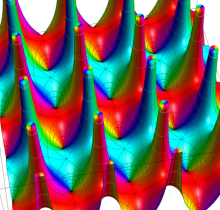
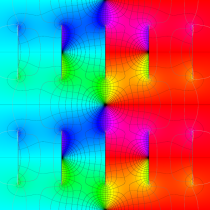
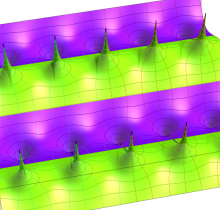
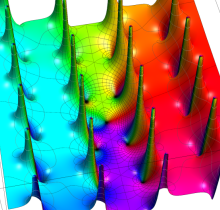
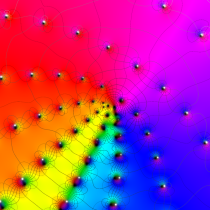
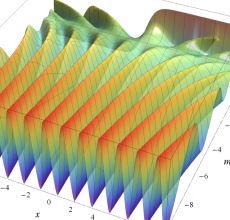
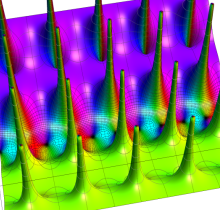
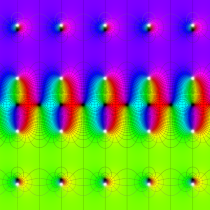
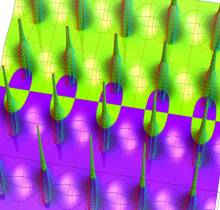
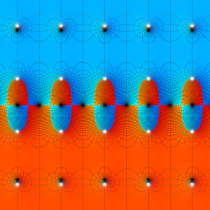
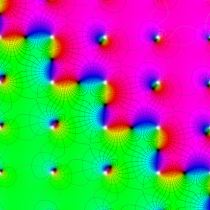
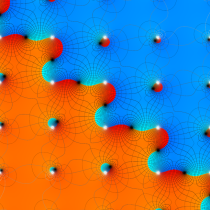
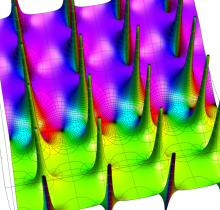
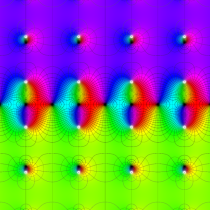
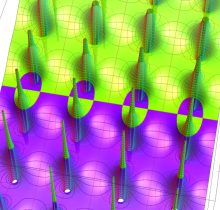
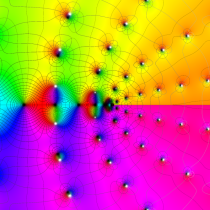
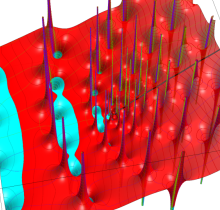
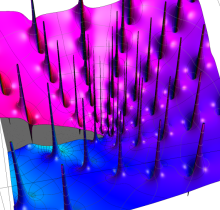
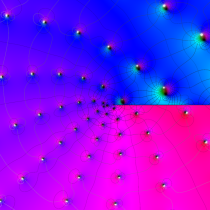
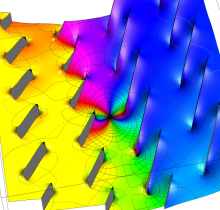
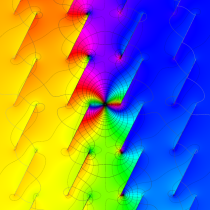
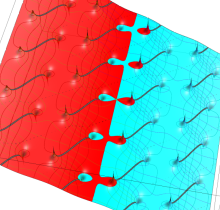
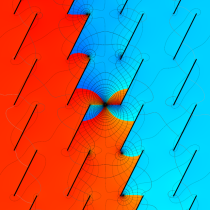
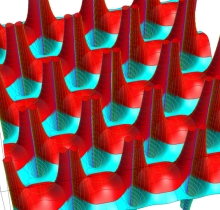
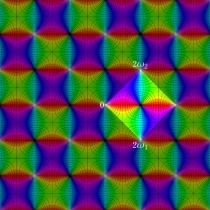
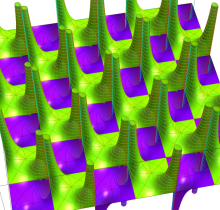
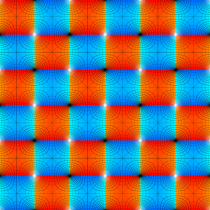
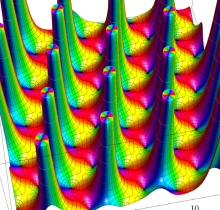
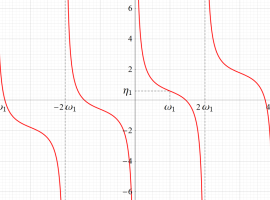
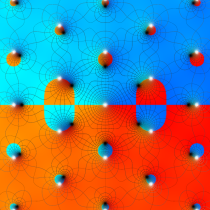
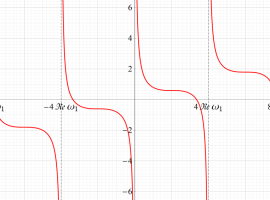
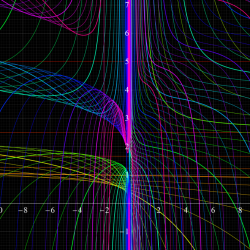
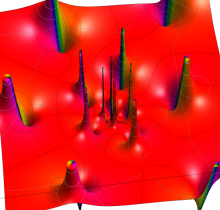
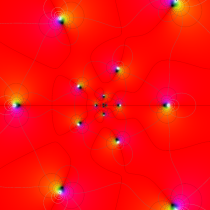
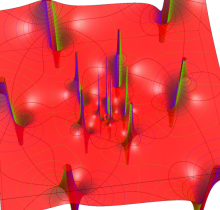
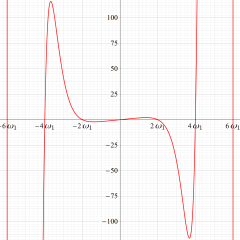
Gauss の楕円関数
の関係を持つように定義される。ただし、Gauss はこれらを楕円関数ではなく 「レムニスケート関数」 と称したので、現在でも
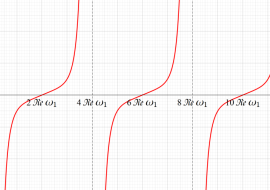
Gauss の楕円関数は、代数的加法公式
を満たす (楕円積分の超越的加法公式としてならば、Euler もこの公式を求めていた)。また併せて、虚数変数のときに
となるので※4、Gauss の楕円関数は二重周期性
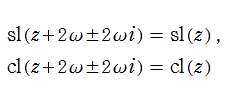
なお、Gauss の楕円関数は、後述する Jacobi の楕円関数の特別な場合として、
と表わせる。
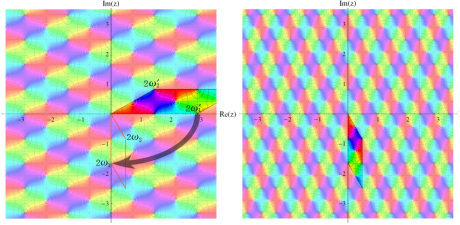
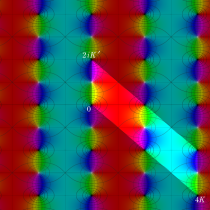
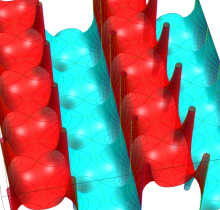
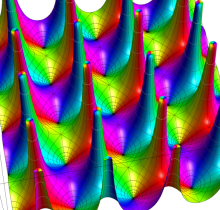
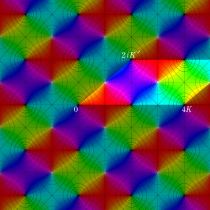
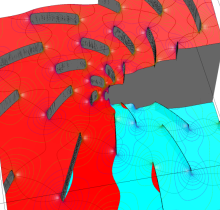
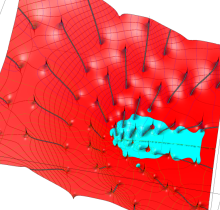
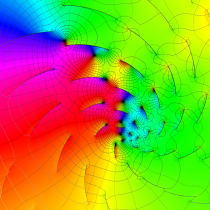
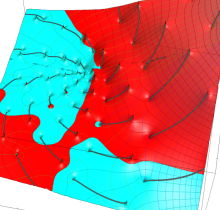
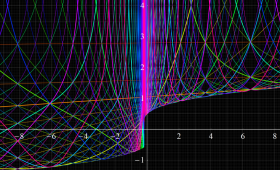
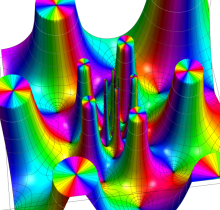
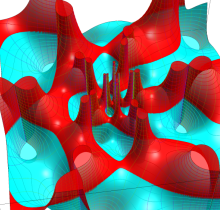
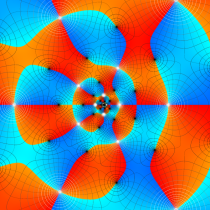
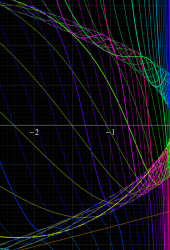
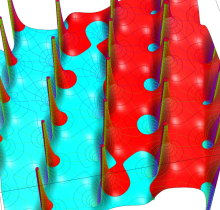
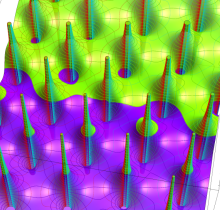
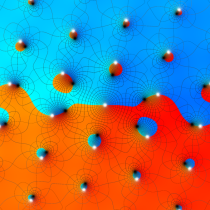
Gauss が楕円関数を複素変数で考察し始めた理由の一つに、レムニスケートの等分問題がある。円の等分問題でも古代ギリシャ時代から大きく飛躍した成果 ―
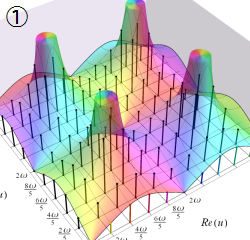
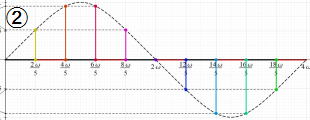
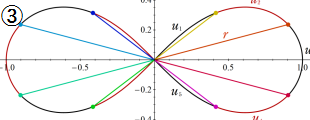
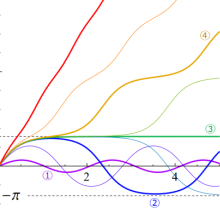
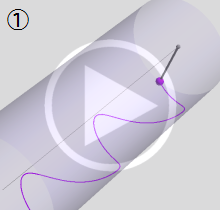
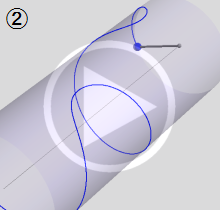
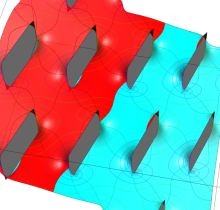
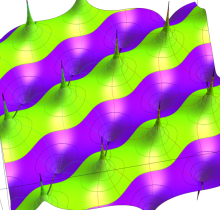
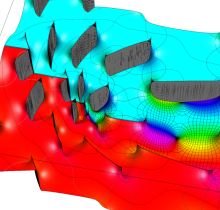
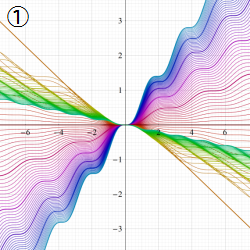
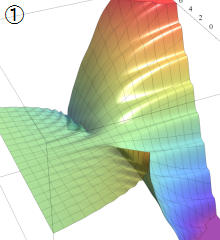
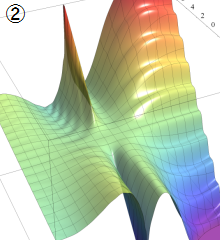
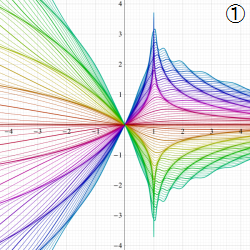
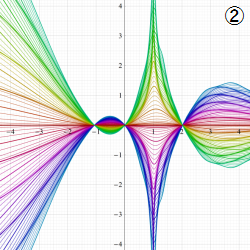
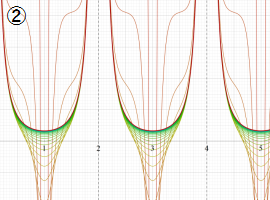
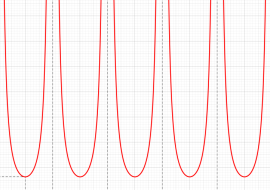
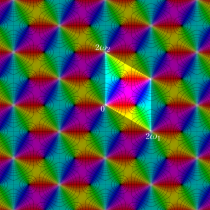
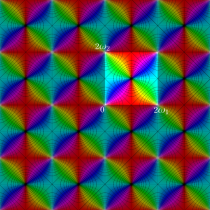
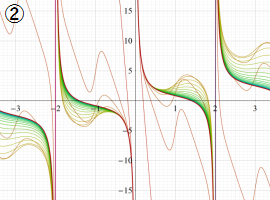
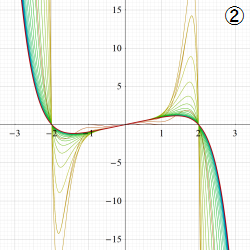
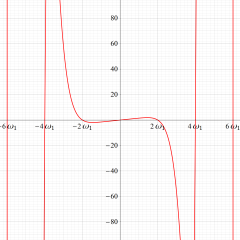
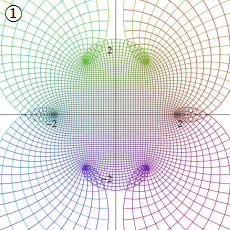
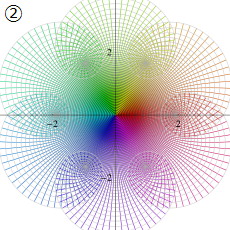
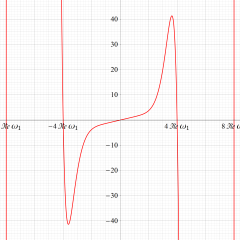
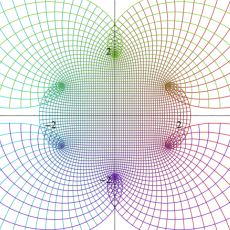
図:レムニスケート (片側) の5等分と Gauss の楕円関数
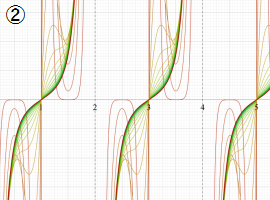
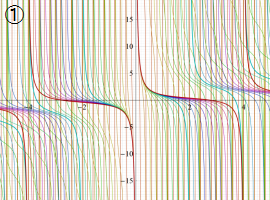
①:レムニスケートの5等分から生じる25次方程式の実数解と複素数解は、格子等分点での Gauss の楕円関数値である。
②:25次方程式の実数解 (2格子分)。5等分の場合は四則演算と平方根のみで表わされる。
③:実際に、レムニスケートの長さを片側について5等分し、②の値との関係を図示する。
①:レムニスケートの5等分から生じる25次方程式の実数解と複素数解は、格子等分点での Gauss の楕円関数値である。
②:25次方程式の実数解 (2格子分)。5等分の場合は四則演算と平方根のみで表わされる。
③:実際に、レムニスケートの長さを片側について5等分し、②の値との関係を図示する。
Gauss は1810年代までに、一般周期の楕円関数、テータ関数、果てはモジュラー・ラムダ関数をも手中にし、約半世紀を先んじていた。しかし、完璧主義者の Gauss はこれらの成果の公表を逡巡し続け、結局すべてが明るみになったのは死後の1860年代であった。
楕円関数の重要な応用先に数論があるが、Gauss の楕円関数で著しいその一例として、4乗剰余 (Biquadratic reciprocity) の相互法則が挙げられる。4乗剰余は平方剰余の拡張であって、4乗剰余記号
で表記される。ここに、
のことを言う。ここに、
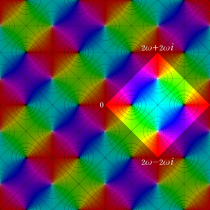
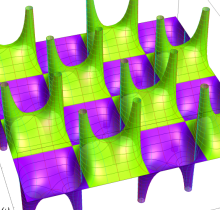
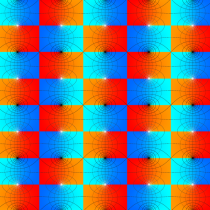
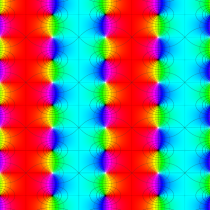
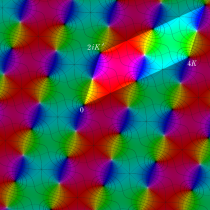
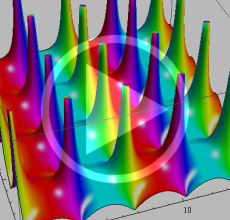
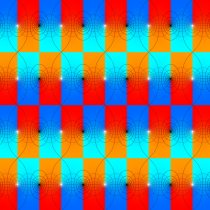
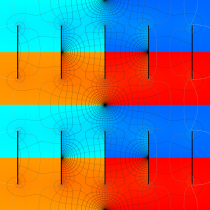
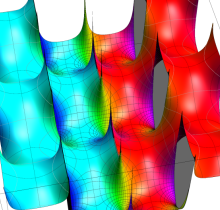
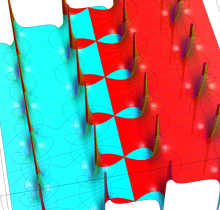
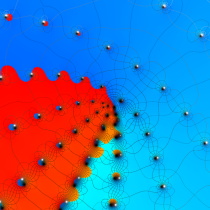
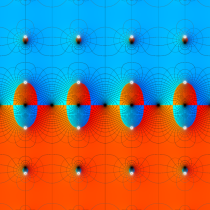
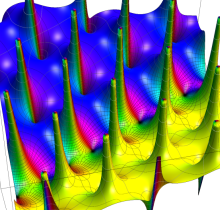
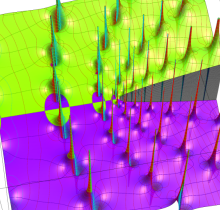
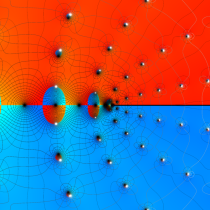
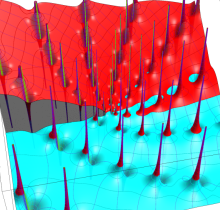
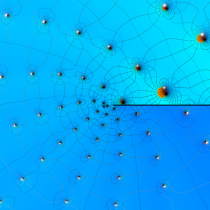
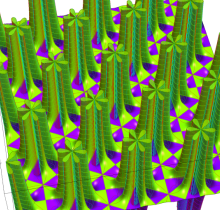
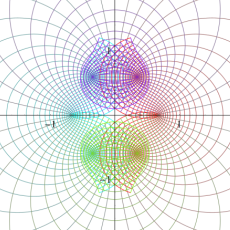
【Dixon の楕円関数】
これは、1890年に A. Dixon が代数曲線
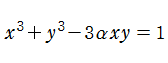
Dixon の楕円関数は、Abel 積分
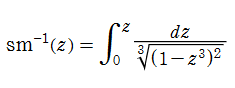
と定義される、位数3の楕円関数である※5。両者は互いに
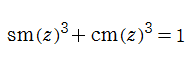
を持つ。
Dixon の楕円関数は、基本領域 (の半分) が正多角形になるという点で、Gauss の楕円関数と類似する。
【註記】
※1:例えば、2階の微分方程式
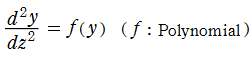
は、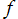 が
が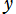 の2次または3次 (定係数) 多項式ならば非線形微分方程式となり、その解は一般に楕円関数になる。一方、1次多項式ならば微分方程式は線形となり、単振動 (正弦・余弦関数) を解として含む。つまり、楕円関数とは単振動に2次または3次の非線形性が加味されたものと言える。それゆえ、楕円関数は自然界等における非線形現象に広く現れる。
の2次または3次 (定係数) 多項式ならば非線形微分方程式となり、その解は一般に楕円関数になる。一方、1次多項式ならば微分方程式は線形となり、単振動 (正弦・余弦関数) を解として含む。つまり、楕円関数とは単振動に2次または3次の非線形性が加味されたものと言える。それゆえ、楕円関数は自然界等における非線形現象に広く現れる。
※2:エラスティカは超越的な (代数的でない) 曲線であるが、第1種楕円積分と第2種楕円積分の差の逆関数で表わせば、幾分か解し易くなるというのが、その動機であった (下図を参照)。
※3:ただし、Euler はこの楕円積分が値域の上下方向に周期的になっていることに気付いており、Legendre は楕円積分を複素変数で考察する必要性を常々強調していた。しかし非常に惜しい事に、両者ともその持論を推し進めることは無かったのである (まだ複素解析学が未整備で、複素数自体も広く受け入れられていなかった事にも原因があった)。
※4:公式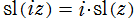 は後述する虚数乗法論の特別な例である。すなわち、「
は後述する虚数乗法論の特別な例である。すなわち、「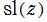 は
は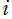 による虚数乗法を持つ」 と解釈される。
による虚数乗法を持つ」 と解釈される。
※5:Abel 積分が楕円関数の逆関数に還元できる場合を調べる 「Abel 積分の還元問題」 も、19世紀以来盛んに研究された。なお、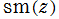 は3位の楕円関数なので、その逆関数は楕円積分にならない。
は3位の楕円関数なので、その逆関数は楕円積分にならない。
※1:例えば、2階の微分方程式
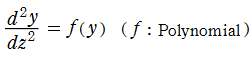
※2:エラスティカは超越的な (代数的でない) 曲線であるが、第1種楕円積分と第2種楕円積分の差の逆関数で表わせば、幾分か解し易くなるというのが、その動機であった (下図を参照)。
※3:ただし、Euler はこの楕円積分が値域の上下方向に周期的になっていることに気付いており、Legendre は楕円積分を複素変数で考察する必要性を常々強調していた。しかし非常に惜しい事に、両者ともその持論を推し進めることは無かったのである (まだ複素解析学が未整備で、複素数自体も広く受け入れられていなかった事にも原因があった)。
※4:公式
※5:Abel 積分が楕円関数の逆関数に還元できる場合を調べる 「Abel 積分の還元問題」 も、19世紀以来盛んに研究された。なお、
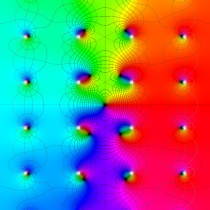
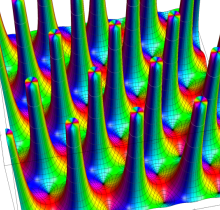
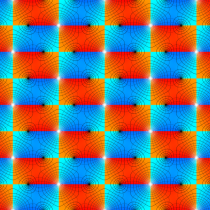
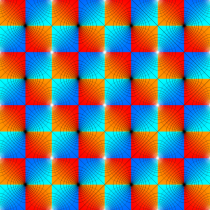
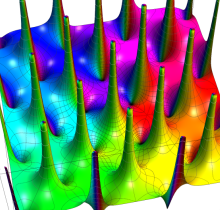
複素変数の Gauss の楕円関数
複素変数の Gauss の楕円関数
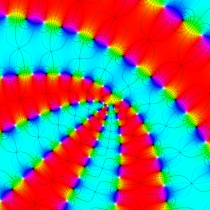
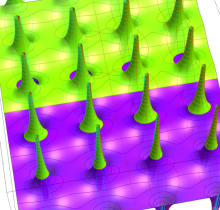
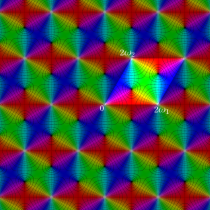
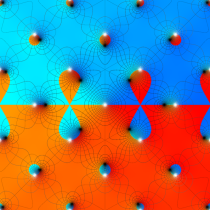
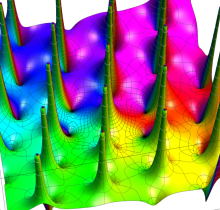
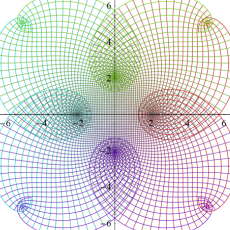
複素変数の Dixon の楕円関数
複素変数の Dixon の楕円関数
Jacobi の楕円関数
日:Jacobiの楕円関数,ヤコビの楕円関数英:Jacobi's elliptic function,仏:Fonction elliptique de Jacobi,独:Jacobische elliptische funktion
前述のとおり、Gauss は研究結果を公表しなかったので、正式な楕円関数の 「先取得権」 は、1827年のほぼ同時期に論文を提出した N. H. Abel と C. G. J. Jacobi に与えられている。両者による楕円関数発見の知らせは、当時の数学界に衝撃をもたらした。多くの数学者が一斉に楕円関数論に取り組むようになり、やがて 「19世紀数学の主要なテーマ」 となっていくのである。この成果を高く評価したパリ科学アカデミーは、1830年に Abel と Jacobi へ賞を授けたが、このとき Abel は結核により既に故人となっていた。
両者が定義した楕円関数は、のちに Legendre - Jacobi の標準形と呼ばれるようになる (第1種) 楕円積分の逆関数であったが、Abel のそれは被積分関数の形が僅かに異なる※1。現在では Jacobi の流儀が定着しており、ここでもそれを扱う。
すなわち、Jacobi の楕円関数は楕円積分
の逆関数であり、
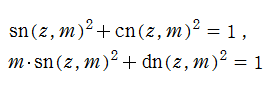
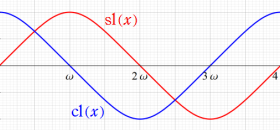
Jacobi 楕円関数の導関数は、それ自身を用いて
と表わされる。よって、楕円関数を逐次微分して得られる任意位数の楕円関数、一般の基本周期を持つ楕円関数など、すべての楕円関数はこの3種類の関数で表わすことができる。
Jacobi の楕円関数は、三角関数と同様に代数的加法公式を満たすが※2、
のように若干複雑である。(式中に現れる第2変数
この代数的加法公式 (並びに 「一致の定理」 等) を用いると、それぞれの Jacobi 楕円関数は、次のような2個の基本周期を持っていることが分かる。(ここに、
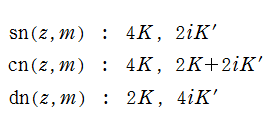
3種類の Jacobi 楕円関数はともに、基本周期の点で囲まれた平行四辺形の内部で、すべての複素数値を2個ずつとり、1位の極と1位の零点とが各々2個分含まれるので、2位の楕円関数である。
Jacobi の楕円関数は、
に還元される (冗長ながら、Gudermann 関数
で定義される。また、実数
Jacobi 楕円関数の級数展開式では、
がよく知られている。このとき、
Jacobi の楕円関数は、2個の楕円テータ関数の商によって
と表わせる。楕円テータ関数は級数の収束が極めて速く、極などの特異点を持たないので扱い易い。Jacobi 楕円関数の数値計算では、前掲の冪級数等ではなく、楕円テータ関数の公式を介した方が便利である。
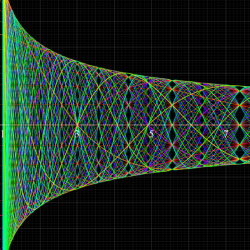
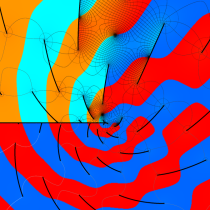
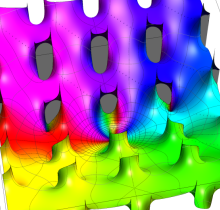
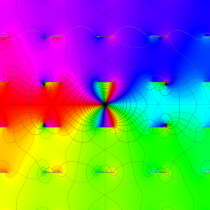
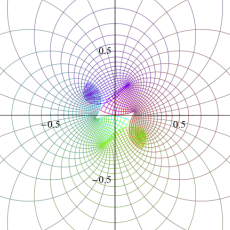
論文提出の前後、互いの研究内容が近いことに気付いた Abel と Jacobi は、半ば競争状態で持論の深化を目指すようになる。Jacobi は前述の楕円テータ関数をも発見し、その膨大な数の公式を導いて楕円関数の計算を容易にするとともに、数論や組合せ論に応用した。楕円テータ関数の対数微分 (第2種楕円関数) を追加して、一般の楕円積分が解けるようにした事も Jacobi の功績である。Abel はより複素領域での楕円関数の性質に傾倒し、虚数乗法論を創始した功績が大きい※3。(虚数乗法の概要については 「Weierstrass の楕円関数」 の所で触れるが) Abel は1827年に、虚数乗法の因子が虚二次体の数に取れること等を示しながら、具体的な例も挙げている (次の図はその事例の一つ)。
図:Abel による虚数乗法の例
【註記】
※1:Abel が扱った第1種楕円積分の形は、Jacobi の場合とは符号等が異なる
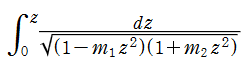
であった。これは虚数変数にすると、根号内の二つの符号が入れ替わるだけになるので、逆関数は虚数方向にも周期を持つことが直ちに分かるという利点を持っていた。
※2:この代数的加法公式を持つという性質が、楕円関数の著しい特徴の一つである。なぜなら、一価の解析関数で代数的加法公式を持つものは、初等有理関数、指数関数 (三角関数の 「加法定理」 はこれに含まれる)、および楕円関数しかないからである。
※3:虚数乗法論はその後、モジュラー関数やイデアル等と関連しつつ、類体論へ結実していく。この豊穣な当時の未開拓地に Abel が到達したかもしれない可能性を思う時、失われた物がいかに大きかったかが分かる。(数学史では有名な話であるが、Abel は更なる不運にも見舞われる。Abel 関数の頁の註記を参照。)
※1:Abel が扱った第1種楕円積分の形は、Jacobi の場合とは符号等が異なる
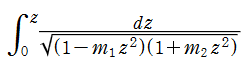
※2:この代数的加法公式を持つという性質が、楕円関数の著しい特徴の一つである。なぜなら、一価の解析関数で代数的加法公式を持つものは、初等有理関数、指数関数 (三角関数の 「加法定理」 はこれに含まれる)、および楕円関数しかないからである。
※3:虚数乗法論はその後、モジュラー関数やイデアル等と関連しつつ、類体論へ結実していく。この豊穣な当時の未開拓地に Abel が到達したかもしれない可能性を思う時、失われた物がいかに大きかったかが分かる。(数学史では有名な話であるが、Abel は更なる不運にも見舞われる。Abel 関数の頁の註記を参照。)
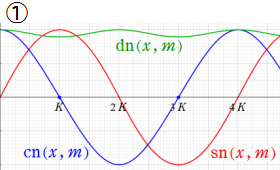
①
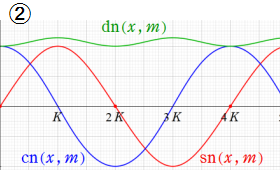
②
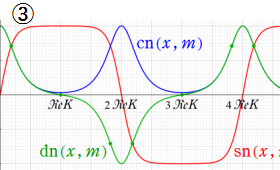
③
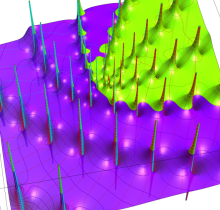
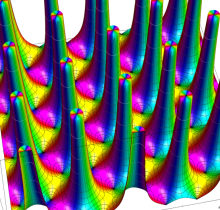
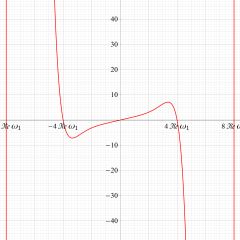
実2変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
アニメーション(10.5MB)
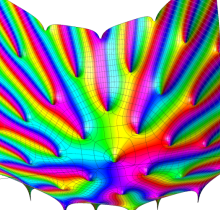
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
実2変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
アニメーション(14.4MB)
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
実2変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
複素変数の Jacobi の楕円関数
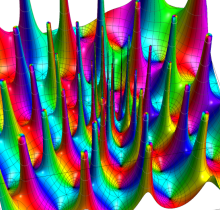
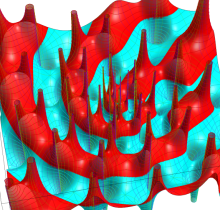
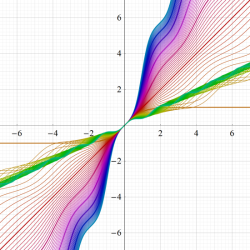
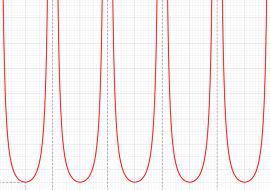
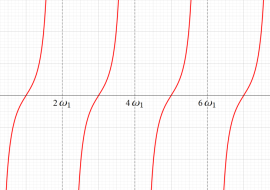
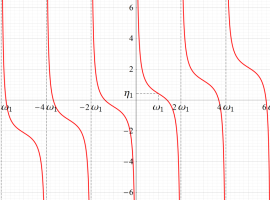
Jacobi の楕円振幅関数
日:Jacobiの楕円振幅関数,ヤコビの振幅関数英:Jacobi's amplitude function,仏:Fonction amplitude de Jacobi,独:Jacobische amplitude funktion
現在定着している Jacobi の楕円関数の記号
Jacobi は物理学等での応用事例を意識して、
の逆関数である楕円振幅関数
と表記していた※1。特に第3番目の式から、楕円振幅関数の定義とも言うべき
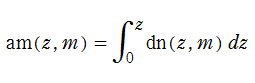
も得られる。
楕円振幅関数自体は楕円関数ではないが、二重の擬周期性
を持つ無限多価関数である※2。また、楕円振幅関数は奇関数で、
に還元される。
単振り子の周期運動は、実変数の楕円振幅関数で表わせる。振り子の腕 (大きく振ることも可能なように剛体棒であると考える) の長さを
となる (ただし、空気抵抗や支点部分の摩擦を無視し、振幅が減衰しないと考える)。これは、
このうち
現在定着しているこの関数名称の 「振幅 (Amplitude)」 とは、物理学における上記の応用事例に因むものである。
【註記】
※1: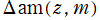 の記号は、楕円関数論で補助的に使用される初等関数
の記号は、楕円関数論で補助的に使用される初等関数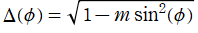 への代入が、元々の意味である。(この初等関数は、楕円積分の頁にも現れた。)
への代入が、元々の意味である。(この初等関数は、楕円積分の頁にも現れた。)
なお C. J. Thomae は、Jacobi の表記法をさらに短縮した合理的な記号 を導入したが、既に時代が経過していたため定着しなかった。
を導入したが、既に時代が経過していたため定着しなかった。
※2:当サイトの楕円振幅関数は、複素変数のグラフに限って (Ver.11以前の) Mathematica と異なる独自の分枝切断線を標準とする。(これは、E. Jahnke,F. Emde 著「Tables of Functions with formulae and curves」にあるグラフと同じです。)
その分枝切断線は、次の級数を使用すると実現できる。
ただし、この級数は収束がやや遅く、原点から遠くなるほど加算項数を増やす必要がある。
※3:その場合、最大振幅角は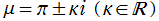 となるが、これは一体何?。
となるが、これは一体何?。
※1:
なお C. J. Thomae は、Jacobi の表記法をさらに短縮した合理的な記号
※2:当サイトの楕円振幅関数は、複素変数のグラフに限って (Ver.11以前の) Mathematica と異なる独自の分枝切断線を標準とする。(これは、E. Jahnke,F. Emde 著「Tables of Functions with formulae and curves」にあるグラフと同じです。)
その分枝切断線は、次の級数を使用すると実現できる。
ただし、この級数は収束がやや遅く、原点から遠くなるほど加算項数を増やす必要がある。
※3:その場合、最大振幅角は
(Mathematica (Ver.11以前) の分枝切断線の場合。単振り子の周期運動はこれを用いるべきである。もし、当サイト独自の分枝切断線を採用したならば、
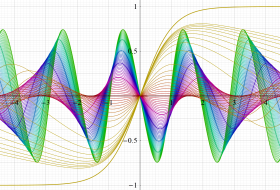
実2変数の Jacobi の楕円振幅関数
複素変数の Jacobi の楕円振幅関数
複素変数の Jacobi の楕円振幅関数
複素変数の Jacobi の楕円振幅関数
複素変数の Jacobi の楕円振幅関数
複素変数の Jacobi の楕円振幅関数
複素変数の Jacobi の楕円振幅関数
複素変数の Jacobi の楕円振幅関数
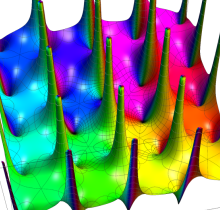
Jacobi の第2種楕円関数
比較的簡単な Jacobi の楕円関数であっても、積分すると本質的に異なる新しい関数が現れる例として、がある。これを Jacobi の第2種楕円関数※1、または Jacobi の楕円イプシロン関数という。
また、
が定義される。これも Jacobi の第2種楕円関数であり、Jacobi の楕円ゼータ関数ともいう※2。更にこれらの関数は、後述する Weierstrass の楕円ゼータ関数とも同クラスであり、互いに他で表わすことができる。
上記の定義式のとおり、第2種楕円積分は楕円関数を代入することによって、初めてその多価性が解消可能となる。換言すれば、(第1種~第3種の) 一般的な楕円積分を解く場合、楕円関数だけでは不足しており、第2種楕円関数や後述の第3種楕円関数 (から導かれる楕円テータ関数) を援用する必要が生じる。
を持っている。また、超越的な加法公式
を満たす。(関数記号から第2変数
【註記】
※1:第2種楕円関数という名称は、一般的に複素平面上において
なる二重の擬周期性を満たす一価有理型関数のことを言う場合もある。
※2:Jacobi の楕円関数の記号 (Gudermann の表記法) に則り、Jacobi の楕円ゼータ関数を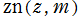 、楕円イプシロン関数を
、楕円イプシロン関数を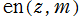 で表記している事例が希にある。
で表記している事例が希にある。
※1:第2種楕円関数という名称は、一般的に複素平面上において
なる二重の擬周期性を満たす一価有理型関数のことを言う場合もある。
※2:Jacobi の楕円関数の記号 (Gudermann の表記法) に則り、Jacobi の楕円ゼータ関数を
実2変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
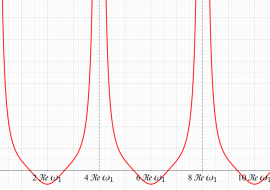
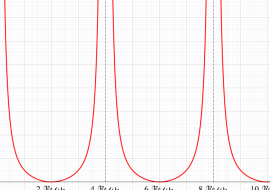
完全楕円積分係数の付加項を持つため、
実2変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
複素変数の Jacobi の第2種楕円関数
Jacobi の第3種楕円関数
Jacobi の楕円関数を積分すると生じ、第3種楕円積分に楕円関数を代入して得られる新しい関数を Jacobi の第3種楕円関数、または Jacobi の楕円パイ関数という※1。特に、上記の第3番目の式から、
が導かれる。この公式は、変数
を持つ無限多価関数である※3。また、超越的な加法公式
を満たす。(同様に、関数記号から
となる (よって、Weierstrass の楕円シグマ関数や、楕円テータ関数のクラスを、第3種楕円関数という場合も多い)。
応用事例として、第3種楕円関数は剛体力学に現れる。特に、独楽の回転運動を記述する目的のために、Jacobi はこの関数を導入した。
【註記】
※1:比較的古い書籍ならば、この関数に言及していることがある。例えば
① 尾本義一・小郷 寛 著 「公式と数表 特殊編」 (電気書院:1964年) の48~49頁
② J. Dieudonné 編 「数学史 ― 1700-1900 (Ⅱ)」 (岩波書店:1985年) の498~499頁
③ E. T. Whittaker, G. N. Watson 「A Course of Modern Analysis」 (1902年) の522~523頁
等がある。
※2:Galois はさらに、第2種・第3種 Abel 積分の間でも同様の可換性が成り立つことを予想したが、これは後に Riemann や Weierstrass 等によって証明された。
※3:以下の複素変数グラフで採用している当サイト独自の分枝切断線は、次の級数を使用すると実現できる。
ただし、この級数は (楕円振幅関数のそれよりも) 収束が遅く、原点から遠くなるほど加算項数が必要。
※1:比較的古い書籍ならば、この関数に言及していることがある。例えば
① 尾本義一・小郷 寛 著 「公式と数表 特殊編」 (電気書院:1964年) の48~49頁
② J. Dieudonné 編 「数学史 ― 1700-1900 (Ⅱ)」 (岩波書店:1985年) の498~499頁
③ E. T. Whittaker, G. N. Watson 「A Course of Modern Analysis」 (1902年) の522~523頁
等がある。
※2:Galois はさらに、第2種・第3種 Abel 積分の間でも同様の可換性が成り立つことを予想したが、これは後に Riemann や Weierstrass 等によって証明された。
※3:以下の複素変数グラフで採用している当サイト独自の分枝切断線は、次の級数を使用すると実現できる。
ただし、この級数は (楕円振幅関数のそれよりも) 収束が遅く、原点から遠くなるほど加算項数が必要。
複素変数の Jacobi の第3種楕円関数
複素変数の Jacobi の第3種楕円関数
複素変数の Jacobi の第3種楕円関数
複素変数の Jacobi の第3種楕円関数
複素変数の Jacobi の第3種楕円関数
複素変数の Jacobi の第3種楕円関数
複素変数の Jacobi の第3種楕円関数
複素変数の Jacobi の第3種楕円関数
複素変数の Jacobi の第3種楕円関数
Weierstrass の楕円関数
日:Weierstrassの楕円関数,ワイエルシュトラスのペー関数英:Weierstrass's elliptic function,仏:Fonction elliptique de Weierstrass,独:Weierstraßsche p-funktion
19世紀中盤になると、次第に楕円関数論は複素領域での研究に主軸が置かれるようになり、また論考の動機や目的も、より純粋数学的な主題から発せられるものが増えていった。そこから理論的に美しく構成された 「Weierstrass の楕円関数 ―
参考までに、
1810~1850年代:A. L. Cauchy 等によって複素解析学の基礎となる諸理論、すなわち、複素線積分と Cauchy の積分定理、留数計算、Laurent 級数等が整備され、程なく楕円関数論を展開する上でも有力な方法となって行った。
1844年:J. Liouville が楕円関数の完全な特徴付けを与える 「Liouville の定理」 を (Cauchy の方法に頼らないで) 導き、楕円関数の存在が直接 ― 楕円積分の逆関数を経由せずに ― 示せるようになった。なお、Cauchy の方法を用いて Liouville の定理を導出することは、C. Hermite (1848年)、Cauchy (1851年) によって実行された。
1847年:Liouville の定理に基づき、有理関数項級数から楕円関数を直接定義する具体的方法が Eisenstein によって論じられ、後の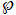 関数とほぼ同等となる関数が導入された (ただし、条件収束級数で定義されていた等の理由で、定着しなかった)。
関数とほぼ同等となる関数が導入された (ただし、条件収束級数で定義されていた等の理由で、定着しなかった)。
1862年頃 (※2):絶対収束する有理関数項級数、および Laurent 級数に基づいた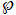 関数の完全な理論が、K. T. W. Weierstrass によって論じられた。言わば Liouville の思想が具体的な楕円関数として結実した。
関数の完全な理論が、K. T. W. Weierstrass によって論じられた。言わば Liouville の思想が具体的な楕円関数として結実した。
1844年:J. Liouville が楕円関数の完全な特徴付けを与える 「Liouville の定理」 を (Cauchy の方法に頼らないで) 導き、楕円関数の存在が直接 ― 楕円積分の逆関数を経由せずに ― 示せるようになった。なお、Cauchy の方法を用いて Liouville の定理を導出することは、C. Hermite (1848年)、Cauchy (1851年) によって実行された。
1847年:Liouville の定理に基づき、有理関数項級数から楕円関数を直接定義する具体的方法が Eisenstein によって論じられ、後の
1862年頃 (※2):絶対収束する有理関数項級数、および Laurent 級数に基づいた
現在では、複素平面上で二重周期を持つ有理型関数を、総称して楕円関数という。その周期全体は、二つの基本周期
で網羅され、平行四辺形の編み目構造を作るので、格子またはラティス (Lattice) と呼ばれる。格子のうち、特に
となる。この基本周期平行四辺形内にある極の位数の和を、その楕円関数の位数という。つまり、基本周期が共通であっても、互いに位数の異なる楕円関数が無数に存在する。これらの楕円関数は、次の 「Liouville の第1~4定理」 で特徴付けられる。これによれば、1位の楕円関数は存在しない (最小の位数は2である) こと等が分かる。
第1定理:二重周期を持つ整関数は、定数 (定数関数) に限る。
第2定理:楕円関数のFPP内に含まれる極の留数の和は0である。
第3定理:楕円関数のFPP内に含まれる零点の位数の和は、楕円関数の位数に等しい。
第4定理:楕円関数のFPP内に含まれる零点の和と極の和との差は、一つの周期に等しい。
第2定理:楕円関数のFPP内に含まれる極の留数の和は0である。
第3定理:楕円関数のFPP内に含まれる零点の位数の和は、楕円関数の位数に等しい。
第4定理:楕円関数のFPP内に含まれる零点の和と極の和との差は、一つの周期に等しい。
同じ基本周期を持った楕円関数どうしの四則演算から得られる関数の集合、または任意の楕円関数とそれを逐次微分して得られる関数の集合は、共通の基本周期を持つ楕円関数を要素とする。この集合は、数体と同じ構造を持つので 「楕円関数体」 と呼ばれる。
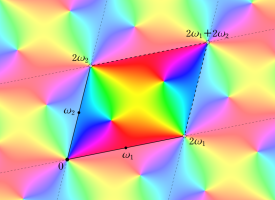
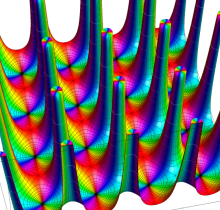
さて、Weierstrass の楕円関数 (
で定義される楕円関数である (上記の総和記号は、以下同様とする)。
は不変量と呼ばれる保型形式の一種である。Weierstrass の楕円関数を Laurent 級数展開したときの係数にも、この不変量が現れる (Laurent 級数展開式および不変量の詳細は、楕円モジュラー形式を参照)。
また、不変量の代わりに 「半周期」 (基本周期を2で割った値) を明示して、Weierstrass の楕円関数を
を満たす。また、公式
は、モジュラー形式としての性質がより鮮明になる。なお、これらの補助変数は、明示しなくても判断できる場合では度々
を持ち、両者は互いに
なる非線形微分方程式で結ばれる。ここに、3次方程式の解と係数の関係から、
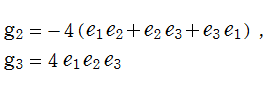
上記のことは、言い換えれば数論等で重要な 「楕円曲線」
が、
また、非線形微分方程式によって、
を満たす。
なる変換を受けるが、これを周期の比
【註記】
※1: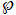 は、Weierstrass の国籍に由来してドイツ語のPと同じく 「ペー」 と読む。記号
は、Weierstrass の国籍に由来してドイツ語のPと同じく 「ペー」 と読む。記号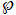 は、時折 Abel 関数にも用いられる (当サイトでは独自に Painlevé 超越関数にも用いた) が、本来は Weierstrass の楕円関数を表わす用途に限られた特殊記号である。多くの文字フォントでサポートされないため、表示できない場合はドイツ花文字 (フラクトゥール) のPで代用することが多い。
は、時折 Abel 関数にも用いられる (当サイトでは独自に Painlevé 超越関数にも用いた) が、本来は Weierstrass の楕円関数を表わす用途に限られた特殊記号である。多くの文字フォントでサポートされないため、表示できない場合はドイツ花文字 (フラクトゥール) のPで代用することが多い。
※2:Weierstrass は最新の持論を学生に教授して広める方法を好み、一方、論文による公表は20~30年後になることも珍しくなかったため、時期を特定できない研究結果が多数ある。
※3:楕円曲線という用語は、楕円関数でパラメータ表示される (一意化と呼ばれる) 曲線との意味であり、元々の由来である 「長円としての楕円」 からは関連が遠くなっている。
楕円曲線はトーラス (円環面) と同一視でき、楕円関数の2個の周期はトーラス上の線形独立な2個の (連続的なホモトピー変形によって1点に退化できない) ループに同一視される (楕円積分の頁にある図を参照)。因みに、円周は三角関数によって一意化される (それゆえ、三角関数は 「円関数」 と呼ばれることもある)。つまり、楕円関数はこの意味でも三角関数の拡張となっている。
楕円曲線は暗号法にも用いられ、今日の高度情報化社会で不可欠となっていることは有名である。
※1:
※2:Weierstrass は最新の持論を学生に教授して広める方法を好み、一方、論文による公表は20~30年後になることも珍しくなかったため、時期を特定できない研究結果が多数ある。
※3:楕円曲線という用語は、楕円関数でパラメータ表示される (一意化と呼ばれる) 曲線との意味であり、元々の由来である 「長円としての楕円」 からは関連が遠くなっている。
楕円曲線はトーラス (円環面) と同一視でき、楕円関数の2個の周期はトーラス上の線形独立な2個の (連続的なホモトピー変形によって1点に退化できない) ループに同一視される (楕円積分の頁にある図を参照)。因みに、円周は三角関数によって一意化される (それゆえ、三角関数は 「円関数」 と呼ばれることもある)。つまり、楕円関数はこの意味でも三角関数の拡張となっている。
楕円曲線は暗号法にも用いられ、今日の高度情報化社会で不可欠となっていることは有名である。
【Equianharmonic Case:
この場合、
実変数の Weierstrass の楕円関数
複素変数の Weierstrass の楕円関数
Equianharmonic Case の3乗
【Pseudo-Equianharmonic Case:
この場合、
実変数の Weierstrass の楕円関数
複素変数の Weierstrass の楕円関数
Pseudo-Equianharmonic Case の3乗
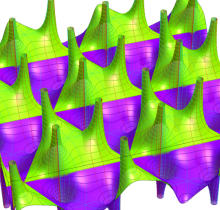
【Lemniscatic Case:
この場合、
実変数の Weierstrass の楕円関数
複素変数の Weierstrass の楕円関数
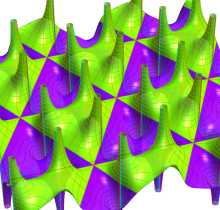
【Pseudo-Lemniscatic Case:
この場合、
実変数の Weierstrass の楕円関数
複素変数の Weierstrass の楕円関数
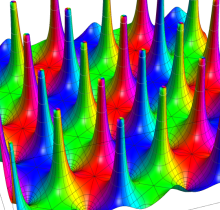
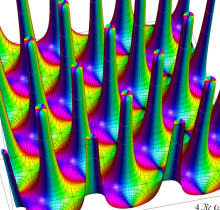
【General Case:
複素変数の Weierstrass の楕円関数
アニメーション(12.2MB)
複素変数の Weierstrass の楕円関数
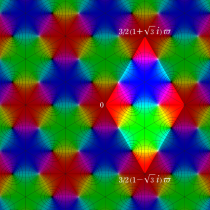
【変数
不変量
複素変数の Weierstrass の楕円関数
不変量
複素変数の Weierstrass の楕円関数
【Equianharmonic Case:
実変数の Weierstrass の楕円関数の導関数
複素変数の Weierstrass の楕円関数の導関数
【Pseudo-Equianharmonic Case:
実変数の Weierstrass の楕円関数の導関数
複素変数の Weierstrass の楕円関数の導関数
【Lemniscatic Case:
実変数の Weierstrass の楕円関数の導関数
複素変数の Weierstrass の楕円関数の導関数
【Pseudo-Lemniscatic Case:
実変数の Weierstrass の楕円関数の導関数
複素変数の Weierstrass の楕円関数の導関数
【General Case:
複素変数の Weierstrass の楕円関数の導関数
【変数
不変量
複素変数の Weierstrass の楕円関数の導関数
不変量
複素変数の Weierstrass の楕円関数の導関数
Weierstrass の楕円ゼータ関数
日:Weierstrassの楕円ゼータ関数,ワイエルシュトラスζ関数英:Weierstrass zeta-function,仏:Fonction zêta de Weierstrass,独:Weierstraßsche zeta-funktion
微分すると、Weierstrass の楕円関数になる関数
を、Weierstrass の楕円ゼータ関数という。この関数は Jacobi の第2種楕円関数に相当し、互いに他で表わすことができる。尤も Weierstrass の楕円ゼータ関数は、より具体的な部分分数展開式
を導入時の定義とすることが多い。
Weierstrass の楕円ゼータ関数は楕円関数ではないが、
を持っている。ここに、附随する定数は、
なる関係を常に満たす。このうち、最後の式は Legendre の関係式に相当する。
Weierstrass の楕円ゼータ関数は、非線形微分方程式
を満たし、超越的加法公式
を介して、
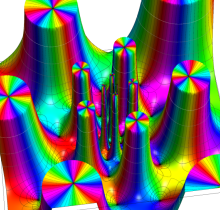
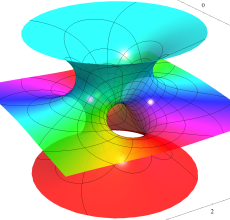
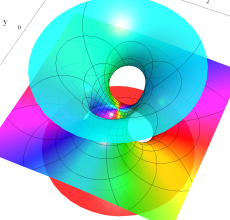
Costa の極小曲面は、Weierstrass の楕円関数および楕円ゼータ関数を用いたパラメトリック曲面として、表わすことができる。
【Equianharmonic Case:
実変数の Weierstrass の楕円ゼータ関数
複素変数の Weierstrass の楕円ゼータ関数
Weierstrass の楕円ゼータ関数
【Pseudo-Equianharmonic Case:
実変数の Weierstrass の楕円ゼータ関数
複素変数の Weierstrass の楕円ゼータ関数
Weierstrass の楕円ゼータ関数
【Lemniscatic Case:
実変数の Weierstrass の楕円ゼータ関数
複素変数の Weierstrass の楕円ゼータ関数
Weierstrass の楕円ゼータ関数
【Pseudo-Lemniscatic Case:
実変数の Weierstrass の楕円ゼータ関数
複素変数の Weierstrass の楕円ゼータ関数
Weierstrass の楕円ゼータ関数
【General Case:
複素変数の Weierstrass の楕円ゼータ関数
Weierstrass の楕円ゼータ関数
【変数
不変量
複素変数の Weierstrass の楕円ゼータ関数
不変量
複素変数の Weierstrass の楕円ゼータ関数
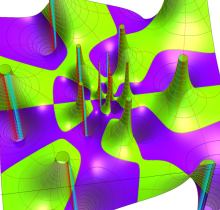
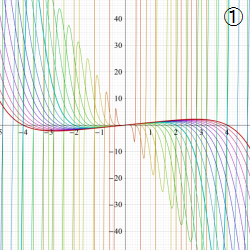
Weierstrass の楕円シグマ関数
日:Weierstrassの楕円シグマ関数,ワイエルシュトラスσ関数英:Weierstrass sigma-function,仏:Fonction sigma de Weierstrass,独:Weierstraßsche sigma-funktion
対数微分すると、Weierstrass の楕円ゼータ関数になる関数
を、Weierstrass の楕円シグマ関数という。この関数は楕円テータ関数に相当し、互いに他で表わすことができる。尤も Weierstrass の楕円シグマ関数は、より具体的な無限乗積展開式
を、導入時の定義とすることが多い。
Weierstrass の楕円シグマ関数は楕円関数ではないが、
を持っている。
Weierstrass の楕円シグマ関数は、非線形微分方程式
を満たし、超越的加法公式に相当する、
を介して、
楕円テータ関数と同様に、Weierstrass の楕円シグマ関数は好ましい対称性を持つので、数論や可解格子模型など多くの分野で応用事例がある。例えば、周期的な境界条件を課した1次元格子系である 「戸田格子 (Toda lattice)」 が挙げられる。指数関数的ポテンシャルを持ち、隣接間で相互作用しながら (例えばバネで連結されて) 運動する格子点を考えるとき、隣接する二つの格子点の座標値の比を
は、戸田格子を表わす方程式の一例になっている (本来は、楕円テータ関数で記述される)。戸田格子は1967年に戸田盛和によって発見され、その後、ソリトン方程式など解が具体的に示せる (可積分な) 非線形系の研究を大いに促すこととなった。
また、19世紀後半には、この関数の多変数化に相当する Riemann テータ関数が導入され、Abel 関数論で主要な役割を果たすとともに、前述の応用分野等を超楕円積分的な場合に拡張することが可能になった。
【Equianharmonic Case:
実変数の Weierstrass の楕円シグマ関数
複素変数の Weierstrass の楕円シグマ関数
Weierstrass の楕円シグマ関数
この事例は、写像元が直交直線座標の①よりも、それを極座標に変えた②の方が状況を把握しやすい。
【Pseudo-Equianharmonic Case:
実変数の Weierstrass の楕円シグマ関数
複素変数の Weierstrass の楕円シグマ関数
Weierstrass の楕円シグマ関数
【Lemniscatic Case:
実変数の Weierstrass の楕円シグマ関数
複素変数の Weierstrass の楕円シグマ関数
Weierstrass の楕円シグマ関数
【Pseudo-Lemniscatic Case:
実変数の Weierstrass の楕円シグマ関数
複素変数の Weierstrass の楕円シグマ関数
Weierstrass の楕円シグマ関数
【General Case:
複素変数の Weierstrass の楕円シグマ関数
Weierstrass の楕円シグマ関数
【変数
不変量
複素変数の Weierstrass の楕円シグマ関数
ただし、関数値が非常に大きくなるので、3次元のグラフは常用対数スケールのみとする。
不変量
複素変数の Weierstrass の楕円シグマ関数
ただし、関数値が非常に大きくなるので、3次元のグラフは常用対数スケールのみとする。