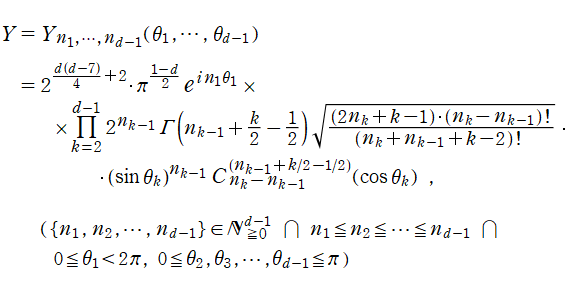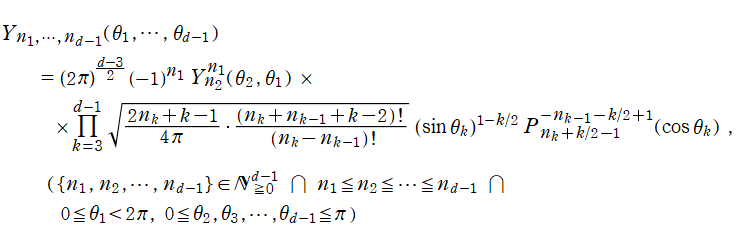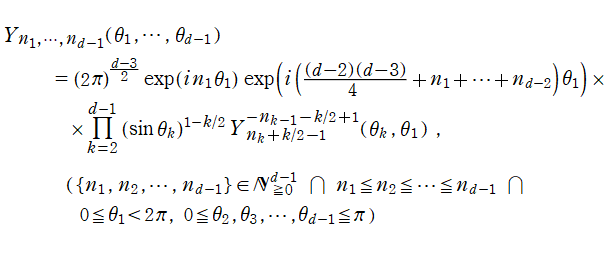Gegenbauer 関数
日:
Gegenbauer関数,
ゲーゲンバウアー関数
英:
Gegenbauer function,仏:
Fonction de Gegenbauer,独:
Gegenbauersche funktion
日:
超球関数
英:
Ultraspherical function,仏:
Fonction ultrasphérique,独:
Ultrasphärische funktion,
Ultrakugelfunktion
2階の線形常微分方程式
は超幾何微分方程式の特別な場合であり、
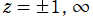
を確定特異点とする。これを Gegenbauer の微分方程式といい、その解の基本系
+b*S[ν, (μ)](z)](siki_spec210/gegenbauer00300.png)
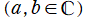
を成す二つの関数を
超幾何関数で表わせば、
となる。これを順に、第1種および第2種 Gegenbauer 関数という※1。このうち、第1種は
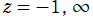
を一般に対数分岐点とし、実軸上の区間
![(-∞, -1]](siki_spec210/gegenbauer00700.png)
に分枝切断線が置かれる。第2種は
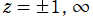
を一般に対数分岐点とし、実軸上の区間
![(-∞, -1]](siki_spec210/gegenbauer00700.png)
および
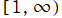
に分枝切断線が置かれる。
Gegenbauer 関数は、
Legendre 陪関数 (Ferrers 型) と本質的に同じクラスの関数であって、
と表わせる。また、この表示式と Legendre 陪関数 (Ferrers 型) の性質を用いれば、
が導かれる。
Gegenbauer 関数は、

に関して線形漸化式および微分漸化式
を満たす。同様に、

に関する漸化式は
となる。ここに
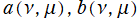
は、
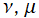
の二変数について1を周期とする任意の周期関数である。
Gegenbauer 関数は

が特別な値のとき、定数関数,
Chebyshev 関数, および Legendre 関数
に還元される。また、

に対して極限を取ると、Chebyshev 関数または
Hermite 関数
に近付く※2。
第1種 Gegenbauer 関数は次数が
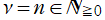
ならば、多項式
に還元され、Gegenbauer 多項式と呼ばれる。Gegenbauer 多項式は
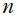
が偶数 (奇数) ならば偶関数 (奇関数) となり、母関数表示式および Rodrigues の公式
によっても表わせる。Gegenbauer 多項式は直交性を持つが、これについては
次節で触れる。
第2種 Gegenbauer 関数については、当サイトと異なる定義がいくつか存在する。例えば 「Higher Transcendental Functions vol.1」 の178~179頁では、
が掲載されている※3。これは、
Legendre 陪関数 (Hobson 型) と本質的に同じクラスの関数であり、
となる。さらに、
](siki_spec210/gegenbauer02200.png)
と
](siki_spec210/gegenbauer02300.png)
の線形結合式
でも表わせるので、
](siki_spec210/gegenbauer02500.png)
は前述と全く同じ線形常微分方程式および

に関する漸化式を満たす。一方、

に関する漸化式は若干形が異なり、
となる。また、
](siki_spec210/gegenbauer02500.png)
は実軸上の区間
![(-∞, 1]](siki_spec210/gegenbauer02700.png)
に分枝切断線を置くことが
, S[ν, (μ)](z)](siki_spec210/gegenbauer02800.png)
と異なる。
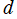
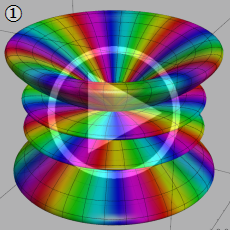
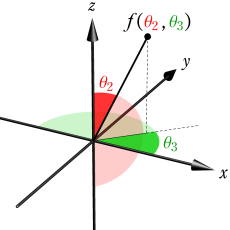
次元 Euclid 空間内の直交直線座標
![{x[1], x[2], …, x[d]}](siki_spec210/gegenbauer02900.png)
を、極座標 (超球座標)
で表わすとき、多変数関数
![ψ = ψ(r, θ[1], …, θ[d-1])](siki_spec210/gegenbauer03100.png)
に超球座標でのラプラシアンを作用させたものは、
となる。このとき、Laplace 方程式
![(Δ[d]^2)ψ = 0](siki_spec210/gegenbauer03300.png)
の解は変数分離が可能で、具体的に
となり、
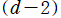
個の天頂角方向で Gegenbauer 関数が現れる※4。それゆえ、Gegenbauer 関数を 「超球関数」 と呼ぶことも多い。Gegenbauer 関数は、高次元空間内で境界条件が超球で定まる物理問題のほか、高次元幾何学、群論に応用される。例えば、量子色力学、相対論的効果を取り入れた調和振動子などが挙げられ、これらは Chebyshev 関数の応用事例とも共通している。
Gegenbauer 関数の名称は、1893年にこの関数を論じた L. B. Gegenbauer に由来する。
【註記】
※1:第2種 Gegenbauer 関数
](siki_spec210/gegenbauer02300.png)
は当サイトが独自に定義したものであって、
](siki_spec210/gegenbauer02200.png)
が余弦関数に相当すると見たとき、
](siki_spec210/gegenbauer02300.png)
は正弦関数に相当する。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針は、別頁
Questions に掲示している。)
※2:
](siki_spec210/gegenbauer03600.png)
は第1種 Gegenbauer 関数の "繰込形式" と呼ばれる。書籍によっては
](siki_spec210/gegenbauer03600.png)
を
](siki_spec210/gegenbauer03700.png)
と表記することもあるが、明らかに両者は同一ではなく、混乱を避けるため当サイトでは区別する。
※3:同著での関数記号は
](siki_spec210/gegenbauer03800.png)
であるが、当サイトでは他の記法に合わせて
](siki_spec210/gegenbauer02500.png)
と表記する。また同著では、正規化していない超幾何関数の閉形式で掲載している。
※4:Gegenbauer 関数の代わりに、Legendre 陪関数 (Ferrers 型) で解を表示することもできる。具体的には
となり、むしろこの方が簡明な形になる。ただし、
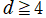
では Legendre 陪関数の次数が半奇数になる場合が現れるため、直交性が適用できない。
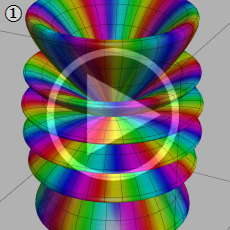
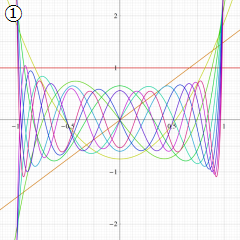
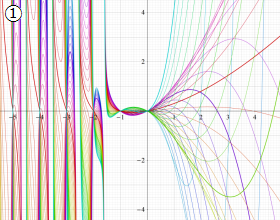
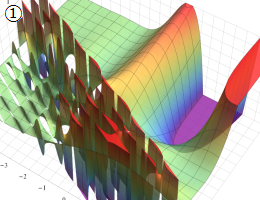
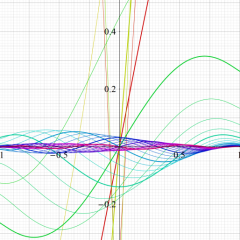
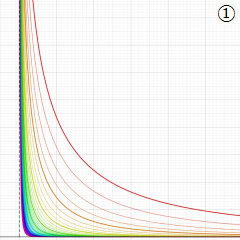
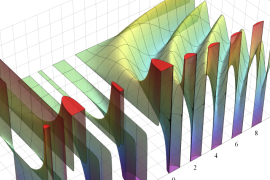
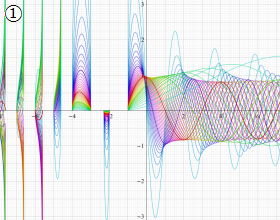
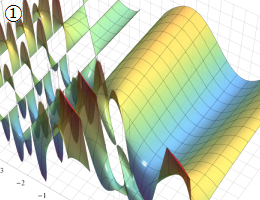
](siki_spec210/gegenbauer06600.png)
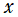
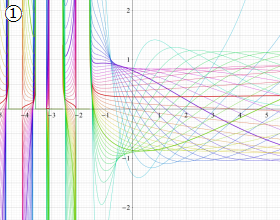
を実変数とする、第1種 Gegenbauer 関数のグラフ。
①整数次
](siki_spec210/gegenbauer04100.png)
(Gegenbauer 多項式)。
②実数次
](siki_spec210/gegenbauer04200.png)
。
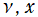
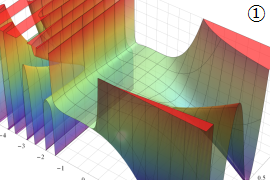
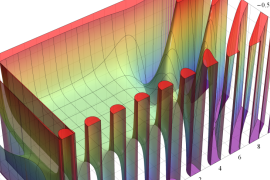
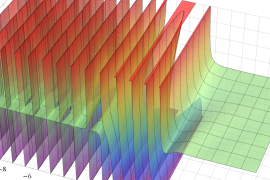
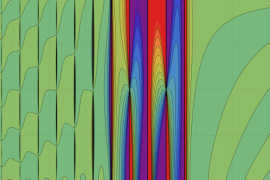
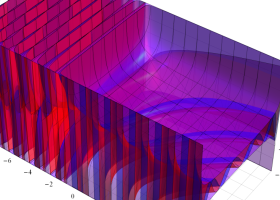
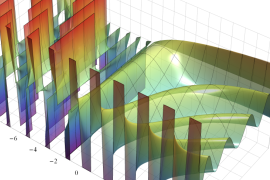
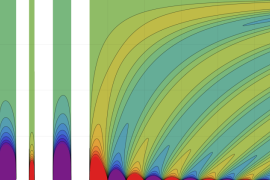
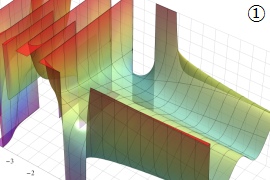
を実2変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer04200.png)
のグラフ。
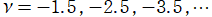
では関数が定義されない。
2番目は、
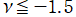
の範囲を拡大した場合。
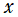
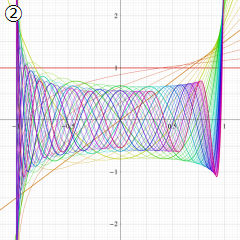
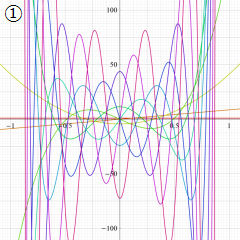
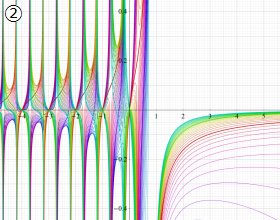
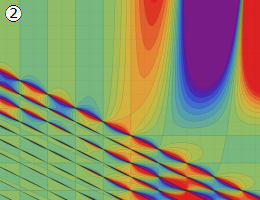
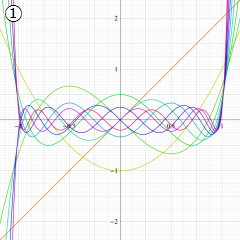
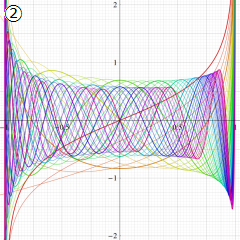
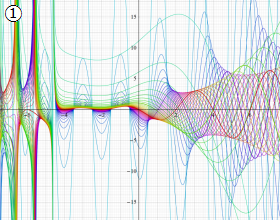
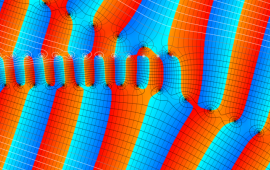
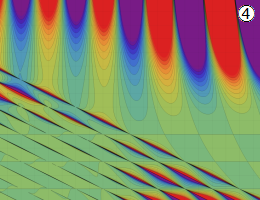
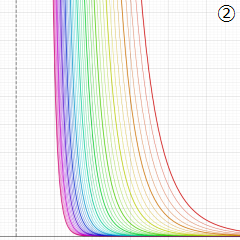
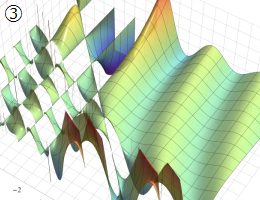
を実変数とする、第1種 Gegenbauer 関数のグラフ。
①整数次
](siki_spec210/gegenbauer04600.png)
(Gegenbauer 多項式)。
②実数次
](siki_spec210/gegenbauer04700.png)
。
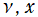
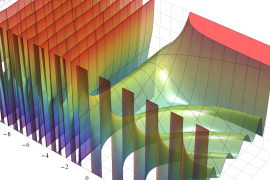
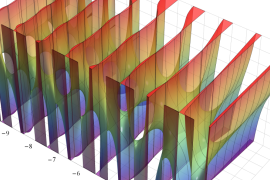
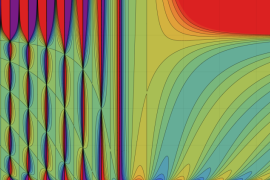
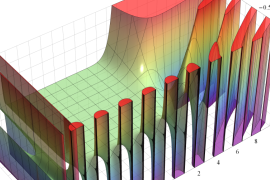
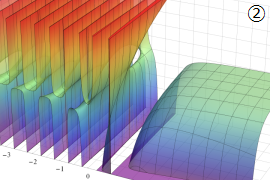
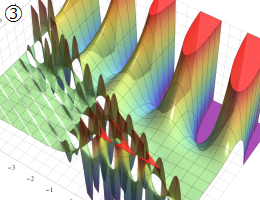
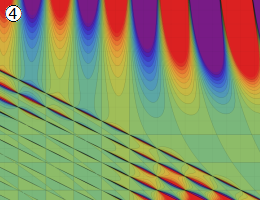
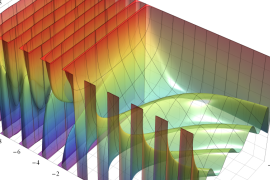
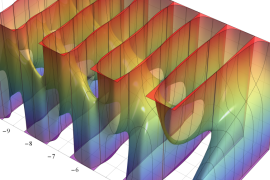
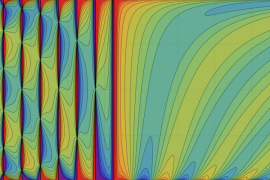
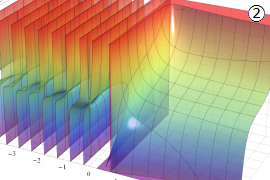
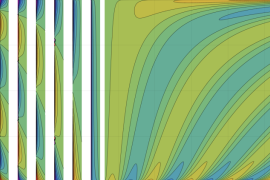
を実2変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer04700.png)
のグラフ。
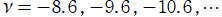
では関数が定義されない。

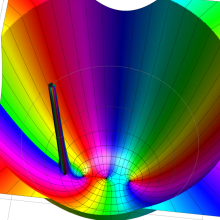
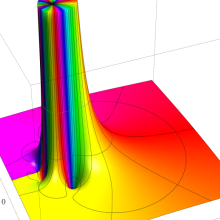
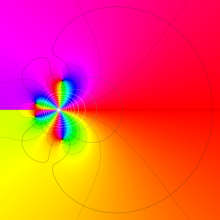
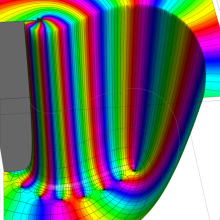
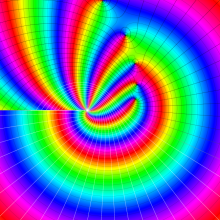
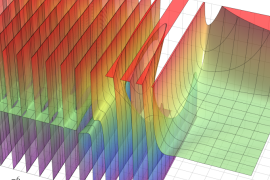
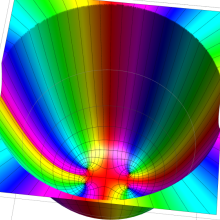
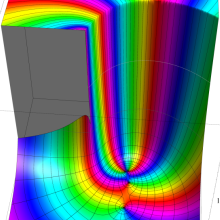
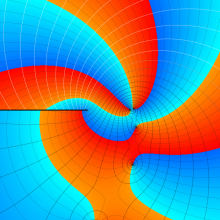
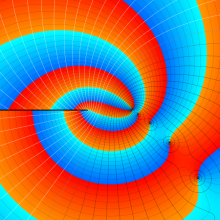
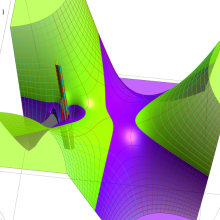
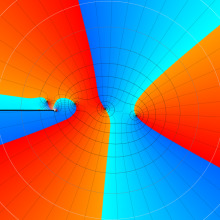
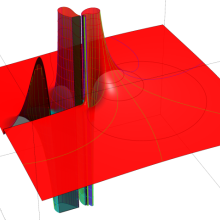
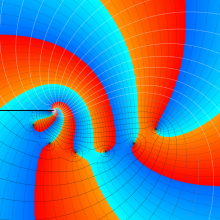
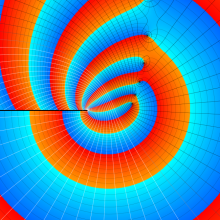
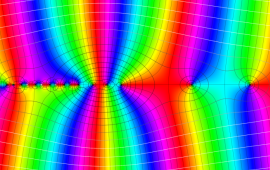
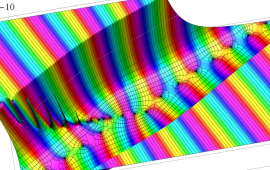
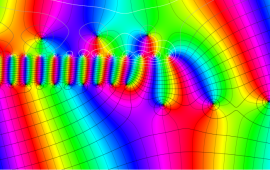
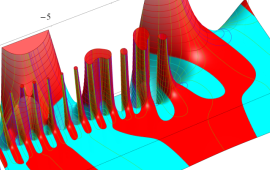
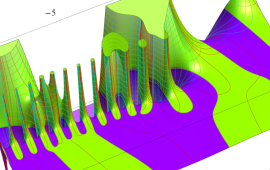
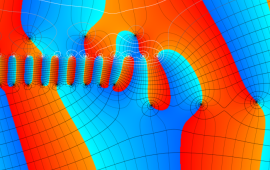
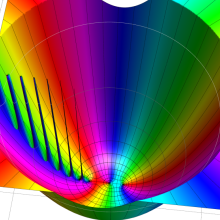
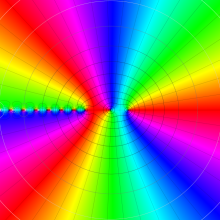
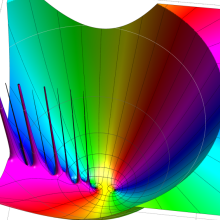
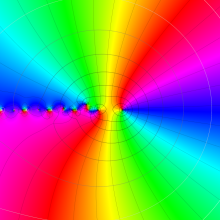
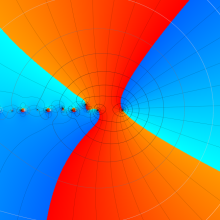
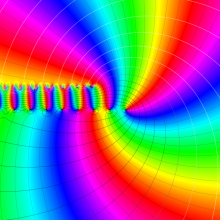
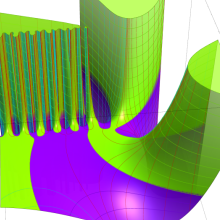
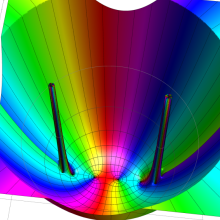
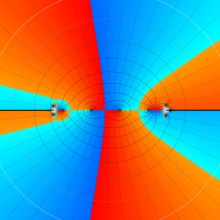
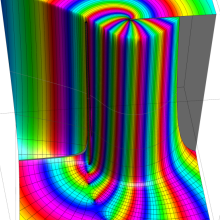
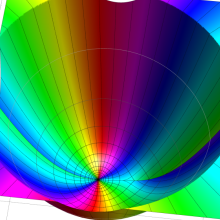
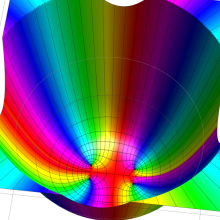
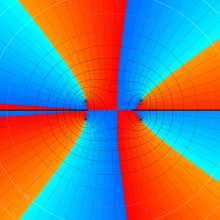
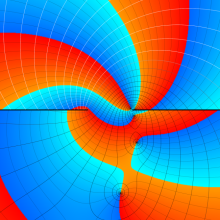
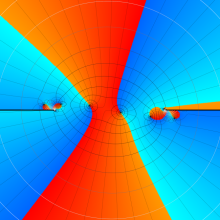
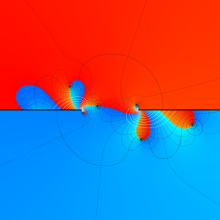
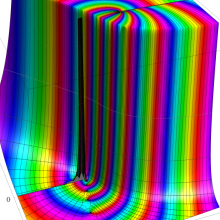
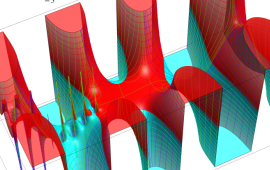
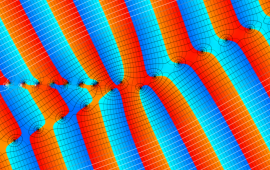
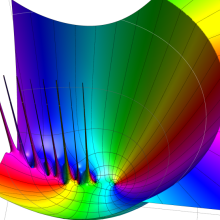
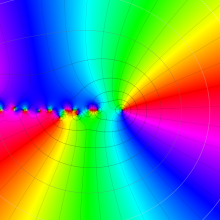
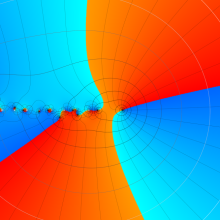
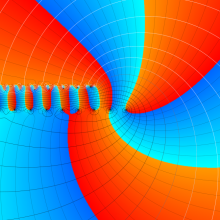
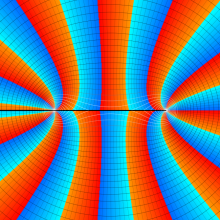
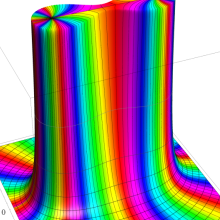
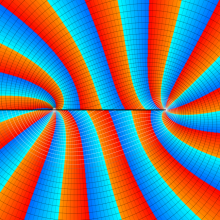
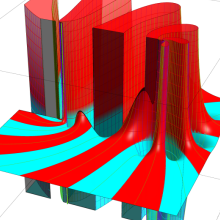
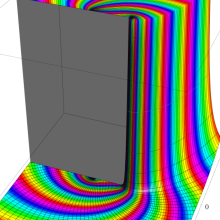
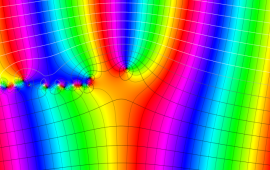
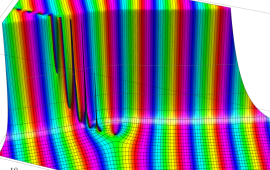
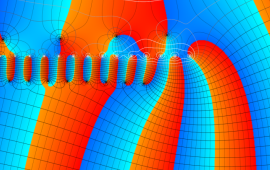
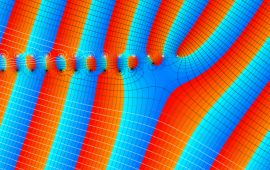
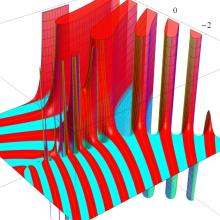
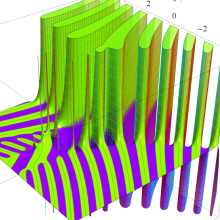
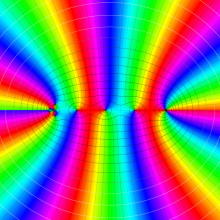
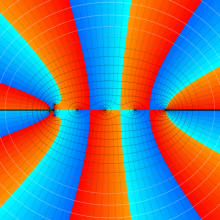
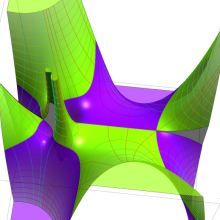
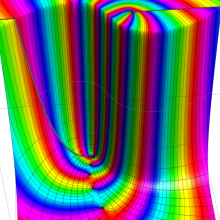
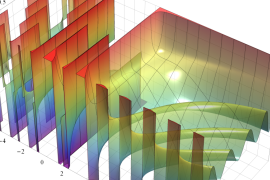
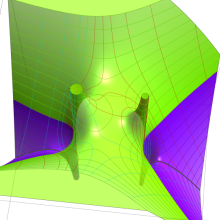
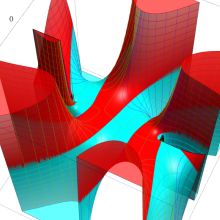
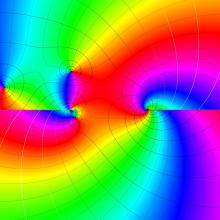
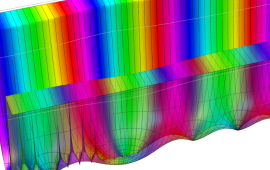
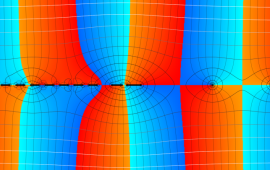
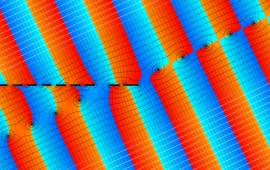
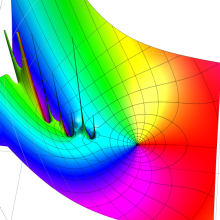
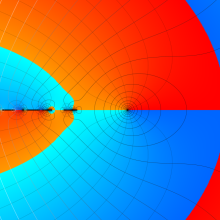
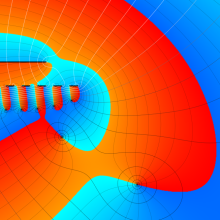
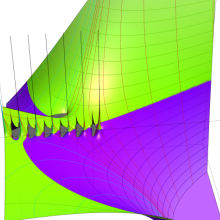
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer04900.png)
のグラフ。

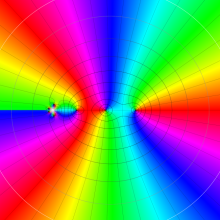
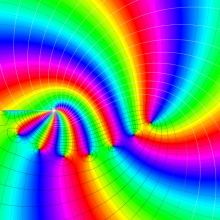
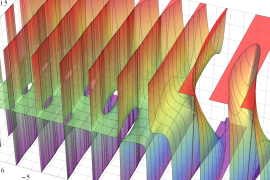
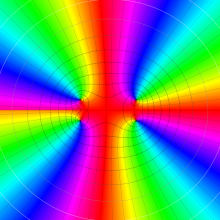
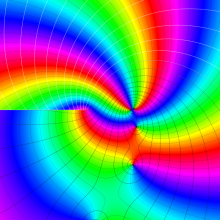
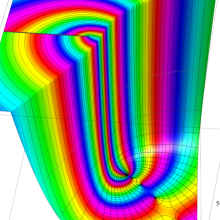
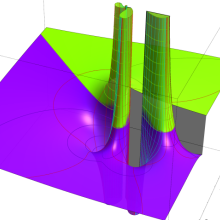
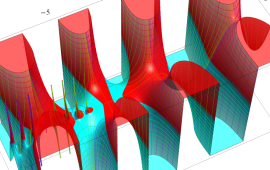
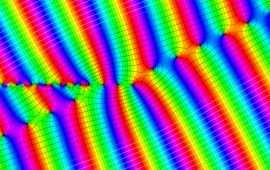
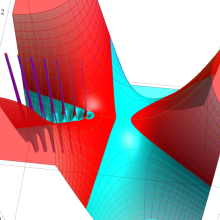
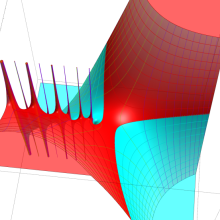
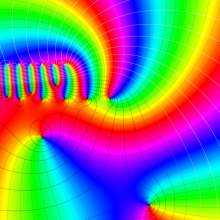
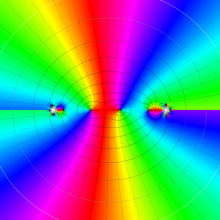
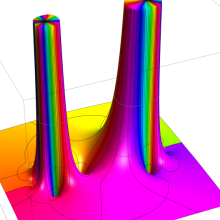
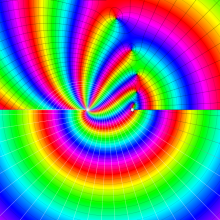
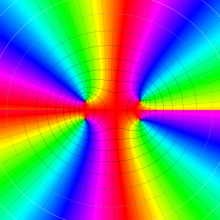
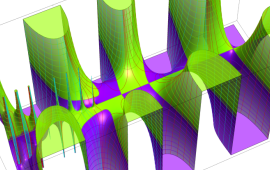
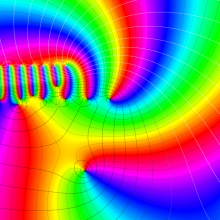
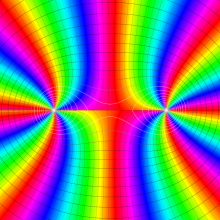
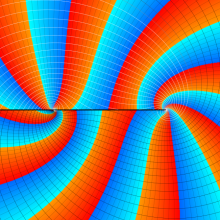
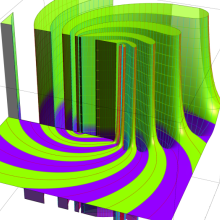
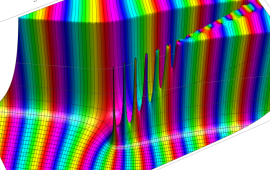
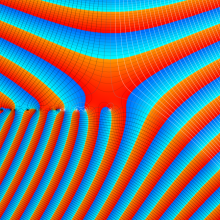
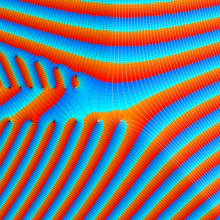
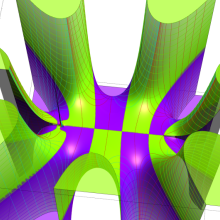
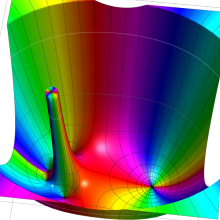
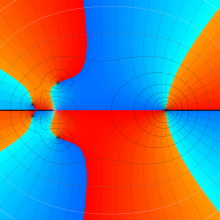
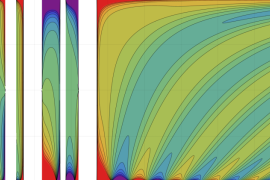
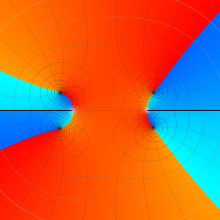
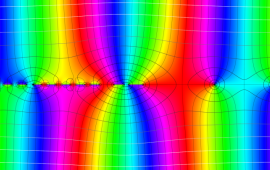
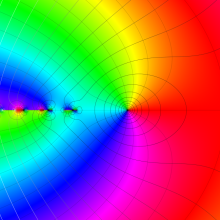
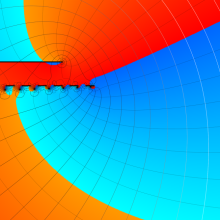
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer05000.png)
のグラフ。

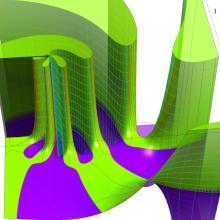
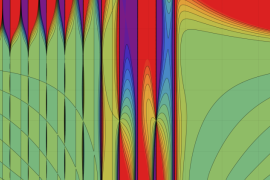
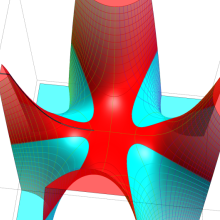
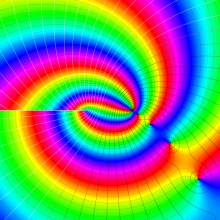
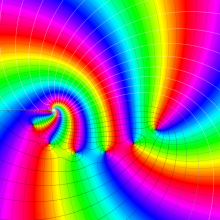
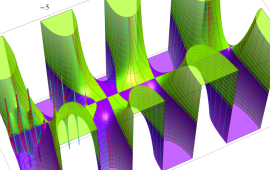
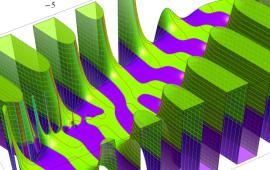
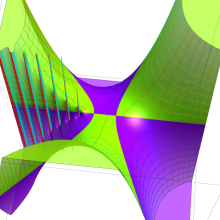
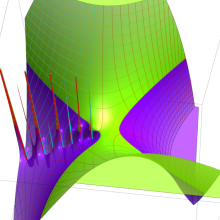
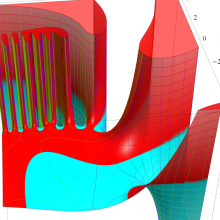
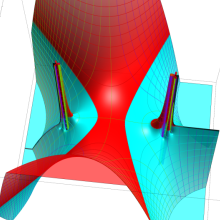
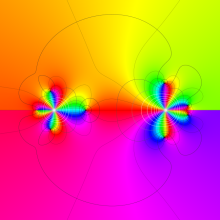
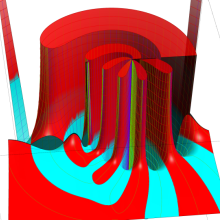
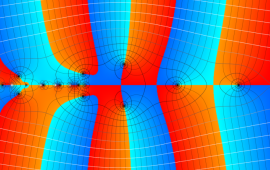
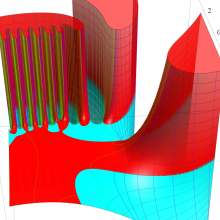
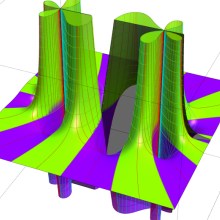
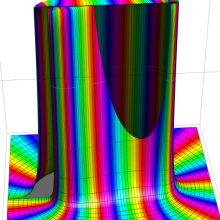
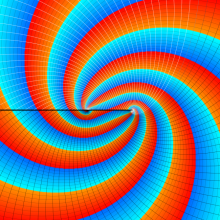
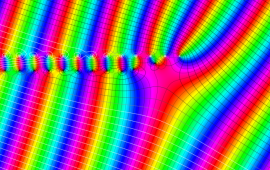
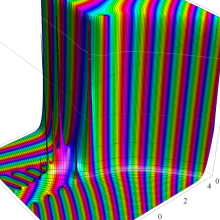
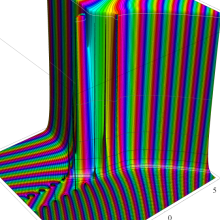
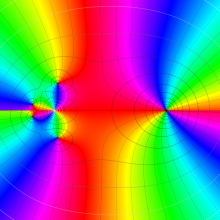
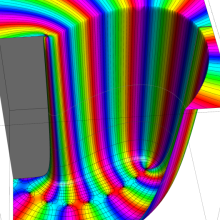
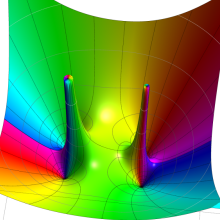
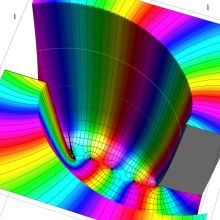
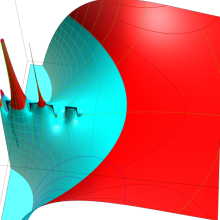
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer05100.png)
のグラフ。

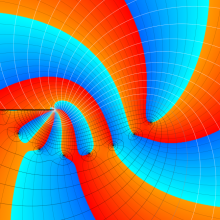
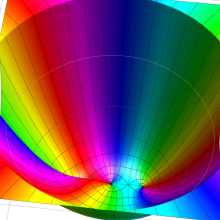
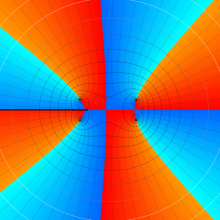
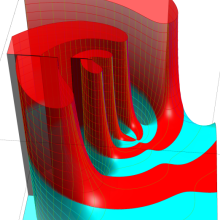
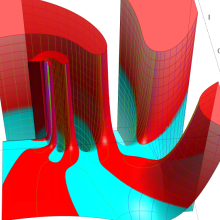
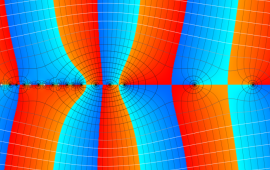
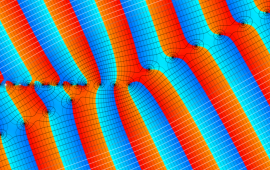
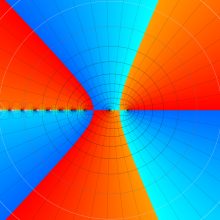
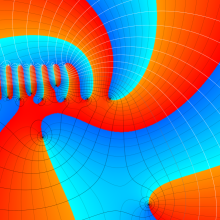
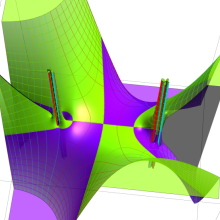
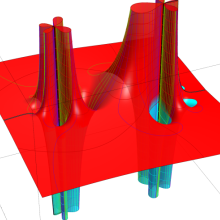
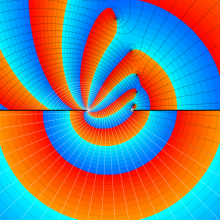
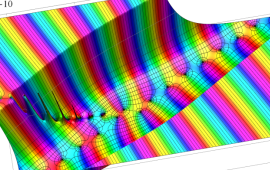
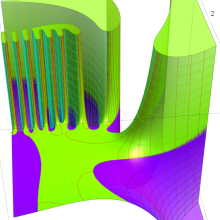
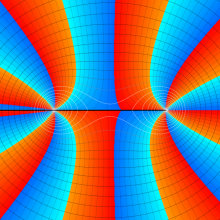
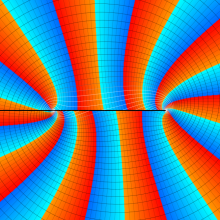
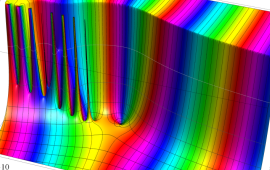
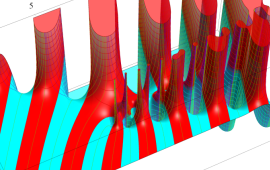
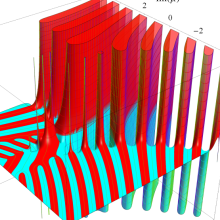
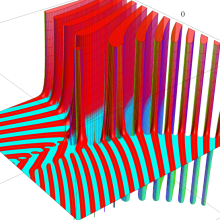
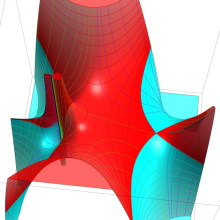
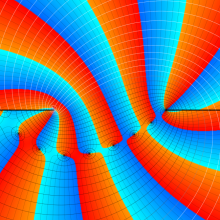
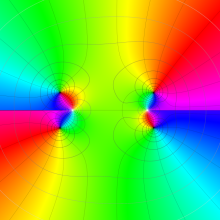
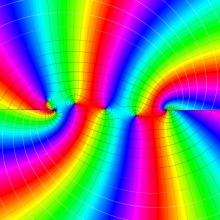
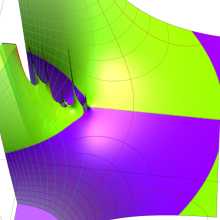
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer05200.png)
のグラフ。
アニメーション
(9.77MB)

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer05300.png)
のグラフ。
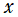
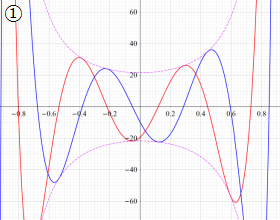
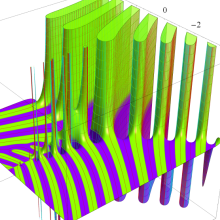
を実変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer05400.png)
のグラフ。
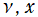
を実2変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer05400.png)
のグラフ。
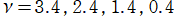
並びに
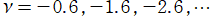
では関数が定義されない。
2番目は、
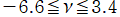
の範囲を拡大した場合。

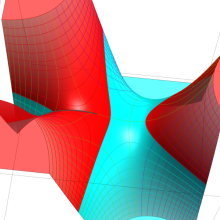
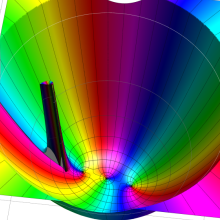
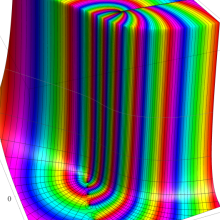
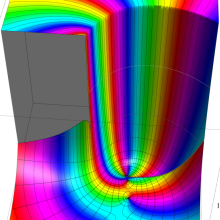
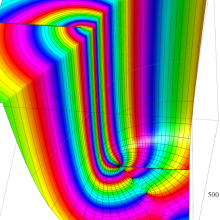
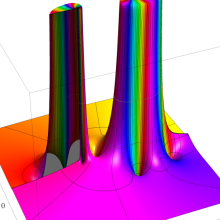
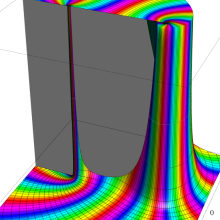
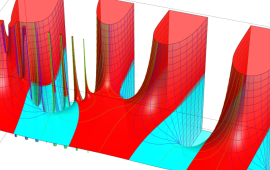
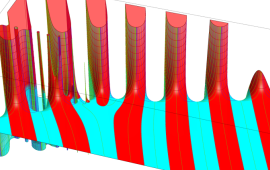
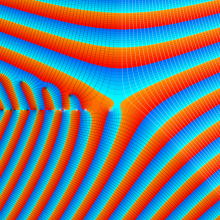
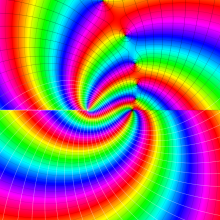
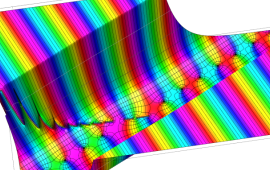
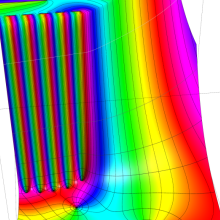
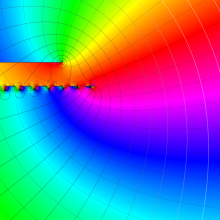
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer05800.png)
のグラフ。

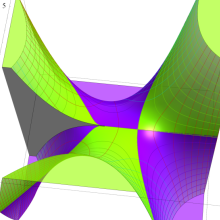
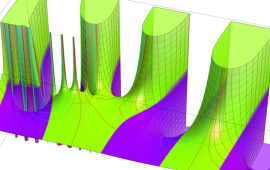
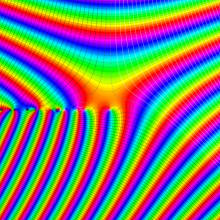
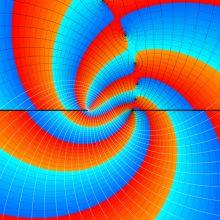
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer05900.png)
のグラフ。

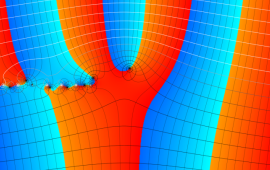
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer06000.png)
のグラフ。

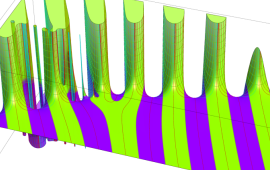
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer06100.png)
のグラフ。

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer06200.png)
のグラフ。

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer06300.png)
のグラフ。

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer06400.png)
のグラフ。

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer06500.png)
のグラフ。
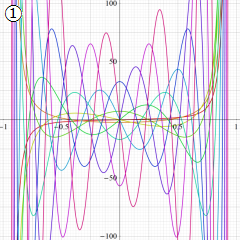
 (変数ν)](siki_spec210/gegenbauer07300.png)

を実変数とする、第1種 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer06700.png)
,
②](siki_spec210/gegenbauer06800.png)
。

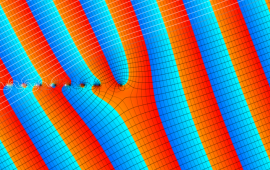
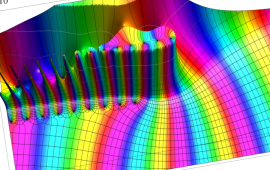
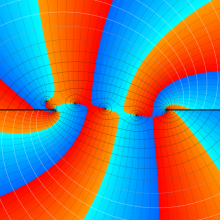
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer06900.png)
のグラフ。

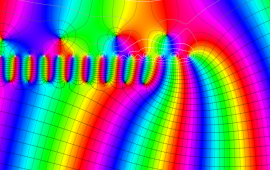
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer07000.png)
のグラフ。

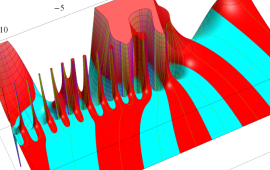
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer07100.png)
のグラフ。

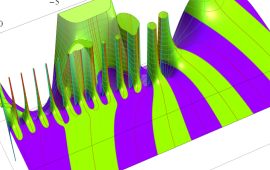
を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer07200.png)
のグラフ。
 (変数μ)](siki_spec210/gegenbauer08100.png)

を実変数とする、第1種 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer07400.png)
,
②](siki_spec210/gegenbauer07500.png)
。
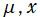
を実2変数とする、第1種 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer07400.png)
,
②](siki_spec210/gegenbauer07500.png)
。

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer07700.png)
のグラフ。

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer07800.png)
のグラフ。

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer07900.png)
のグラフ。

を複素変数とする、第1種 Gegenbauer 関数
](siki_spec210/gegenbauer08000.png)
のグラフ。
 (変数ν,μ)](siki_spec210/gegenbauer08500.png)
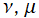
を実2変数とする、第1種 Gegenbauer 関数のグラフ。
①,
②](siki_spec210/gegenbauer08300.png)
。
③,
④](siki_spec210/gegenbauer08400.png)
。
, C[ν,(μ)](z)/μ](siki_spec210/gegenbauer09000.png)
冒頭で触れたとおり、繰込形式の Gegenbauer 関数
](siki_spec210/gegenbauer03600.png)
は実質的に第1種 Chebyshev 関数である。よって、

を複素変数とする
](siki_spec210/gegenbauer03600.png)
のグラフは省略する。
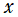
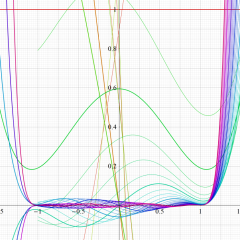
を実変数とする、繰込形式の Gegenbauer 関数のグラフ。
①整数次
](siki_spec210/gegenbauer08600.png)
(Gegenbauer 多項式),
②実数次
](siki_spec210/gegenbauer08700.png)
。
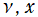
を実2変数とする、繰込形式の Gegenbauer 関数
](siki_spec210/gegenbauer08700.png)
のグラフ。
極限を取る前の、繰込形式の Gegenbauer 関数
/μ](siki_spec210/gegenbauer08800.png)
と、その
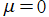
への連続的な推移。
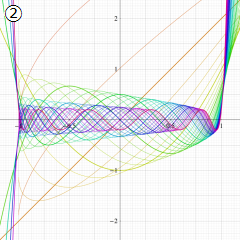
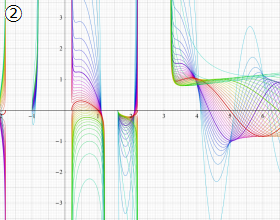
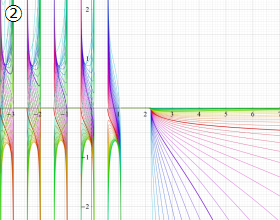
](siki_spec210/gegenbauer10900.png)
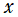
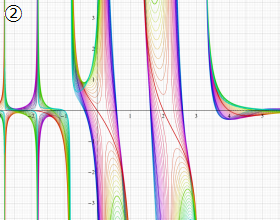
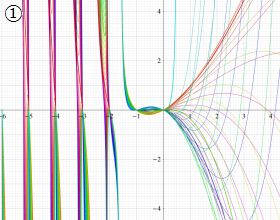
を実変数とする、第2種 Gegenbauer 関数のグラフ。
①整数次
](siki_spec210/gegenbauer09100.png)
,
②実数次
](siki_spec210/gegenbauer09200.png)
。
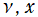
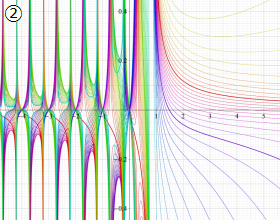
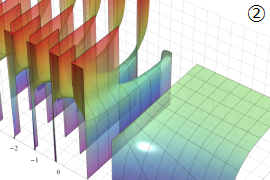
を実2変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer09200.png)
のグラフ。
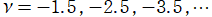
では関数が定義されない。
2番目は、
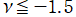
の範囲を拡大した場合。
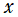
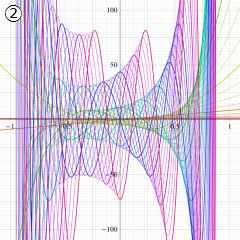
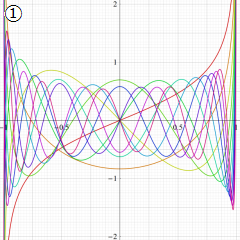
を実変数とする、第2種 Gegenbauer 関数のグラフ。
①整数次
](siki_spec210/gegenbauer09300.png)
,
②実数次
](siki_spec210/gegenbauer09400.png)
。
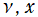
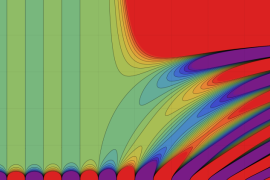
を実2変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer09400.png)
のグラフ。
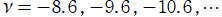
では関数が定義されない。

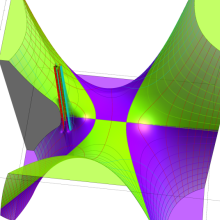
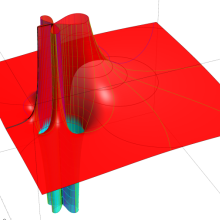
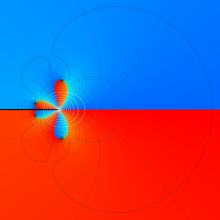
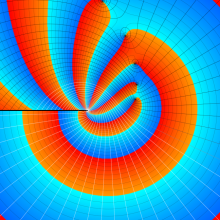
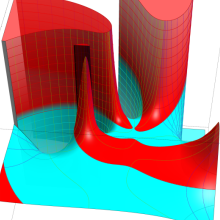
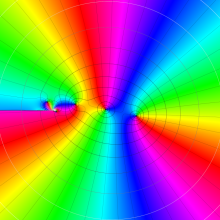
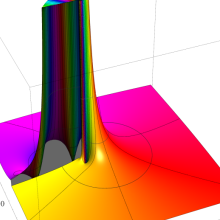
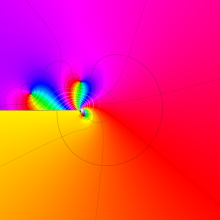
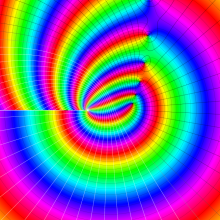
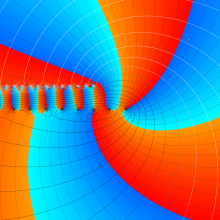
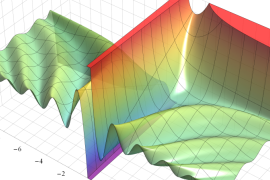
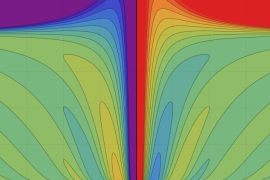
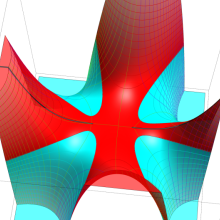
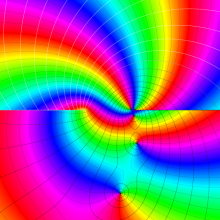
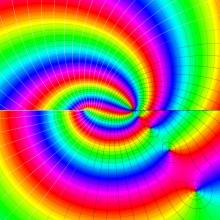
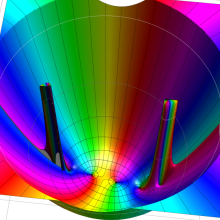
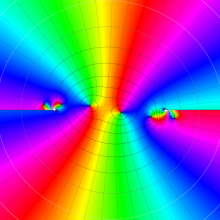
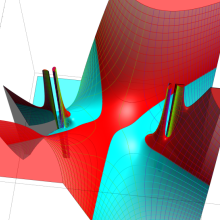
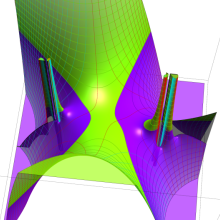
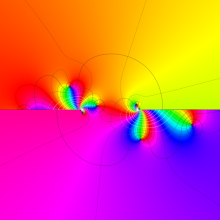
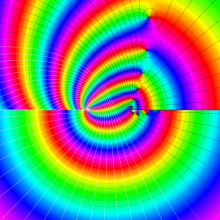
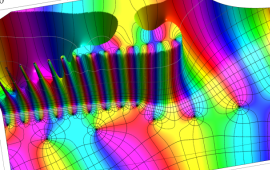
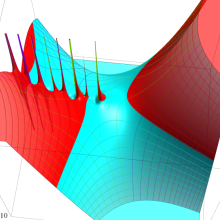
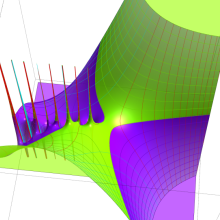
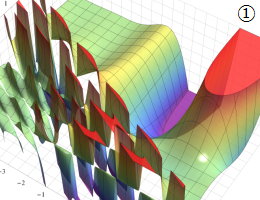
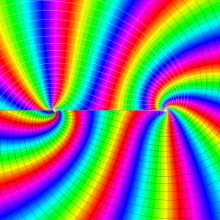
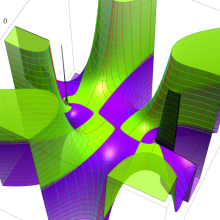
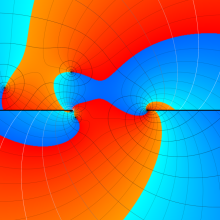
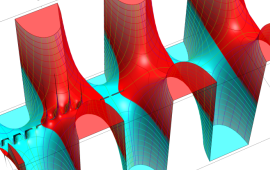
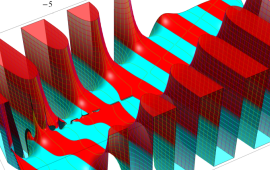
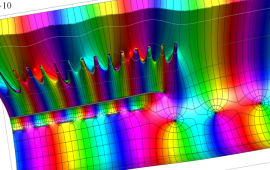
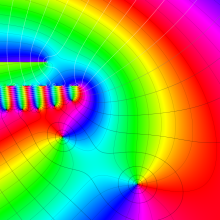
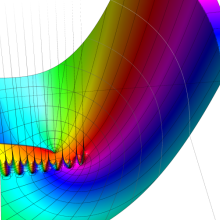
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer09500.png)
のグラフ。

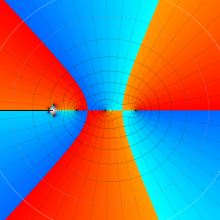
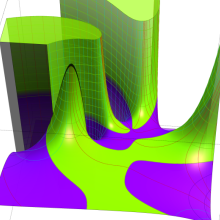
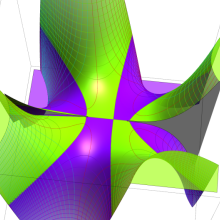
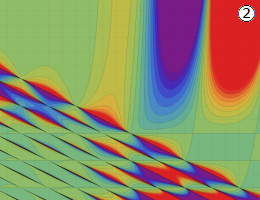
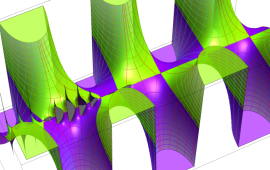
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer09600.png)
のグラフ。

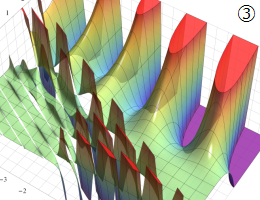
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer09700.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer09800.png)
のグラフ。
アニメーション
(11.0MB)

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer09900.png)
のグラフ。
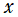
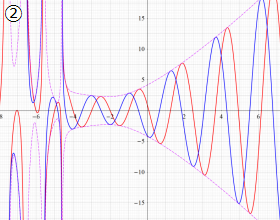
を実変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10000.png)
のグラフ。
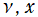
を実2変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10000.png)
のグラフ。
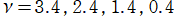
並びに
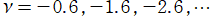
では関数が定義されない。
2番目は、
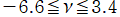
の範囲を拡大した場合。

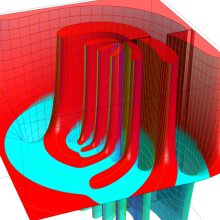
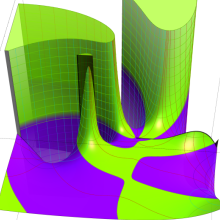
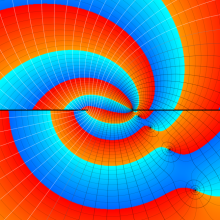
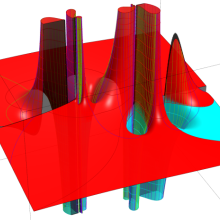
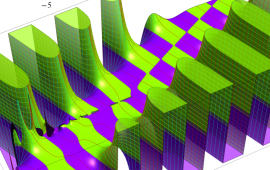
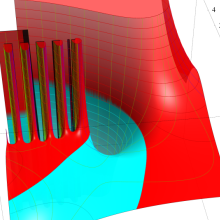
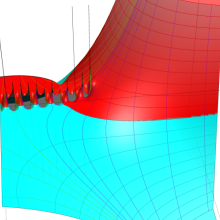
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10100.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10200.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10300.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10400.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10500.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10600.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10700.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer10800.png)
のグラフ。
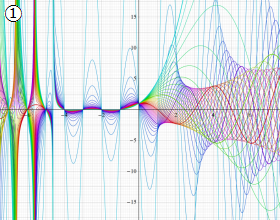
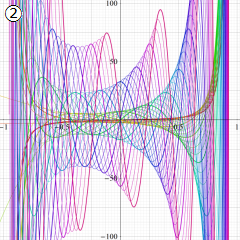
 (変数ν)](siki_spec210/gegenbauer11600.png)

を実変数とする、第2種 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer11000.png)
,
②](siki_spec210/gegenbauer11100.png)
。

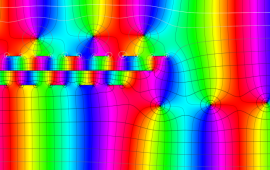
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer11200.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer11300.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer11400.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer11500.png)
のグラフ。
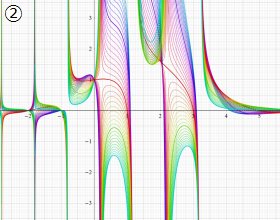
 (変数μ)](siki_spec210/gegenbauer12300.png)

を実変数とする、第2種 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer11700.png)
,
②](siki_spec210/gegenbauer11800.png)
。
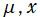
を実2変数とする、第2種 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer11700.png)
,
②](siki_spec210/gegenbauer11800.png)
。

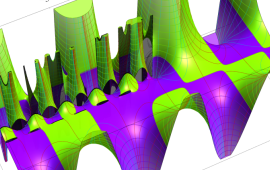
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer11900.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer12000.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer12100.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer12200.png)
のグラフ。
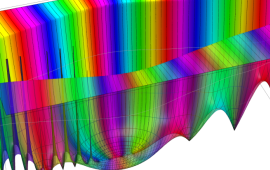
 (変数ν,μ)](siki_spec210/gegenbauer12600.png)
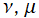
を実2変数とする、第2種 Gegenbauer 関数のグラフ。
①,
②](siki_spec210/gegenbauer12400.png)
。
③,
④](siki_spec210/gegenbauer12500.png)
。
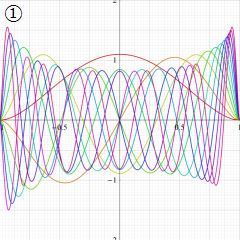
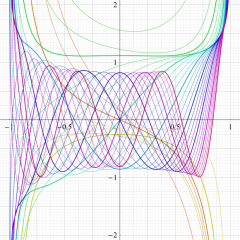
とS[ν,(μ)](z)の関係](siki_spec210/gegenbauer13000.png)
余弦・正弦関数に類似した
](siki_spec210/gegenbauer12700.png)
と
](siki_spec210/gegenbauer12800.png)
の関係。このとき、両者の包絡線は
^2+S[ν,(μ)](z)^2)](siki_spec210/gegenbauer12900.png)
となる。
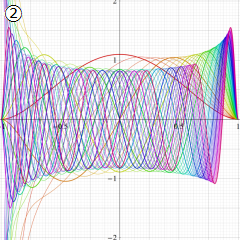
実2変数
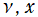
の場合。
](siki_spec210/gegenbauer14000.png)
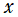
を実変数とする、第2種 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer13100.png)
,
②](siki_spec210/gegenbauer13200.png)
。

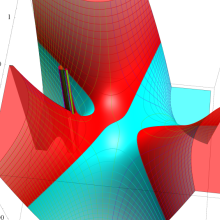
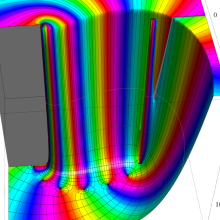
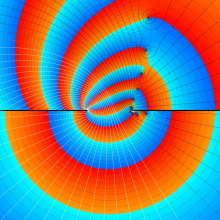
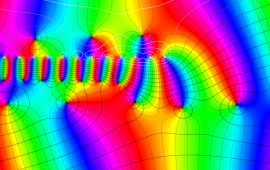
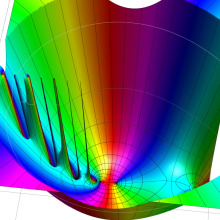
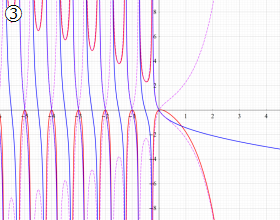
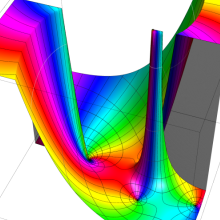
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer13300.png)
のグラフ。

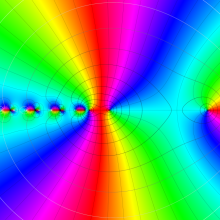
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer13400.png)
のグラフ。

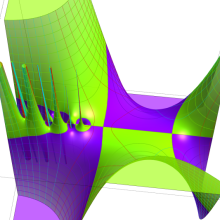
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer13500.png)
のグラフ。
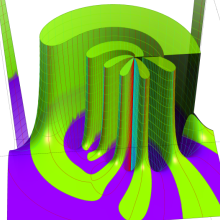
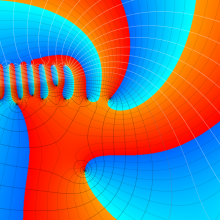
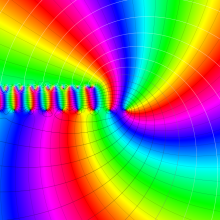
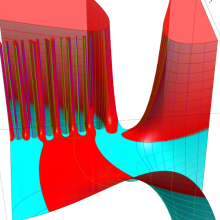
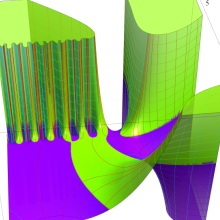
アニメーション
(22.9MB)

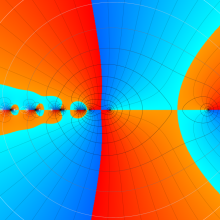
を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer13600.png)
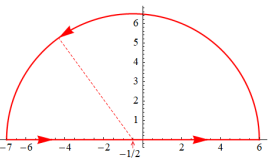
のグラフ。ここに次数は、複素

平面上を2番目の図のように動く。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer13700.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer13800.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer13900.png)
のグラフ。
 (変数ν)](siki_spec210/gegenbauer14600.png)

を実変数とする第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14100.png)
は、
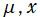
が実数であっても一般に実数値を取らない。よって、そのグラフは省略する。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14200.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14300.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14400.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14500.png)
のグラフ。
 (変数μ)](siki_spec210/gegenbauer15100.png)

を実変数とする第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14100.png)
は、
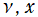
が実数であっても一般に実数値を取らない。よって、そのグラフは省略する。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14700.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14800.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer14900.png)
のグラフ。

を複素変数とする、第2種 Gegenbauer 関数
](siki_spec210/gegenbauer15000.png)
のグラフ。
Gegenbauer 多項式
](siki_spec210/gegenbauer15200.png)
は、直交区間を
![[-1, 1]](siki_spec210/gegenbauer15300.png)
とする直交多項式であり、重み関数を伴う直交性
を持っている。超球面調和関数の正規化因子を求める場合等では、上記に
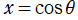
の置換積分を施した
の形が必要になる※1。Gegenbauer 多項式は、超幾何関数系で Jacobi 多項式に次いで複雑な直交性を持つ古典的直交多項式であり、その q-類似も含めて組合せ論的な研究が進展している。
さて、当サイトでは Gegenbauer 関数に対しても、独自に
を導入し、正規化 Gegenbauer 関数と呼ぶ※2。よって、
} (n ∈ N≧0)](siki_spec210/gegenbauer15800.png)
は
正規直交関数系を成すとともに、重み関数が現れない直交性
を満たす。
これまでに現れた関係式から、正規化 Gegenbauer 関数は Legendre 陪関数と、
の違いしかないことが分かる※3。
【註記】
※1:Legendre 陪関数と異なり、この直交性は

が正の実数ならば成立するので、超球面調和関数を構成するときに大変都合が良い。(Gegenbauer 関数を導入する意義は、正にこの事に尽きる。)
※2:関数記号は正規化 (Normalization) に基づく。また、当サイトでは
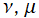
および

を複素数まで許容する。
※3:したがって、グラフの掲載数を若干削減する。
](siki_spec210/gegenbauer17600.png)
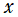
を実変数とする、正規化 Gegenbauer 関数のグラフ。
①整数次
](siki_spec210/gegenbauer16100.png)
,
②実数次
](siki_spec210/gegenbauer16200.png)
。
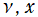
を実2変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer16200.png)
のグラフ。
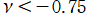
では関数が実数値を取らない

の帯状領域がある。
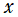
を実変数とする、正規化 Gegenbauer 関数のグラフ。
①整数次
](siki_spec210/gegenbauer16400.png)
,
②実数次
](siki_spec210/gegenbauer16500.png)
。
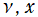
を実2変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer16500.png)
のグラフ。
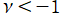
では関数が実数値を取らない

の帯状領域がある。

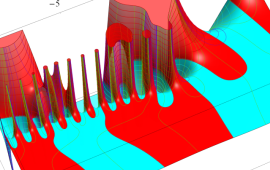
を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer16700.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer16800.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer16900.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer17000.png)
のグラフ。
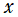
を実変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer17100.png)
のグラフ。
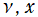
を実2変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer17100.png)
のグラフ。
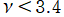
では関数が実数値を取らない

の帯状領域がある。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer17300.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer17400.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer17500.png)
のグラフ。
 (変数ν)](siki_spec210/gegenbauer18300.png)

を実変数とする、正規化 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer17700.png)
,
②](siki_spec210/gegenbauer17800.png)
。

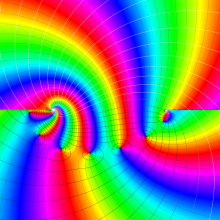
を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer17900.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer18000.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer18100.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer18200.png)
のグラフ。
 (変数μ)](siki_spec210/gegenbauer18900.png)

を実変数とする、正規化 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer18400.png)
,
②](siki_spec210/gegenbauer18500.png)
。
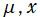
を実2変数とする、正規化 Gegenbauer 関数のグラフ。
①](siki_spec210/gegenbauer18400.png)
,
②](siki_spec210/gegenbauer18500.png)
。

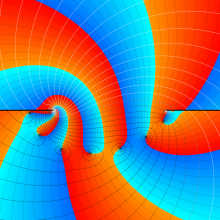
を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer18600.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer18700.png)
のグラフ。

を複素変数とする、正規化 Gegenbauer 関数
](siki_spec210/gegenbauer18800.png)
のグラフ。
 (変数ν,μ)](siki_spec210/gegenbauer19200.png)
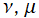
を実2変数とする、正規化 Gegenbauer 関数のグラフ。
①,
②](siki_spec210/gegenbauer19000.png)
。
③,
④](siki_spec210/gegenbauer19100.png)
。
日:
超球面調和関数,
高次元球面調和関数
英:
Ultraspherical harmonics,
Hyperspherical harmonics,仏:
Harmonique ultrasphérique,独:
Ultrakugelflächenfunktion
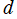
次元超球座標で変数分離した Laplace 方程式の一般解
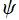
は、すでに冒頭の節で与えられている。このうち、方位角および天頂角方向の解は第1種の基本解のみ (つまり、
![B[l] = 0 (l = 1, 2, …, d-1))](siki_spec210/gegenbauer19300.png)
となる場合) を採用した特別な固有関数解を選び、しかも動径方向
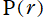
を除外した多変数関数
を考える。超球面全体にわたる積分が1となる要請
のうち、さらに具体的な条件
を課せば、正規化因子
![A[l]](siki_spec210/gegenbauer19800.png)
が決定される。特に
![A[1] = 1/Sqrt(2π)](siki_spec210/gegenbauer19900.png)
となるが、
![A[k] (k = 2, 3, …, d-1)](siki_spec210/gegenbauer20000.png)
は前述の Gegenbauer 多項式の直交性から求められ、
となる。以上の手順を経て、超球面調和関数
が導かれる※1。名称については、高次元球面調和関数 (または特定の次元数を冠して
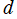
次元球面調和関数) と呼ぶこともある。
既に述べた公式および
ガンマ関数の倍数公式等を用いれば、Gegenbauer 多項式の部分を Legendre 陪関数および
球面調和関数に書き換えて (つまり、Legendre 陪関数の直交性を経由せずに)、
と表示することもできる。特に
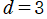
の超球面調和関数は、球面調和関数と Condon - Shortley の位相だけ異なることが分かる※2。
通常、球面調和関数の次数は整数に限定されるが、これが半奇数の場合でも (階乗をガンマ関数で置き換えて) 計算可能であると定義するならば、超球面調和関数を球面調和関数の有限積
で表わすことができる※2。
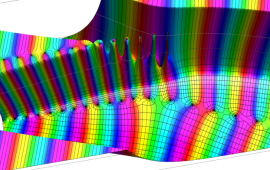
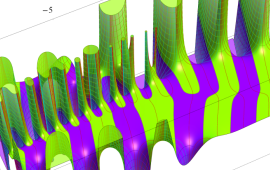
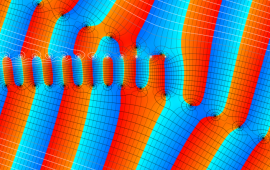
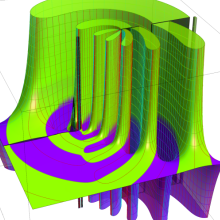
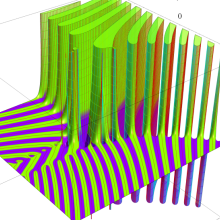
超球面調和関数をそのままグラフで視覚化するのは難しい。当サイトでは、
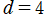
の場合のみを扱い、しかも
![θ[1], θ[2], θ[3]](siki_spec210/gegenbauer20700.png)
のいずれかを動かしたときのアニメーションを中心に掲載する。
また、球面調和関数に付随して
Wigner の 3-j 記号が現れたように、
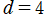
の超球面調和関数では 「6-j 記号」 並びに 「9-j 記号」 が現れるが、当サイトでは詳述しない※3。
【註記】
※1:この表示式は、サイト管理人が上記の手順に則って独自に求めたものである。したがって、論文等で採用されている表示式および記号と、見かけが異なるかもしれない。
※2:つまり
 = (-1)^n[1]*Y[n2, n1](θ[2], θ[1])](siki_spec210/gegenbauer20800.png)
となる。(次数および変数の順序が逆になる不都合は、当サイトが採用した超球座標の表記法に由来する。)
※3:6-j 記号, 9-j 記号自体の詳細は、
NIST の Chapter34 にある。
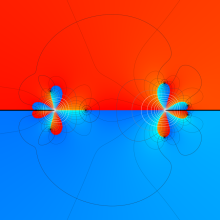
](siki_spec210/gegenbauer22000.png)
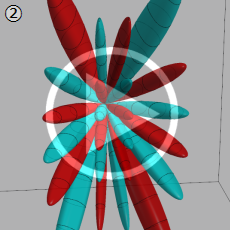
![θ[1], θ[2]](siki_spec210/gegenbauer20900.png)
を変数とする超球面調和関数
①)](siki_spec210/gegenbauer21000.png)
,
②))](siki_spec210/gegenbauer21200.png)
,
③))](siki_spec210/gegenbauer21300.png)
のグラフを、
![0 ≦ θ[3] ≦ π](siki_spec210/gegenbauer21100.png)
で動かした場合のアニメーション
(2.96~3.26MB)。末尾の図は座標の取り方を示す (以下同様)。
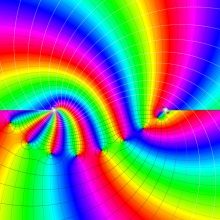
![θ[1], θ[3]](siki_spec210/gegenbauer21400.png)
を変数とする超球面調和関数
①)](siki_spec210/gegenbauer21000.png)
,
②))](siki_spec210/gegenbauer21200.png)
,
③))](siki_spec210/gegenbauer21300.png)
のグラフを、
![0 ≦ θ[2] ≦ π](siki_spec210/gegenbauer21500.png)
で動かした場合のアニメーション
(3.27~3.50MB)。
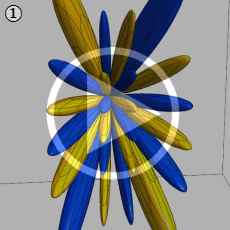
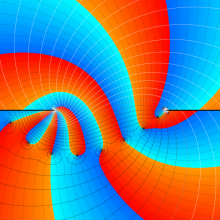
![θ[2], θ[3]](siki_spec210/gegenbauer21600.png)
を変数とする超球面調和関数
①)](siki_spec210/gegenbauer21000.png)
,
②))](siki_spec210/gegenbauer21200.png)
,
③))](siki_spec210/gegenbauer21300.png)
のグラフを、
![0 ≦ θ[1] ≦ 2π/5](siki_spec210/gegenbauer21700.png)
で動かした場合のアニメーション
(3.06~5.94MB)。
(
![0 ≦ θ[1] ≦ 2π/5](siki_spec210/gegenbauer21700.png)
が周期ゆえ、
![0 ≦ θ[1] ≦ 2π](siki_spec210/gegenbauer21800.png)
で動かすと5周期 ― コマ数が冗長 ― となる。)
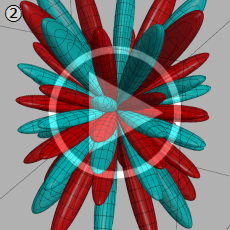
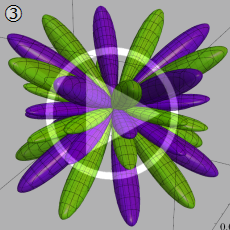
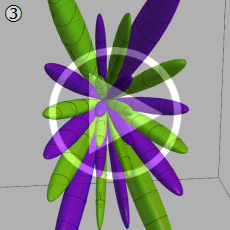
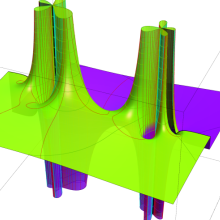
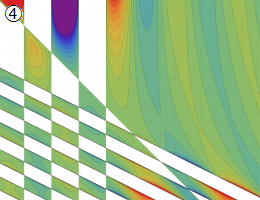
![θ[1], θ[2], θ[3]](siki_spec210/gegenbauer20700.png)
を変数とする超球面調和関数
①)](siki_spec210/gegenbauer21000.png)
,
②))](siki_spec210/gegenbauer21200.png)
,
③))](siki_spec210/gegenbauer21300.png)
のグラフを、直交直線座標
![{θ[1], θ[2], θ[3]}](siki_spec210/gegenbauer21900.png)
で描画する。
](siki_spec210/gegenbauer02300.png) は当サイトが独自に定義したものであって、
は当サイトが独自に定義したものであって、](siki_spec210/gegenbauer02200.png) が余弦関数に相当すると見たとき、
が余弦関数に相当すると見たとき、](siki_spec210/gegenbauer02300.png) は正弦関数に相当する。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針は、別頁 Questions に掲示している。)
は正弦関数に相当する。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針は、別頁 Questions に掲示している。)](siki_spec210/gegenbauer03600.png) は第1種 Gegenbauer 関数の "繰込形式" と呼ばれる。書籍によっては
は第1種 Gegenbauer 関数の "繰込形式" と呼ばれる。書籍によっては](siki_spec210/gegenbauer03600.png) を
を](siki_spec210/gegenbauer03700.png) と表記することもあるが、明らかに両者は同一ではなく、混乱を避けるため当サイトでは区別する。
と表記することもあるが、明らかに両者は同一ではなく、混乱を避けるため当サイトでは区別する。](siki_spec210/gegenbauer03800.png) であるが、当サイトでは他の記法に合わせて
であるが、当サイトでは他の記法に合わせて](siki_spec210/gegenbauer02500.png) と表記する。また同著では、正規化していない超幾何関数の閉形式で掲載している。
と表記する。また同著では、正規化していない超幾何関数の閉形式で掲載している。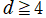 では Legendre 陪関数の次数が半奇数になる場合が現れるため、直交性が適用できない。
では Legendre 陪関数の次数が半奇数になる場合が現れるため、直交性が適用できない。 が正の実数ならば成立するので、超球面調和関数を構成するときに大変都合が良い。(Gegenbauer 関数を導入する意義は、正にこの事に尽きる。)
が正の実数ならば成立するので、超球面調和関数を構成するときに大変都合が良い。(Gegenbauer 関数を導入する意義は、正にこの事に尽きる。)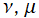 および
および を複素数まで許容する。
を複素数まで許容する。 = (-1)^n[1]*Y[n2, n1](θ[2], θ[1])](siki_spec210/gegenbauer20800.png) となる。(次数および変数の順序が逆になる不都合は、当サイトが採用した超球座標の表記法に由来する。)
となる。(次数および変数の順序が逆になる不都合は、当サイトが採用した超球座標の表記法に由来する。)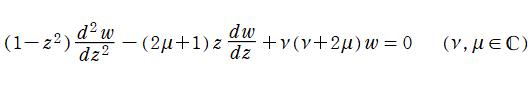
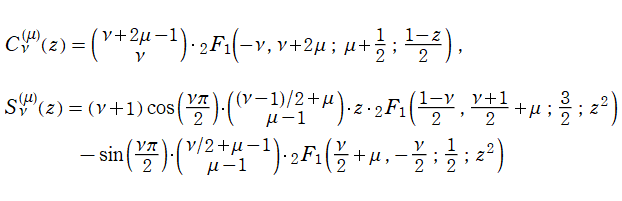
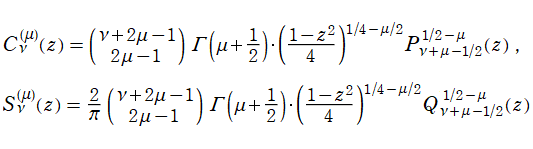
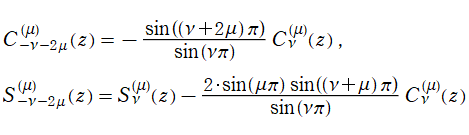
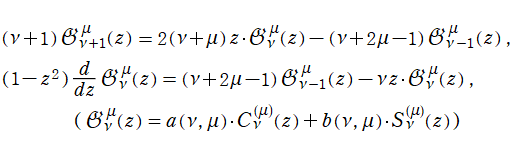
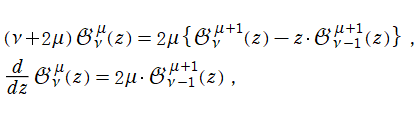
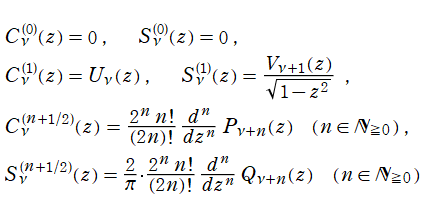
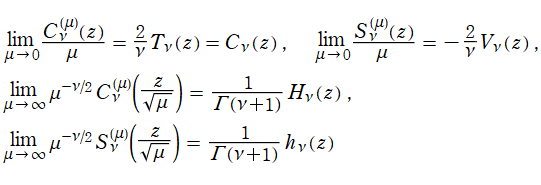
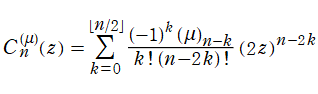
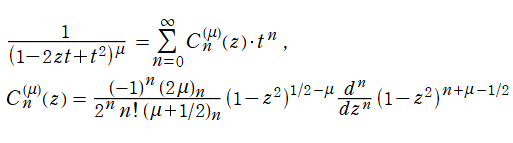
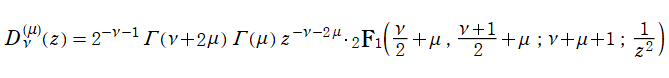
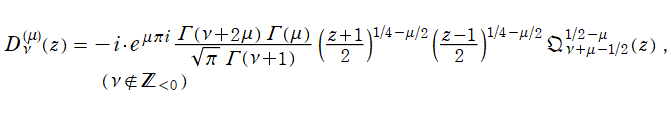
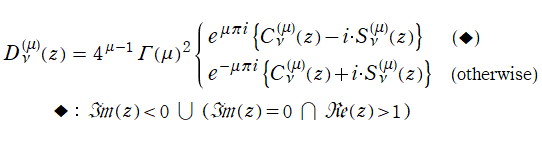
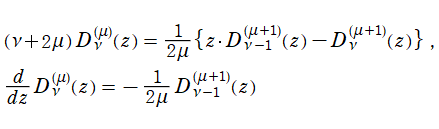
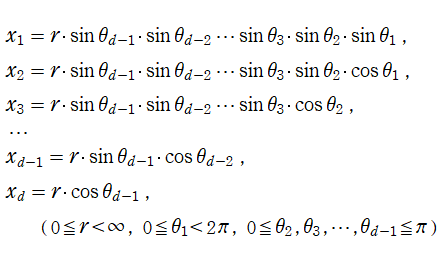
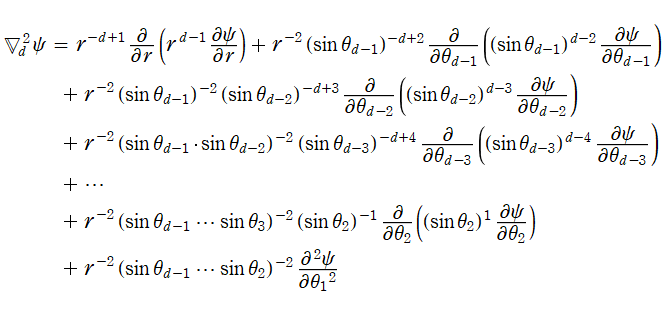
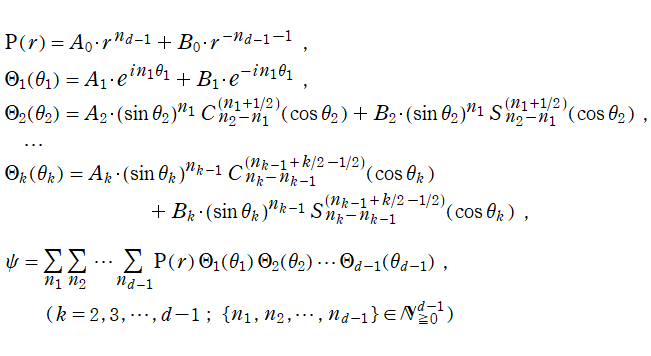
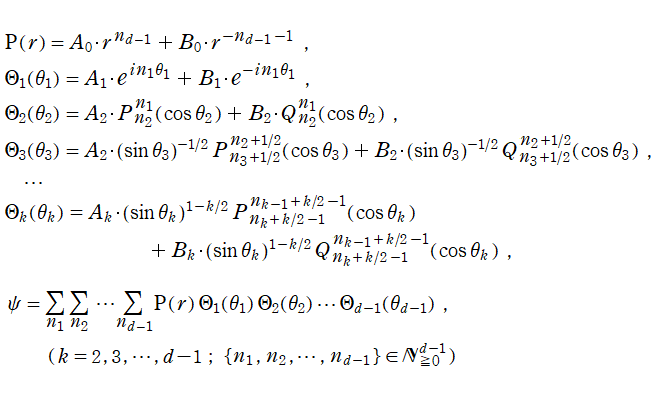






































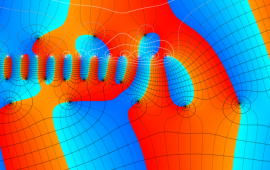
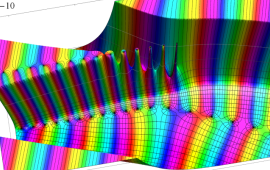
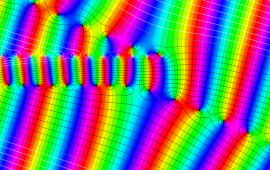
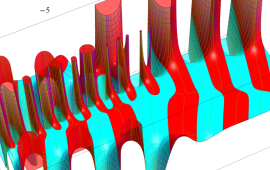































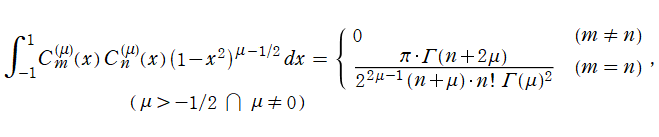
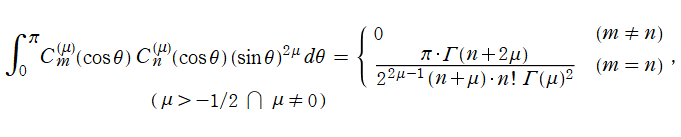
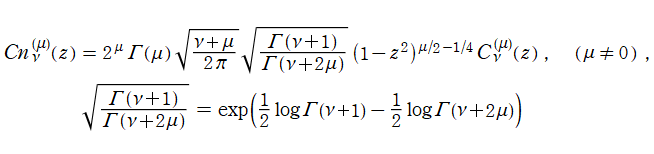
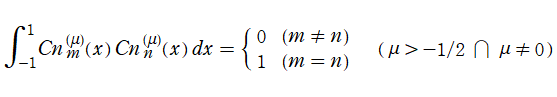
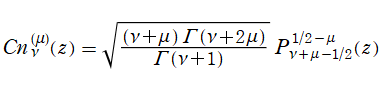
















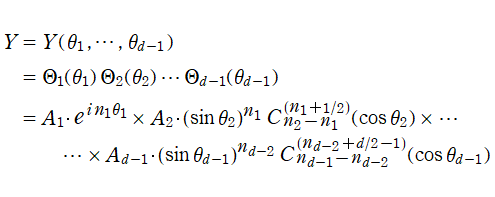
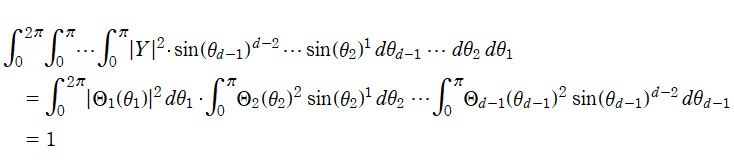
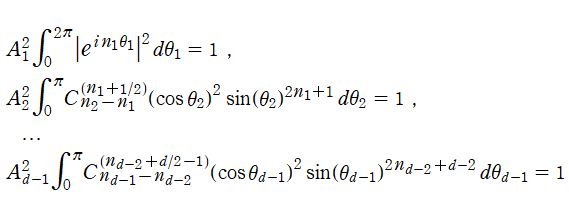
![A[k] (2≦k≦d-1)の値](siki_spec210/gegenbauer20100.png)