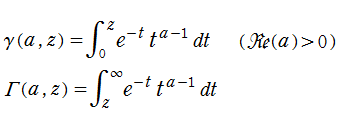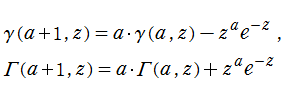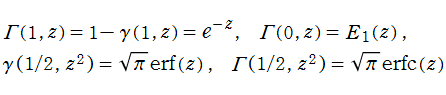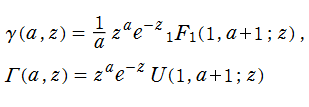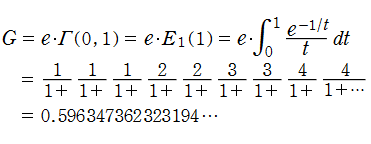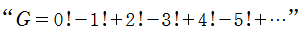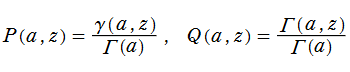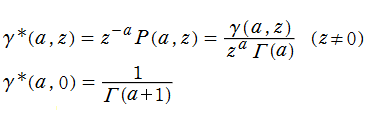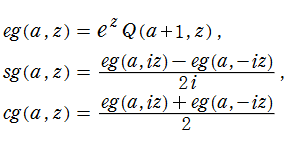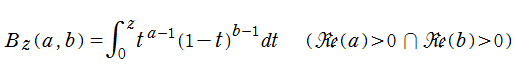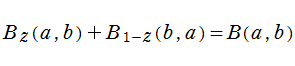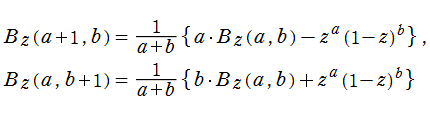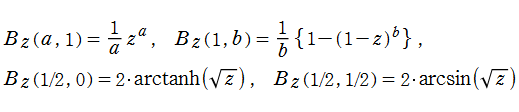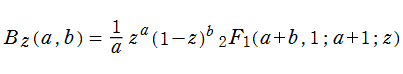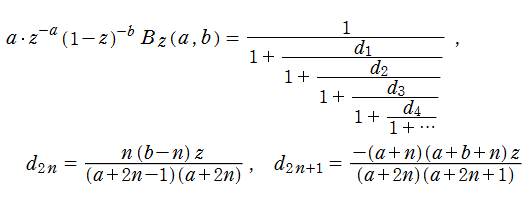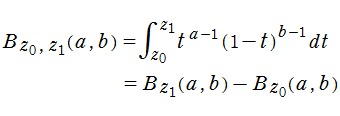特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
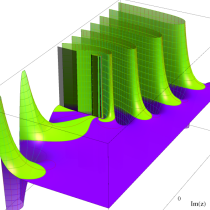
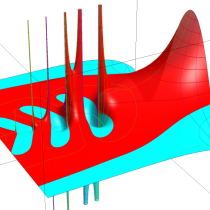
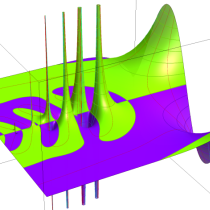
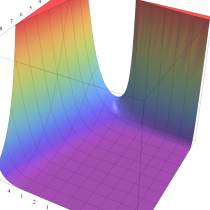
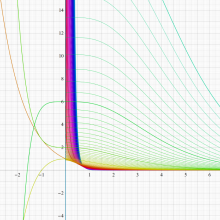
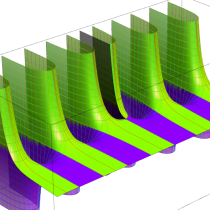
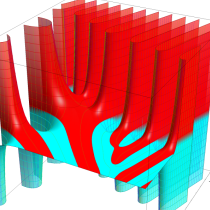
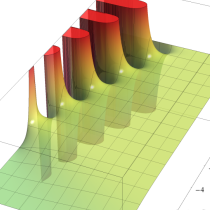
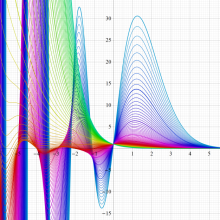
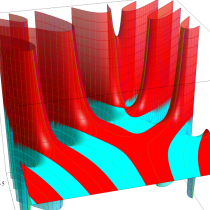
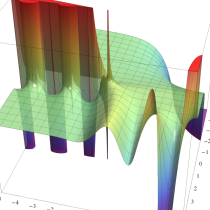
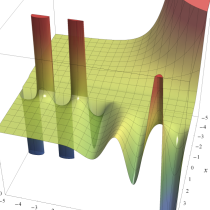
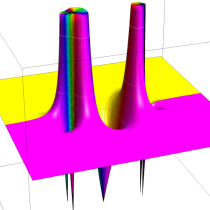
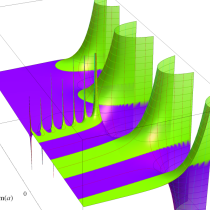
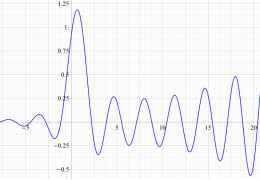
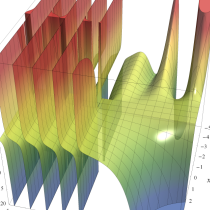
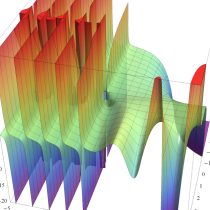
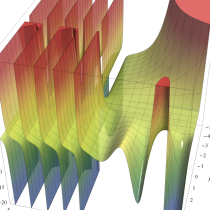
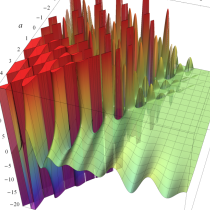
不完全ガンマ関数
不完全ガンマ関数
日:不完全ガンマ関数,不完全Γ関数英:Incomplete gamma function,仏:Fonction gamma incompléte,独:Unvollständige Gammafunktion
不完全ガンマ関数は、ガンマ関数の積分表示式 (第2種 Euler 積分) の積分区間を変数化した、二つの関数
である。区別して呼ぶ場合は 「不完全ガンマ関数」 の名称に、
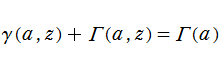
を満たす。
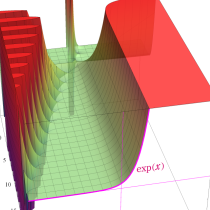
特別な
のように初等関数、積分指数関数、および誤差関数に還元されるので、先の関数等式を適用すれば、隣接する
不完全ガンマ関数は、合流型超幾何関数の特別な場合として
と表わすことができ、大半の性質はこれから導かれる。例えば、
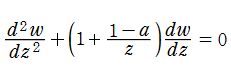
に展開できる。なお、後者の連分数展開式等に値を代入して得られる定数
は、「Gompertz の定数」 と呼ばれている※1。
不完全ガンマ関数は、ガンマ関数と同様に種々の積分計算に伴って現れる。例えば、Dirichlet 級数の積分表示式を求める場合や Euler - Maclaurin 和の公式を適用した計算などで現れる。
諸科学への応用例もいくつかあり、特に、統計学での各種確率分布の累積関数が著しい。その他にも、量子化学の Gauss 軌道および Slater 軌道、タンパク質の緩和時間における対数的振動、生態系および集団生物学への応用等がある。
不完全ガンマ関数は、A. M. Legendre がガンマ関数の研究に関連して1818年に定義したが、「不完全ガンマ関数」 なる名称は、1871年に O. X. Schlömilch が初めて使用して以降、一般に定着した。
【註記】
※1:1756年に L. Euler は、今日で言うところの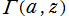 の漸近級数に値を強引に代入し、これと Gompertz の定数の連分数表示を比較することで、
の漸近級数に値を強引に代入し、これと Gompertz の定数の連分数表示を比較することで、
なる発散級数の意味付けが可能であるとした。(勿論、正しい推察ではない。Borel 総和法の意味では正しい。)
※1:1756年に L. Euler は、今日で言うところの
なる発散級数の意味付けが可能であるとした。(勿論、正しい推察ではない。Borel 総和法の意味では正しい。)
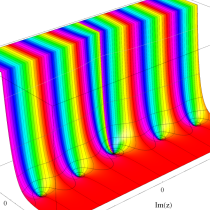
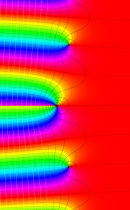
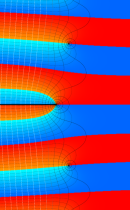
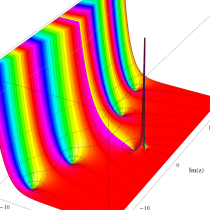
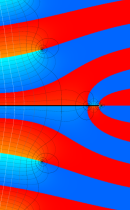
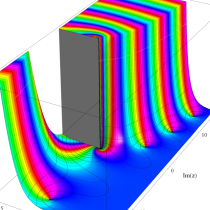
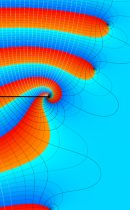
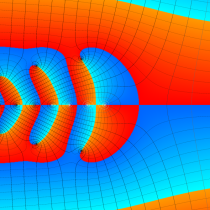
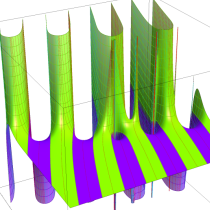
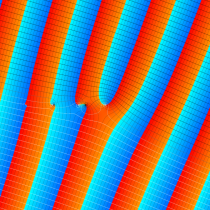
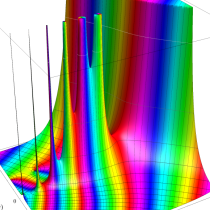
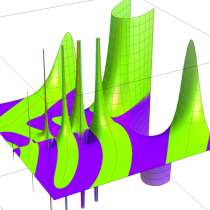
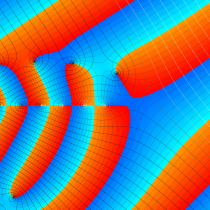
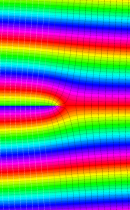
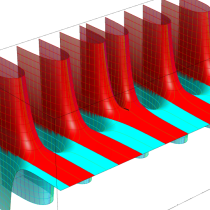
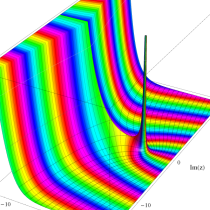
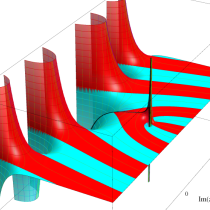
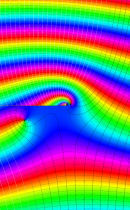
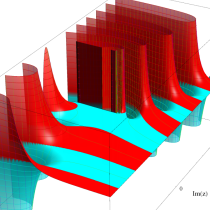
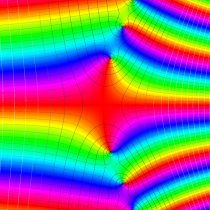
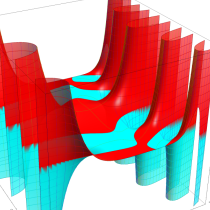
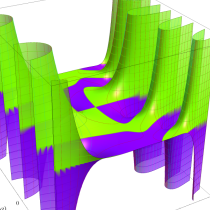
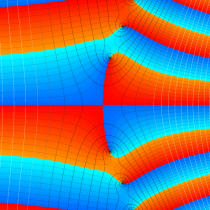
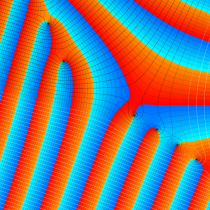
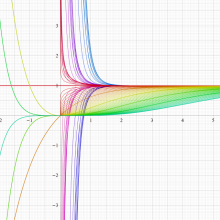
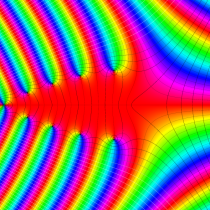
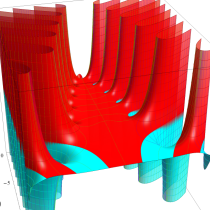
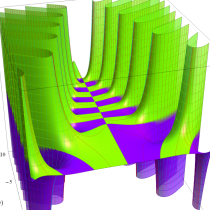
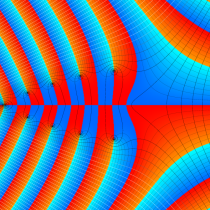
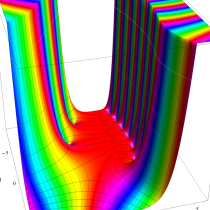
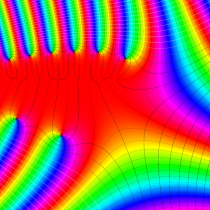
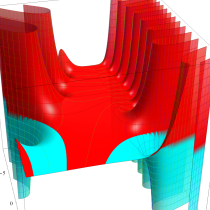
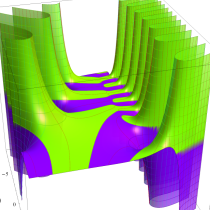
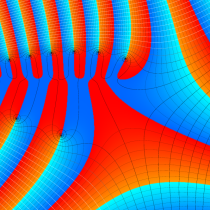
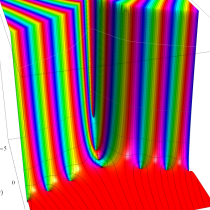
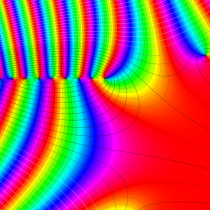
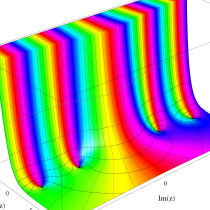
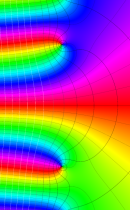
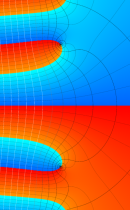
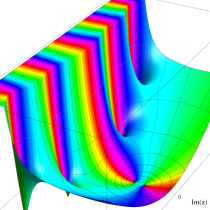
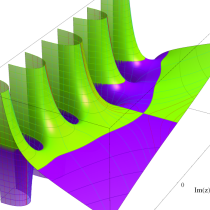
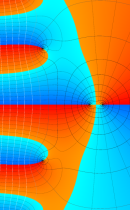
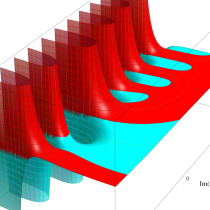
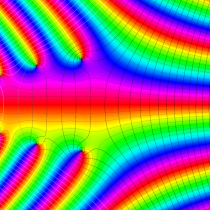
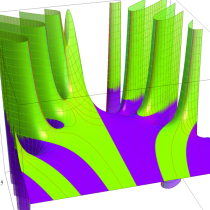
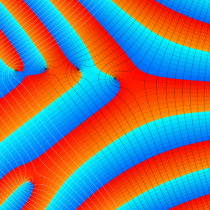
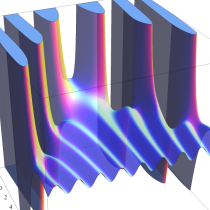
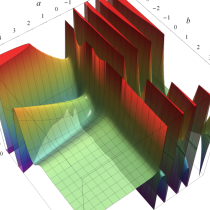
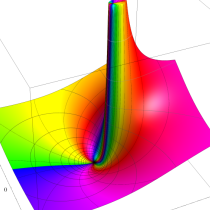
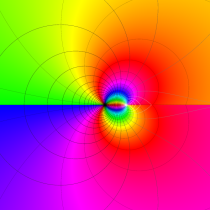
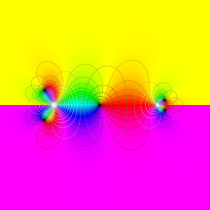
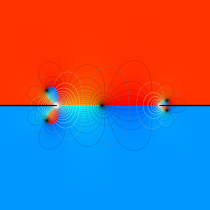
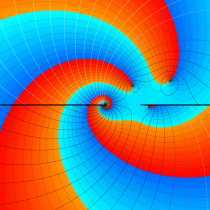
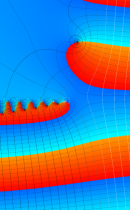
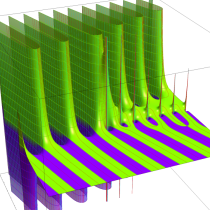
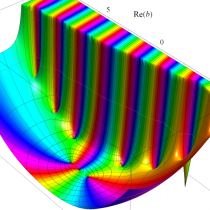
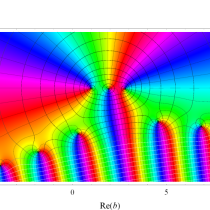
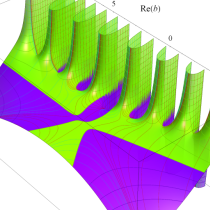
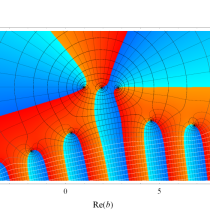
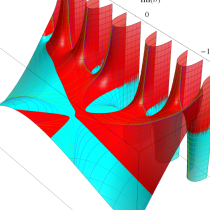
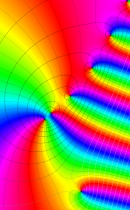
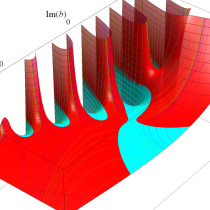
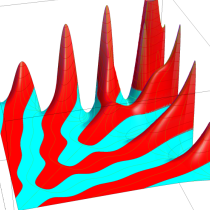
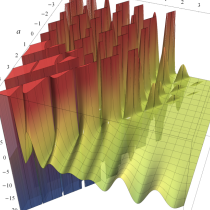
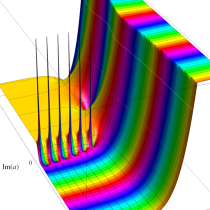
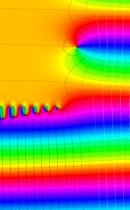
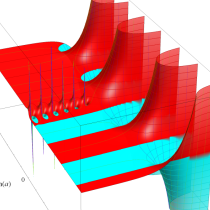
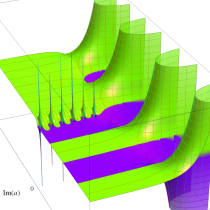
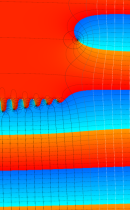
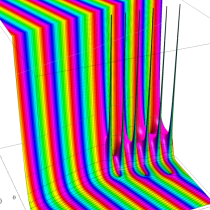
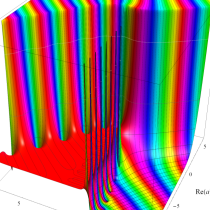
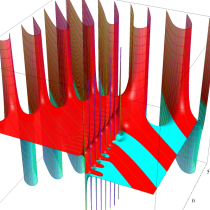
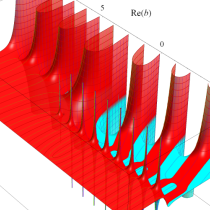
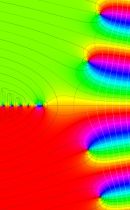
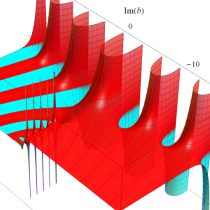
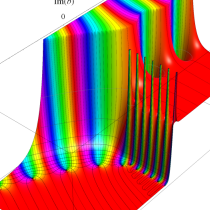
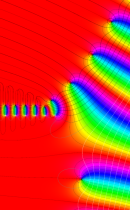
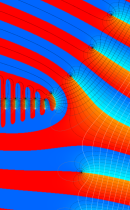
複素変数の不完全ガンマ関数
複素変数の不完全ガンマ関数
複素変数の不完全ガンマ関数
複素変数の不完全ガンマ関数
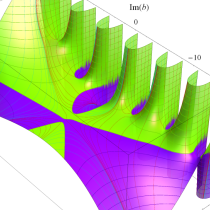
複素変数の不完全ガンマ関数
複素変数の不完全ガンマ関数
複素変数の不完全ガンマ関数
複素変数の不完全ガンマ関数
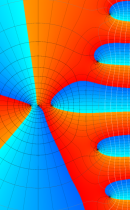
複素変数の不完全ガンマ関数
複素変数の不完全ガンマ関数
複素変数の不完全ガンマ関数
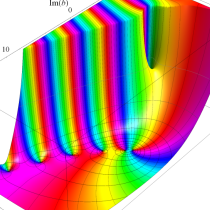
複素変数の不完全ガンマ関数
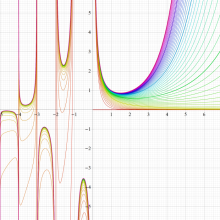
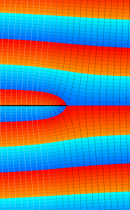
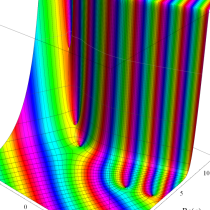
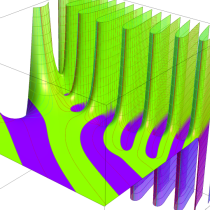
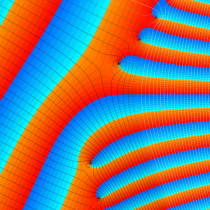
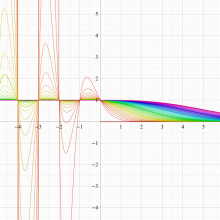
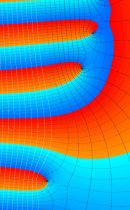
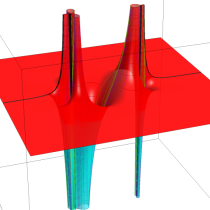
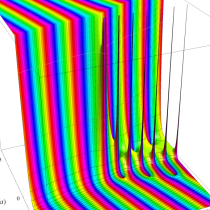
正則化不完全ガンマ関数
正則化不完全ガンマ関数とは、と定義することによって、
この定義から、両者は
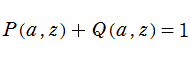
なお、これを更に正則化した関数、
も定義されている。
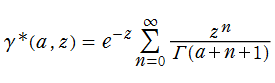
応用では不完全ガンマ関数と同等に扱われるが、特に、統計学では
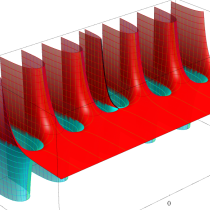
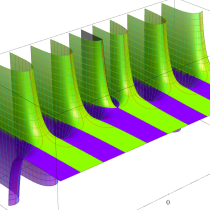
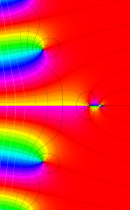
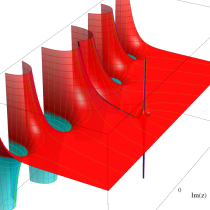
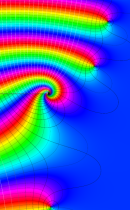
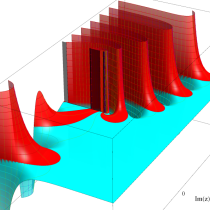
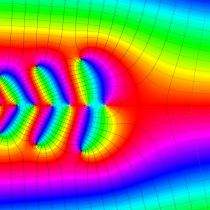
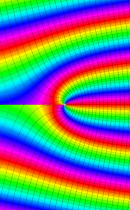
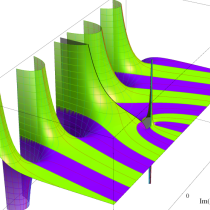
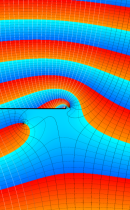
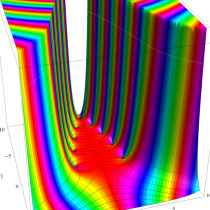
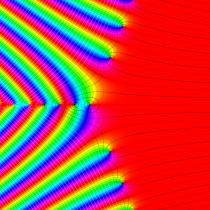
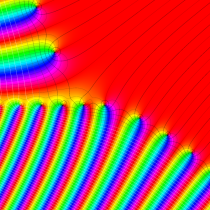
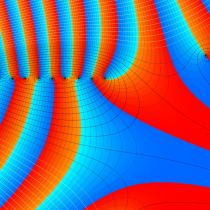
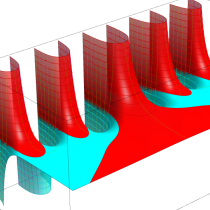
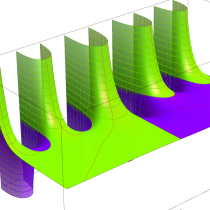
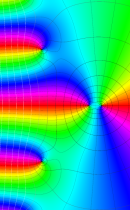
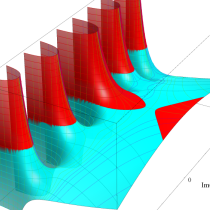
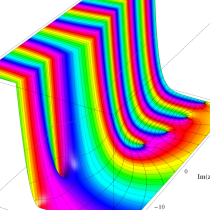
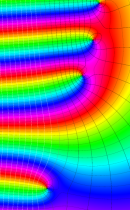
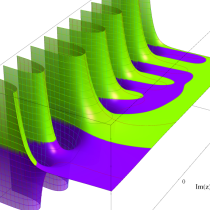
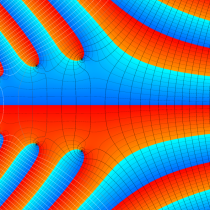
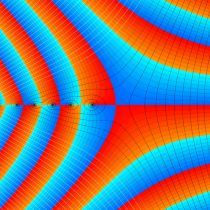
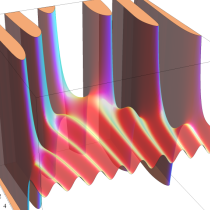
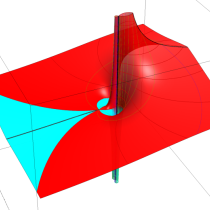
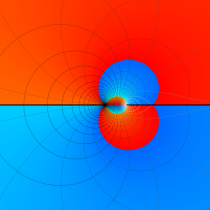
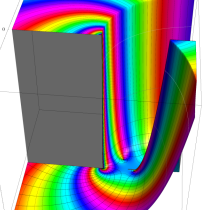
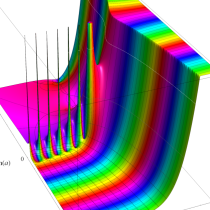
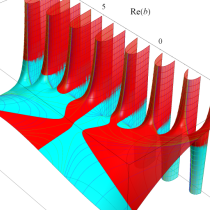
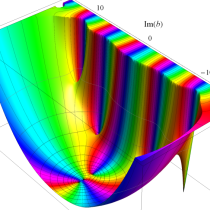
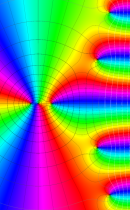
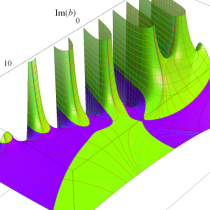
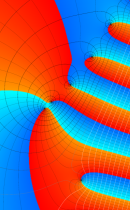
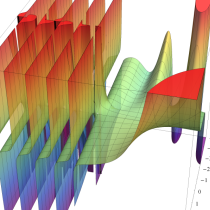
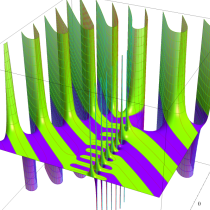
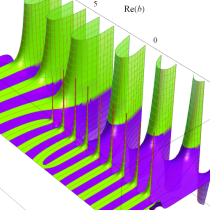
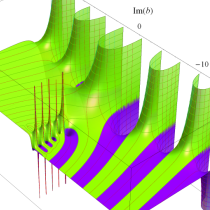
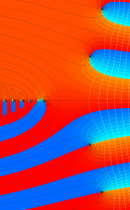
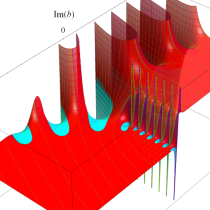
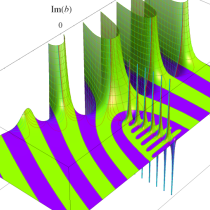
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
一方、
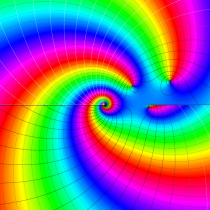
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
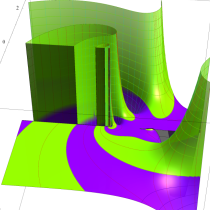
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
複素変数の正則化不完全ガンマ関数
は、
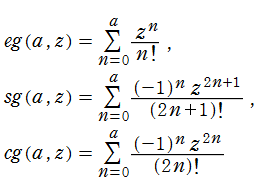
アニメーション:
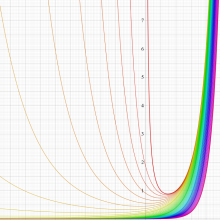
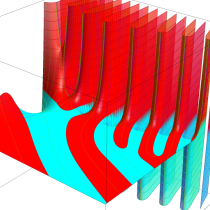
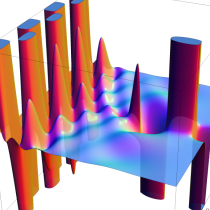
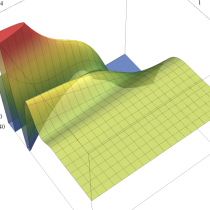
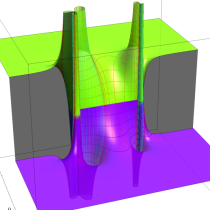
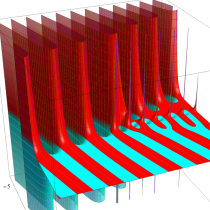
不完全ベータ関数
日:不完全ベータ関数英:Incomplete beta function,仏:Fonction bêta incompléte,独:Unvollständige Betafunktion
現在では、ベータ関数の積分表示式 (第1種 Euler 積分) に対しても積分区間を変数化した、不完全ベータ関数
が定義されている。以下に見るとおり、不完全ベータ関数が満たす公式の多くは、不完全ガンマ関数のそれに類似している。
例えば、変数
は、二つの不完全ガンマ関数間の関係式に相当している。また、不完全ベータ関数は関数等式
を満たす。
特別な
のように初等関数に還元される。先の関数等式を適用すれば、隣接する
不完全ベータ関数は、超幾何関数の特別な場合として
と表わすことができ、大半の性質はこれから導かれる。
また、不完全ベータ関数は連分数
に展開できる。
不完全ベータ関数
不完全ベータ関数 (後述の正則化も含めて) の著しい応用事例は、統計学におけるベータ分布の累積関数であるが、他にも、軟質または粒状物体のパッキング分析、物質を含み宇宙定数を持つ膨張宇宙の成長因子に関する数式などがある。
不完全ベータ関数の起源は、I. Newton (1676年)、J. Stirling (1730年)、並びに P. S. Laplace (1778年) 等による定積分の公式を求める研究にあり、その後、次第に不完全ガンマ関数と対をなす現在の形に整備された。
アニメーション(10.0MB)
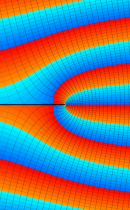
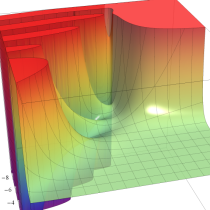
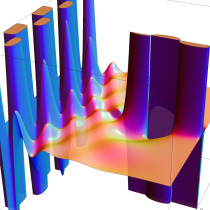
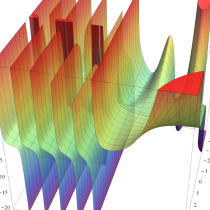
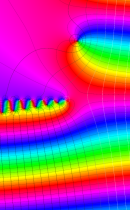
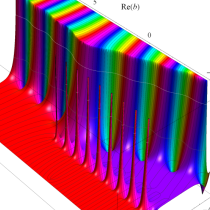
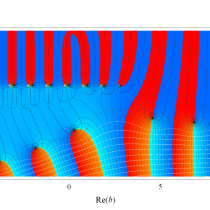
複素変数の不完全ベータ関数
複素変数の不完全ベータ関数
複素変数の不完全ベータ関数
複素変数の不完全ベータ関数
複素変数の不完全ベータ関数
複素変数の不完全ベータ関数
複素変数の不完全ベータ関数
複素変数の不完全ベータ関数
複素変数の不完全ベータ関数
が定義できる。ここでは、特別な一例のみを描画する。
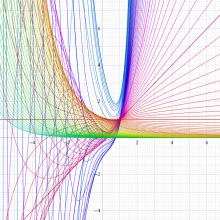
実変数の一般化不完全ベータ関数
複素変数の一般化不完全ベータ関数
正則化不完全ベータ関数
正則化不完全ガンマ関数と同様に、正則化不完全ベータ関数も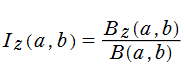
正則化不完全ベータ関数の性質は、不完全ベータ関数のそれに上記の定義式を適用すれば直ちに導かれる。例えば、
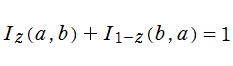
正則化不完全ベータ関数は、統計力学におけるモンテカルロ法のサンプリング式に現れる他、不完全ベータ関数と同じ応用事例で現れることが多い。
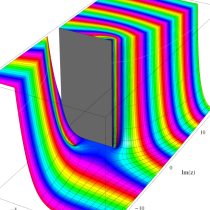
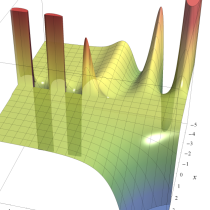
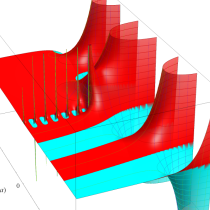
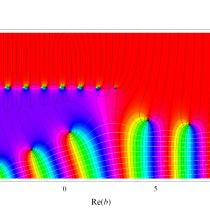
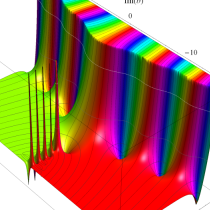
複素変数の正則化不完全ベータ関数
複素変数の正則化不完全ベータ関数
複素変数の正則化不完全ベータ関数
複素変数の正則化不完全ベータ関数
複素変数の正則化不完全ベータ関数
複素変数の正則化不完全ベータ関数