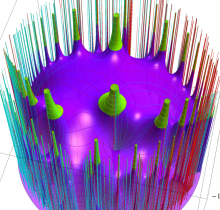
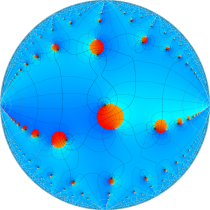
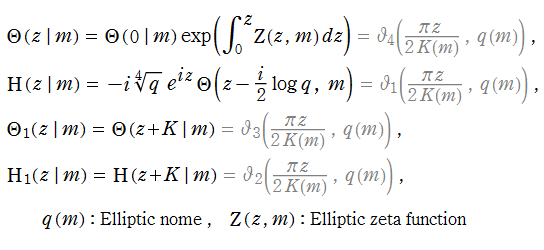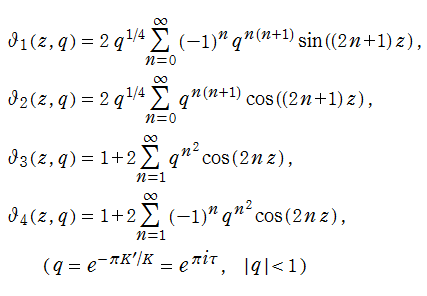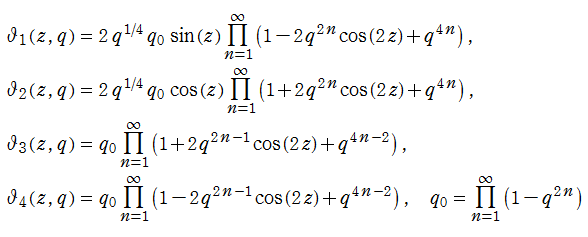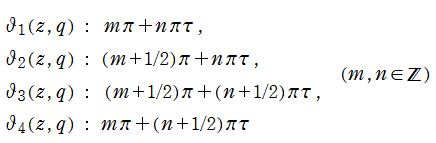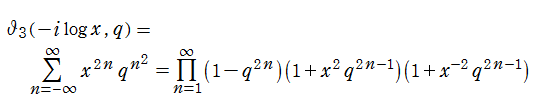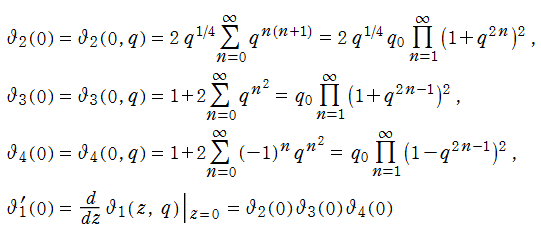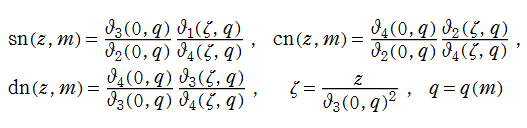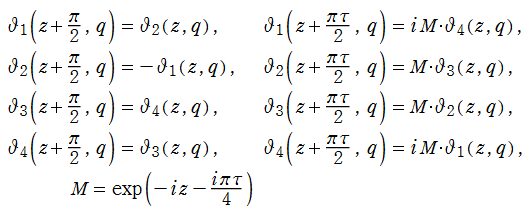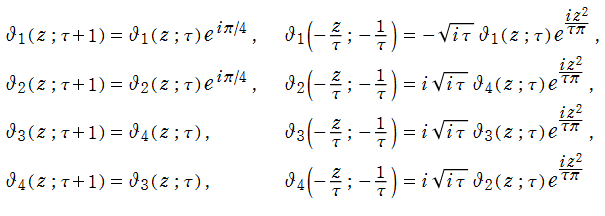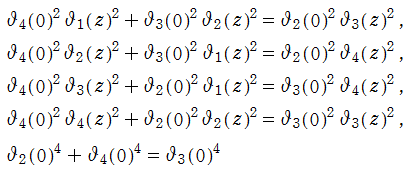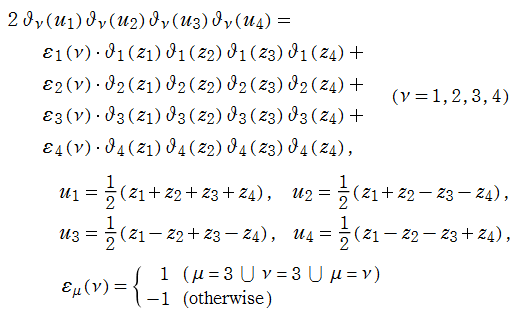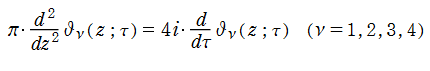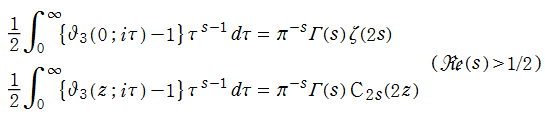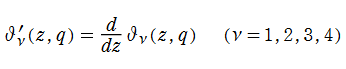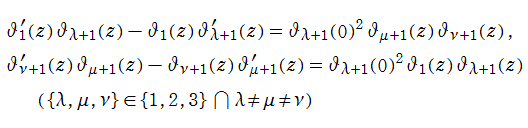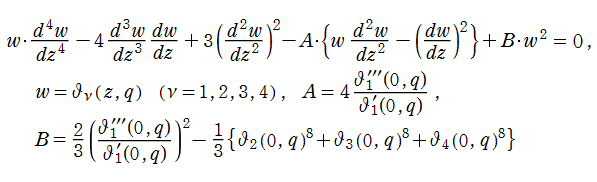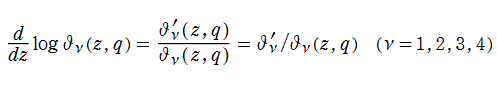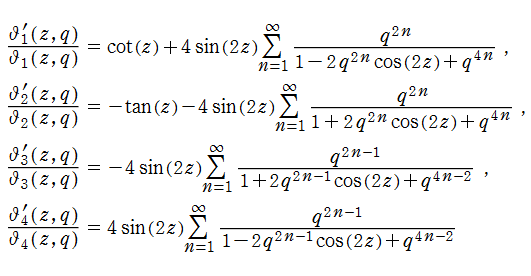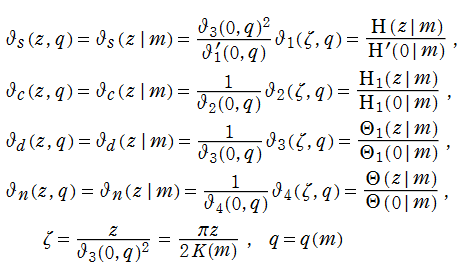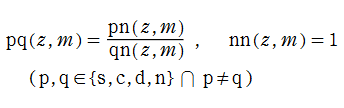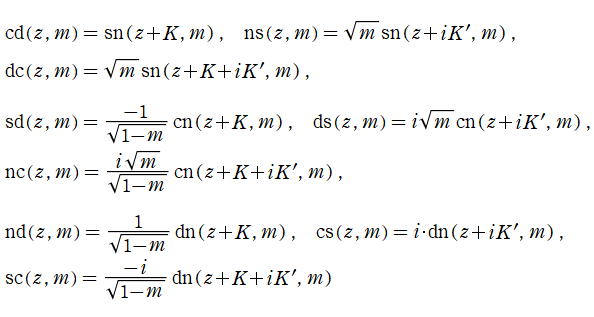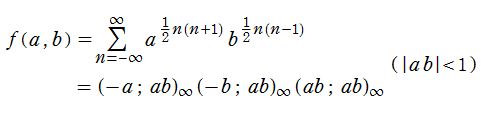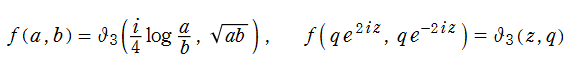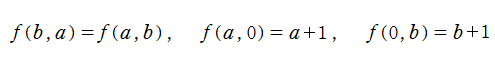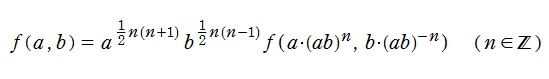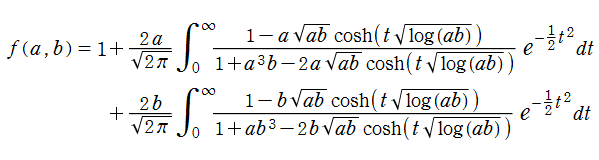特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
楕円テータ関数
楕円テータ関数
日:楕円テータ関数,テータ関数,θ関数英:Elliptic Theta function,仏:Fonction thêta,独:Thetafunktion
楕円テータ関数 (略称または広義として、単に 「テータ関数」 とも呼ばれる) は、楕円関数の発見に附随して現れた。すべての有理型関数は、その零点と極を分離したとき、各々と同じ位置に零点を持つ二つの超越整関数の商で表わされる。これを考える利点は、超越整関数が複素平面上で極を持たないことにあり、級数の収束範囲等で有理型関数よりも扱い易い場合が多いからである。実際、C. F. Gauss は自身の発見した楕円関数 ― それは有理型関数である ― に対してこの手順を踏み、(後のテータ関数と同等な) 4種類の超越整関数を導いている。しかし、楕円関数と同様、この発見についても Gauss は生前に結果を公表しなかったので、テータ関数の正式な第1発見者は C. G. J. Jacobi に帰せられている。
Jacobi が最初に定義したテータ関数は、実は 「テータ」 と 「エータ」
であったが※1、程なく Jacobi 自身によって、より洗練された定義 (第1変数と第2変数の完全な分離等) と関数記号に改められた。それが、現在定着している楕円テータ関数
であり※2、多くの場合、この Fourier 級数が導入時の定義として選ばれる。特に、この級数は
なお、第2変数を
楕円テータ関数は、無限乗積展開式
によっても表わされる。これも収束が非常に速いので数値計算に適している。また、この無限乗積展開式から、複素
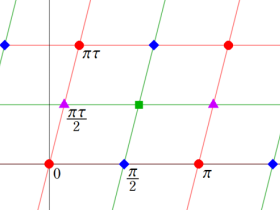
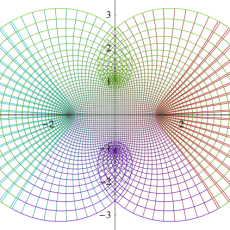
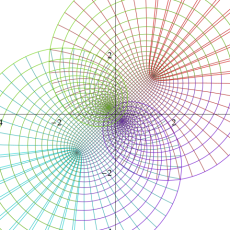
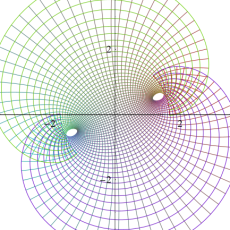
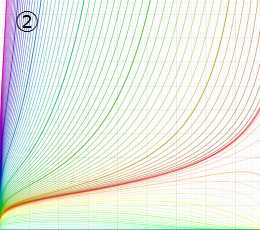
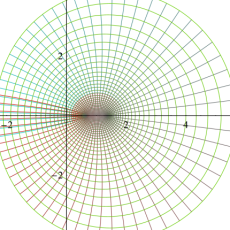
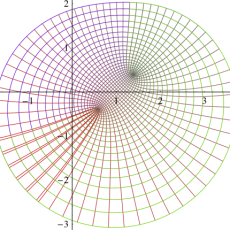
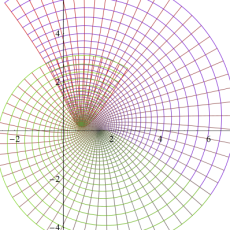
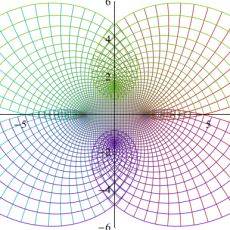
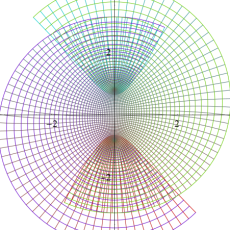
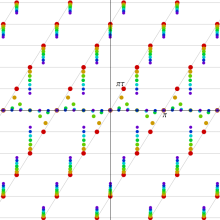
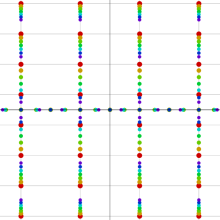
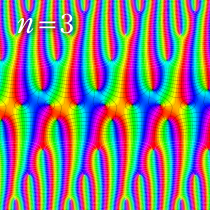
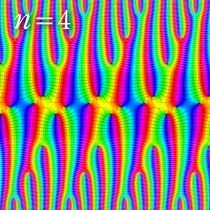
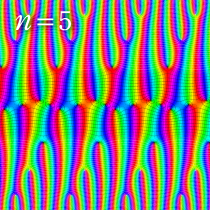
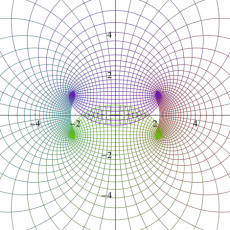
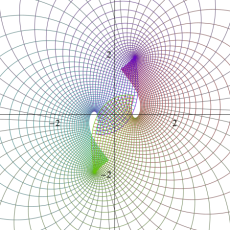
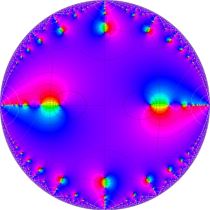
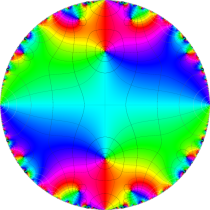
図:楕円テータ関数の零点の位置
の位置にあることも容易に分かる。
上記の無限乗積展開式は、q-解析学の端緒の一つで現在の量子群などに繋がるので、歴史的に見ても重要な公式である。例えば、上記の Fourier 級数と無限乗積展開式を比較して得られる
は、Jacobi の三重積公式 (Jacobi's triple product) と呼ばれ、Euler の五角数定理と並ぶ代表的な q-解析学の恒等式である。
も、「テータ零値」 と呼ばれる
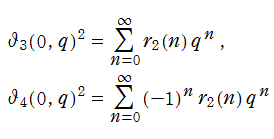
Jacobi が楕円テータ関数を導入した目的も、冒頭で述べた Gauss のそれと同じであった、すなわち、Jacobi の楕円関数は、二つの楕円テータ関数の商
で表わされる。以上のことから、楕円関数の数値計算も容易になる。(Weierstrass の楕円関数を楕円テータ関数で表わす公式もあるが、掲載は省略する。詳細は、NIST の 23.6(i) 等を参照。)
楕円テータ関数は非常に多くの関係式を持っている。そのうち、代表的なものを次に列挙する。
(周期性・擬周期性)
(擬保型性)
(相互関係式):これは 「Riemann の関係式」 とも呼ばれる。
(超越的加法公式)
(熱拡散方程式):物理学への応用から得られる公式※3。
(楕円テータ関数の Mellin 変換):Riemann ゼータ関数等との関係。
ここに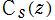 は、一般 Clausen 関数である。
は、一般 Clausen 関数である。
楕円テータ関数と同クラスの関数は他にも、定数因子が若干異なる Neville のテータ関数、楕円テータ関数に変数が2次の指数関数を掛けたものに相当する Weierstrass のシグマ関数などがある (つまり、Weierstrass のシグマ関数は 「より一般的な基本周期から構成されたテータ関数」 である)。また、実質は楕円テータ関数と同じであるが、同時にテータ零値の二変数化にもなっている Ramanujan のテータ関数がある。(擬保型性)
(相互関係式):これは 「Riemann の関係式」 とも呼ばれる。
(超越的加法公式)
(熱拡散方程式):物理学への応用から得られる公式※3。
(楕円テータ関数の Mellin 変換):Riemann ゼータ関数等との関係。
ここに
ここまで掲載してきた公式のいくつかは、楕円テータ関数が数論や組合せ論および古典物理学に応用され得ることを既に物語っているが、他にも、代数幾何学、ソリトン方程式などの可積分系、矩形ポテンシャルに関する量子力学、分数量子ホール効果 (Fractional quantum Hall effect)、球充填 (Sphere packing)、符号理論 (Coding theory) など、実に多くの応用事例が知られている。さらに、虚数乗法論、4乗剰余の相互法則、流体力学や電磁気学における等角写像など、楕円関数の応用分野の多くでは代わりにテータ関数を用いることが可能で、むしろ、その方が融通が利き、エレガントな理論が展開できる場合もある。
【註記】
※1:このテータ関数とエータ関数のグラフは、Neville のテータ関数のそれに似ていると思われる。
※2:記号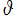 はギリシャ文字
はギリシャ文字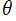 (Theta) の筆記体で 「Curly Theta」 と呼ばれる。しかし、使用可能な書体の制限上
(Theta) の筆記体で 「Curly Theta」 と呼ばれる。しかし、使用可能な書体の制限上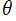 を用いることも多い。また、日本語訳ではこの関数を 「テータ関数」 と読む習慣が定着しているが、これを 「シータ関数」 と読んでも誤りではない (実際、そう表記している書籍等もある)。
を用いることも多い。また、日本語訳ではこの関数を 「テータ関数」 と読む習慣が定着しているが、これを 「シータ関数」 と読んでも誤りではない (実際、そう表記している書籍等もある)。
関数記号の付番は相違が多く注意を要する。特に、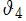 を
を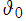 で表記している事例は多い (因みに Jacobi は
で表記している事例は多い (因みに Jacobi は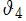 のみを
のみを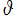 と付番なしで表記した)。また、
と付番なしで表記した)。また、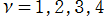 の代わりに
の代わりに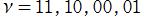 なる付番 (
なる付番 (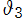 の零点格子からの半格子ずれを表わした付番 ― C. Hermite が始めた) を採用していることも結構ある。
の零点格子からの半格子ずれを表わした付番 ― C. Hermite が始めた) を採用していることも結構ある。
さらに、同じ記号・付番であっても、定義域または値域の定数倍、指数関数因子が異なる定義になっていることがあり、混乱を招きやすい。
※3:S. D. Poisson と J. B. J. Fourier は、この熱拡散方程式のテータ関数解を Fourier 級数展開式として求めている。(テータ関数を発見した訳ではない。)
※1:このテータ関数とエータ関数のグラフは、Neville のテータ関数のそれに似ていると思われる。
※2:記号
関数記号の付番は相違が多く注意を要する。特に、
さらに、同じ記号・付番であっても、定義域または値域の定数倍、指数関数因子が異なる定義になっていることがあり、混乱を招きやすい。
※3:S. D. Poisson と J. B. J. Fourier は、この熱拡散方程式のテータ関数解を Fourier 級数展開式として求めている。(テータ関数を発見した訳ではない。)
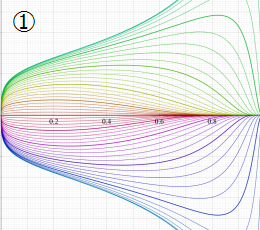
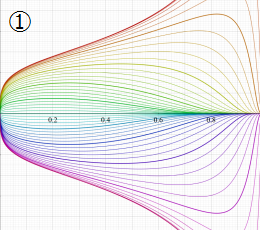
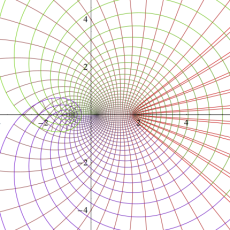
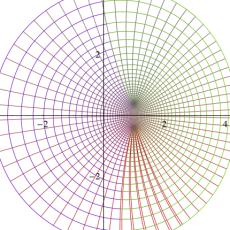
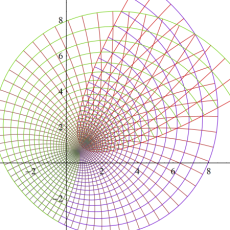
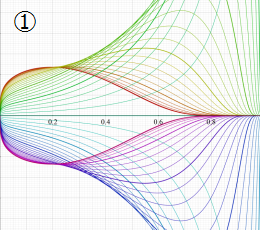
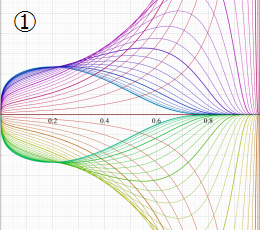
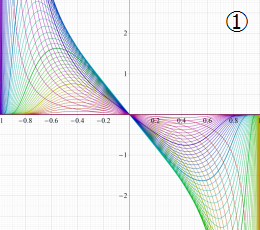
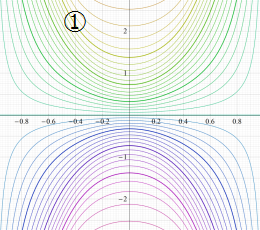
曲線上の点は
因みに、実数
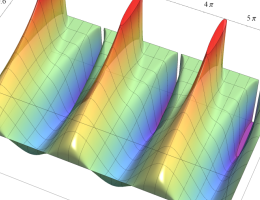
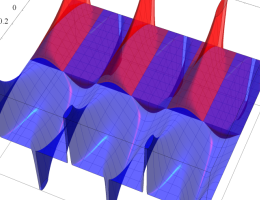
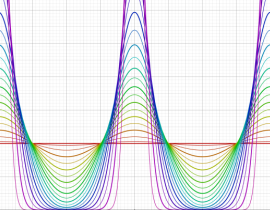
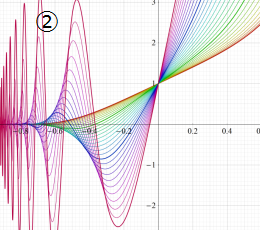
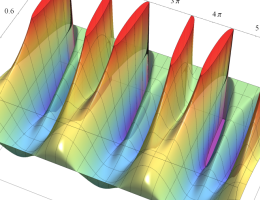
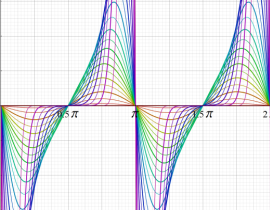
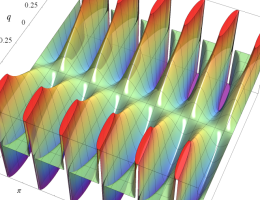
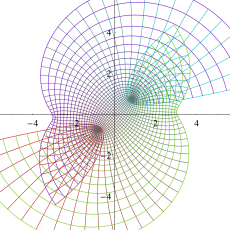
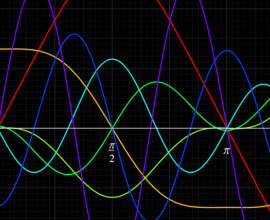
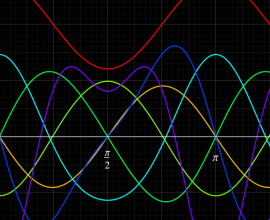
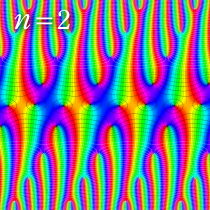
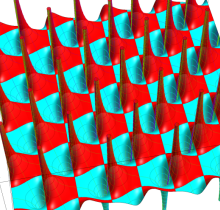
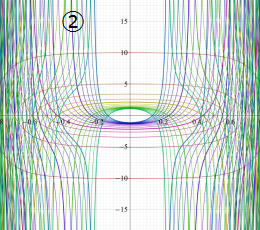
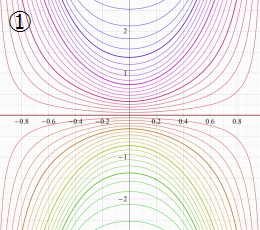
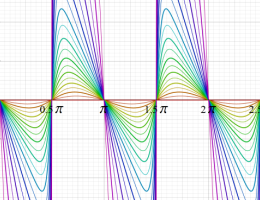
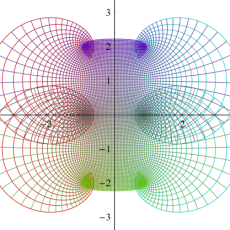
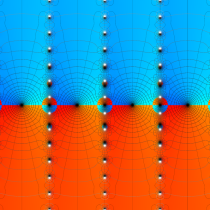
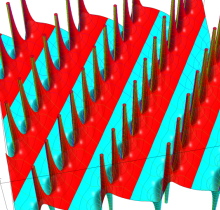
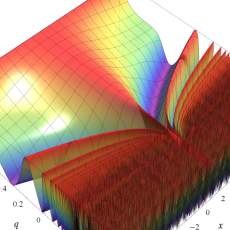
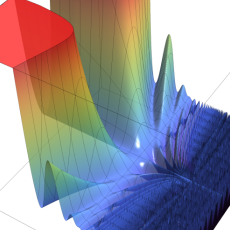
実2変数の楕円テータ関数
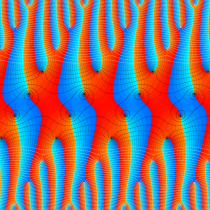
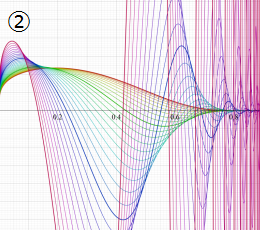
2番目は、その実部と虚部のグラフであり、
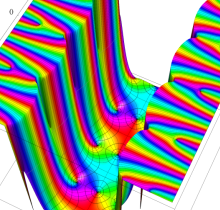
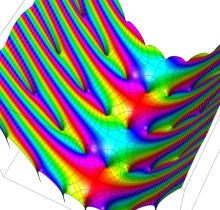
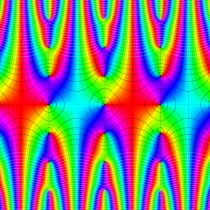
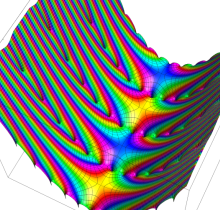
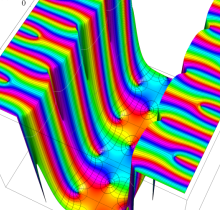
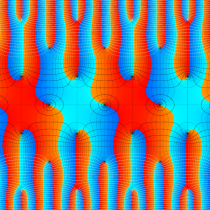
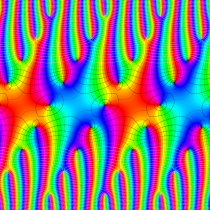
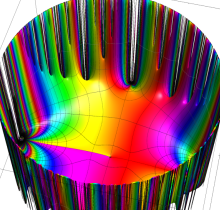
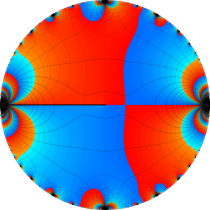
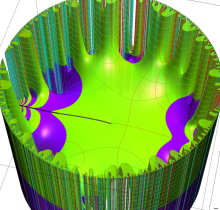
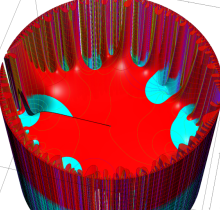
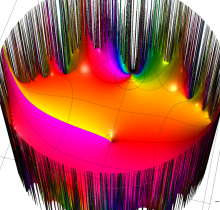
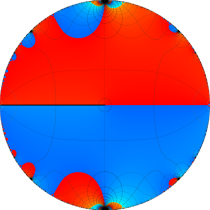
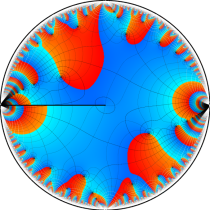
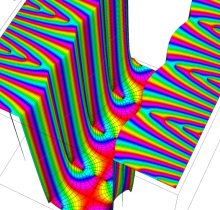
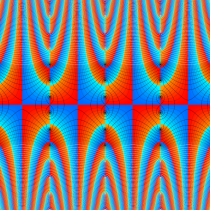
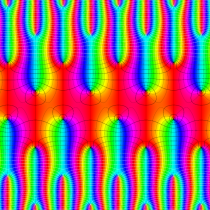
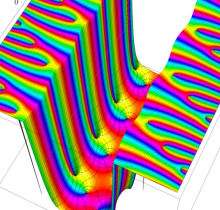
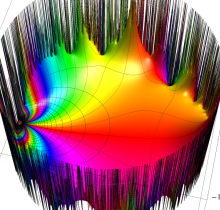
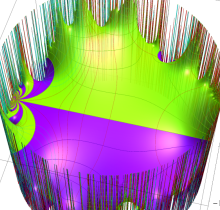
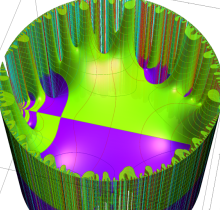
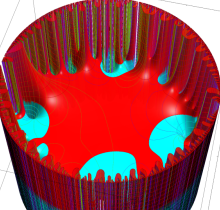
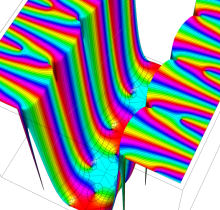
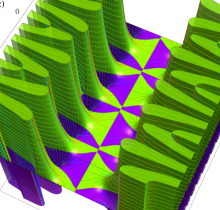
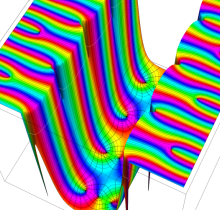
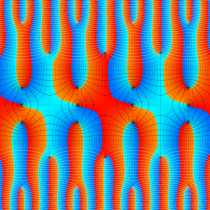
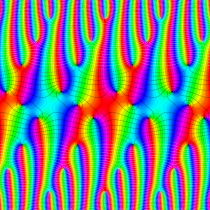
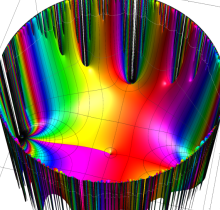
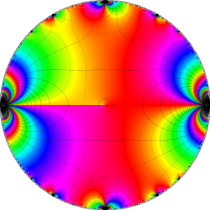
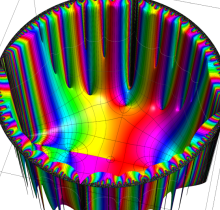
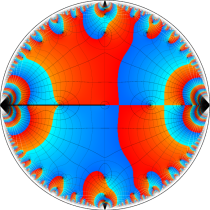
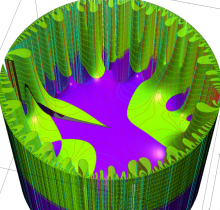
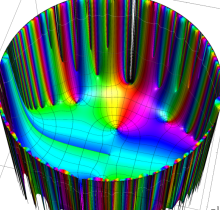
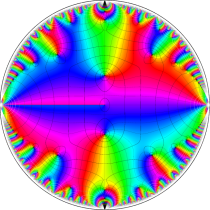
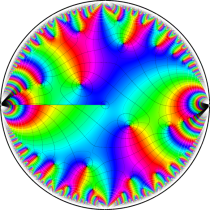
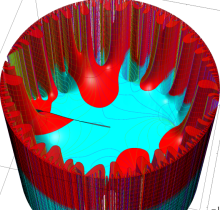
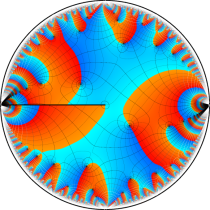
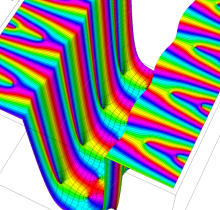
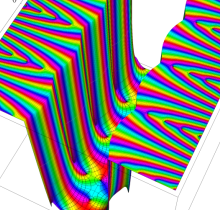
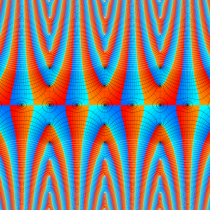
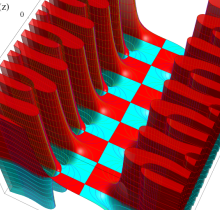
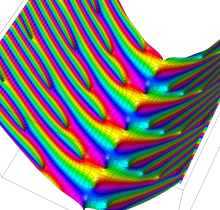
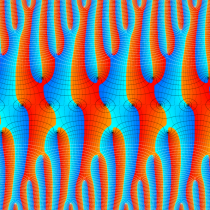
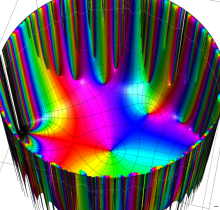
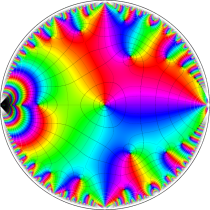
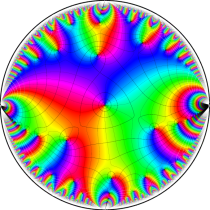
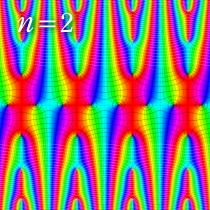
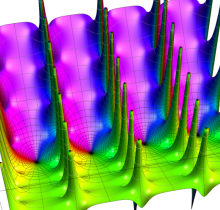
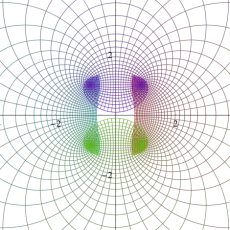
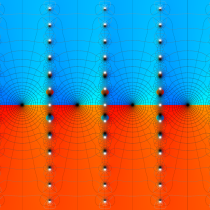
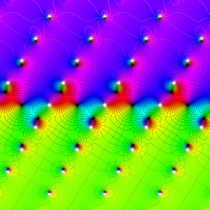
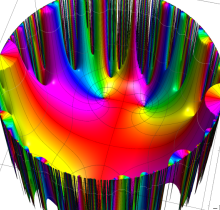
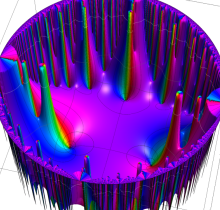
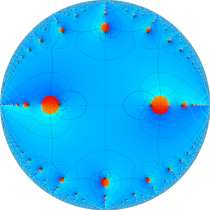
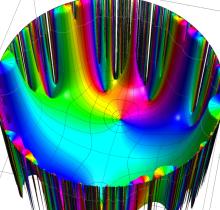
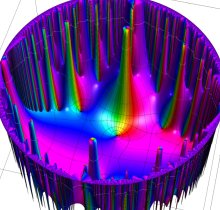
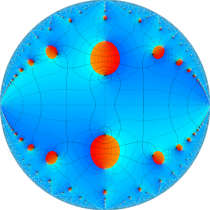
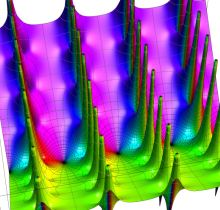
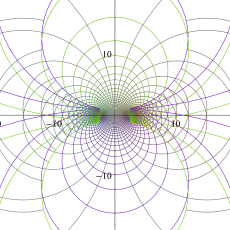
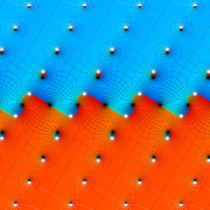
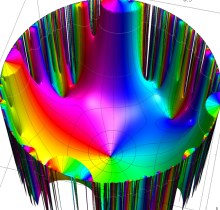
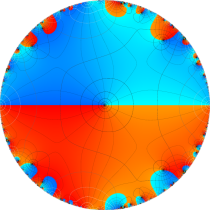
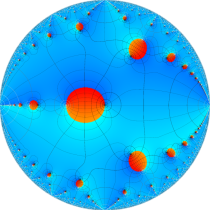
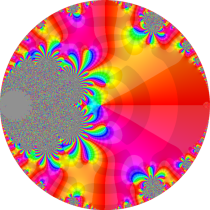
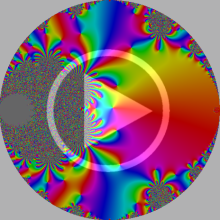
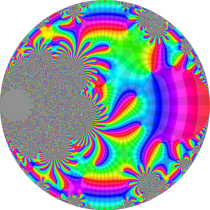
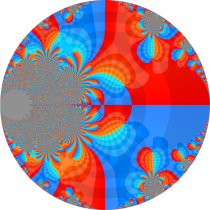
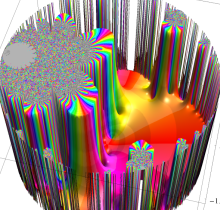
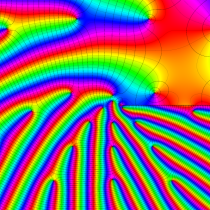
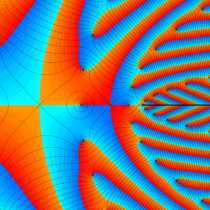
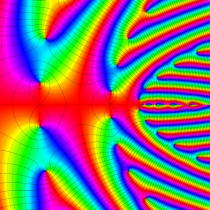
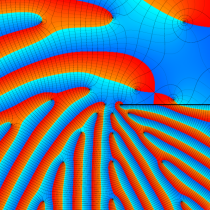
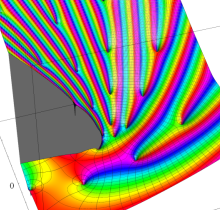
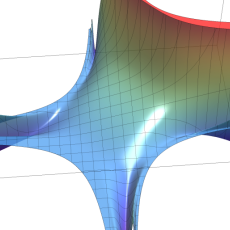
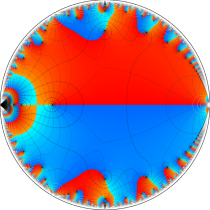
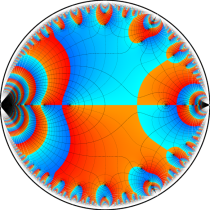
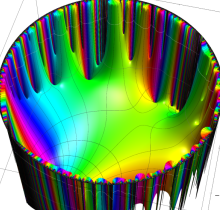
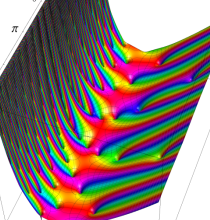
複素変数の楕円テータ関数
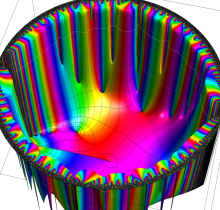
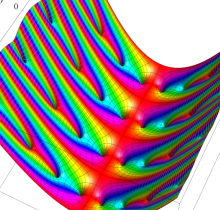
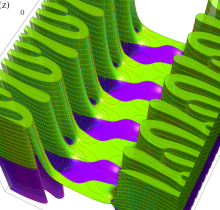
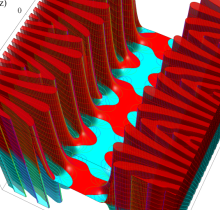
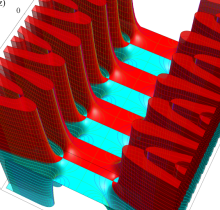
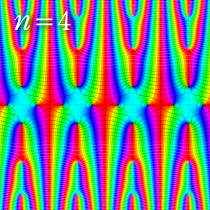
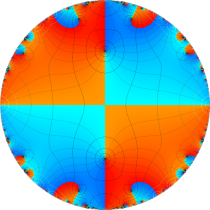
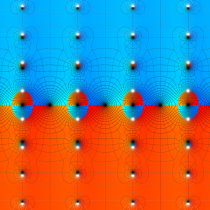
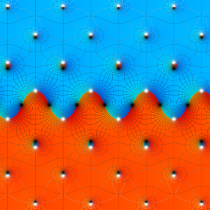
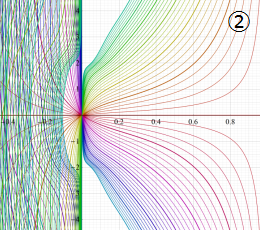
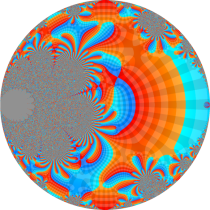
楕円テータ関数
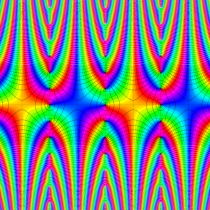
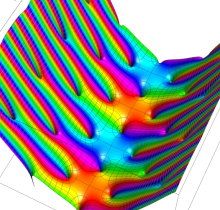
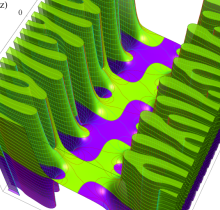
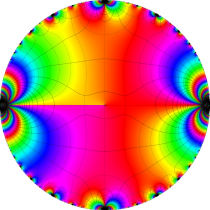
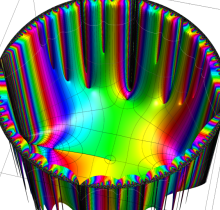
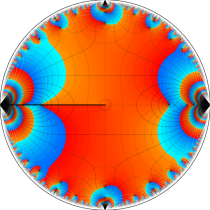
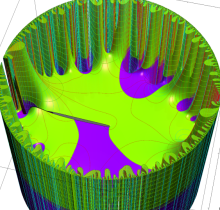
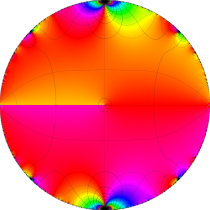
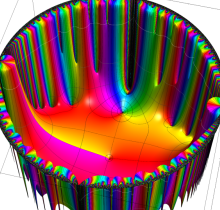
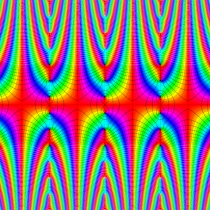
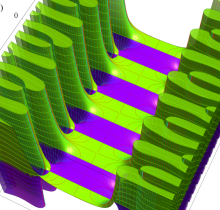
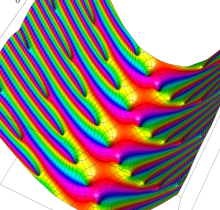
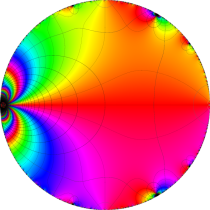
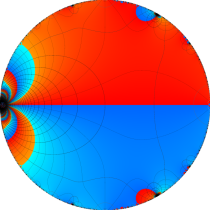
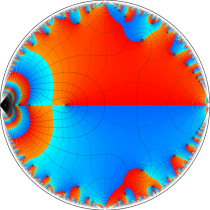
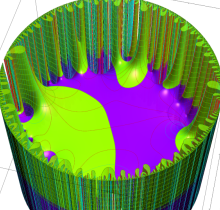
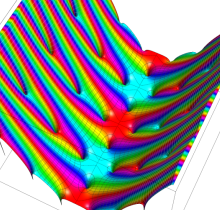
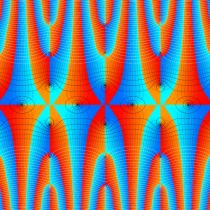
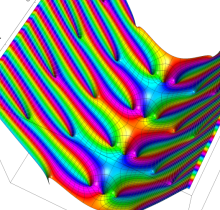
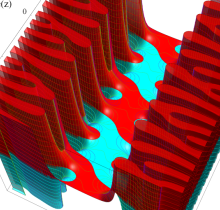
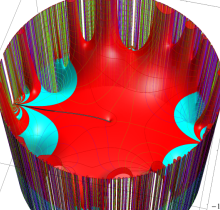
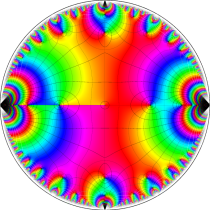
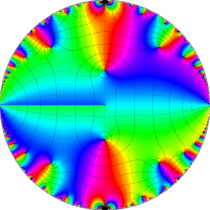
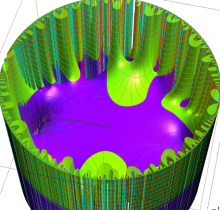
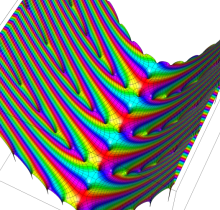
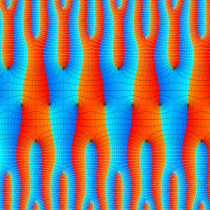
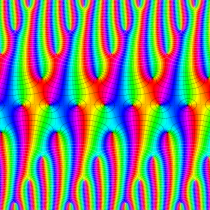
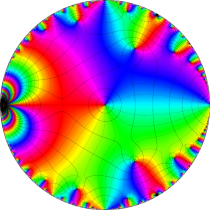
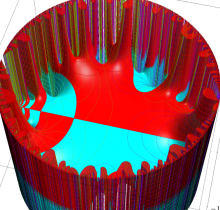
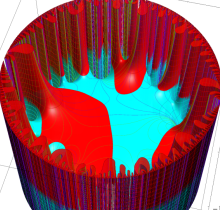
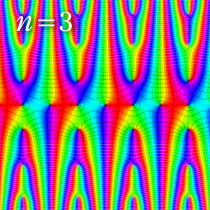
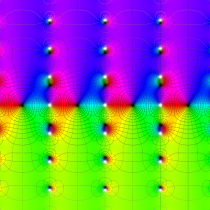
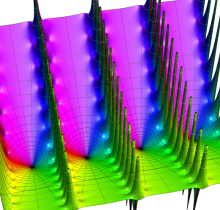
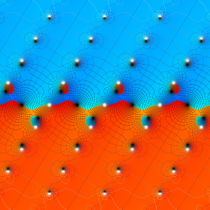
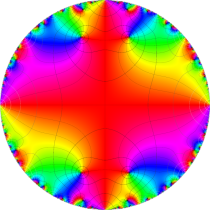
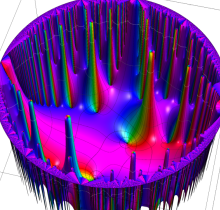
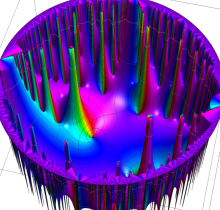
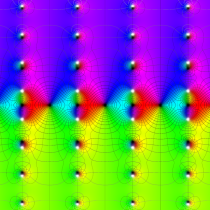
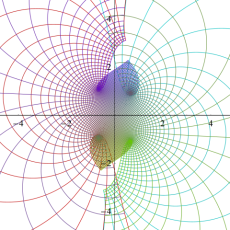
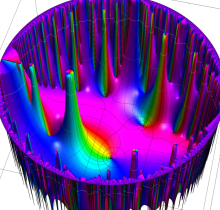
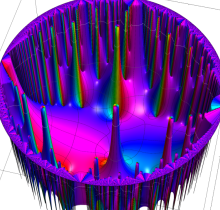
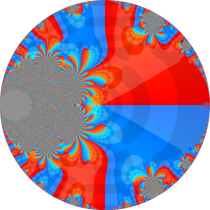
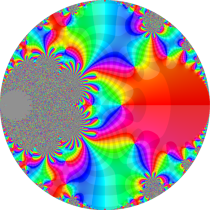
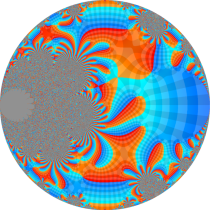
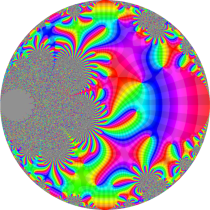
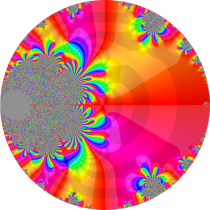
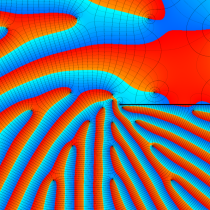
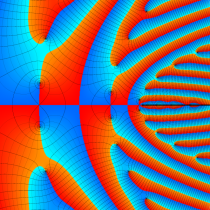
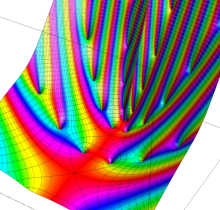
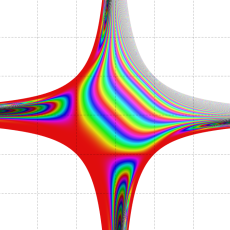
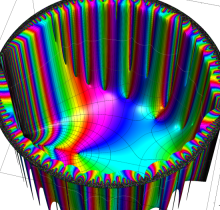
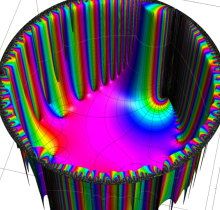
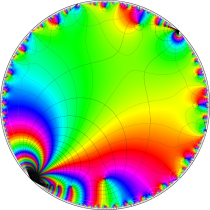
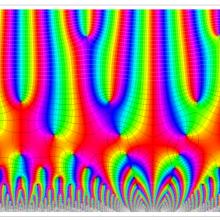
複素変数の楕円テータ関数
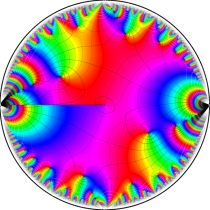
楕円テータ関数
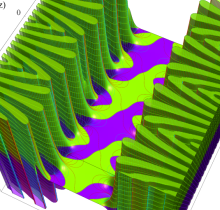
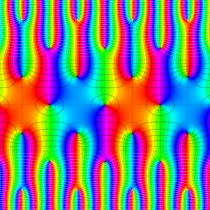
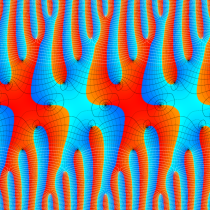
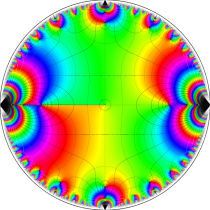
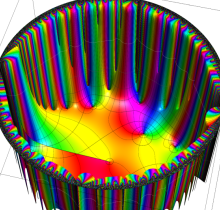
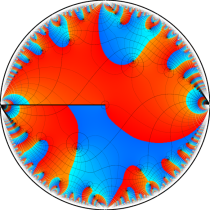
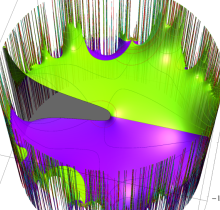
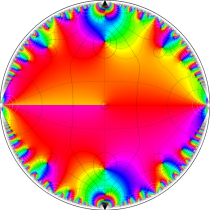
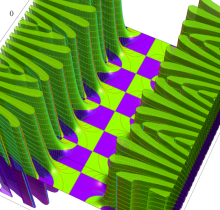
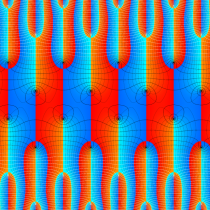
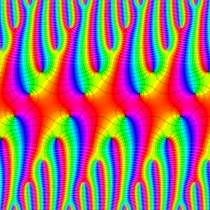
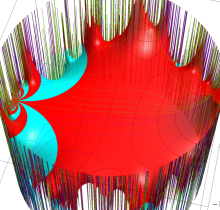
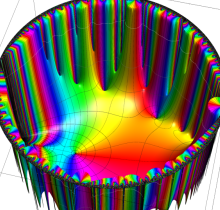
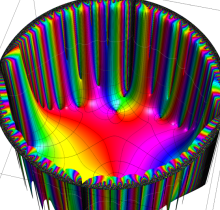
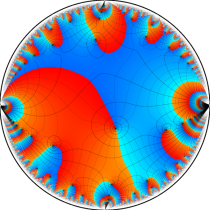
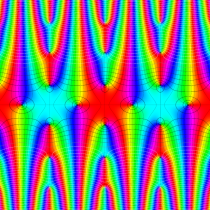
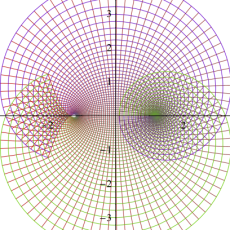
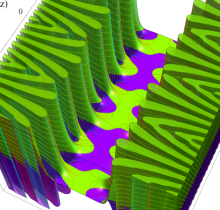
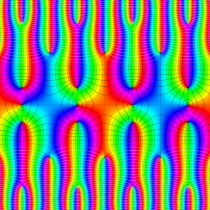
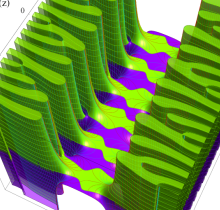
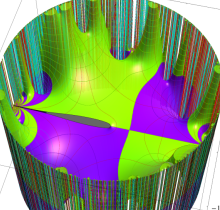
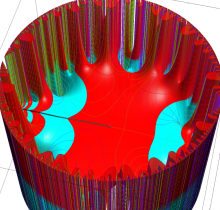
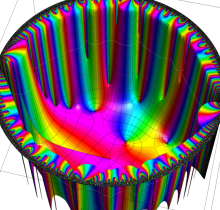
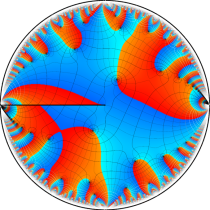
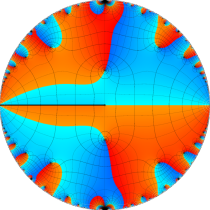
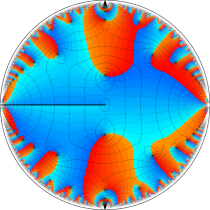
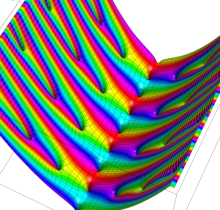
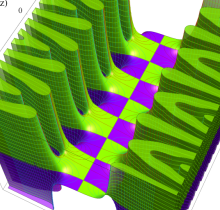
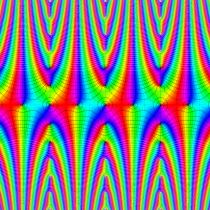
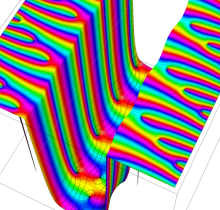
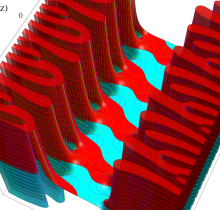
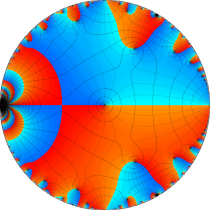
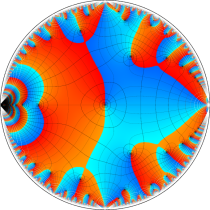
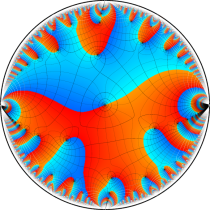
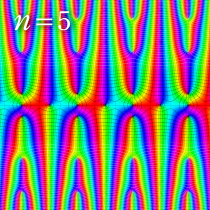
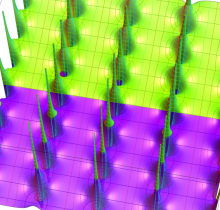
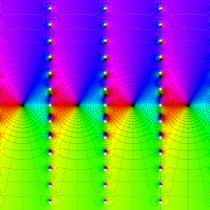
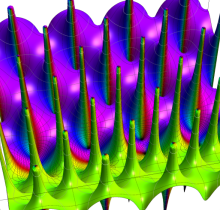
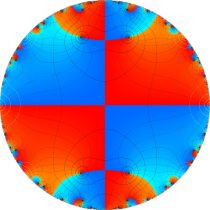
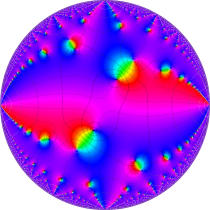
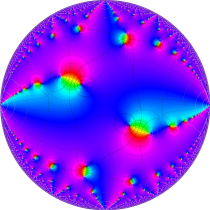
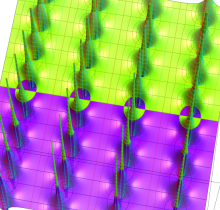
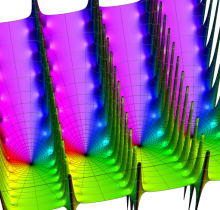
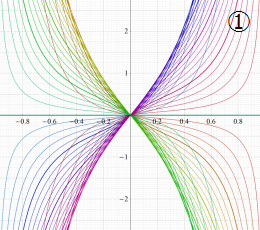
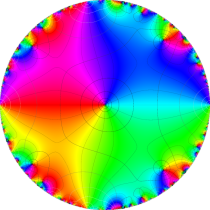
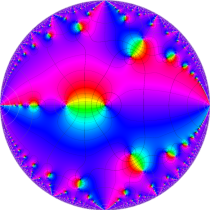
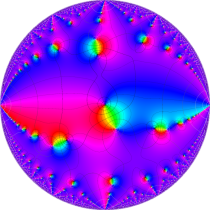
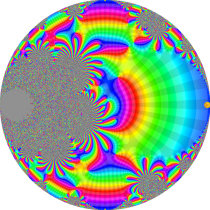
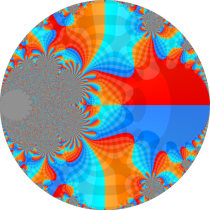
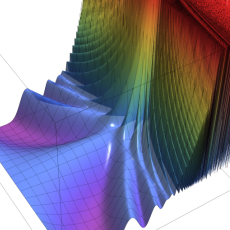
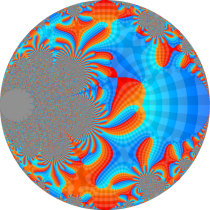
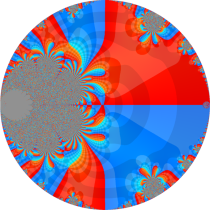
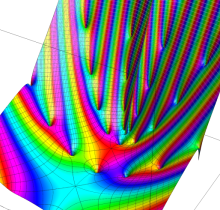
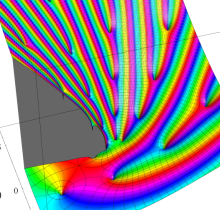
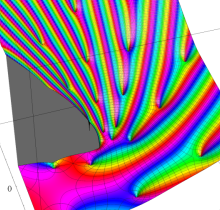
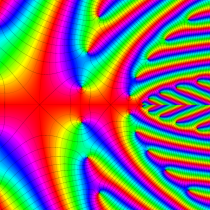
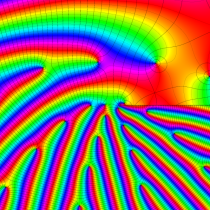
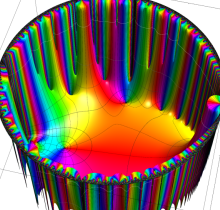
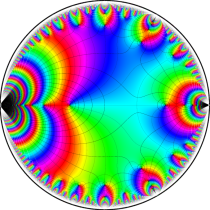
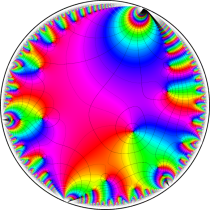
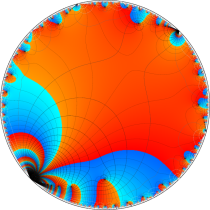
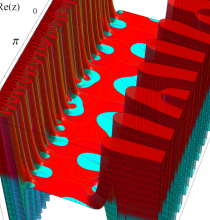
複素変数の楕円テータ関数
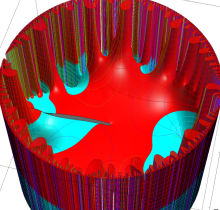
楕円テータ関数
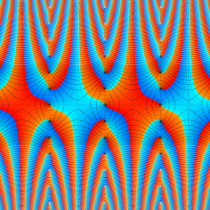
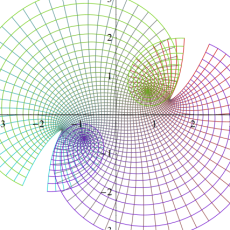
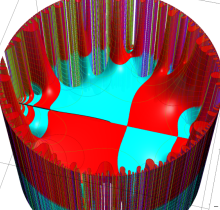
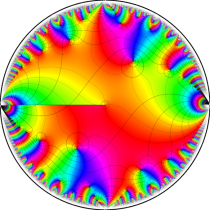
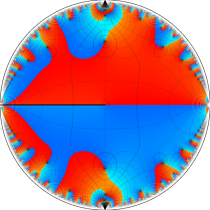
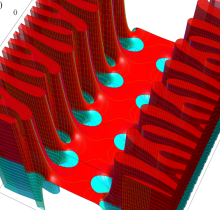
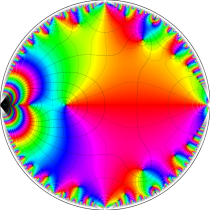
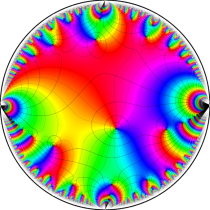
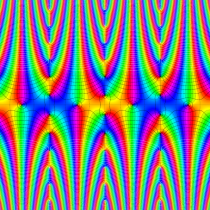
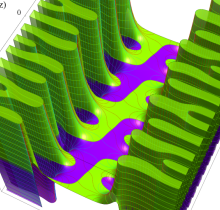
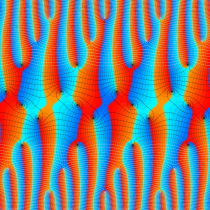
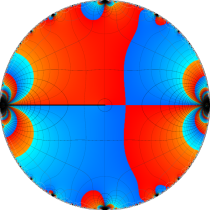
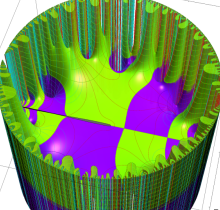
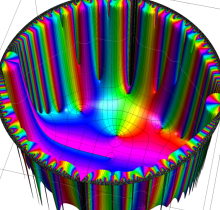
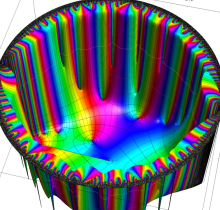
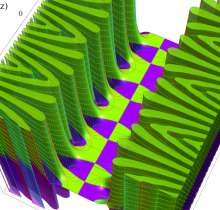
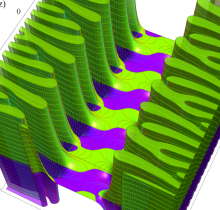
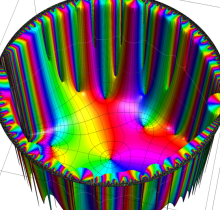
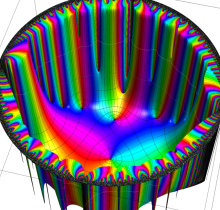
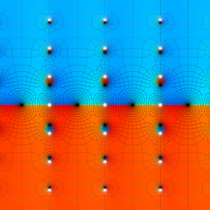
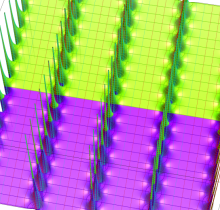
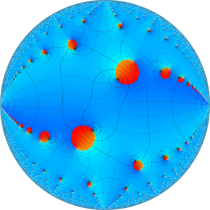
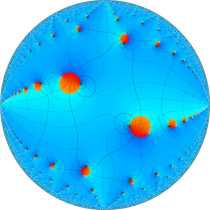
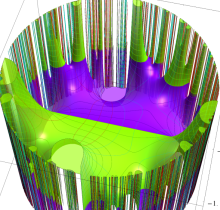
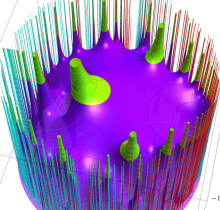
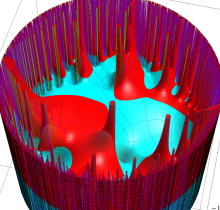
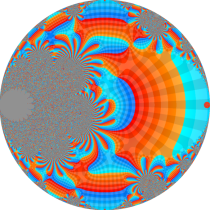
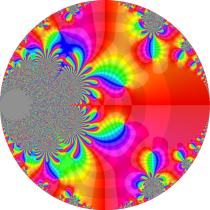
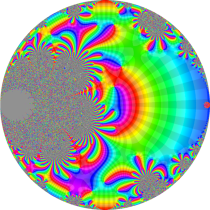
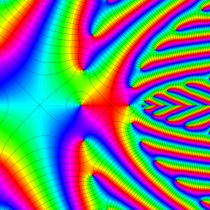
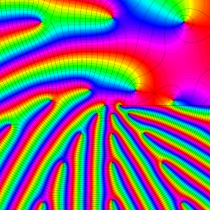
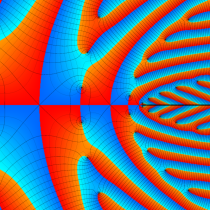
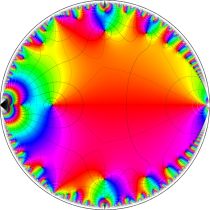
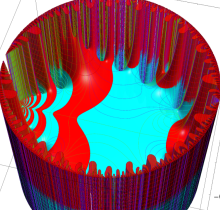
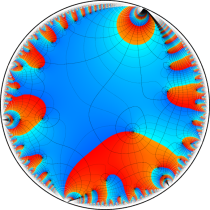
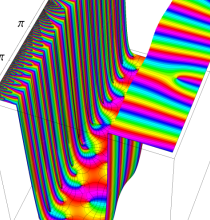
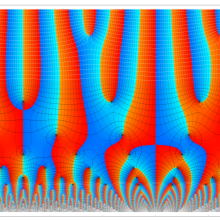
複素変数の楕円テータ関数
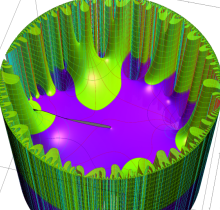
楕円テータ関数
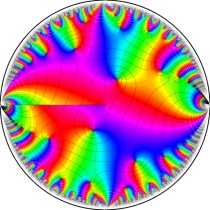
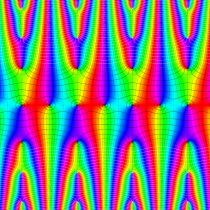
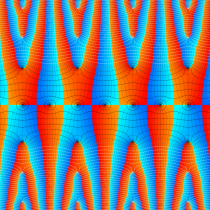
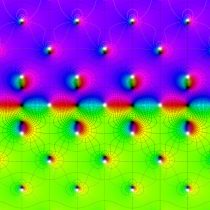
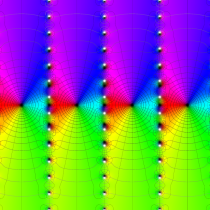
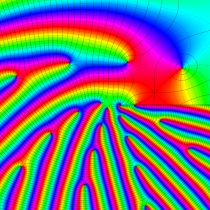
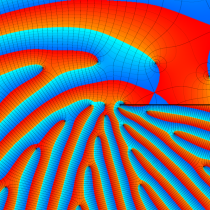
複素変数の楕円テータ関数
複素変数の楕円テータ関数
複素変数の楕円テータ関数
アニメーション(7.01MB)
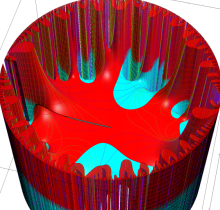
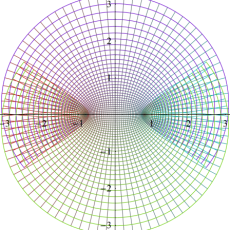
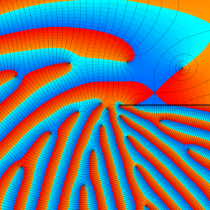
複素変数の楕円テータ関数
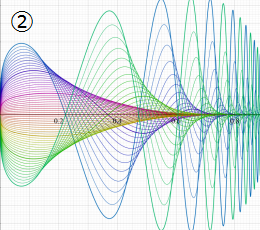
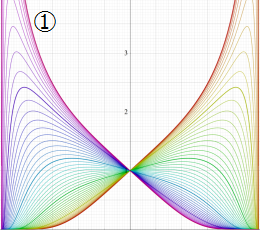
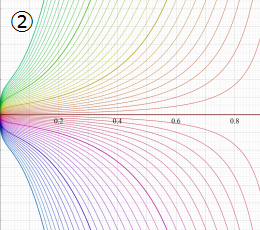
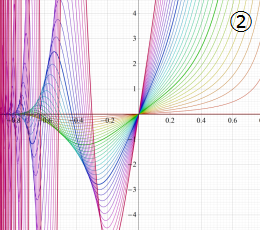
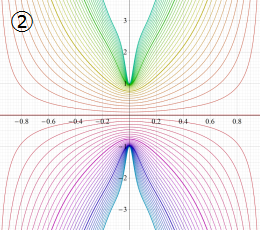
②における薄色の曲線は、①のグラフを重ねたものである。
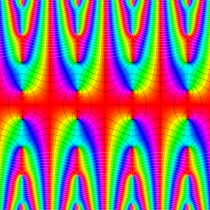
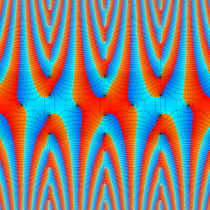
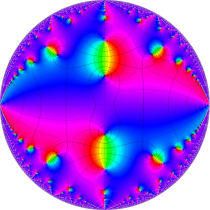
複素変数の楕円テータ関数
複素変数の楕円テータ関数
複素変数の楕円テータ関数
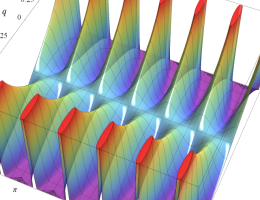
実2変数の楕円テータ関数
複素変数の楕円テータ関数
楕円テータ関数
複素変数の楕円テータ関数
楕円テータ関数
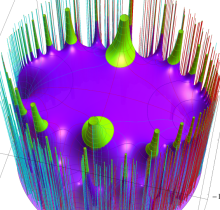
複素変数の楕円テータ関数
楕円テータ関数
複素変数の楕円テータ関数
楕円テータ関数
複素変数の楕円テータ関数
複素変数の楕円テータ関数
複素変数の楕円テータ関数
アニメーション(7.11MB)
複素変数の楕円テータ関数
楕円テータ関数の導関数
楕円テータ関数は、も併せて用意すると都合が良い。なぜならば、超越的加法公式を特別な場合に還元すると得られる公式には、導関数を含む関係式
等があり、応用でも楕円テータ関数の導関数は度々出現するからである。また、Fourier 級数展開式を
4種類の楕円テータ関数はいずれも、代数的な4階の非線形微分方程式
を満たす。なお、楕円テータ関数は各項が陰関数で結ばれた3階の非線形微分方程式 (式は複雑なので省略する) も満たすので、3階以上の導関数は2階導関数までの代数関数で表わせる※1。
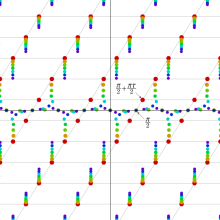
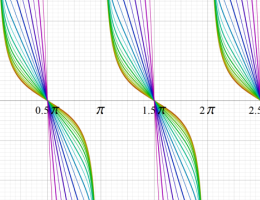
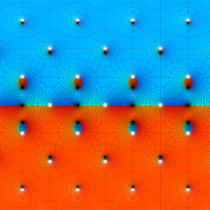
楕円テータ関数の導関数も超越整関数であるが、複素零点は格子から若干ずれた位置になる。また、実零点は
【註記】
※1:当サイトでは主に1階導関数のグラフを掲載する (2階以上は、零点の位置に関するグラフのみを掲載する)。
※1:当サイトでは主に1階導関数のグラフを掲載する (2階以上は、零点の位置に関するグラフのみを掲載する)。
因みに、実数
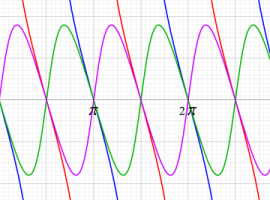
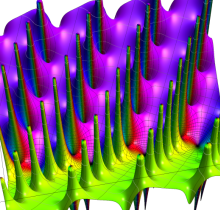
実2変数の楕円テータ導関数
2番目は、その実部と虚部のグラフであり、
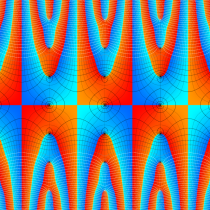
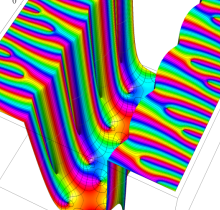
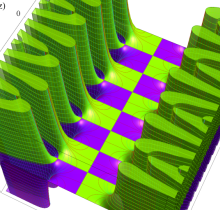
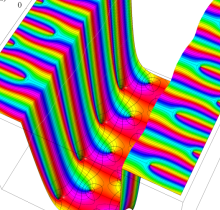
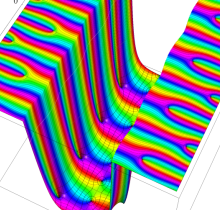
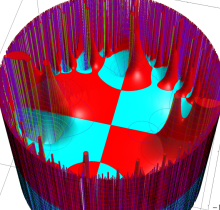
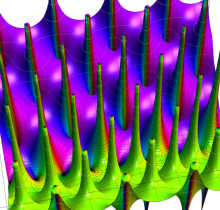
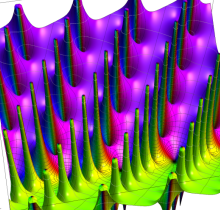
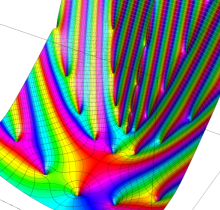
複素変数の楕円テータ導関数
楕円テータ導関数
複素変数の楕円テータ導関数
楕円テータ導関数
複素変数の楕円テータ導関数
楕円テータ導関数
複素変数の楕円テータ導関数
楕円テータ導関数
複素変数の楕円テータ導関数
複素変数の楕円テータ導関数
複素変数の楕円テータ導関数
複素変数の楕円テータ導関数
複素変数の楕円テータ導関数
複素変数の楕円テータ導関数
実2変数の楕円テータ導関数
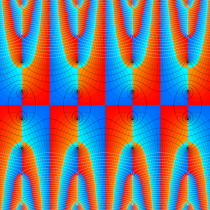
複素変数の楕円テータ導関数
楕円テータ導関数
複素変数の楕円テータ導関数
楕円テータ導関数
複素変数の楕円テータ導関数
楕円テータ導関数
複素変数の楕円テータ導関数
楕円テータ導関数
複素変数の楕円テータ導関数
複素変数の楕円テータ導関数
複素変数の楕円テータ導関数
(曲線の色は、後掲の零点の位置図と対応する。)
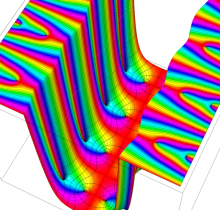
複素変数の楕円テータ関数の逐次導関数
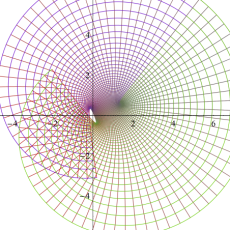
零点
複素変数の楕円テータ関数の逐次導関数
零点
(曲線の色は、後掲の零点の位置図と対応する。)
複素変数の楕円テータ関数の逐次導関数
零点
複素変数の楕円テータ関数の逐次導関数
零点
楕円テータ関数の対数微分
楕円テータ関数の数値計算では、無限乗積展開式も収束が速いため便利であった。しかし、これはを考えれば、(もはや無限乗積ではないが) 新たな有理三角関数項の無限級数
が得られる。これら4個の関数は、楕円テータ関数が零点を持つ格子点上で、代わりに1位の極を持つ有理型関数となる。楕円テータ関数の対数微分は、さらに逐次微分しても極の位置が変わらず、任意位数の楕円関数を生じる。実際、この考え方で Jacobi は自身の楕円関数を演繹した。
楕円テータ関数の対数微分は、Jacobi の楕円ゼータ関数・イプシロン関数、Weierstrass の楕円ゼータ関数と同クラスであり、互いに一次関数を加減した違いしかない。
因みに、実数
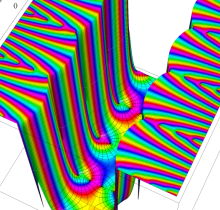
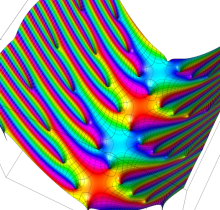
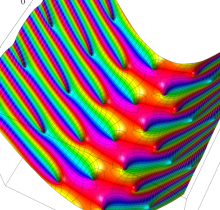
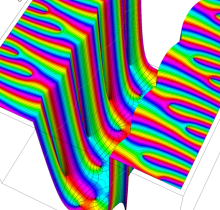
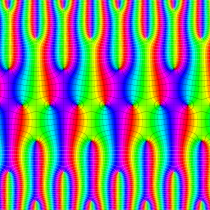
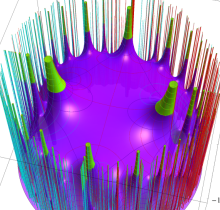
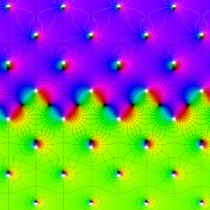
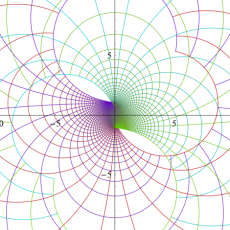
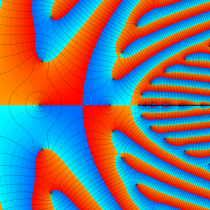
複素変数の楕円テータ関数の対数微分
楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
複素変数の楕円テータ関数の対数微分
Neville のテータ関数
日:Nevilleのテータ関数,ネヴィル テータ関数英:Neville theta function,仏:Fonction thêta de Neville,独:Nevillesche Thetafunktion
Neville のテータ関数は、
で定義される※1。これは、E. H. Neville が1944年に著した楕円関数の解説書 「Jacobian elliptic functions」 で初めて導入された※2。その主な利点は、
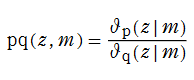
で表わすことを言う。例えば、
なお、Glaisher 表記の Jacobi 楕円関数は、商や逆数ではなく定数倍と半周期等の平行移動によって、
と表わすこともできる※3。
【註記】
※1:したがって、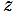 を変数とする Neville のテータ関数は、楕円テータ関数の定義域と値域を定数倍したものにすぎない。一方、
を変数とする Neville のテータ関数は、楕円テータ関数の定義域と値域を定数倍したものにすぎない。一方、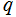 は第2変数のみならず第1変数の
は第2変数のみならず第1変数の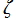 にも含まれているため、
にも含まれているため、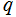 または
または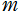 を変数とする Neville のテータ関数は、楕円テータ関数の振る舞いとかなり異なる。
を変数とする Neville のテータ関数は、楕円テータ関数の振る舞いとかなり異なる。
※2:Neville はこの著書中で、他にも楕円関数に対して合理的な定義を提案しているが、残念ながら現在ではほとんど顧みられる事が無い。
※3:それゆえ、Glaisher 表記の Jacobi 楕円関数のグラフ (特に複素変数) は、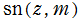 ,
, 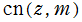 ,
, 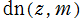 のそれと似ている。当サイトでは掲載個数を削減する理由で、それらのグラフを載せていない。
のそれと似ている。当サイトでは掲載個数を削減する理由で、それらのグラフを載せていない。
その他:※1の理由から、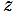 が変数の Neville テータ関数は実変数のグラフのみを掲載し、複素変数のグラフは専ら
が変数の Neville テータ関数は実変数のグラフのみを掲載し、複素変数のグラフは専ら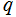 または
または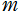 が変数の場合を掲載する。また、
が変数の場合を掲載する。また、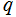 を複素変数とする場合のグラフは大変複雑なため、等高線を入れるとメモリーオーバーを起こす。したがって、代わりに FunctionPlot.m を使用する。
を複素変数とする場合のグラフは大変複雑なため、等高線を入れるとメモリーオーバーを起こす。したがって、代わりに FunctionPlot.m を使用する。
※1:したがって、
※2:Neville はこの著書中で、他にも楕円関数に対して合理的な定義を提案しているが、残念ながら現在ではほとんど顧みられる事が無い。
※3:それゆえ、Glaisher 表記の Jacobi 楕円関数のグラフ (特に複素変数) は、
その他:※1の理由から、
曲線上の点は
因みに、実数
曲線上の点は
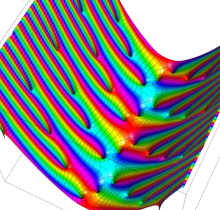
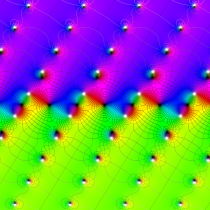
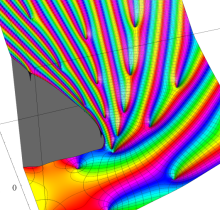
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
アニメーション(13.2MB)
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
(以降、
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
複素変数の Neville のテータ関数
Ramanujan のテータ関数
日:Ramanujanのテータ関数,ラマヌジャン テータ関数英:Ramanujan theta function,仏:Fonction thêta de Ramanujan,独:Ramanujan-Thetafunktion
第1変数と第2変数を対称的な形に定めたテータ関数
を、Ramanujan の (一般) テータ関数という。これは、
となるので、実質は楕円テータ関数
Ramanujan のテータ関数は、自明な公式
のほか、やや複雑な恒等式
など、多数の関係式を満たす。また、積分表示式
を持っている。
Ramanujan のテータ関数の応用事例は、ほとんどが q-解析学などの純粋数学であるが、超弦理論やM理論における最大次元数の問題にも現れる。
【註記】
※1:実は、上記の定義級数と q-シフト因子との関係式が、Jacobi の三重積公式に相当する。
また、Ramanujan が主張した公式の一部は、B. C. Berndt が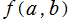 を用いて証明している。Berndt 著 「Ramanujan's Notebooks, Part III. (Springer-Verlag, 1985年)」 の第16章等を参照。
を用いて証明している。Berndt 著 「Ramanujan's Notebooks, Part III. (Springer-Verlag, 1985年)」 の第16章等を参照。
※1:実は、上記の定義級数と q-シフト因子との関係式が、Jacobi の三重積公式に相当する。
また、Ramanujan が主張した公式の一部は、B. C. Berndt が
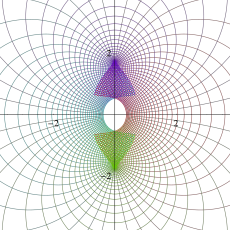
二つの直角双曲線で囲まれた領域の (原点を含む側の) 内部のみで存在する。
複素変数の Ramanujan のテータ関数
複素変数の Ramanujan のテータ関数
複素変数の Ramanujan のテータ関数
複素変数の Ramanujan のテータ関数
アニメーション(4.13MB)
複素変数の Ramanujan のテータ関数
一般に Ramanujan のテータ関数は、存在領域の円の半径が1(単位円) とは限らない。
複素変数の Ramanujan のテータ関数
一般に、