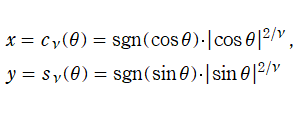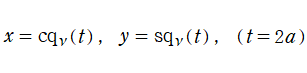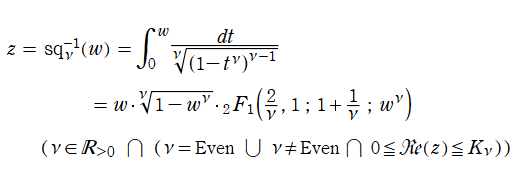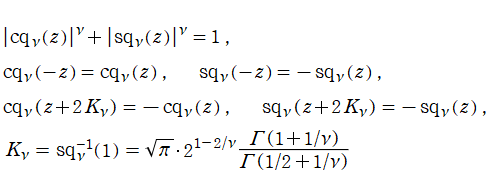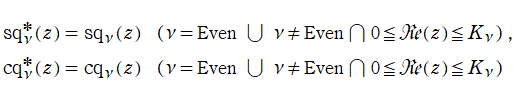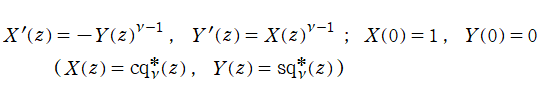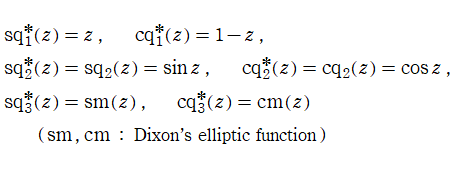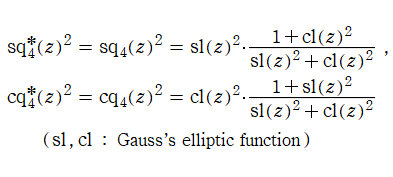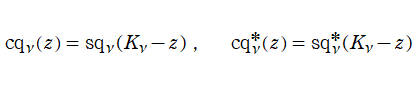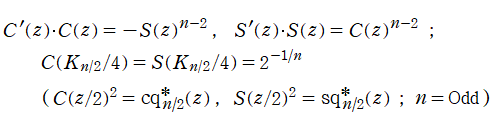特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
Abel 関数
Abel 関数
日:Abel関数,アーベル関数英:Abelian function,仏:Fonction Abélienne,独:Abelsche funktion
Abel 関数は、多変数の楕円関数ともいうべき関数で、
19世紀前半には楕円積分の拡張として、根号内が5次以上の多項式となる超楕円積分、さらには代数関数の積分である Abel 積分が考察対象として本格的に扱われるようになり、それらの積分も楕円積分と同様に、第1種~第3種の標準形に帰着できること等が次第に判明した。また、楕円関数との類似性から、その逆関数に相当するものを求めることが当時の数学界における中心的課題となり、「超楕円積分の逆関数問題」 と呼ばれるようになった。
まず始めに C. G. J. Jacobi は (多項式が6次の) 超楕円積分の逆関数を求めたが、それは4重周期関数であるものの二価関数であった。種数
さらに1840年代には J. G. Rosenhain, A. Göpel, および C. Hermite 等が、種数2の Abel 関数を具体的な2変数テータ関数の商で表わすことに成功した。
一般の種数
に対する逆関数、すなわち
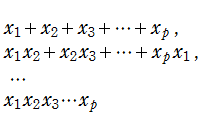
一方、Riemann は、自身の産み出した Riemann 面の概念とその面上での線積分を用いて、種数
第1種 Abel 積分の被積分関数である代数関数は、種数
このとき、
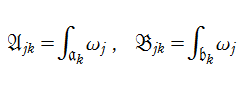
を定義すると、積
さて、ここで取り扱う具体的な Abel 関数は、
なお、この Abel 関数は、値:
Riemann モジュール行列
と表わされる。
Abel 関数論は、前述のとおり Weierstrass, および Riemann によって一応の完成段階に達し、しばしば19世紀数学の最高到達点の一つと称される。現在では、解析的な側面として演繹的に Abel 関数論が含まれるように 「代数関数論」 が整備され、その過程で重要視されるようになった Riemann 面の概念や代数多様体は、それ自体が研究対象として興味を引き、位相幾何学など新しい分野との繋がりも見出された。Abel 関数は、一変数複素関数論に比べて (現在でも) 不明な点がある多変数複素関数論において、具体的な考察対象を与えるものとしても重要である。
Abel 関数の純粋数学的な応用としては、高次の代数曲線や代数曲面 (例えば Kummer 曲面など) を Abel 関数によってパラメータ表示すること等、19世紀後半からの研究がある。これは、現在では 「代数幾何学」 と呼ばれる大きな分野に発展している。整数論では、代数多様体を代数体の類似と見て、前者に付随して定義される 「合同ゼータ関数」 では Riemann 予想が成立していることを、1974年に P. Deligne が証明した等の著しい成果がある。
物理学においても、重力下で固定点を持つ剛体 (独楽など) の回転運動を記述する Euler 運動方程式は、種数2の Abel 関数によって表わされる特別な解を持つことを、S. V. Kovalevskaya が発見したこと等、種々の応用事例がある。
【註記】
※1:これは、数学史上の事件とも言うべき出来事として知られている。概ね次のように経過した。
1826年:Abel からアカデミーへ論文が提出される。審査は主に A. M. Legendre と A. L. Cauchy が行う。論文の字が薄くて読めないとの結論になり、再提出を Abel に求める事および論文の保管が Cauchy に託された。
1829年:Jacobi は Legendre に手紙を送り、Abel から提出されたはずの論文に注目するよう促す。(因みに、その約1週間前に Abel は亡くなる。)
1830年:フランス7月革命。王政復古時代が終わり、保守支持を表明していた Cauchy は亡命する。
1838年:Cauchy が亡命先から帰国するが、Abel の論文は再び忘れ去られる。
1841年:アカデミーから論文が公表される (論文提出は1826年であった旨の断り付き)。
※1:これは、数学史上の事件とも言うべき出来事として知られている。概ね次のように経過した。
1826年:Abel からアカデミーへ論文が提出される。審査は主に A. M. Legendre と A. L. Cauchy が行う。論文の字が薄くて読めないとの結論になり、再提出を Abel に求める事および論文の保管が Cauchy に託された。
1829年:Jacobi は Legendre に手紙を送り、Abel から提出されたはずの論文に注目するよう促す。(因みに、その約1週間前に Abel は亡くなる。)
1830年:フランス7月革命。王政復古時代が終わり、保守支持を表明していた Cauchy は亡命する。
1838年:Cauchy が亡命先から帰国するが、Abel の論文は再び忘れ去られる。
1841年:アカデミーから論文が公表される (論文提出は1826年であった旨の断り付き)。
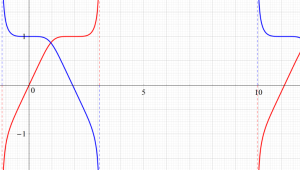
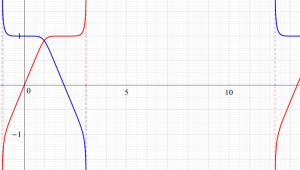
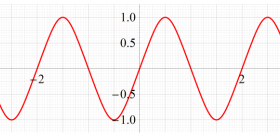
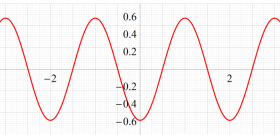
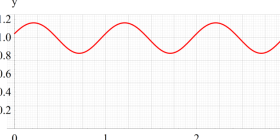
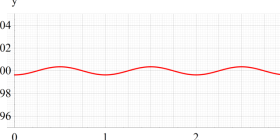
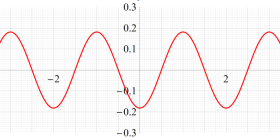
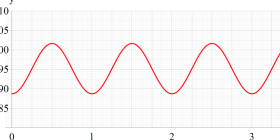
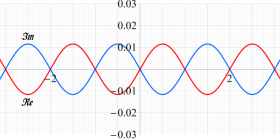
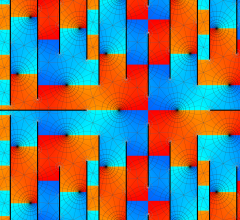
実変数、および複素変数の Abel 関数
ここで、上記の Abel 関数が実際に4個の基本周期を持つことを確認しよう。前述の奇関数の定義式、および後述の Riemann テータ関数の諸公式を用いれば、周期性は
となることが分かる。ここに、指標の要素は0または1からなるので、指数関数因子は必ず±1になることに注意する。さらに、ここで考察している事例は、
であるから、周期性の式は
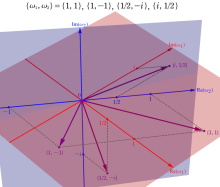
に簡略化される。ここで、指数関数因子が1となるためには
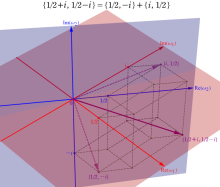
の4個選べることが分かる。つまり、この Abel 関数の任意の周期はすべて、この4個の基本周期の有限和で表わされる。
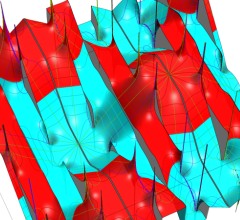
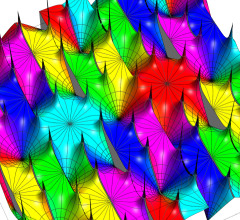
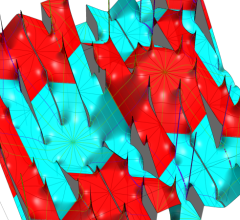
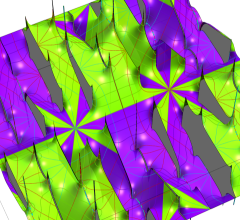
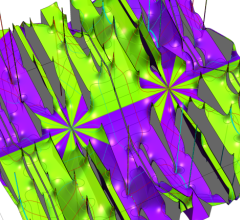
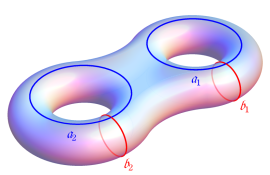
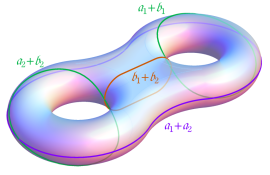
4個の基本周期、基本周期の和の一例、および基本周期からなる格子を、4次元空間内のベクトルとして視覚化すると次のようになる。
また、変数が基本周期の2区間分を動いたときの
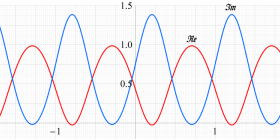
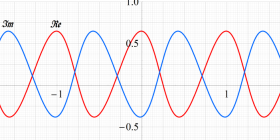
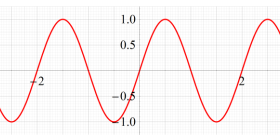
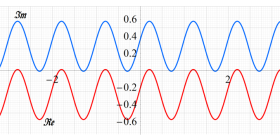
実変数、および複素変数の Abel 関数
実変数、および複素変数の Abel 関数
実変数、および複素変数の Abel 関数
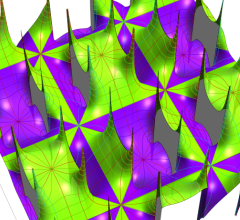
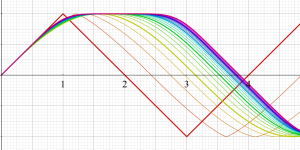
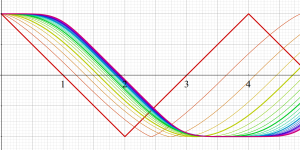
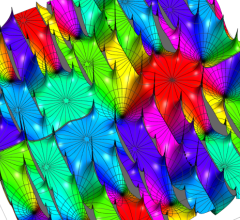
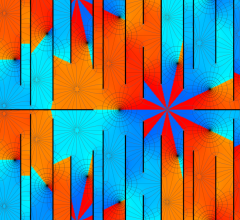
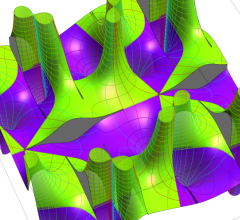
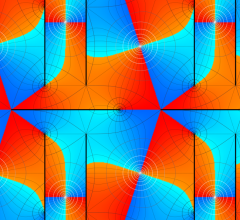
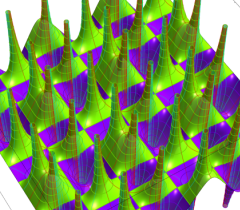
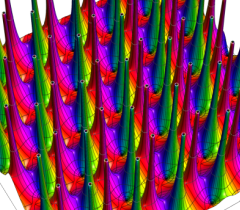
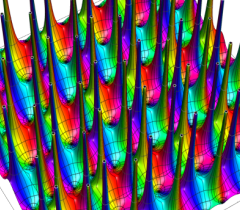
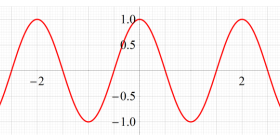
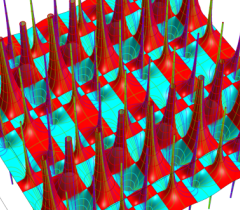
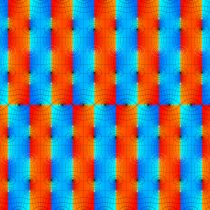
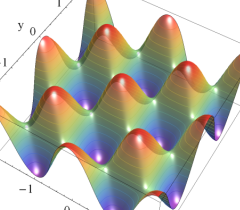
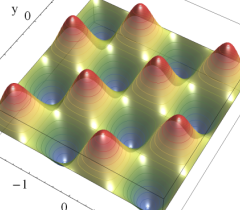
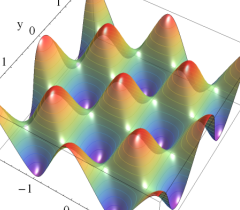
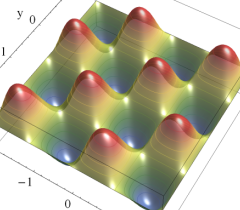
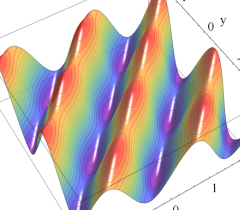
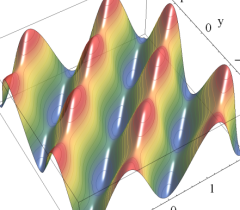
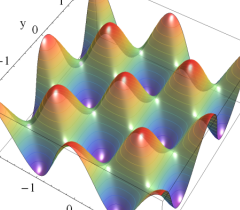
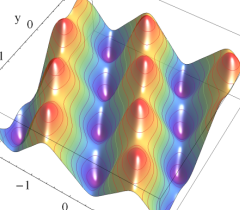
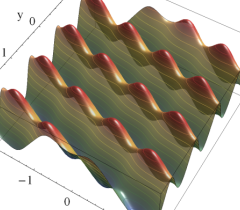
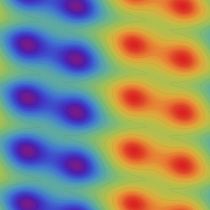
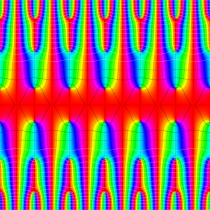
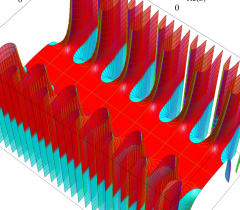
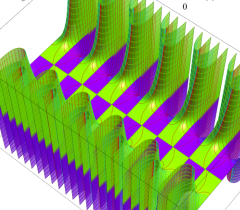
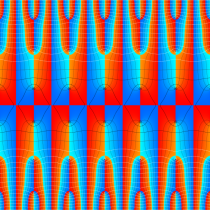
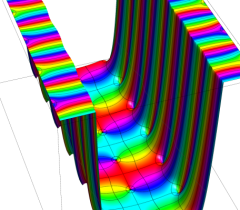
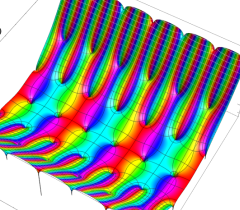
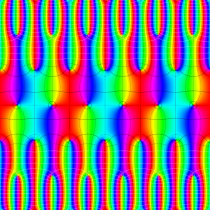
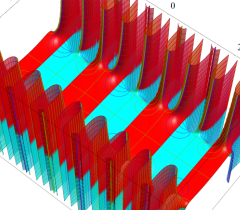
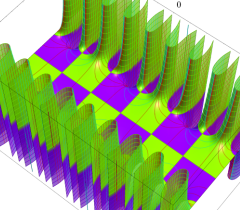
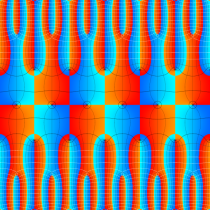
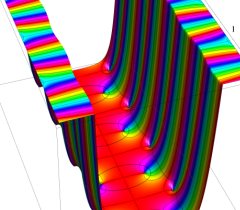
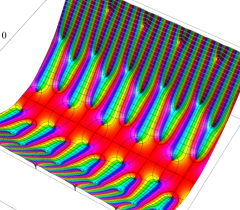
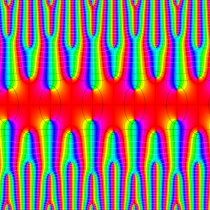
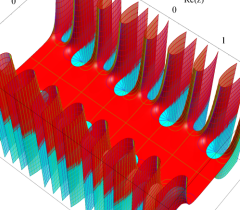
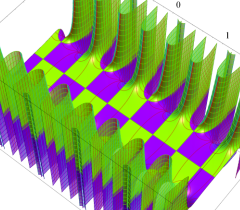
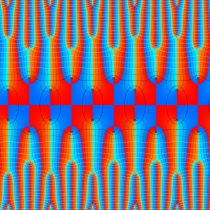
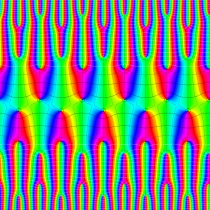
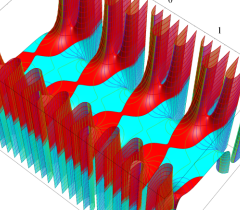
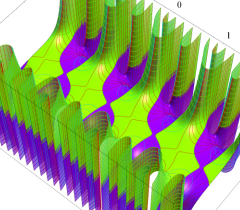
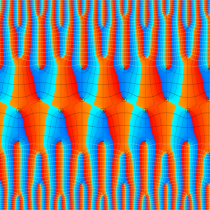
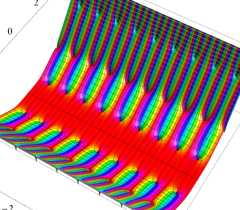
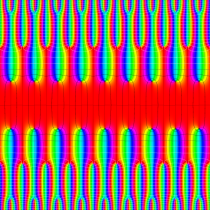
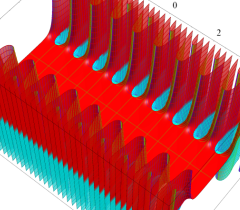
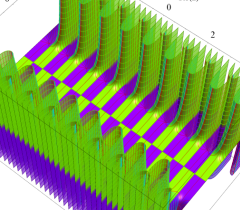
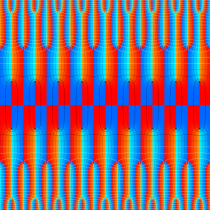
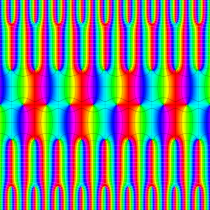
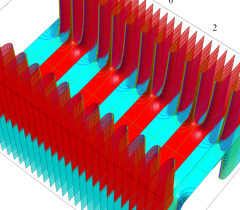
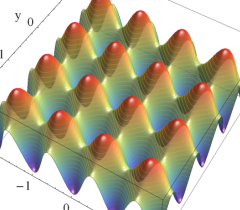
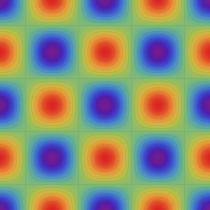
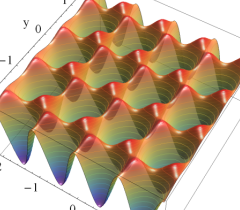
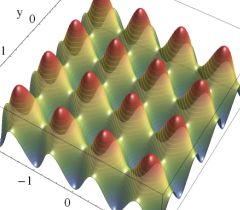
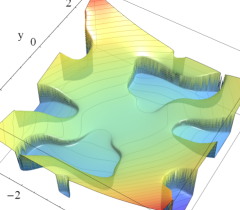
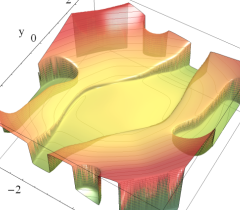
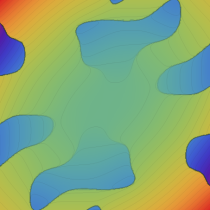
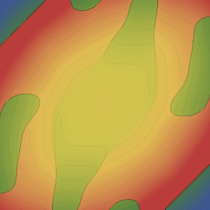
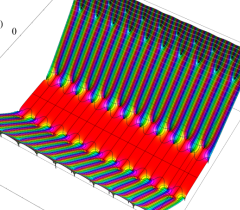
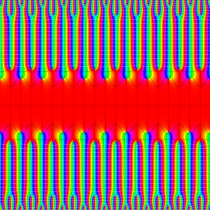
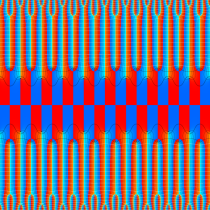
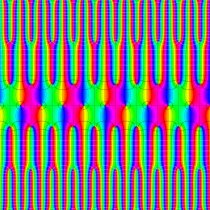
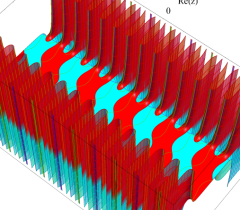
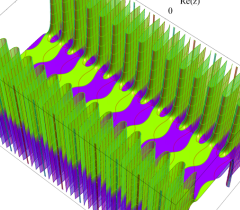
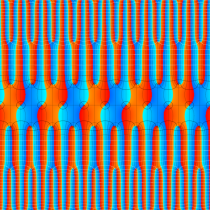
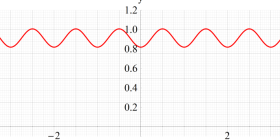
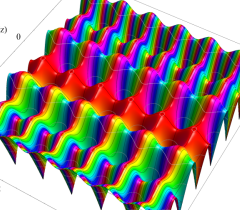
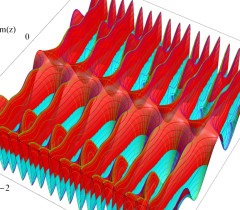
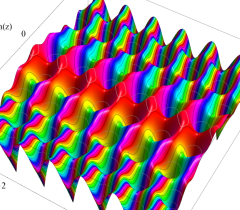
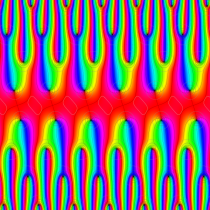
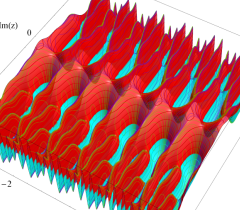
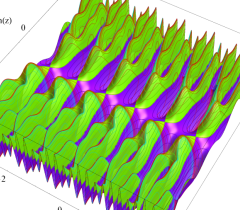
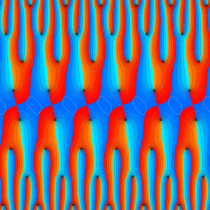
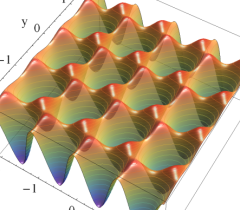
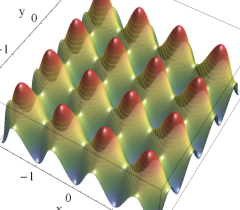
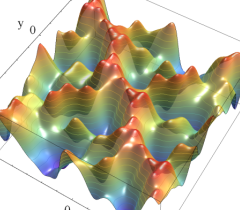
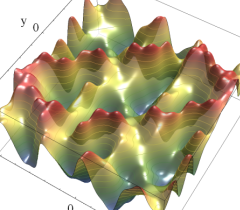
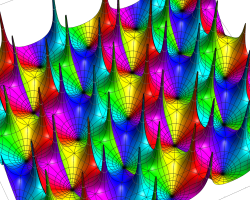
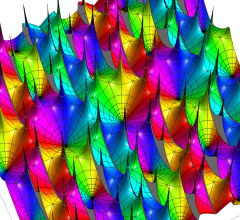
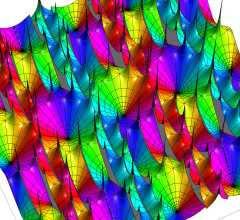
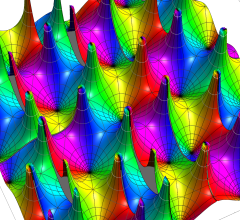
実2変数の Abel 関数
実2変数の Abel 関数
実2変数の Abel 関数
実2変数の Abel 関数
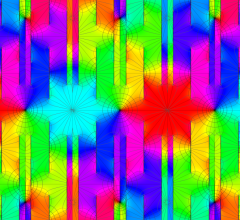
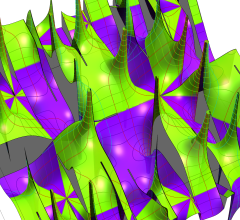
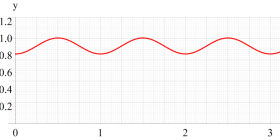
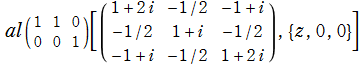 のグラフ。
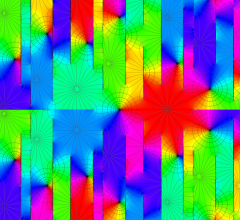
のグラフ。実変数、および複素変数の Abel 関数
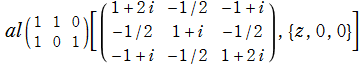 のグラフ。
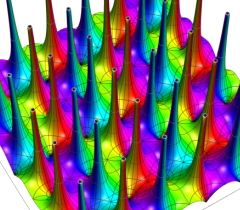
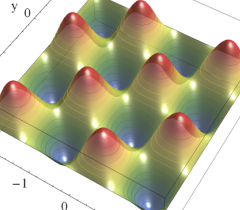
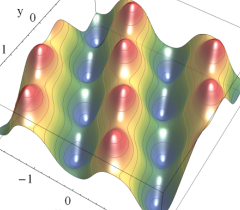
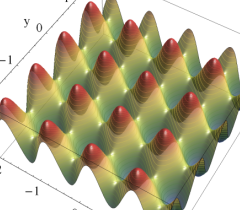
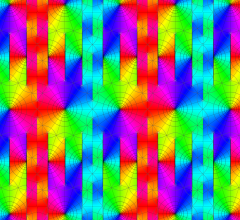
のグラフ。実2変数の Abel 関数
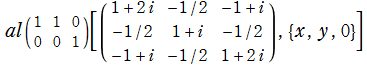 のグラフ。
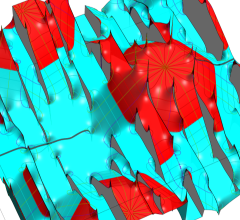
のグラフ。実2変数の Abel 関数
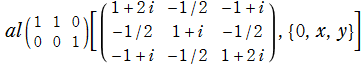 のグラフ。
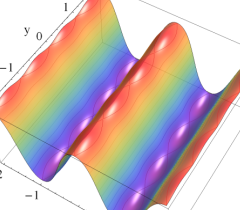
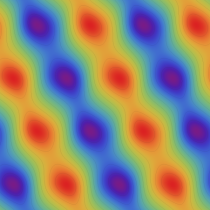
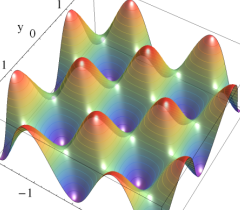
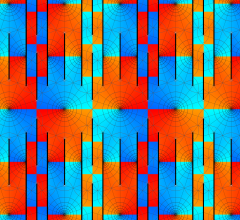
のグラフ。実2変数の Abel 関数
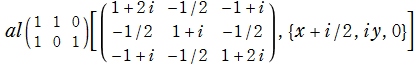 のグラフ。
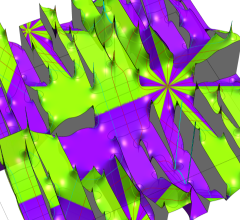
のグラフ。実2変数の Abel 関数
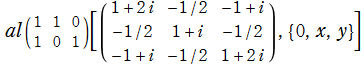 のグラフ。
のグラフ。Riemann テータ関数
日:Riemannテータ関数,リーマンθ関数英:Riemann Theta Function,仏:Fonction thêta de Riemann,独:Riemannsche thetafunktion
歴史的に Riemann テータ関数は、それらの商として Abel 関数を表わすために導入された。Abel 関数が
種数
と表わされる。ここに、
特に、種数2のときを具体的に表記すれば (
Riemann テータ関数の
と表わされる。また、Riemann テータ関数は
併せて、「指標付き Riemann テータ関数」 がしばしば定義される。
と表わされる。ここに、簡略形記号は前述と同じであり、
指標付き Riemann テータ関数は、次のように (指標無し) Riemann テータ関数で表わすことができる。
特に、種数2の場合を具体的に記述すれば (
となる。
種数1の場合に楕円テータ関数になることを具体的に表記すれば、
となる。ここに、
一方、Riemann テータ関数は Riemann モジュール行列
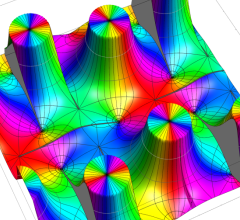
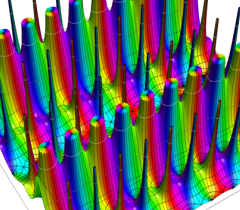
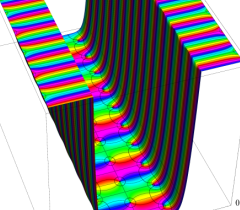
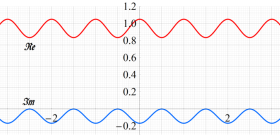
実変数、および複素変数の Riemann テータ関数
実変数、および複素変数の Riemann テータ関数
実変数、および複素変数の Riemann テータ関数
実変数、および複素変数の Riemann テータ関数
実変数、および複素変数の Riemann テータ関数
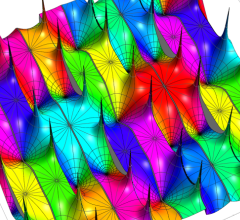
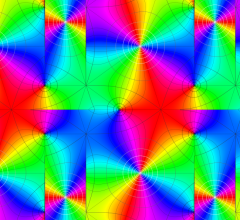
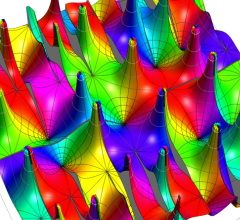
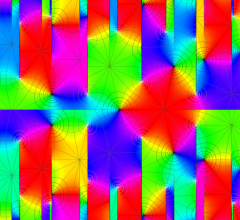
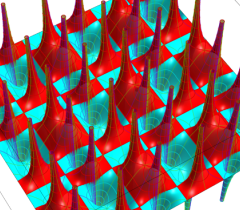
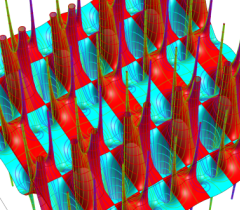
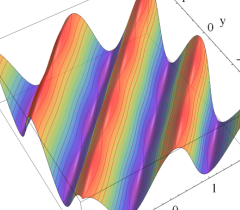
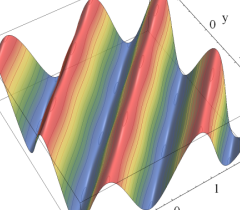
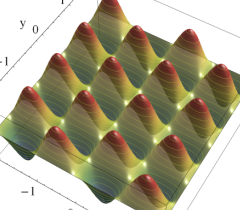
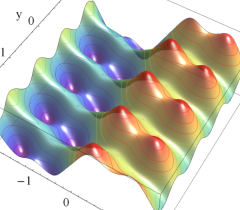
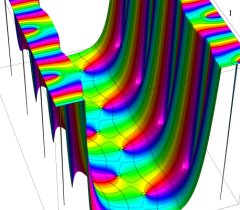
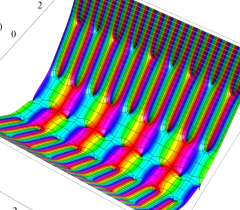
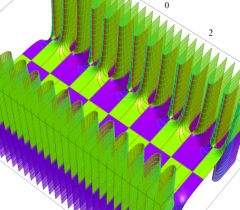
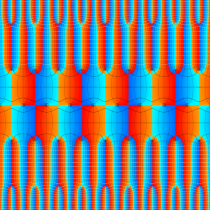
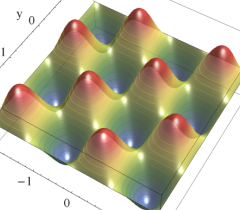
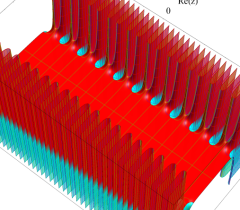
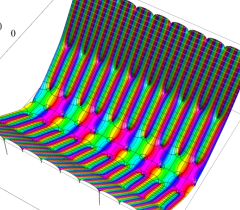
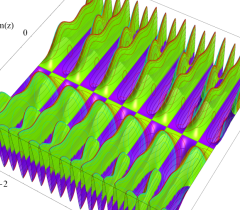
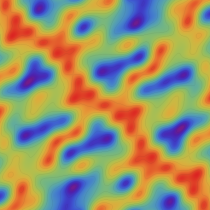
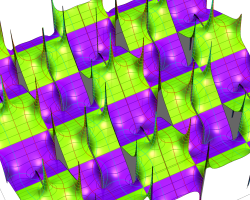
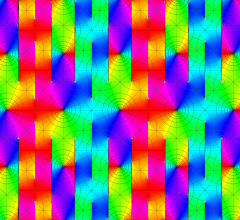
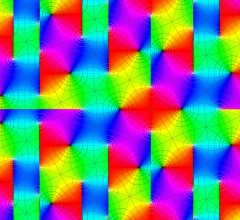
実2変数の Riemann テータ関数
実2変数の Riemann テータ関数
実2変数の Riemann テータ関数
実2変数の Riemann テータ関数
(ただしこの場合は、関数値が極端に大きくなるため、実部・虚部それぞれの逆双曲線正弦値をとっている。)
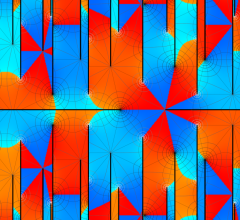
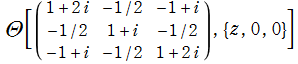 のグラフ。
のグラフ。実変数、および複素変数の Riemann テータ関数
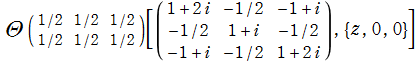 のグラフ。
のグラフ。Scaled - Riemann テータ関数
通常の Riemann テータ関数に指数関数因子を乗じた、Scaled - Riemann テータ関数を定義することがある (例えば、「NIST Handbook of Mathematical Functions」 など)。ここに、
Scaled - Riemann テータ関数は複素ベクトル変数
実変数、複素変数の Scaled - Riemann テータ関数
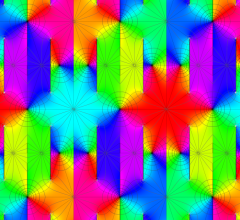
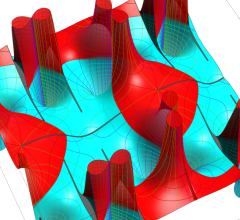
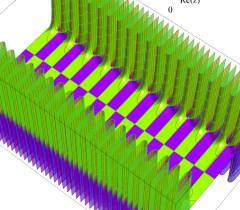
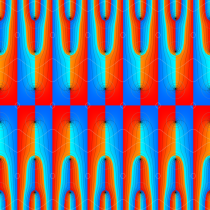
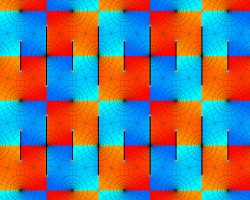
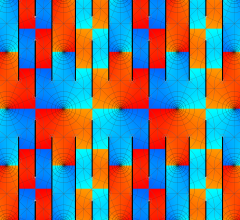
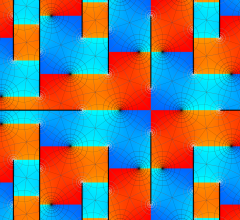
実2変数の Scaled - Riemann テータ関数
実2変数の Scaled - Riemann テータ関数
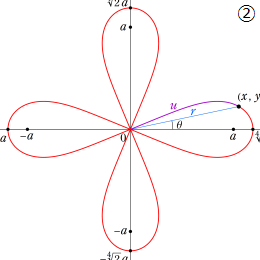
超レムニスケート関数
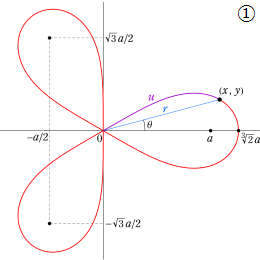
レムニスケート (連珠形) が原点から延びる弦 (動径) によって切り取られて弧を作るとき、弦の長さは、弧の長さを変数とする Gauss の楕円関数で表わされるのであった。ここでレムニスケートを拡張し、原点を中心とし半径が
となるので、これを整理すれば
が得られる。(下図は、①3焦点のレムニスケート, ②4焦点のレムニスケートである。)
ここに、
の逆関数であり、Gauss の楕円関数 (レムニスケート正弦関数) を拡張したものに相当するので、当サイトでは
となる※2。
また、
となるので、実質は楕円関数の無理関数であることが分かる。
【註記】
※1:NDSolveComplexDomain.m に収録している超レムニスケート関数のコードは、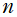 が非整数である場合も一応計算できるが、そのグラフは正当性に疑念が残る概形になる (非複素解析的な結果になるので、恐らく誤っている)。
が非整数である場合も一応計算できるが、そのグラフは正当性に疑念が残る概形になる (非複素解析的な結果になるので、恐らく誤っている)。
※2:C. F. Gauss は、三角関数の拡張を企図して楕円関数の発見に至るまでの過程で、ここで言うところの](siki_spec360/abel10300.png) についても検証している。高木貞治 著 「近世数学史談」 の第6章冒頭 (p.36~37) を参照。
についても検証している。高木貞治 著 「近世数学史談」 の第6章冒頭 (p.36~37) を参照。
※1:NDSolveComplexDomain.m に収録している超レムニスケート関数のコードは、
※2:C. F. Gauss は、三角関数の拡張を企図して楕円関数の発見に至るまでの過程で、ここで言うところの
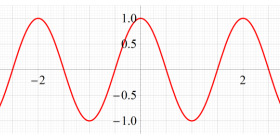
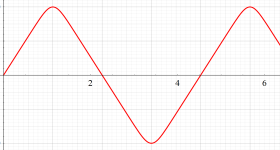
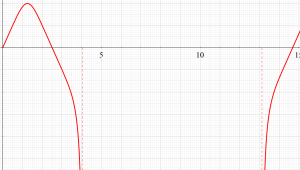
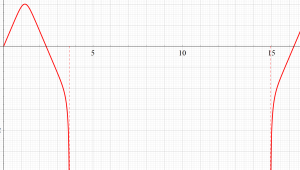
超レムニスケート関数:実変数
超レムニスケート関数:実変数
超レムニスケート関数:実変数
(複素変数の3番目のグラフは、放射状の分枝切断線を採用した場合。)
超レムニスケート関数:実変数
(複素変数の3番目のグラフは、放射状の分枝切断線を採用した場合。)
実変数の超レムニスケート関数
多価関数である超レムニスケート関数
関数
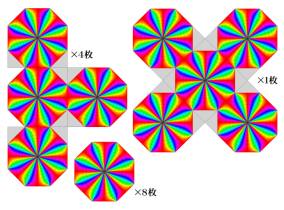
原点を含む正8角形の領域を
Euclid 平面上では、頂点を介して8枚分の正8角形を敷き詰めることはできないが、非 Euclid 平面 (双曲幾何) 上では可能である。したがって、正8角形を円弧正8角形に移す写像 (Schwarz - Christoffel 変換等、複数種の等角写像の合成) によって、
なお、合同な円弧正8角形のみから成る Schwarz の保型関数は無数にあるため、写像先の円弧正8角形は、これが唯一ではない。例えば Schwarz の保型関数
以下は、
用意した組み立てパーツ。
組み立て中の状態。貼り合わせは瞬間接着剤を用いた。
完成。横から見ると、フリル状に歪んでいるので、これを平面と呼ぶのは無理がある。しかし、それは Euclid 空間に住む人間の感覚である。この曲面上のみを移動可能な 「2次元生命体」 が存在したならば、彼らは 「我々の世界は平坦で歪みがない。ここでは正8角形を隙間なく敷き詰めることができる。」 と言うであろう。フリル状の歪みは、この非 Euclid 平面が負の曲率を持つ (双曲幾何である) ことに由来する。
なお、深い論考を伴ったもっと複雑な紙細工が、「Home page of Gerard Westendorp」 (http://westy31.home.xs4all.nl/Geometry/Geometry.html) に多数掲載されている。
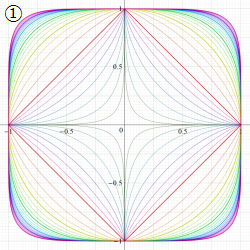
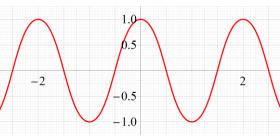
Squigonometric 関数
日:Squigonometric 関数※1英:Squigonometric function,Trigonometric function in ν-norm
ここでは、前節の超レムニスケート関数とよく似ている別の関数を取り上げる。以降、断らない限り
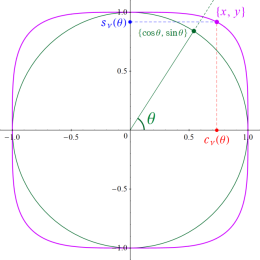
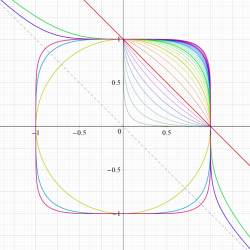
円の陰関数表示式を拡張した
Squircle は、媒介変数表示式
で表わすこともできるが、この
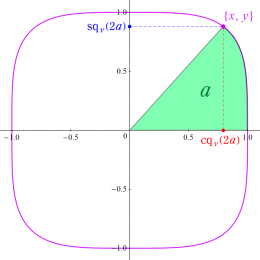
そこで、点
で記述できる関数
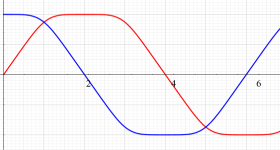
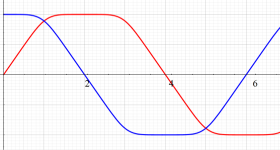
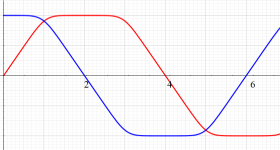
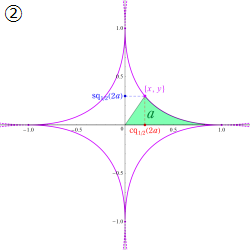
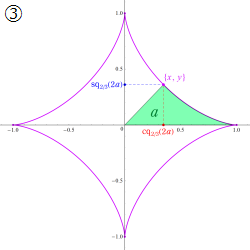
具体的に、Squigonometric 正弦関数
の逆関数であり、Squigonometric 余弦関数
を持つ。ただし、周期性は Squircle の定義式に絶対値記号が使われていることに因る。このため、一般に Squigonometric 関数は、複素領域で技巧的な分枝切断線が無数に入り、互いに連結していない分枝が生じてしまう。そこで当サイトでは、解析接続が施されて分枝が単連結となる Squigonometric 関数
を併せて定義する。両者は、非線形連立微分方程式の解
となる。(実際の数値計算では、上記のうち初期条件を
関数
となる。また、
となるので、楕円関数の無理関数に帰着される。(→ Gauss および Dixon の楕円関数)
Squigonometric 余弦関数は、
であるから、いずれの複素変数グラフも、Squigonometric 正弦関数のそれを原点で180°回転し、さらに
【註記】
※1:恐らく Squigonometric function は新しい名称で、適当な訳語もまだ存在しない。当サイトでは敢えて (検索に掛かりやすいキーワードとして) "Squigonometric" を残し、「Squigonometric 関数」 と呼ぶことにする。もし、次の※2を踏まえて全訳したならば、「矩形円関数」 または 「方円関数」 となるだろうか?。
※2:Squircle なる名称も、Square (矩形, 四角形) と Circle (円) から成る比較的新しい造語であって、統一された訳語は存在しない。中国語ではこれを 「方圓形」 と訳すようである。なお、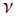 が偶数ならば Squircle と一致する定義
が偶数ならば Squircle と一致する定義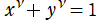
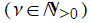 の場合を、「Fermat 曲線」 と呼ぶことがある。
の場合を、「Fermat 曲線」 と呼ぶことがある。
さらに、Squircle を一般化した曲線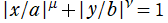
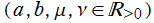 は、「スーパー楕円」 または 「Lamé 曲線」 と呼ばれている。スーパー楕円に対応した Squigonometric 関数も既に研究されているが、当サイトはそこまで深入りしない。
は、「スーパー楕円」 または 「Lamé 曲線」 と呼ばれている。スーパー楕円に対応した Squigonometric 関数も既に研究されているが、当サイトはそこまで深入りしない。
※3:通常ならば、Squigonometric 関数は, cos[ν](z)](siki_spec360/abel14800.png) で表記されるが、残念ながら当サイトでは同じ記号を q-三角関数で使用したので、代わりに
で表記されるが、残念ながら当サイトでは同じ記号を q-三角関数で使用したので、代わりに, cq[ν](z)](siki_spec360/abel13000.png) で表記する。
で表記する。
※4:NDSolveComplexDomain.m に収録している Squigonometric 関数のコードは、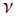 が整数または半奇数ならば複素変数まで正しい。その他の
が整数または半奇数ならば複素変数まで正しい。その他の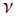 では実変数のみ正しい。
では実変数のみ正しい。
因みに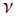 が半奇数のときは、代替の非線形連立微分方程式
が半奇数のときは、代替の非線形連立微分方程式
を用いる。(この微分方程式は、逆関数である Abel 積分の置換積分から導くことができる。)
※1:恐らく Squigonometric function は新しい名称で、適当な訳語もまだ存在しない。当サイトでは敢えて (検索に掛かりやすいキーワードとして) "Squigonometric" を残し、「Squigonometric 関数」 と呼ぶことにする。もし、次の※2を踏まえて全訳したならば、「矩形円関数」 または 「方円関数」 となるだろうか?。
※2:Squircle なる名称も、Square (矩形, 四角形) と Circle (円) から成る比較的新しい造語であって、統一された訳語は存在しない。中国語ではこれを 「方圓形」 と訳すようである。なお、
さらに、Squircle を一般化した曲線
※3:通常ならば、Squigonometric 関数は
※4:NDSolveComplexDomain.m に収録している Squigonometric 関数のコードは、
因みに
を用いる。(この微分方程式は、逆関数である Abel 積分の置換積分から導くことができる。)
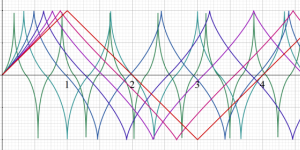
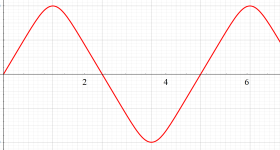
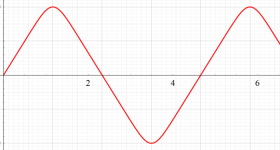
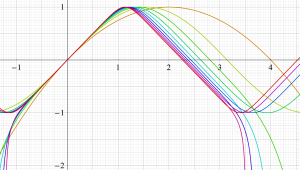
複素変数の Squigonometric 関数
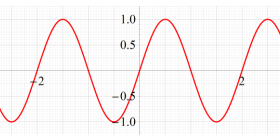
実変数の Squigonometric 関数
複素変数の Squigonometric 関数
実変数の Squigonometric 関数
複素変数の Squigonometric 関数
実変数の Squigonometric 関数
複素変数の Squigonometric 関数
実変数の Squigonometric 関数
実変数の Squigonometric 関数
アニメーション(9.42MB)
一定長の線分の2端点のうち、一方が常に横軸上、他の一方が常に縦軸上を動くとき、線分群の包絡線はアステロイドになる。
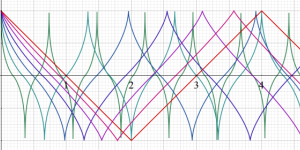
複素変数の Squigonometric 関数
実変数の Squigonometric 関数
複素変数の Squigonometric 関数
複素変数の Squigonometric 関数
複素変数の Squigonometric 関数
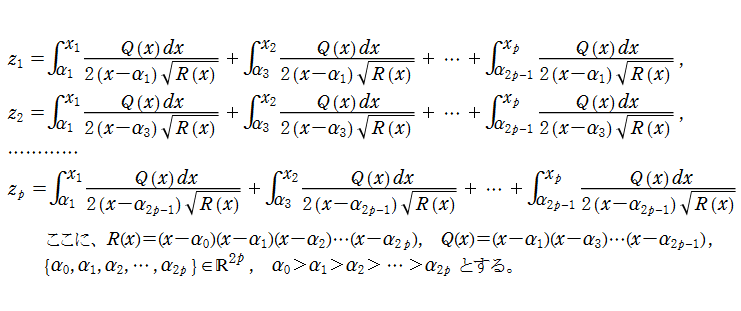
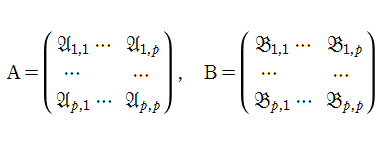
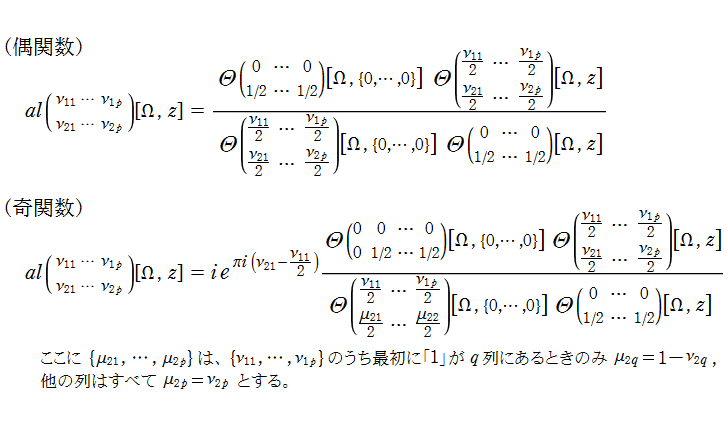


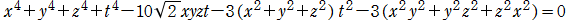






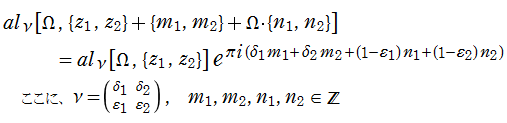
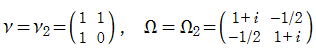
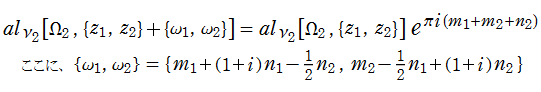
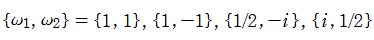
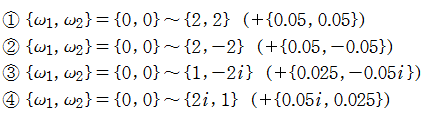










































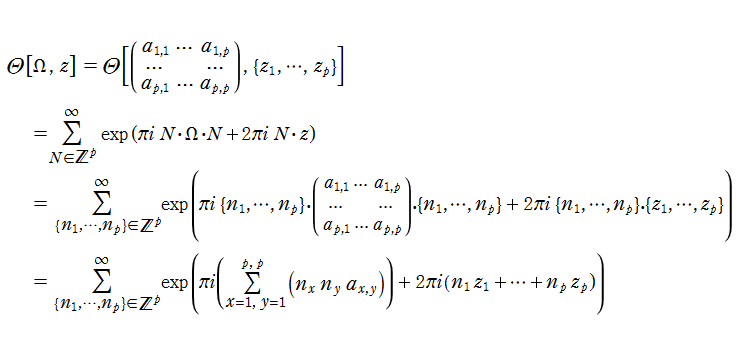
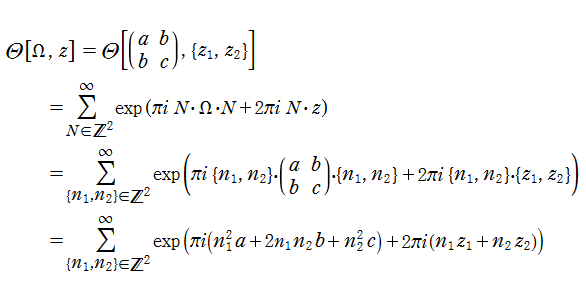
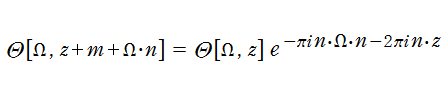
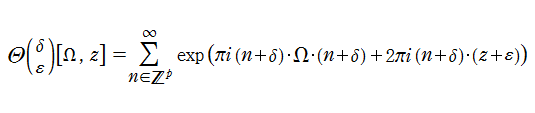
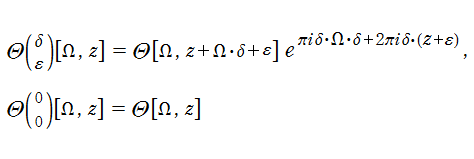
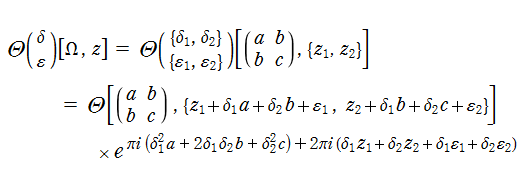
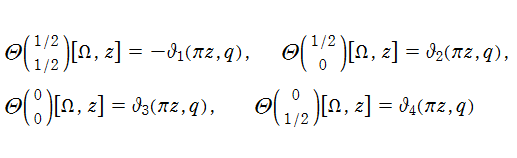









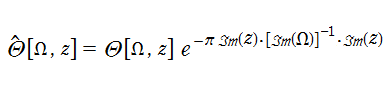



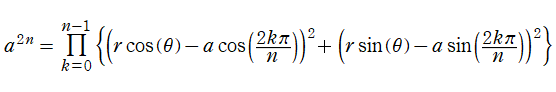
 a))(過程・結果)](siki_spec360/abel10000.png)
![z = sl[n]-1(w) = Integral[0,w](1/Sqrt(1-t^n))dt](siki_spec360/abel10200.png)
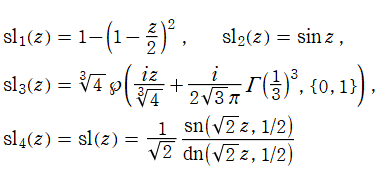
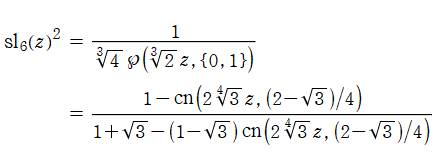














^8のグラフ](gazou_spec360/360_1770_thumb.png)