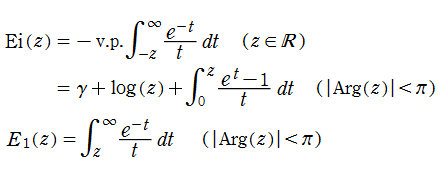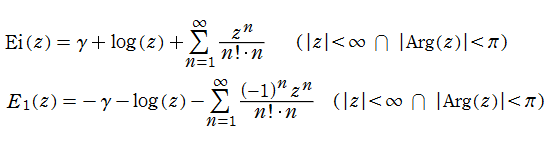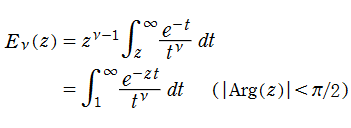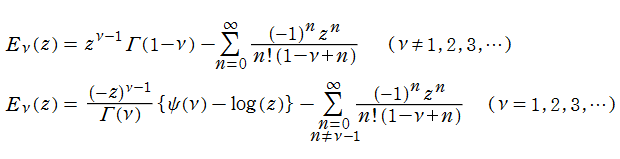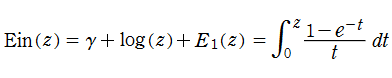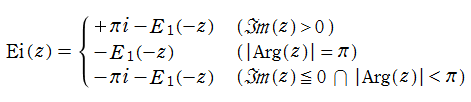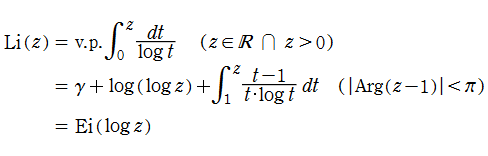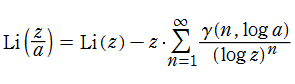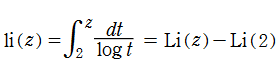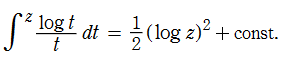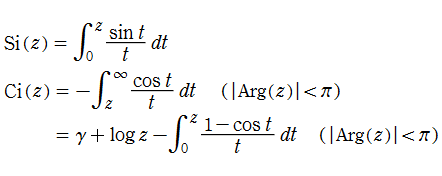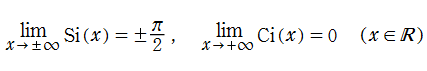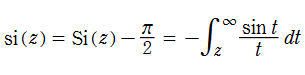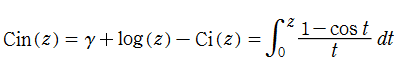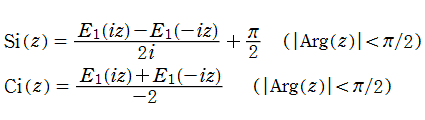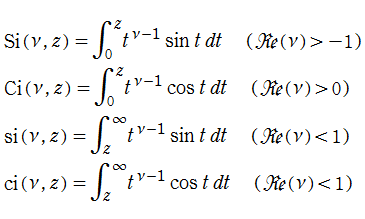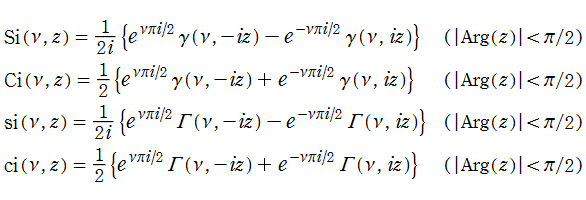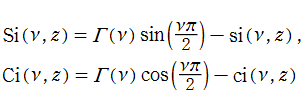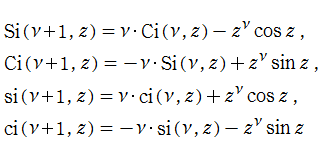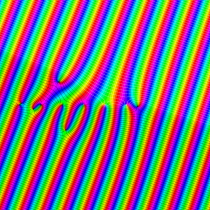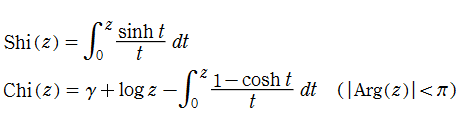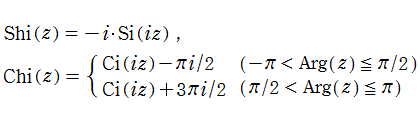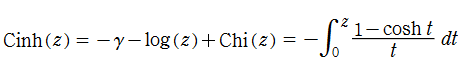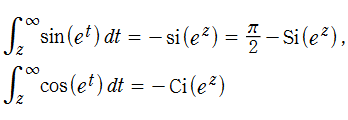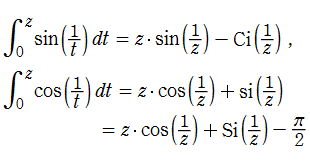特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
積分指数関数
積分指数関数
日:積分指数関数,指数積分英:Exponential integral,仏:Exponentielle intégrale,独:Integralexponentialfunktion
初等関数の積分が、再び初等関数にならず全く新しい関数になる例は、17世紀以降の積分計算に伴って多数発見されてきた。そのうち、本頁の積分指数関数系、次頁以降で述べる誤差関数系や楕円積分は、被積分関数の形が簡潔で、かつ、諸科学での出現頻度も高いことから特に注目され、現在に至るまで詳しい研究の積み重ねがある。このため、これらの関数は、特殊関数としての地位が比較的早くから確立している。
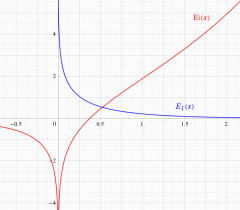
さて、積分指数関数とは、積分表示式で定義された次の二つの関数
のことである。ここに、
積分指数関数は、
なる冪級数に展開できる。このほか、漸近級数など多様な級数展開表示が知られている。
さらに現在では、一般積分指数関数
も定義されている。勿論、この関数は
一般積分指数関数は、不完全ガンマ関数 (と本質的に同じ関数)、合流型超幾何関数の特別な場合として、
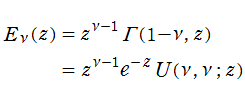
に展開できる。
以上のほか、対数に由来する多価性を取り除いて超越整関数にした、相補 (complementary -) 積分指数関数
が併用されることもある。
積分指数関数は、上記以外にも置換積分等によって得られる夥しい数の積分表示式があり、それらは公式集で網羅的に掲載されていることが多い。現在の数式処理システムにも、その変換規則が反映されている。
応用面では、後述の積分対数関数や積分三角関数とともに用いられることが多いが、積分指数関数が単独で現れる応用事例としては、量子力学、恒星や惑星の大気における熱放射平衡、地下帯水層からの坑井を介した揚水理論 (C. V. Theis 法) などがある。
積分指数関数の研究は、A. M. Legendre (1811年)、O. X. Schlömilch (1846年)、および J. W. L. Glaisher (1870年) 等が手掛けている。
【註記】
※1:逆に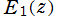 なる関数記号は、一般積分指数関数が導入された後に定着したものである。それ以前は
なる関数記号は、一般積分指数関数が導入された後に定着したものである。それ以前は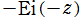 で表記されることもあったが、両者は多価性と Cauchy の主値に由来する違いがある。
で表記されることもあったが、両者は多価性と Cauchy の主値に由来する違いがある。
実のところ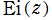 は、
は、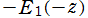 に複素定数を加減した関数の分枝と本質的に同じであるが、実軸上では Cauchy の主値を考慮して更なる場合分けが必要になる。具体的には
に複素定数を加減した関数の分枝と本質的に同じであるが、実軸上では Cauchy の主値を考慮して更なる場合分けが必要になる。具体的には
とすれば、複素領域における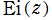 の定義となり、数値計算上も扱い易い。
の定義となり、数値計算上も扱い易い。
※1:逆に
実のところ
とすれば、複素領域における
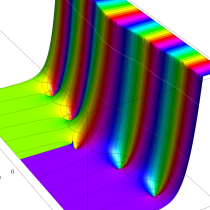
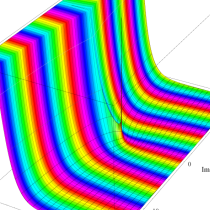
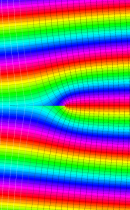
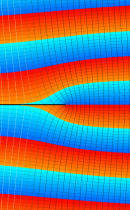
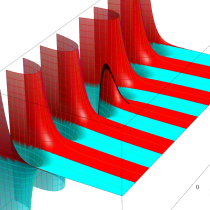
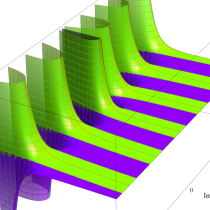
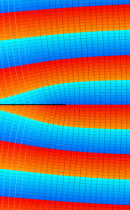
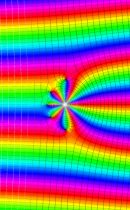
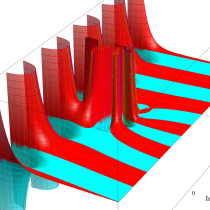
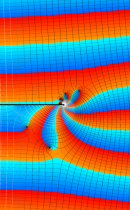
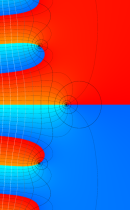
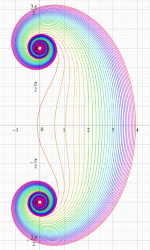
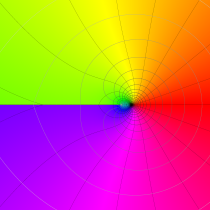
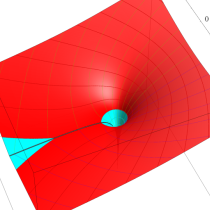
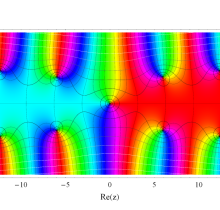
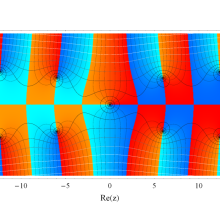
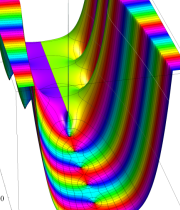
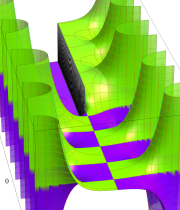
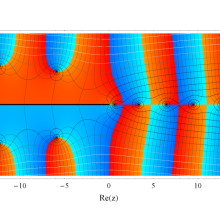
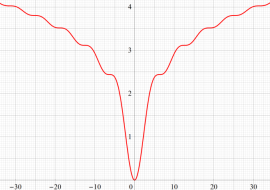
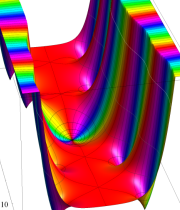
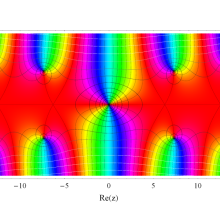
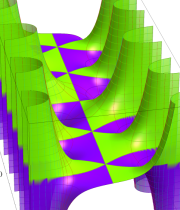
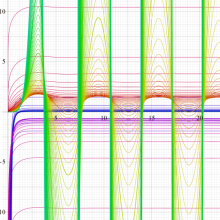
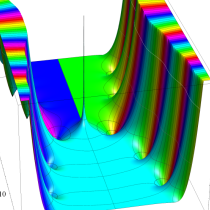
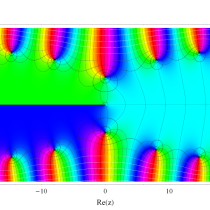
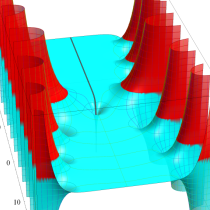
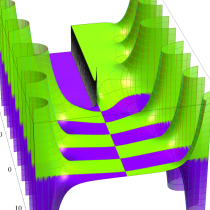
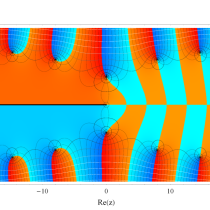
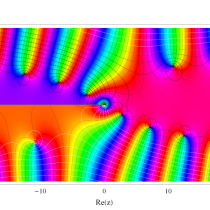
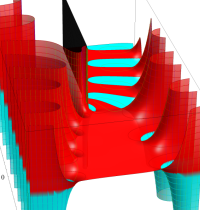
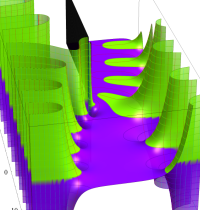
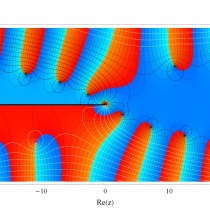
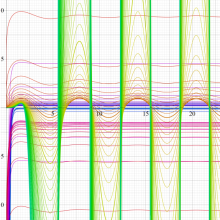
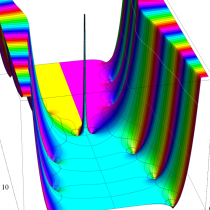
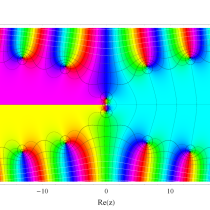
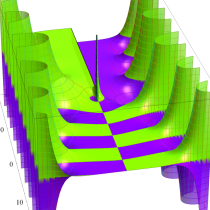
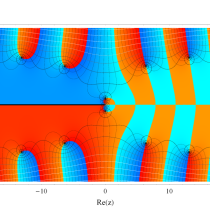
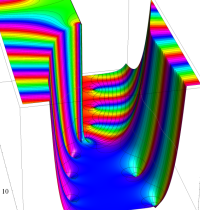
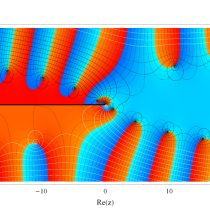
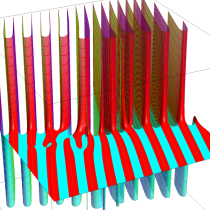
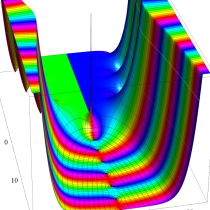
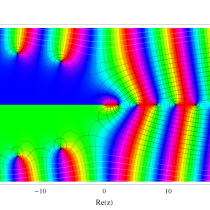
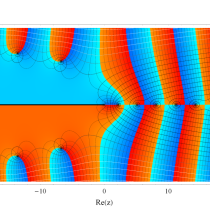
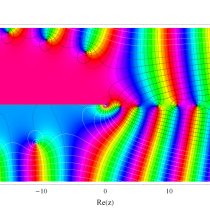
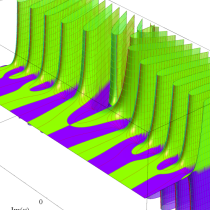
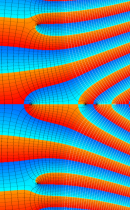
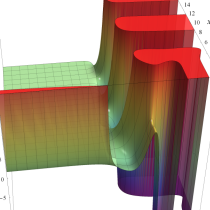
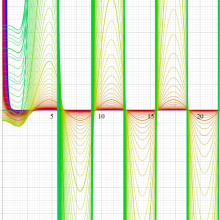
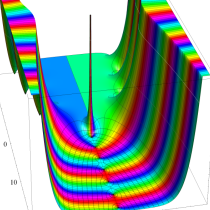
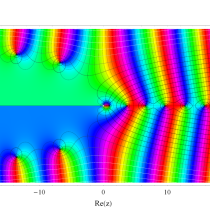
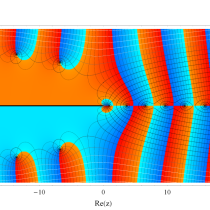
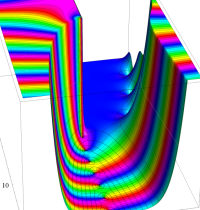
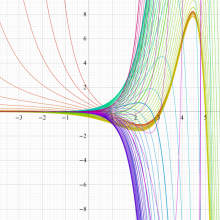
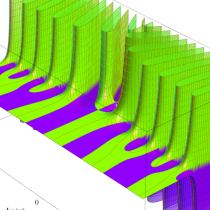
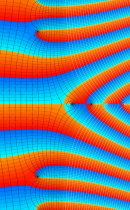
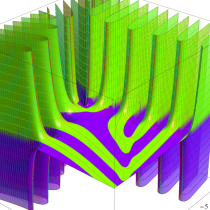
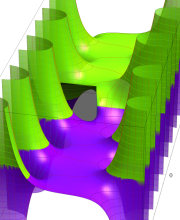
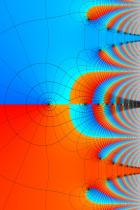
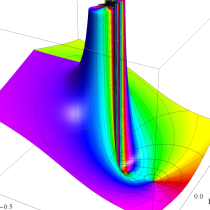
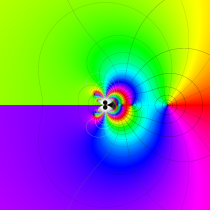
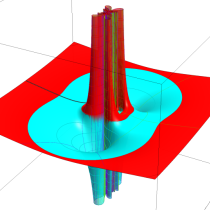
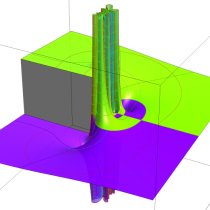
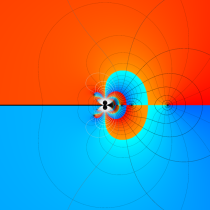
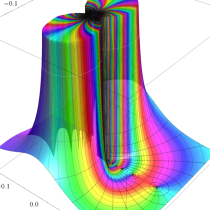
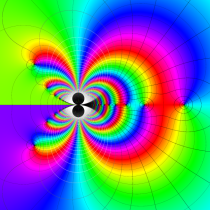
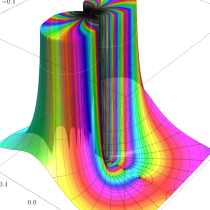
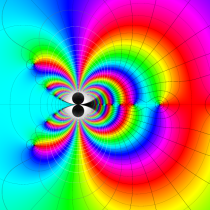
複素変数の積分指数関数
複素変数の積分指数関数
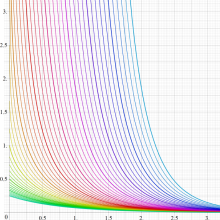
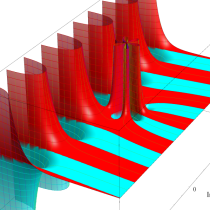
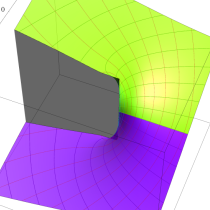
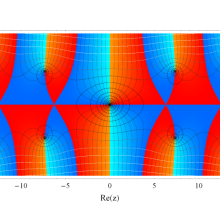
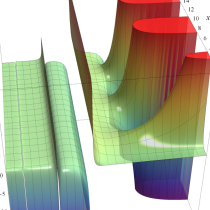
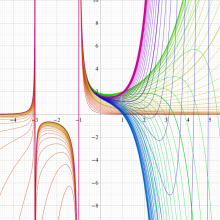
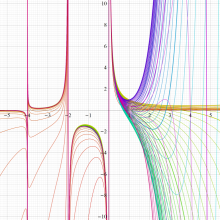
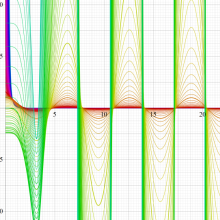
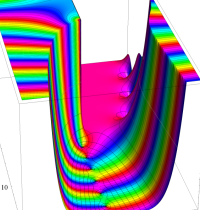
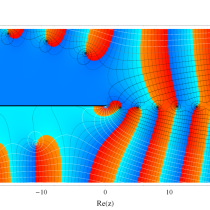
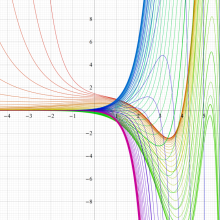
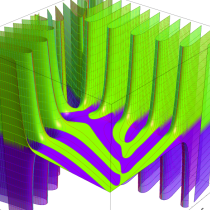
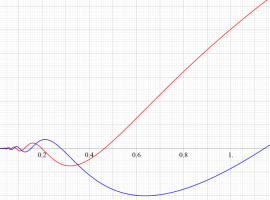
実変数の一般積分指数関数
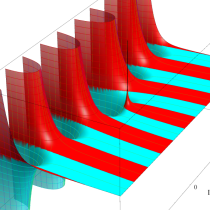
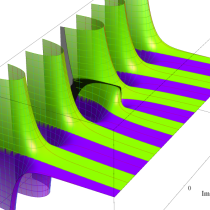
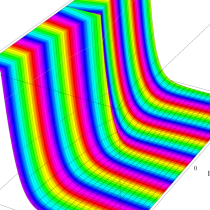
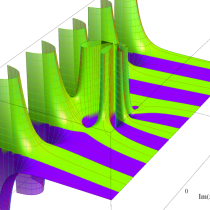
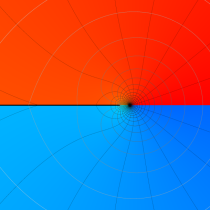
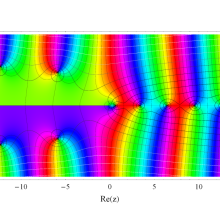
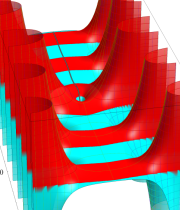
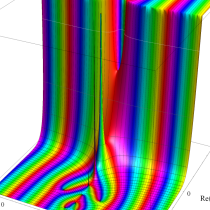
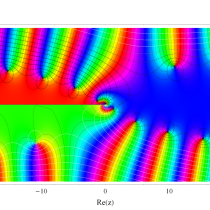
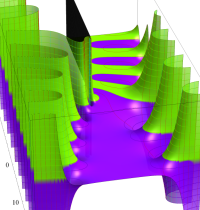
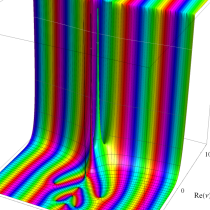
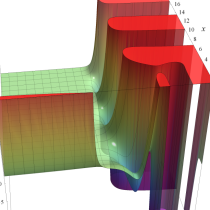
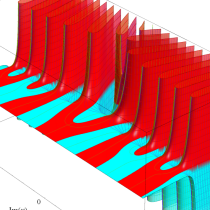
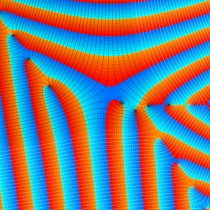
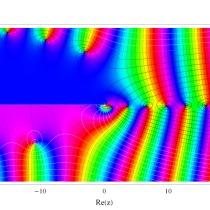
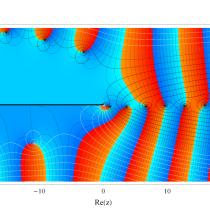
複素変数の一般積分指数関数
複素変数の一般積分指数関数
複素変数の一般積分指数関数
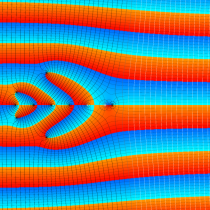
複素変数の相補積分指数関数
積分対数関数
日:積分対数関数,対数積分英:Logarithmic integral,仏:Logarithme intégrale,独:Integrallogarithmus
積分対数関数は、積分指数関数の引数に対数関数を代入した、
で定義される※1。ここに、
積分対数関数の基本的な性質の多くは積分指数関数のそれから導けるので、次の比較的自明でない公式を掲載するのみとし、他は省略する。この公式は、F. W. Bessel によって発見された。
積分対数関数は、物理学等で応用されることはあまりないが、数論、特に素数分布論では頻繁に用いられ、種々の深遠な結果とも関係しているため重要視される。そのうち、「素数定理」 や 「Riemann - von Mangoldt 公式」 は、最もよく知られている応用事例である。後者では、引数が複素数冪になった
数論等では、
を用いることもある※2。この積分区間による定義は、Cauchy の主値をとらなくて済むことに利点があるが、素数定理ではどちらを用いても本質的な違いは生じない。なお、Riemann - von Mangoldt 公式では明確に
実軸上にある
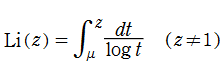
積分対数関数の研究は、L. Euler (1768年)、L. Mascheroni (1790年)、J. von Soldner (1809年)、および C. A. Bretschneider (1837年) 等が手掛けている。記号
【註記】
※1:積分指数関数系の定義方法に倣えば、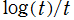 の積分を考えたくなるが、これは
の積分を考えたくなるが、これは
のとおり、初等関数になってしまう。
※2:現在では、当サイトとは逆に、主値をとる関数を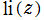 、積分区間を2から始める関数を
、積分区間を2から始める関数を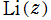 と表記するほうが主流になりつつある。
と表記するほうが主流になりつつある。
※1:積分指数関数系の定義方法に倣えば、
のとおり、初等関数になってしまう。
※2:現在では、当サイトとは逆に、主値をとる関数を
次は、
実際には、より扱いやすい
これは、素数分布論における Riemann - von Mangoldt 公式に関連しており、点
複素変数の積分対数関数
積分三角関数
日:積分三角関数,三角積分英:Trigonometric integral,仏:Trigonométrique intégrale,独:Integraltrigonometrischefunktion
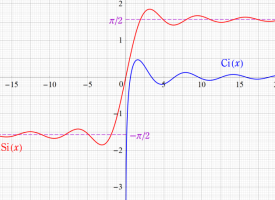
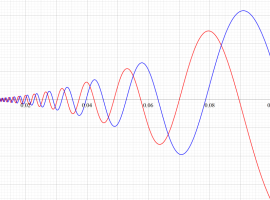
積分三角関数とは、積分表示式で定義された次の二つの関数
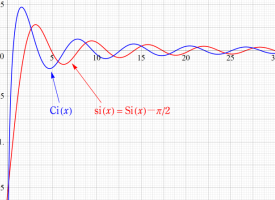
の総称であって、
を持つので、
が用いられることも多い。
が併せて定義されている。
積分三角関数は、虚変数の積分指数関数と
の関係にあり、Euler の公式と類似している。したがって、積分三角関数の基本的性質の大半は、積分指数関数のそれから導かれる。
さらに現在では、一般積分三角関数
も定義されている。この関数については、「NIST-Handbook of Mathematical Functions」 の Chapter 8. 21:p.188~189 に記述がある※1。
一般積分三角関数は不完全ガンマ関数を用いて、
と表わすことができる。ただし、条件を超える領域では不完全ガンマ関数を解析接続する。
一般積分三角関数は、正弦型または余弦型どうしの間に、
の関係がある。また、積分表示式に部分積分を適用すると、
が得られる。このような性質の大半は、不完全ガンマ関数のそれからも導かれる。
一般積分三角関数はいずれも、
積分三角関数の数学・諸科学への応用で特に有名な事例としては、Fourier 級数等における Gibbs 現象の解析、半波長ダイポール (Dipole) アンテナからの電磁波放射などがある。
積分三角関数の研究は、L. Mascheroni (1790年)、F. W. Bessel (1812年)、C. A. Bretschneider (1843年)、O. X. Schlömilch (1846年)、および J. W. L. Glaisher (1870年) 等が手掛けている。
【註記】
※1:一般積分三角関数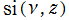 ,
, 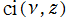 は、1939年の P. E. Böhmer による研究に基づき、「Böhmer 積分」 と呼ばれることもある。また、A. Erdelyi 他3名(著)
「Higher Transcendental Functions (Ⅱ)」 の149頁では、この関数を 「Generalized Fresnel
integral」 と称している。(ただし、関数記号と引数の順序は
は、1939年の P. E. Böhmer による研究に基づき、「Böhmer 積分」 と呼ばれることもある。また、A. Erdelyi 他3名(著)
「Higher Transcendental Functions (Ⅱ)」 の149頁では、この関数を 「Generalized Fresnel
integral」 と称している。(ただし、関数記号と引数の順序は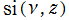 ,
, 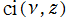 と異なる。
と異なる。
※1:一般積分三角関数
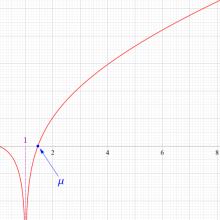
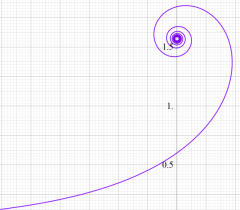
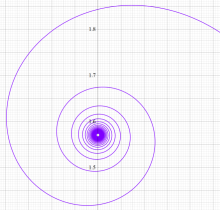
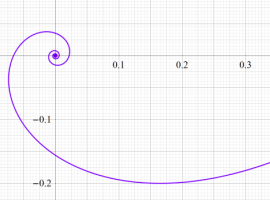
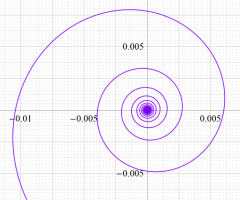
このパラメトリック曲線
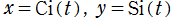 は、「Nielsen の螺線」 または 「積分螺線」 と呼ばれる。曲率が曲線長の指数関数で表わされる曲線は Nielsen の螺線と合同で、これを平行移動したものと一致する。
は、「Nielsen の螺線」 または 「積分螺線」 と呼ばれる。曲率が曲線長の指数関数で表わされる曲線は Nielsen の螺線と合同で、これを平行移動したものと一致する。複素変数の積分三角関数
複素変数の積分三角関数
複素変数の積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
(これは、
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
(これは、
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
複素変数の一般積分三角関数
アニメーション(5.99MB)
一般積分三角関数によるパラメトリック曲線
積分双曲線関数
日:積分双曲線関数,双曲線積分英:Hyperbolic integral,仏:Hyperbolique intégrale,独:Integralhyperbelfunktion
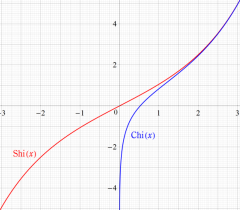
積分双曲線関数とは、積分表示式で定義された次の二つの関数
の総称であって、
となる。
が併せて定義されている。
積分双曲線関数は、数学で種々の積分公式に現れることもあるが、その数は少ない。諸科学への応用事例もあまり知られていない。
積分双曲線関数は、C. A. Bretschneider が1843年に積分三角関数を研究した際に併せて導入した。
複素変数の積分双曲線関数
複素変数の積分双曲線関数
複素変数の積分双曲線関数
その他の積分関数(積分三角関数関連)
積分三角関数に置換積分を施すと、様々な定積分の値を求めることができる。ここでは、被積分関数が比較的簡潔な形になる例を取り扱う。
引数が指数関数である三角関数の積分
は、右辺の積分三角関数を解析接続した関数で表わせる。ともに超越整関数であり、無限遠点の他に特異点を持たない。特に積分余弦関数の多価性は、この形にすることによって解消され、一価関数となる。
引数が分数関数である三角関数の積分も、積分三角関数を用いて
と表わせる。両者は
複素変数の
複素変数の
次は、曲率が原点からの曲線長の逆数で表わされる螺線
複素変数の
複素変数の