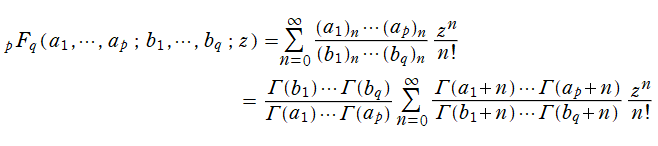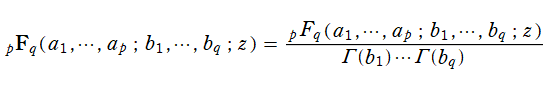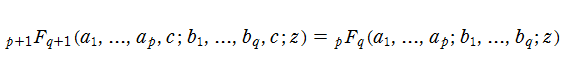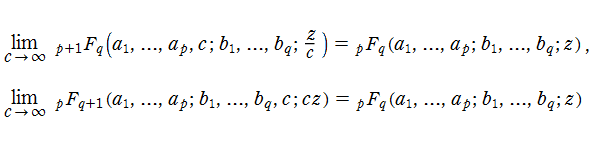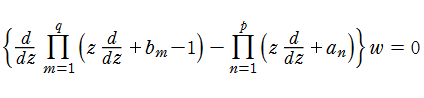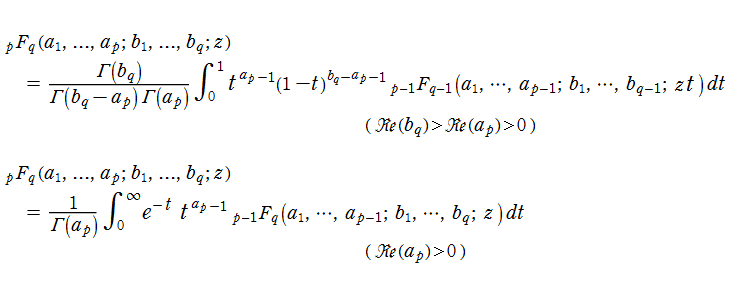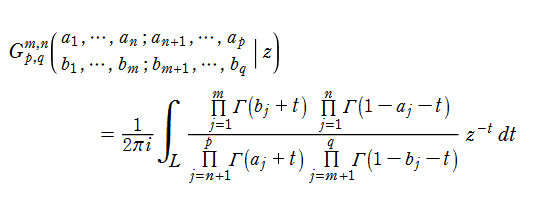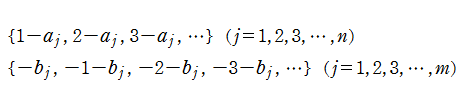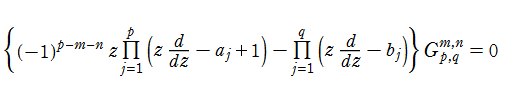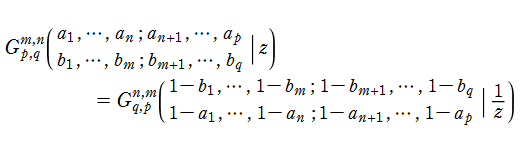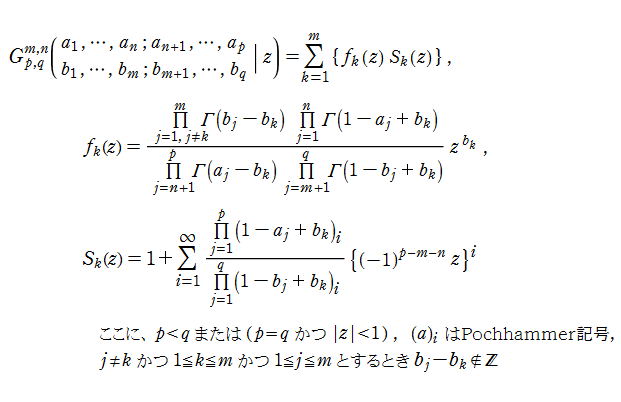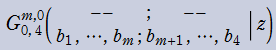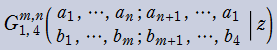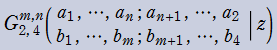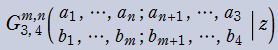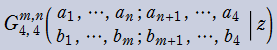特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
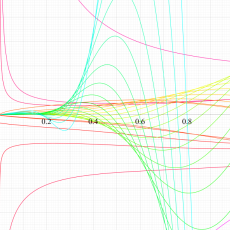
一般超幾何関数
一般超幾何関数
日:一般超幾何関数英:Generalized hypergeometric function,仏:Fonction hypergéométrique généralisée
独:Generalihypergeometrischen funktion
(Gauss の) 超幾何関数、(Kummer の) 合流型超幾何関数を一般化した
を、(Pochhammer の) 一般超幾何関数という。つまり、記号
一般超幾何関数に対して、ガンマ関数因子に由来する不定性を取り除いた 「正規化された一般超幾何関数」
は、数値計算等で好都合なため多用される。
当然ながら、
となる。また、極限操作によっても
のように異なるクラスの一般超幾何関数に移り変わる。
一般超幾何関数は、階数が
を満たす(乗積記号は、微分演算子の非可換な積として解釈する)。
一般超幾何関数は、積分表示式
で表わされる。また、この他にも様々な積分表示式で表わせる。
一般超幾何関数は、
一般超幾何関数は、超幾何関数の場合よりもさらに複雑な種々の積分値や級数総和値の表示、他の特殊関数どうしの関係式、特殊関数の一般論に用いられる。物理学等では、一般超幾何関数が単独で用いられることは少ない。
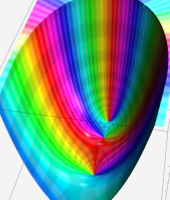
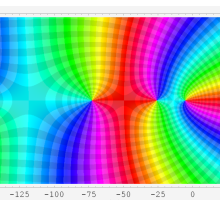
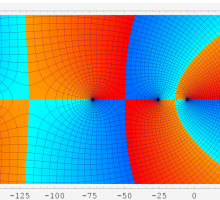
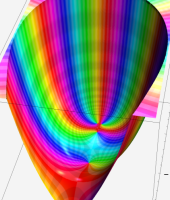
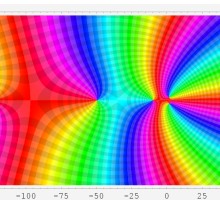
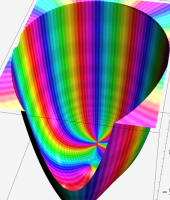
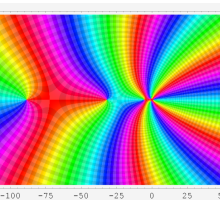
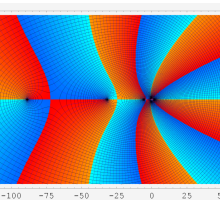
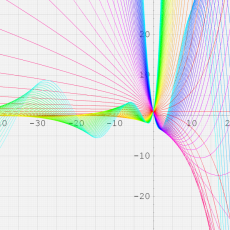
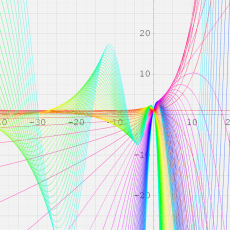
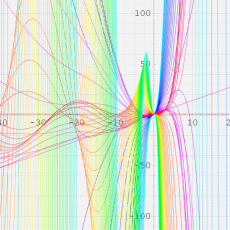
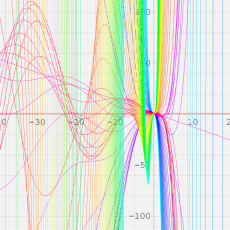
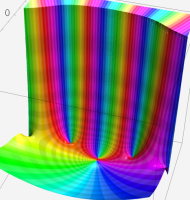
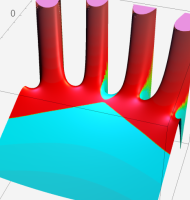
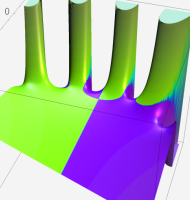
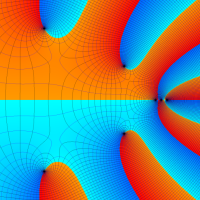
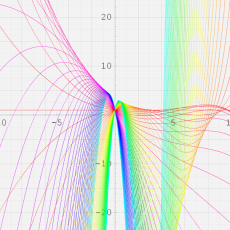
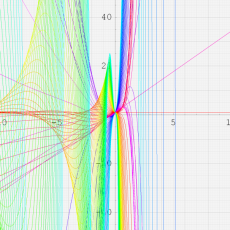
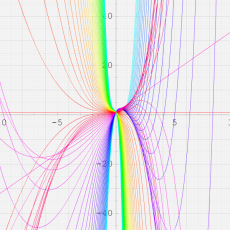
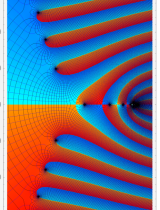
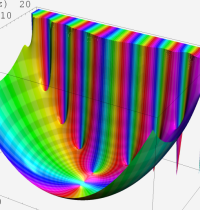
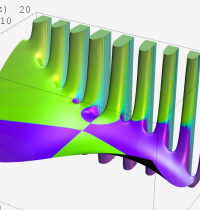
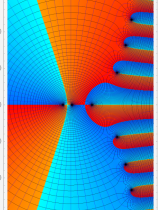
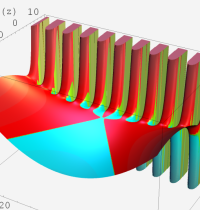
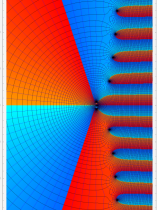
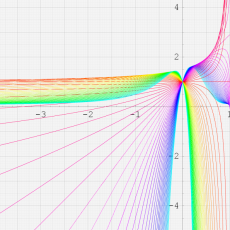
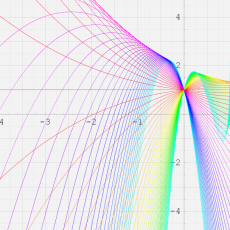
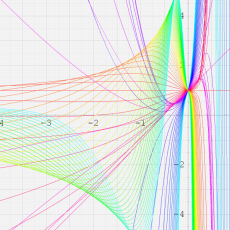
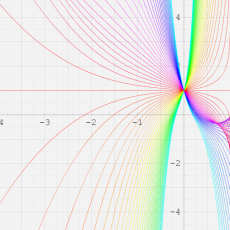
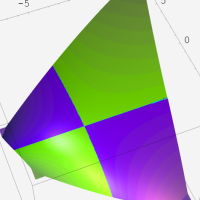
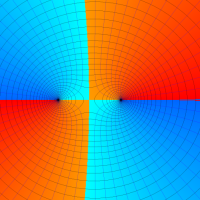
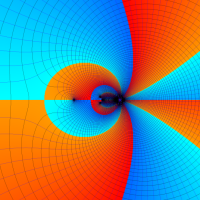
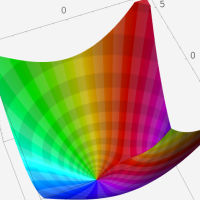
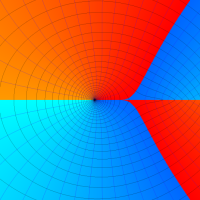
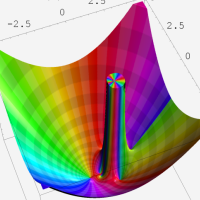
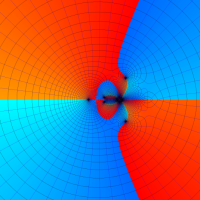
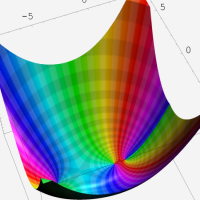
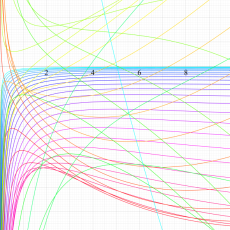
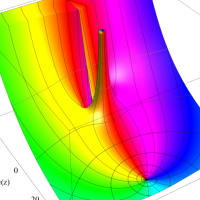
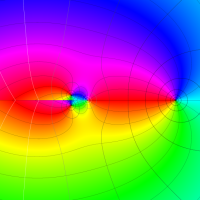
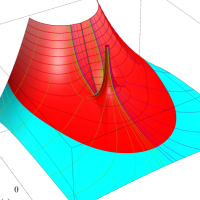
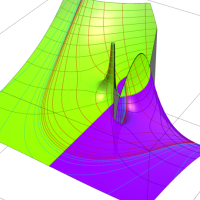
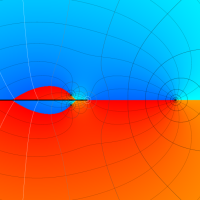
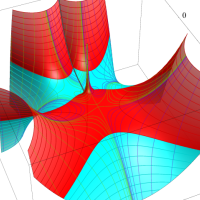
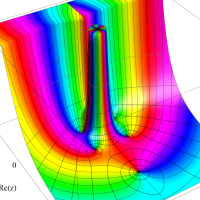
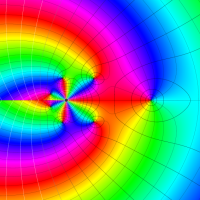
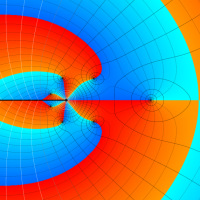
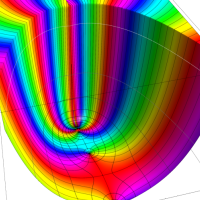
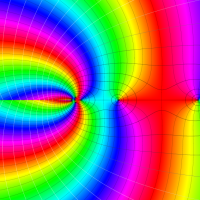
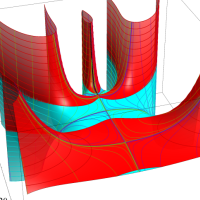
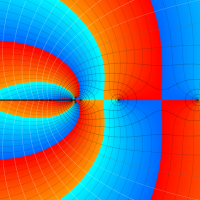
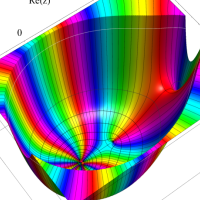
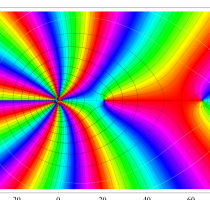
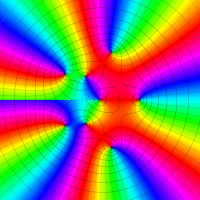
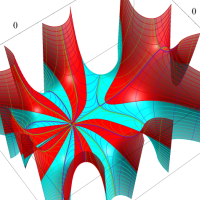
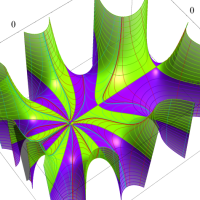
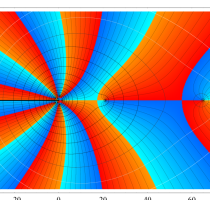
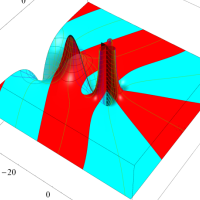
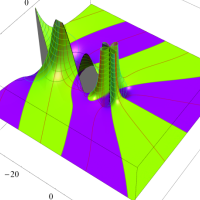
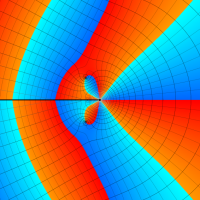
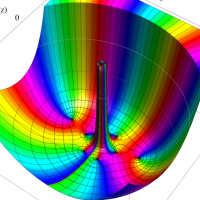
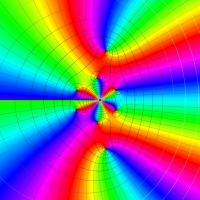
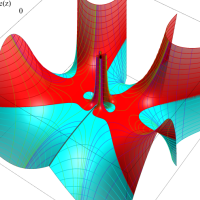
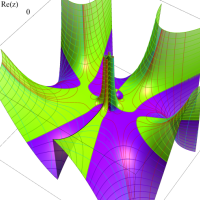
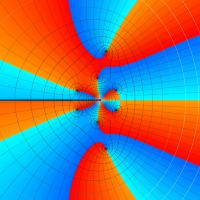
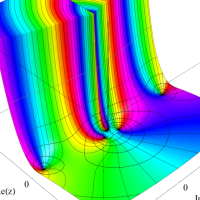
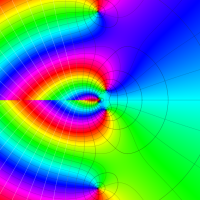
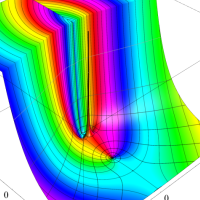
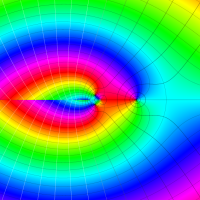
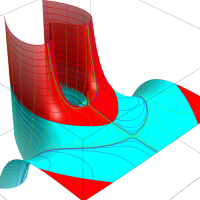
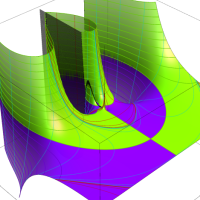
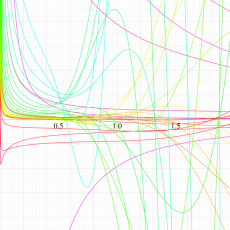
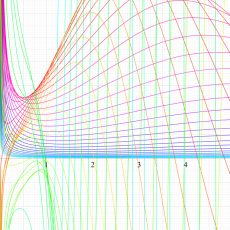
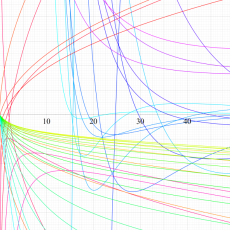
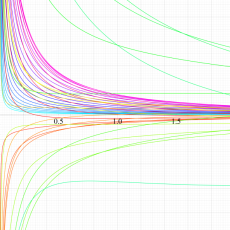
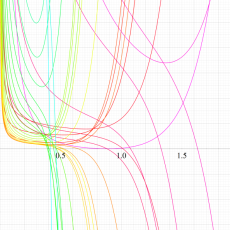
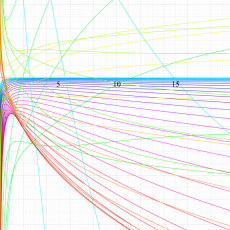
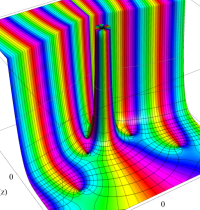
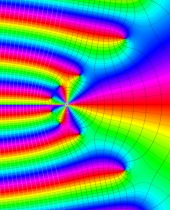
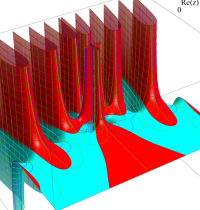
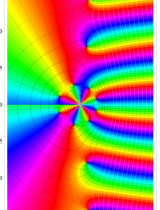
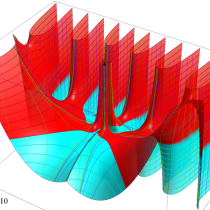
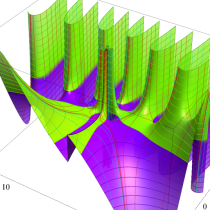
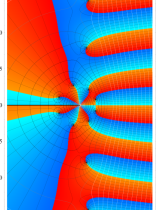
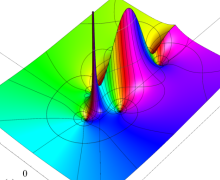
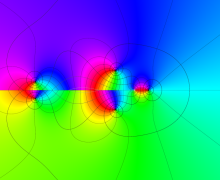
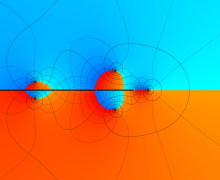
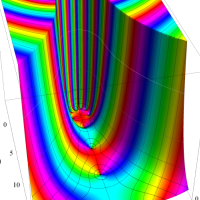
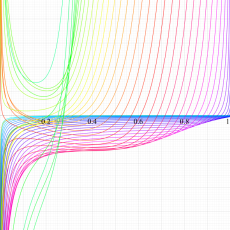
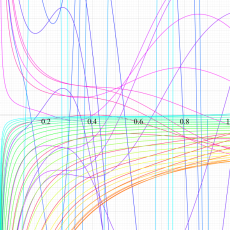
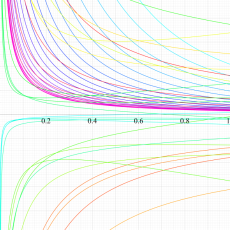
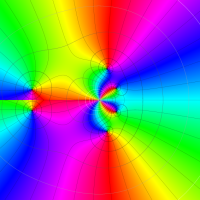
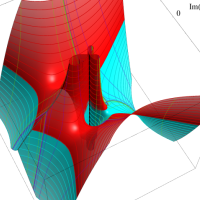
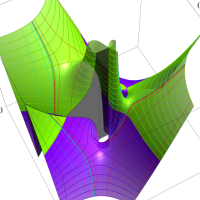
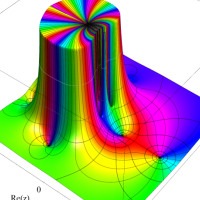
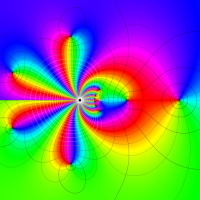
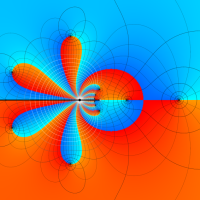
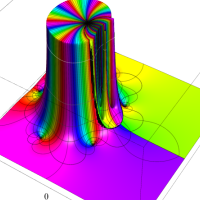
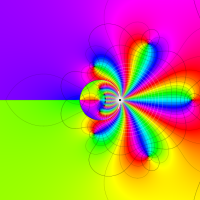
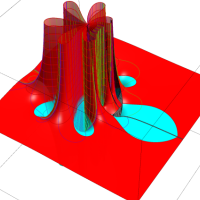
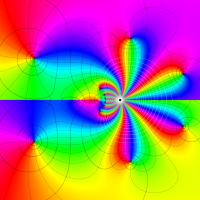
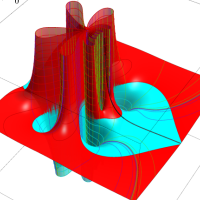
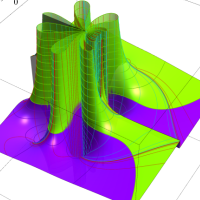
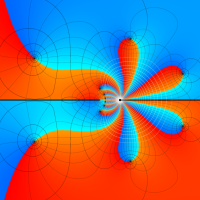
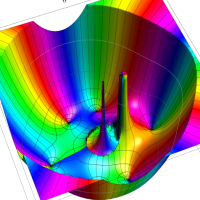
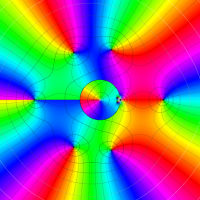
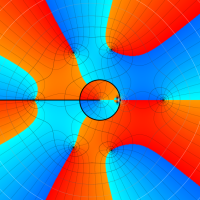
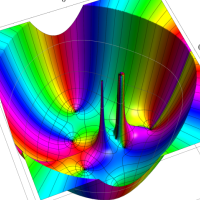
複素変数における一般超幾何関数
以下では、
の場合は取り扱わない。
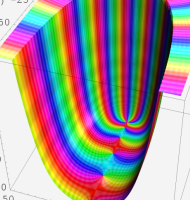
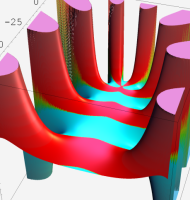
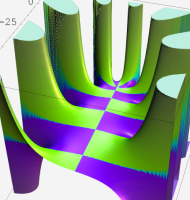
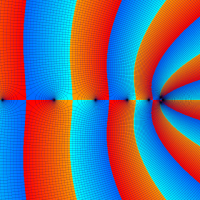
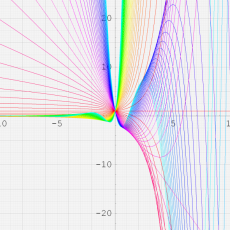
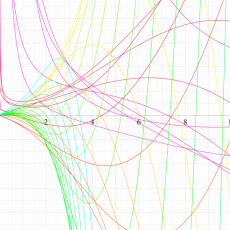
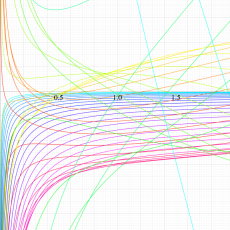
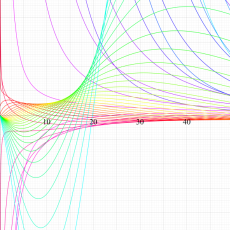
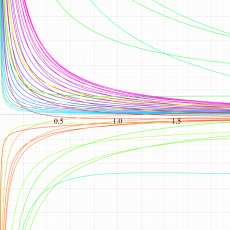
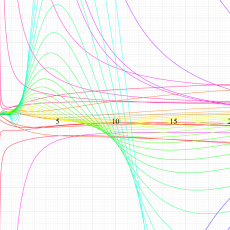
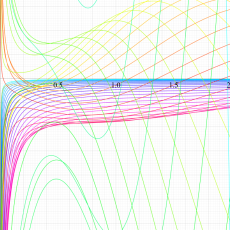
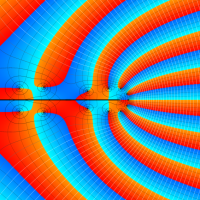
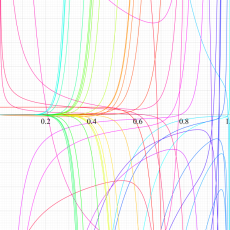
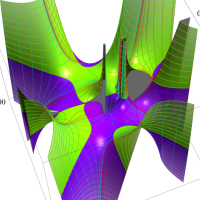
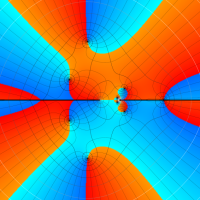
複素変数の一般超幾何関数
複素変数の一般超幾何関数
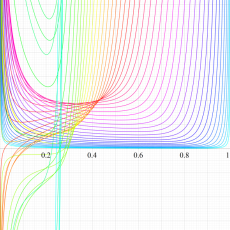
複素変数の一般超幾何関数
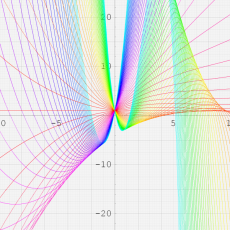
複素変数の一般超幾何関数
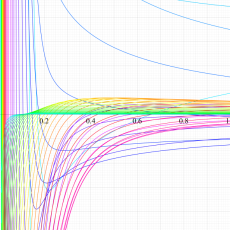
複素変数の一般超幾何関数
複素変数の一般超幾何関数
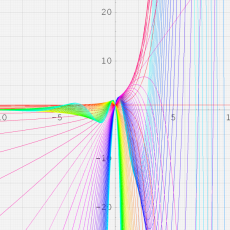
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
複素変数の一般超幾何関数
Meijer のG関数
日:MeijerのG関数,マイヤーのG関数英:Meijer G-function,仏:Fonction G de Meijer,独:Meijersche G-funktion
Meijer のG関数は、Pochhammer の一般超幾何関数等をも包含する、さらに一般化された超幾何関数である。換言すれば、初等関数および超幾何関数系の特殊関数は、Meijer のG関数を用いて表わせる。
Meijer のG関数の最初の定義は、1936 年の C. S. Meijer による冪級数を用いた定義であったが、より現代的で完全な定義は、1953年の A. Erdélyi によって導入された、複素平面上の経路積分を用いた次の定義である。その積分表示式は、逆 Mellin 変換と見なすことができる等の理由で都合が良い。
ここに、4組(ベクトル)のパラメータ
なお、歴史的な理由により、関数記号のインデックスは
積分経路
の周囲を、前者は時計回り(経路の進行方向に対して右側に極があるよう)に、後者は反時計回り(経路の進行方向に対して左側に極があるよう)に進むものとする。3種類のタイプに応じて、積分の収束範囲や
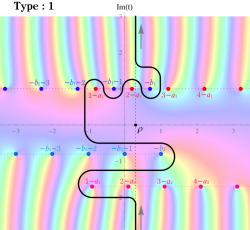
【タイプ1】
複素平面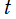 上において、
上において、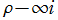 から
から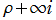
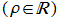 に至る、虚軸に平行な経路。この場合の積分の収束範囲は、
に至る、虚軸に平行な経路。この場合の積分の収束範囲は、
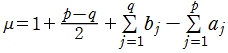 である(以下同様)。
である(以下同様)。
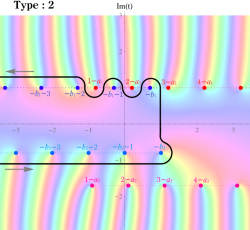
【タイプ2】
複素平面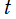 上において、
上において、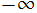 から
から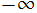 に戻るループを形成する経路。この場合の積分の収束範囲は、
に戻るループを形成する経路。この場合の積分の収束範囲は、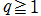 を前提に、
を前提に、
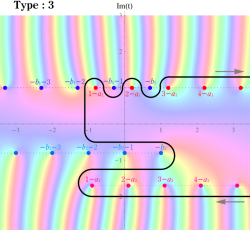
【タイプ3】
複素平面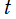 上において、
上において、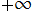 から
から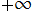 に戻るループを形成する経路。この場合の積分の収束範囲は、
に戻るループを形成する経路。この場合の積分の収束範囲は、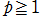 を前提に、
を前提に、
具体的に複素平面
*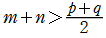 ならば、
ならば、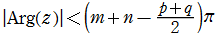
*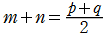 かつ
かつ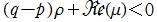 ならば、
ならば、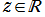 かつ
かつ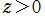
となる。ここに、*
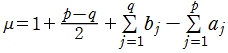 である(以下同様)。
である(以下同様)。【タイプ2】
複素平面
*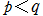 ならば、すべての有界な
ならば、すべての有界な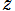
*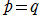 ならば、
ならば、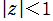
*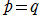 かつ
かつ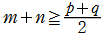 かつ
かつ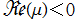 ならば、
ならば、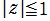
となる。*
*
【タイプ3】
複素平面
*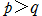 ならば、すべての有界な
ならば、すべての有界な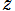
*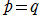 ならば、
ならば、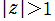
*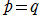 かつ
かつ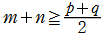 かつ
かつ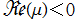 ならば、
ならば、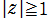
となる。*
*
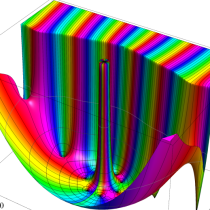
Meijer のG関数は、階数が
を満たす(乗積記号は、微分演算子の非可換な積として解釈する)。
また、Meijer のG関数は種々の関数等式を満たす。特に、単位円の外部と内部をつなぐ反転公式
が成り立つ。
多くの数式処理システムは、直接計算用とともに内部変換処理用として Meijer のG関数を実装している。Mathematica における Meijer のG関数は、特異点が
Meijer のG関数の
となる。この級数は収束する場合であっても、前述の合理的な分枝とは必ずしも一致するとは限らず、別の分枝を表わすことがある。また、
当サイトではこの場合に限り、分枝切断線を単位円周に置く通常の関数とともに、
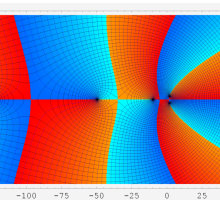
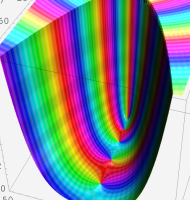
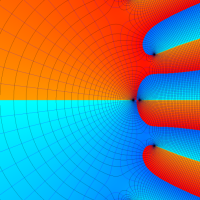
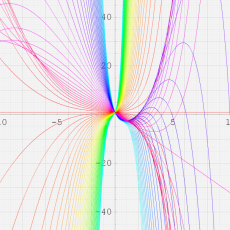
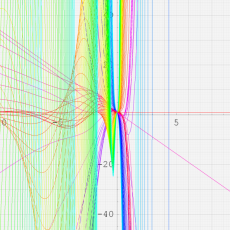
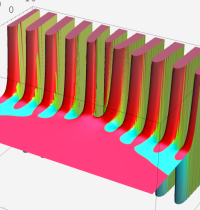
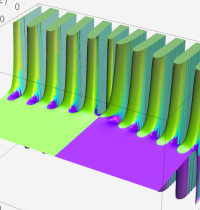
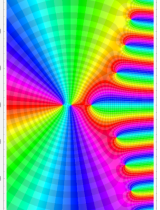
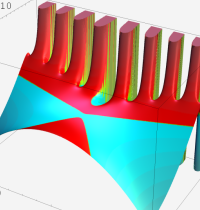
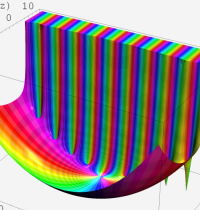
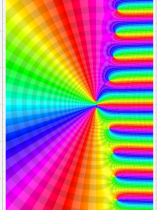
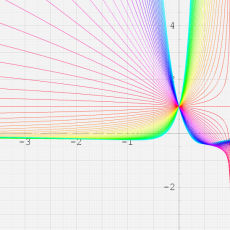
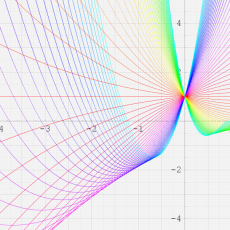
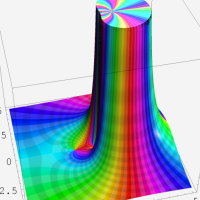
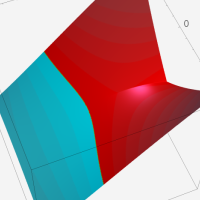
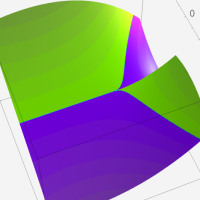
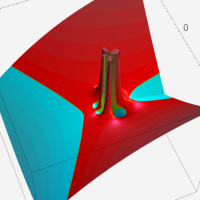
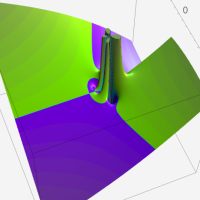
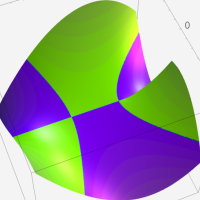
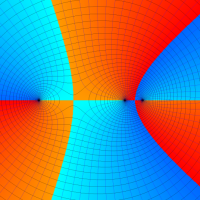
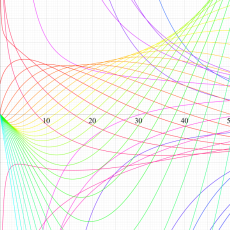
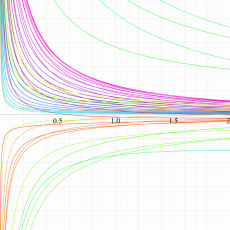
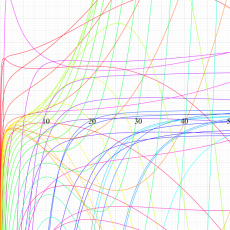
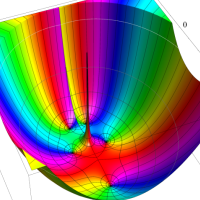
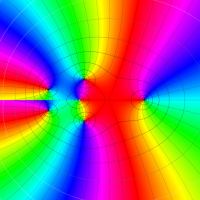
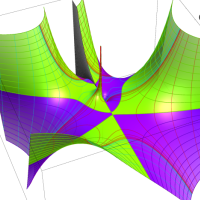
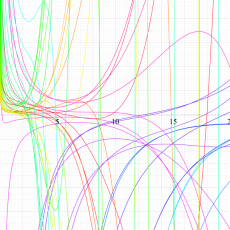
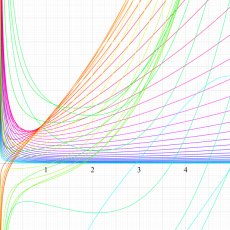
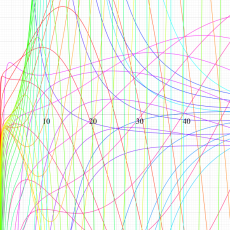
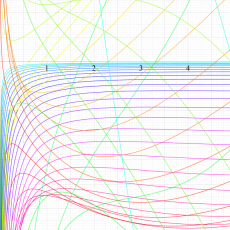
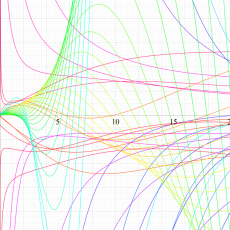
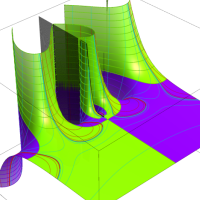
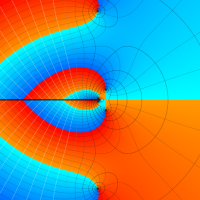
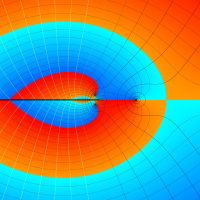
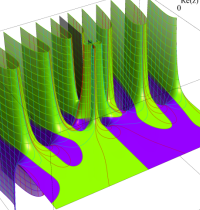
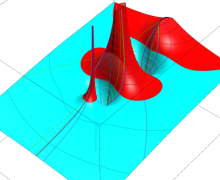
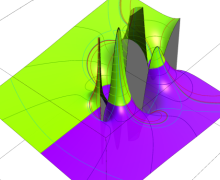
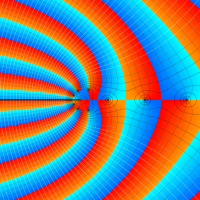
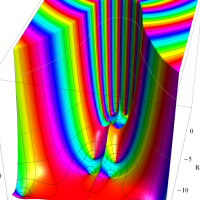
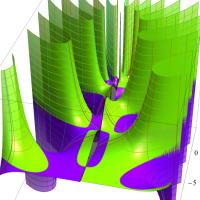
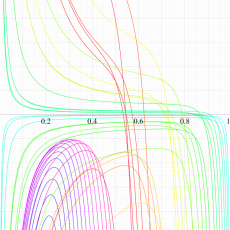
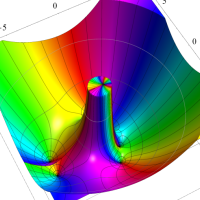
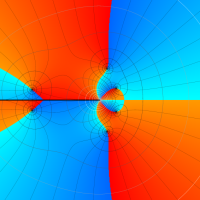
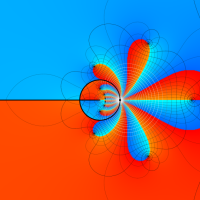
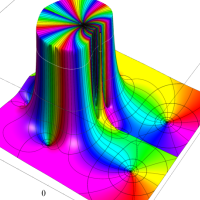
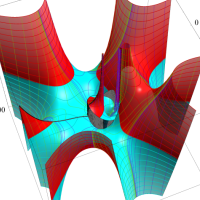
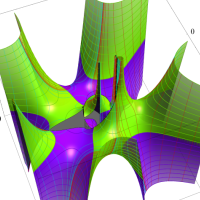
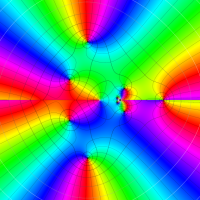
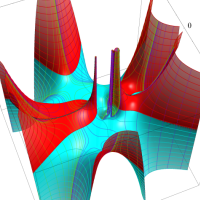
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
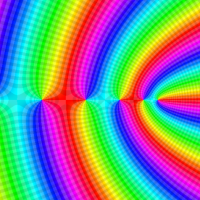
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
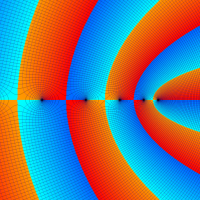
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
複素変数の Meijer のG関数
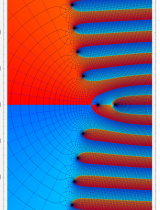
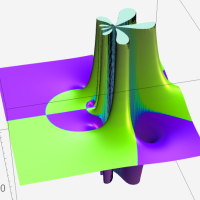
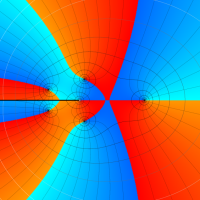
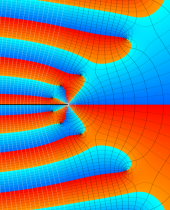
【単位円周上に分枝切断線を置く場合。】
【単位円周上に分枝切断線を置かない場合。】
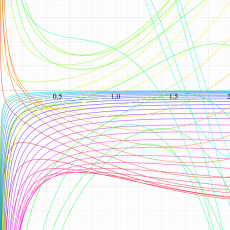
複素変数の Meijer のG関数
【単位円周上に分枝切断線を置く場合。】
【単位円周上に分枝切断線を置かない場合。】