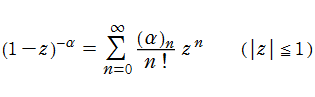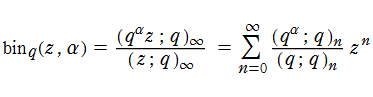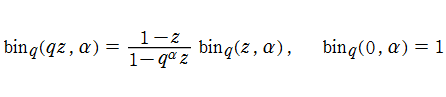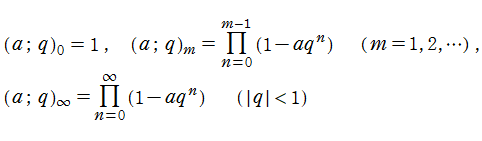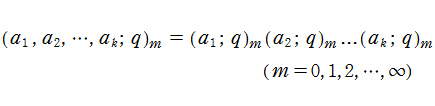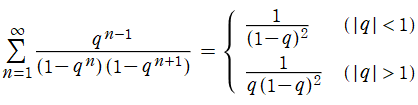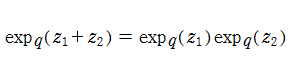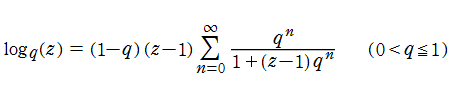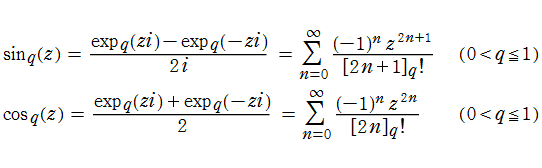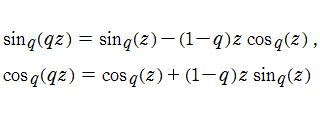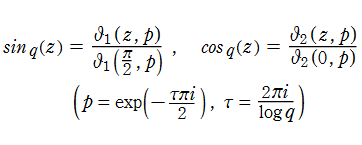特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
q-特殊関数 Menu
q-初等関数
q-二項展開
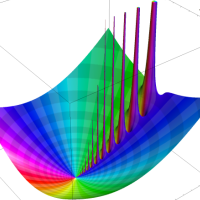
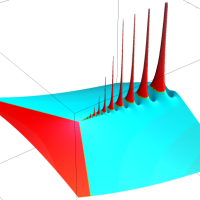
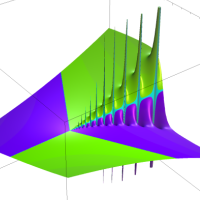
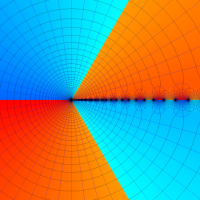
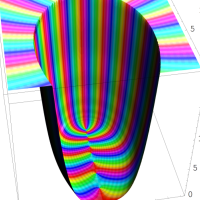
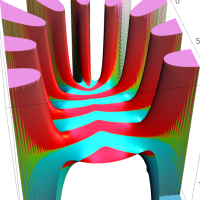
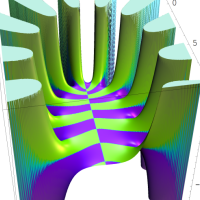
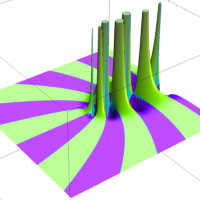
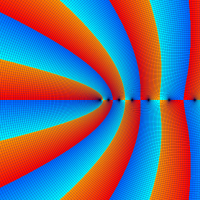
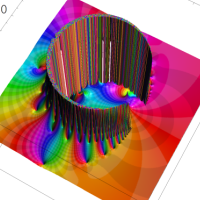
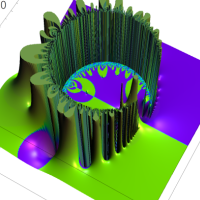
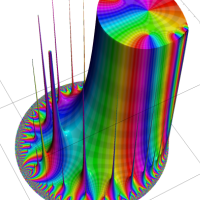
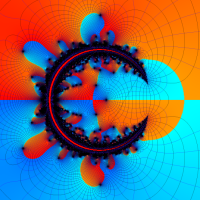
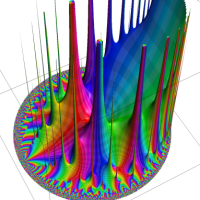
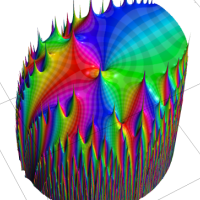
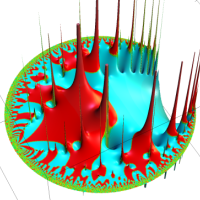
通常の二項展開を q-類似した次の式を、q-二項展開という。
q-二項展開は極限操作
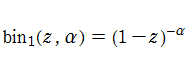
を満たす。また、
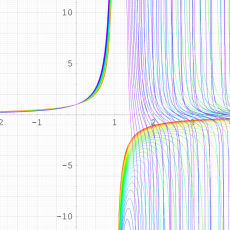
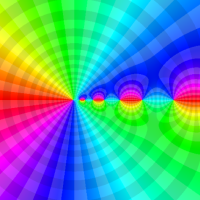
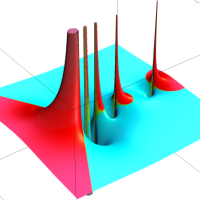
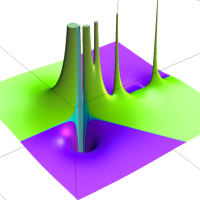
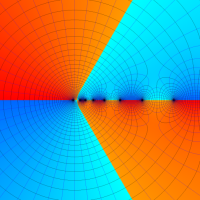
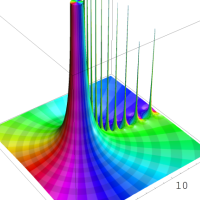
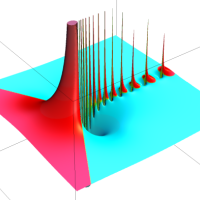
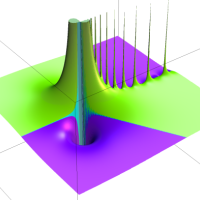
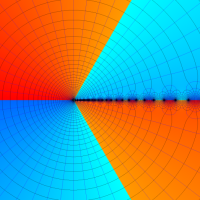
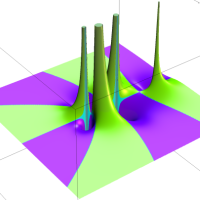
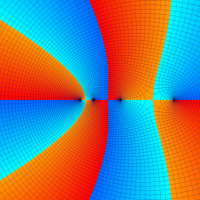
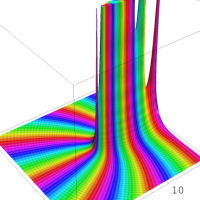
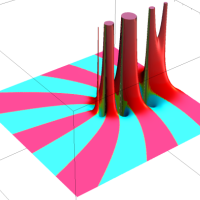
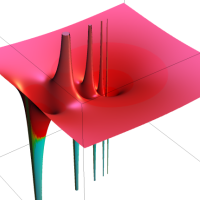
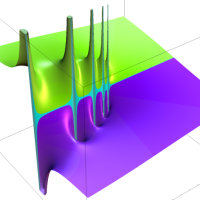
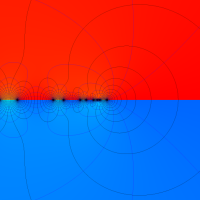
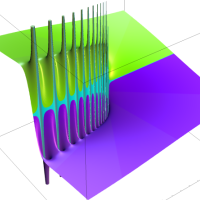
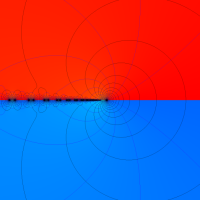
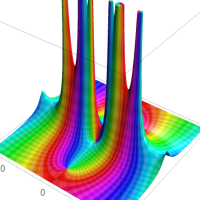
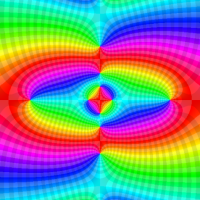
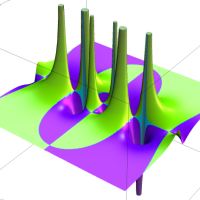
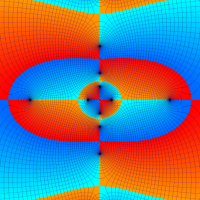
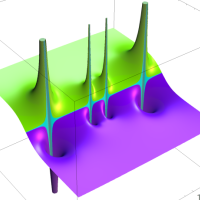
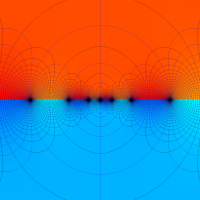
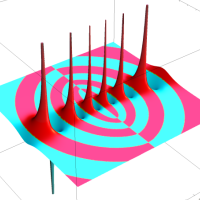
複素解析関数としての q-二項展開は、一位の極を
q-シフト因子
日:q-シフト因子,q-シフト階乗英:q-shifted factorial,仏:q-décalé factorielle,独:q-verschoben fakultät
日:q-Pochhammer記号,q-ポッホハンマー記号
英:q-Pochhammer symbol,仏:q-symbole de Pochhammer,独:q-Pochhammer-symbol
q-解析学において頻繁に現れる有限積あるいは無限積
は、q-シフト因子 (q-shifted factorial) と呼ばれ、一つの因数のように扱って計算を簡略化する。有限積
q-シフト因子は、q-Pochhammer 記号と呼ばれることも多い。しかし、Pochhammer 記号
変数
前述の無限積において
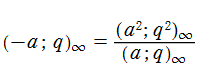
しばしば、q-解析学においては複数の q-シフト因子の積を
のように表記する。
q-解析学に現れる q-特殊関数には、多くの q-シフト因子が連なった複雑な式で定義されるものが多い。
【註記】
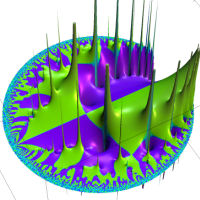
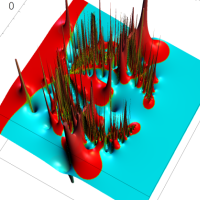
※1:以降および q-特殊関数の頁にあるいくつかのグラフのとおり、当サイトでは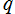 を変数とする q-特殊関数が、単位円の外部でも "計算され得る" 場合はその結果で掲載している。しかし、自然境界を越えた (関数が存在しない余白への) 定義域の拡張方法は唯一ではないゆえ、厳密には解析接続ではない。この事は、K. T. W. Weierstrass および J. H. Poincaré 等によって論証されている。
を変数とする q-特殊関数が、単位円の外部でも "計算され得る" 場合はその結果で掲載している。しかし、自然境界を越えた (関数が存在しない余白への) 定義域の拡張方法は唯一ではないゆえ、厳密には解析接続ではない。この事は、K. T. W. Weierstrass および J. H. Poincaré 等によって論証されている。
また、元々は自然境界を持たない関数であるが、単位円の内部と外部で異なる有理関数に収束する無限級数
のような例も存在する。これは、結果が初等関数になるため、二つの関数は互いに他の解析接続になっていないことが明確に分かる。
※1:以降および q-特殊関数の頁にあるいくつかのグラフのとおり、当サイトでは
また、元々は自然境界を持たない関数であるが、単位円の内部と外部で異なる有理関数に収束する無限級数
のような例も存在する。これは、結果が初等関数になるため、二つの関数は互いに他の解析接続になっていないことが明確に分かる。
q-指数関数
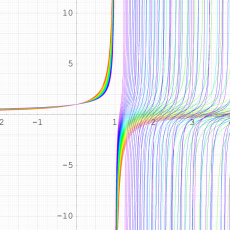
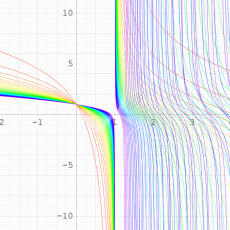
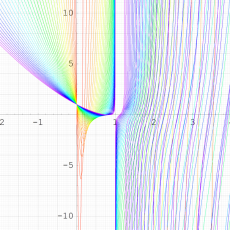
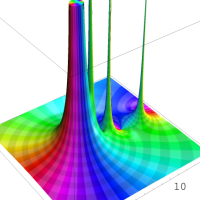
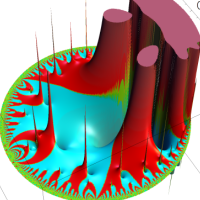
指数関数を q-類似したを、q-指数関数という。ここに、冪級数に現れた係数は「q-階乗」と呼ばれる。(→ q-ガンマ関数を参照。)
q-指数関数は極限操作
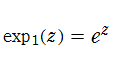
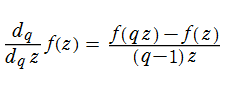
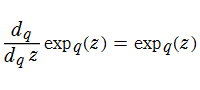
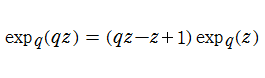
も成立することとなる。(通常の数の場合は成立しない。)
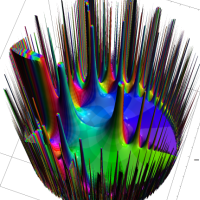
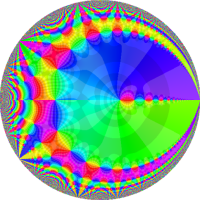
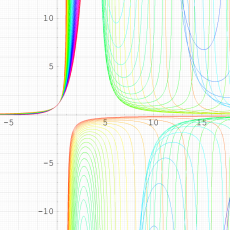
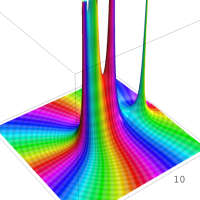
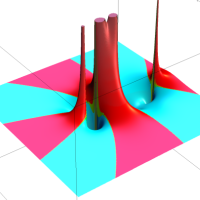
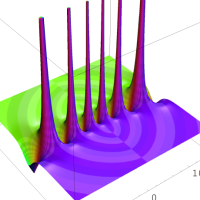
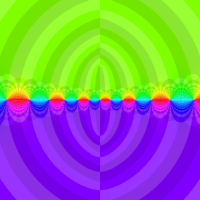
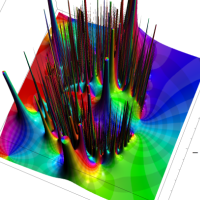
複素解析関数としての q-指数関数は、一位の極を
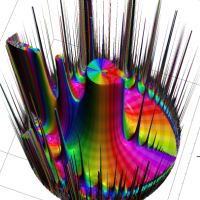
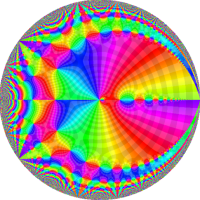
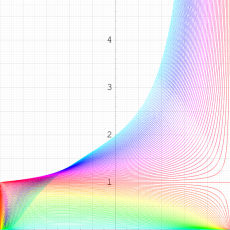
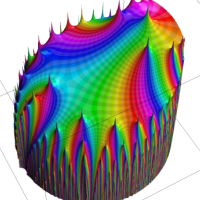
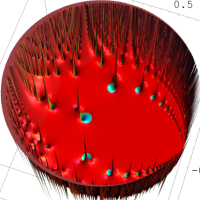
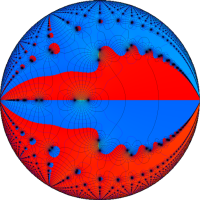
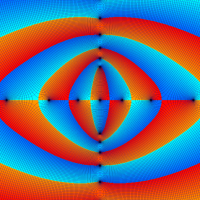
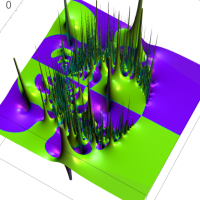
次は、前掲の ①, ②, ④, ⑤のグラフにおいて、描画範囲を単位円内部に限った場合。
次は、前掲の ①, ②, ④, ⑤のグラフにおいて、描画範囲を単位円内部に限った場合。
q-対数関数
q-二項展開に対し、C. J. Thomae の 「q-積分」 を適用して導くことができる、を、q-対数関数という (これとはかなり異なる定義も存在する)。
q-対数関数は極限操作
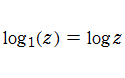
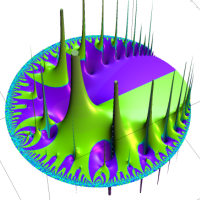
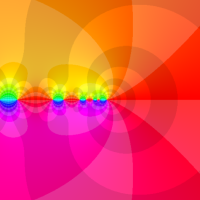
複素解析関数としての q-対数関数は、一位の極を負の実軸上に持つ有理型関数である。
q-三角関数
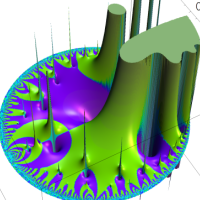
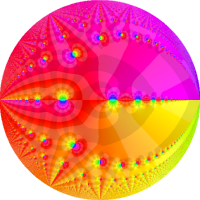
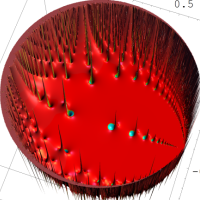
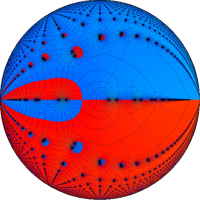
Euler の公式に倣い、q-指数関数から定義されるを、q-三角関数 (q-正弦関数, q-余弦関数) という。
q-三角関数は極限操作
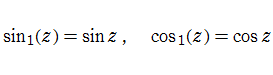
を満たす。このほか、通常の三角関数に倣って q-正接関数, q-余接関数, q-正割関数, および q-余割関数
が定義される。
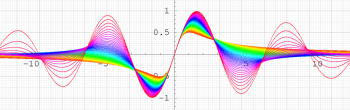
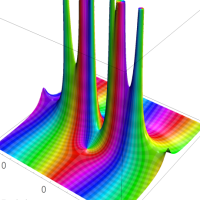
複素解析関数としての q-三角関数は、一位の極を
なお、上記とは異なる定義である
を q-三角関数とすることもある。しかしこれは楕円テータ関数そのものであり、グラフは既にその箇所で触れているので、ここでの描画は省略する (ただし、別頁の 「q-超幾何関数」 系の関数を定義する際に、係数として現れる)。この関数についても、前述と同様に q-正接関数, q-余接関数等が定義される。
アニメーション(6.00MB)
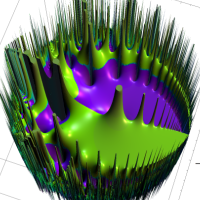
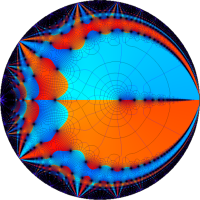
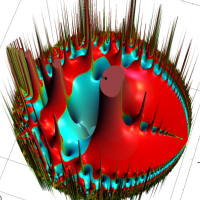
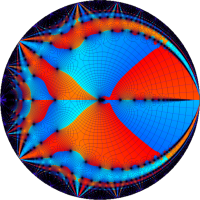
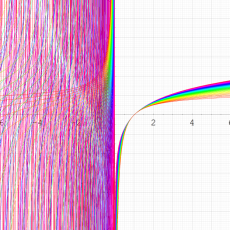
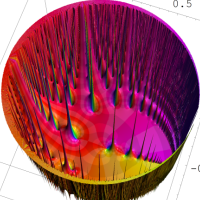
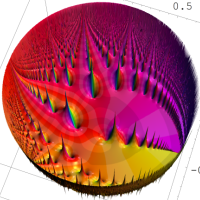
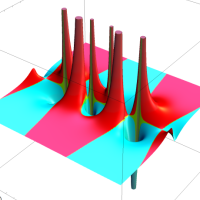
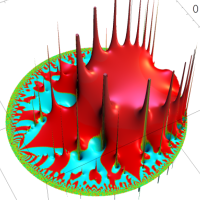
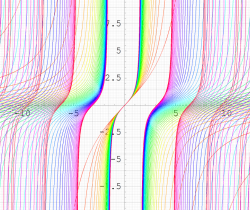
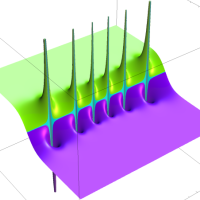
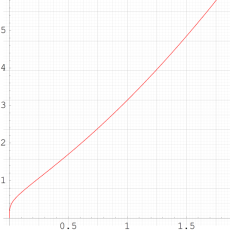
②は、①のグラフの垂直軸を、常用対数目盛にした場合。
次は、前掲の ①, ②, ④, ⑤のグラフにおいて、描画範囲を単位円内部に限った場合。
②は、①のグラフの垂直軸を、常用対数目盛にした場合。
次は、前掲の ①, ②, ④, ⑤のグラフにおいて、描画範囲を単位円内部に限った場合。
q-円周率
q-円周率とは、q-ガンマ関数を用いて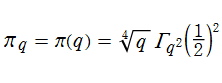
q-円周率は極限操作
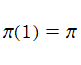
複素関数としての q-円周率は、