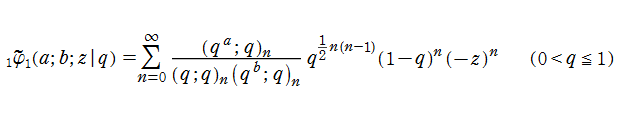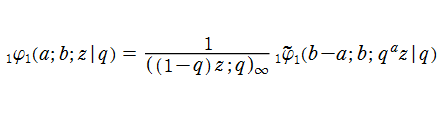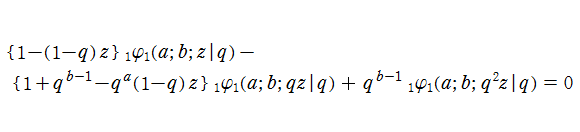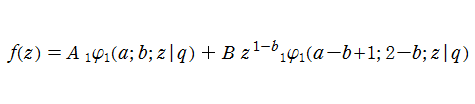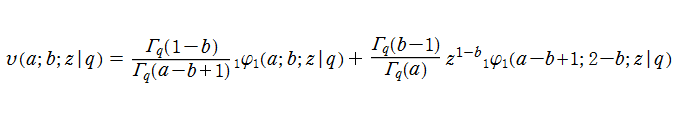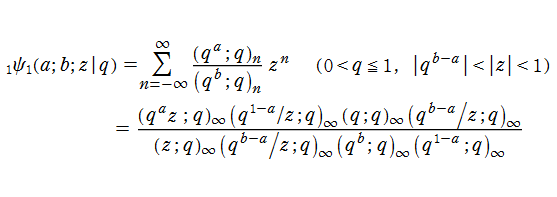q-合流型超幾何関数
Kummer の
合流型超幾何関数を q-類似した
を、第1種 q-合流型超幾何関数という。また、級数の収束がより速い
を 第1種 q-合流型超幾何関数の定義とすることも多い。両者は互いに、
の関係にある。(因みに Heine の
q-超幾何関数の場合は、
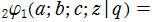
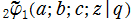
となる。)
q-合流型超幾何関数は2階の q-差分方程式を満たし、これから関数等式
を満たすことが分かる。逆に、この2階 q-差分方程式を満たす一般解
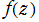
は、
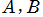
を任意の複素定数とするとき、
となる。これを満たす
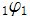
とは異なる基本解で、
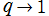
なる極限によって
第2種合流型超幾何関数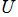
に還元される、
を、第2種 q-合流型超幾何関数という。
q-超幾何関数と同様に、q-合流型超幾何関数も q-解析学において要となる関数のひとつである。
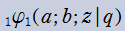
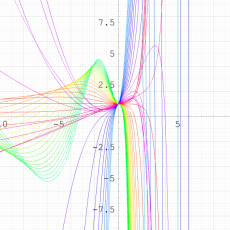
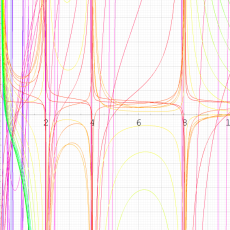
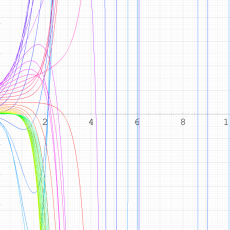
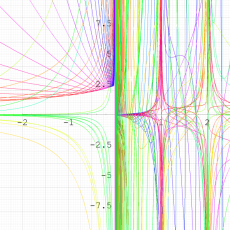
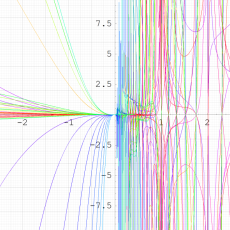
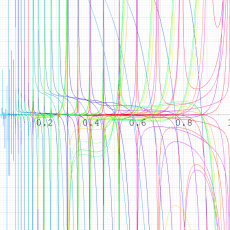
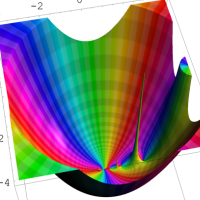
実変数の第1種 q-合流型超幾何関数のグラフ。順に、①
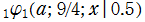
, ②
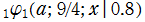
, ③
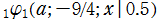
, ④
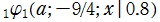
。いずれも
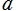
=-3.99~4.01 (+0.2)。
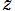
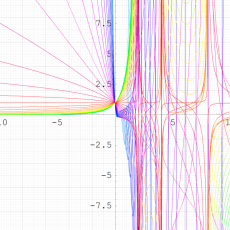
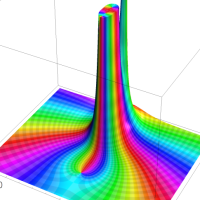
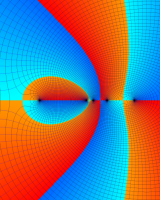
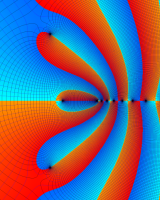
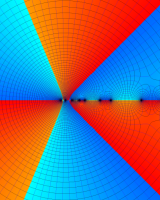
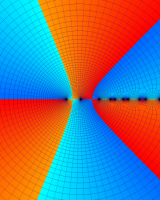
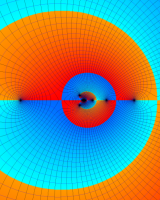
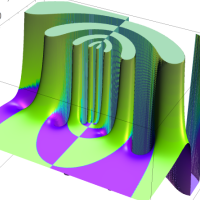
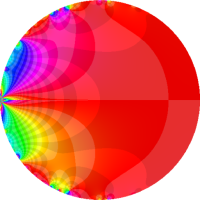
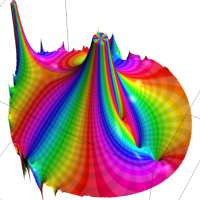
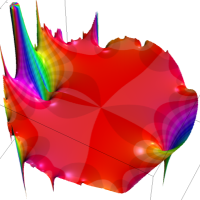
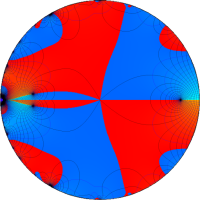
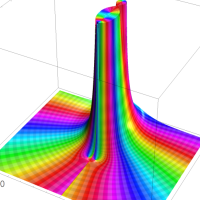
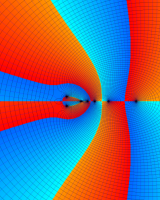
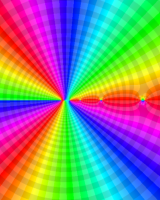
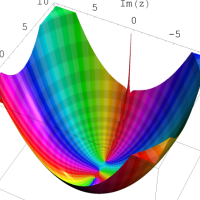
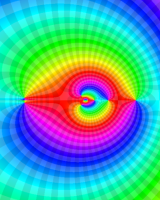
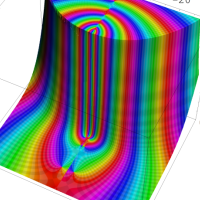
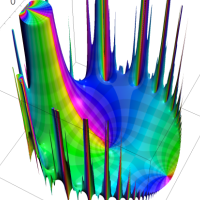
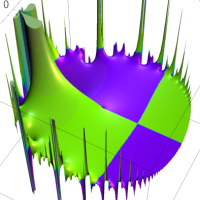
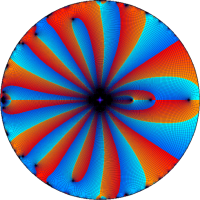
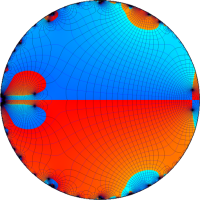
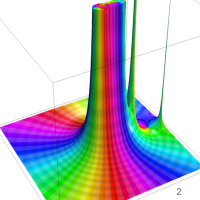
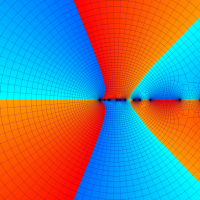
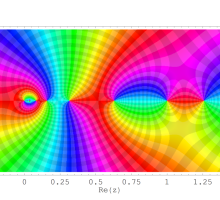
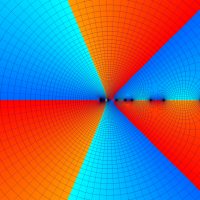
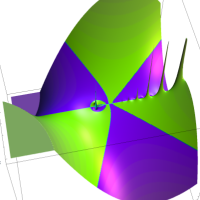
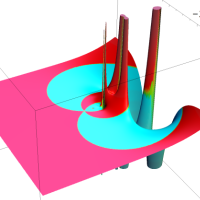
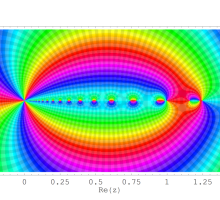
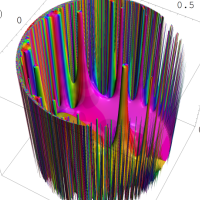
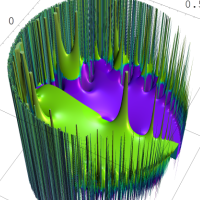
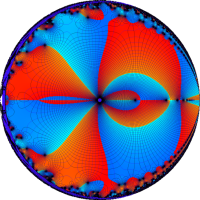
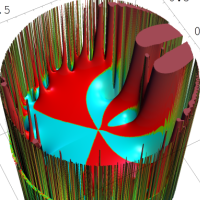
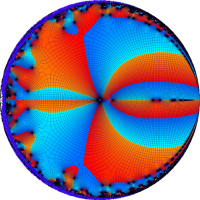
を複素変数とする第1種 q-合流型超幾何関数
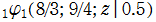
のグラフ。
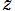
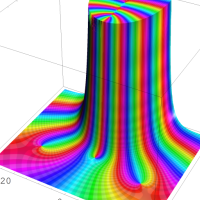
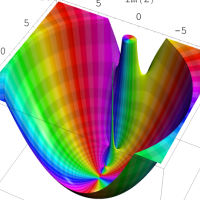
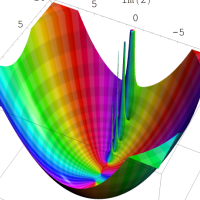
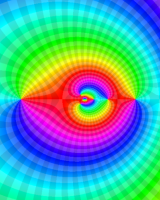
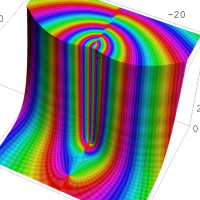
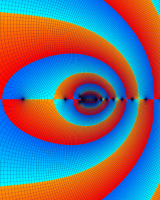
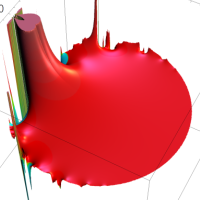
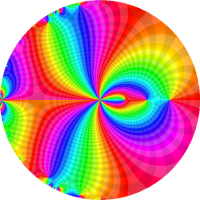
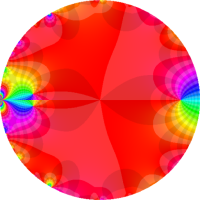
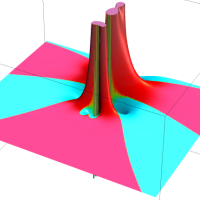
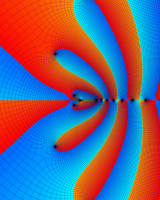
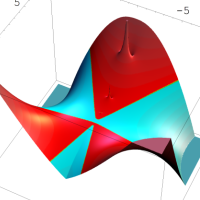
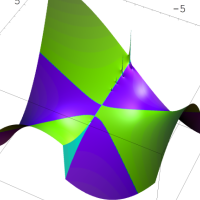
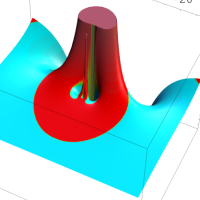
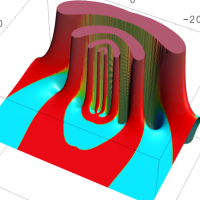
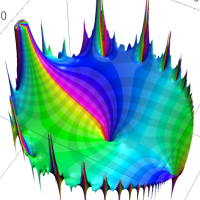
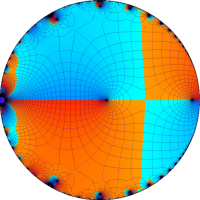
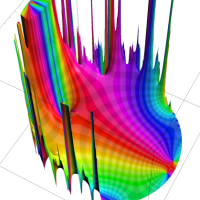
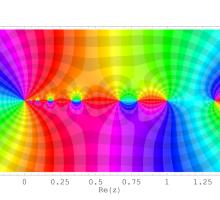
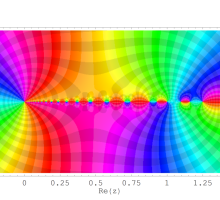
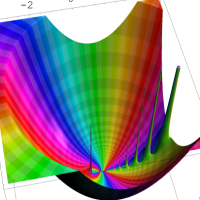
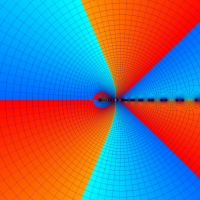
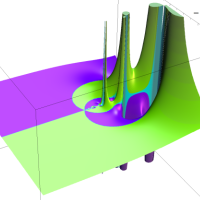
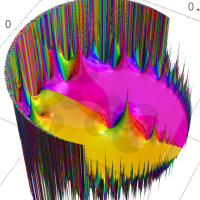
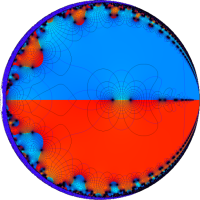
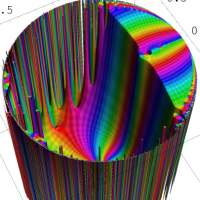
を複素変数とする第1種 q-合流型超幾何関数
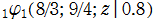
のグラフ。
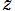
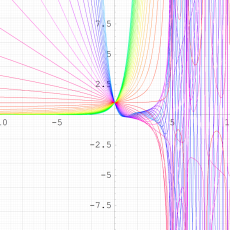
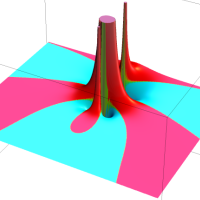
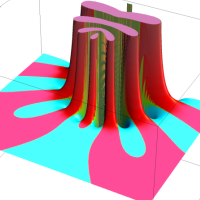
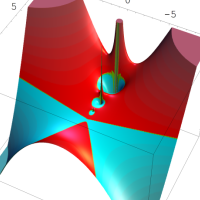
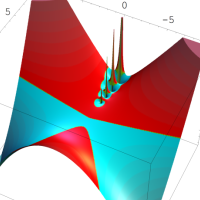
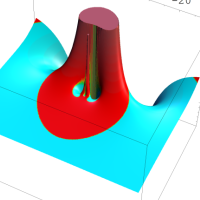
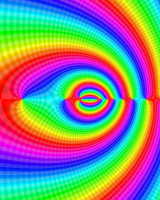
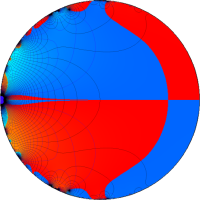
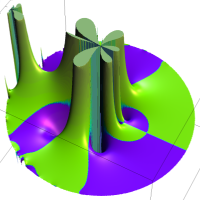
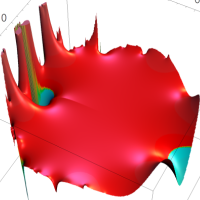
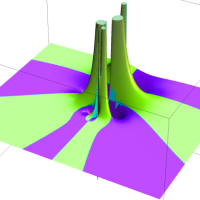
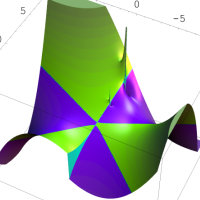
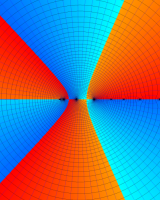
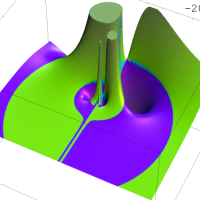
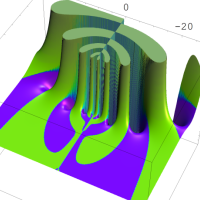
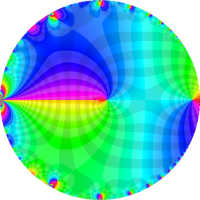
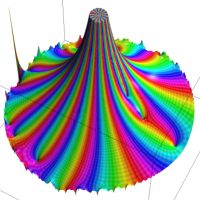
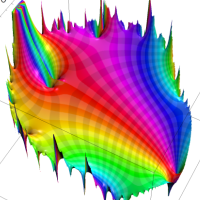
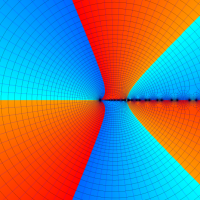
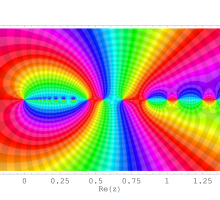
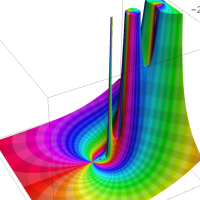
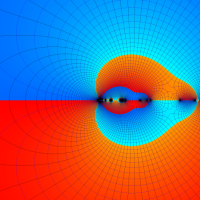
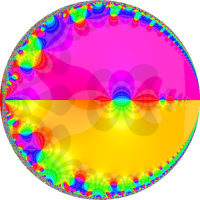
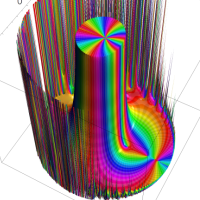
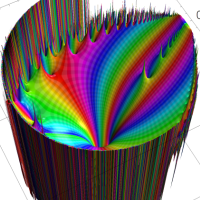
を複素変数とする第1種 q-合流型超幾何関数
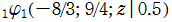
のグラフ。
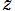
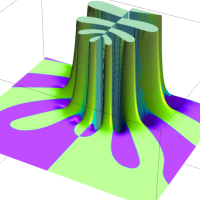
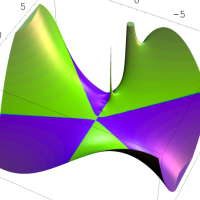
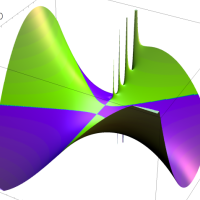
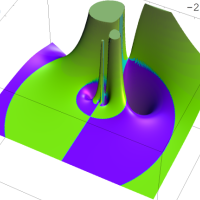
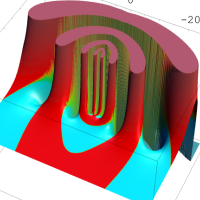
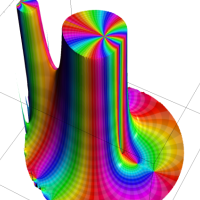
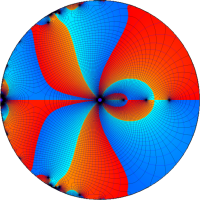
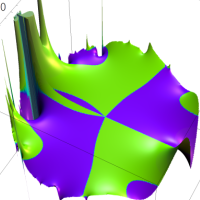
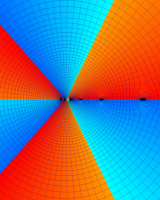
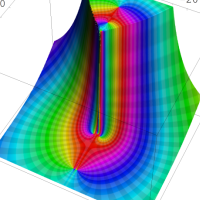
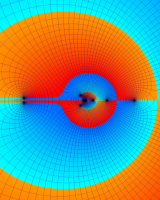
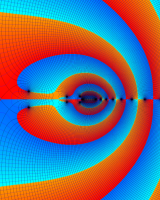
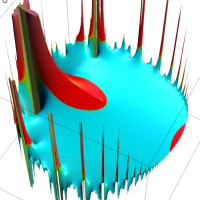
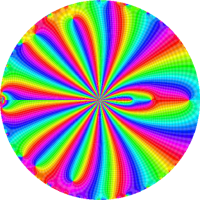
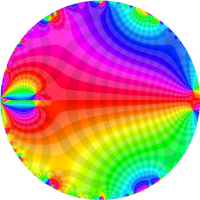
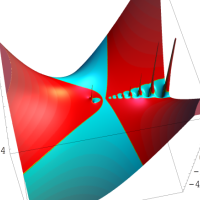
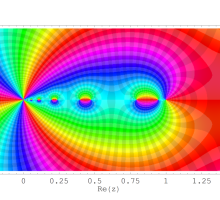
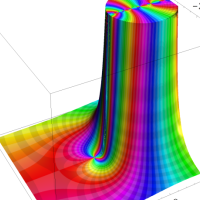
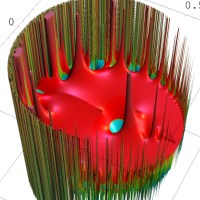
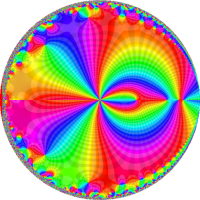
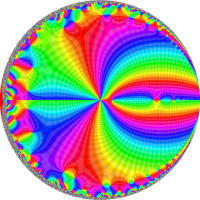
を複素変数とする第1種 q-合流型超幾何関数
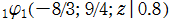
のグラフ。
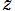
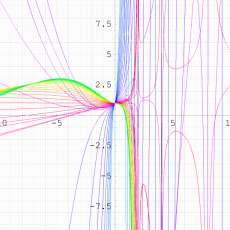
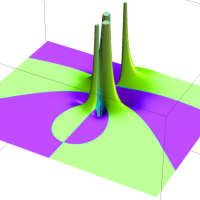
を複素変数とする第1種 q-合流型超幾何関数
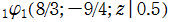
のグラフ。
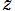
を複素変数とする第1種 q-合流型超幾何関数
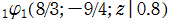
のグラフ。
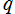
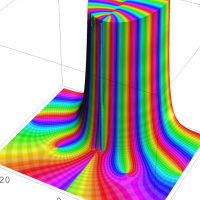
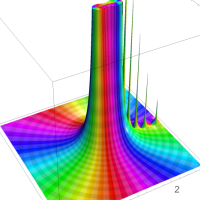
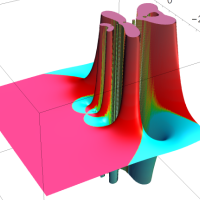
を複素変数とする第1種 q-合流型超幾何関数
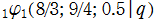
のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。
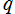
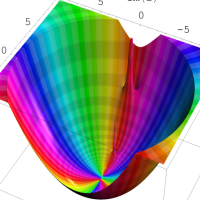
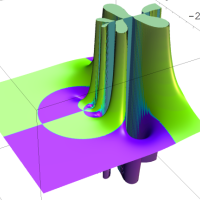
を複素変数とする第1種 q-合流型超幾何関数

のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。
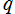
を複素変数とする第1種 q-合流型超幾何関数
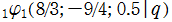
のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。
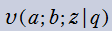
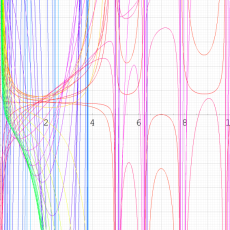
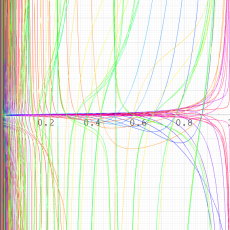
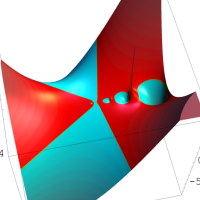
実変数の第2種 q-合流型超幾何関数のグラフ。順に、①
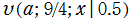
, ②
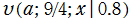
, ③
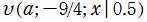
, ④
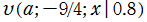
。いずれも
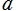
=-3.99~4.01 (+0.2)。
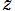
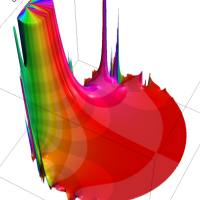
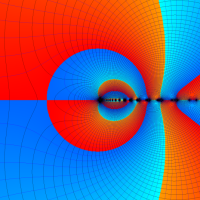
を複素変数とする第2種 q-合流型超幾何関数
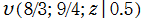
のグラフ。
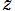
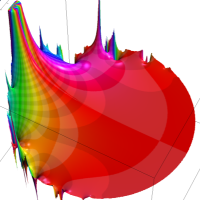
を複素変数とする第2種 q-合流型超幾何関数
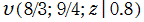
のグラフ。
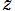
を複素変数とする第2種 q-合流型超幾何関数
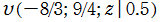
のグラフ。
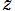
を複素変数とする第2種 q-合流型超幾何関数
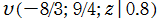
のグラフ。
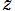
を複素変数とする第2種 q-合流型超幾何関数
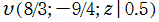
のグラフ。
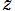
を複素変数とする第2種 q-合流型超幾何関数
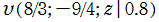
のグラフ。
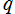
を複素変数とする第2種 q-合流型超幾何関数
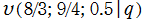
のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。
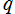
を複素変数とする第2種 q-合流型超幾何関数
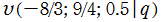
のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。
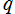
を複素変数とする第2種 q-合流型超幾何関数
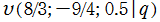
のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。
q-合流型超幾何関数に類似した
を、Ramanujan の
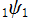
関数という。
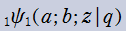
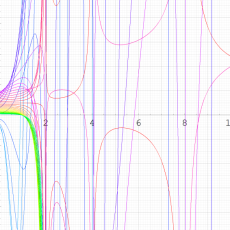
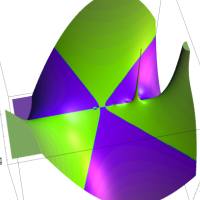
実変数の Ramanujan
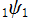
関数のグラフ。順に、①
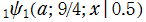
。②
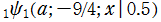
。
③:①の一部を拡大したグラフ。④:②の一部を拡大したグラフ。いずれも
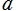
=-3.99~4.01 (+0.2)。
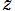
を複素変数とする Ramanujan
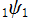
関数
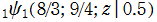
のグラフ。3番目は、2番目のグラフの原点付近を拡大した場合。
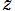
を複素変数とする Ramanujan
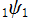
関数
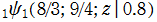
のグラフ。3番目は、2番目のグラフの原点付近を拡大した場合。
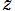
を複素変数とする Ramanujan
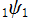
関数
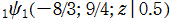
のグラフ。3番目は、2番目のグラフの原点付近を拡大した場合。
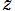
を複素変数とする Ramanujan
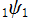
関数
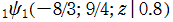
のグラフ。3番目は、2番目のグラフの原点付近を拡大した場合。
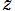
を複素変数とする Ramanujan
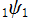
関数
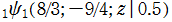
のグラフ。3番目は、2番目のグラフの原点付近を拡大した場合。
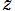
を複素変数とする Ramanujan
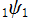
関数
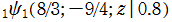
のグラフ。3番目は、2番目のグラフの原点付近を拡大した場合。
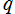
を複素変数とする Ramanujan
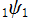
関数
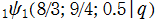
のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。
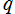
を複素変数とする Ramanujan
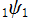
関数
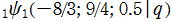
のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。
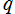
を複素変数とする Ramanujan
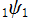
関数
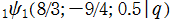
のグラフ。2番目は、1番目のグラフの垂直軸を常用対数目盛にした場合。