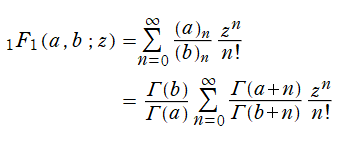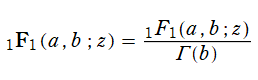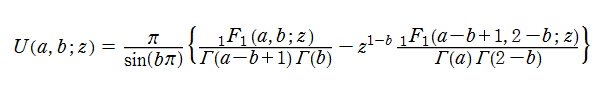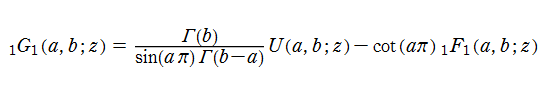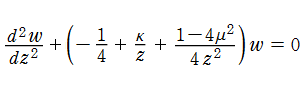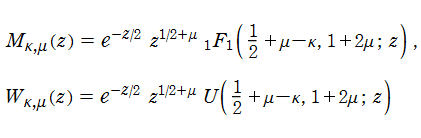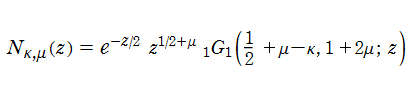特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
合流型超幾何関数
合流型超幾何関数
日:合流型超幾何関数英:Confluent hypergeometric function,仏:Fonction hypergéométrique confluente
独:Konfluente hypergeometrische funktion
二階線形常微分方程式
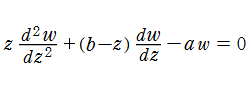
そのうち、原点で有限となる基本解
を、第1種合流型超幾何関数という。特に、この級数は合流型超幾何級数と呼ばれ、その収束半径は
第1種合流型超幾何関数に対して、ガンマ関数因子に由来する不定性を取り除いた 「正規化された合流型超幾何関数」
は、数値計算等で好都合なため多用される。
一方、原点で無限大となる、
を、第2種合流型超幾何関数という。ただし、
も、ここでは第2種合流型超幾何関数として採用する (第2種 Laguerre 陪関数から類推される独自定義の関数。超幾何関数系の第2種関数の定義方法に対する当サイトでの方針は、別頁「Questions」を参照)。これも発散する場合は極限をとり、その無限級数は対数項を含む。
合流型超幾何関数は、積分表示式
で表わされ、逆にこれをもって合流型超幾何関数の定義とする場合もある。この積分は
一般に合流型超幾何関数は、複素平面上
合流型超幾何関数は、単独で物理学等に用いられることは少なく、むしろ応用上重要な種々の特殊関数どうしの関係、特殊関数の一般論が問題となる場合に用いられることが多い。
歴史的背景については、超幾何関数と発展をともにしているので、詳細は「超幾何関数」の概要に譲る。
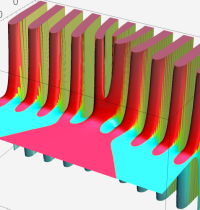
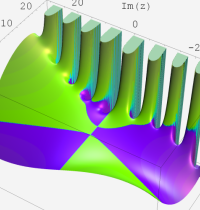
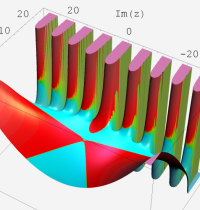
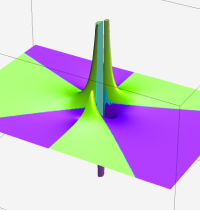
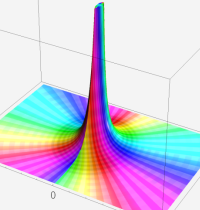
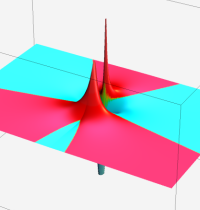
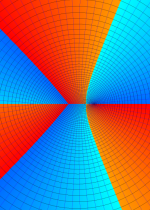
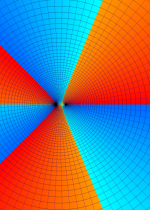
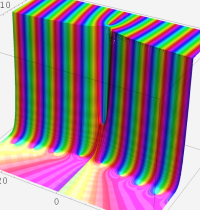
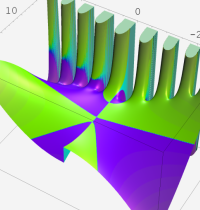
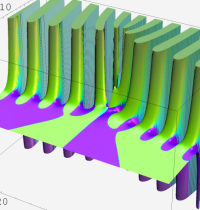
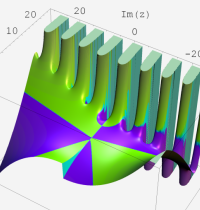
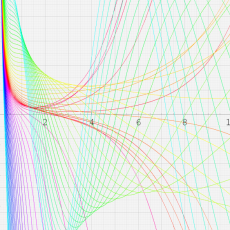
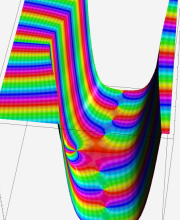
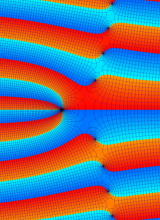
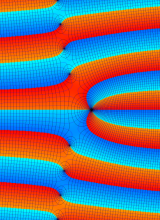
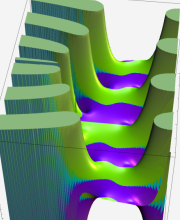
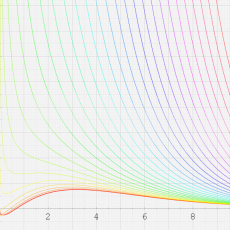
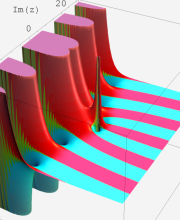
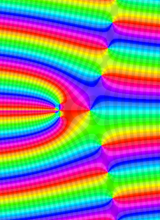
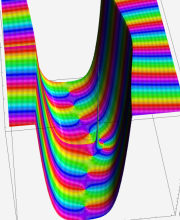
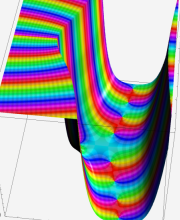
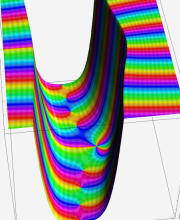
複素変数の第1種合流型超幾何関数
複素変数の第1種合流型超幾何関数
複素変数の第1種合流型超幾何関数
複素変数の第1種合流型超幾何関数
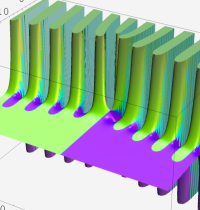
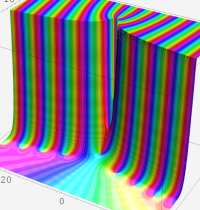
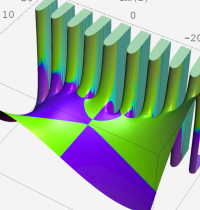
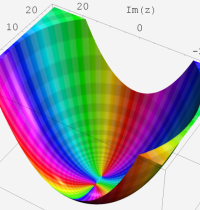
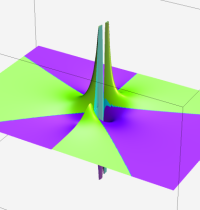
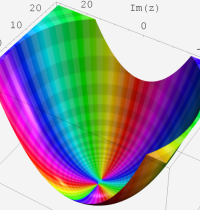
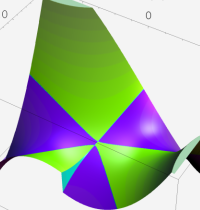
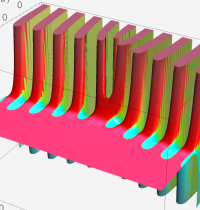
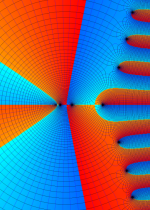
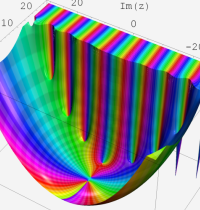
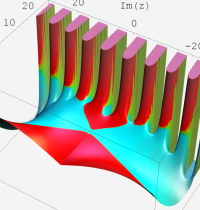
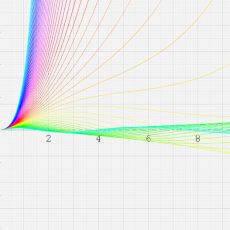
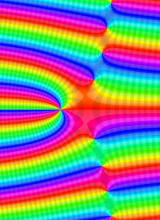
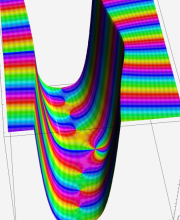
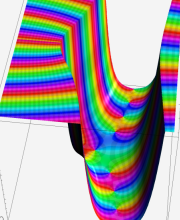
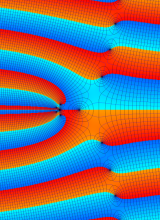
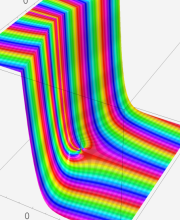
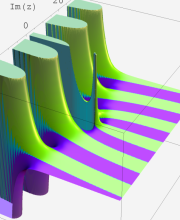
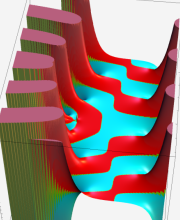
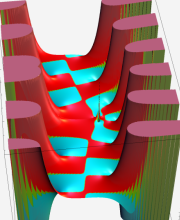
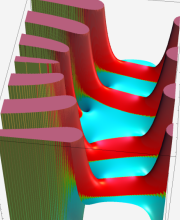
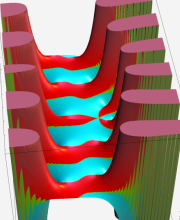
複素変数の第2種合流型超幾何関数
複素変数の第2種合流型超幾何関数
複素変数の第2種合流型超幾何関数
複素変数の第2種合流型超幾何関数
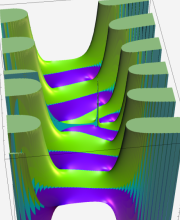
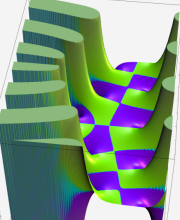
複素変数の第2種合流型超幾何関数
複素変数の第2種合流型超幾何関数
複素変数の第2種合流型超幾何関数
複素変数の第2種合流型超幾何関数
Whittaker 関数
日:Whittaker関数,ホイッタカー関数英:Whittaker function,仏:Fonction de Whittaker,独:Whittakersche funktion
Whittaker 関数は、本質的には合流型超幾何関数であり、その違いは初等関数因子だけである。しかし、Whittaker の微分方程式と呼ばれる二階線形常微分方程式
を満たすため、合流型超幾何関数よりも理論的に若干扱いやすくなる。この微分方程式の互いに線形独立な二つの解
を、第1種・第2種 Whittaker 関数という。因みに、
なお、第2種 Whittaker 関数は常に
また併せて、Whittaker の微分方程式を満たすが
を、別の第2種 Whittaker 関数として独自定義する (これも、別頁「Questions」にある理由による)。
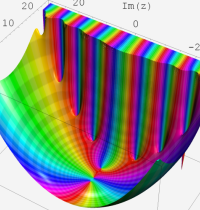
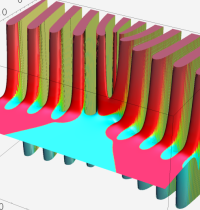
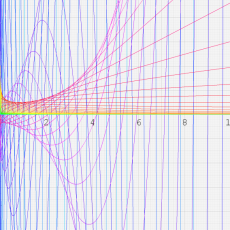
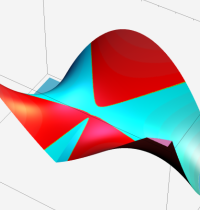
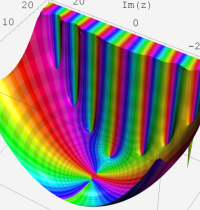
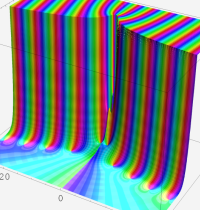
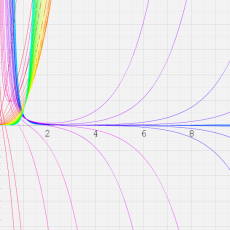
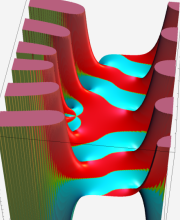
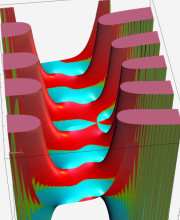
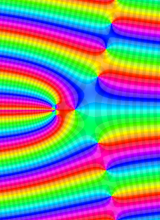
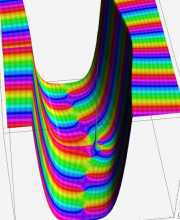
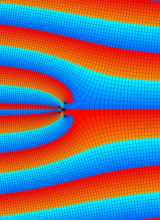
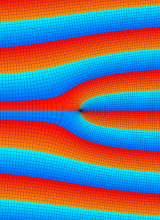
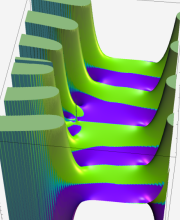
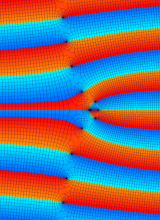
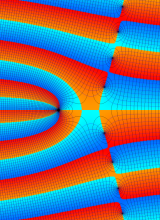
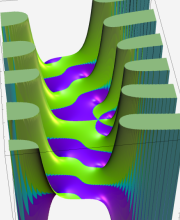
複素変数の第1種 Whittaker 関数
複素変数の第1種 Whittaker 関数
複素変数の第1種 Whittaker 関数
複素変数の第1種 Whittaker 関数
順に、①
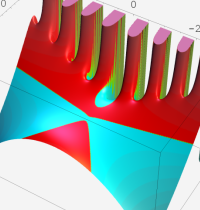
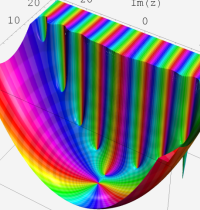
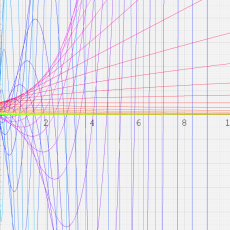
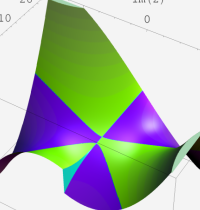
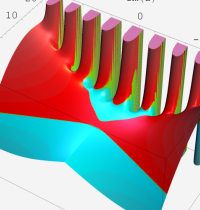
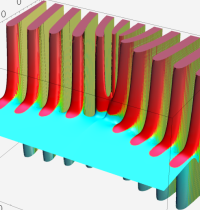
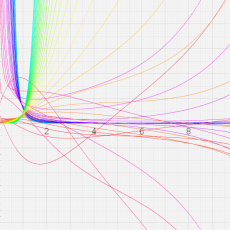
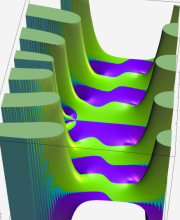
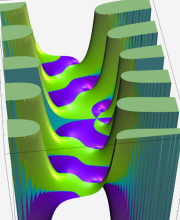
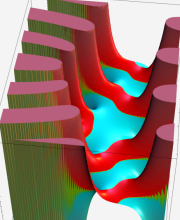
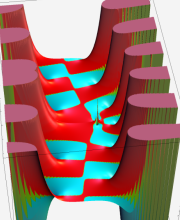
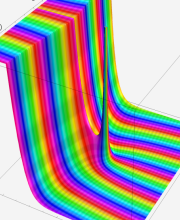
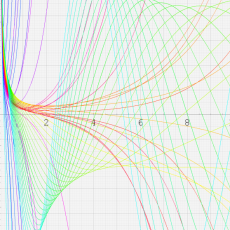
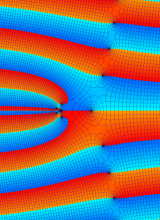
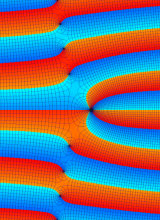
複素変数の第2種 Whittaker 関数
複素変数の第2種 Whittaker 関数
複素変数の第2種 Whittaker 関数
複素変数の第2種 Whittaker 関数
複素変数の第2種 Whittaker 関数
複素変数の第2種 Whittaker 関数