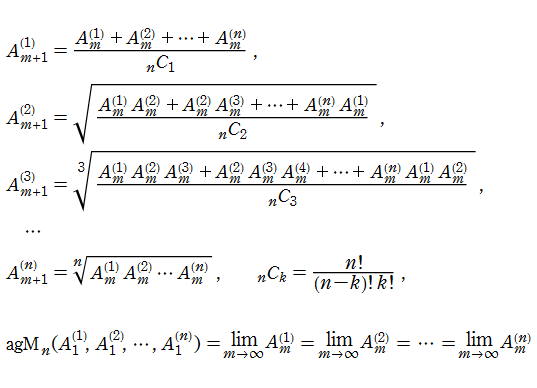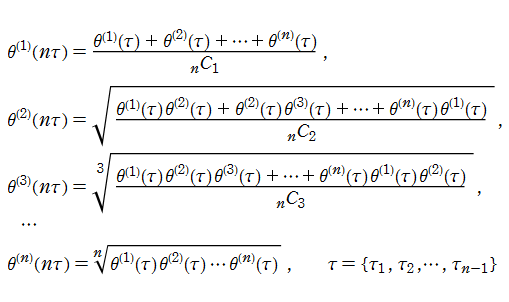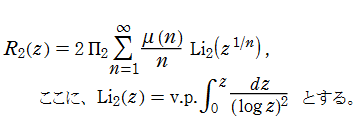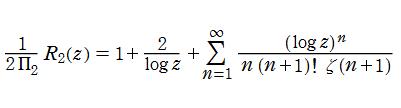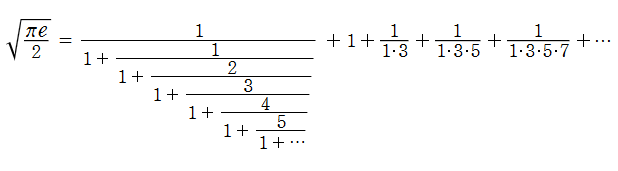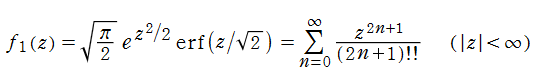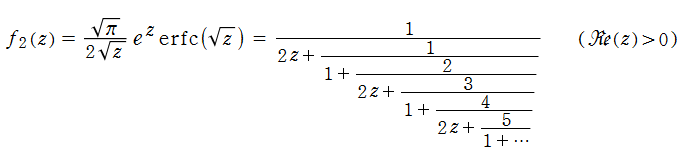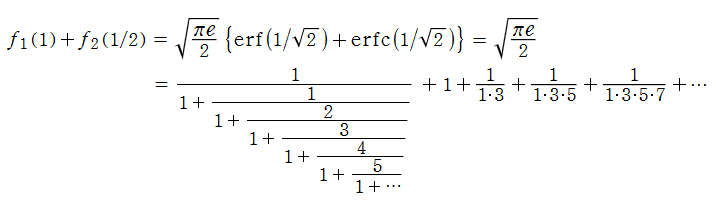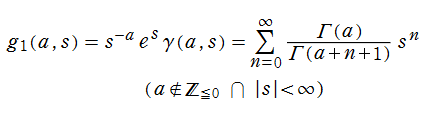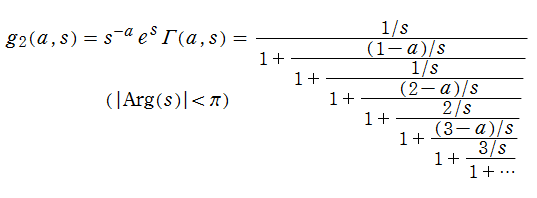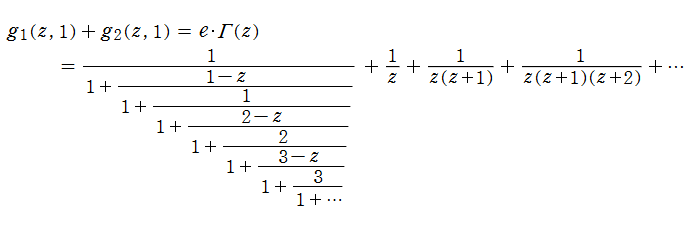特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
Home Menu
Questions
特殊関数についての、個人的な未解決事項・疑問・および妄想 …。
多項間算術幾何平均
Gauss の算術幾何平均(を(勝手に)多項間算術幾何平均と呼んでいる。Gauss の算術幾何平均と同様に、何らかの積分値と一致するような気がするが、これが全く分からない。
Gauss の場合から推測すると、
のような形の?…。
つまり、
しかし、現在も不明である。
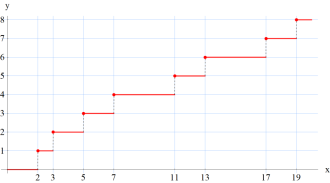
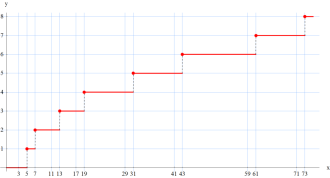
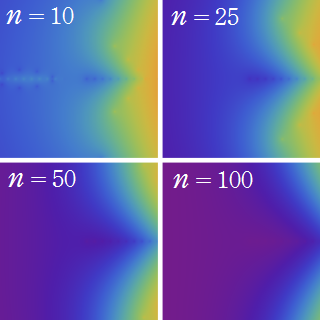
双子素数階段関数の近似
実数同様に、実数
また、この双子素数の分布に関連して、次の関数を考える。
ここに、
実際の計算においては、これを Gram 級数化した、
を用いる。これは、通常の素数計数関数から Gram 級数を導く方法(積分対数関数
このとき、
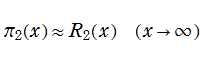
*******
双子素数階段関数因みに、
(
関数の定義における謎
現在定着している関数の定義について、当サイト管理人が長らく抱いている疑問点の数々。第2種Legendre関数
個人的には、第2種 Legendre 陪関数はしかし、実際に定着している定義はこれではない (理由は不明)。
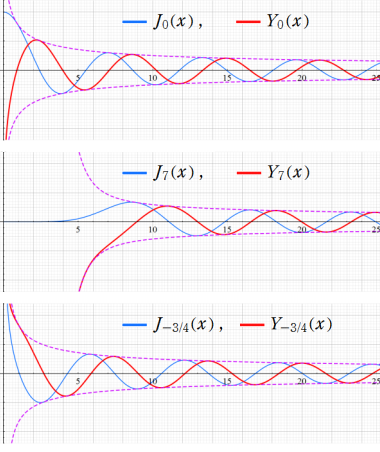
因みに、第1種と第2種の Bessel 関数は、同じ包絡線を持つ。
第2種の Hermite 関数、Laguerre 関数、Gegenbauer 関数、および Jacobi 関数の定義は(あまり応用されないこともあって)一定していない。実は、当サイトで採用しているこれらの第2種関数は、すべて第1種関数と同じ包絡線を持つような定義となっている (文献等を調べても、恐らく同じ定義は載っていないと思われる※)。
【註記】
※ 第2種 Hermite 関数については、森口繁一・宇田川銈久・一松 信「岩波 数学公式Ⅲ 特殊関数」p.94 に当サイトとほぼ同じ定義 (ただし整数次のみ) の記述がある。
※ 第2種 Hermite 関数については、森口繁一・宇田川銈久・一松 信「岩波 数学公式Ⅲ 特殊関数」p.94 に当サイトとほぼ同じ定義 (ただし整数次のみ) の記述がある。
ガンマ関数
ガンマ関数は階乗の連続化であるが、正確には1ずれている。Euler の業績を分析・整理していた A. M. Legendre が、Euler の定義した階乗関数を「ガンマ関数」と呼ぶことにした際、1ずれた形で定義したためである。その理由はよく分からないが、Legendre はガンマ関数の積分表示形(第2種 Euler 積分)を考察したときに、広義積分のなお、H. Jeffreys など一部の数学者は、階乗と一致した
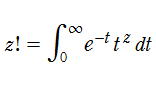
しかし、余程のことがない限り、変更されることは無いだろう。
【註記】
※ G. B. Arfken 著,権平健一郎・神原武志・小山直人:共訳「基礎物理数学2 関数論」p.279。
※ G. B. Arfken 著,権平健一郎・神原武志・小山直人:共訳「基礎物理数学2 関数論」p.279。

「連分数+級数」 型の表示式
(2019年8月29日 掲載記事)次は、S. Ramanujan によって得られた、大変美しい式である。
しかし、連分数と級数に現れる数字のパターンから、何となく合流型超幾何関数系の公式との関連が窺える。実際、これは誤差関数を用いて導くことができる。
NISTの公式:7.6.2の冪級数展開式から、
また、NISTの公式:7.9.1の連分数展開式をやや変形すると、
となる。因みに Ramanujan は、これとほとんど同じ連分数展開式を (自力で) 求めている。
よって、
が得られる (このような種明かしは、むしろ 「Ramanujan 的な神秘性が損なわれて興ざめ」 かもしれない…)。
当サイト管理人は、この方法を不完全ガンマ関数にも適用した。第1種不完全ガンマ関数の冪級数展開式から、
また、第2種不完全ガンマ関数の連分数展開式から、
よって、
が得られた。導出方法自体に注目すべき所は何もないが、この表示式は結構美しい (?)。
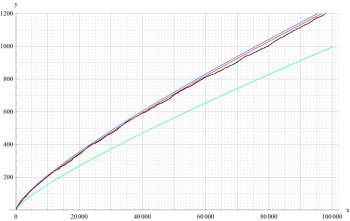
次のグラフは、この表示式 (両辺を
ガンマ関数の頁に掲載した漸近級数と組み合わせて (複素平面上で適用範囲を区分して) コードを記述すれば、割合効率的な実装になるのではなかろうか。
さて、ほとんど終わりに近付いたが、ここからが本題の "妄想" である。
他の特殊値や関数についても、「連分数+級数」 または 「連分数+連分数」 の表示式があるだろうか?。しかも、それらが数値計算法上も有用で、関数等の性質について洞察を与え、かつ、規則性がある表示式であれば更に都合が良い。例えば、
① 超越数論で問題となる定数:Euler - Mascheroni 定数, 奇数でのゼータ関数値など。
② 未解決問題を有する関数:ゼータ関数, 保型関数など。
③ 計算が難しい定数や関数。
に対して、そのような表示式が得られないだろうか?。(②のうち Riemann ゼータ関数の表示式を、当サイト管理人は Debye 関数 (不完全ゼータ関数) から求めようとしたが、現在は行き詰まっている。)② 未解決問題を有する関数:ゼータ関数, 保型関数など。
③ 計算が難しい定数や関数。
【工事中】
工事中:ここに新規項目の追加を計画しています。Under construction:I'm planning to add a new contents here.