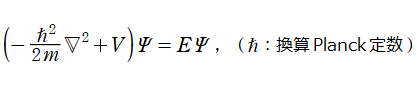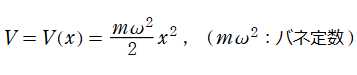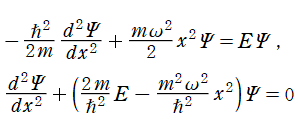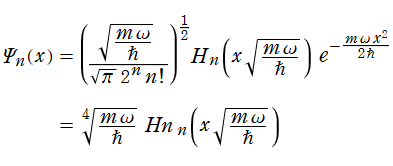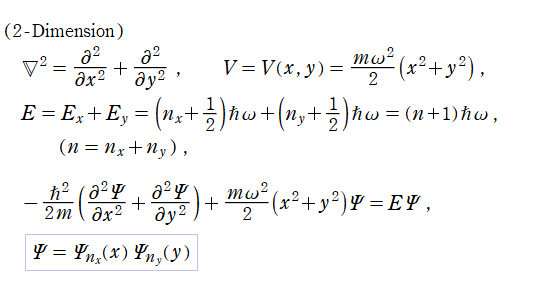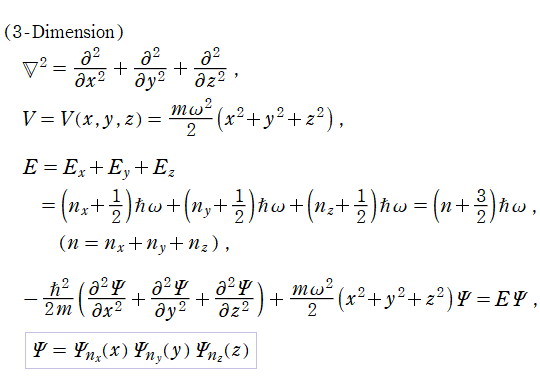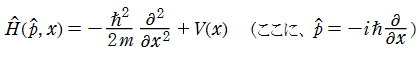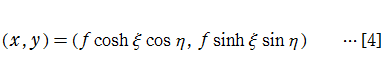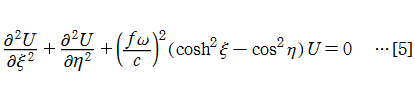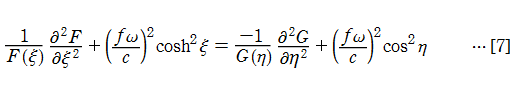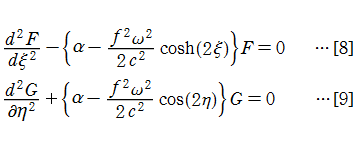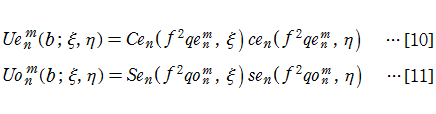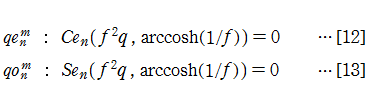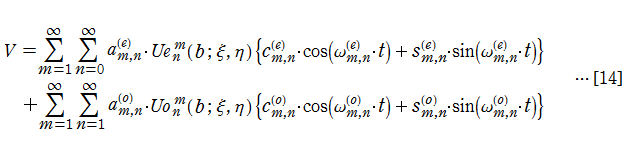特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
Home Menu
特殊関数 応用編
水素原子における電子の存在確率
3次元直交直線座標である。ただし、具体的な
上記の Schrödinger 方程式を、球座標
によって変換すれば、
となる。さらに、解が変数分離形
となり、各々の座標方向が独立に変動しても恒等的に成り立つ式になる。つまり、各項が定数に等しいと置いて式全体が0となるように定めることができる。そこで、解が既知の関数に帰着されるよう定数
が得られる。
まず①において、
よって、物理的に
となり、さらに変換
となる。この微分方程式の有界な解が、正規化 Laguerre 陪関数によって
と表わされるためには、
が得られる※3。逆変換
となる。
が課せられるので、ここから
と求まる※4。
②は単に式変形すれば
となり、その解は Legendre 陪関数 (Ferrers 型) に余弦関数を代入したものになるが、このうち有界な解として第2種 Legendre 陪関数を含まない、
を選ばなければならない。
同様に、③も簡単な式変形によって、
となることが直ちに分かるが、
を選ぶ。このとき
となっている。
よって、
となる※5。この解の全体に対して絶対値を取って2乗した式が、水素原子における電子の存在確率を表わす※6。
【註記】
※1:一般的な原子の場合は、いわゆる 「多体問題」 が生じる等の理由から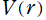 の式が複雑になるため、既知の関数で明示された形に解くことが難しい。しかし水素原子の場合は、陽子と電子が1個ずつの単純な構造であるため多体問題が生じず、しかも陽子は電子の約1836倍の質量があるため、陽子は原点に固定されていると仮定できる。それゆえ、この場合は上記のように解くことができる。(ただし、水素原子に外力が与えられていないとか、相対性理論からの効果を無視する等、他にもいくつかの仮定を含む。)
の式が複雑になるため、既知の関数で明示された形に解くことが難しい。しかし水素原子の場合は、陽子と電子が1個ずつの単純な構造であるため多体問題が生じず、しかも陽子は電子の約1836倍の質量があるため、陽子は原点に固定されていると仮定できる。それゆえ、この場合は上記のように解くことができる。(ただし、水素原子に外力が与えられていないとか、相対性理論からの効果を無視する等、他にもいくつかの仮定を含む。)
※2: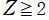 の場合とは、電子を1個のままで原子核を一般的な元素のそれに置き換えた想像上の原子に相当する。これは 「水素様原子」 (水素型原子 = Hydrogen-like atom) と呼ばれる。
の場合とは、電子を1個のままで原子核を一般的な元素のそれに置き換えた想像上の原子に相当する。これは 「水素様原子」 (水素型原子 = Hydrogen-like atom) と呼ばれる。
※3:むしろ本来の順序では、この式が Bohr 半径の (国際量体系での) 定義として先に与えられる。Bohr 半径は、基底 (最低エネルギー) 状態の水素原子における電子の軌道半径に相当する長さの単位であって、概ね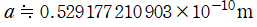 とされる。名称は、N. H. D. Bohr に由来する。
とされる。名称は、N. H. D. Bohr に由来する。
※4:この定積分は次の方法で求める。まず、Laguerre 陪関数が満たす漸化式
から、正規化 Laguerre 陪関数が満たす漸化式
を得る。この両辺に](siki_home040/applic_1_04500.png) を掛けて積分すると、
を掛けて積分すると、
となるが、右辺にある定積分は重み関数が現れない正規直交性ゆえ1または0になる。よって、
が得られる。(当サイトでは、解の導出にあたって正規化 Laguerre 陪関数を介したが、勿論これは必須ではなく、通常は Laguerre 陪多項式で求める。)
※5:特に、![ψ[n, 0, 0]](siki_home040/applic_1_04800.png) は角運動量が零になる 「s 状態」 の軌道を表わす。古典力学で s 状態を説明しようとすると、電子が原子核に落下して軌道が潰れてしまうとの結論が導かれてしまう。これは、現実とも矛盾する。しかし量子力学によれば、s 状態でも固有エネルギーを持ち、確率分布にしたがって電子は存在するとの結論になり、軌道が潰れないことを上手く説明できる。
は角運動量が零になる 「s 状態」 の軌道を表わす。古典力学で s 状態を説明しようとすると、電子が原子核に落下して軌道が潰れてしまうとの結論が導かれてしまう。これは、現実とも矛盾する。しかし量子力学によれば、s 状態でも固有エネルギーを持ち、確率分布にしたがって電子は存在するとの結論になり、軌道が潰れないことを上手く説明できる。
※6:以下のグラフは全て、Bohr 半径を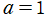 , 陽子数を
, 陽子数を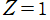 として描画する。
として描画する。
( グラフのコードは 「Mathematica Code」 の頁に掲載しています。)
グラフのコードは 「Mathematica Code」 の頁に掲載しています。)
※1:一般的な原子の場合は、いわゆる 「多体問題」 が生じる等の理由から
※2:
※3:むしろ本来の順序では、この式が Bohr 半径の (国際量体系での) 定義として先に与えられる。Bohr 半径は、基底 (最低エネルギー) 状態の水素原子における電子の軌道半径に相当する長さの単位であって、概ね
※4:この定積分は次の方法で求める。まず、Laguerre 陪関数が満たす漸化式
から、正規化 Laguerre 陪関数が満たす漸化式
を得る。この両辺に
となるが、右辺にある定積分は重み関数が現れない正規直交性ゆえ1または0になる。よって、
が得られる。(当サイトでは、解の導出にあたって正規化 Laguerre 陪関数を介したが、勿論これは必須ではなく、通常は Laguerre 陪多項式で求める。)
※5:特に、
※6:以下のグラフは全て、Bohr 半径を
(
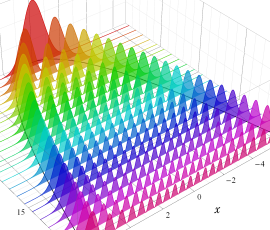
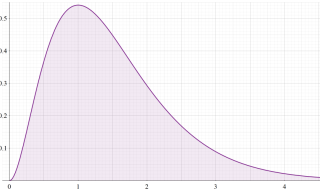
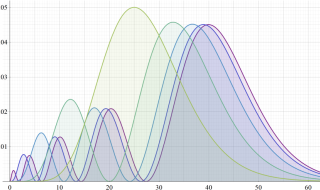
動径方向の波動関数
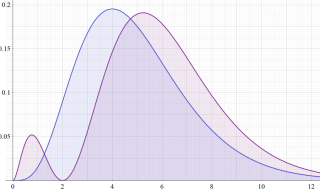
動径方向K 殻 (
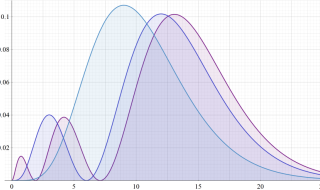
L 殻 (
M 殻 (
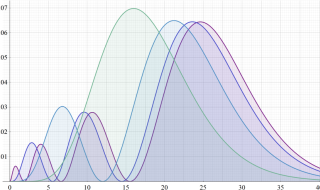
N 殻 (
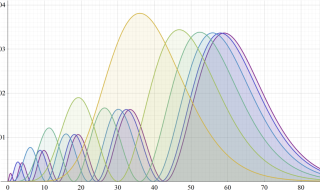
O 殻 (
P 殻 (
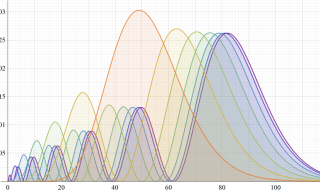
Q 殻 (
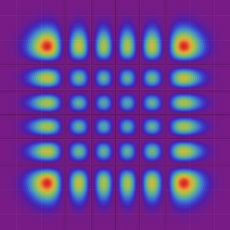
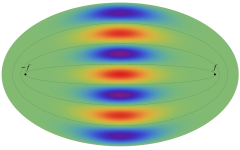
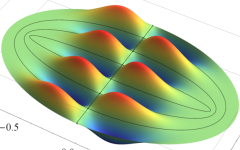
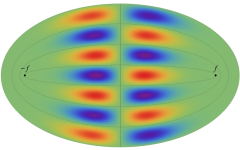
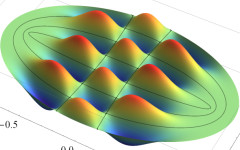
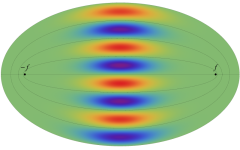
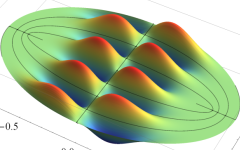
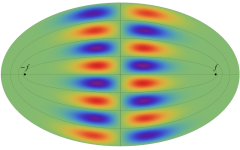
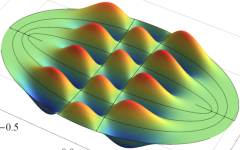
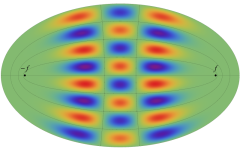
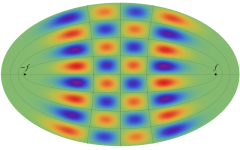
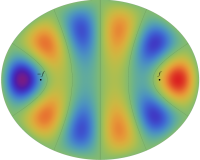
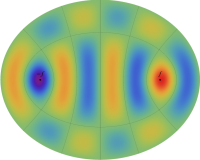
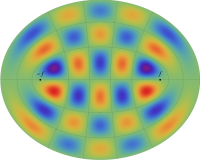
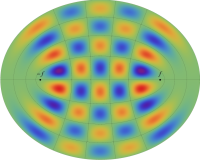
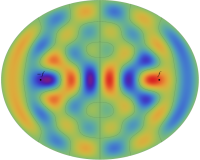
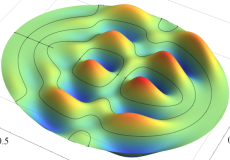
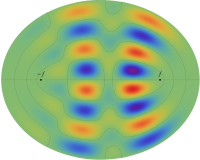
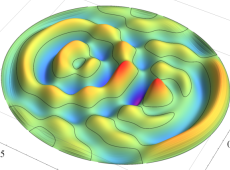
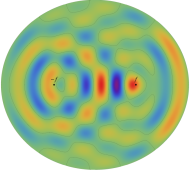
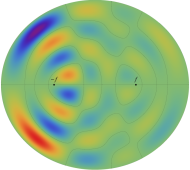
電子の存在確率の「雲」
前述の解なお、電子雲の色は疑似カラーであって、現実とは異なる (可視光線の波長は原子半径の概ね数千倍もあるので、原子の規模について色を問うこと自体が無意味)。また、原点にある原子核を強調するため赤点を置いたが、その電子雲に対する実際の大きさは、図よりも遙かに小さい。
【色の凡例】
以下のグラフで使用する色の凡例。赤字は、Og (オガネソン) までの元素の電子配置には現れないと推定されている原子軌道。
(表中の文字をクリックすると、当該グラフの掲載箇所にジャンプします。)
| s | p | d | f | g | h | i | |
|---|---|---|---|---|---|---|---|
| K | 1s | ||||||
| L | 2s | 2p | |||||
| M | 3s | 3p | 3d | ||||
| N | 4s | 4p | 4d | 4f | |||
| O | 5s | 5p | 5d | 5f | 5g | ||
| P | 6s | 6p | 6d | 6f | 6g | 6h | |
| Q | 7s | 7p | 7d | 7f | 7g | 7h | 7i |
【1s: K殻・s状態】
【2s: L殻・s状態】
【2p: L殻・p状態】
【3s: M殻・s状態】
【3p: M殻・p状態】
【3d: M殻・d状態】
【4s: N殻・s状態】
【4p: N殻・p状態】
【4d: N殻・d状態】
【4f: N殻・f状態】
【5s: O殻・s状態】
【5p: O殻・p状態】
【5d: O殻・d状態】
【5f: O殻・f状態】
【5g: O殻・g状態】
【6s: P殻・s状態】
【6p: P殻・p状態】
【6d: P殻・d状態】
【6f: P殻・f状態】
【6g: P殻・g状態】
【6h: P殻・h状態】
【7s: Q殻・s状態】
【7p: Q殻・p状態】
【7d: Q殻・d状態】
【7f: Q殻・f状態】
【7g: Q殻・g状態】
【7h: Q殻・h状態】
【7i: Q殻・i状態】
【 Petite Galerie 】
"量子力学的" 太極図
(N. H. D. Bohr は自身の紋章に太極図を採用している。)
(N. H. D. Bohr は自身の紋章に太極図を採用している。)
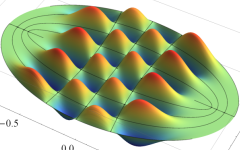
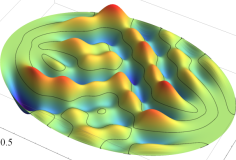
調和振動子の存在確率
結晶内の原子が、熱エネルギーによって振動する場合などの格子振動現象は、古典力学における単振り子やバネの運動を、量子力学の (時間に依存しない) Schrödinger 方程式によって量子化したもので説明される。ここに、
最も簡単な事例として、原子が1次元的に並び、しかも原点からの距離に比例する引力が各原子に影響している場合を考える。古典力学的な1次元調和振動子のポテンシャルエネルギー関数
となるのでそのまま代入し、ラプラシアンの部分は (1次元ゆえ) 単なる2階の常微分演算子になる。よって、Schrödinger 方程式は
に変形される※1。
上記の Schrödinger 方程式は、正規化 Hermite 多項式が満たす微分方程式と実質同じ形であるから、解が正規化 Hermite 多項式で表わされる事を期待するならば、固有エネルギーは

よって、前掲の Schrödinger 方程式の解
が得られる。この解の全体に対して絶対値を取り、さらに2乗した式が、1次元調和振動子の存在確率を表わす。
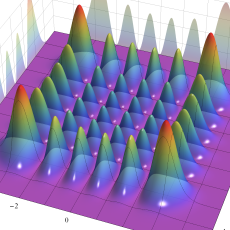
多次元調和振動子は、Schrödinger 方程式が変数分離形になるため、次元数個の1次元調和振動子の (上記の) 解を掛け合わせた形になる。具体的に、2次元ならば
となり、3次元ならば
となる。いずれの場合も同様に、存在確率は解の絶対値の2乗となる。
以下では、1次元, 2次元, および3次元調和振動子の存在確率のグラフを掲載しているが、簡単のため全てのグラフを、バネ定数については
(
【註記】
※1:古典的な Newton 力学に従う1次元運動の場合、その物理系の Hamilton 関数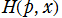 は、ポテンシャルエネルギー関数を
は、ポテンシャルエネルギー関数を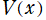 とするとき、
とするとき、
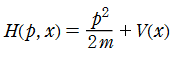
となる (右辺の第1項は、運動エネルギーを表わす)。この場合、Hamilton 関数を量子化した 「Hamilton 演算子」
によって、Newton 方程式を置き換えた、
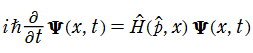
が Schrödinger 方程式となる。
※1:古典的な Newton 力学に従う1次元運動の場合、その物理系の Hamilton 関数
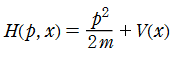
によって、Newton 方程式を置き換えた、
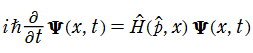
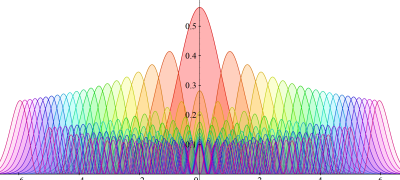
1次元調和振動子
1次元調和振動子の存在確率を表わす波動関数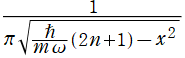 に近くなる。(グラフは
に近くなる。(グラフは2次元調和振動子
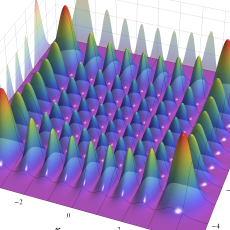
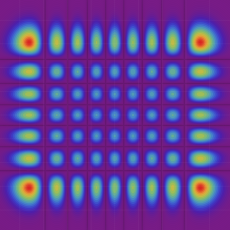
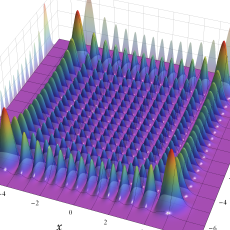
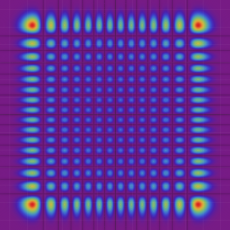
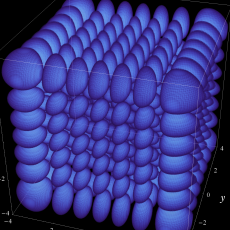
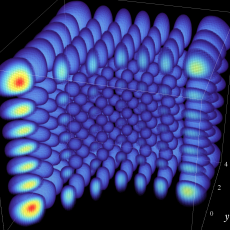
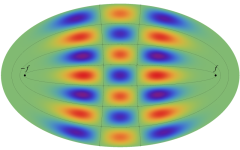
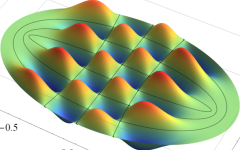
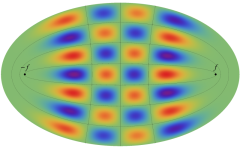
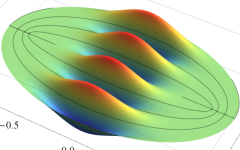
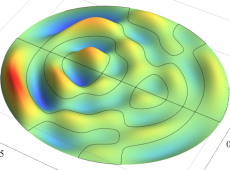
2次元調和振動子の存在確率を表わす波動関数(格子の内部より、辺や頂点に位置する原子の周辺の方が、電子の存在確率は高くなることが分かる。)
2次元調和振動子の存在確率を表わす波動関数
2次元調和振動子の存在確率を表わす波動関数
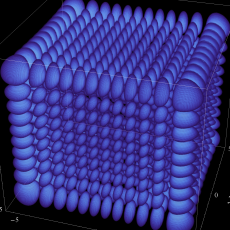
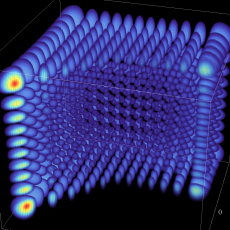
3次元調和振動子
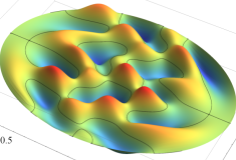
3次元調和振動子の存在確率を表わす波動関数2番目は、1番目の一部領域を切り取って、内部が分かるようにしたグラフである (以下同様)。
3次元調和振動子の存在確率を表わす波動関数
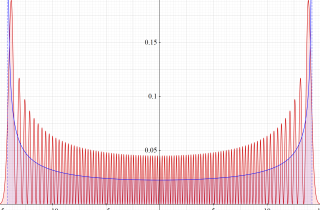
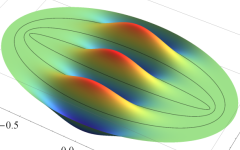
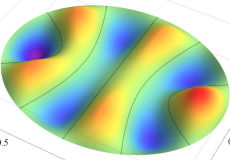
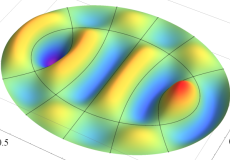
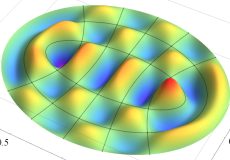
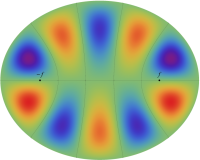
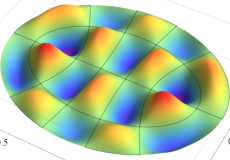
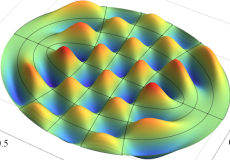
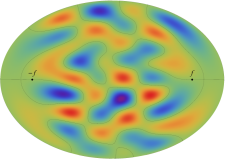
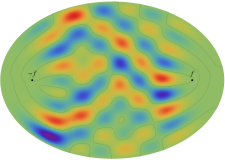
楕円形膜の振動
太鼓などの膜の振動現象は、膜の形状が簡単であれば特殊関数を用いて表わせる。円形膜の場合は、動径方向に第1種 Bessel 関数が現れる事例として、多くの書籍・ウェブサイト等で詳しい解説がある。ここでは、比較的取り上げられることが少ない事例として、第1種 Mathieu 関数が現れる楕円形膜の場合を扱う (方法そのものは円形膜の場合と変わらない)。
速さ
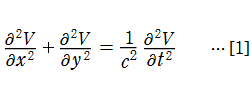
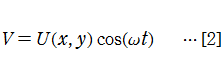
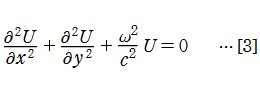
を用いれば、[3]は
に変形される。このとき解
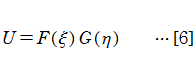
になる。これは
が得られる。[8]は変形された Mathieu の微分方程式、[9]は Mathieu の微分方程式に他ならない。よって、固有振動関数
となる。ここに
の正の実数解
より一般的な楕円形膜の振動は、
となる。ここに
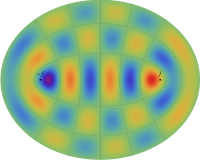
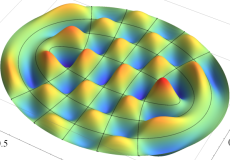
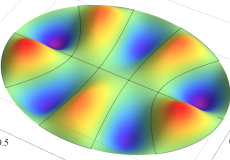
固有振動関数(偶関数・奇関数)
固有振動関数は、時刻(
①②:
①②:
①②:
①②:
①②:
①②:
①②:
①②:
アニメーション(2.14MB)
楕円形膜の固有振動 (偶関数)。
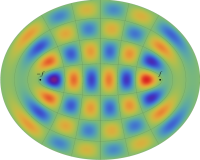
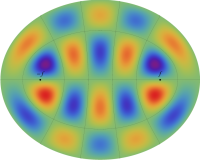
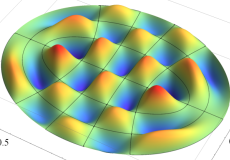
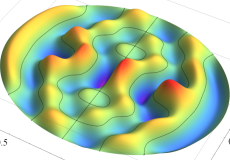
固有振動関数の和
楕円形膜の振動の一般的な例として、複数個の固有振動関数を足し合わせた場合を以下に示す。これは、時刻①②:
③④:
①②:
③④:
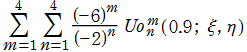
①②:
③④:
【工事中】
工事中:ここに新規項目の追加を計画しています。Under construction:I'm planning to add a new contents here.


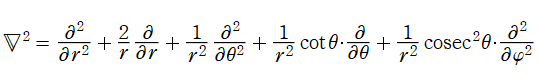
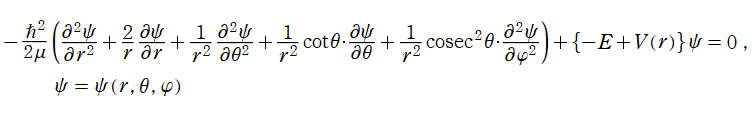
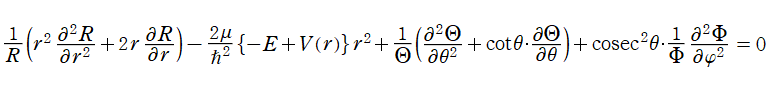
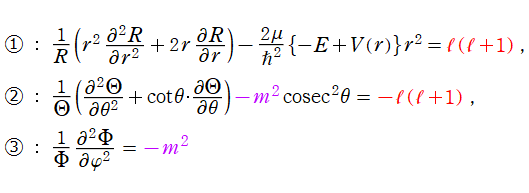

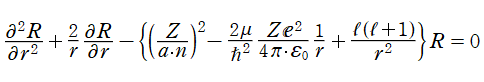
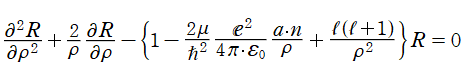
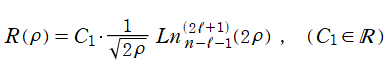
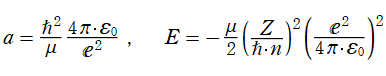
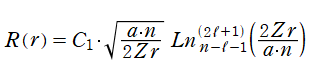
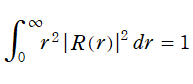
![具体的なC[1]の表示](siki_home040/applic_1_02800.png)
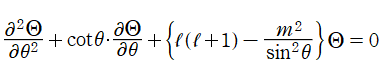
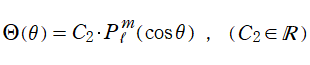
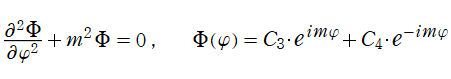
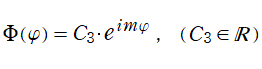
![具体的なC[2]とC[3]の表示](siki_home040/applic_1_03700.png)
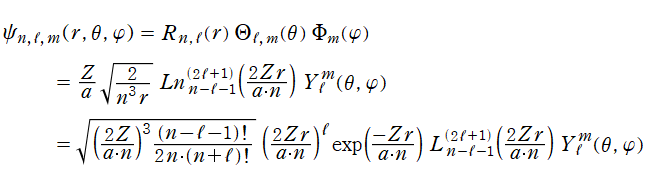
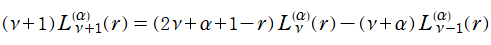
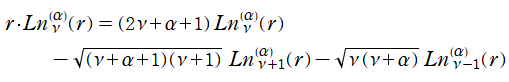
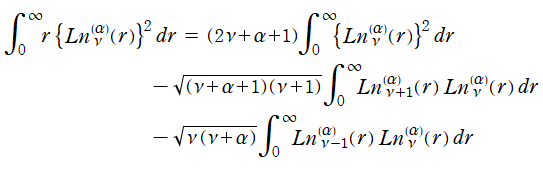
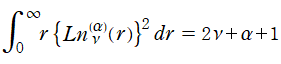
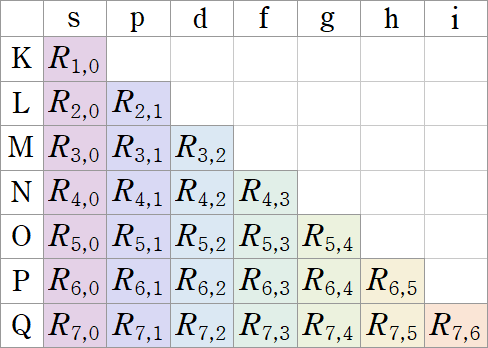
![ψ[1, 0, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen100s_thumb.png)
![ψ[1, 0, 0]の電子雲(3次元)](gazou_home040/190_hydrogen100t_thumb.png)
![ψ[2, 0, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen200s_thumb.png)
![ψ[2, 0, 0]の電子雲(3次元)](gazou_home040/190_hydrogen200t_thumb.png)
![ψ[2, 1, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen210s_thumb.png)
![ψ[2, 1, 0]の電子雲(3次元)](gazou_home040/190_hydrogen210t_thumb.png)
![ψ[2, 1, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen211s_thumb.png)
![ψ[2, 1, 1]の電子雲(3次元)](gazou_home040/190_hydrogen211t_thumb.png)
![ψ[3, 0, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen300s_thumb.png)
![ψ[3, 0, 0]の電子雲(3次元)](gazou_home040/190_hydrogen300t_thumb.png)
![ψ[3, 1, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen310s_thumb.png)
![ψ[3, 1, 0]の電子雲(3次元)](gazou_home040/190_hydrogen310t_thumb.png)
![ψ[3, 1, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen311s_thumb.png)
![ψ[3, 1, 1]の電子雲(3次元)](gazou_home040/190_hydrogen311t_thumb.png)
![ψ[3, 2, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen320s_thumb.png)
![ψ[3, 2, 0]の電子雲(3次元)](gazou_home040/190_hydrogen320t_thumb.png)
![ψ[3, 2, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen321s_thumb.png)
![ψ[3, 2, 1]の電子雲(3次元)](gazou_home040/190_hydrogen321t_thumb.png)
![ψ[3, 2, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen322s_thumb.png)
![ψ[3, 2, 2]の電子雲(3次元)](gazou_home040/190_hydrogen322t_thumb.png)
![ψ[4, 0, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen400s_thumb.png)
![ψ[4, 0, 0]の電子雲(3次元)](gazou_home040/190_hydrogen400t_thumb.png)
![ψ[4, 1, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen410s_thumb.png)
![ψ[4, 1, 0]の電子雲(3次元)](gazou_home040/190_hydrogen410t_thumb.png)
![ψ[4, 1, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen411s_thumb.png)
![ψ[4, 1, 1]の電子雲(3次元)](gazou_home040/190_hydrogen411t_thumb.png)
![ψ[4, 2, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen420s_thumb.png)
![ψ[4, 2, 0]の電子雲(3次元)](gazou_home040/190_hydrogen420t_thumb.png)
![ψ[4, 2, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen421s_thumb.png)
![ψ[4, 2, 1]の電子雲(3次元)](gazou_home040/190_hydrogen421t_thumb.png)
![ψ[4, 2, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen422s_thumb.png)
![ψ[4, 2, 2]の電子雲(3次元)](gazou_home040/190_hydrogen422t_thumb.png)
![ψ[4, 3, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen430s_thumb.png)
![ψ[4, 3, 0]の電子雲(3次元)](gazou_home040/190_hydrogen430t_thumb.png)
![ψ[4, 3, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen431s_thumb.png)
![ψ[4, 3, 1]の電子雲(3次元)](gazou_home040/190_hydrogen431t_thumb.png)
![ψ[4, 3, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen432s_thumb.png)
![ψ[4, 3, 2]の電子雲(3次元)](gazou_home040/190_hydrogen432t_thumb.png)
![ψ[4, 3, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen433s_thumb.png)
![ψ[4, 3, 3]の電子雲(3次元)](gazou_home040/190_hydrogen433t_thumb.png)
![ψ[5, 0, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen500s_thumb.png)
![ψ[5, 0, 0]の電子雲(3次元)](gazou_home040/190_hydrogen500t_thumb.png)
![ψ[5, 1, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen510s_thumb.png)
![ψ[5, 1, 0]の電子雲(3次元)](gazou_home040/190_hydrogen510t_thumb.png)
![ψ[5, 1, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen511s_thumb.png)
![ψ[5, 1, 1]の電子雲(3次元)](gazou_home040/190_hydrogen511t_thumb.png)
![ψ[5, 2, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen520s_thumb.png)
![ψ[5, 2, 0]の電子雲(3次元)](gazou_home040/190_hydrogen520t_thumb.png)
![ψ[5, 2, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen521s_thumb.png)
![ψ[5, 2, 1]の電子雲(3次元)](gazou_home040/190_hydrogen521t_thumb.png)
![ψ[5, 2, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen522s_thumb.png)
![ψ[5, 2, 2]の電子雲(3次元)](gazou_home040/190_hydrogen522t_thumb.png)
![ψ[5, 3, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen530s_thumb.png)
![ψ[5, 3, 0]の電子雲(3次元)](gazou_home040/190_hydrogen530t_thumb.png)
![ψ[5, 3, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen531s_thumb.png)
![ψ[5, 3, 1]の電子雲(3次元)](gazou_home040/190_hydrogen531t_thumb.png)
![ψ[5, 3, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen532s_thumb.png)
![ψ[5, 3, 2]の電子雲(3次元)](gazou_home040/190_hydrogen532t_thumb.png)
![ψ[5, 3, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen533s_thumb.png)
![ψ[5, 3, 3]の電子雲(3次元)](gazou_home040/190_hydrogen533t_thumb.png)
![ψ[5, 4, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen540s_thumb.png)
![ψ[5, 4, 0]の電子雲(3次元)](gazou_home040/190_hydrogen540t_thumb.png)
![ψ[5, 4, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen541s_thumb.png)
![ψ[5, 4, 1]の電子雲(3次元)](gazou_home040/190_hydrogen541t_thumb.png)
![ψ[5, 4, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen542s_thumb.png)
![ψ[5, 4, 2]の電子雲(3次元)](gazou_home040/190_hydrogen542t_thumb.png)
![ψ[5, 4, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen543s_thumb.png)
![ψ[5, 4, 3]の電子雲(3次元)](gazou_home040/190_hydrogen543t_thumb.png)
![ψ[5, 4, 4]の電子雲(x-z断面)](gazou_home040/190_hydrogen544s_thumb.png)
![ψ[5, 4, 4]の電子雲(3次元)](gazou_home040/190_hydrogen544t_thumb.png)
![ψ[6, 0, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen600s_thumb.png)
![ψ[6, 0, 0]の電子雲(3次元)](gazou_home040/190_hydrogen600t_thumb.png)
![ψ[6, 1, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen610s_thumb.png)
![ψ[6, 1, 0]の電子雲(3次元)](gazou_home040/190_hydrogen610t_thumb.png)
![ψ[6, 1, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen611s_thumb.png)
![ψ[6, 1, 1]の電子雲(3次元)](gazou_home040/190_hydrogen611t_thumb.png)
![ψ[6, 2, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen620s_thumb.png)
![ψ[6, 2, 0]の電子雲(3次元)](gazou_home040/190_hydrogen620t_thumb.png)
![ψ[6, 2, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen621s_thumb.png)
![ψ[6, 2, 1]の電子雲(3次元)](gazou_home040/190_hydrogen621t_thumb.png)
![ψ[6, 2, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen622s_thumb.png)
![ψ[6, 2, 2]の電子雲(3次元)](gazou_home040/190_hydrogen622t_thumb.png)
![ψ[6, 3, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen630s_thumb.png)
![ψ[6, 3, 0]の電子雲(3次元)](gazou_home040/190_hydrogen630t_thumb.png)
![ψ[6, 3, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen631s_thumb.png)
![ψ[6, 3, 1]の電子雲(3次元)](gazou_home040/190_hydrogen631t_thumb.png)
![ψ[6, 3, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen632s_thumb.png)
![ψ[6, 3, 2]の電子雲(3次元)](gazou_home040/190_hydrogen632t_thumb.png)
![ψ[6, 3, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen633s_thumb.png)
![ψ[6, 3, 3]の電子雲(3次元)](gazou_home040/190_hydrogen633t_thumb.png)
![ψ[6, 4, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen640s_thumb.png)
![ψ[6, 4, 0]の電子雲(3次元)](gazou_home040/190_hydrogen640t_thumb.png)
![ψ[6, 4, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen641s_thumb.png)
![ψ[6, 4, 1]の電子雲(3次元)](gazou_home040/190_hydrogen641t_thumb.png)
![ψ[6, 4, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen642s_thumb.png)
![ψ[6, 4, 2]の電子雲(3次元)](gazou_home040/190_hydrogen642t_thumb.png)
![ψ[6, 4, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen643s_thumb.png)
![ψ[6, 4, 3]の電子雲(3次元)](gazou_home040/190_hydrogen643t_thumb.png)
![ψ[6, 4, 4]の電子雲(x-z断面)](gazou_home040/190_hydrogen644s_thumb.png)
![ψ[6, 4, 4]の電子雲(3次元)](gazou_home040/190_hydrogen644t_thumb.png)
![ψ[6, 5, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen650s_thumb.png)
![ψ[6, 5, 0]の電子雲(3次元)](gazou_home040/190_hydrogen650t_thumb.png)
![ψ[6, 5, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen651s_thumb.png)
![ψ[6, 5, 1]の電子雲(3次元)](gazou_home040/190_hydrogen651t_thumb.png)
![ψ[6, 5, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen652s_thumb.png)
![ψ[6, 5, 2]の電子雲(3次元)](gazou_home040/190_hydrogen652t_thumb.png)
![ψ[6, 5, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen653s_thumb.png)
![ψ[6, 5, 3]の電子雲(3次元)](gazou_home040/190_hydrogen653t_thumb.png)
![ψ[6, 5, 4]の電子雲(x-z断面)](gazou_home040/190_hydrogen654s_thumb.png)
![ψ[6, 5, 4]の電子雲(3次元)](gazou_home040/190_hydrogen654t_thumb.png)
![ψ[6, 5, 5]の電子雲(x-z断面)](gazou_home040/190_hydrogen655s_thumb.png)
![ψ[6, 5, 5]の電子雲(3次元)](gazou_home040/190_hydrogen655t_thumb.png)
![ψ[7, 0, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen700s_thumb.png)
![ψ[7, 0, 0]の電子雲(3次元)](gazou_home040/190_hydrogen700t_thumb.png)
![ψ[7, 1, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen710s_thumb.png)
![ψ[7, 1, 0]の電子雲(3次元)](gazou_home040/190_hydrogen710t_thumb.png)
![ψ[7, 1, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen711s_thumb.png)
![ψ[7, 1, 1]の電子雲(3次元)](gazou_home040/190_hydrogen711t_thumb.png)
![ψ[7, 2, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen720s_thumb.png)
![ψ[7, 2, 0]の電子雲(3次元)](gazou_home040/190_hydrogen720t_thumb.png)
![ψ[7, 2, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen721s_thumb.png)
![ψ[7, 2, 1]の電子雲(3次元)](gazou_home040/190_hydrogen721t_thumb.png)
![ψ[7, 2, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen722s_thumb.png)
![ψ[7, 2, 2]の電子雲(3次元)](gazou_home040/190_hydrogen722t_thumb.png)
![ψ[7, 3, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen730s_thumb.png)
![ψ[7, 3, 0]の電子雲(3次元)](gazou_home040/190_hydrogen730t_thumb.png)
![ψ[7, 3, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen731s_thumb.png)
![ψ[7, 3, 1]の電子雲(3次元)](gazou_home040/190_hydrogen731t_thumb.png)
![ψ[7, 3, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen732s_thumb.png)
![ψ[7, 3, 2]の電子雲(3次元)](gazou_home040/190_hydrogen732t_thumb.png)
![ψ[7, 3, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen733s_thumb.png)
![ψ[7, 3, 3]の電子雲(3次元)](gazou_home040/190_hydrogen733t_thumb.png)
![ψ[7, 4, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen740s_thumb.png)
![ψ[7, 4, 0]の電子雲(3次元)](gazou_home040/190_hydrogen740t_thumb.png)
![ψ[7, 4, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen741s_thumb.png)
![ψ[7, 4, 1]の電子雲(3次元)](gazou_home040/190_hydrogen741t_thumb.png)
![ψ[7, 4, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen742s_thumb.png)
![ψ[7, 4, 2]の電子雲(3次元)](gazou_home040/190_hydrogen742t_thumb.png)
![ψ[7, 4, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen743s_thumb.png)
![ψ[7, 4, 3]の電子雲(3次元)](gazou_home040/190_hydrogen743t_thumb.png)
![ψ[7, 4, 4]の電子雲(x-z断面)](gazou_home040/190_hydrogen744s_thumb.png)
![ψ[7, 4, 4]の電子雲(3次元)](gazou_home040/190_hydrogen744t_thumb.png)
![ψ[7, 5, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen750s_thumb.png)
![ψ[7, 5, 0]の電子雲(3次元)](gazou_home040/190_hydrogen750t_thumb.png)
![ψ[7, 5, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen751s_thumb.png)
![ψ[7, 5, 1]の電子雲(3次元)](gazou_home040/190_hydrogen751t_thumb.png)
![ψ[7, 5, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen752s_thumb.png)
![ψ[7, 5, 2]の電子雲(3次元)](gazou_home040/190_hydrogen752t_thumb.png)
![ψ[7, 5, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen753s_thumb.png)
![ψ[7, 5, 3]の電子雲(3次元)](gazou_home040/190_hydrogen753t_thumb.png)
![ψ[7, 5, 4]の電子雲(x-z断面)](gazou_home040/190_hydrogen754s_thumb.png)
![ψ[7, 5, 4]の電子雲(3次元)](gazou_home040/190_hydrogen754t_thumb.png)
![ψ[7, 5, 5]の電子雲(x-z断面)](gazou_home040/190_hydrogen755s_thumb.png)
![ψ[7, 5, 5]の電子雲(3次元)](gazou_home040/190_hydrogen755t_thumb.png)
![ψ[7, 6, 0]の電子雲(x-z断面)](gazou_home040/190_hydrogen760s_thumb.png)
![ψ[7, 6, 0]の電子雲(3次元)](gazou_home040/190_hydrogen760t_thumb.png)
![ψ[7, 6, 1]の電子雲(x-z断面)](gazou_home040/190_hydrogen761s_thumb.png)
![ψ[7, 6, 1]の電子雲(3次元)](gazou_home040/190_hydrogen761t_thumb.png)
![ψ[7, 6, 2]の電子雲(x-z断面)](gazou_home040/190_hydrogen762s_thumb.png)
![ψ[7, 6, 2]の電子雲(3次元)](gazou_home040/190_hydrogen762t_thumb.png)
![ψ[7, 6, 3]の電子雲(x-z断面)](gazou_home040/190_hydrogen763s_thumb.png)
![ψ[7, 6, 3]の電子雲(3次元)](gazou_home040/190_hydrogen763t_thumb.png)
![ψ[7, 6, 4]の電子雲(x-z断面)](gazou_home040/190_hydrogen764s_thumb.png)
![ψ[7, 6, 4]の電子雲(3次元)](gazou_home040/190_hydrogen764t_thumb.png)
![ψ[7, 6, 5]の電子雲(x-z断面)](gazou_home040/190_hydrogen765s_thumb.png)
![ψ[7, 6, 5]の電子雲(3次元)](gazou_home040/190_hydrogen765t_thumb.png)
![ψ[7, 6, 6]の電子雲(x-z断面)](gazou_home040/190_hydrogen766s_thumb.png)
![ψ[7, 6, 6]の電子雲(3次元)](gazou_home040/190_hydrogen766t_thumb.png)