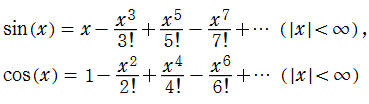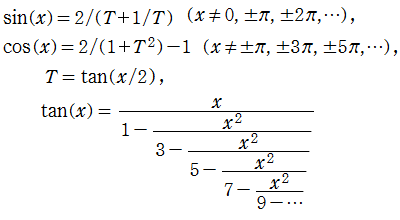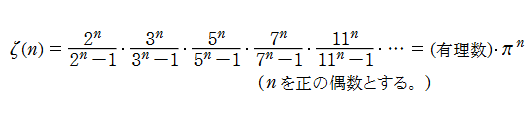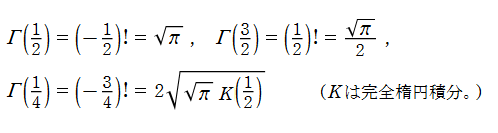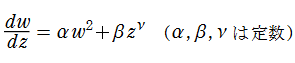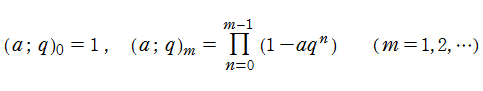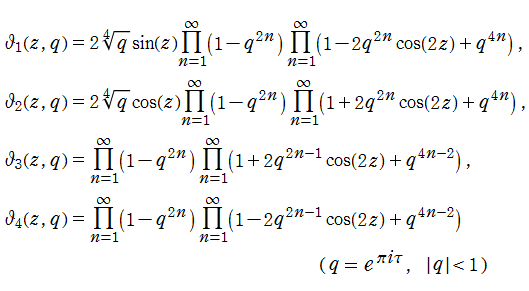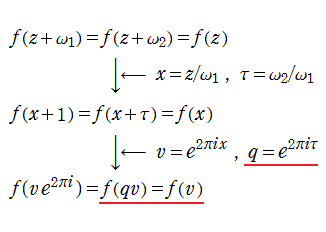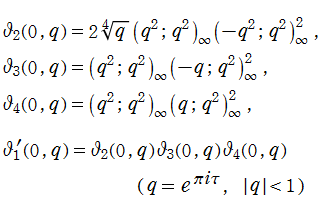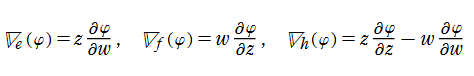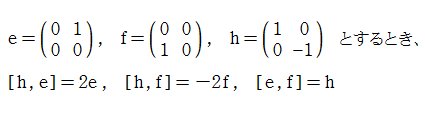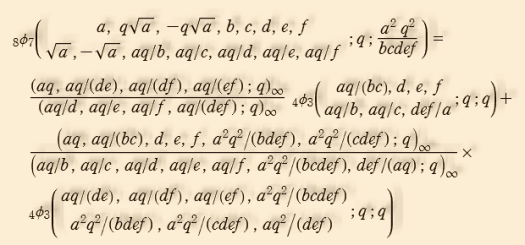特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
Home Menu
特殊関数 概説
ガウスが進んだ道は即ち数学の進む道である。その道は帰納的である。特殊から一般へ! それが標語である。(高木貞治 「近世数学史談」)
できあがった数学理論は、試行錯誤や帰納の苦汁を、いっさい取り払い、演繹的に美しく構成される。しかしそれは、真に新しいものを産み出さない。
具体性 ― それこそが真の独創をはらんでいる。(難波 誠 「複素関数 三幕劇」)
できあがった数学理論は、試行錯誤や帰納の苦汁を、いっさい取り払い、演繹的に美しく構成される。しかしそれは、真に新しいものを産み出さない。
具体性 ― それこそが真の独創をはらんでいる。(難波 誠 「複素関数 三幕劇」)
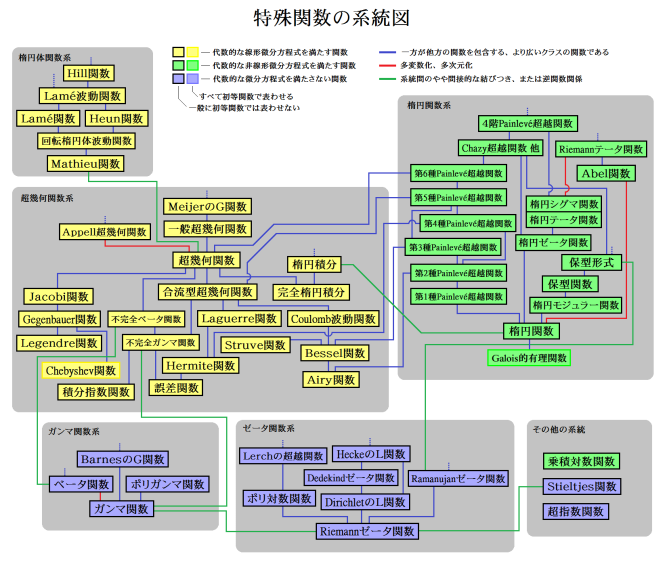
特殊関数の系統図
(注1)q-特殊関数、楕円特殊関数はこの系統図に含めていない。また、初等関数との関係も省略している。
(注2)当然ながら、この図とは異なる見解に基づいた様々な系統図が存在する。
(注2)当然ながら、この図とは異なる見解に基づいた様々な系統図が存在する。
「このうち要となる特殊関数は?」
出現頻度、理論の発展性、現代数学への影響なども考慮すると、個人的な選定では、
3大特殊関数 : 超幾何関数 ,保型形式 ,Riemannゼータ関数
5大特殊関数 : 3大特殊関数 + Abel 関数 ,Painlevé 超越関数
になると思いますが、どうでしょう?。5大特殊関数 : 3大特殊関数 + Abel 関数 ,Painlevé 超越関数
「楕円体関数系は馴染みがないですが?」
楕円体関数系は、Bessel 関数や Legendre 関数と同じく、主に曲面座標での変数分離によって生じる特殊関数ですが、様相が複雑なため(狭義では)特殊関数に含めないことも多々あります。 逆に、楕円体関数系にも触れている特殊関数の書籍は、かなり専門的と見てよいのかもしれません。
特殊関数とは?
数学の「関数」といえば、普通は指数関数や三角関数などが思い浮かぶ。これらは一般に「初等関数」という枠組みでまとめられ、しばしば特殊関数と対比される。日本の(現在の)中等教育課程までに現れる関数はすべて、この初等関数の範囲内である。(一変数の)初等関数を分類的に示すと、次のようになる。
初等代数関数
→ 初等整関数(多項式),有理関数(分数関数),無理関数
初等超越関数 (「超越」とは、「代数的であることを超えている」の意味がある。)
→ 指数関数,対数関数,三角関数,逆三角関数,双曲線関数,逆双曲線関数
一方、「特殊関数」は高等教育(大学)課程でなければ現れないため一般に馴染みは薄い※1。最近はあまり使われなくなった別名の「高等超越関数」(英:Higher
Transcendental Functions)であれば、さらに「特殊」で近寄り難い印象を受ける。→ 初等整関数(多項式),有理関数(分数関数),無理関数
初等超越関数 (「超越」とは、「代数的であることを超えている」の意味がある。)
→ 指数関数,対数関数,三角関数,逆三角関数,双曲線関数,逆双曲線関数
しかし実際は、「初等関数ほど頻繁ではないが、初等関数に続いてよく現れる関数」というのが、特殊関数のもっともらしい説明であり※2、初等関数から孤絶した高等な存在ではない。
例えば、教科書や技術書などで、「三角関数表」を見たことのある人は多いと思う。変数
の有限項までの和、つまり多項式で近似しているのである※3。実は特殊関数も、計算法やその理論的背景は多くの場合、初等関数と共通で、単に見かけが複雑なだけである場合が多い。
また時折、「特殊関数とは、初等関数に四則演算や合成を施しただけでは表わすことができない関数」との説明がなされるが、これは部分的に正しくない。なぜなら、Chebyshev 関数のように、いかなる場合でも初等関数のみで表わせるが、特殊関数として広く認知されている関数が含まれているからである。したがって単純に、特殊関数は初等関数の対義語としての意味だけに留まらない。
特殊関数が「特殊」である所以は、むしろその「有用性と特異性」にあるだろう。それを、応用数学的な観点と、純粋数学的な観点から見れば、以下のようになるだろうか?。
【註記】
※1:高校数学の 「統計処理」 で現れる正規分布に従う確率の数表 「正規分布表」 は、本質的に誤差関数の数表でもあるという意味では、高等学校でも特殊関数との接点がある。(ただし、それが既知の関数で表わせない事は、簡単な言及のみで終わると思うが。)
※2:しかしながら、このサイトでは「ほとんど現れない」関数についても、いくつか取り上げている。
※3:実際には、もっと効率的な方法で得られた値かもしれない。例えば、次の連分数を用いる計算法は、冪級数近似よりも速く収束する (複素変数の場合も、冪級数より扱い易い)。
(因みに、当サイト管理人は初めて三角関数 (三角比) の数表を見た時、「これは広大な平地に巨大な直角三角形を作図して実測したに違いない…」 と思っていました。)
※1:高校数学の 「統計処理」 で現れる正規分布に従う確率の数表 「正規分布表」 は、本質的に誤差関数の数表でもあるという意味では、高等学校でも特殊関数との接点がある。(ただし、それが既知の関数で表わせない事は、簡単な言及のみで終わると思うが。)
※2:しかしながら、このサイトでは「ほとんど現れない」関数についても、いくつか取り上げている。
※3:実際には、もっと効率的な方法で得られた値かもしれない。例えば、次の連分数を用いる計算法は、冪級数近似よりも速く収束する (複素変数の場合も、冪級数より扱い易い)。
(因みに、当サイト管理人は初めて三角関数 (三角比) の数表を見た時、「これは広大な平地に巨大な直角三角形を作図して実測したに違いない…」 と思っていました。)
数理物理学に不可欠な「道具」
特殊関数が自然科学、特に物理学において「使える」ということが、特殊関数が現在まで命脈を保ち、多彩な世界を形成するうえで、常に原動力となっていた。逆に、物理学等での示唆や必要に応える形で、新しい特殊関数が産み出されるというプロセスも、また常に存在した。Bessel 関数や Legendre 関数の起源は、全く物理学からの派生であるし、Mathieu 関数が物理学と無関係な、純粋数学で応用されるような例は極めて少ない。微分方程式は、特殊関数の存在意義を保証する母胎のひとつである。自然や社会の現象などを科学的に捉えようとするとき、多くの場合で微分方程式は避けて通れない。その解は、時間などの物理量を変数とする関数になる。科学者等は18世紀以降、その解が初等関数で表わされない場合、特殊関数に帰着させようと努め、あるいは新しい特殊関数を導入した。現在では電子計算機の出現によって、微分方程式の解を直接数値的に求められるようになったため、特殊関数の重要性は若干減ったとも言われている。しかし、解を具体的な関数で表わすことができれば、その解の構造や性質を理解するうえで、より明快な手がかりを得たことになる。よって、特殊関数は依然として重要な「道具」なのである。
物理学には、特殊関数と密接な関係にあるものが二つある。
一つは偏微分方程式、特に Laplace 方程式や Helmholtz 方程式を、三次元空間の曲面座標系の各成分に変数分離して解く方法である。この場合、超幾何関数系や楕円体関数系の特殊関数が現れる。この方法は非常に有用で、物体の振動、電磁波の伝播と散乱、回転流体の平衡形状など、古典的な物理問題の多岐に及ぶ。
もう一つが量子力学で、特殊関数の重要性をさらに確固たるものにする。最もよく知られた例は、簡単な条件下での Schrödinger 方程式の解(波動関数)が、Hermite 関数や Laguerre 関数、球面調和関数によって表現できることである。
調和と神秘を体現する「数学的実在」
前述に反して純粋数学では、個々の理論や数学的対象物が実世界において「有用である」ことよりも、数学世界の中で、それ自体が調和や均整に満ち、時として驚くような意外な結びつきを垣間見せるということに重点を置いた探求がなされる。いわゆる「数学のための数学」という色彩が強くなる※1。特殊関数は、ここでも個性的かつ印象的な立ち現れ方をする。逆に、特殊関数が新しい理論を産み出し、その後の発展に決定的な影響を与えることさえ少なくない。その最たる分野は数論である。そのような例の多くは、その深遠さを正確に述べようとするならば難解な理論を必要とするので、到底私の及ぶところではない。二三の断片的な数式によってその雰囲気を示すに留めようと思う。
多くの人が認めるように、ガンマ関数やゼータ関数は「汲み尽くせない不思議」に満ちている。例えば、L. Euler が発見した、次の素数列からなる無限乗積は、円周率と関係する。
また、分数のガンマ関数値(つまり整数でない階乗!)は、円周率や楕円積分の値と関係する※2。
19世紀初頭、C. F. Gauss は算術幾何平均から延びる 「特殊関数の鉱脈」 を知っていた。それは以後、約60年間の数学を予見するものであった。
解析的整数論、代数幾何学など現代数学の成立に至る過程では、このような美と神秘を湛えた式や関数から多くのインスピレーションを受けている。特殊関数は、これからも新しい数学の源泉となり続けるに違いない。
【註記】
※1:それが「実生活で役に立たない」とは限らない。遠い将来、有用になる可能性もある。
※2:当サイトでは、楕円積分の母数は Mathematica に準拠しているため、この場合の完全楕円積分の引数は1/2となるが、大抵の公式集等では、これの平方根で表記されている。その次の Gauss の式も全く同じ理由から、変数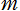 は
は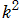 で表記されることが多い。
で表記されることが多い。
* * *※1:それが「実生活で役に立たない」とは限らない。遠い将来、有用になる可能性もある。
※2:当サイトでは、楕円積分の母数は Mathematica に準拠しているため、この場合の完全楕円積分の引数は1/2となるが、大抵の公式集等では、これの平方根で表記されている。その次の Gauss の式も全く同じ理由から、変数
特殊関数の歴史
数学も、人類が築き上げた数々の文化の一つであり、長い歴史を有している。近年、数学自体もさることながら、「数学史」にも注目が集まっている。科学館や博物館での数学をテーマにした催事が予想以上に好評を博するのも、数学が単に学術や技術に留まらず、文化的・歴史的な話題を多く持っていることにも一因があるのだろう。「和算」への関心も、全くこの流れに沿うものと言える。今や数学の諸分野は複雑かつ広大になっており、数学者のような専門家であってもその全貌を掴むことが次第に難しくなりつつある。しかしながら、数学は一見すると無関係に思える分野間に、想像を超えた繋がりが発見されることがあり、またそれを目標の一つにしながら数学者等は研究をおこなっているので、専門外の分野についても歴史的経緯や現在の内容に精通するよう求められる。それゆえ、数学史は数学科のカリキュラムとして以前より重要視されるようになった。
特殊関数の歴史は、(それが明確に意識されるようになって以降という意味では) かなり短いが、近年であるということもあって、比較的詳しく伝えられている※1。以下では、その大まかな歴史を示そうと思う。
前史:断片的成果と微積分学の創始
中世から近代の時期は、まだ特殊関数は本格的に姿を現していない。特殊関数に繋がる断片的な成果ならば、いくつかが知られている。特に円周率などの数学定数や、特定の図形の面積・体積を無限級数で表わすことは古くから行われてきた。例えば、14世紀に N. Oresme は無限調和級数が発散すること、すなわち
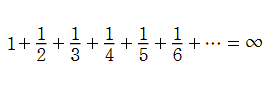
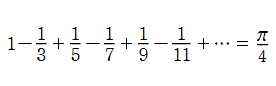
また、16~17世紀になると、自然現象等を司る法則を記述するための言葉として、数学が用いられるべきとの思想が流布し、その有効性がまず天体力学で示された。1609年に J. Kepler が解明した惑星の楕円軌道の理論はその最たる事例であるが、後に Kepler の方程式と呼ばれる超越方程式がそこから現れた。その解は初等関数に還元不能であり、18世紀以降に進展する研究で特殊関数に繋がる。
一方、特殊関数を考える上で基礎的な道具立てとなる座標や関数概念は、この 「前史」 から始まっている。R. Descartes は1637年の著書 「方法序説」 の中で、二つの実数値の組を平面上の点として表示する方法に触れており、一般にこれが座標の創始とされる。以降、数式や関数が曲線などの図形と結びつくことで、代数学や幾何学が飛躍的に理解しやすくなった。計算実務上の道具としての対数や三角比は、古くから (対数は16世紀末から、三角比は紀元前100年頃?から) 利用されてきたが、これらを単なる演算規則と見るだけでなく、複数の連動して変化する量の関係を表わしていると見る 「関数概念」 が、17世紀頃からはっきりと意識されるようになった。実際、Leibniz はこの関数 (概念) を指す言葉として、ラテン語の 「functio (機能)」 を初めて用いた。西洋数学が座標や関数概念に到達できた事こそが、後の微分積分学の発展を決定的にし、延いては自然科学全盛の時代を準備したと言っても過言ではない。
微分と積分は、別々の概念として既にいくつかの研究成果が得られていたが、1650年頃から 「微分積分学の基本定理」 が現れて、微積分演算がより容易に実行できるようになり、それまでの数学が一新されることとなった。1690年代になると、微分方程式に関する論文が C. Huygens,Leibniz,Jak. Bernoulli 等によって発表されるようになった。同じ頃 Joh. Bernoulli は、微分積分学を応用して種々の曲線の長さを求めていた。これは次世紀の楕円積分の研究へと繋がっていく。
18世紀:「大陸学派」の貢献
Leibniz の記号哲学が良かったこともあって、微分積分学はイギリスよりも次第にヨーロッパの大陸側で発展した (それでも、階乗関数や調和級数の漸近近似 (J. Stirling:1730年)、後述の冪級数解法などは、非大陸側の数学者による寄与が大きい)。特に17世紀以来、Bernoulli 家は代々数学者を輩出し、解析学とその物理学への応用で貢献が著しい。特殊関数では D. Bernoulli が重い鎖の微小振動の解析から初めて Bessel 関数を、惑星などの回転楕円体における重力の問題から Legendre 関数 (に繋がる) を研究している。また、L. Euler はこの時代における最大と言ってもよい数学者で、数学や物理学に与えた影響は計り知れない。特殊関数に限っても、ガンマ関数、超幾何関数を発見し、後に Riemann が名付けたゼータ関数について先駆的な研究をおこなった。後述の楕円積分も同様である。18世紀の初期には既に、簡単な微分方程式であっても解が初等関数で表わせない場合が多いことに、数学者等は気付き始めた。J. F. Riccati が1722年に発見した 「Riccati の微分方程式」
もそのような例である (後年、この解は Bessel 関数で表わせることが判明する)。特に物理学から、応用上重要な2階線形常微分方程式が多数生じたが、その解を冪級数で求める「級数解法」がこの時代から整備され始め、特殊関数が初等関数の延長線上にあるものとして受け入れられる一助にもなった。解を漸近級数で表わすことも盛んになり、大きな変数に対する数値計算にも道を開いた (現在では、この級数解法およびその周辺理論を(狭義の)特殊関数論と呼ぶこともある)。
Fourier 級数論の萌芽もこの時代に見出せるが、当時はまだ級数の収束性に充分な注意が払われておらず、関数や実数の連続性についても理解が曖昧であったため、具体的な事例の研究に留まり一般論の展開には無理があった。Fourier 級数の厳密的な扱いへの第一歩は、19世紀前半にもたらされることになる。
1733年に A. de Moivre は二項分布の極限として正規分布を初めて論じ、誤差関数を扱った。これは、16~17世紀以来発展し続けてきた確率論に、微分積分学の手法を援用する流れを作り現在に至っている (そのため今では、確率論は解析学に含まれる)。
G. C. Fagnano は、Bernoulli 家による曲線の長さの問題に興味を抱き、1715~1750年の間に得られた成果をベルリン科学アカデミーに送付した。これは1751年12月23日に Euler の関心を惹き、楕円積分の加法定理の証明に繋がる (後に C. G. J. Jacobi は、この日を「楕円関数の誕生日」と称した)。しかし、Euler はこれの逆関数を考察することに着手しなかったため、楕円関数の発見は19世紀に持ち越された (1797年、19歳の Gauss は既に楕円関数を知っていたが、結局公表しなかった)。
18世紀の数学者を、特殊関数論への影響力の大きさで挙げたとき、前半が Euler ならば、後半は P. S. Laplace になるかもしれない。1780年に彼が導入した Laplace 変換は、特殊関数に対しても多くの積分表示式を与えることとなり、また Laplace は、確率論に関連して不完全ベータ関数を研究している。さらには、天体力学における重力ポテンシャルの研究から現れた Laplace 方程式は、その解 (調和関数) が具体的な境界条件のときに超幾何関数系および楕円体関数系の特殊関数となり、19世紀の大量発見をもたらす一因になる。
19世紀:最大の発展期
前述のとおり、19世紀初頭になると一般的な Fourier 級数が研究されるようになったが、その収束性等を初めて厳密に論じたのは J. P. G. L. Dirichlet であった。さらにこの時代、三角関数以外の固有関数列に級数展開される場合にも拡張され、直交関数系の理論や積分変換論が生じた。これらは、現在でも特殊関数を支える基礎理論として欠かすことができない。しかし特殊関数史に限れば、19世紀は1827年の楕円関数の発見によって始まったと言える。なぜなら、N. H. Abel と Jacobi によるこの発見は当時の数学界を驚嘆させ、19世紀数学の方向性をある程度決定付けた出来事だったからである。これは、依然として懐疑的に見られていた複素数の存在が次第に認知される機会を与えるとともに、複素数を積極的に微分積分学に導入した「複素解析学」が A. L. Cauchy 等によって確立されるのを後押しした。同時に、級数の収束性や無限大の扱い等について微分積分学が厳密化されるなど、周辺分野に与えた影響が大きかった点でも意義深い出来事であった。
楕円関数の多変数化すなわち Abel 関数を求めることは、既に Abel と É. Galois が重要な示唆を与えており、19世紀数学の主要な問題であり続けた。その過程で登場した、Riemann 面による位相幾何学的な見方、様々な曲率を持つ曲面を抽象的に扱う多様体論は、複素領域における代数関数の多価構造について本質的な理解をもたらした。
同じように楕円モジュラー関数、保型関数も楕円関数から派生して、複素解析学など当時の新しい数学理論の威力をいかんなく発揮する分野となった。これらの楕円関数的な特殊関数は、その二重周期性や保型性に着目した群論的アプローチが F. Klein によって整理され、彼が1872年に示した指針「エルランゲン・プログラム」は、変換群に基づいた幾何学への刷新を促した。
特殊関数の数論への応用では、Dirichlet と G. F. Riemann の寄与を忘れてはならない。特に Riemann は1859年、ゼータ関数と素数との結びつきを明らかにしたうえで「Riemann 予想」を提起した。これは、前述の保型関数が代数的整数論に深く関係するのに対して、解析的整数論のあらゆる研究課題に関係している。
複素領域における線形常微分方程式の大域的な理論が充実したのもこの時代である。ここでは超幾何関数が中心的役割を演ずる。2階線形常微分方程式の2つの基本解からなる線形結合式の係数を決定するために、モノドロミー群などの理論が導入されて、解の多価性が明確に説明できるようになった。同時に、線形常微分方程式をその特異点から分類・理解することが、L. I. Fuchs,G. G. Stokes 等によって推し進められた。H. Poincaré は、一般的な線形常微分方程式がその2基本解の比の逆関数によって生じる保型関数で統制されることを示した(1881~1884年)。
時代に合うように特殊関数の各論を洗練することも、19世紀の多くの数学者の関心事であった。また、膨大な種類に増えた特殊関数を鳥瞰し、互いに帰着できるものを統合してその数を減らすよう努力した。その結果、現在「古典的特殊関数」と呼ばれる主要な特殊関数の一群は、19世紀末までにほぼ出揃った。その頃 E. T. Whittaker と G. N. Watson は、これらの成果を収集・編纂する作業に着手し、有名な書籍「A Course of Modern Analysis」を1902年に著した。
20世紀:深化と電子計算機の登場
19世紀的な意識、すなわち 「新しい特殊関数を発見する」 という動機は、20世紀に入って一段落しつつも、決して衰退することはなかった。数学者等は、前世紀以降に得られた線形常微分方程式の根幹を成す諸理論が、非線形常微分方程式にも拡張できないか模索し始めた。早速1900~1902年には、P. Painlevé 等が2階の場合について顕著な成果を得た。この結果の意義はすぐには理解されなかったが、1970年代に具体的な応用例が見つかり、その後は、可積分系や微分 Galois 理論等と関連しながら今なお発展し続けている。1913年、G. H. Hardy によって S. Ramanujan が 「発見」 され、世に明るみとなった数々の公式は、未知の関数がまだ多く存在することを強く示唆した。保型形式に関する新事実やモックテータ関数の発見は、まさに Ramanujan の金字塔と称するに相応しい。
20世紀はまた、ゼータ関数の研究が深化した時代である。まず19世紀終盤から、代数体のイデアル類の各種性質を解明する過程で Dedekind のゼータ関数が駆使されていたが、これは1920年、高木貞治による類体論の完成を見ることになった。このような成功例もあって、ゼータ関数は数学の諸問題解決の究極的な鍵と見なされ、それゆえに膨大な数のゼータ関数が定義されている。そのうち、有限体上の代数関数体に対する合同ゼータ関数、および特殊線形群の素な共役類全体をわたる Euler 積で表わされる Selberg のゼータ関数は、20世紀中に Riemann 予想の類似が証明された貴重な例である。また、この時代を通じて研究が積み重ねられた楕円曲線に附随するゼータ関数は、記憶に新しい1995年の A. J. Wiles と R. L. Taylor による 「Fermat の最終定理」 の証明という成果をもたらした。
全般的に20世紀は、数学自体の抽象化が推し進められ、また後述の電子計算機の出現もあって、特殊関数は前世紀ほど重要視されなくなった。一方で、特殊関数も抽象的な理論に基づく解釈が試みられるようになった。例えば、Laplace 方程式から得られる作用素の対称性を Lie 群で表現し、これを超幾何関数系の特殊関数の統一的扱いに適用した例や、量子群が持つ非可換性によって初めて q-特殊関数の真の性質が把握された例などがある。後者からは q-超幾何関数系の直交多項式が新たに多数得られ、組合せ論と特殊関数論との間に太い水脈が通じた。
20世紀を通じて概ね純粋数学が持て囃された傾向があったが、1980年代になると反動のように数理物理学が脚光を浴びるようになり、ゲージ理論や超弦理論等では保型関数・保型形式を応用して研究に一定の進展が見られた。これが刺激となって、(用いる理論は新しいが) 特殊関数をメインに扱う論文も再び増えつつある。また、一部の数学者に 「古典愛好」 が支持され、数学史研究の隆盛とも相俟って、特殊関数を見直す動きが更に加速している。この特殊関数の 「復権」 は、21世紀初頭になっても続いている。
計算機の構想は古くから存在したが、20世紀中葉になると電子計算機が実現して、人類の計算能力を指数関数的に高めていった。1950年代頃までは、特殊関数の計算の多くは大型汎用計算機を用いた数表作成という国家プロジェクトであり、その目的は主にレーダーの性能向上などの軍事であった。そこで得られた新しい計算法や数表は徐々に民間にも浸透し、1964年にはアメリカ合衆国国立標準局 (現:国立標準技術研究所) の M. Abramowitz と I. Stegun によって 「Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables」 が編集・出版された※2。この参考書は計算を必要とする科学者等にとって必携の書となった。
当サイト管理者が所蔵する 「A&S」 の写真 ※3。
その後、電子計算機が次第に身近になってくるとともに、誰もが数値計算や数式処理をおこなえる汎用ソフトウェアや小型計算機が登場し、数学を 「紙と鉛筆だけの学問」 と呼ぶ事実は過去のものとなった。数学も他の自然科学と同様に、個々の事例を具体的に検証することが可能となり、「計算科学」 や 「実験数学」 なる言葉も造られる程になっている。
【註記】
※1:下記URLでは、特殊関数の歴史についての詳しい解説、例えば、当サイトが触れなかったロシアでの状況等について記述がある (ただし英文。また後半は Mathematica における特殊関数の歴史になっている)。
Stephen Wolfram.com 「The History and Future of Special Functions」
※2:現在、その内容はインターネット上で自由に閲覧できる。例えば、Link 集に掲載している C. B. Macdonald 氏のサイトから、オンライン閲覧またはPDF版のダウンロードが可能である。
※3:A&S自体は、米国ではパブリックドメインとなっていますが、上記写真は Dover社による商業出版社版を撮影したものであるため、念のため拡大表示は控えます。
* * *※1:下記URLでは、特殊関数の歴史についての詳しい解説、例えば、当サイトが触れなかったロシアでの状況等について記述がある (ただし英文。また後半は Mathematica における特殊関数の歴史になっている)。
Stephen Wolfram.com 「The History and Future of Special Functions」
※2:現在、その内容はインターネット上で自由に閲覧できる。例えば、Link 集に掲載している C. B. Macdonald 氏のサイトから、オンライン閲覧またはPDF版のダウンロードが可能である。
※3:A&S自体は、米国ではパブリックドメインとなっていますが、上記写真は Dover社による商業出版社版を撮影したものであるため、念のため拡大表示は控えます。
q-特殊関数・楕円特殊関数とは?
「q-特殊関数」とは非常に大雑把に言えば、通常の特殊関数に文字これは「q-シフト因子」または「q-Pochhammer 記号」と呼ばれるもので、極限
q-特殊関数の萌芽は、L. Euler による分割数の研究などに見られるが、前述の観点は19世紀の Jacobi 辺りから始まっている。しかし、q-特殊関数がどのような数学世界を背景にしているのかについては不明であった。ところが1985年頃に、神保道夫と V. G. Drinfeld によって量子群の理論が導入され、曖昧であった q-解析学や q-特殊関数の本質が解明された。
*******
しかし、大多数の人が抱くもっともな疑問は、むしろ「なぜ q-何々と呼ぶようになったのか?」, 「なぜ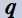 は楕円テータ関数から
は楕円テータ関数から
実は、ある通常の特殊関数でも前述の q-シフト因子が頻繁に現れる。それは楕円テータ関数である。Jacobi は楕円テータ関数を無限乗積で定義した。Jacobi はこのとき、助変数も上記のとおり
この助変数
と解釈される。このとき、最後の式は乗法的な差分方程式で、「q-差分」の起源でもある。
一方、
これはまた楕円モジュラー関数にも繋がり、多くの深遠な数学理論を生むこととなった。
つまり、もし Jacobi が
人を魅了する文字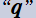
Jacobi がQから始まる英単語は他に比べるとかなり少ない。その中に
quaint : 風変わりで面白い, quest : 探求, quantum : 量子, quasi-☆ : ☆の類似, quintessence : 真髄, quotation : 引用
など。因みに、量子群は q-特殊関数の約150年後に登場したので、Qで一致するのは恐らく偶然であろう。欧文において、もともとQの出現頻度が低いということは、言いかえれば文章中で「気になる存在」に映るということではないだろうか?。もしこれが正解であれば、数式においても同じことが言えるかもしれない。新しい数学を言い表わす時に、どのような記号や文字を用いるかによって、重大な違いを生むことがある。I. Newton が採用した微分積分学の記号はいくつかの欠点があったため、その後しばらくの間イギリスで数学が停滞する一因となった。その意味で、Jacobi の選択は(結果的にせよ人々に受け入れられたので)良かったことになる。(もっとも、数字の9と見間違えやすいとの反論もありそうだが…。)
人は無意識のうちに
It's a  World
World
あらゆる q-特殊関数が住むという「量子群」とは、一体どのような世界なのであろうか?。難解な現代数学の一分野であるため、詳細は当サイトのレベルを遙かに超える。上野喜三雄氏が、月刊誌「数学のたのしみ」No.2 (1997年8月)に掲載した論文「q 解析学と量子群」において、量子平面などの例を用いて分かりやすく解説している。以下では、その内容を参考にしつつ(それでも不完全に理解したうえでの)説明をしたい※1。
【註記】
※1:実際は、説明と言える内容には程遠いと思うので、量子群についてもっと正確な情報が必要な場合は、前述の上野氏の論文をはじめ、種々の文献等をご覧になることをお勧めします。下記の楕円量子群についても同様です。
※1:実際は、説明と言える内容には程遠いと思うので、量子群についてもっと正確な情報が必要な場合は、前述の上野氏の論文をはじめ、種々の文献等をご覧になることをお勧めします。下記の楕円量子群についても同様です。
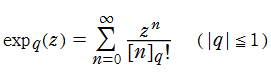
と定義される。q-指数関数は q-微分(実質は乗法的差分)
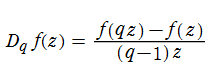
しかし、数学者とは恐るべき自由人である。逆に、指数法則を満たすように
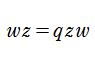
これを、現在では(後述の「量子群」が背景にあるので)「量子平面」と呼ぶ。
【註記】
※1:しかしながら当サイトでは、q-特殊関数のグラフはすべて、通常の数を変数とする関数として描画する。既に述べたように、歴史的には q-特殊関数は通常の関数として始まったからである。
(そして本当の理由は、「非可換変数関数など描ける訳がない!」。)
※1:しかしながら当サイトでは、q-特殊関数のグラフはすべて、通常の数を変数とする関数として描画する。既に述べたように、歴史的には q-特殊関数は通常の関数として始まったからである。
(そして本当の理由は、「非可換変数関数など描ける訳がない!」。)
数学者(だけが入れる?)の遊園地
あまりにも直前の話は奇妙すぎてローラーコースターのように目眩がしそうだが、いよいよこれに確固たる理論付けがなされる。「量子群」の登場である。まず「量子」であるが、察しが付くように、これは「量子力学」のことである。複数の演算子
この
ところで、
は、各々
これと同じ代数構造は、3種類の行列を用いて
と言いかえることができる。これは Lie 群
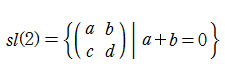
量子平面
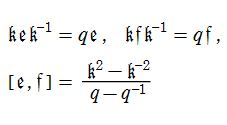
複雑な q-級数の例 (Bailey's Transformation)
「特殊関数の差分化 楕円関数風に…」
非常に曖昧な説明になるが、「楕円特殊関数」とは、q-特殊関数において度々現れるこれは、1968~1971年に導入された Yang - Baxter 方程式(関係式)の解に示唆を受けて考え出されるようになった関数で、代表的な例は、1997年に I. B. Frenkel と V. G. Turaev が定義した「楕円超幾何関数」である※1。
また1985年頃に登場した量子群は、Yang - Baxter 方程式の三角関数解との関連が指摘されると、ただちに量子群の楕円関数化すなわち「楕円量子群」への拡張が試みられるようになった。神保道夫、今野 均など、多くの日本人数学者が組織的な研究を進めており、今後が期待される。
近年、世界的に注目が集まっている Painlevé 方程式に平行して、q-Painlevé 方程式や楕円差分 Painlevé 方程式などへの関心も高まっている。ここでも日本人数学者の寄与が著しい。
これらの分野はまだ非常に新しくて、不明な点も数多く残っているようである。また、関数の定義も数学者によって微妙に異なる場合が多く、内容はやや流動的な感がある。
【註記】
※1:このサイトでは、まだグラフの描画は実現していない (将来、追加するかもしれない)。
※1:このサイトでは、まだグラフの描画は実現していない (将来、追加するかもしれない)。
「三角関数の次は楕円関数」という "お約束"
Yang - Baxter 方程式や楕円量子群についても正確な説明は到底無理なので、今回も、ごく簡単に仄めかすような記述で済ますことをお許し願いたい。ある条件下で Yang - Baxter 方程式は行列解を持つが、その成分は、初等整関数、指数関数、楕円テータ関数のどれかを用いて表わされる。その一因として、それぞれの有理型関数、つまり初等有理関数、三角関数、楕円関数がいずれも代数的加法公式を持つことがあげられる。これらのうち三角関数行列解は、その代数的構造が量子群と関連している。そこで、これを包含し、より複雑な楕円関数行列解に対応する「量子群の楕円関数化」があるのではないか?、という発想に到達する。楕円量子群の研究はここから始まっている。
前述のように量子群は積の非可換性が根底にある代数系であるが、楕円量子群の定める代数系は更に複雑になる。今野 均の研究によれば、楕円量子群には「頂点型」と「面型」の2種類があるとのことである(これも説明は難しい…)。
ところで、超幾何関数、q-超幾何関数、および楕円超幾何関数の冪級数展開式を一括して
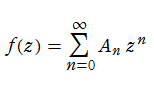
超幾何関数 → 実質的に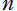 の初等有理関数になる。(既知)
の初等有理関数になる。(既知)
q-超幾何関数 → 実質的に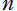 の三角関数になる。(既知)
の三角関数になる。(既知)
楕円超幾何関数 → 実質的に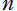 の楕円関数になる。(新しい)
の楕円関数になる。(新しい)
となるように楕円超幾何関数についても定義する。ここに、具体的な楕円特殊関数を得る指導原理が見出されたのである。Frenkel と Turaev の定義による楕円超幾何関数は、3番目の具体例のひとつであり、楕円量子群との関連性についても研究が進められている。q-超幾何関数 → 実質的に
楕円超幾何関数 → 実質的に
楕円関数への憧憬…