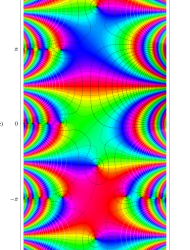
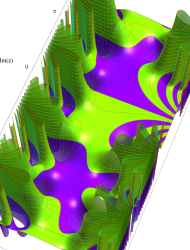
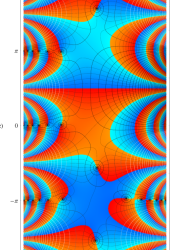
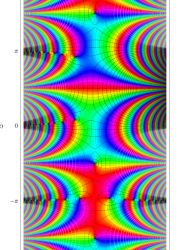
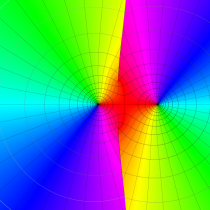
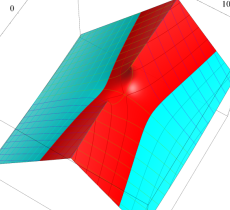
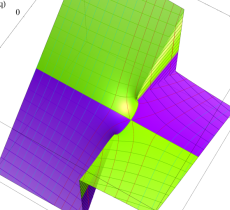
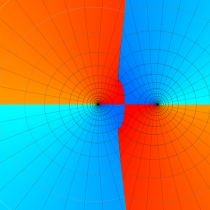
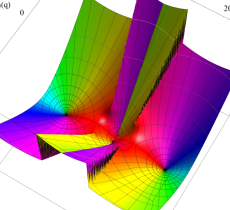
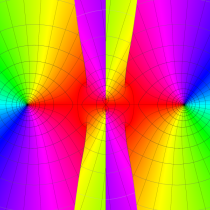
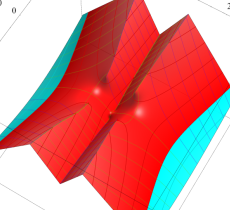
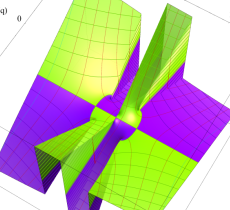
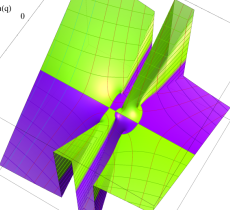
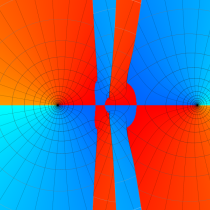
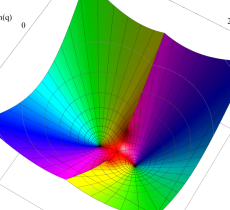
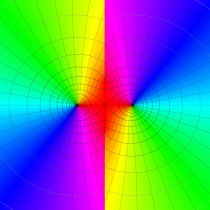
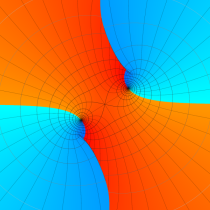
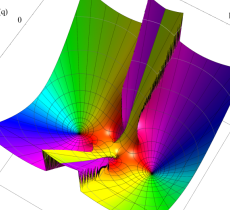
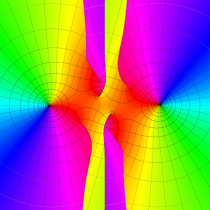
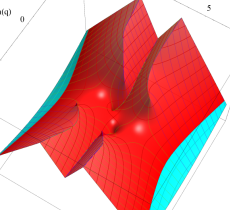
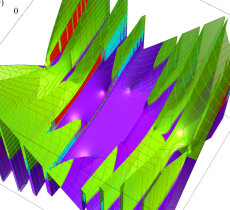
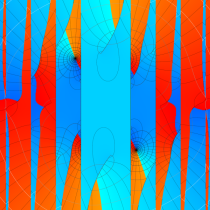
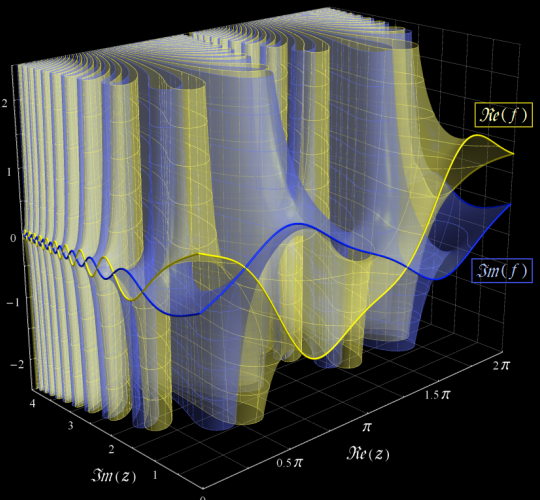
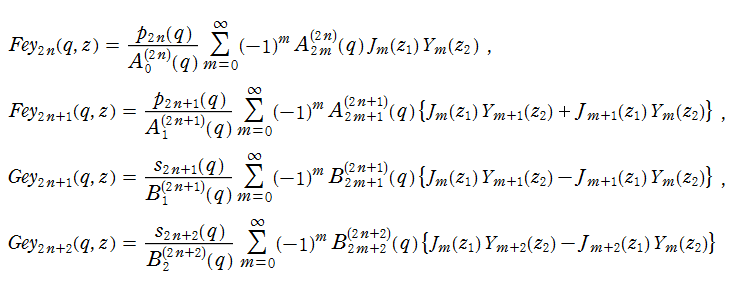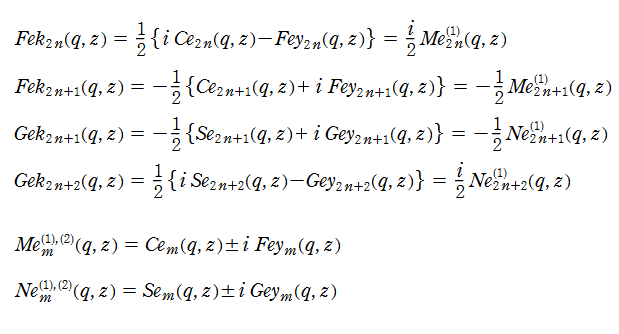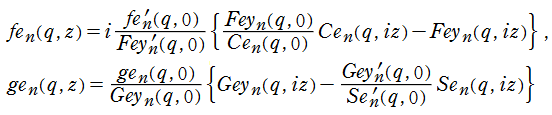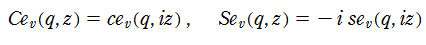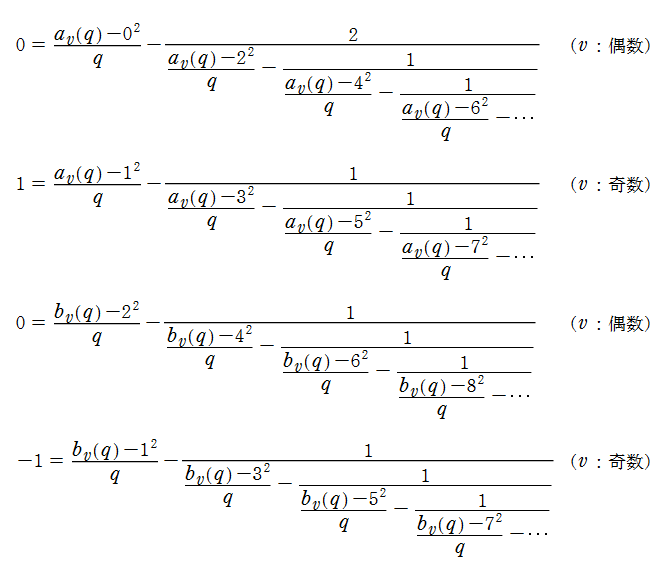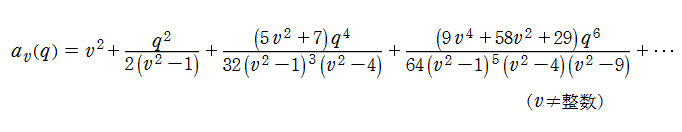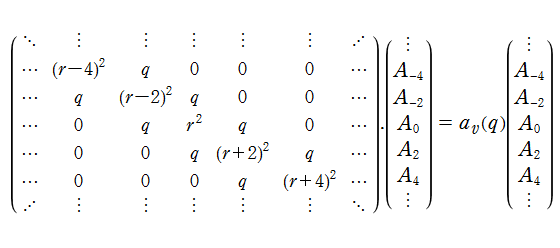特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
Mathieu 関数
Mathieu 関数
日:Mathieu関数,マシュー関数(マチウ関数)英:Mathieu function,仏:Fonction de Mathieu,独:Mathieusche funktion
Laplace の方程式または Helmholtz の方程式を楕円柱座標で変数分離すると、楕円成分・双曲線成分の満たす微分方程式は、それぞれ
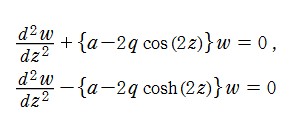
Mathieu の微分方程式は
に変形される。代数的な Mathieu の微分方程式は、
Mathieu の微分方程式は、より一般的な Hill の微分方程式
の特別な場合である。
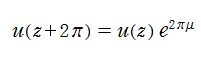
これを Mathieu の微分方程式に適用すると、二つの基本解の一方が周期
(整数次) 第1種 Mathieu 関数は、直交性
を有するので、任意の関数は (整数次) 第1種 Mathieu 関数の無限級数に展開できる。例えば、後述の (整数次) 第2種 Mathieu 関数をこの方法で定義する例があるが、詳細は省略する※1。
(整数次) 第1種 Mathieu 関数は周期関数であるため、次のような Fourier 級数に展開できる。
ここに、Fourier 係数
また、(整数次) 第1種 Mathieu 関数に対する非周期的な第2の基本解をそれぞれ
で表わされる。ここに Fourier 係数や定数
なお、非整数次
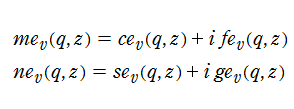
一般に Mathieu 関数は超越整関数のため、無限遠点のほかに特異点を持たない。代数的な Mathieu の微分方程式の解としての Mathieu 関数は、複素平面上
Mathieu 関数は楕円柱関数という別名があるとおり、楕円形膜の振動問題のように境界が楕円柱である場合などの物理問題に現れる。このほかにも電磁波の散乱現象など近年は応用面が増えつつあるが、Bessel 関数などに比べるとずっと少ない。それは Mathieu 関数の計算が複雑で取り扱いが難しいことにもよる。
Mathieu 関数をはじめ、回転楕円体波動関数、Lamé 関数、Lamé 波動関数等は、超幾何関数よりも高等な楕円体関数と呼ばれる系統に含まれる。しかし、超幾何関数系が、漸化式や隣接関係式などによって統制され、モノドロミー群が具体的かつ簡易な形で求められる等、比較的見通しの良い性質に基づいて纏められるのに対して、楕円体関数系は、全体を特徴付ける共通した性質が限られており、固有値の間隔によって次数が決まるため制約も多い。つまり、純粋数学的な観点から見れば、あまり "美しくない" とも言える※3。
【註記】
※1 : J. Meixner,F. W. Schäfke 著 「Mathieusche Funktionen und Sphäroidfunktionen」 の p.194 を参照。
※2 : 第2種用の Fourier 係数を求める他の方法として、N. W. McLachlan 著 「Theory and Application of Mathieu Functions」 の§7.50,§7.52,および§7.55 がある。
※3 : サイト管理人にとっては、好奇心をそそられる "素敵な" 関数の一群でもある。
※1 : J. Meixner,F. W. Schäfke 著 「Mathieusche Funktionen und Sphäroidfunktionen」 の p.194 を参照。
※2 : 第2種用の Fourier 係数を求める他の方法として、N. W. McLachlan 著 「Theory and Application of Mathieu Functions」 の§7.50,§7.52,および§7.55 がある。
※3 : サイト管理人にとっては、好奇心をそそられる "素敵な" 関数の一群でもある。
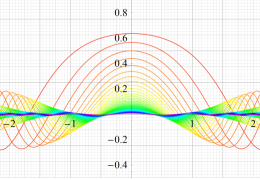
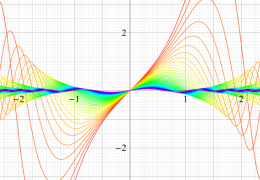
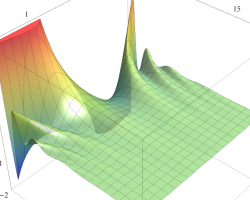
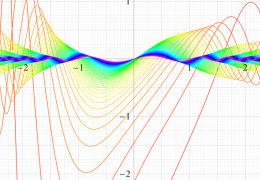
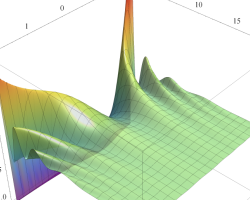
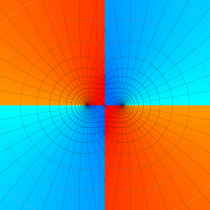
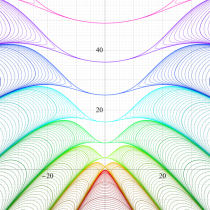
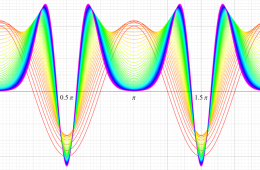
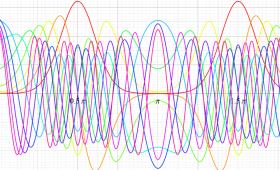
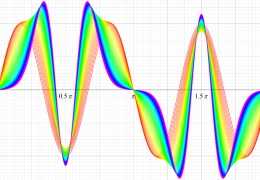
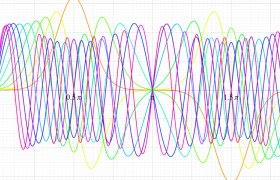
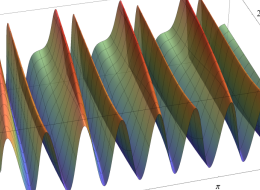
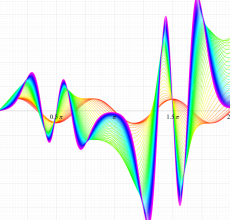
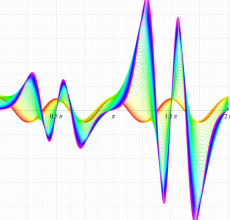
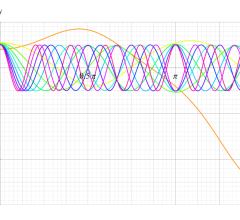
順に、①
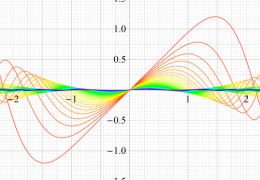
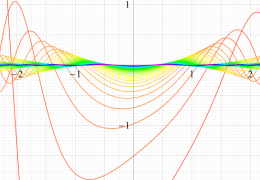
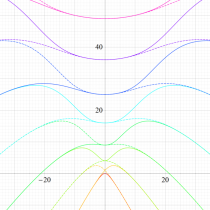
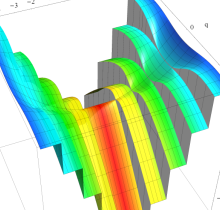
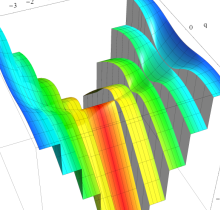
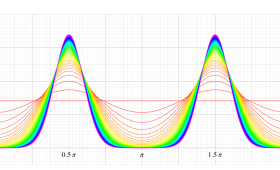
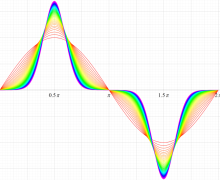
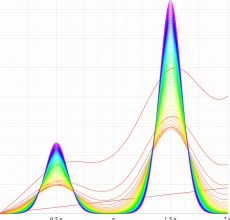
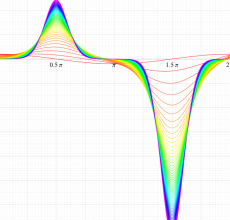
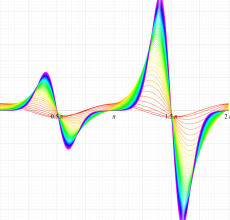
実変数の第1種 Mathieu 関数のグラフ。
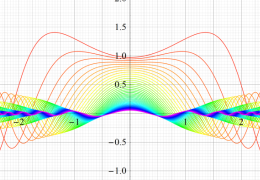
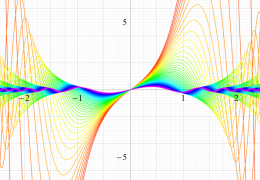
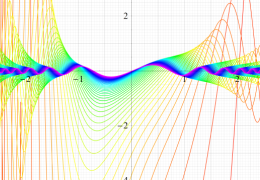
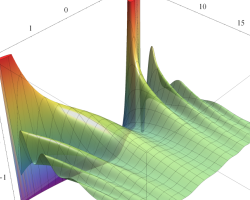
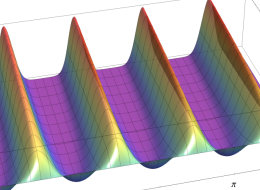
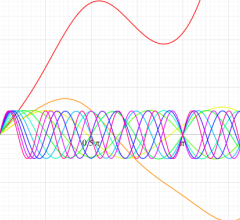
順に、①
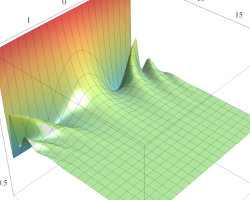
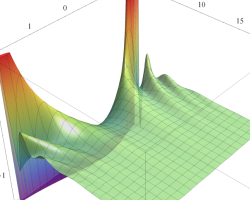
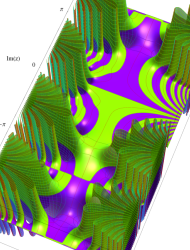
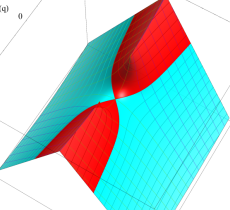
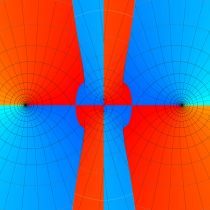
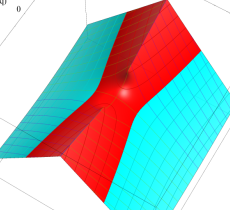
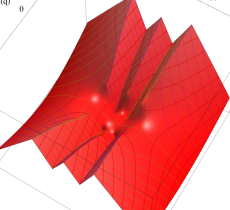
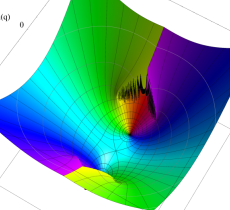
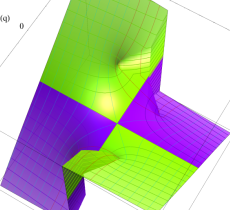
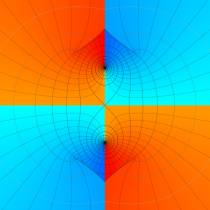
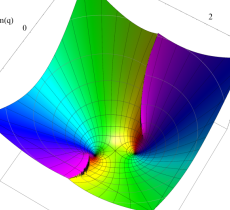
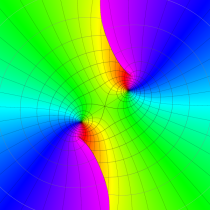
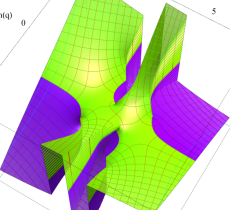
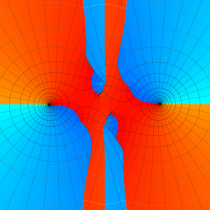
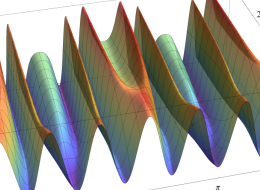
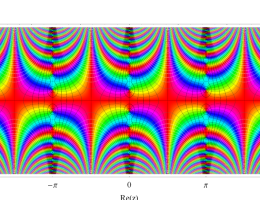
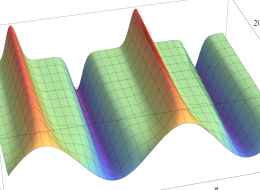
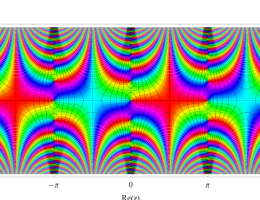
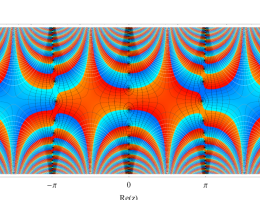
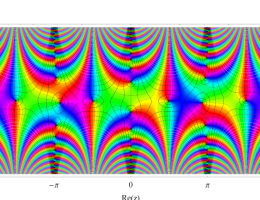
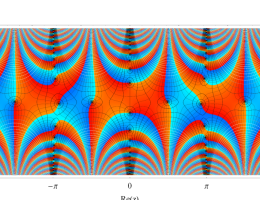
実2変数の第1種 Mathieu 関数のグラフ。順に、①
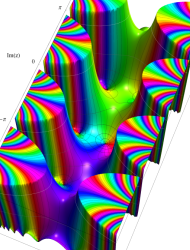
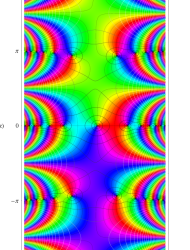
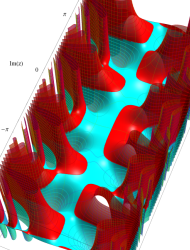
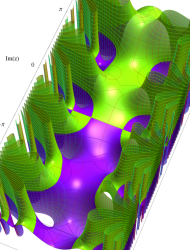
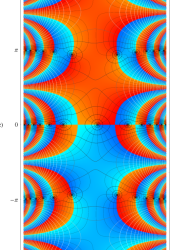
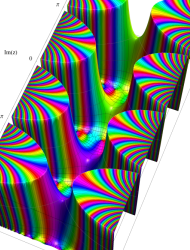
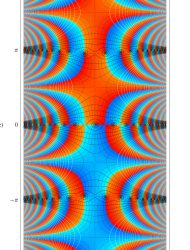
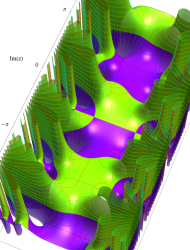
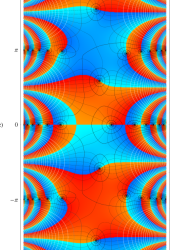
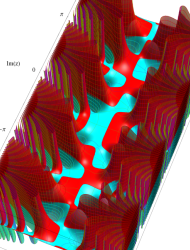
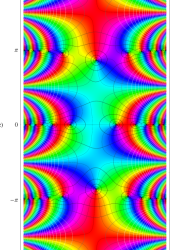
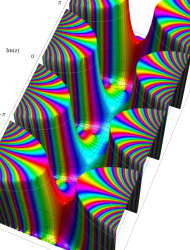
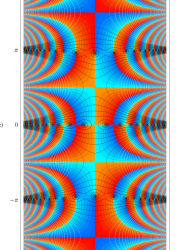
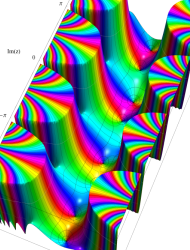
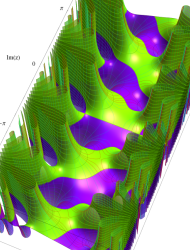
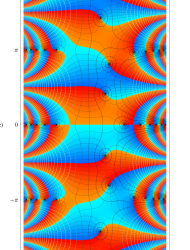
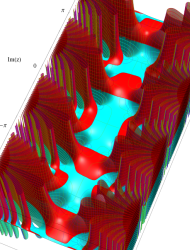
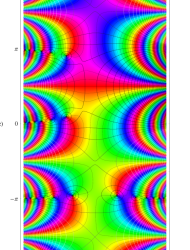
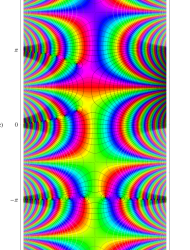
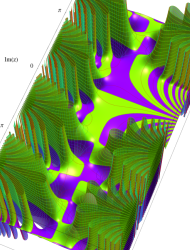
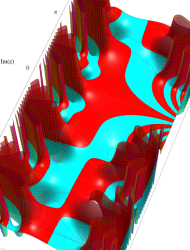
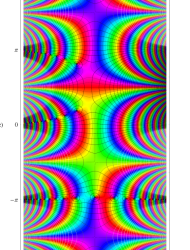
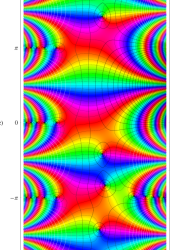
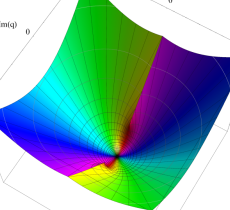
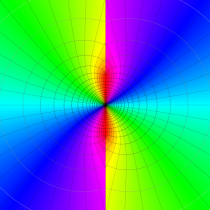
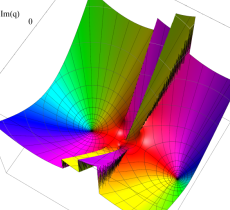
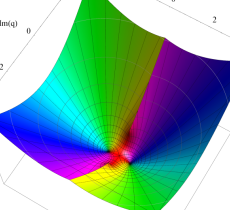
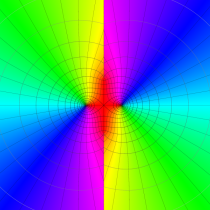
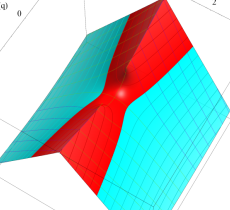
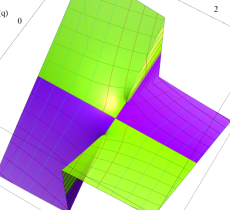
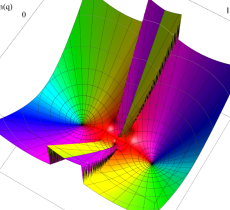
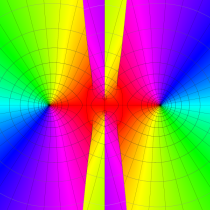
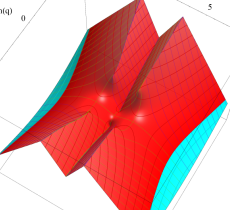
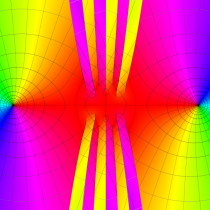
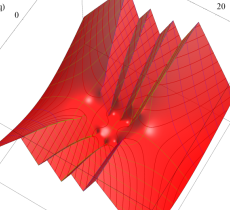
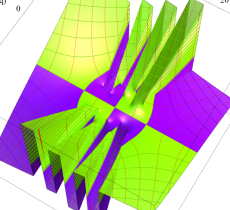
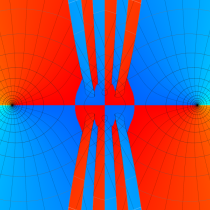
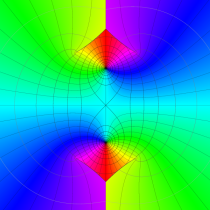
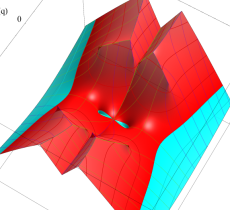
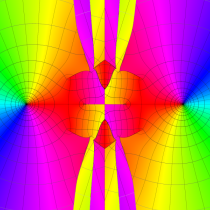
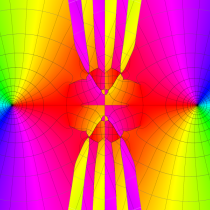
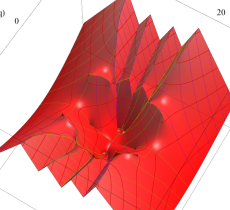
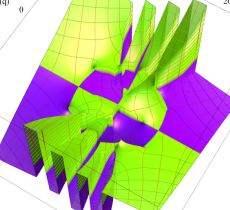
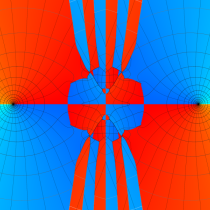
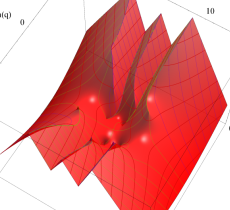
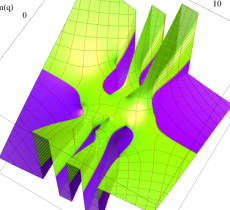
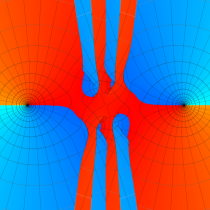
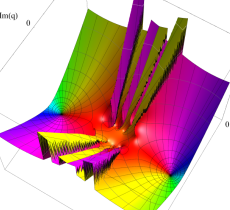
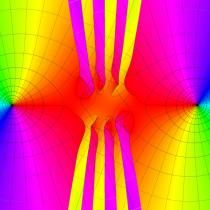
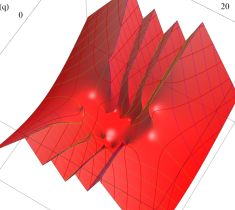
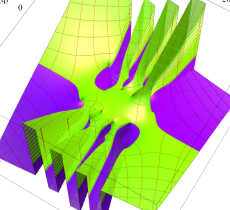
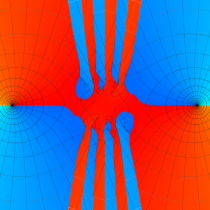
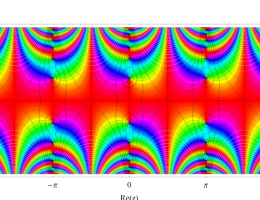
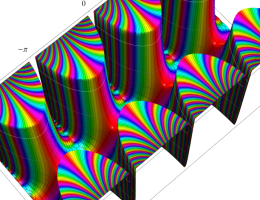
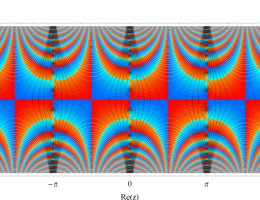
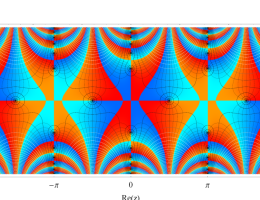
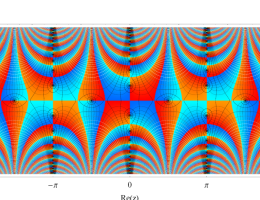
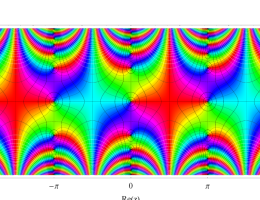
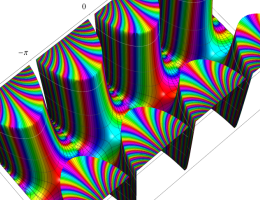
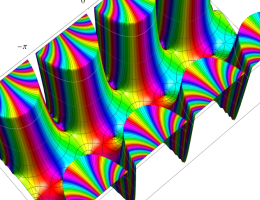
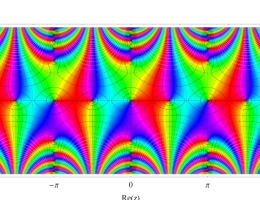
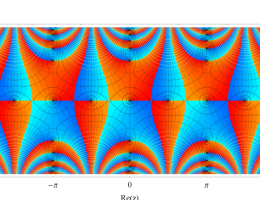
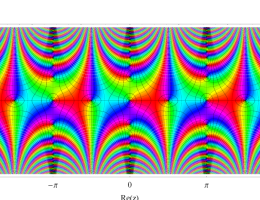
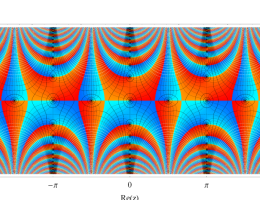
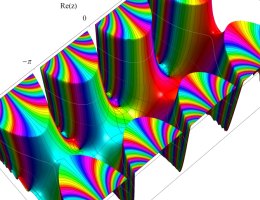
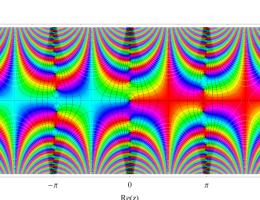
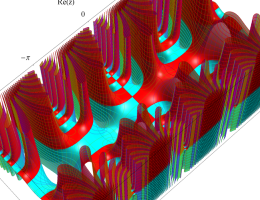
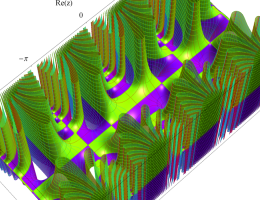
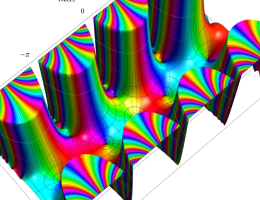
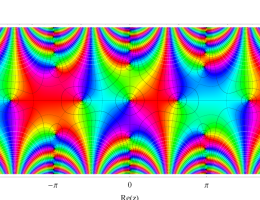
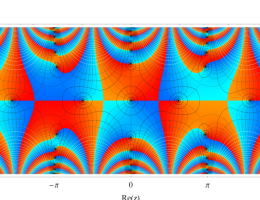
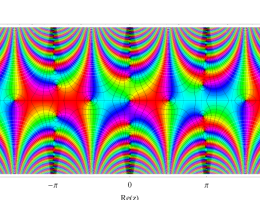
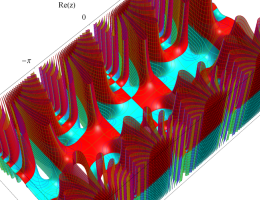
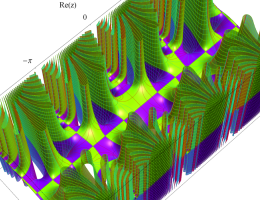
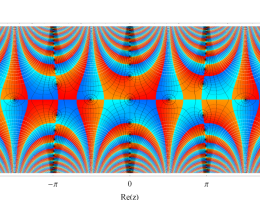
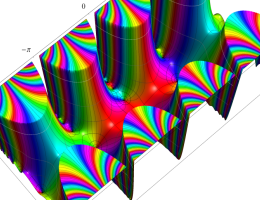
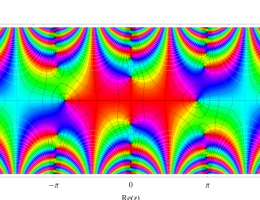
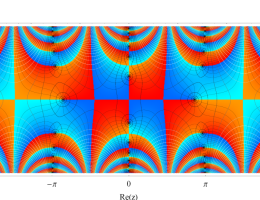
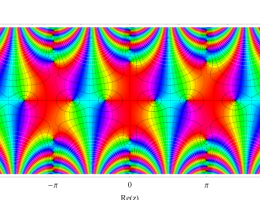
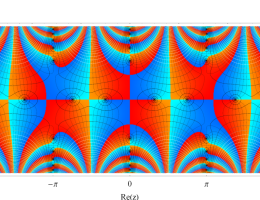
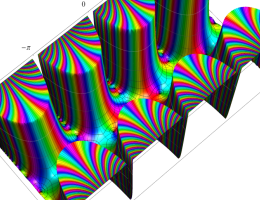
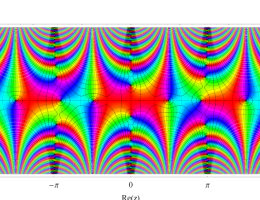
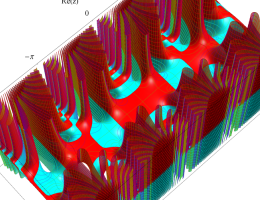
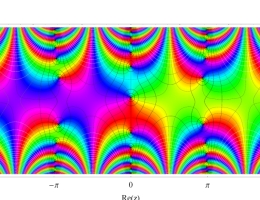
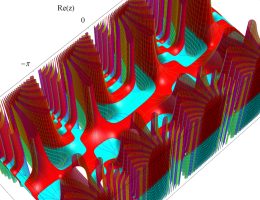
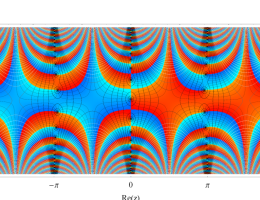
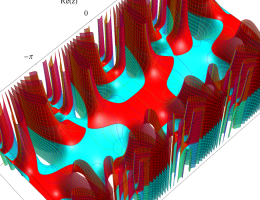
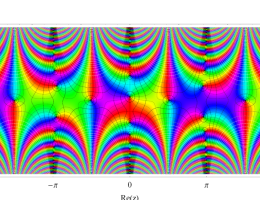
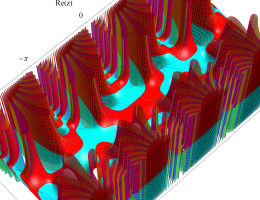
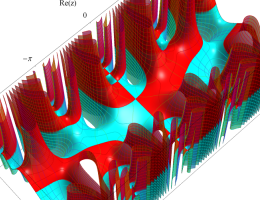
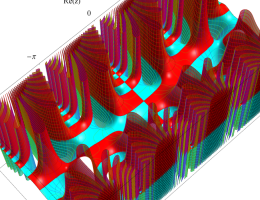
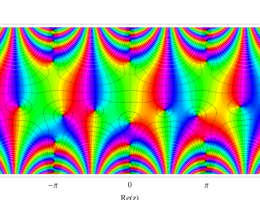
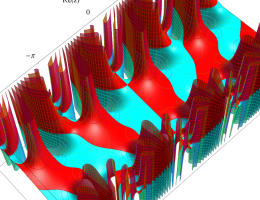
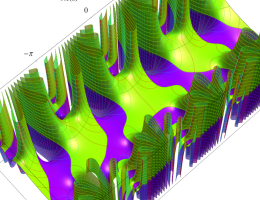
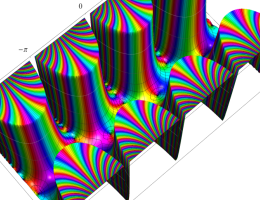
複素変数の第1種 Mathieu 関数
複素変数の第1種 Mathieu 関数
複素変数の第1種 Mathieu 関数
複素変数の第1種 Mathieu 関数
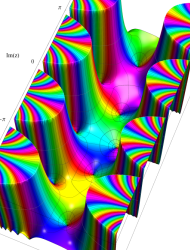
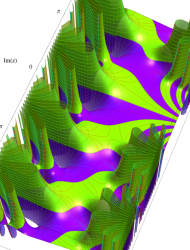
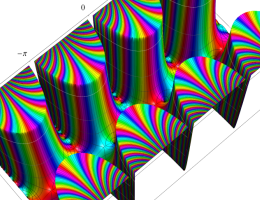
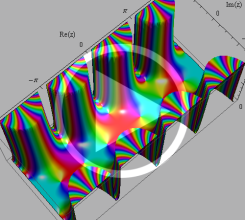
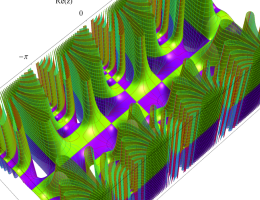
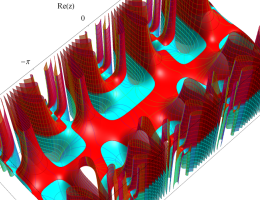
アニメーション(6.12MB)
複素変数の第1種 Mathieu 関数
整数次のときに動きが滑らかでない理由は、固有値が不安定域を跨ぐからである。
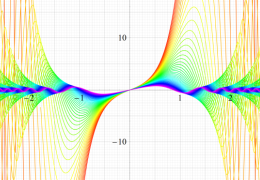
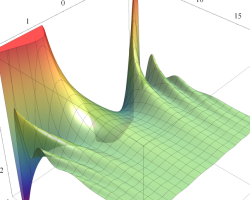
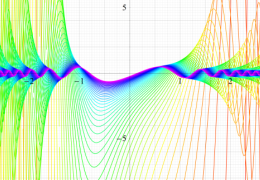
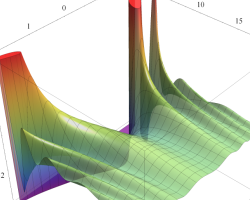
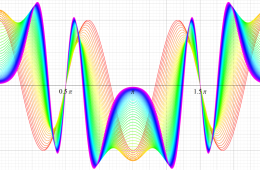
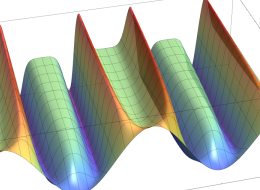
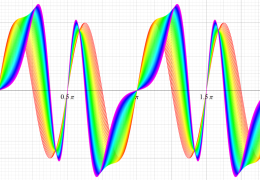
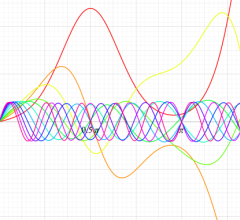
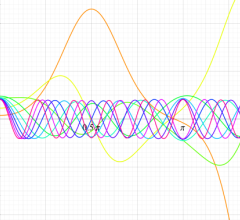
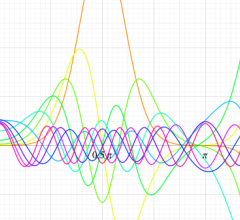
順に、①
実変数の第1種 Mathieu 関数のグラフ。
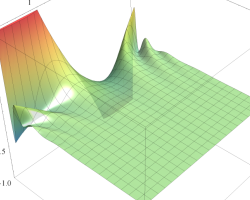
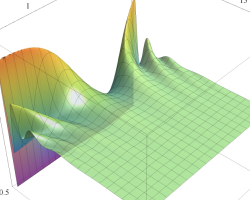
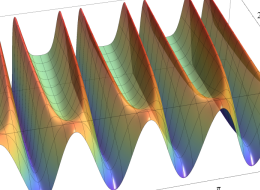
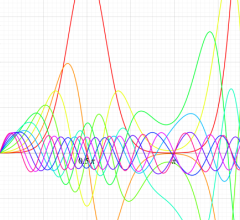
順に、①
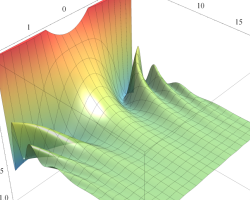
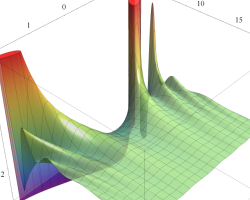
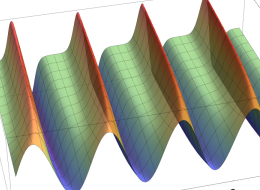
実2変数の第1種 Mathieu 関数のグラフ。順に、①
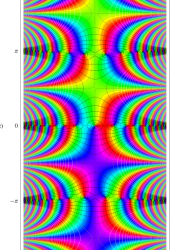
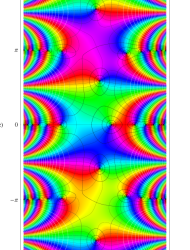
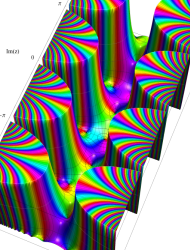
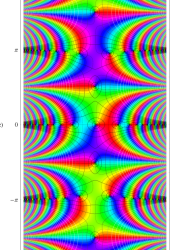
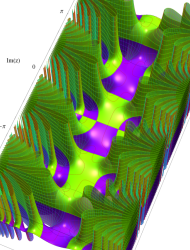
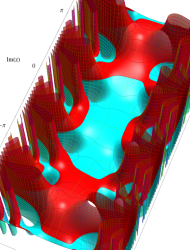
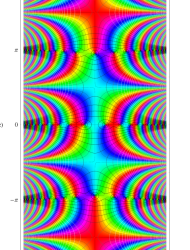
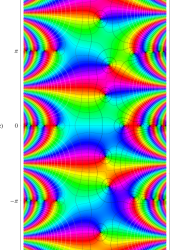
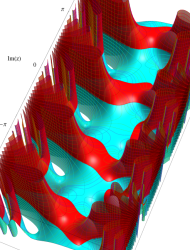
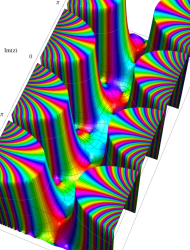
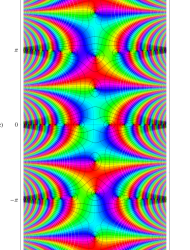
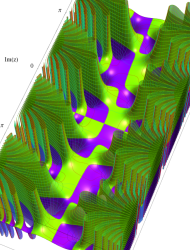
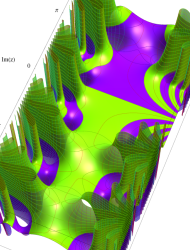
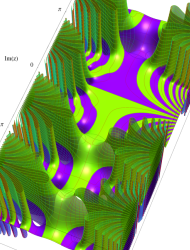
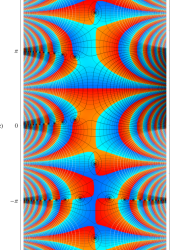
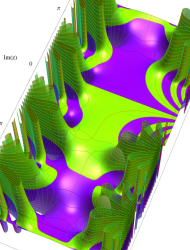
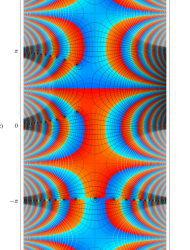
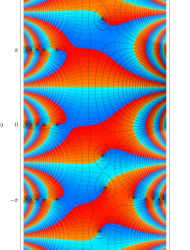
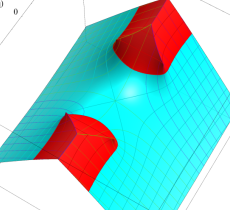
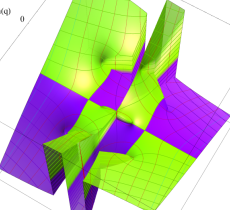
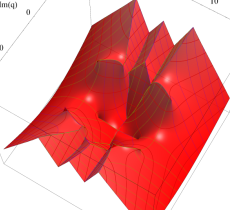
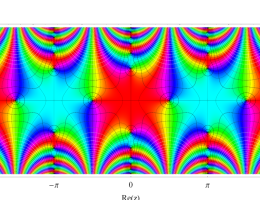
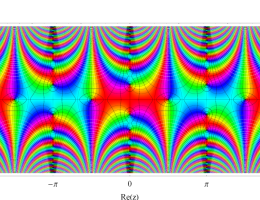
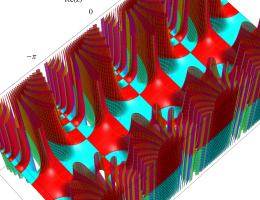
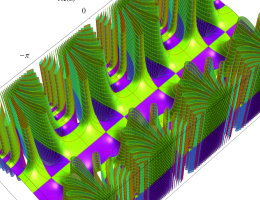
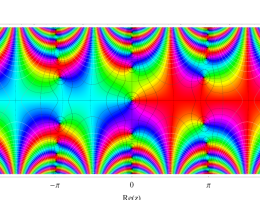
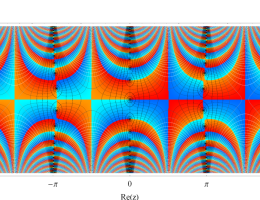
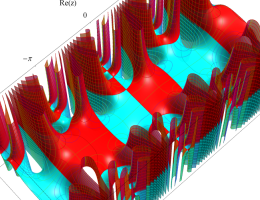
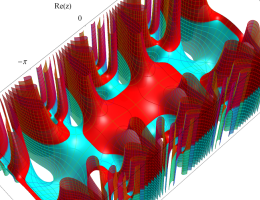
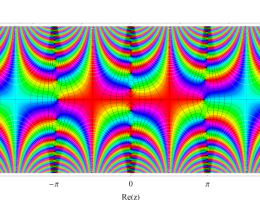
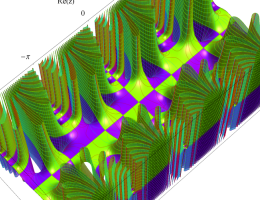
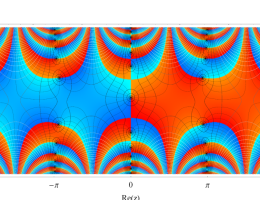
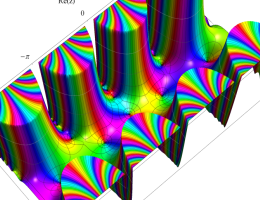
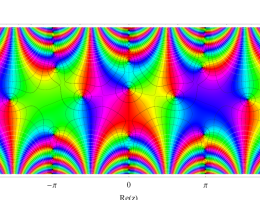
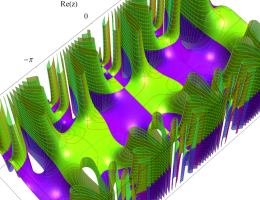
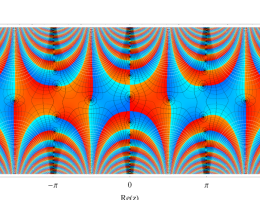
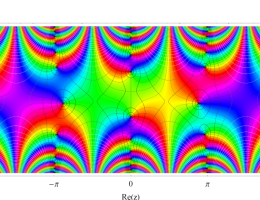
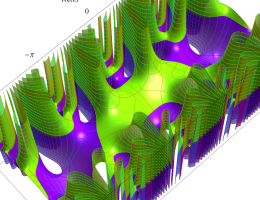
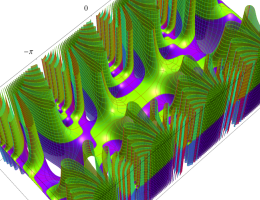
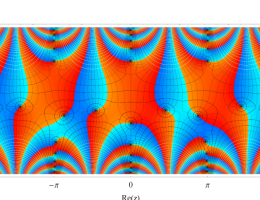
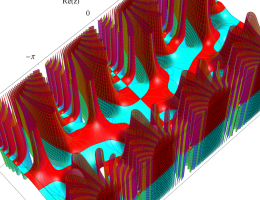
複素変数の第1種 Mathieu 関数
複素変数の第1種 Mathieu 関数
複素変数の第1種 Mathieu 関数
複素変数の第1種 Mathieu 関数
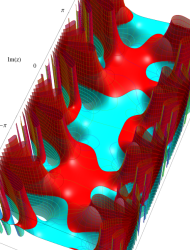
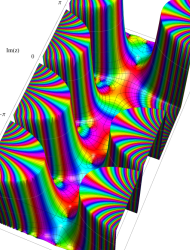
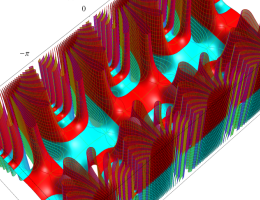
アニメーション(6.59MB)
複素変数の第1種 Mathieu 関数
同様に、固有値が不安定域を跨ぐ次数のときは、動きが滑らかにならない。
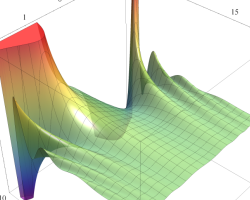
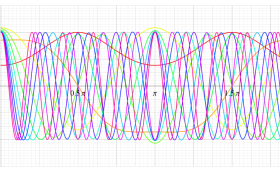
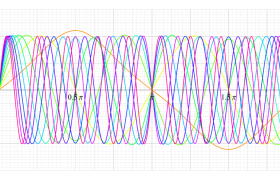
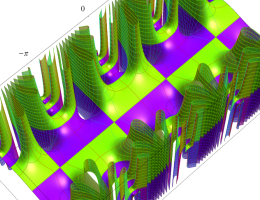
順に、①
1番目のグラフのうち、
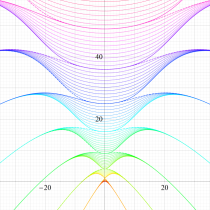
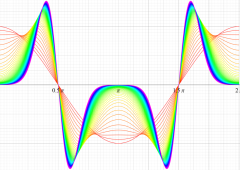
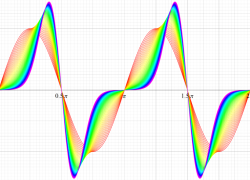
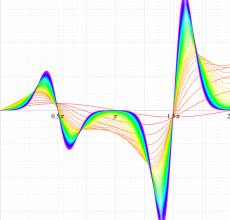
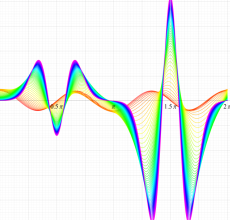
実変数の第2種 Mathieu 関数のグラフ。
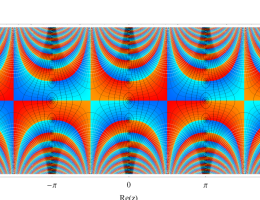
順に、①
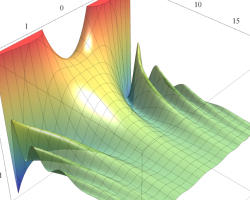
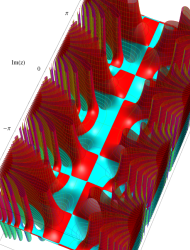
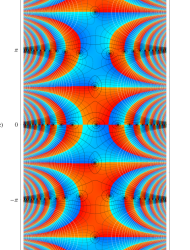
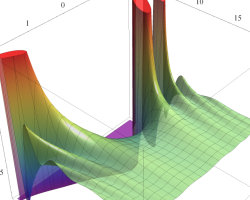
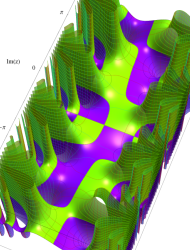
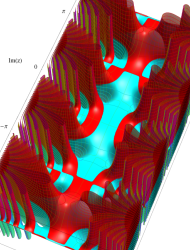
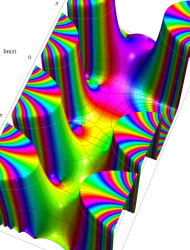
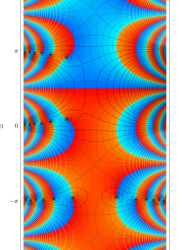
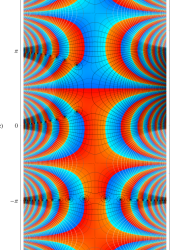
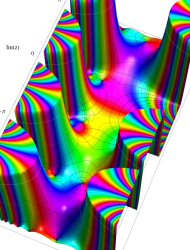
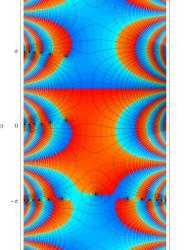
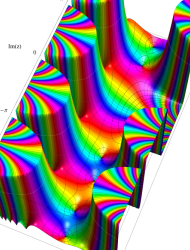
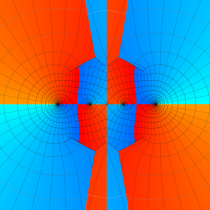
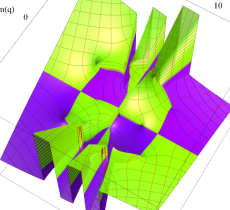
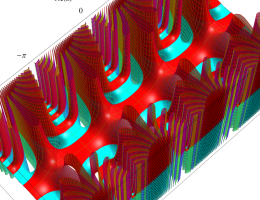
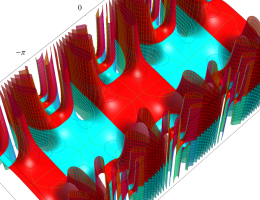
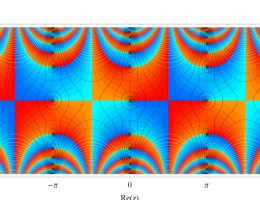
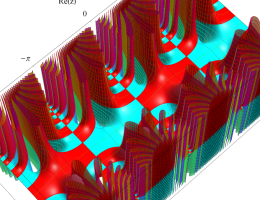
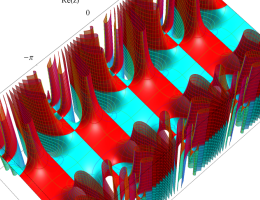
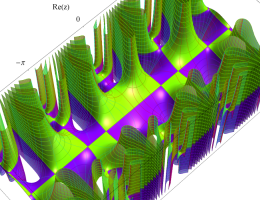
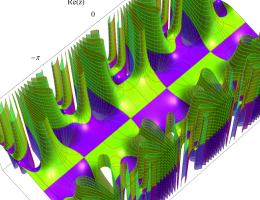
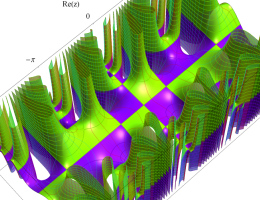
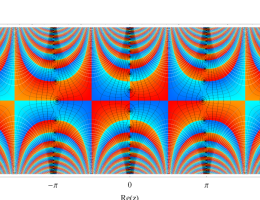
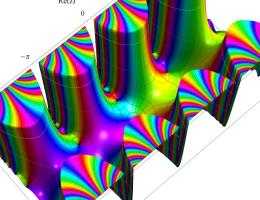
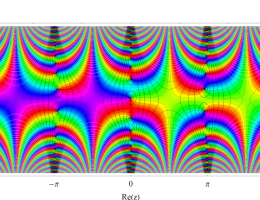
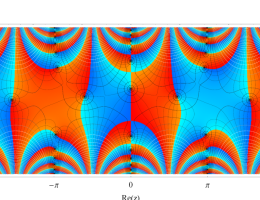
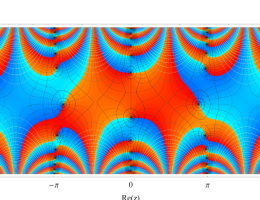
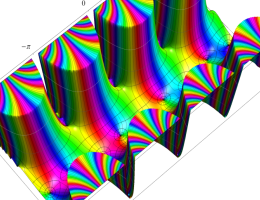
複素変数の第2種 Mathieu 関数
複素変数の第2種 Mathieu 関数
複素変数の第2種 Mathieu 関数
複素変数の第2種 Mathieu 関数
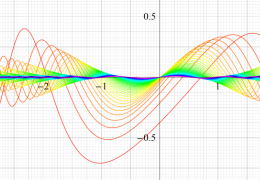
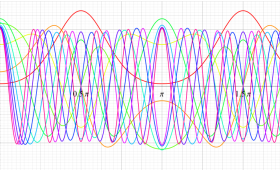
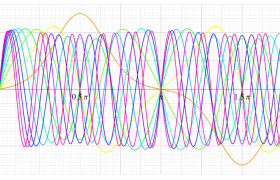
順に、①
実変数の第2種 Mathieu 関数のグラフ。
順に、①
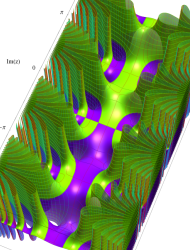
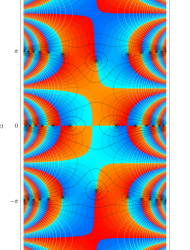
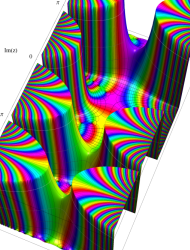
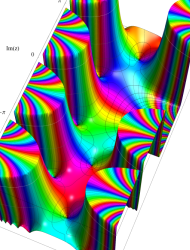
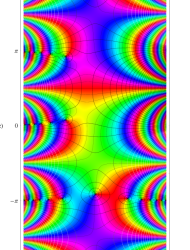
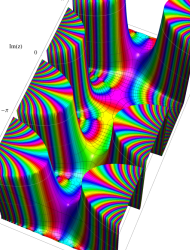
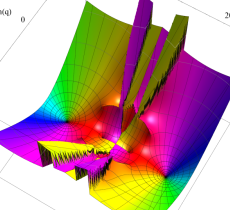
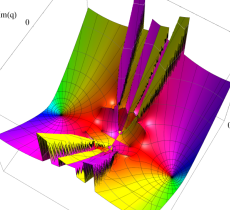
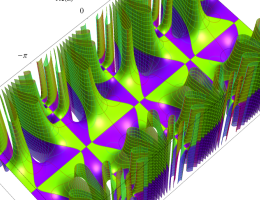
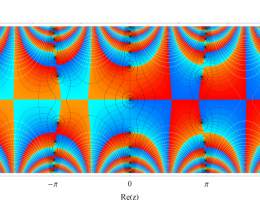
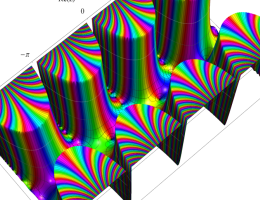
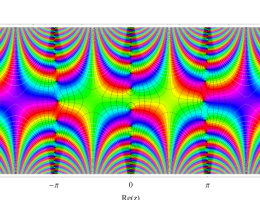
複素変数の第2種 Mathieu 関数
複素変数の第2種 Mathieu 関数
複素変数の第2種 Mathieu 関数
複素変数の第2種 Mathieu 関数
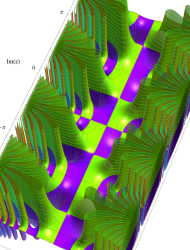
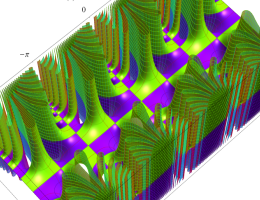
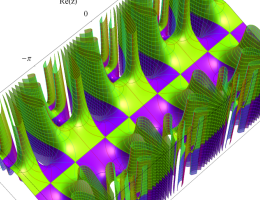
複素変数の第3種 Mathieu 関数
複素変数の第3種 Mathieu 関数
複素変数の第3種 Mathieu 関数
複素変数の第3種 Mathieu 関数
複素変数の第3種 Mathieu 関数
複素変数の第3種 Mathieu 関数
複素変数の第3種 Mathieu 関数
複素変数の第3種 Mathieu 関数
変形 Mathieu 関数
変換この変換によって、第1種・第2種変形 Mathieu 関数は
となる。
(以下、
ここに、Fourier 係数
である。
さらにこの展開式において、引数が
も変形された Mathieu の微分方程式を満たし、
このほか、第3種変形 Mathieu 関数として
が定義される。これは指数関数 (に余弦関数を代入した関数) に漸近するため、その振る舞いが簡単になる。関数記号の
以上の第2種・第3種の解は、
【註記】
※1 : 「NIST - Handbook of Mathematical Functions」, 「(A&S) Handbook of Mathematical Functions …」 で採用されているのは、Meixner - Schäfke の規格化である。これは、上記の関数と定数倍の違いしかない。なお、Mathematica のコード 「Mathieu.m」 では、2種類の規格化をともに搭載した。
※2 : 冒頭で述べた Fourier 級数を数値計算に使用すると、実軸から遠くなるほど丸め誤差が累積して精度が悪くなる。このような領域では、上記の Bessel 関数による級数展開式を用いると高精度で計算できる。その際、変形 Mathieu 関数から Mathieu 関数へ切り替える場合、特に第2種については、
なる線形結合式を用いる。
※1 : 「NIST - Handbook of Mathematical Functions」, 「(A&S) Handbook of Mathematical Functions …」 で採用されているのは、Meixner - Schäfke の規格化である。これは、上記の関数と定数倍の違いしかない。なお、Mathematica のコード 「Mathieu.m」 では、2種類の規格化をともに搭載した。
※2 : 冒頭で述べた Fourier 級数を数値計算に使用すると、実軸から遠くなるほど丸め誤差が累積して精度が悪くなる。このような領域では、上記の Bessel 関数による級数展開式を用いると高精度で計算できる。その際、変形 Mathieu 関数から Mathieu 関数へ切り替える場合、特に第2種については、
なる線形結合式を用いる。
より、両者は互いに90
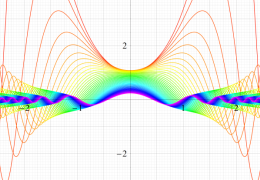
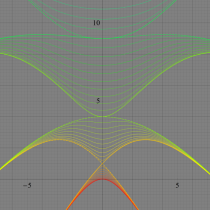
実変数の第1種変形 Mathieu 関数のグラフ。
順に、①
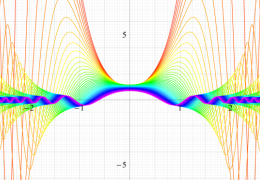
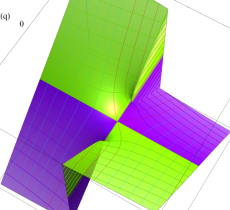
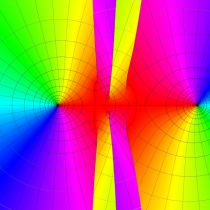
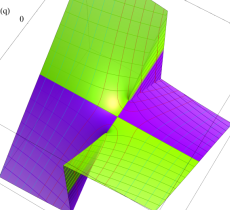
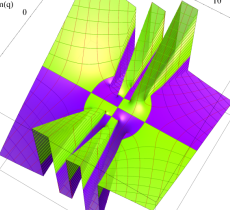
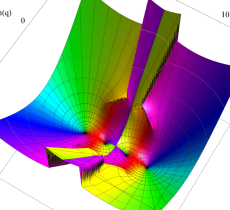
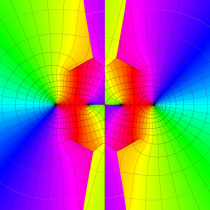
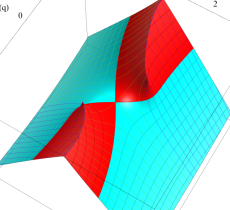
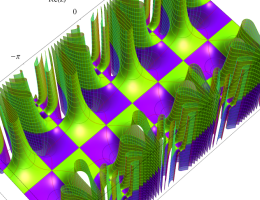
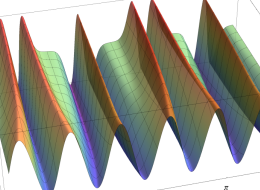
実2変数の第1種変形 Mathieu 関数のグラフ。順に、①
実変数の第1種変形 Mathieu 関数のグラフ。
順に、①
実2変数の第1種変形 Mathieu 関数のグラフ。順に、①
順に、①
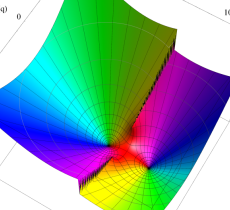
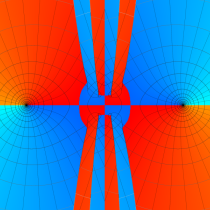
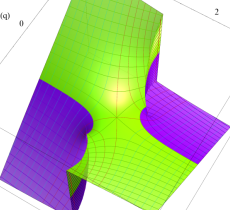
実2変数の第2種変形 Mathieu 関数のグラフ。順に、①
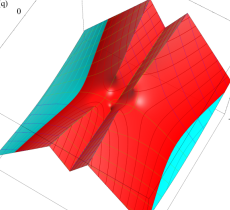
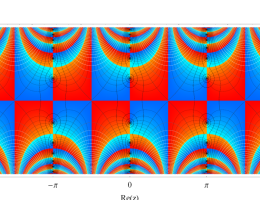
複素変数の第2種変形 Mathieu 関数
複素変数の第2種変形 Mathieu 関数
複素変数の第2種変形 Mathieu 関数
複素変数の第2種変形 Mathieu 関数
順に、①
実2変数の第2種変形 Mathieu 関数のグラフ。順に、①
複素変数の第2種変形 Mathieu 関数
複素変数の第2種変形 Mathieu 関数
複素変数の第2種変形 Mathieu 関数
複素変数の第2種変形 Mathieu 関数
複素変数の第3種変形 Mathieu 関数
複素変数の第3種変形 Mathieu 関数
複素変数の第3種変形 Mathieu 関数
複素変数の第3種変形 Mathieu 関数
複素変数の第3種変形 Mathieu 関数
複素変数の第3種変形 Mathieu 関数
複素変数の第3種変形 Mathieu 関数
複素変数の第3種変形 Mathieu 関数
Mathieu 固有値関数
Floquet の定理により、Mathieu の微分方程式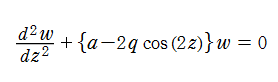
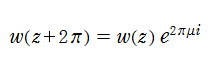
解の様相は次の①~③に分類される。
① 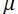 が実数となるとき → 擬周期性基本解は一般に概周期関数になる
が実数となるとき → 擬周期性基本解は一般に概周期関数になる
② 特に①のうち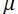 が有理数となるとき → 擬周期性基本解は周期関数になる
が有理数となるとき → 擬周期性基本解は周期関数になる
以上①,②の場合、擬周期性基本解の値は実定義域上で有界となる。このような② 特に①のうち
③ 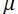 が①,②以外のとき → 二つの基本解の一方は擬周期関数になるが、いずれも有界な解ではない
が①,②以外のとき → 二つの基本解の一方は擬周期関数になるが、いずれも有界な解ではない
となるようなまた固有値
特に、
を満たす。また、
と表わされる。
電子計算機での数値計算においては、前述の無限連分数方程式に Newton 法を適用するか、無限次元三重対角行列の固有値に基づく線形代数方程式
を直接解くのが便利である。ここに
なお、
となる。ここに
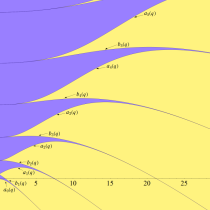
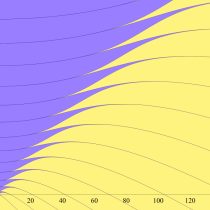
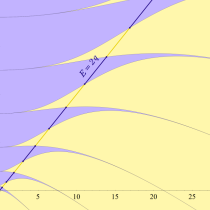
Mathieu 固有値関数の物理学での応用例として、量子力学における (無限に広がる) 一次元結晶格子内部の自由電子が取りうるエネルギー範囲がある。この場合の Schrödinger 方程式とその解である波動関数は、Mathieu の微分方程式と (整数次) 第1種 Mathieu 関数になり、波動関数が存在する条件とは、固有値 (すなわち電子の取りうるエネルギー) が安定域にあることに他ならない。原子が単独または間隔が疎ならば、その周囲の電子はエネルギーが断続的な特定値 (量子数) を取るが、原子が密集する金属等の自由電子では、エネルギーがある程度の幅を持った連続値を取るようになる。これは 「帯構造 (Band structure)」 と呼ばれ、エネルギーの取り得る区間を 「許容帯 (Energy band)」、そうでない区間を 「禁制帯 (Energy gap)」 と言う。Mathieu 固有値関数の安定域と不安定域は、帯構造の形状を表わす一例となっている。
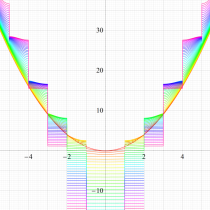
なお、前述の自由電子が取りうるエネルギー範囲 (許容帯) とは、下図の原点を通る直線上 (ただし、Planck 定数で決まる値より小さくはならない) で、かつ、安定域と重なる無数の線分区間になる。一方、各線分の間には不安定域を挟むギャップ (禁制帯) が存在し、そこでは波動関数は存在せず、エネルギーを考えることもできなくなる。
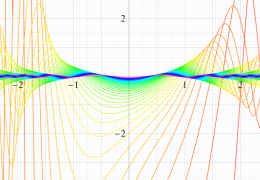
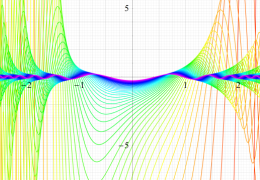
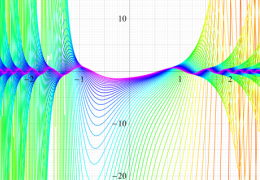
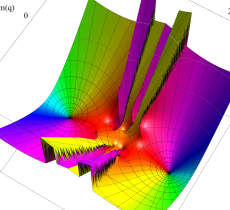
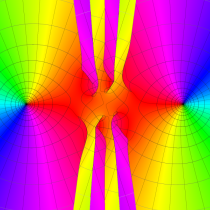
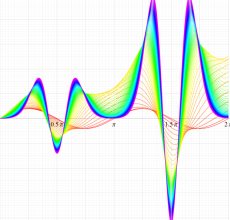
実変数の Mathieu 固有値関数のグラフ。①
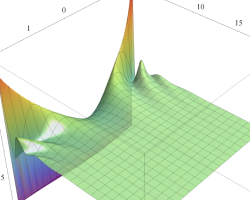
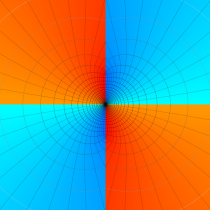
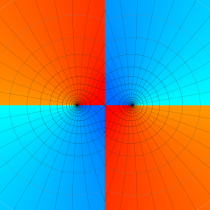
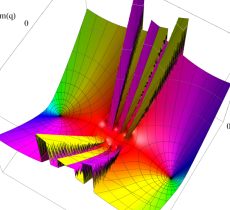
実2変数の Mathieu 固有値関数のグラフ。①
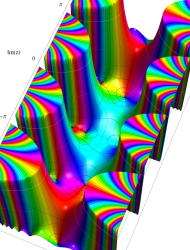
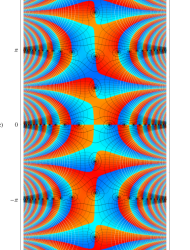
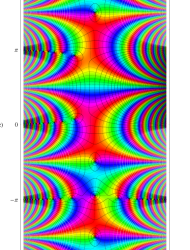
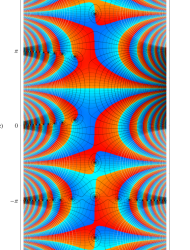
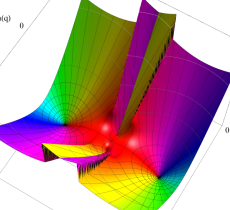
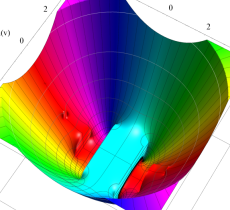
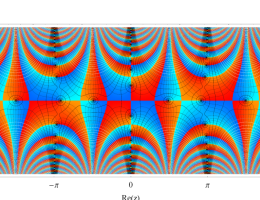
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
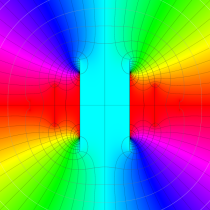
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
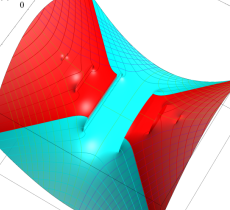
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
実変数の Mathieu 固有値関数
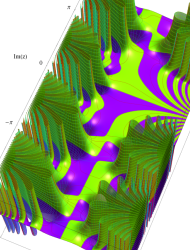
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
複素変数の Mathieu 固有値関数
【 Petite Galerie 】
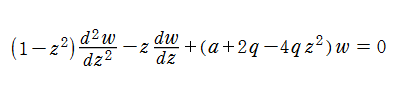
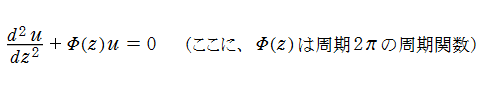
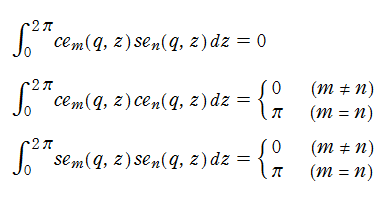
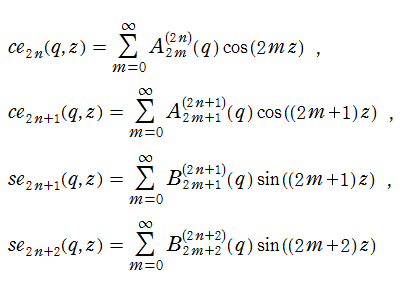
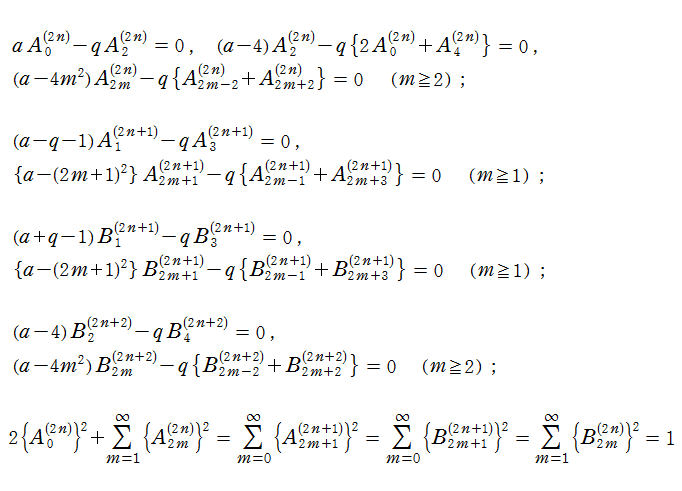
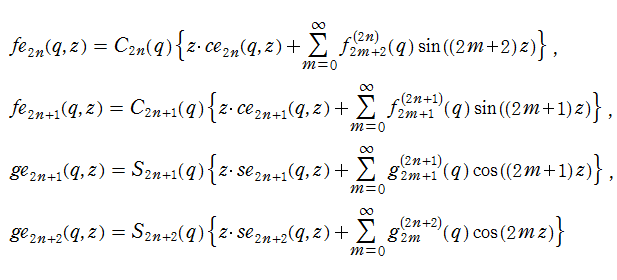
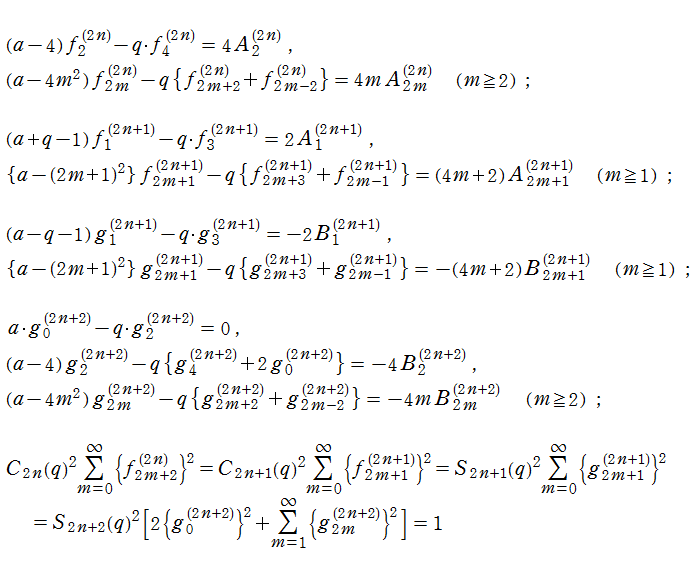
























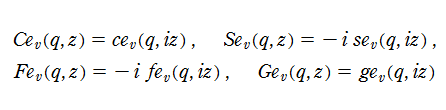
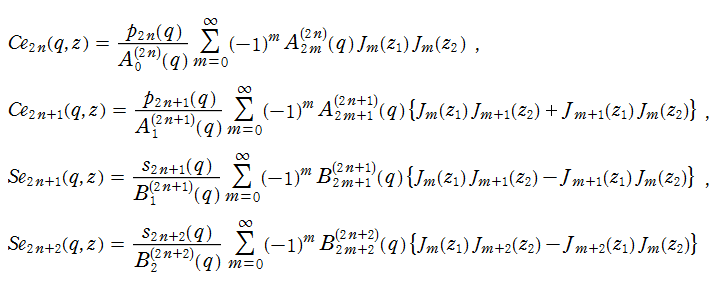
, s[n](q)](siki_spec270/mathieu765.png)