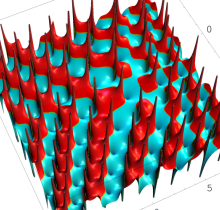
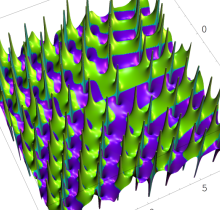
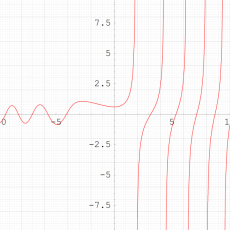
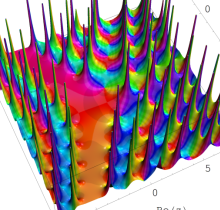
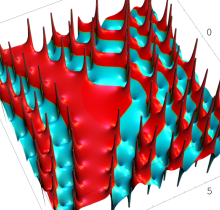
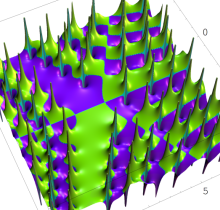
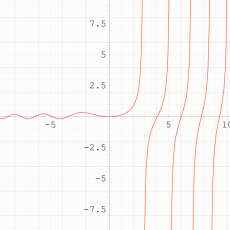
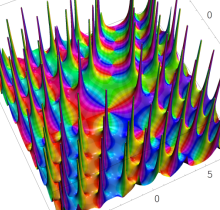
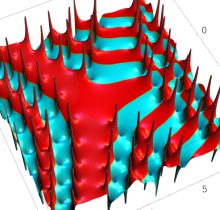
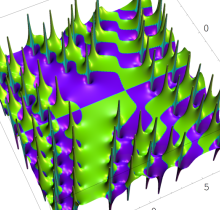
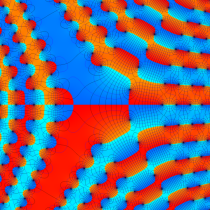
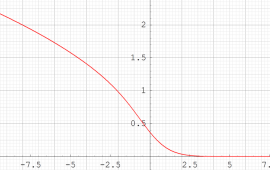
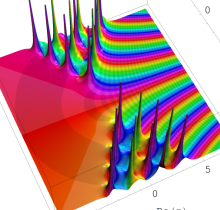
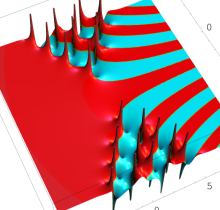
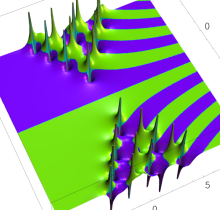
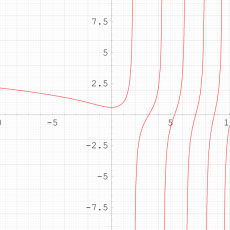
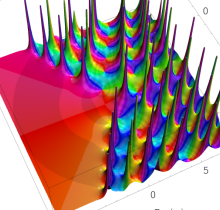
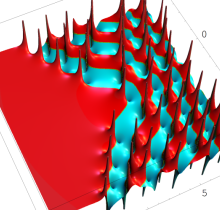
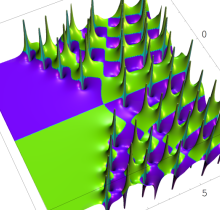
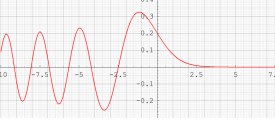
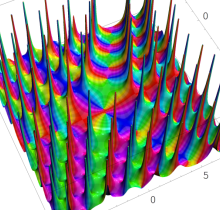
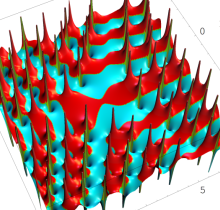
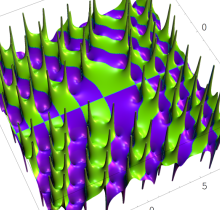
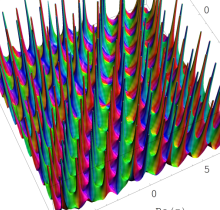
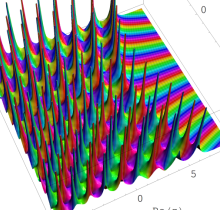
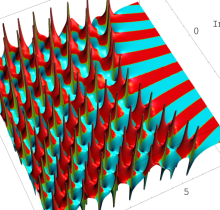
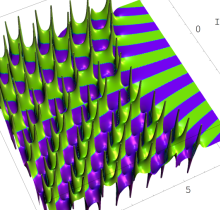
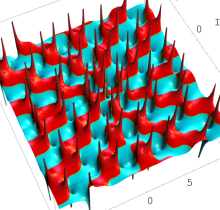
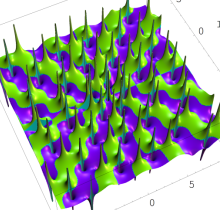
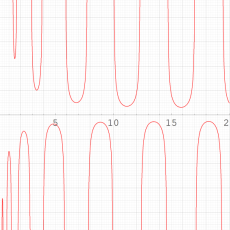
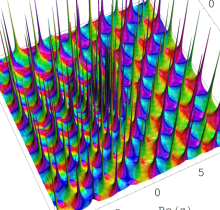
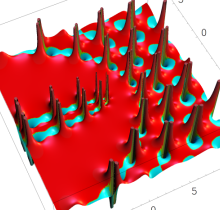
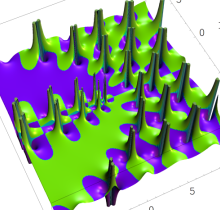
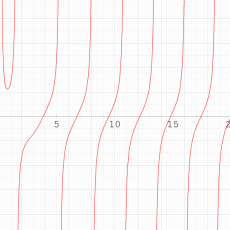
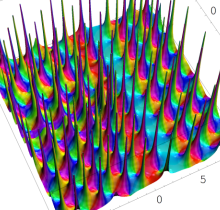
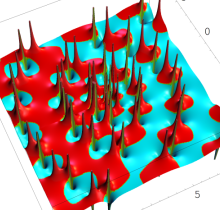
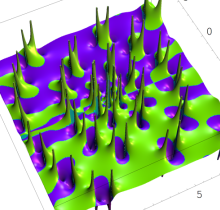
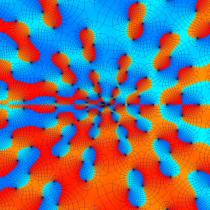
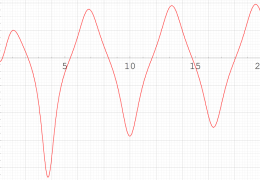
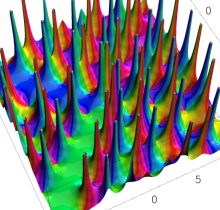
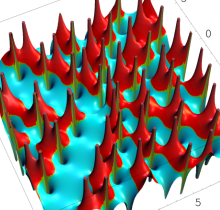
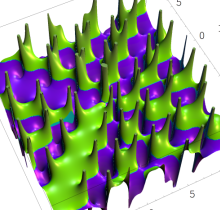
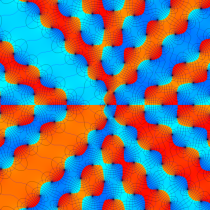
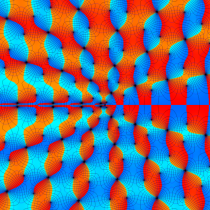
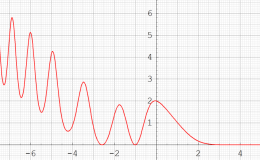
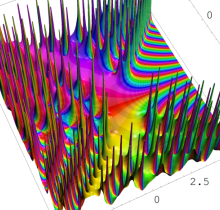
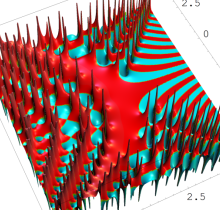
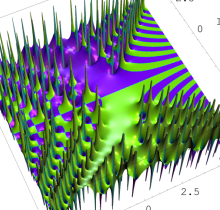
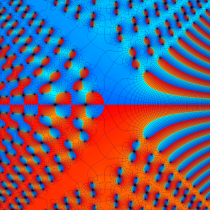
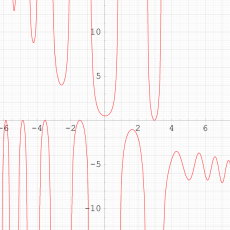
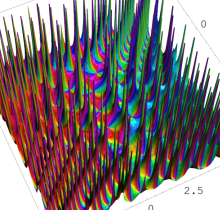
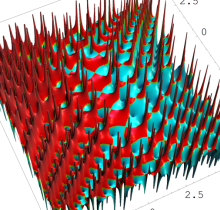
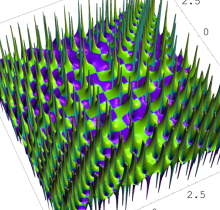
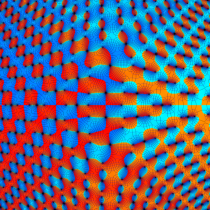
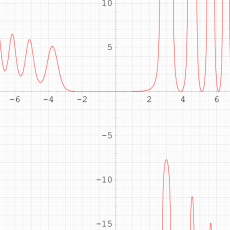
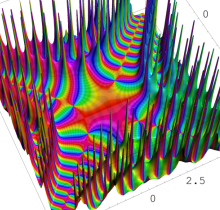
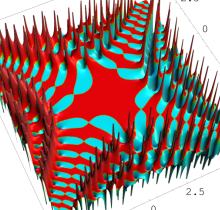
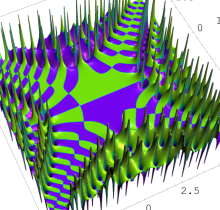
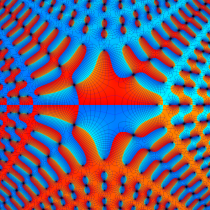
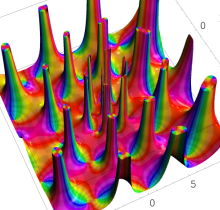
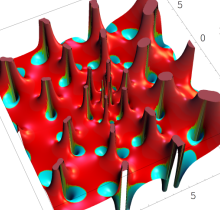
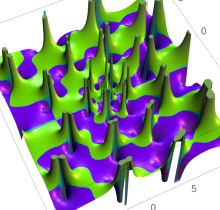
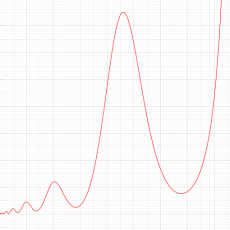
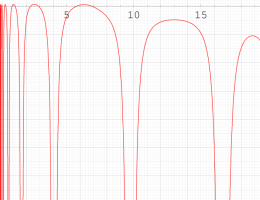
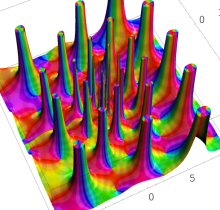
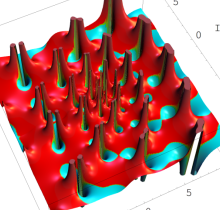
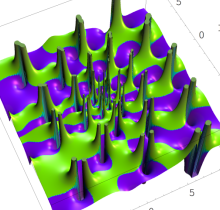
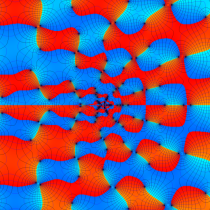
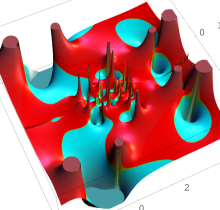
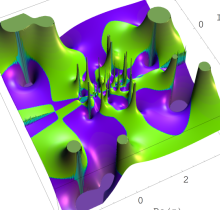
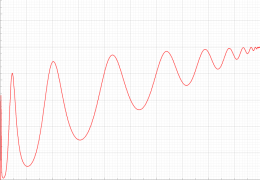
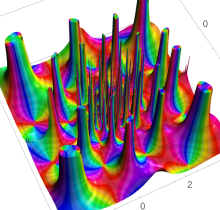
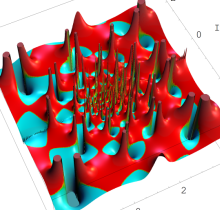
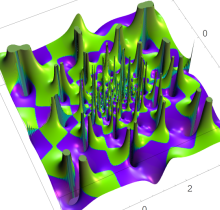
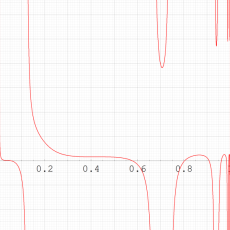
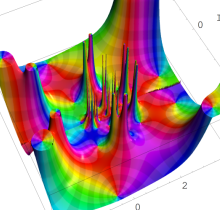
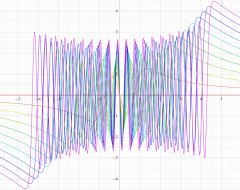
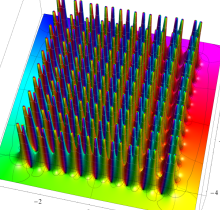
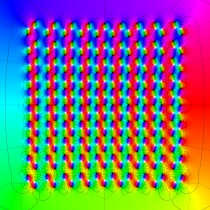
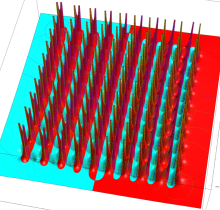
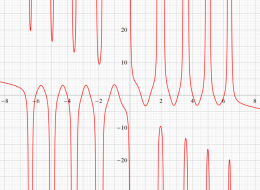
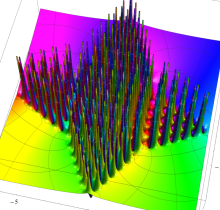
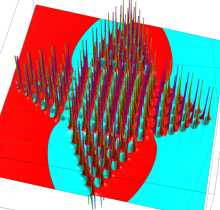
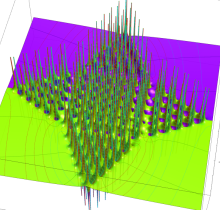
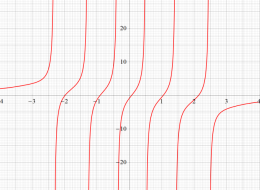
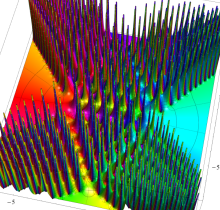
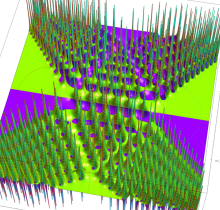
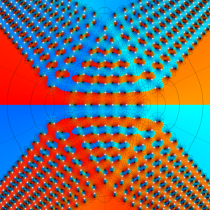
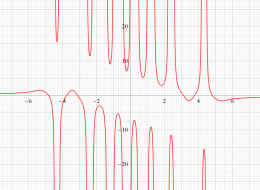
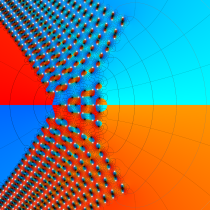
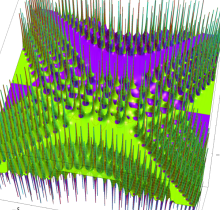
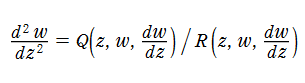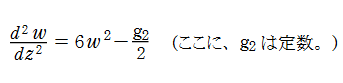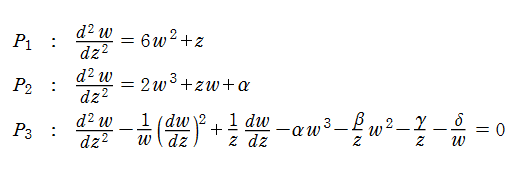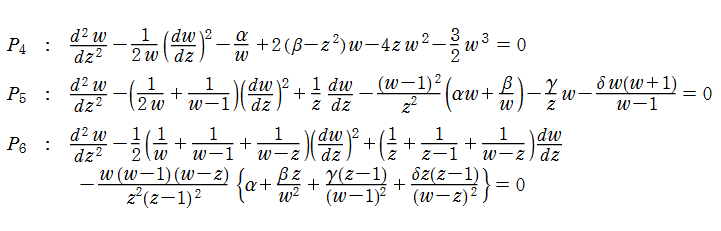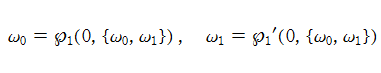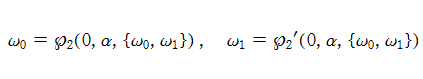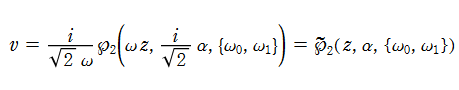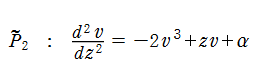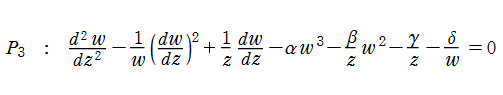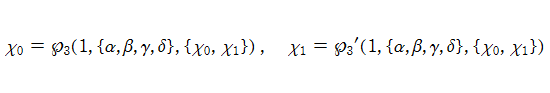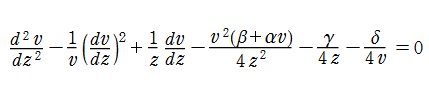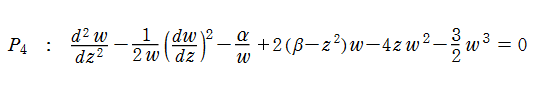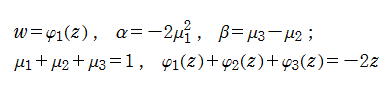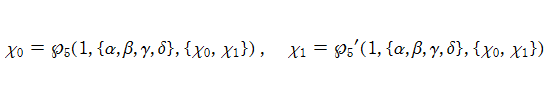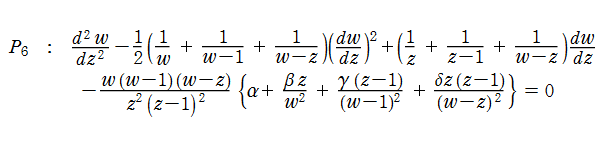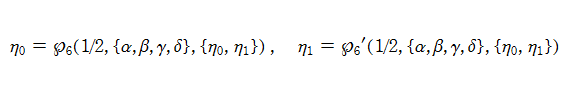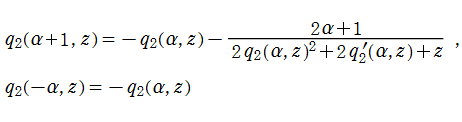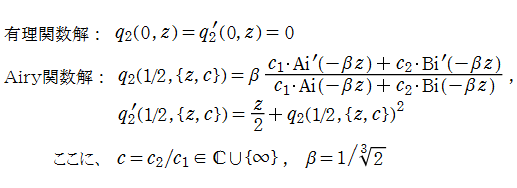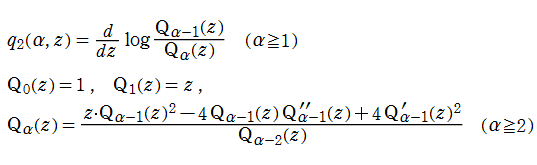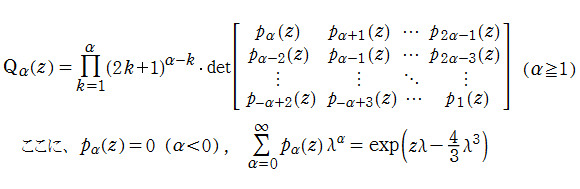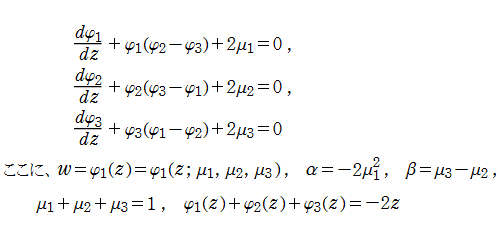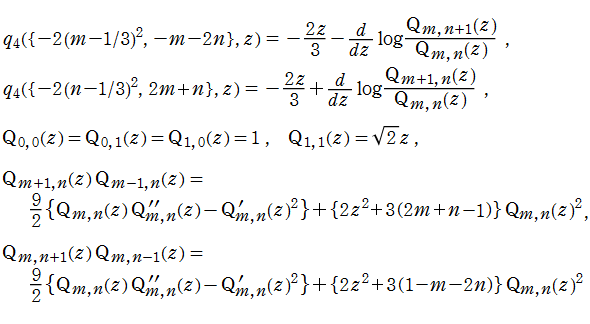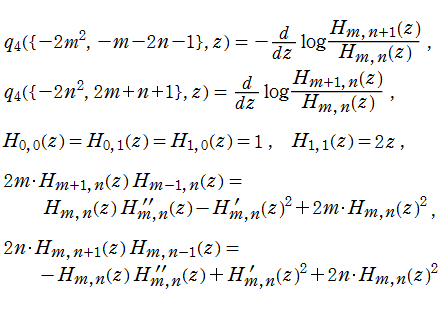特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
Painlevé 超越関数
第1種 Painlevé 超越関数
日:Painlevé超越関数,パンルヴェ超越関数,パンルヴェ関数英:Painlevé transcendents,仏:Fonctions transcendantes de Painlevé,独:Painlevésche transzendente
線形常微分方程式の解の特異点(極、分岐点など)は、方程式中の任意定数や解の初期値に係わらず、必ずその係数(関数)の特異点と一致する。したがって、それらの特異点は個々の解によって位置が変わらない。これを「動かない特異点(fixed singular point)」という。一方、非線形常微分方程式の場合は、一般に動かない特異点を持つと同時に、方程式中の任意定数等によって特異点の位置が変わる「動く特異点(movable singular point)」を持つ。
1階の代数的な非線形常微分方程式
の解にどのような種類の関数が現れるかについては、L. I. Fuchs,H. Poincaré 以来多くの研究を経て、ある程度の解決を見ている。特に、その解の動く特異点が極に限られる場合(これは「Painlevé 性」と呼ばれる)は、線形常微分方程式で定義される特殊関数と楕円関数、および初等関数によって表わされる。よってここからは、19世紀末までに既知の特殊関数(いわゆる古典的特殊関数)以外の新しい関数は生じない。
2階の代数的な非線形常微分方程式
についても、同時代の C. É. Picard,P. Painlevé 等が、方程式の型の分類、出現する特殊関数の研究に着手したが、2階になると一般的に動く分岐点が現れるため困難を極めた。元々、解の様相が完全に解明されている非線形常微分方程式はあまり多くない。例外的に、Weierstrass の楕円関数が満たす非線形常微分方程式
は、楕円関数が種々の良い性質を持つため、明快に論ずることができる (この2階非線形微分方程式は、1階非線形微分方程式に変換できる。さらに、それは変数分離法で解けて、解が第1種楕円積分の逆関数、すなわち楕円関数になる事が分かる)。
そこで Painlevé は、楕円関数と同様に動く特異点が極のみである場合に限ってこの研究を進め、50個の標準的な方程式を見出した。ここから解が既知の関数になる場合を順次除外し、次の3個の方程式を見出した(1900~1902年)。
さらに、Painlevé の計算誤りを修正した B. O. Gambier によって
現在では、これら6個の微分方程式を総称して Painlevé 方程式と呼び、
Painlevé 方程式は、パラメータ
Painlevé 超越関数は、ある特定のパラメータでの解がひとつ与えられると、それを元にした漸化式によって、次々と異なるパラメータの解を得ることができる。この変換は「Bäcklund 変換」と呼ばれている。
6個の Painlevé 方程式の(前述の還元される特別な場合を除いた)一般的な解が、本当に新しい特殊関数であるかどうかについては、Painlevé の時代から既に論争が起こっていたが、西岡 啓二と梅村 浩による1980年代末の一連の研究によって肯定的に証明された。
M. E. R. Fuchs が楕円体微分方程式のモノドロミー保存変形問題を解く過程で
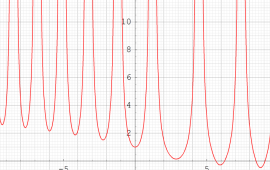
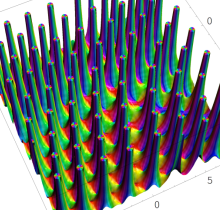
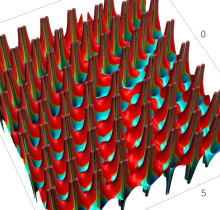
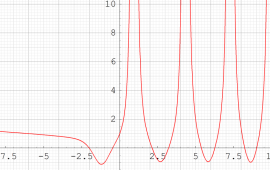
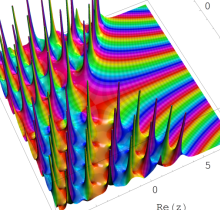
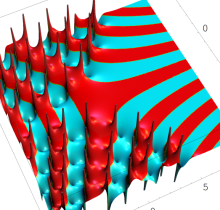
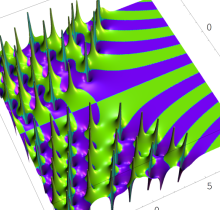
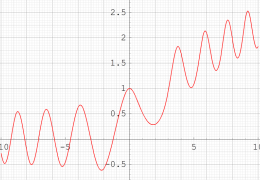
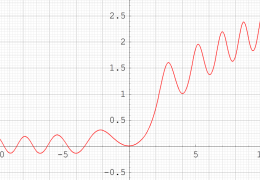
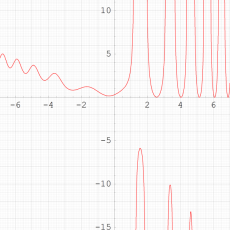
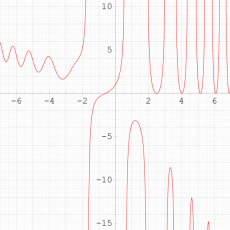
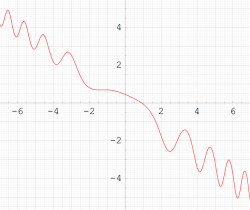
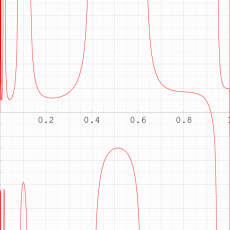
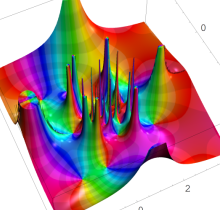
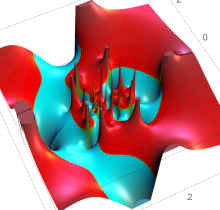
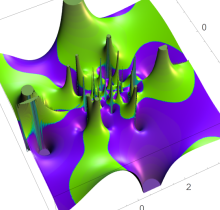
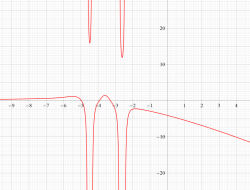
ここでは、第1種 Painlevé 方程式
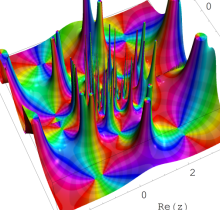
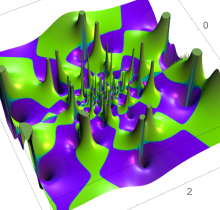
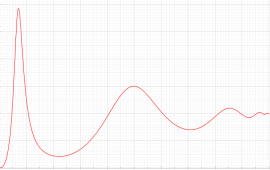
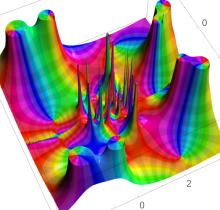
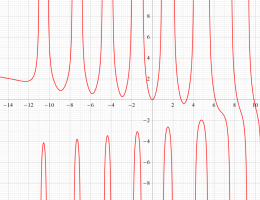
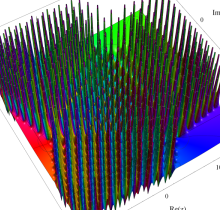
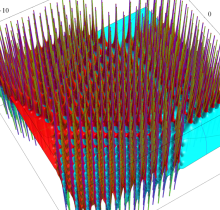
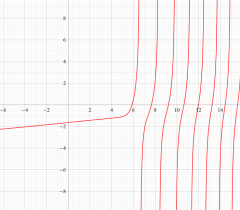
である。第1種 Painlevé 超越関数の動く極は、常に2位である。計算は、W. Fair と Y. L. Luke による連分数近似法による。
【註記】
※1:M. E. R. Fuchs は、冒頭で述べた L. I. Fuchs の息子である。
※1:M. E. R. Fuchs は、冒頭で述べた L. I. Fuchs の息子である。
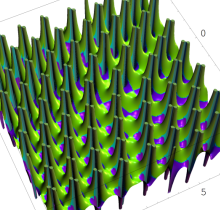
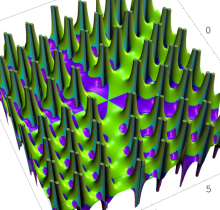
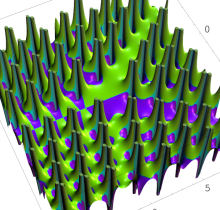
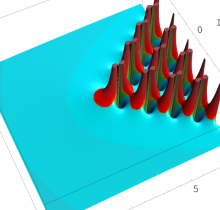
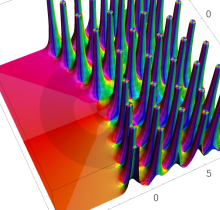
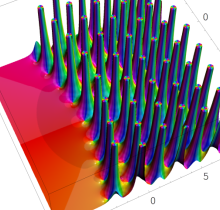
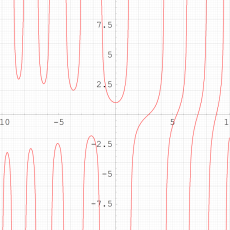
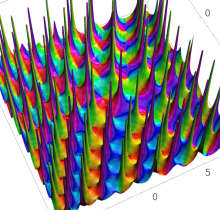
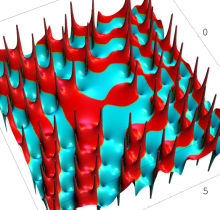
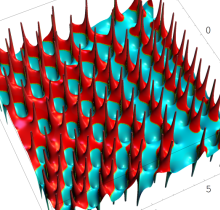
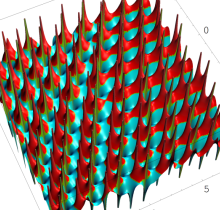
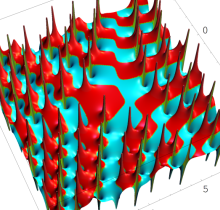
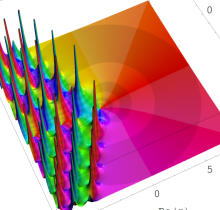
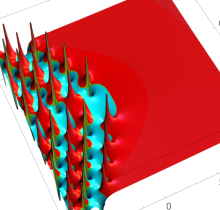
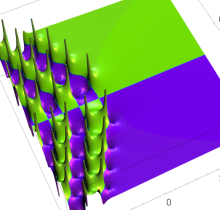
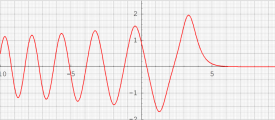
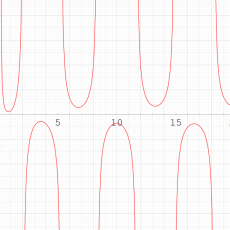
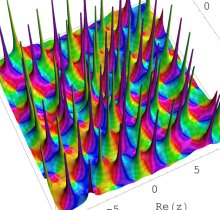
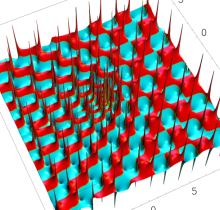
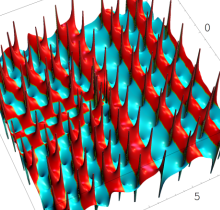
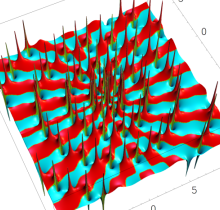
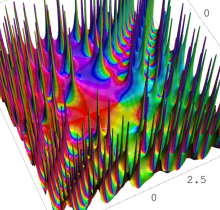
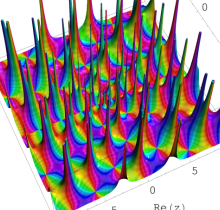
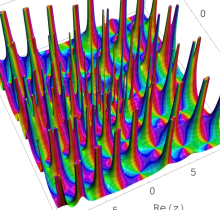
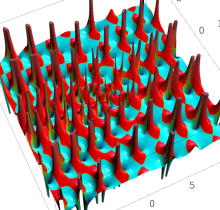
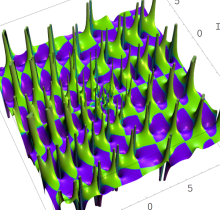
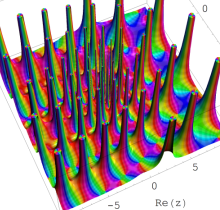
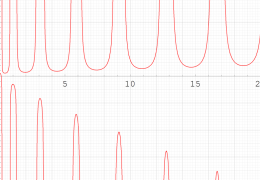
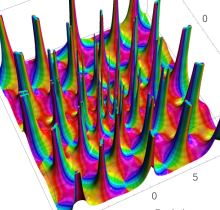
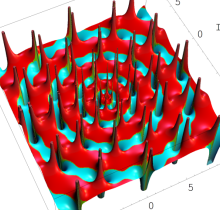
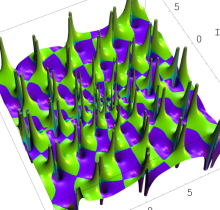
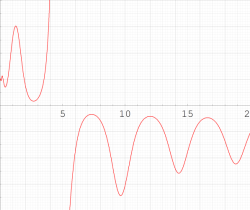
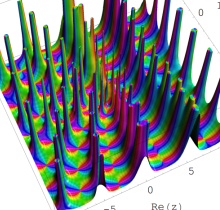
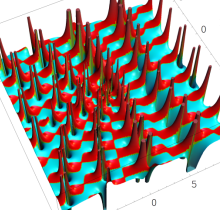
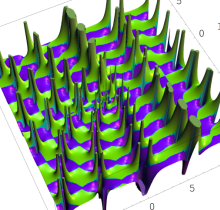
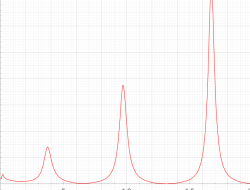
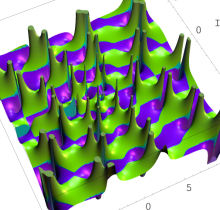
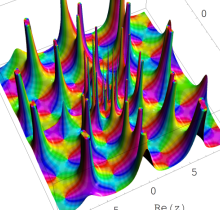
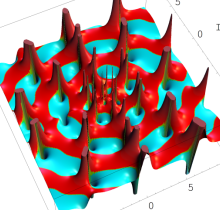
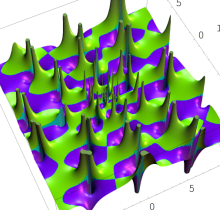
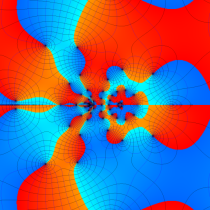
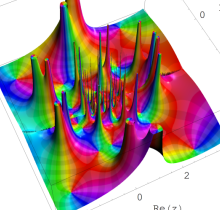
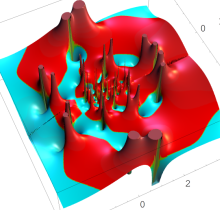
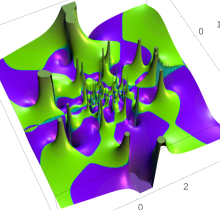
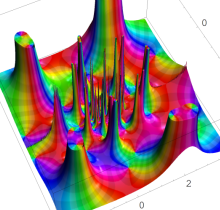
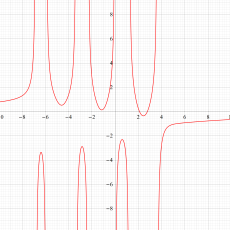
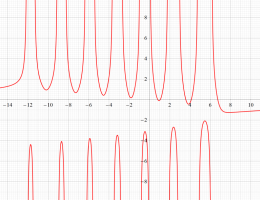
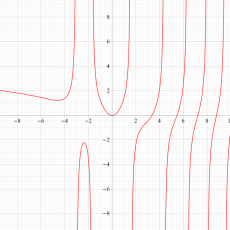
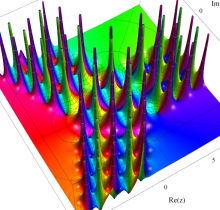
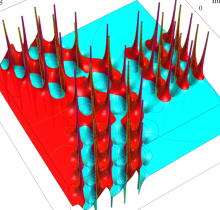
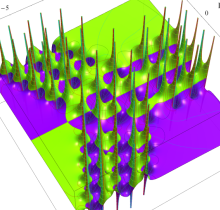
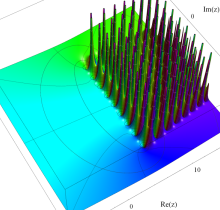
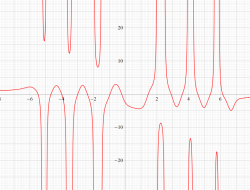
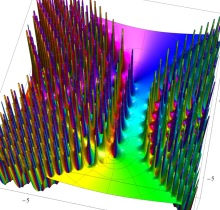
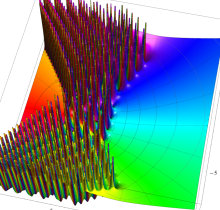
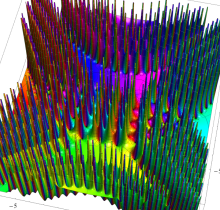
複素変数の第1種 Painlevé 超越関数
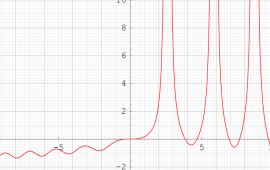
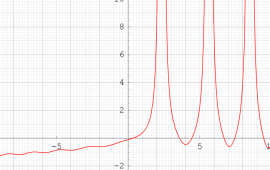
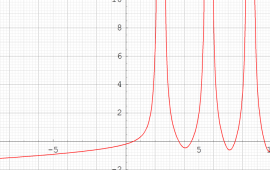
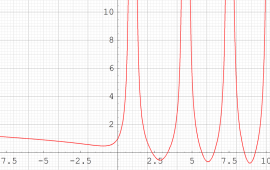
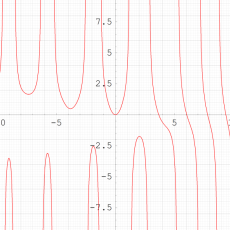
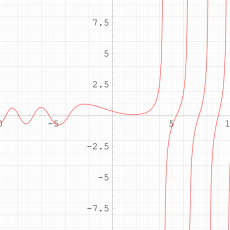
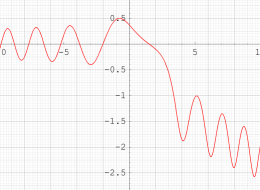
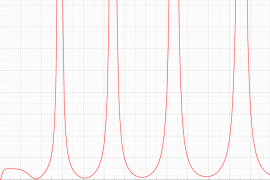
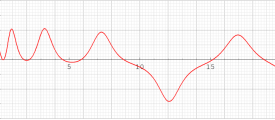
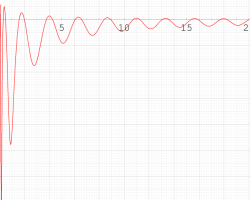
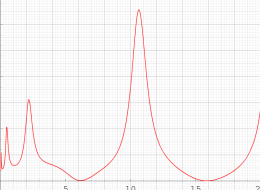
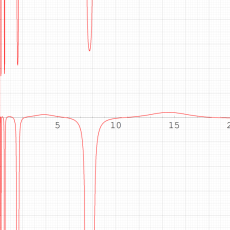
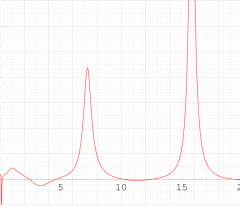
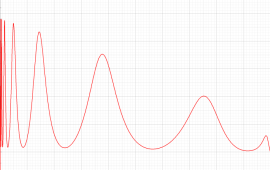
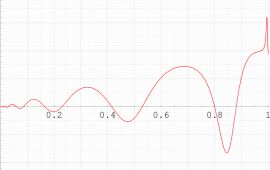
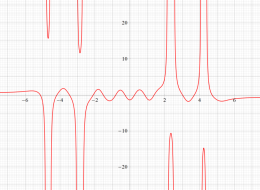
実変数の第1種 Painlevé 超越関数
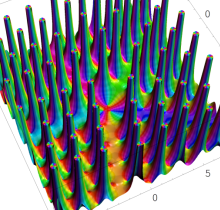
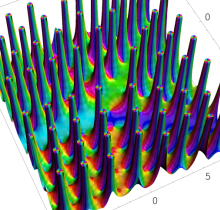
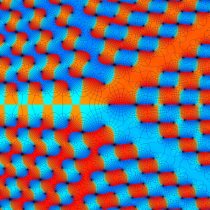
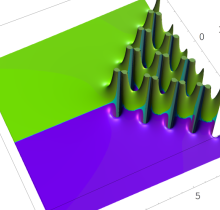
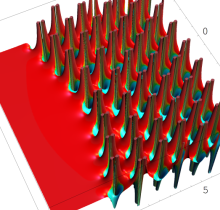
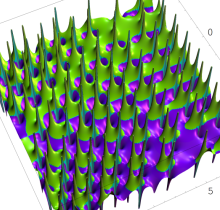
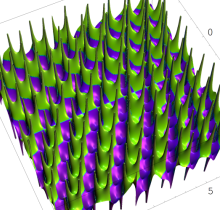
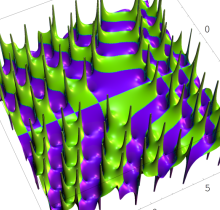
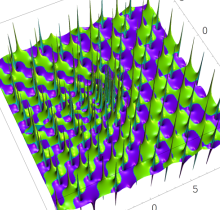
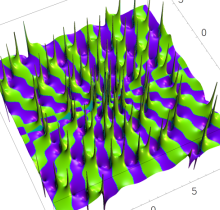
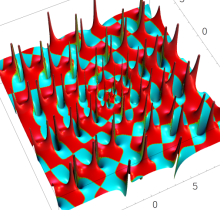
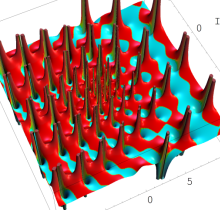
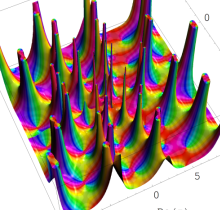
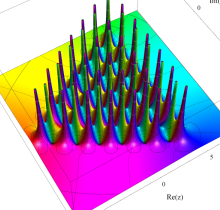
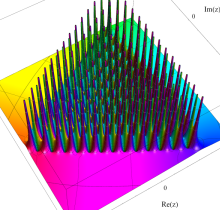
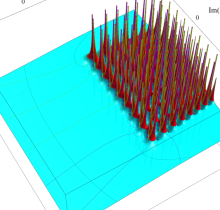
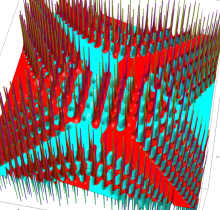
複素変数の第1種 Painlevé 超越関数
実変数の第1種 Painlevé 超越関数
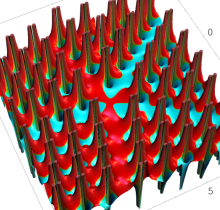
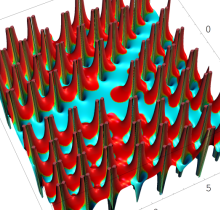
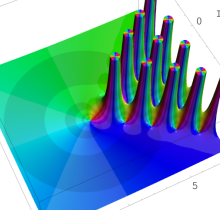
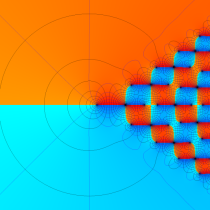
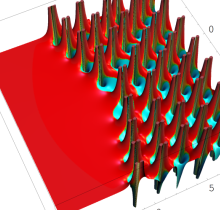
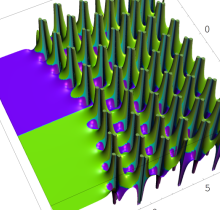
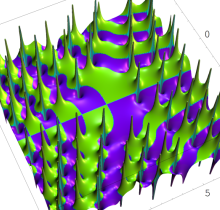
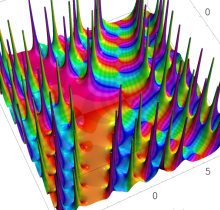
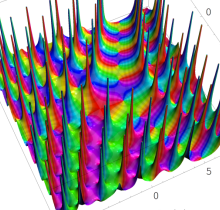
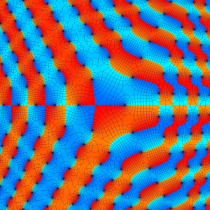
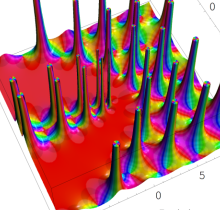
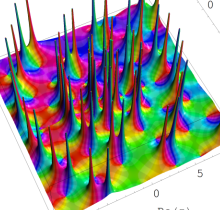
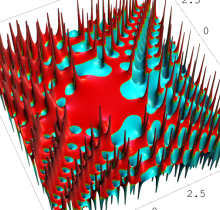
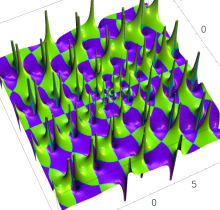
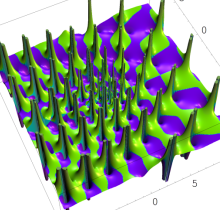
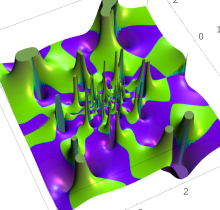
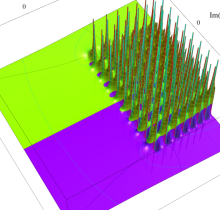
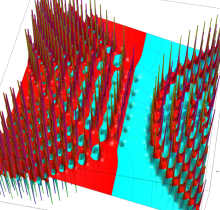
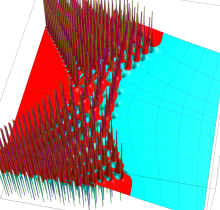
複素変数の第1種 Painlevé 超越関数
実変数の第1種 Painlevé 超越関数
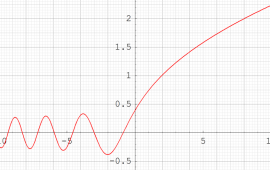
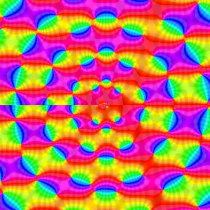
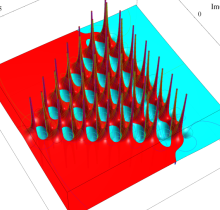
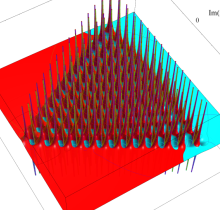
複素変数の第1種 Painlevé 超越関数
実変数の第1種 Painlevé 超越関数
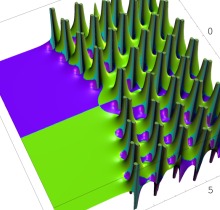
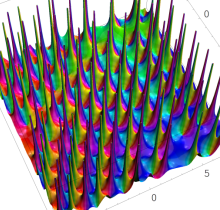
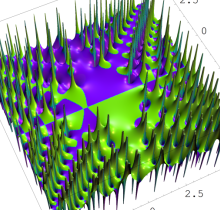
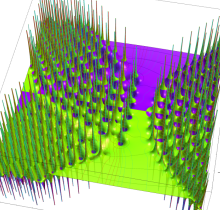
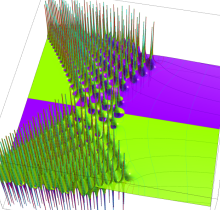
複素変数の第1種 Painlevé 超越関数
実変数の第1種 Painlevé 超越関数
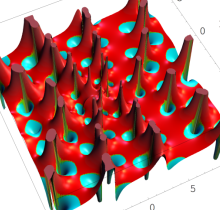
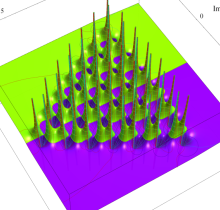
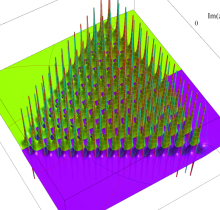
複素変数の第1種 Painlevé 超越関数
第2種 Painlevé 超越関数
Painlevé 方程式のうちでも、第2種は、同じく解が一価有理型関数になる
数学や物理学への応用例も、Painlevé 方程式の中では比較的多い方になるが、特に興味深い事例として、ランダム行列理論における Tracy - Widom 分布が挙げられる。この分布の確率密度関数は、
ここでは、第2種 Painlevé 方程式
である。第2種 Painlevé 超越関数の動く極は、常に1位である。
は、微分方程式
を満たす。計算は、W. Fair と Y. L. Luke による連分数近似法による。
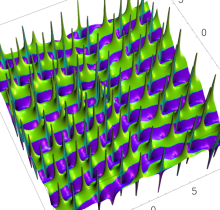
複素変数の第2種 Painlevé 超越関数
実変数の第2種 Painlevé 超越関数
複素変数の第2種 Painlevé 超越関数
実変数の第2種 Painlevé 超越関数
複素変数の第2種 Painlevé 超越関数
実変数の第2種 Painlevé 超越関数
複素変数の第2種 Painlevé 超越関数
実変数の第2種 Painlevé 超越関数
複素変数の第2種 Painlevé 超越関数
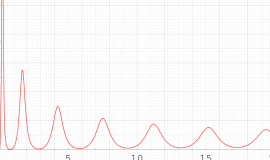
実変数の第2種 Painlevé 超越関数(Hastings - McLeod 解)
複素変数の第2種 Painlevé 超越関数(Hastings - McLeod 解)
実変数の第2種 Painlevé 超越関数
複素変数の第2種 Painlevé 超越関数
実変数の第2種 Painlevé 超越関数
複素変数の第2種 Painlevé 超越関数
アニメーション(12.30MB)
複素変数の第2種 Painlevé 超越関数
複素変数の第2種変形 Painlevé 超越関数
実変数の第2種変形 Painlevé 超越関数
複素変数の第2種変形 Painlevé 超越関数
実変数の第2種変形 Painlevé 超越関数
複素変数の第2種変形 Painlevé 超越関数
実変数の第2種変形 Painlevé 超越関数
複素変数の第2種変形 Painlevé 超越関数
実変数の第2種変形 Painlevé 超越関数
複素変数の第2種変形 Painlevé 超越関数
実変数の第2種変形 Painlevé 超越関数
複素変数の第2種変形 Painlevé 超越関数
第3種 Painlevé 超越関数
ここでは、第3種 Painlevé 方程式の解を具体的に
である。第3種 Painlevé 超越関数は原点に対数分岐点を持ち、通常は
しばしば、「Alternative な形」と呼ばれる
の解
計算は、W. Fair と Y. L. Luke による連分数近似法を拡張した方法による。
複素変数の第3種 Painlevé 超越関数
実変数の第3種 Painlevé 超越関数
複素変数の第3種 Painlevé 超越関数
実変数の第3種 Painlevé 超越関数
複素変数の第3種 Painlevé 超越関数
実変数の第3種 Painlevé 超越関数
複素変数の第3種 Painlevé 超越関数
実変数の第3種 Painlevé 超越関数
複素変数の第3種 Painlevé 超越関数
実変数の第3種 Painlevé 超越関数
複素変数の第3種 Painlevé 超越関数
実変数の第3種 Painlevé 超越関数
複素変数の第3種 Painlevé 超越関数
実変数の第3種 Painlevé 超越関数
複素変数の第3種 Painlevé 超越関数
第4種 Painlevé 超越関数
第4種 Painlevé 方程式は、解が一価有理型関数になり、特別な場合として古典的関数解を含むなど、
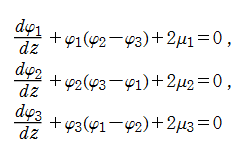
である。これらの対称的な関数を用いると、第4種 Painlevé 方程式の Bäcklund 変換は大変簡潔に表現できる。またこれに付随して、
Painlevé 方程式の対称形式については、第4種のほかに第2種、第5種でも発見されており、これらは野海正俊・山田泰彦による研究が端緒になっている。逆に、対称性を持つ連立非線形微分方程式から、Painlevé 性などの良い性質を持つ3階以上の非線形常微分方程式を導くという方法も、現在盛んに研究されている。
ここでは、第4種 Painlevé 方程式
である。
計算は、W. Fair と Y. L. Luke による連分数近似法を拡張した方法による。
【註記】
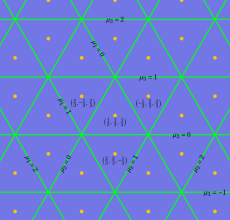
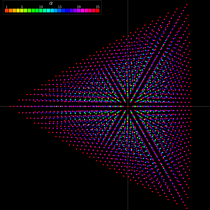
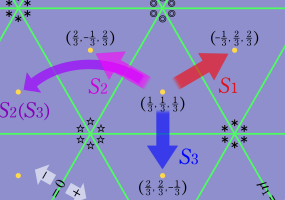
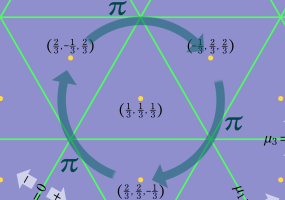
※1:このことを、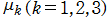 の三角座標上の領域として図示すると、次のようになる。(第4種 Painlevé 方程式の Bäcklund 変換の詳細は、後述の 「第4種 Painlevé 方程式の古典関数解」 に記載している。)
の三角座標上の領域として図示すると、次のようになる。(第4種 Painlevé 方程式の Bäcklund 変換の詳細は、後述の 「第4種 Painlevé 方程式の古典関数解」 に記載している。)
※1:このことを、
複素変数の第4種 Painlevé 超越関数
実変数の第4種 Painlevé 超越関数
複素変数の第4種 Painlevé 超越関数
実変数の第4種 Painlevé 超越関数
複素変数の第4種 Painlevé 超越関数
実変数の第4種 Painlevé 超越関数
複素変数の第4種 Painlevé 超越関数
実変数の第4種 Painlevé 超越関数
複素変数の第4種 Painlevé 超越関数
実変数の第4種 Painlevé 超越関数
複素変数の第4種 Painlevé 超越関数
実変数の第4種 Painlevé 超越関数
複素変数の第4種 Painlevé 超越関数
第5種 Painlevé 超越関数
ここでは、第5種 Painlevé 方程式の解を具体的に
である。第5種 Painlevé 超越関数は原点に対数分岐点を持ち、通常は
計算は、W. Fair と Y. L. Luke による連分数近似法を拡張した方法による。
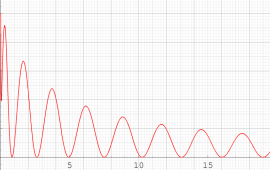
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
実変数の第5種 Painlevé 超越関数
複素変数の第5種 Painlevé 超越関数
第6種 Painlevé 超越関数
ここでは、第6種 Painlevé 方程式の解を具体的に
である。第6種 Painlevé 超越関数は
M. E. R. Fuchs は、代数的な (Fuchs 型の) 楕円体微分方程式が持つ4個の確定特異点が Riemann 球面上を動くとき、微分方程式の解の多価性 (モノドロミー群) が不変となるように固有値 (アクセサリーパラメーター) を決定するための必要十分条件を求めたが、それは、固有値が確定特異点の位置に依存する値を変数とし、第6種 Painlevé 方程式を満たす関数になるという結果であった。これを、(特異点4個の Fuchs 型微分方程式に対する) モノドロミー保存変形問題という※1。
線形常微分方程式の理論において超幾何関数が要の存在であるように、非線形常微分方程式版のそれは第6種 Painlevé 超越関数になるだろうとの予想もあり、今後の発展が特に期待されている。
計算は、W. Fair と Y. L. Luke による連分数近似法を拡張した方法による。
【註記】
※1:もし、確定特異点が3個ならば、固有値が生じずモノドロミー群 (および一次分数変換の群) が具体的に書き表わせるので、保型関数の Gauss - Schwarz 理論が可能となる。モノドロミー保存変形問題はこれの拡張として現れたものである。逆に、確定特異点が5個以上ならば、固有値は関数として多変数 Painlevé 方程式 (Garnier 方程式) の解となる。
※1:もし、確定特異点が3個ならば、固有値が生じずモノドロミー群 (および一次分数変換の群) が具体的に書き表わせるので、保型関数の Gauss - Schwarz 理論が可能となる。モノドロミー保存変形問題はこれの拡張として現れたものである。逆に、確定特異点が5個以上ならば、固有値は関数として多変数 Painlevé 方程式 (Garnier 方程式) の解となる。
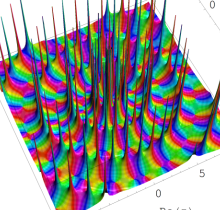
複素変数の第6種 Painlevé 超越関数
実変数の第6種 Painlevé 超越関数
複素変数の第6種 Painlevé 超越関数
実変数の第6種 Painlevé 超越関数
複素変数の第6種 Painlevé 超越関数
実変数の第6種 Painlevé 超越関数
複素変数の第6種 Painlevé 超越関数
実変数の第6種 Painlevé 超越関数
複素変数の第6種 Painlevé 超越関数
実変数の第6種 Painlevé 超越関数
複素変数の第6種 Painlevé 超越関数
実変数の第6種 Painlevé 超越関数
複素変数の第6種 Painlevé 超越関数
第2種 Painlevé 方程式の古典関数解
日:Yablonskii-Vorob'ev多項式,ヤブロンスキー・ヴォロビエフ多項式英:Yablonskii-Vorob'ev polynomials,仏:Polynôme de Yablonskii-Vorob'ev,独:Yablonskii-Vorob'ev Polynom
第2種 Painlevé 方程式
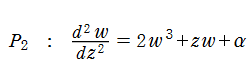
によって求めることができる。特に、
を初期関数 (Seed 解) として前述の Bäcklund 変換を繰り返し施したもので尽くされる。
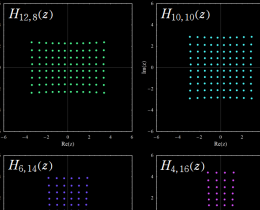
このうち有理関数解は、多項式の対数微分形の式
として表わすことができる。この多項式
から導かれる。
なお、第1種を除く Painlevé 方程式、ある種の高階 Painlevé 方程式についても有理関数解があり、同様の性質が見出されている。併せて有理関数解は扱い易いため、特定の非線形常微分方程式が Painlevé 性を持つ理由、各種 Painlevé 方程式の一般解全体の構造など、諸研究の手掛かりにもなっている。
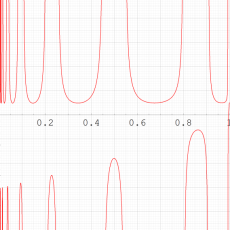
第2種 Painlevé 方程式の有理関数解
第2種 Painlevé 方程式の有理関数解
第2種 Painlevé 方程式の有理関数解
第2種 Painlevé 方程式の Airy 関数解
第2種 Painlevé 方程式の Airy 関数解
第2種 Painlevé 方程式の Airy 関数解
第2種 Painlevé 方程式の Airy 関数解
第2種 Painlevé 方程式の Airy 関数解
アニメーション(7.52MB)
第2種 Painlevé 方程式の Airy 関数解
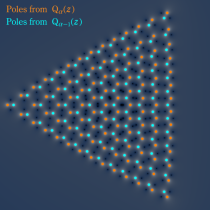
第2種 Painlevé 方程式の有理関数解
(前述のように有理関数解は対数微分で表わされるので、その分母は必ず2個の Yablonskii - Vorob'ev 多項式の積になる。)
第4種 Painlevé 方程式の古典関数解
第4種 Painlevé 方程式の Bäcklund 変換は、前述のとおり対称な3連1階非線形微分方程式
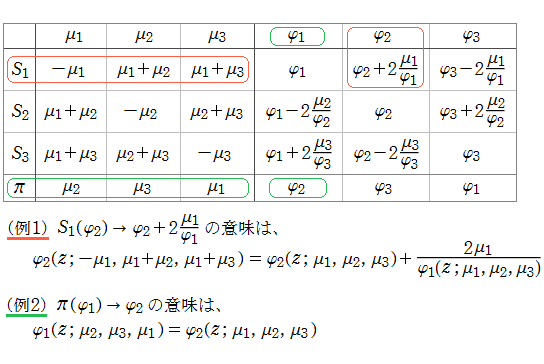
で考えたほうが分かりやすい。上記3種類の関数およびパラメーター間では、4種類の Bäcklund 変換
また、三角座標
以上のもとで、有理関数解および Hermite 関数解は、
を初期関数 (Seed 解) として前述の Bäcklund 変換を繰り返し施したもので尽くされる。以下では、これらの
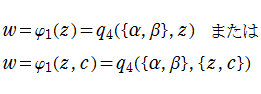
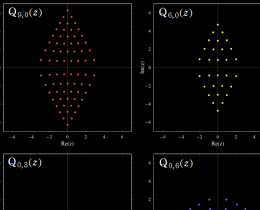
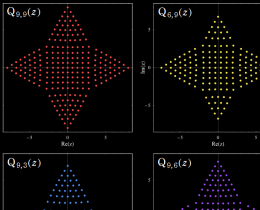
一般岡本多項式
このうち、
一般 Hermite 多項式
これらの多項式も Schur 関数型の表示式(記述は省略する)を持ち、種々の組合わせ論的な性質が発見される等、第2種の場合と同様の理論が展開されている。
【註記】
※1:タウ関数に成り得る他の例としては Weierstrass の楕円シグマ関数がある。その2階対数微分が Weierstrass の楕円関数となる事と上記の話とは類似関係になっている。(実際、これらの多項式のグラフは原点周辺に限れば、Weierstrass の楕円シグマ関数のそれに似ている。)
※1:タウ関数に成り得る他の例としては Weierstrass の楕円シグマ関数がある。その2階対数微分が Weierstrass の楕円関数となる事と上記の話とは類似関係になっている。(実際、これらの多項式のグラフは原点周辺に限れば、Weierstrass の楕円シグマ関数のそれに似ている。)
②
第4種 Painlevé 方程式の (有理) Hermite 多項式解
第4種 Painlevé 方程式の (有理)岡本多項式解
第4種 Painlevé 方程式の (有理)岡本多項式解
第4種 Painlevé 方程式の (有理)岡本多項式解
第4種 Painlevé 方程式の (有理) Hermite 関数解
第4種 Painlevé 方程式の (有理) Hermite 関数解
第4種 Painlevé 方程式の (有理) Hermite 関数解
第4種 Painlevé 方程式の (有理) Hermite 関数解
第4種 Painlevé 方程式の (有理) Hermite 関数解
第4種 Painlevé 方程式の (有理) Hermite 関数解
第4種 Painlevé 方程式の (有理) Hermite 関数解
第4種 Painlevé 方程式の (有理) Hermite 関数解
第4種 Painlevé 方程式の (有理) Hermite 関数解
一般 Hermite 多項式
第4種 Painlevé 方程式の (有理) Hermite 多項式解
(前述のように有理関数解は対数微分で表わされるので、その分母は必ず2個の一般 Hermite 多項式の積になる。)
一般岡本多項式
第4種 Painlevé 方程式の (有理)一般岡本多項式解
(同様に、この有理関数解の分母は必ず2個の一般岡本多項式の積になる。)
一般岡本多項式
一般岡本多項式
第4種 Painlevé 方程式の (有理)一般岡本多項式解
(同様に、この有理関数解の分母は必ず2個の一般岡本多項式の積になる。)