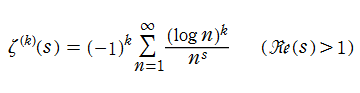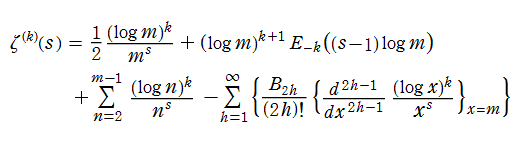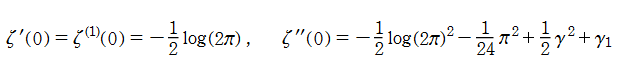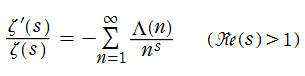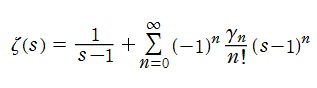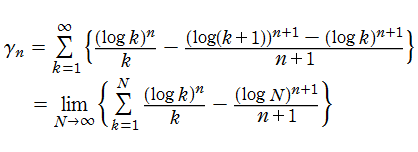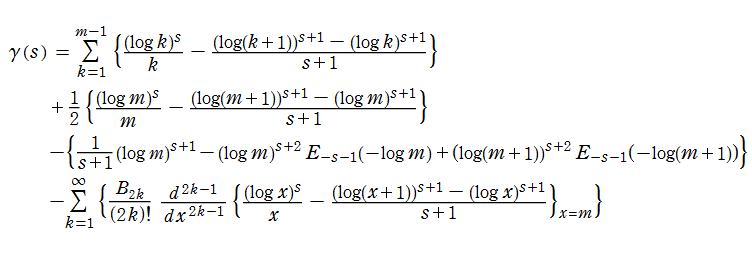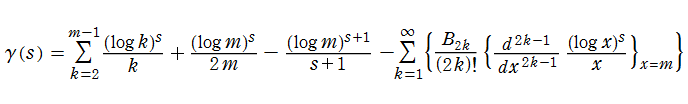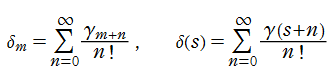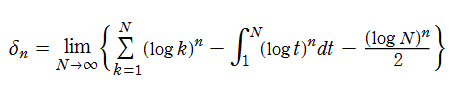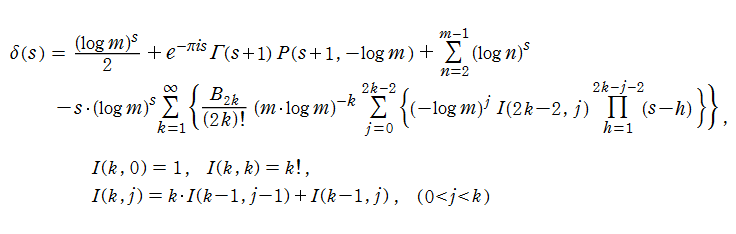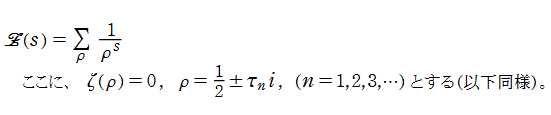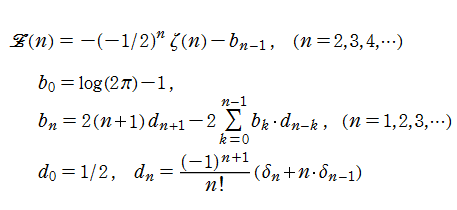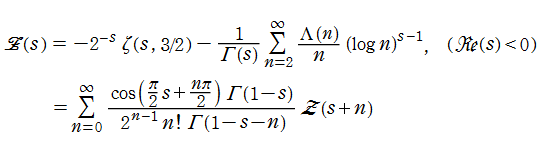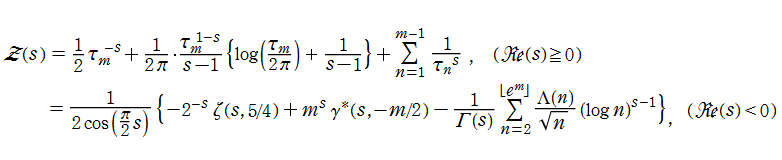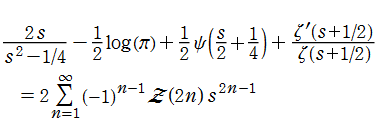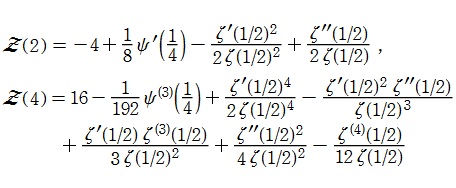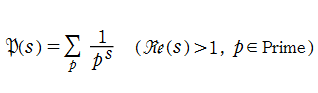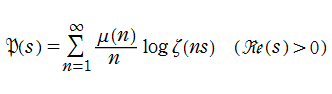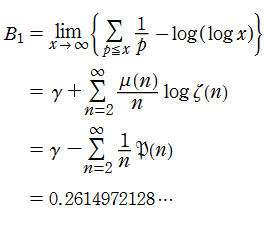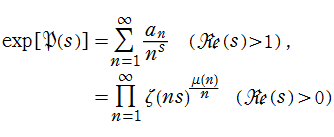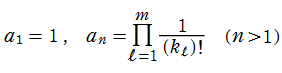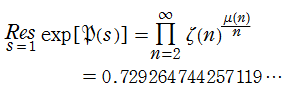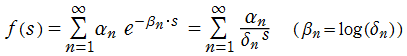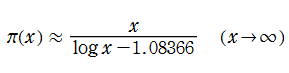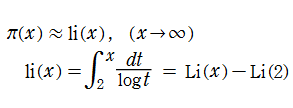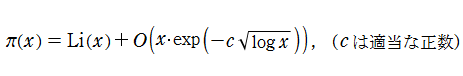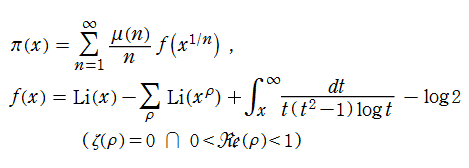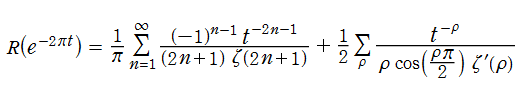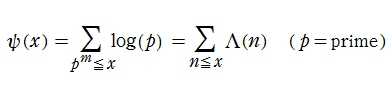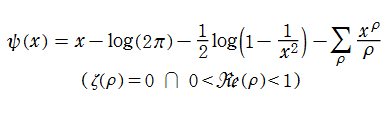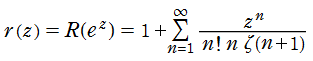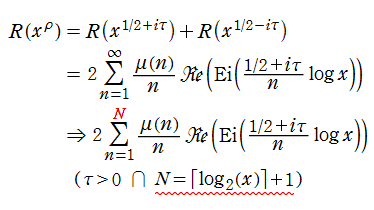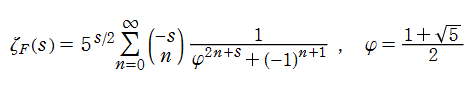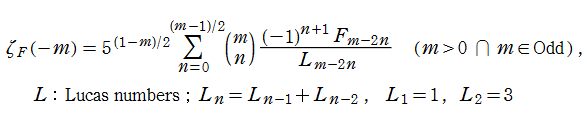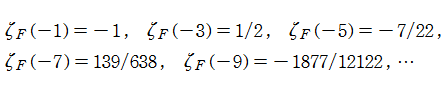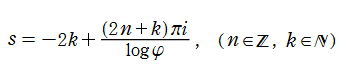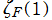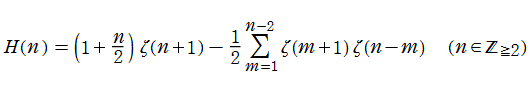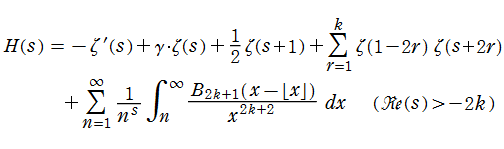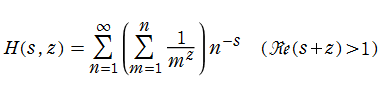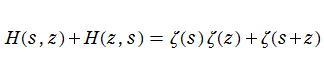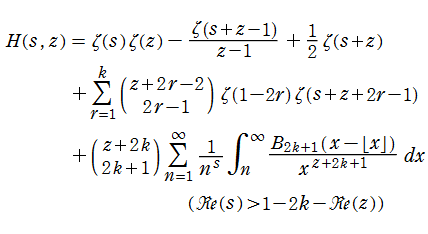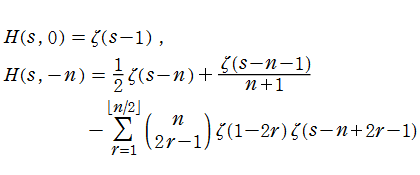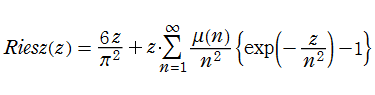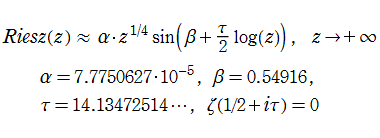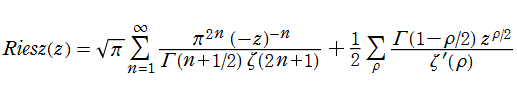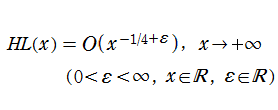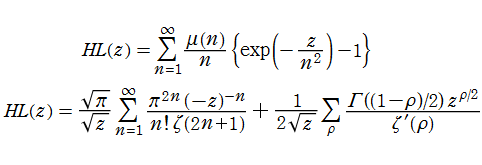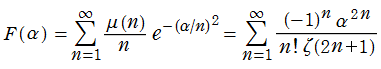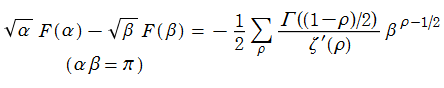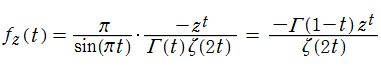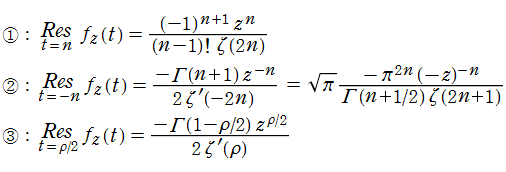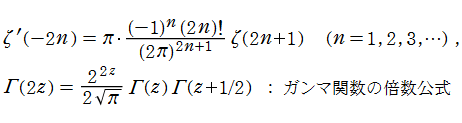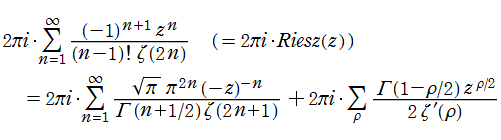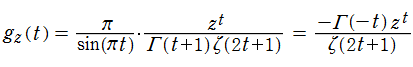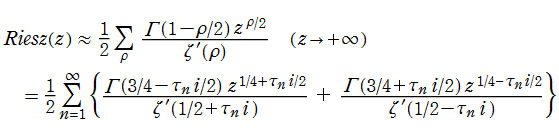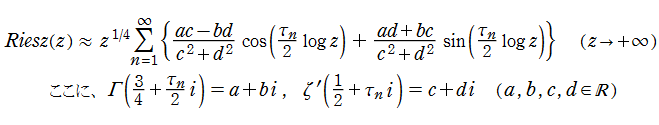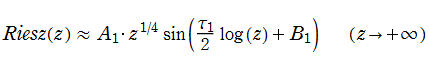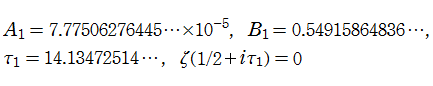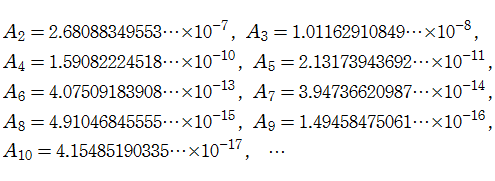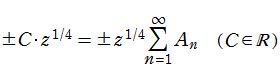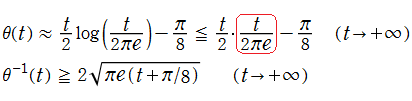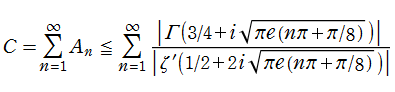特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
ゼータ関数に関連する関数
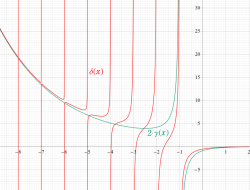
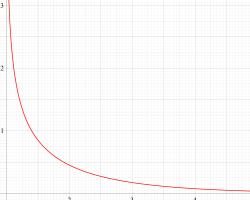
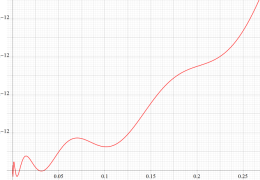
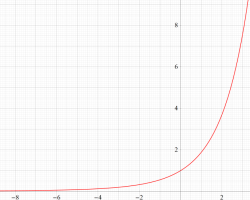
Riemann ゼータ関数の導関数
Riemann ゼータ関数の導関数は、Dirichlet 級数展開式をによって表わされる (和は
を使用すれば計算できる。ここに
Riemann ゼータ関数の導関数は、
等の特殊値がよく知られている。ここに、
また、Riemann ゼータ関数の対数微分は、Dirichlet 級数
に展開される。ここに、
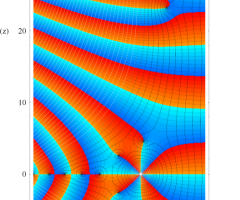
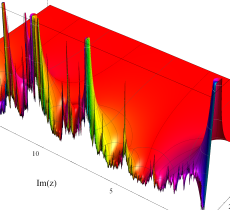
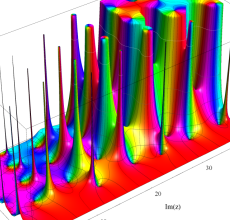
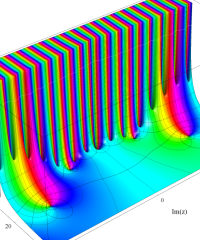
複素関数としての Riemann ゼータ関数の導関数
【註記】
※1 : このような相違点を踏まえて、Riemann ゼータ関数とは異なる頁に掲載することとした。
※2 : A. Speiser 「Geometrisches zur Riemannschen Zetafunktion」 Mathematische Annalen, 110, (1935), No.1, p.514-521
※3 : N. Levinson, H. L. Montgomery 「Zeros of the derivatives of the Riemann zeta-function」 Acta Mathematica, 133, (1974), p.49-65
※1 : このような相違点を踏まえて、Riemann ゼータ関数とは異なる頁に掲載することとした。
※2 : A. Speiser 「Geometrisches zur Riemannschen Zetafunktion」 Mathematische Annalen, 110, (1935), No.1, p.514-521
※3 : N. Levinson, H. L. Montgomery 「Zeros of the derivatives of the Riemann zeta-function」 Acta Mathematica, 133, (1974), p.49-65
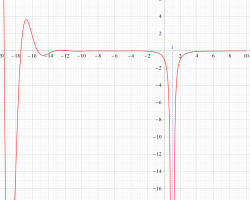
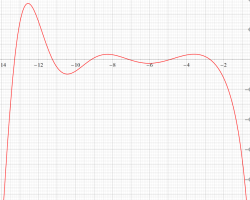
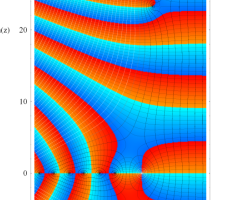
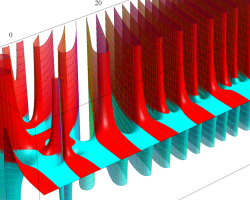
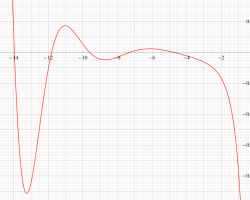
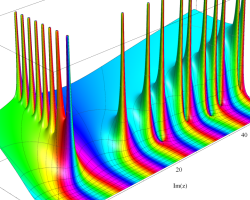
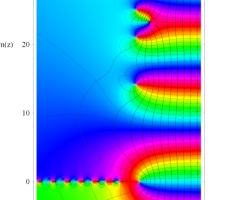
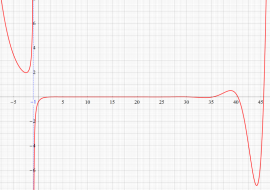
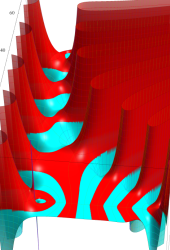
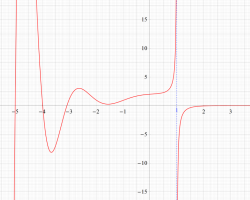
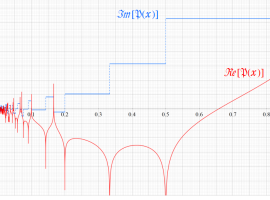
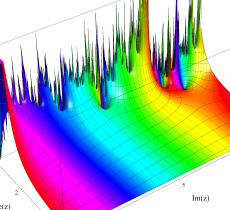
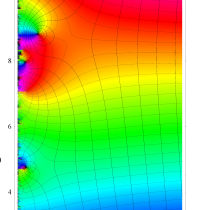
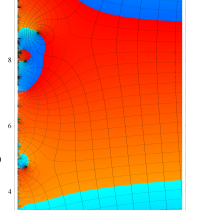
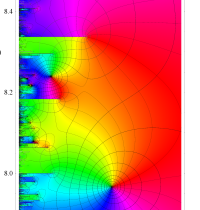
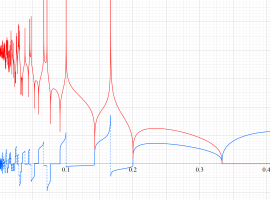
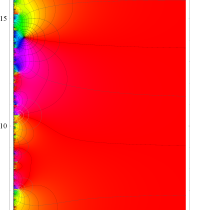
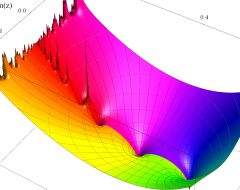
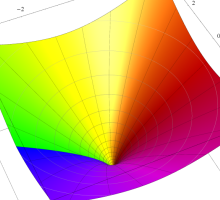
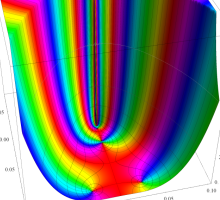
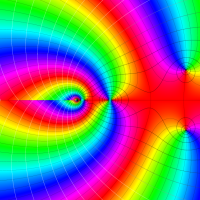
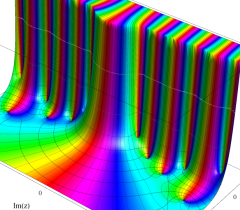
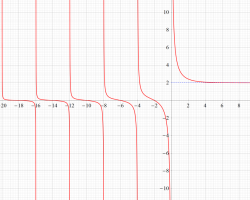
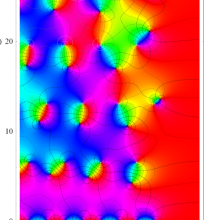
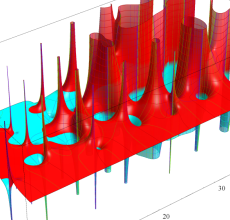
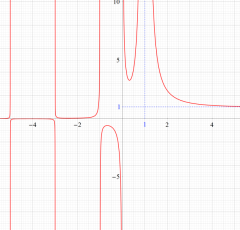
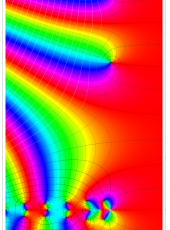
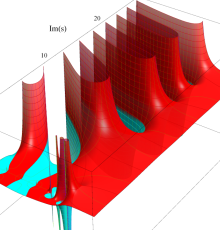
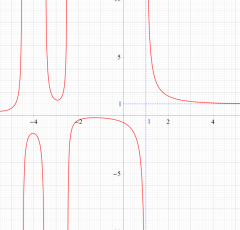
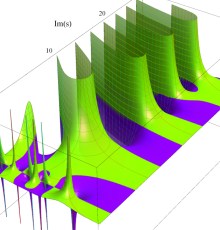
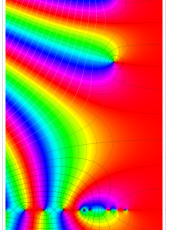
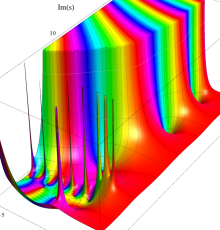
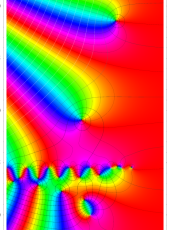
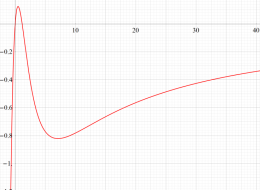
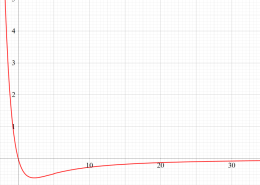
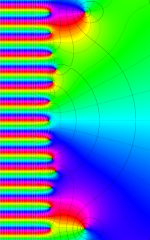
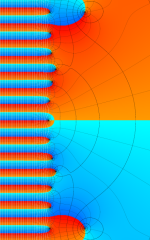
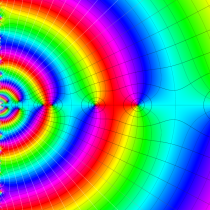
②負の定義域のうち、関数の絶対値が小さくなる部分を拡大したグラフ。
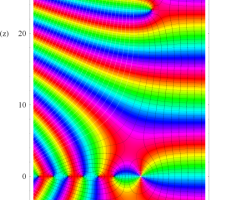
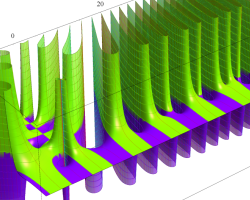
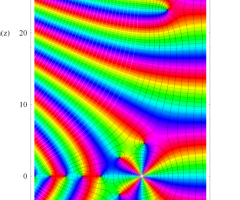
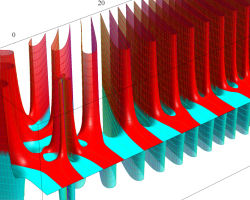
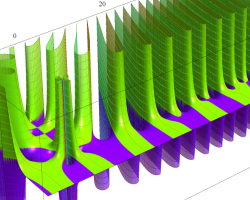
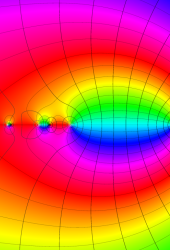
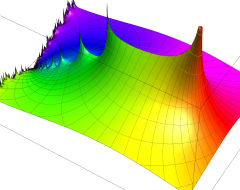
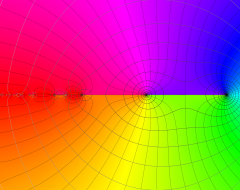
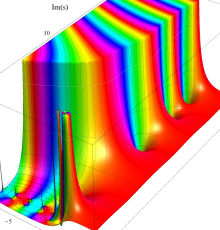
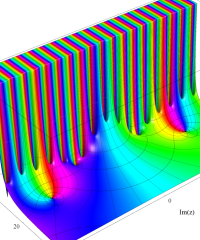
複素変数の Riemann ゼータ関数の導関数のグラフ。
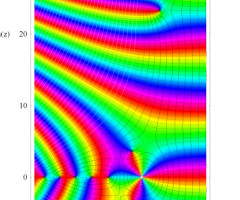
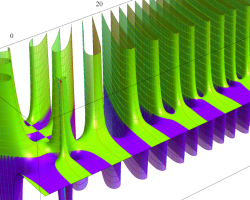
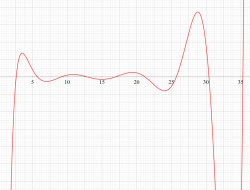
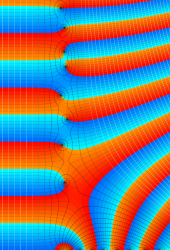
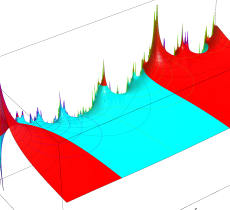
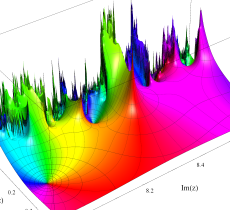
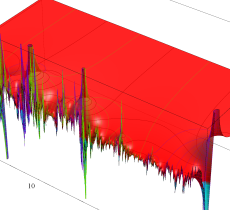
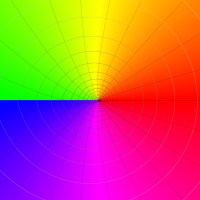
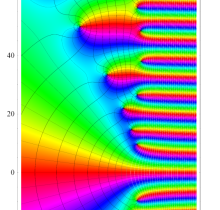
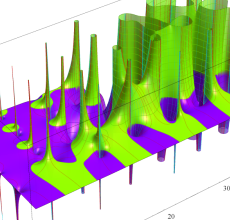
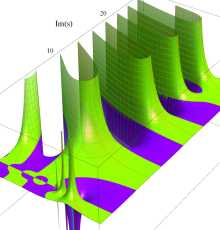
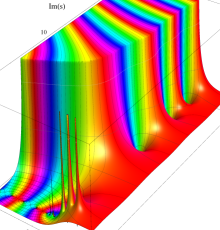
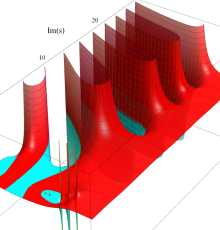
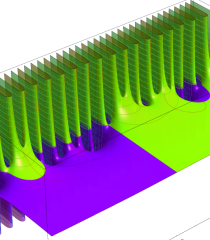
②負の定義域のうち、関数の絶対値が小さくなる部分を拡大したグラフ。
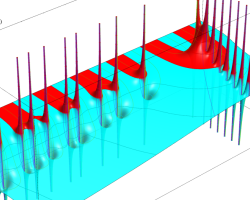
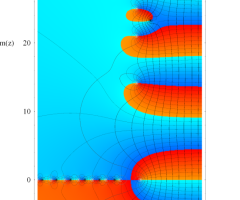
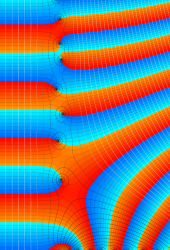
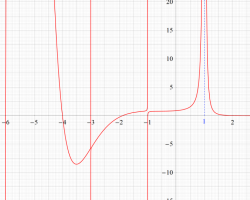
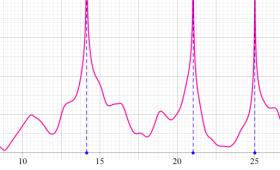
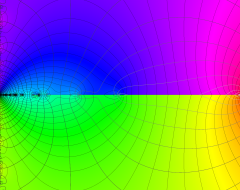
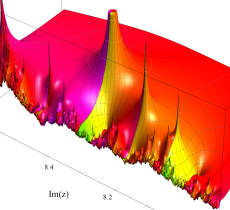
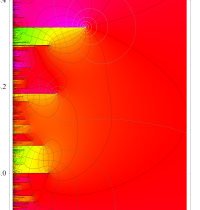
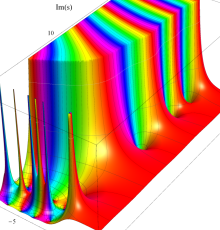
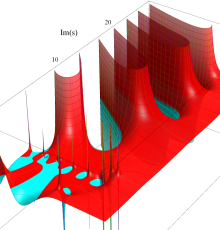
複素変数の Riemann ゼータ関数の2位導関数のグラフ。
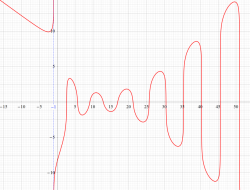
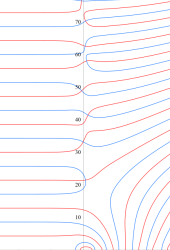
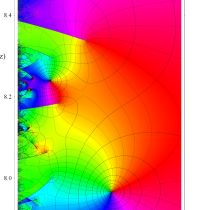
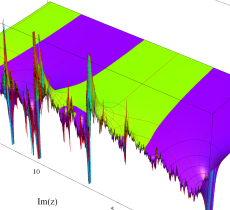
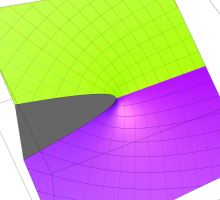
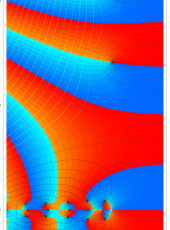
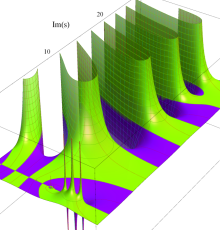
②負の定義域のうち、関数の絶対値が小さくなる部分を拡大したグラフ。
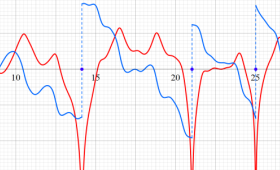
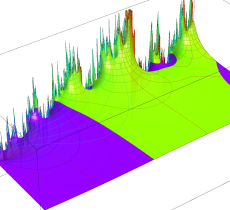
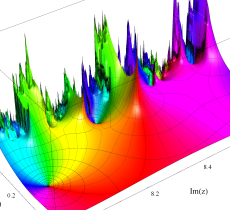
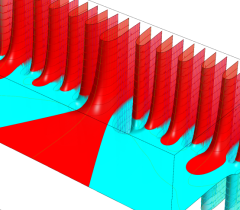
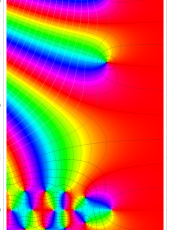
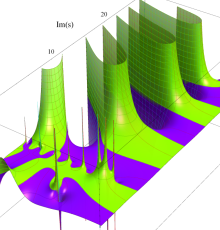
複素変数の Riemann ゼータ関数の3位導関数のグラフ。
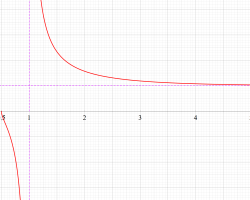
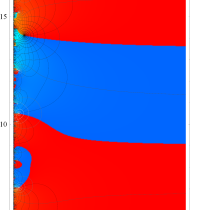
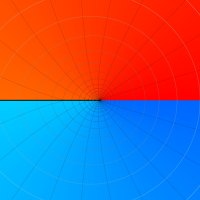
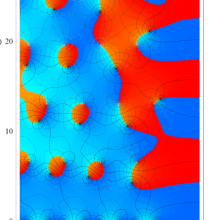
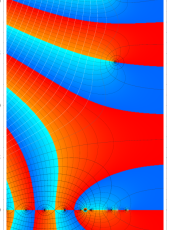
②負の定義域のうち、関数の絶対値が小さくなる部分を拡大したグラフ。
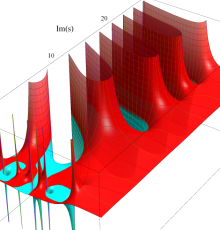
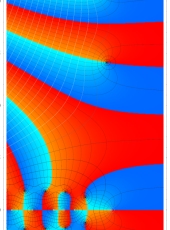
複素変数の Riemann ゼータ関数の対数微分のグラフ。
Stieltjes 関数
日:Stieltjes関数,スティルチェス関数英:Stieltjes function,仏:Fonction de Stieltjes,独:Stieltjes funktion
Riemann のゼータ関数の極
に現れる係数
によって定義され、特に
この定義式はともに、変数
上記の無限級数の収束は大変遅いので、実際の数値計算では、これに 「Euler - Maclaurin 総和公式」 を適用して得られる式
を使用する。ここに
さらに、Stieltjes 関数は
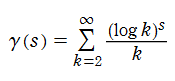
が得られる。この式はさらに収束が速く、数値計算に便利である。
後述の Sitaramachandrarao 関数は、Stieltjes 関数によって表わすことができる。すなわち、両者は
の関係にある。
複素関数としての Stieltjes 関数は、
【註記】
※1 : J. Bohman & C. E. Fröberg 「The Stieltjes function - Definition and properties」 Mathematics of Computation, vol.51 (1988) pp.281-289
※1 : J. Bohman & C. E. Fröberg 「The Stieltjes function - Definition and properties」 Mathematics of Computation, vol.51 (1988) pp.281-289
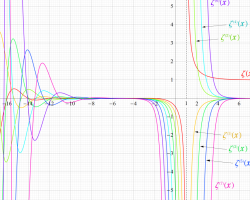
②正の定義域のうち、関数の絶対値が小さくなる部分を拡大したグラフ。
③ J. Bohman & C. E. Fröberg の論文にあるものと同じ、
複素変数の Stieltjes 関数のグラフ。
J. Bohman & C. E. Fröberg の論文にあるものと同様のグラフ。
非自明零点の Dirichlet 級数
唯一の極を解消した Riemann のゼータ関数が、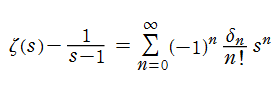
Sitaramachandrarao 定数は、極限式
によって定義されるが、この式を直接計算するのは難しい。極限式は複素数
実際の計算では、上記の極限式に Euler - Maclaurin 総和公式を適用した式
を使用する。ここに
複素関数としての Sitaramachandrarao 関数は、負の整数上でガンマ関数に由来する1位の極を持つ有理型関数である。また、正の実軸上に零点を持つほか複素零点も持つ。それらの位置に Riemann ゼータ関数のような規則性は見られず、グラフの概形も、前述の極の周辺を除いて Stieltjes 関数と似ている。
Lehmer の論文によれば、Riemann ゼータ関数の非自明零点に関する Dirichlet 級数※1
の引数
と表わされる※2。 複素関数としての
André Voros著 「Zeta functions over zeros of zeta functions」 Lecture Notes of the Unione Matematica Italiana, Vol.8 (2010), Springer) によれば、
となる。ここに
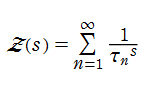
によって計算できる。ここに
のように冪級数展開式の係数として求められる。例えば具体的に、
となる。
関数
【註記】
※1 : 1914年に G. H. Hardy によって、少なくとも臨界線上の非自明零点は無限個存在することが証明されているので、これらは無限級数になる。また、級数の定義方法から分かるとおり、Riemann 予想の成立を仮定している。
※2 : この Dirichlet 級数の値を用いて、Stieltjes 定数を表現することも可能である。例えば、J. B. Keiper の論文 「Power series expansions of Riemann's ξ function」 Mathematics of Computation, vol.58 (1992) pp.765-773 等。これまでの結果を大雑把に解釈すれば、母関数や特殊値を介した次のような特殊関数の系列が存在すると言える。
※1 : 1914年に G. H. Hardy によって、少なくとも臨界線上の非自明零点は無限個存在することが証明されているので、これらは無限級数になる。また、級数の定義方法から分かるとおり、Riemann 予想の成立を仮定している。
※2 : この Dirichlet 級数の値を用いて、Stieltjes 定数を表現することも可能である。例えば、J. B. Keiper の論文 「Power series expansions of Riemann's ξ function」 Mathematics of Computation, vol.58 (1992) pp.765-773 等。これまでの結果を大雑把に解釈すれば、母関数や特殊値を介した次のような特殊関数の系列が存在すると言える。
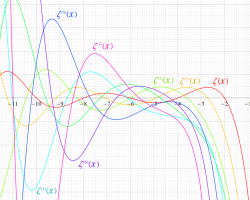
②負の実数方向へ更に広い範囲を描画する。変曲点が Stieltjes 関数の2倍に近づく。
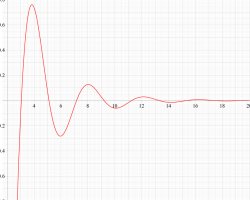
③正の定義域のうち、関数の絶対値が小さくなる部分を拡大したグラフ。振動していることが分かる。
複素変数の Sitaramachandrarao 関数のグラフ。3番目は、2番目のグラフの原点周辺を拡大した場合。
②正の定義域のうち、関数の絶対値が小さくなる部分を確認するため、代わりに
複素変数の、非自明零点に関する Dirichlet 級数
複素変数の、非自明零点に関する Dirichlet 級数
素数ゼータ関数
日:素数ゼータ関数,素数ζ関数英:Prime zeta function,仏:Fonction zêta des nombres premiers,独:Primzetafunktion
素数の逆数列に関する Dirichlet 級数で表わされる関数
は、現在では素数ゼータ関数と呼ばれている※1。この関数については、19世紀後半の J. W. L. Glaisher 等による研究結果が知られているが、後述のとおり、関数の着想自体はもっと古くから存在したと推測される。
素数ゼータ関数は、Landau - Hurwitz の公式 (ただし、発見者は恐らく Glaisher (1891年) と思われる。)
によってさらに広い領域へ解析接続される。ここに
複素関数としての素数ゼータ関数は、Landau - Hurwitz の公式から明らかなように、正の方向から虚軸に近付くにつれて Riemann ゼータ関数の非自明零点に由来する対数分岐点が集積するため、虚軸が解析関数としての自然境界となる※2。また、平方因子を含まない自然数を
素数ゼータ関数は主に素数分布論で現れるが、Riemann のゼータ関数に比べると頻度は少ない。L. Euler は Riemann ゼータ関数の素数積表示式を用いて、素数が無限個存在することの新しい証明、および素数の逆数和が発散することの証明を与えた (1737年)。これは
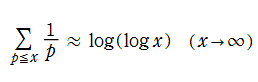
と求められており、「Meissel - Mertens 定数」 と呼ばれる。ここに
素数ゼータ関数を指数関数に代入した関数は、Dirichlet 級数、および Landau - Hurwitz の公式から得られる無限乗積
で表わされる。ここに係数
であるとする。無限乗積の形から
である。
前述の無限乗積は複素数値計算に適しているが、その結果は
【註記】
※1 : 素数ゼータ関数,副次的ゼータ関数,Fibonacci ゼータ関数等は、一般 Dirichlet 級数
に該当するため 「ゼータ」 を含む名称で呼ばれるが、その性質は多くの点で Riemann ゼータ関数と異なることから、通常はゼータ関数の一種であるとは考えない。
本文のとおり、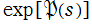 は通常の Dirichlet 級数で表示できるものの、そのグラフは依然として Riemann ゼータ関数との相違点が多い。
は通常の Dirichlet 級数で表示できるものの、そのグラフは依然として Riemann ゼータ関数との相違点が多い。
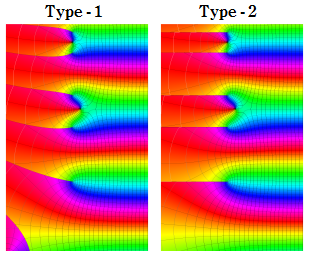
※2 : Landau - Hurwitz の公式における Riemann ゼータ関数の対数は、単純に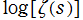 で計算すると分枝切断線が 「Type-1」 のようになる。当サイトでは、すべての分枝切断線が実軸に平行となる 「Type-2」 を採用する。(因みに、Mathematica の素数ゼータ関数で採用されている分枝切断線は、このいずれとも異なる。)
で計算すると分枝切断線が 「Type-1」 のようになる。当サイトでは、すべての分枝切断線が実軸に平行となる 「Type-2」 を採用する。(因みに、Mathematica の素数ゼータ関数で採用されている分枝切断線は、このいずれとも異なる。)
* 素数ゼータ関数は、独自定義の 「素数正弦関数・素数ガンマ関数」 の対数微分を冪級数展開したときの係数としても現れます。
※1 : 素数ゼータ関数,副次的ゼータ関数,Fibonacci ゼータ関数等は、一般 Dirichlet 級数
に該当するため 「ゼータ」 を含む名称で呼ばれるが、その性質は多くの点で Riemann ゼータ関数と異なることから、通常はゼータ関数の一種であるとは考えない。
本文のとおり、
※2 : Landau - Hurwitz の公式における Riemann ゼータ関数の対数は、単純に
* 素数ゼータ関数は、独自定義の 「素数正弦関数・素数ガンマ関数」 の対数微分を冪級数展開したときの係数としても現れます。
②原点に近い実軸上における素数ゼータ関数のグラフ (実部と虚部)。
①臨界線上の素数ゼータ関数のグラフ (絶対値)。
②臨界線上の素数ゼータ関数のグラフ (実部と虚部)。
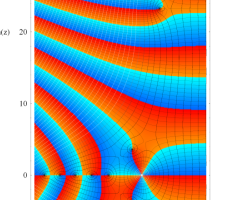
複素変数の素数ゼータ関数のグラフ。
複素変数のうち、原点に近い領域を拡大したグラフ。
複素変数のうち、虚軸に近い領域を拡大したグラフ。
複素変数のうち、虚軸に近い領域を拡大したグラフ (Type-1 の分枝切断線を採用した場合)。
②原点に近い実軸上における
①臨界線上:
②臨界線上:
複素変数の
複素変数のうち、原点に近い領域を拡大したグラフ。
複素変数のうち、虚軸に近い領域を拡大したグラフ。
Riemann 素数計数関数
日:Riemann素数計数関数,英:Riemann prime counting function, 仏:Fonction de compte des nombres premiers,
独:Riemannsche Primzahlfunktion
一般に広く知られているように素数は自然数の中で不規則に現れる。素数列そのものを定義する方程式や関数を見つけるという研究も古くから存在するが、それらは概ね発展性に乏しく、重要な成果があったとは言い難い※1。そこで多くの数学者は、代わりに素数の出現頻度を個数で捉え、その増加傾向を広い範囲で大まかに評価するという問題に視点を移した。一見すると素数との結びつきが前者に比べて間接的に見えるが、素数ゼータ関数の所でも述べたとおり、その着想は素数が無限個あることの解析的な証明法に起源があり、その後は大いに発展して前者とは比較にならないほどの成果が得られた。
現在では、素数の出現頻度を見積る方法、およびこれに関連する理論は 「素数分布論」 と呼ばれており、数論の重要な一分野となっている。特に素数分布論は、複素関数論等で得られた解析学の方法を積極的に数論に援用する 「解析的整数論」 の主要分野とされる。素数に関する多くの未解決問題、とりわけ Riemann 予想 (→ Riemann のゼータ関数を参照) との重要な接点が19世紀に発見されたため、以降は常に数学者等の関心を集めるようになったが、まだ多くが未解決で残っていることからも分かるように、この分野の研究は相当の困難が伴う。
素数の個数を捉える具体的な関数はいくつか例があるが、そのうち最も単純な定義は、正の実数
Legendre は1798年に近似
を推察した。しかしこの推察は正しくないことが、1838年に P. L. Chebyshev によって証明された (後述の素数定理に見るように定数
Gauss も1792年に
なる近似を推察した。ここに、
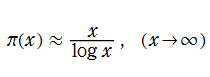
の形で証明される。この結果は、Riemann ゼータ関数の非自明零点の実部は1より小さいという事実と同値である。誤差項を改良する研究は現在でも続けられているが、1901年に N. F. H. von Koch は、Riemann 予想が正しいと仮定すれば得られる結果
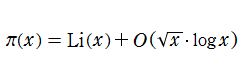
一方 Riemann は、ベルリン学士院月報1859年11月号に掲載された有名な論文 「与えられた数より小さい素数の個数について」 中で、素数の個数が (素数定理とは別の意味で) ゼータ関数の非自明零点と密接に関係していることを明らかにした。それは現在 「Riemann - von Mangoldt 公式」 と呼ばれている無限級数
であるが、(それまでの近似法を超えて) 驚くべきことに
Riemann - von Mangoldt 公式の意味を大雑把に (イメージ的に) 解釈すれば、補間間隔が不規則な素数列になるように変形された Fourier 級数によって
結果的にその後の歴史では、素数定理の証明自体に Riemann - von Mangoldt 公式は必要でなくなり、逆に最良の誤差項評価は Riemann 予想の成立と同値になることが判明したが、恐らく Riemann も素数定理とその誤差項評価を意識して、前述の論文を著したと思われる。
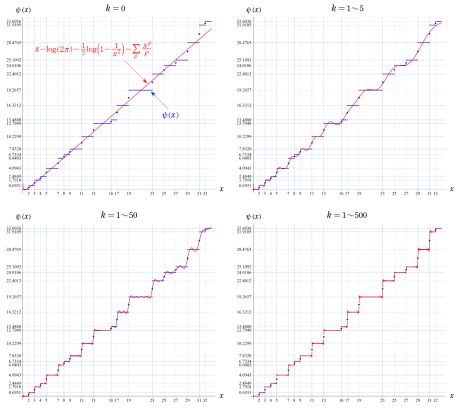
ところで、Riemann - von Mangoldt 公式において
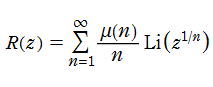
なお、この関数は 「Gram 級数」 と呼ばれる無限級数
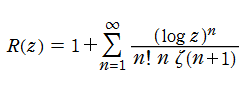
複素関数としての Riemann 素数計数関数は、複素平面上
によって計算できる※3。
Riemann 素数計数関数を導出する方法を、非自明零点の項、および積分と定数の項にも適用すると、Riemann 素数計数関数のみを用いた Riemann - von Mangoldt 公式の表示
が得られる。この表示式では、Riemann ゼータ関数の極とすべての零点からの影響が明確に見て取れ、さらに、自明零点をわたる和の項は (上記の範囲に限って) 初等関数に還元される。
素数分布論では
がある (ここでは、第1 Chebyshev 関数には触れない)。
となる。これは
【註記】
※1 : 大抵の結果は、入れ子になった累乗や床関数などの区分定義関数を使用した 「不自然で技巧的な」 関数となるため、そこから素数に関する何らかの知見を得ることはほとんど望めない。
(例えば、P. Ribenboim 著 「素数の世界:その探索と発見」 第3章が、この問題点等について詳しく論じている。)
※2 : この名称は Mathematica の言語解説ページ https://reference.wolfram.com/language/ref/RiemannR.html に従っているが、単に Riemann のR関数と呼ぶこともある。通常、Riemann 素数計数関数なる名称は、当サイトでの Riemann - von Mangoldt 公式 を指す場合が多い。なお、 も普通は素数階段関数ではなく 「素数計数関数」 と呼ばれることが多い。
も普通は素数階段関数ではなく 「素数計数関数」 と呼ばれることが多い。
※3 : Folkmar Bornemann の論文 「Solution of a Problem Posed by Jörg Waldvogel, (2003).」 http://www-m3.ma.tum.de/Allgemeines/FolkmarBornemannPublications を参照。(公開はインターネット上のみ。)
※1 : 大抵の結果は、入れ子になった累乗や床関数などの区分定義関数を使用した 「不自然で技巧的な」 関数となるため、そこから素数に関する何らかの知見を得ることはほとんど望めない。
(例えば、P. Ribenboim 著 「素数の世界:その探索と発見」 第3章が、この問題点等について詳しく論じている。)
※2 : この名称は Mathematica の言語解説ページ https://reference.wolfram.com/language/ref/RiemannR.html に従っているが、単に Riemann のR関数と呼ぶこともある。通常、Riemann 素数計数関数なる名称は、当サイトでの Riemann - von Mangoldt 公式 を指す場合が多い。なお、
※3 : Folkmar Bornemann の論文 「Solution of a Problem Posed by Jörg Waldvogel, (2003).」 http://www-m3.ma.tum.de/Allgemeines/FolkmarBornemannPublications を参照。(公開はインターネット上のみ。)
複素変数の Riemann 素数計数関数のグラフ。
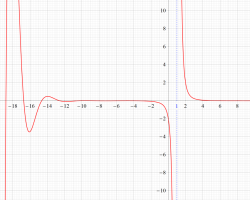
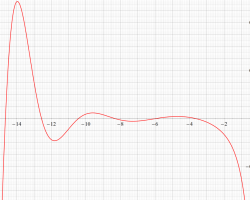
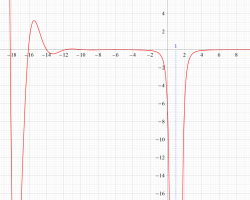
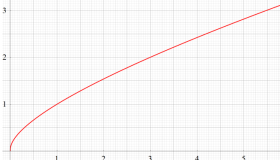
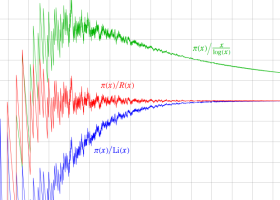
実変数の Riemann 素数計数関数
複素変数の Riemann 素数計数関数
になる。これは超越整関数であり、絶対値が非常に大きい負数の実零点が無数に存在する。
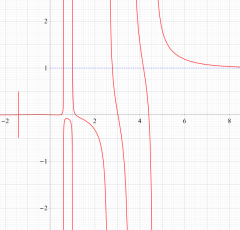
実変数の Riemann 素数計数指数関数のグラフ。
複素変数の Riemann 素数計数指数関数のグラフ。
描画領域を非常に大きくした場合の、実変数の Riemann 素数計数指数関数のグラフ。
つまり (指数関数を代入しない) Riemann 素数計数関数では、零点が原点の右側近傍に圧縮されている。
描画領域を非常に大きくした場合の、複素変数の Riemann 素数計数指数関数のグラフ。
なお、
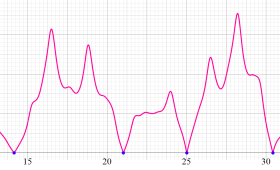
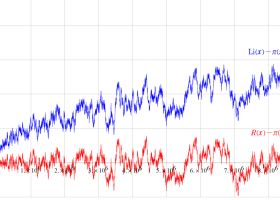
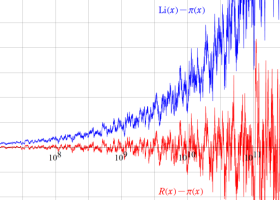
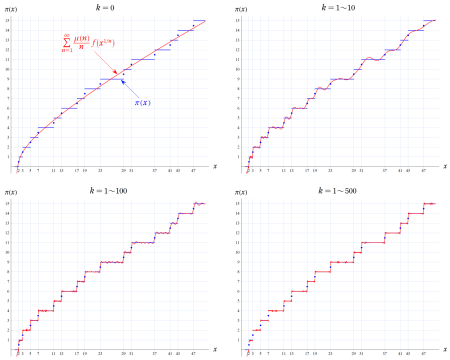
①若干狭い範囲のグラフ (
②より広い範囲のグラフ (
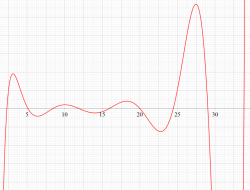
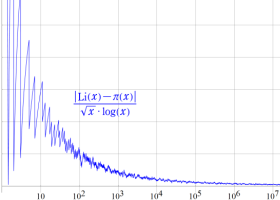
上限評価の誤差項を伴う素数定理のグラフ。
実は、このグラフは近似が鋭敏になるよう、非自明零点項の無限和を
アニメーション(2.64MB)
Riemann - von Mangoldt 公式が
このグラフは、Riemann - von Mangoldt 公式のような技法を用いなくても描画できる。
アニメーション(2.01MB)
Fibonacci ゼータ関数
Fibonacci 数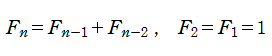
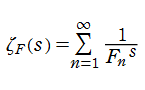
実際の数値計算、特に領域
を用いると便利である※1。また、この公式から負の奇数での特殊値が、有理数
になることも分かる。最初の5個の特殊値を具体的に示すと、
となる。
複素関数としての Fibonacci ゼータ関数は、複素平面上において無限個の一位の極
を持つ有理型関数である。特に実軸上において、極は
因みに超越数論では、変数が自然数のときの Fibonacci ゼータ関数の値について、超越数や無理数であるかどうかを問題とする。
ここに、
【註記】
※1 : L. Navas「Analytic continuation of the Fibonacci Dirichlet series」The Fibonacci Quarterly, vol.39, (2001) p. 409-418.
※2 :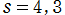 における Fibonacci ゼータ関数の特殊値を、独自研究の頁に掲載しています。
における Fibonacci ゼータ関数の特殊値を、独自研究の頁に掲載しています。
※1 : L. Navas「Analytic continuation of the Fibonacci Dirichlet series」The Fibonacci Quarterly, vol.39, (2001) p. 409-418.
※2 :
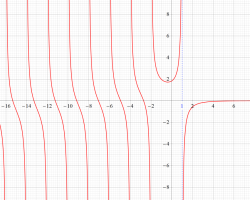
複素変数の Fibonacci ゼータ関数のグラフ。
次のグラフ上の平行な直線はすべて等間隔で、実線の交点に Fibonacci ゼータ関数の極がある。
Euler 和(調和級数係数の Dirichlet 級数)
日:Euler 和,英:Euler sum, 仏:Somme d'Euler,独:Eulersche Summe
調和級数の値を係数とする Dirichlet 級数
は現在、Euler 和 (Euler Sum) と呼ばれている。この関数は、例えば 「NIST - Handbook of Mathematical Functions」 の613頁 (25. 16 (ii)) に記載がある。
Euler 和は、1742年の 「C. Goldbach からL. Euler への手紙」 の内容に着想を得た Euler が考察を始めたもので、
この結果も、Euler によって得られた。
なお、次の公式を用いれば、前述の Dirichlet 級数が収束しない複素数
ここに、
調和級数部分を一般化した、
は一般 Euler 和と呼ばれ※1、同様に特殊値が知られており、またそれらを用いれば他の様々な無限級数の値を表わせる。一般 Euler 和は、
がある。同様に、
によって、前述の Dirichlet 級数が収束しない複素数
を用いればよい。
複素変数
【註記】
※1 : 次の式を 一般 Euler 和とする定義もある。
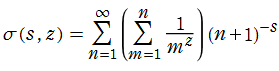 これは、ここでの 一般 Euler 和の定義と
これは、ここでの 一般 Euler 和の定義と
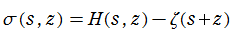 の関係にある。
の関係にある。
※1 : 次の式を 一般 Euler 和とする定義もある。
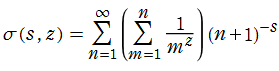
複素変数の Euler 和
複素変数の一般 Euler 和
実変数の一般 Euler 和
複素変数の一般 Euler 和
複素変数の一般 Euler 和
Riesz 関数
日:Riesz 関数,リース関数,英:Riesz function, 仏:Fonction de Riesz,独:Riesz funktion
Riesz 関数は、冪級数展開式
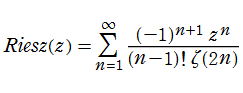
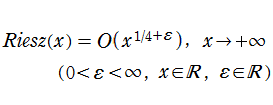
そのため数値計算においても、引数が極端に大きい正数での Riesz 関数の振る舞いが関心事となる。ところが、上記の冪級数の収束半径は理論上
は、より広い複素領域で実際の数値計算が可能になる。また、Riesz 関数の漸近評価式
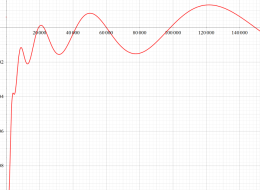
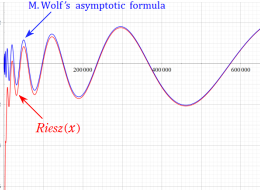
が Marek Wolf によって (Riemann 予想の成立を仮定して) 与えられている※1。この結果から、Riesz 関数は正の実軸上に絶対値が非常に大きい零点を無数に持つことが分かる。
Riesz 関数の冪級数展開式が、Riemann 素数計数指数関数
が得られる※2。ここに
Riesz 関数に類似した関数
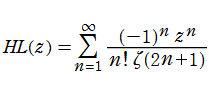
もし、
が成立するならば、Riemann 予想も成立する (必要十分条件でもある)。すなわち Hardy - Littlewood 関数は、Riemann ゼータ関数の奇数での特殊値と非自明零点との関係を表現する。
Hardy - Littlewood 関数も、正の実軸上に絶対値が非常に大きい零点を無数に持ち、Riesz 関数と状況が良く似ている。Hardy - Littlewood 関数に関する公式
も、Riesz 関数で用いた方法を応用すれば得られる。
【註記】
※1 : M. Wolf の論文 「Evidence in favor of the Baez-Duarte criterion for the Riemann hypothesis」 Computational Methods in Science and Technology, 14 (1), p.47-54 (2008) を参照。
※2 : 後述の 「Riesz 関数の漸近公式について」 で、この事の証明と検証結果を掲示していますので、併せて参照願います。
※1 : M. Wolf の論文 「Evidence in favor of the Baez-Duarte criterion for the Riemann hypothesis」 Computational Methods in Science and Technology, 14 (1), p.47-54 (2008) を参照。
※2 : 後述の 「Riesz 関数の漸近公式について」 で、この事の証明と検証結果を掲示していますので、併せて参照願います。
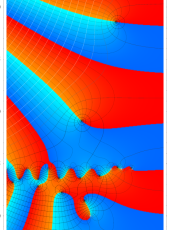
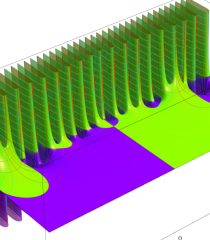
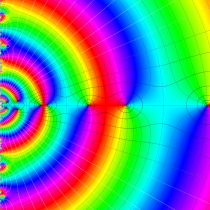
複素変数の Riesz 関数のグラフ。
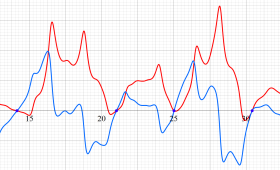
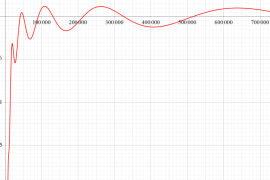
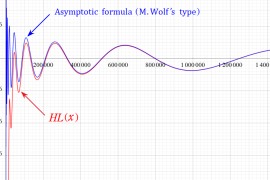
実変数の Riesz 関数のグラフ。正の実軸上にある零点を確認するため、非常に広い範囲を描画するとともに、漸近評価式との比較も行う。
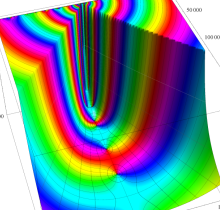
複素変数の Riesz 関数のグラフ。正の実軸上にある零点を確認するため、非常に広い範囲を描画する。
アニメーション(10.50MB)
複素変数の Riesz 関数のグラフ。原点周辺の狭い範囲から非常に広い範囲に描画領域を拡大する動画。
複素変数の Hardy - Littlewood 関数のグラフ。
実変数の Hardy - Littlewood 関数のグラフ。正の実軸上にある零点を確認するため、非常に広い範囲を描画するとともに、漸近評価式との比較も行う。
複素変数の Hardy - Littlewood 関数のグラフ。正の実軸上にある零点を確認するため、非常に広い範囲を描画する。
は、実は当サイト管理人である私が独自に導いたものですが、既に説明したように Folkmar Bornemann の論文 「Solution of a Problem Posed by Jörg Waldvogel, (2003).」 http://www-m3.ma.tum.de/Allgemeines/FolkmarBornemannPublications (公開はインターネット上のみ) にある方法を応用して導出した公式であり、私の独創だけで得られた結果ではありません。
しかし、この公式は恐らく他に言及例が無いと思われ、また、公式の右辺第2項は級数の初項のみをとると M. Wolf の漸近評価式と一致する等、面白い事実も判明したので、以下、その導出過程を掲示することにしました。
(2018年6月23日 追加記事)
Hardy - Littlewood 関数の漸近公式自体は、既に G. H. Hardy と J. E. Littlewood が論文 「Contributions to the Theory of the Riemann Zeta-Function and the Theory of the Distribution of Primes, Acta Mathematica. 41, p.119–196」 で触れていることが判明しました。ただし、それを導く方法は若干異なり、始めに関数
を用意し、逆 Mellin 変換等を用いてより一般的な関数等式
を導くというものです。ここで、具体的に
【証明】
次の関数を用意する。
これは、やや天下り的ではあるものの、右辺の第1項の形は、Riesz 関数の元々の定義式である冪級数
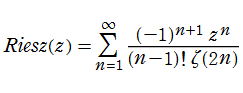
で網羅されることが分かる。①, ②はすべて1位の極である。③は上記の仮定によりすべて1位となる。それぞれの極に対する留数は、
となる。ここに、②の式変形では次の公式を用いる。
ここで、
となる (留数定理は積分経路が閉曲線であることを条件とするが、Fig.1 の経路でも Riemann 球面上に写像すれば本質は閉曲線であることが分かる)。ゆえに、両辺を整理すれば目標の公式が得られる。■
(Fig.1) Riesz 関数に関する積分経路図
因みに、Hardy - Littlewood 関数の場合は、次の関数を上記と同じ経路で積分し、留数定理を適用すると同様の公式が得られる。(したがって、導出過程は掲示しない。)
上記の新しい漸近公式から、容易に M. Wolf の漸近評価式を導くことができる。
新しい漸近公式の右辺第1項は、いかなる自然数
非自明零点
となる。さらに、
となり、単振動 (余弦+正弦関数) の合成公式によって、新しい漸近評価式
が得られる。ここで、級数項を
となり、これは M. Wolf の漸近評価式に他ならない。なぜなら実際に、
となるからである。
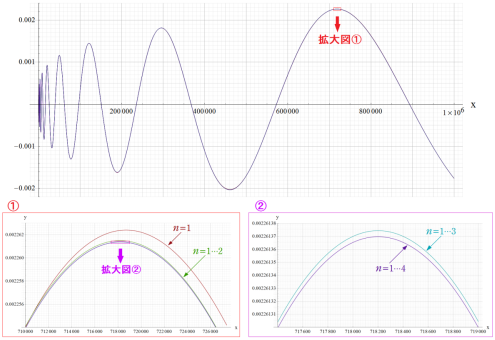
新しい漸近評価式において
となっており、その寄与は
(Fig.2) 新しい漸近評価式の有限級数部分のグラフ
以上の結果から、新しい漸近評価式は上限・下限値
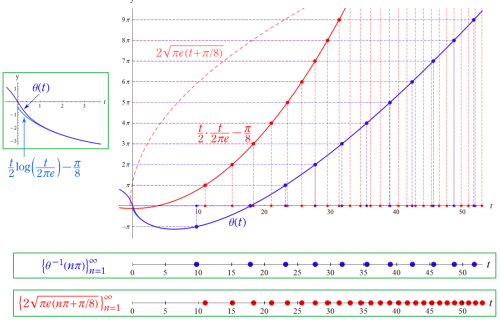
を超えない。Riemann-Siegel シータ関数およびその逆関数の増大傾向は、
となるから、
(Fig.3) Riemann-Siegel シータ関数とその逆関数の増大傾向
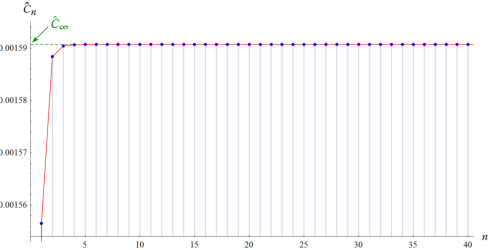
したがって、
となる。最後尾の無限級数は急速に値
(Fig.4) 上限値へ収束する点列のグラフ