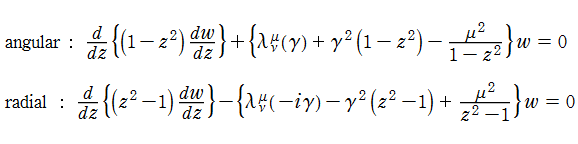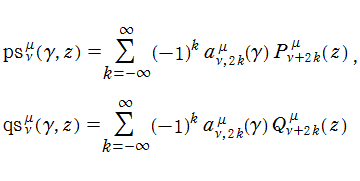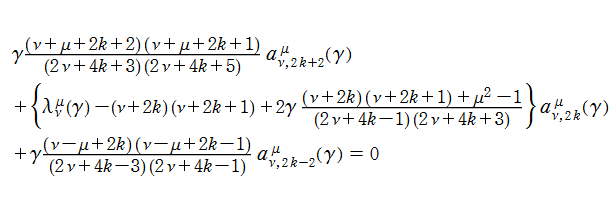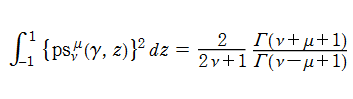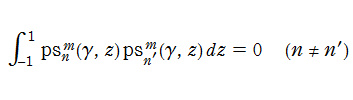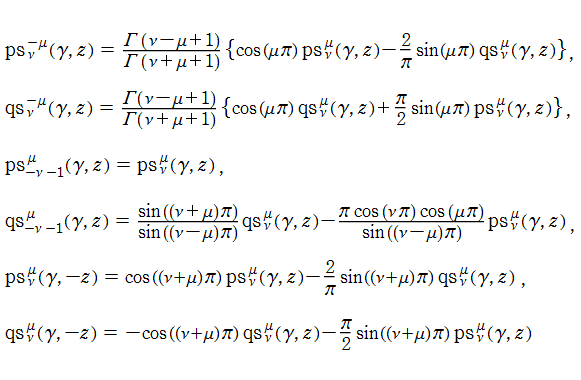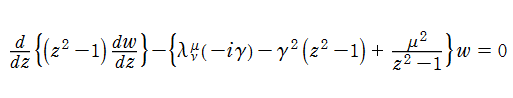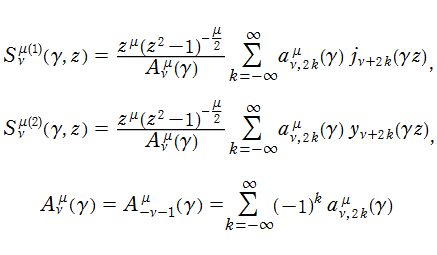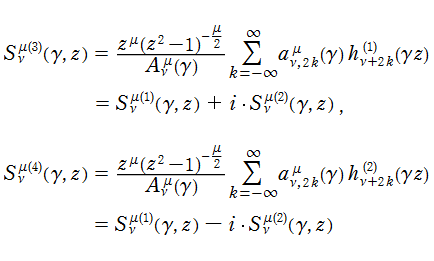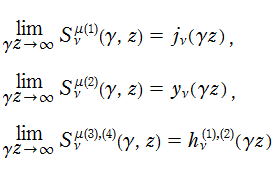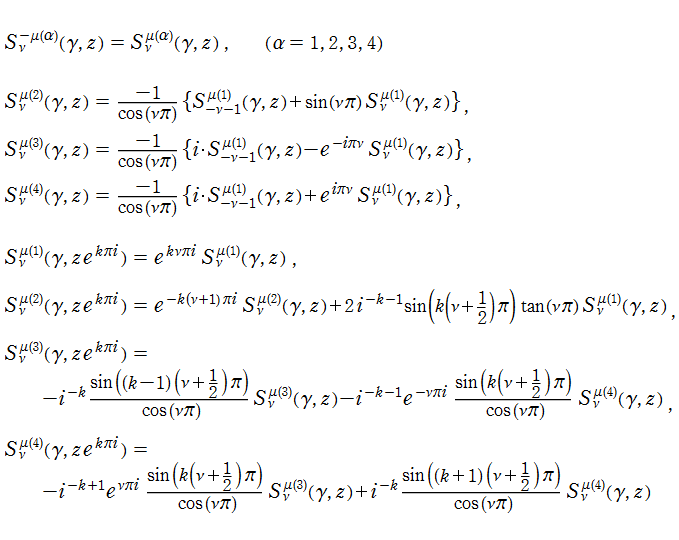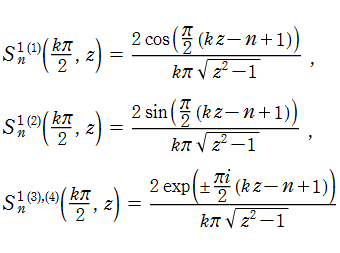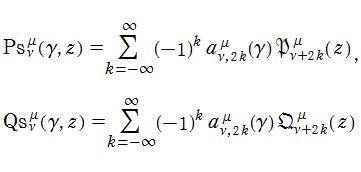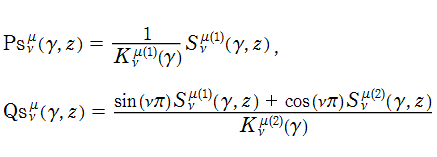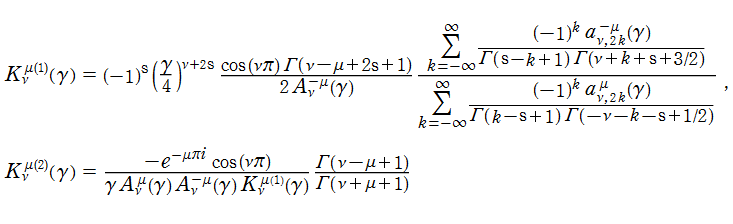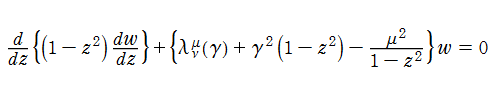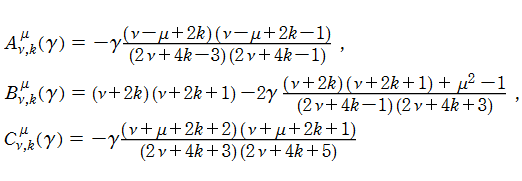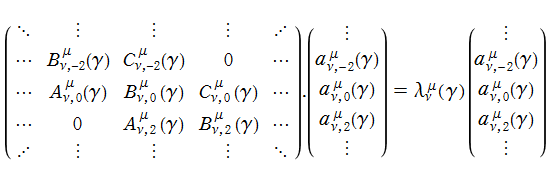特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
回転楕円体波動関数
扁長回転楕円体波動関数 (角度関数)
日:回転楕円体波動関数,スフェロイド関数英:Spheroidal wave function,仏:Fonctions d'ondes sphéroidale,独:Sphäroidfunktion
Helmholtz の方程式を扁長回転楕円体座標で変数分離すると、角度 (angular) 成分、動径 (radial) 成分の満たす微分方程式は、それぞれ
になる。両者を併せて、扁長回転楕円体微分方程式という。また、扁平回転楕円体座標のときは全てにおいて
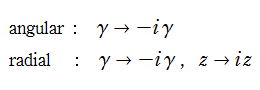
回転楕円体微分方程式は、
この関数記号及び以下に述べる定数規格化 (正規化) は、それを定義した数学者の名を取って「Meixner - Schäfke の規格化」と呼ばれる。このほかにも「Flammer の規格化」など、幾つかの定義があり関数記号も異なる。しかし、いずれも本質的な違いは定数倍だけであり、同一の微分方程式を満たす。
回転楕円体波動関数 (角度関数) は、次のように Legendre 陪関数 (Ferrers 型) の級数に展開できる。
ここに
「Meixner - Schäfke の規格化」は、次の定義によって成される。
(整数次の) 第1種回転楕円体波動関数 (角度関数) は、直交性
を有する。(
回転楕円体波動関数 (角度関数) は、Legendre 陪関数と同様の公式
等を満たす。
なお、
一般に扁長回転楕円体波動関数 (角度関数) は、複素平面上
回転楕円体波動関数はスフェロイド関数とも呼ばれ、境界条件が回転楕円体 (スフェロイド) で定まる物理問題に現れる。Mathieu 関数と同様に、初期の応用事例は音響学※1・電磁波の散乱理論等に限られていたが、これは数値計算が複雑であることに大きな原因があった※2。実際、回転楕円体波動関数の数表が現れ始めたのは1950年代になってからである。しかし、21世紀初頭になると、二原子から成る分子における電子分布など応用事例数が次第に増えている。
回転楕円体波動関数は、Helmholtz 方程式を回転楕円体座標で解く目的のため、1880年に C. Niven が初めて導入した※3。しかし、本格的な理論の整備を手掛け、現在の規格化と関数記号を定着させたのは、その後に現れた多数の数学者・物理学者等である。その過程で、回転楕円体波動関数の数値計算法も改良が重ねられて、これが前述のような応用面の拡充を促している。併せて、電子計算機の性能の向上および数式処理システムへの実装が進んだ時代と並行していた事も、応用をさらに容易にした。
【註記】
※1:これの興味深い応用例として、耳が音源の方向を音波の回折や散乱によって感知する特性を研究する際に用いる擬似頭 (HATS:Head And Torso Simulator) を回転楕円体とみなし、頭部周辺の音波を回転楕円体波動関数で近似する方法がある。言い換えると、聴覚器官や脳がいかに複雑な処理をおこなっているかが伺えるような事例である。
※2:例えば、前述の漸化式をよく見ると、(通常は必要な) 初期項が定義されていない。これは理論的には規格化の積分式で決定される定数になるのだが、求めようとする関数が被積分関数になっているので、容易には求められない。そこで、漸化式を無限回反復したときの値を漸近評価し、漸化式を遡及してすべての係数を求める等、いくつかの代替方法がある。回転楕円体波動関数の他、楕円体関数系では皆このような複雑な計算が伴う。
※3:C. Niven 「On the conduction of heat in ellipsoids of revolution」 Philosophical transactions of the Royal Society of London, No.171, (1880), p.117-151
※1:これの興味深い応用例として、耳が音源の方向を音波の回折や散乱によって感知する特性を研究する際に用いる擬似頭 (HATS:Head And Torso Simulator) を回転楕円体とみなし、頭部周辺の音波を回転楕円体波動関数で近似する方法がある。言い換えると、聴覚器官や脳がいかに複雑な処理をおこなっているかが伺えるような事例である。
※2:例えば、前述の漸化式をよく見ると、(通常は必要な) 初期項が定義されていない。これは理論的には規格化の積分式で決定される定数になるのだが、求めようとする関数が被積分関数になっているので、容易には求められない。そこで、漸化式を無限回反復したときの値を漸近評価し、漸化式を遡及してすべての係数を求める等、いくつかの代替方法がある。回転楕円体波動関数の他、楕円体関数系では皆このような複雑な計算が伴う。
※3:C. Niven 「On the conduction of heat in ellipsoids of revolution」 Philosophical transactions of the Royal Society of London, No.171, (1880), p.117-151
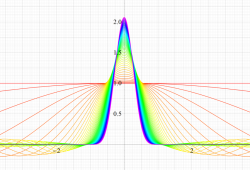
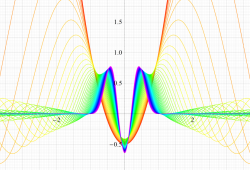
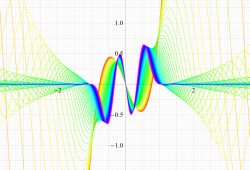
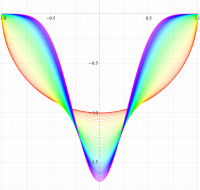
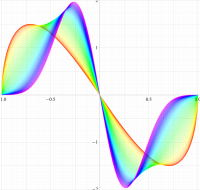
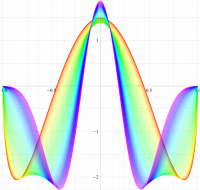
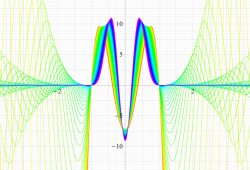
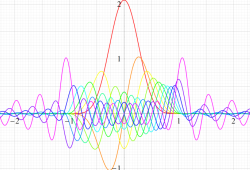
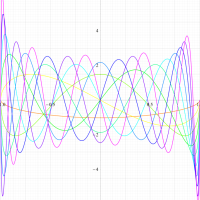
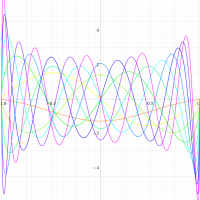
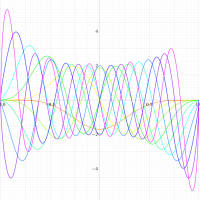
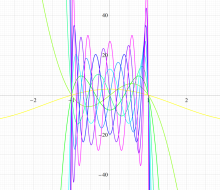
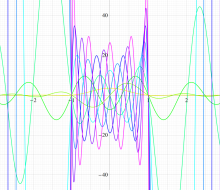
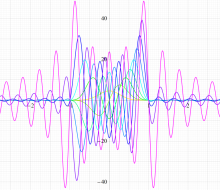
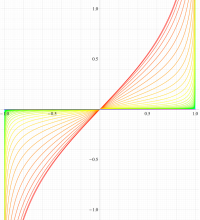
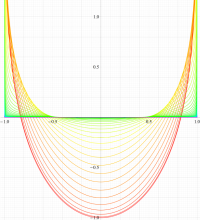
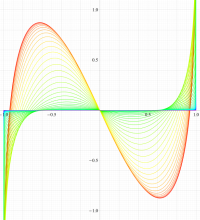
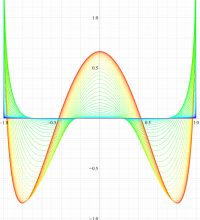
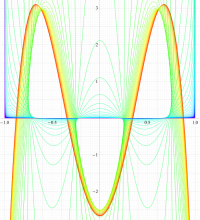
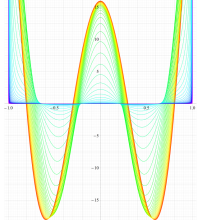
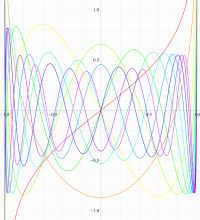
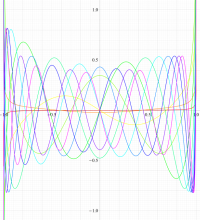
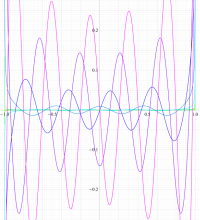
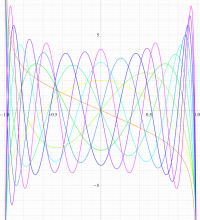
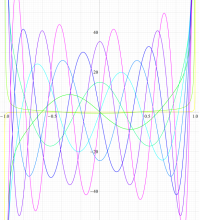
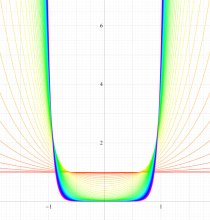
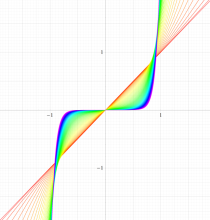
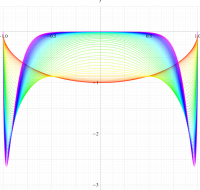
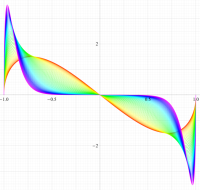
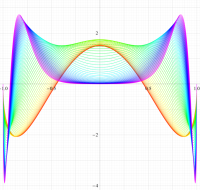
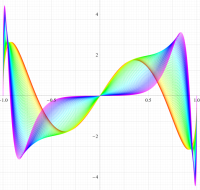
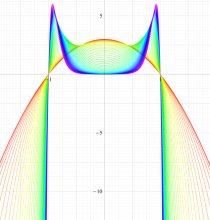
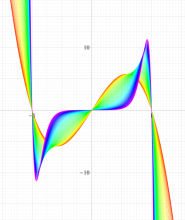
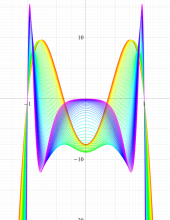
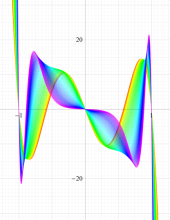
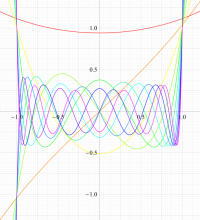
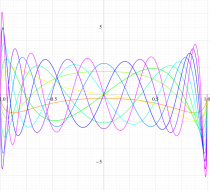
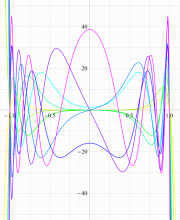
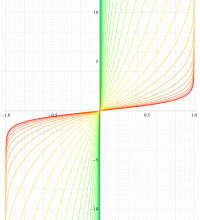
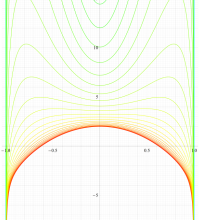
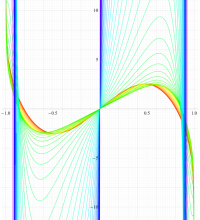
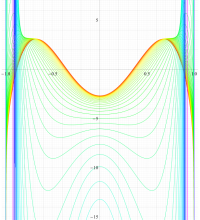
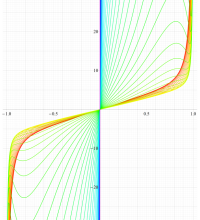
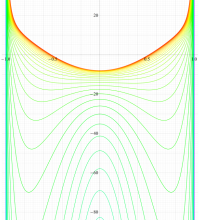
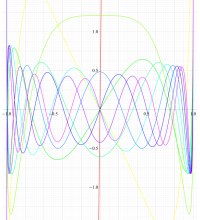
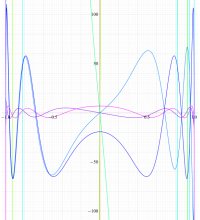
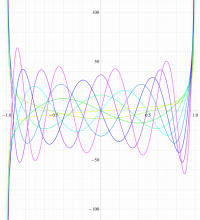
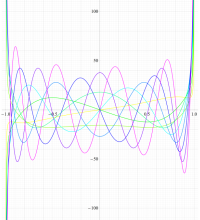
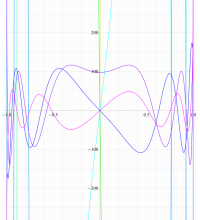
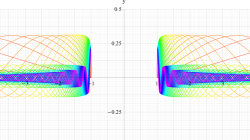
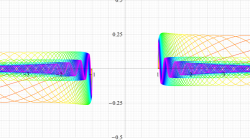
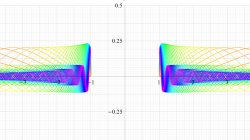
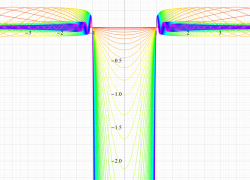
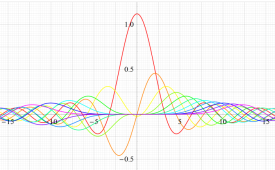
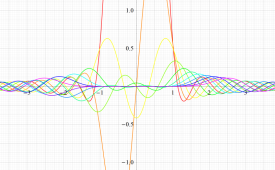
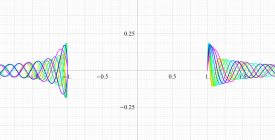
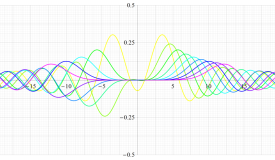
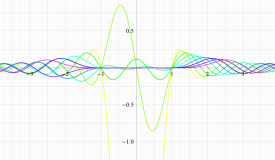
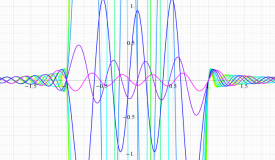
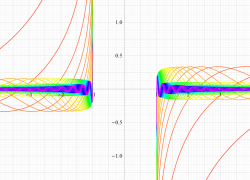
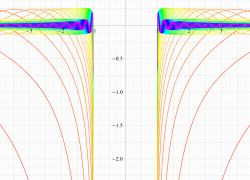
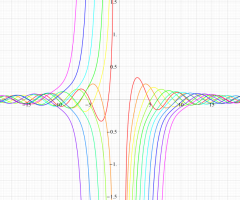
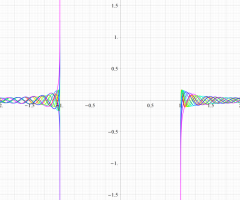
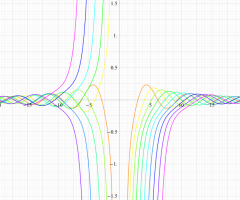
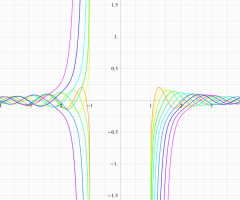
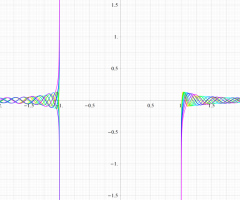
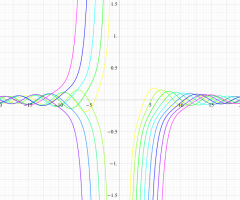
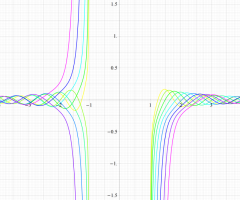
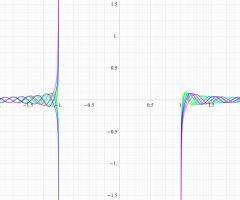
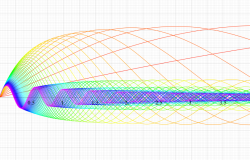
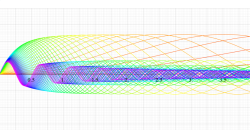
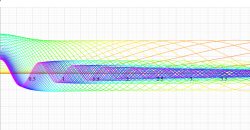
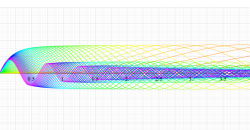
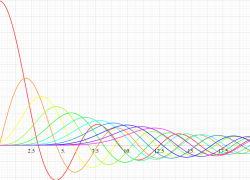
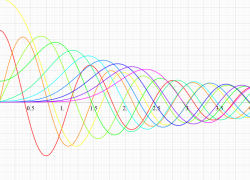
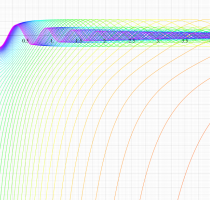
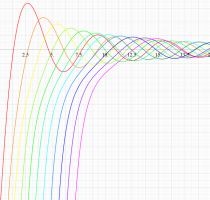
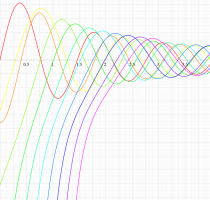
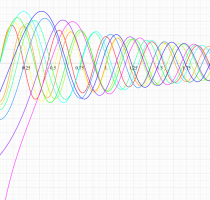
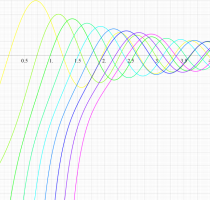
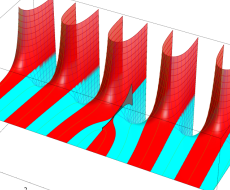
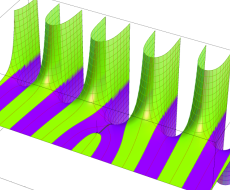
実変数の第1種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
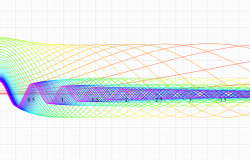
実変数の第1種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
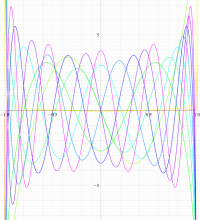
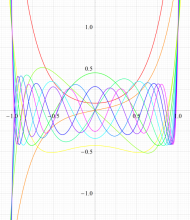
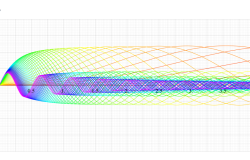
実変数の第1種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
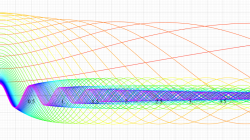
実変数の第1種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
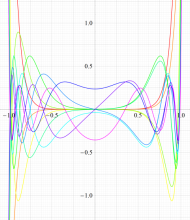
実変数の第1種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
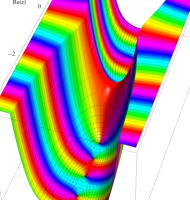
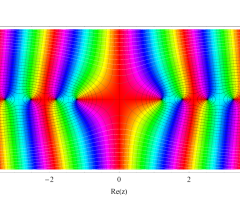
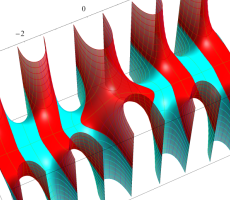
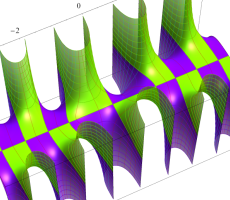
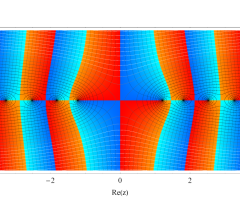
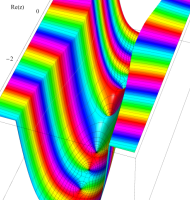
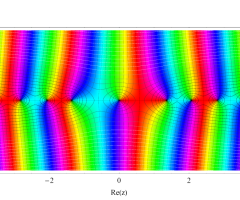
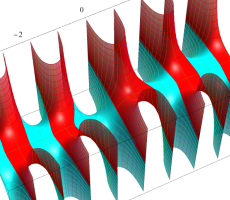
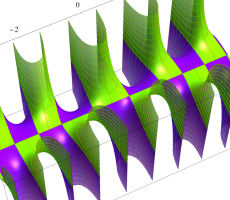
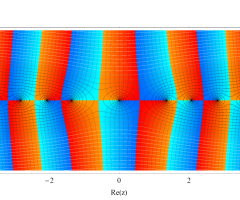
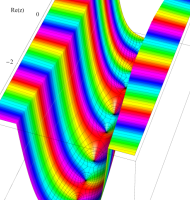
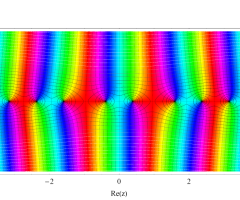
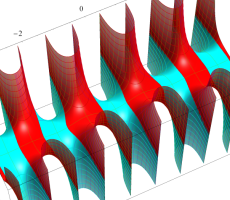
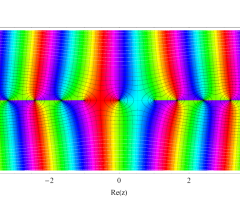
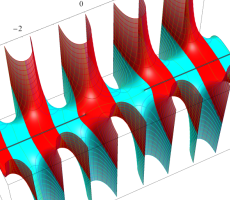
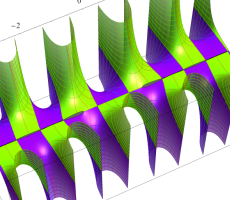
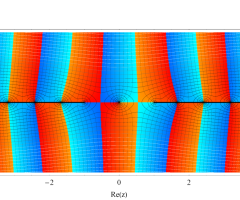
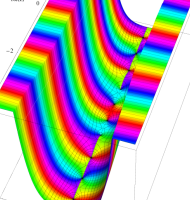
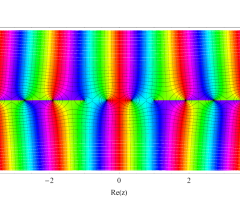
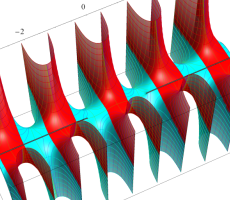
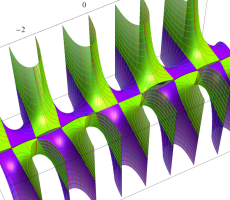
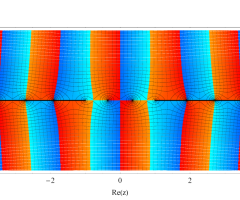
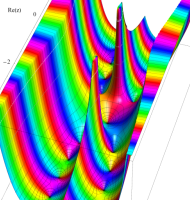
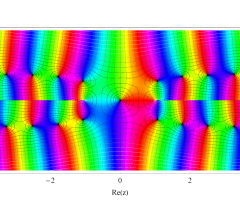
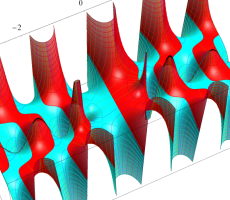
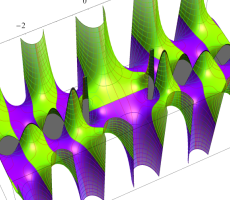
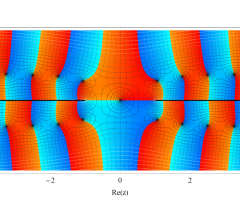
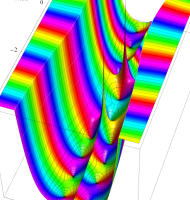
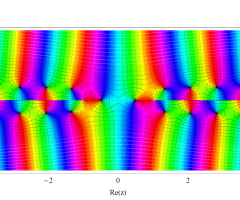
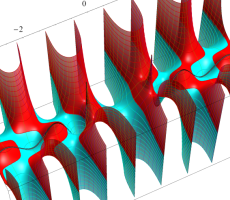
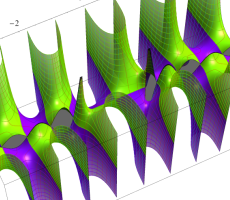
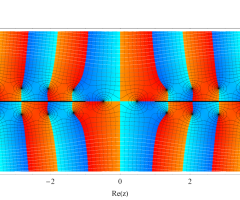
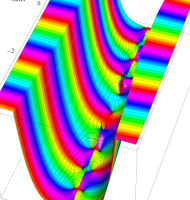
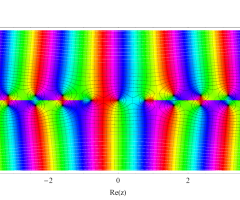
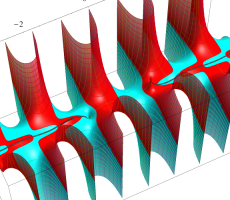
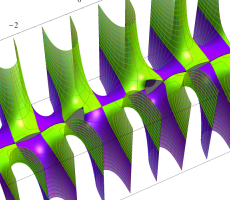
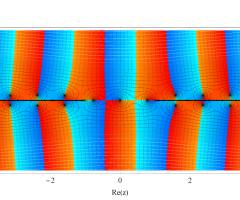
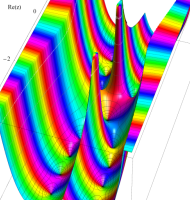
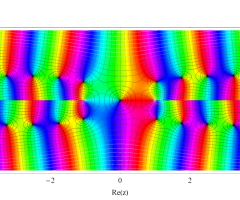
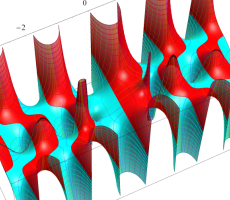
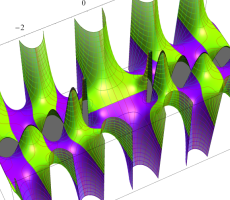
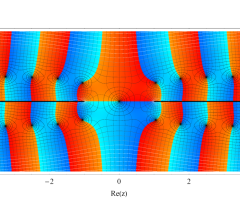
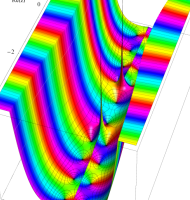
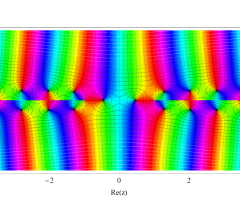
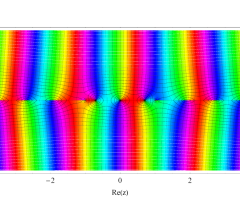
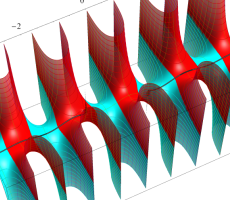
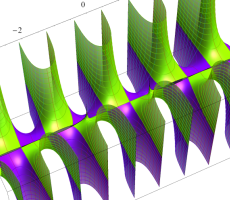
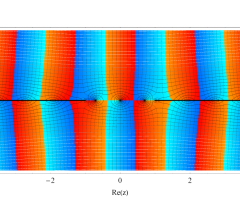
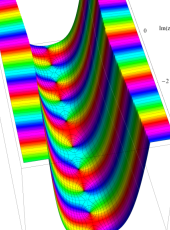
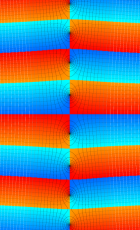
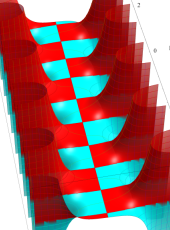
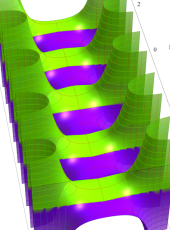
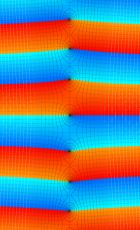
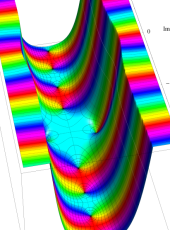
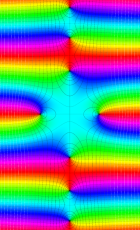
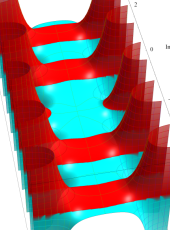
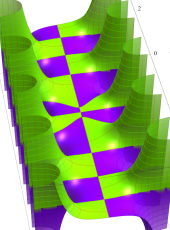
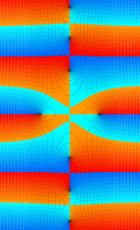
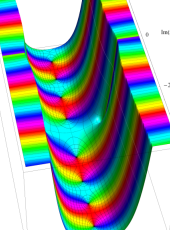
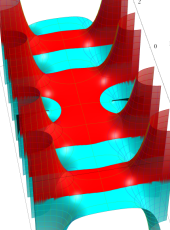
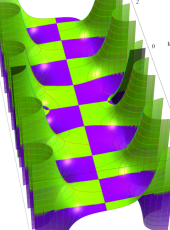
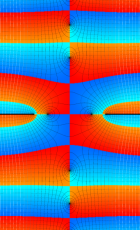
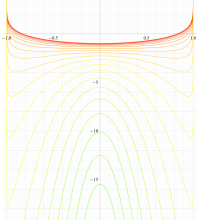
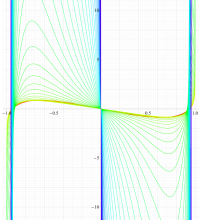
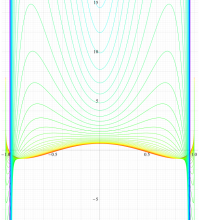
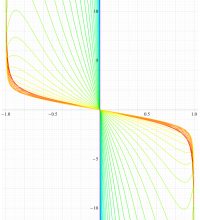
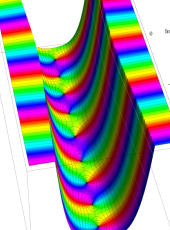
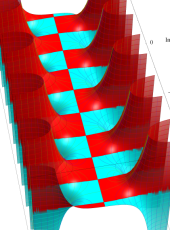
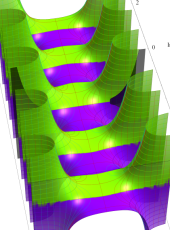
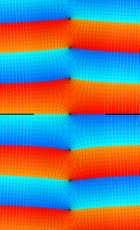
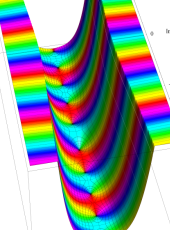
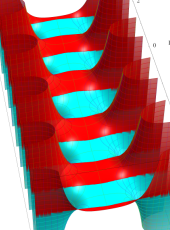
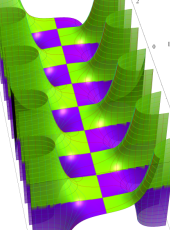
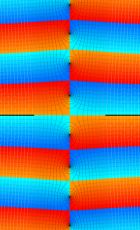
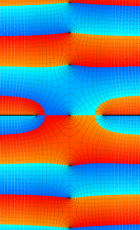
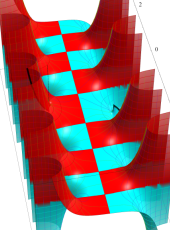
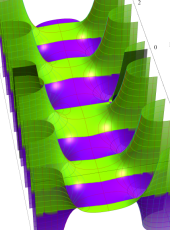
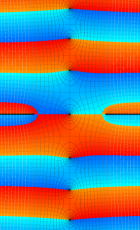
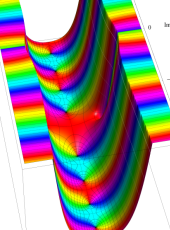
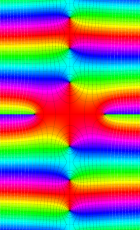
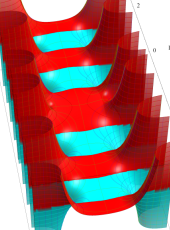
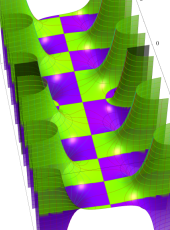
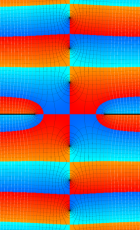
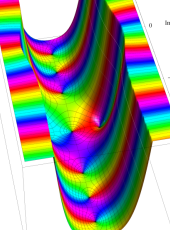
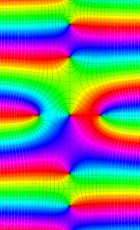
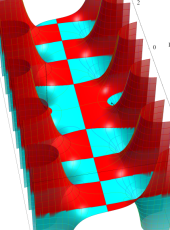
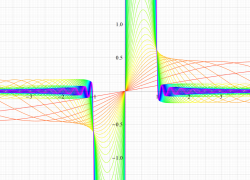
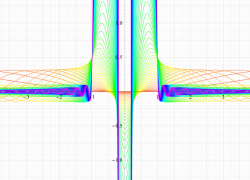
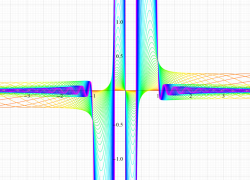
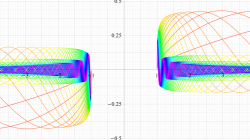
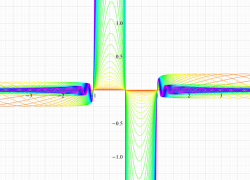
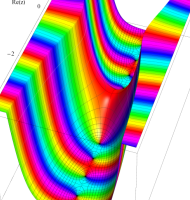
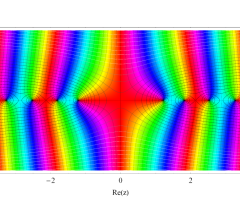
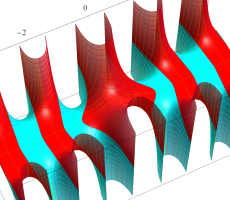
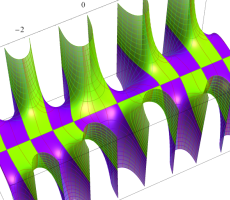
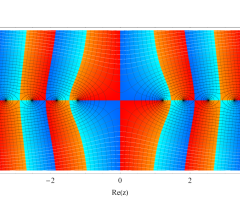
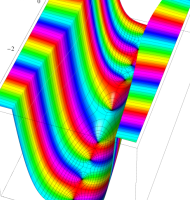
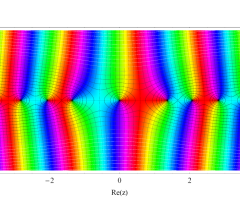
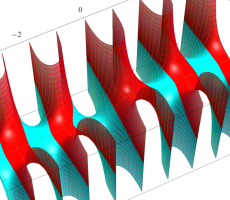
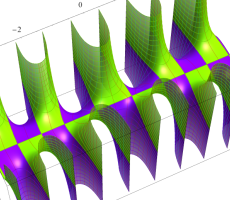
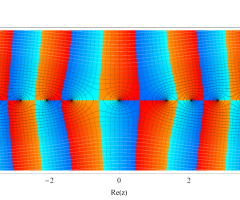
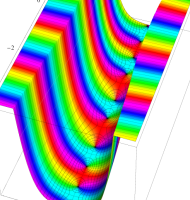
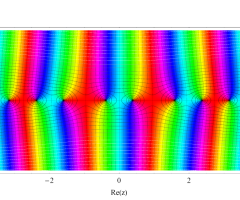
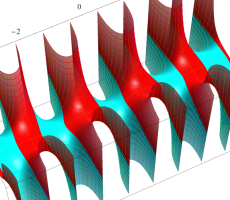
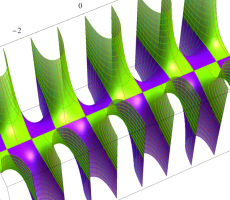
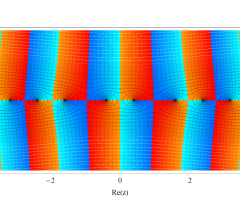
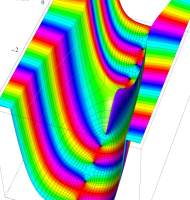
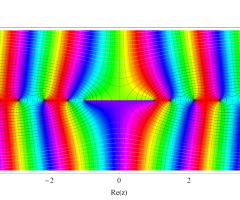
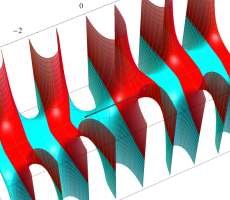
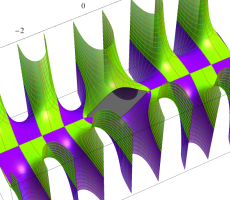
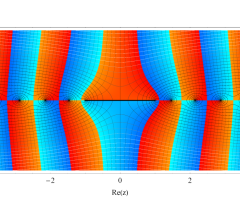
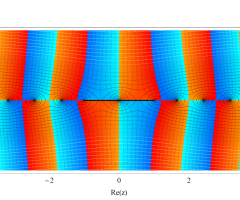
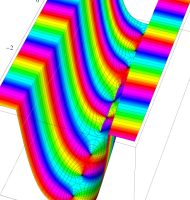
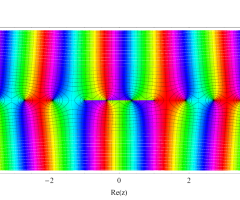
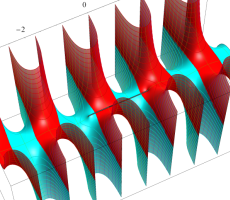
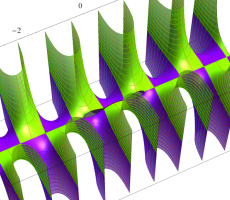
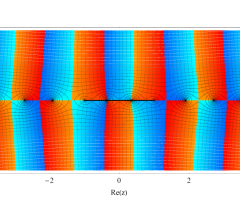
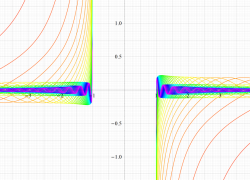
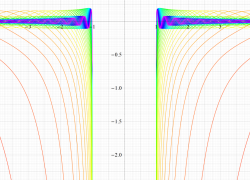
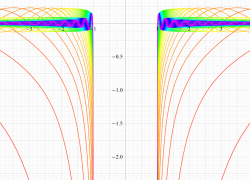
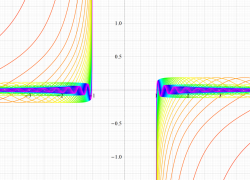
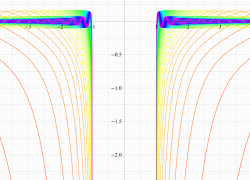
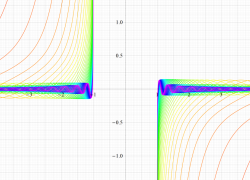
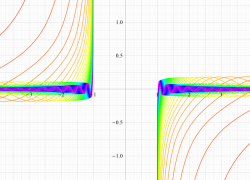
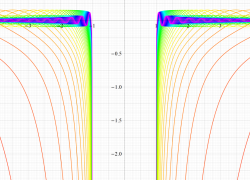
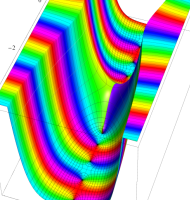
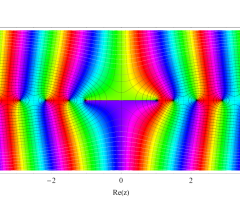
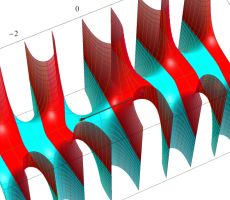
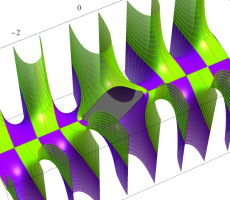
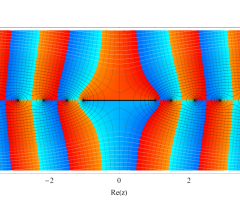
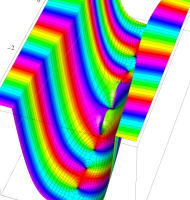
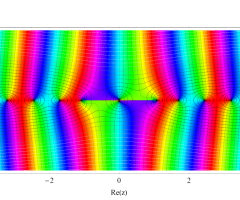
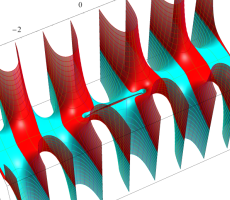
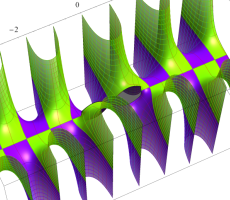
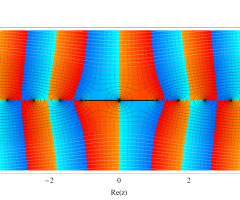
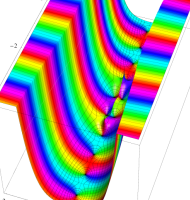
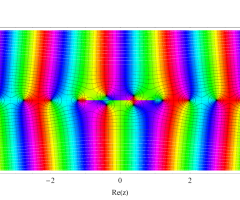
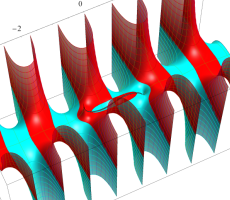
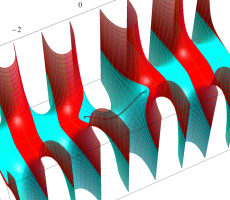
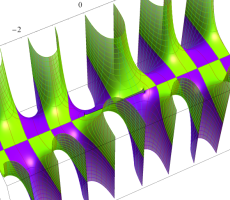
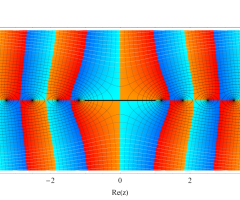
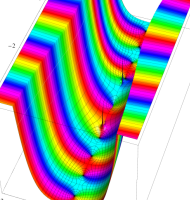
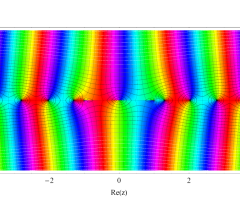
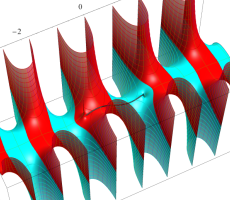
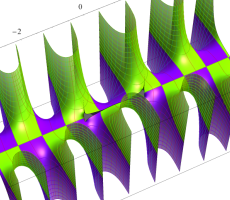
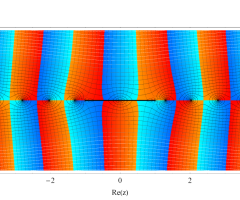
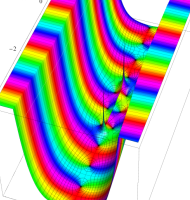
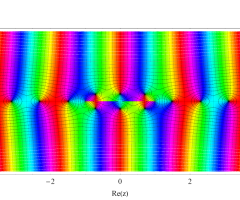
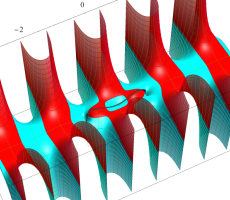
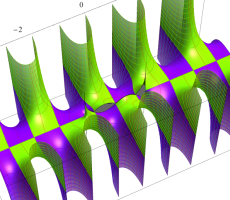
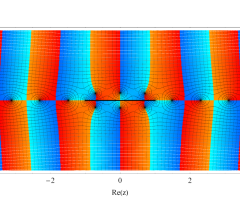
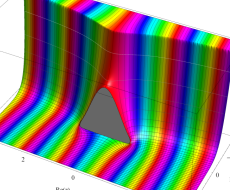
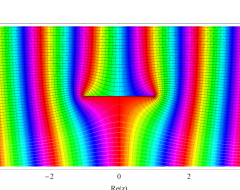
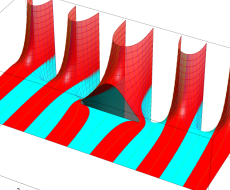
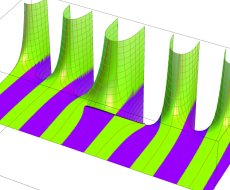
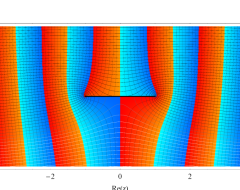
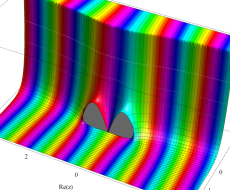
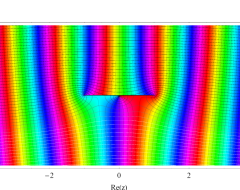
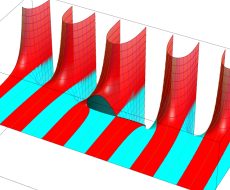
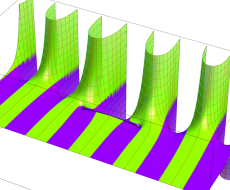
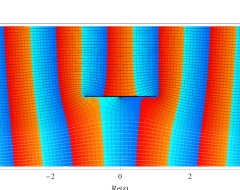
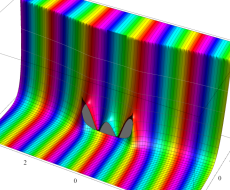
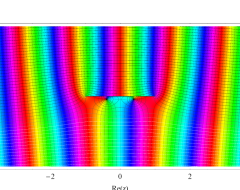
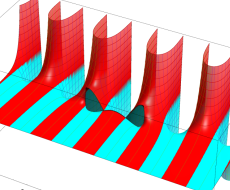
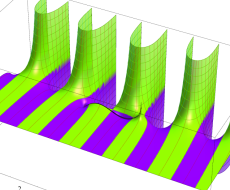
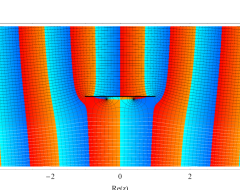
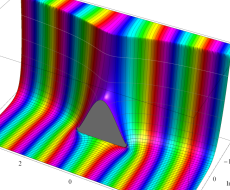
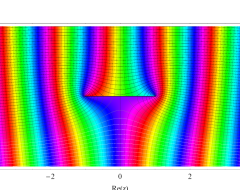
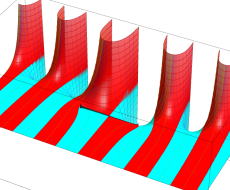
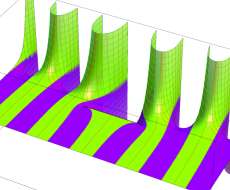
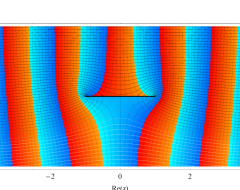
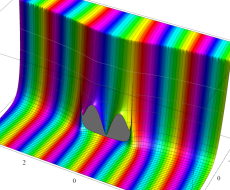
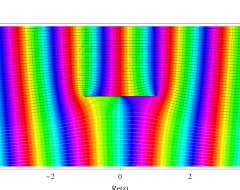
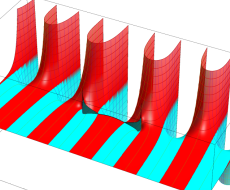
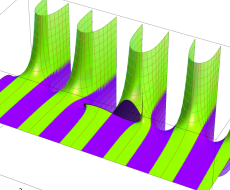
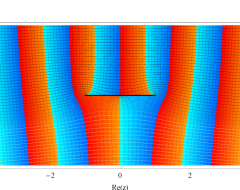
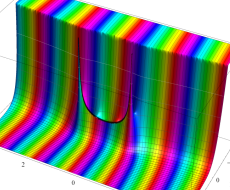
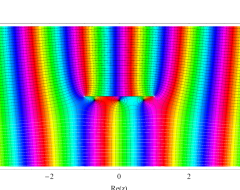
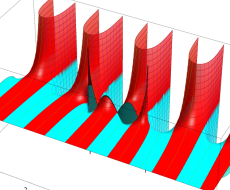
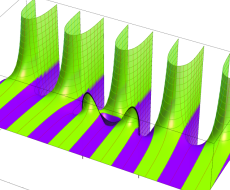
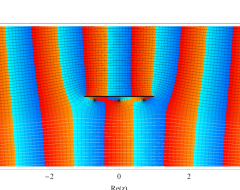
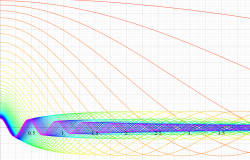
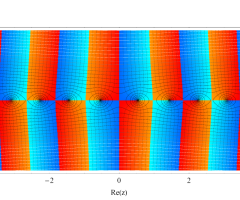
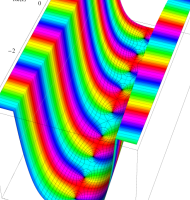
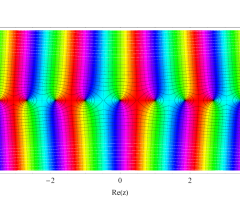
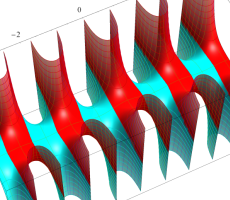
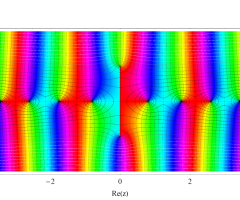
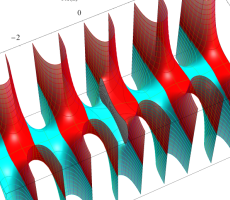
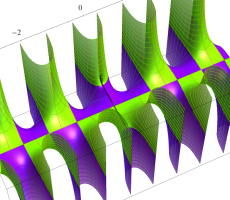
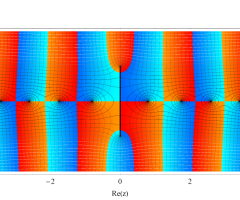
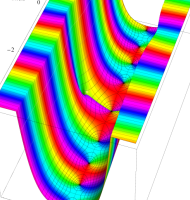
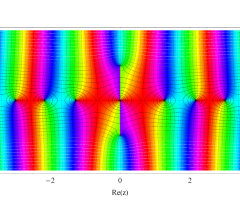
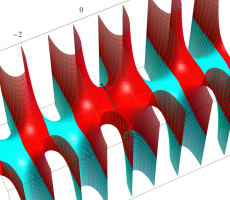
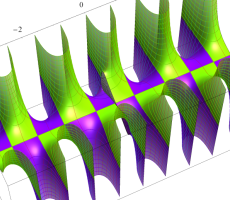
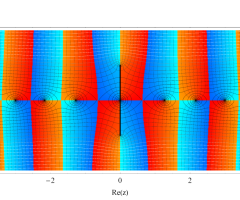
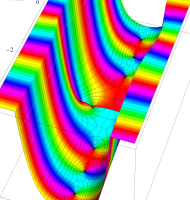
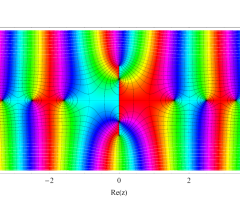
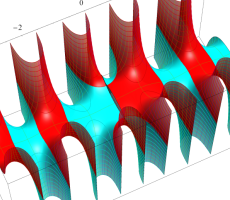
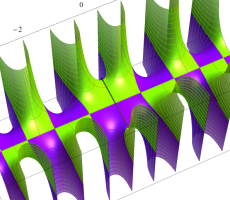
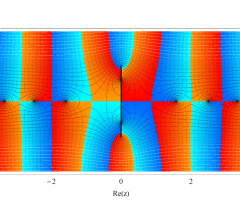
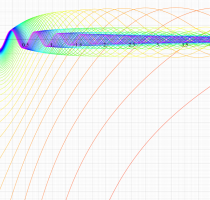
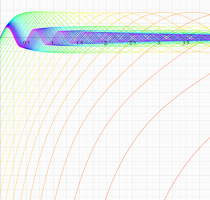
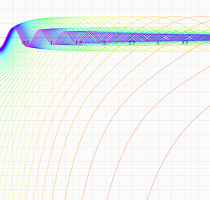
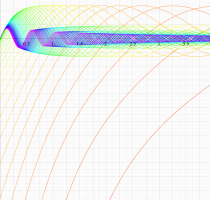
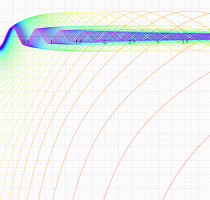
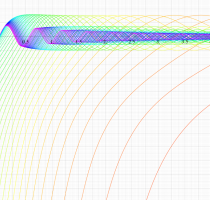
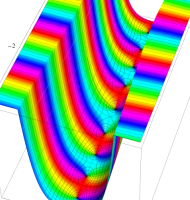
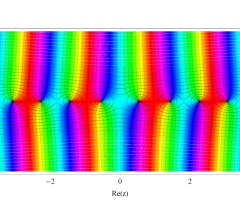
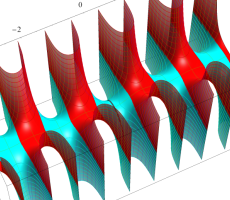
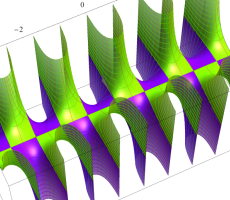
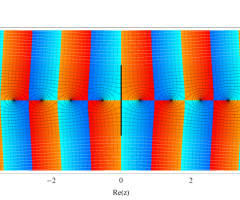
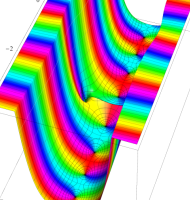
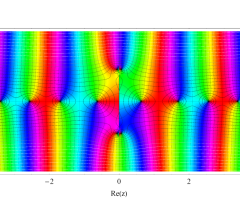
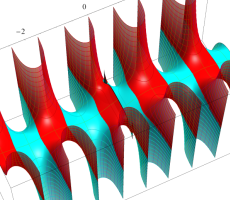
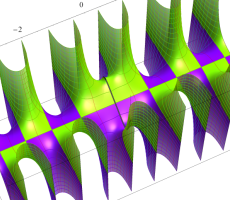
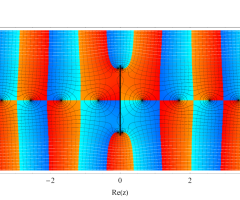
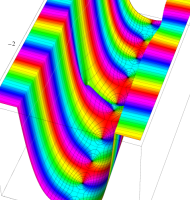
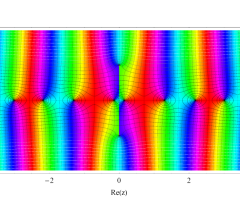
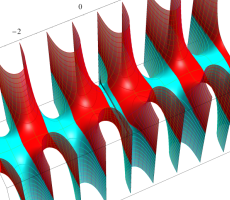
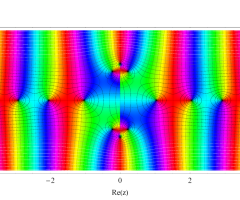
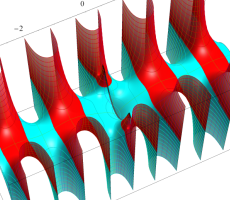
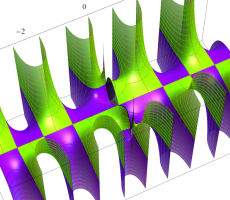
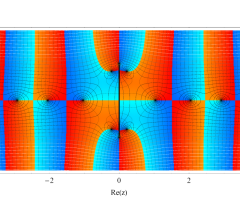
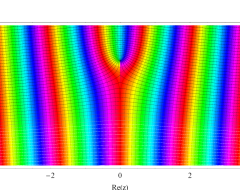
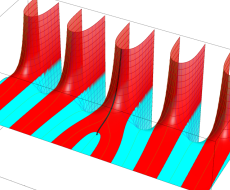
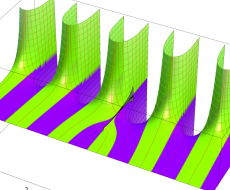
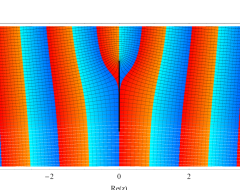
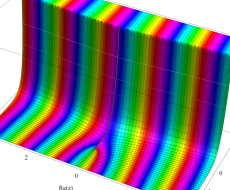
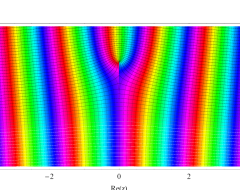
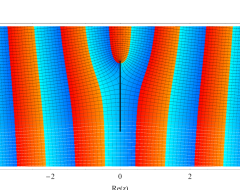
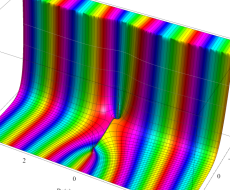
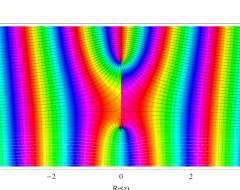
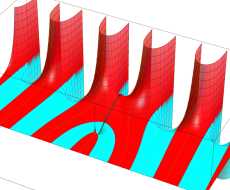
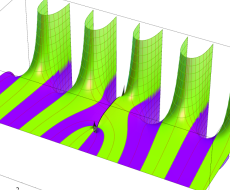
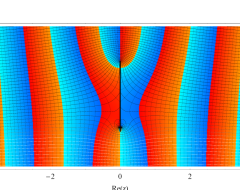
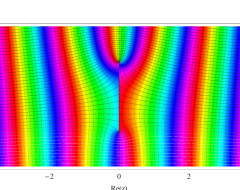
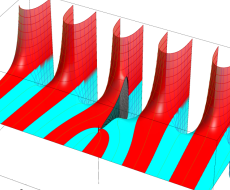
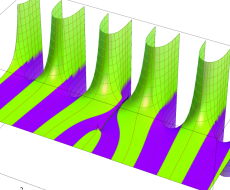
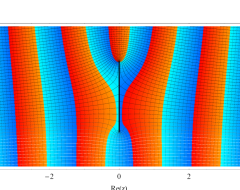
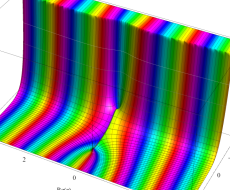
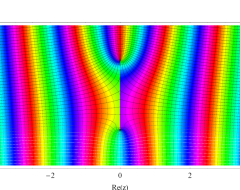
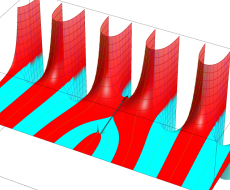
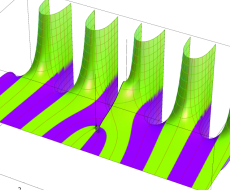
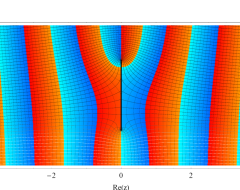
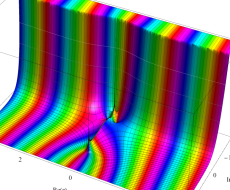
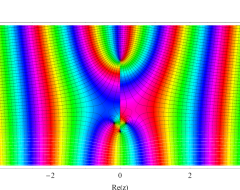
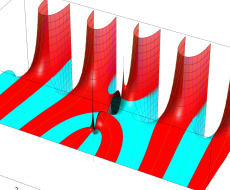
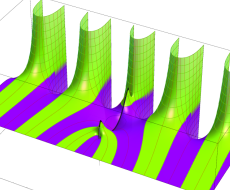
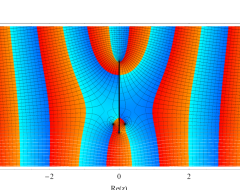
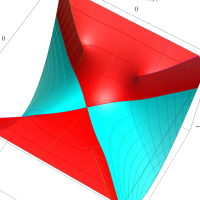
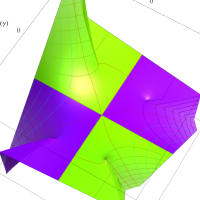
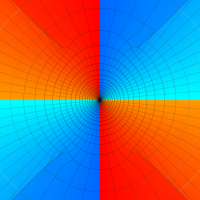
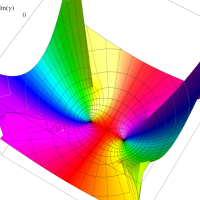
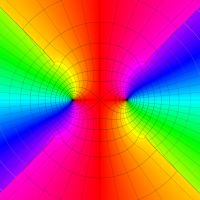
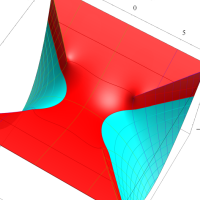
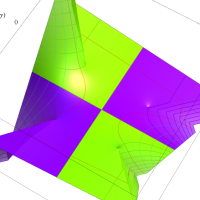
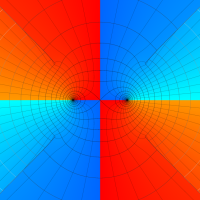
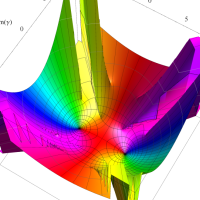
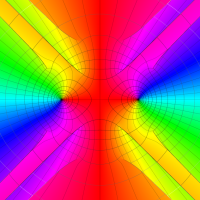
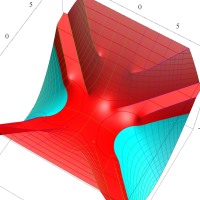
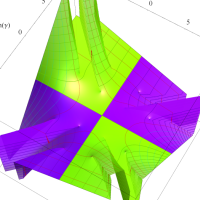
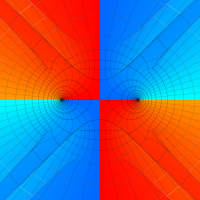
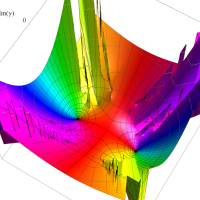
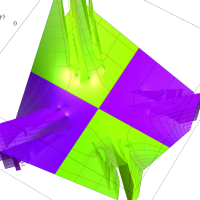
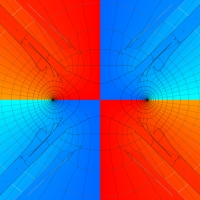
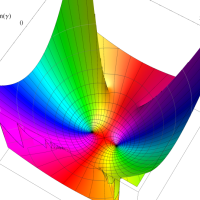
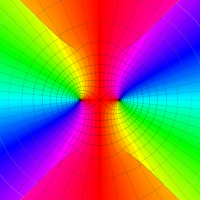
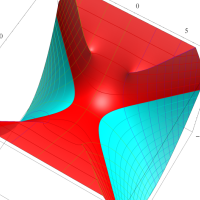
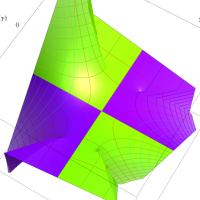
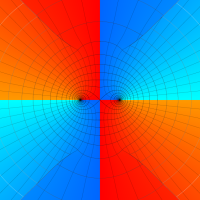
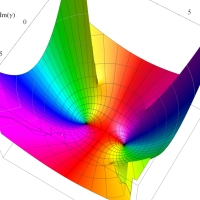
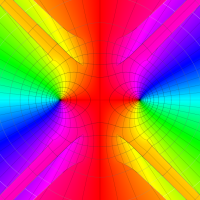
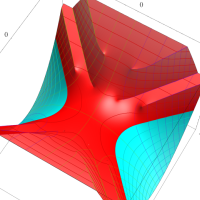
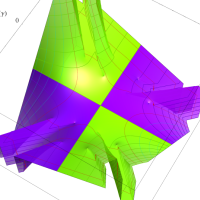
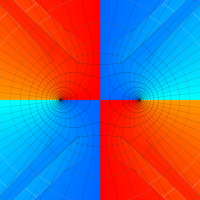
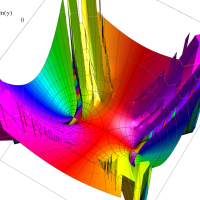
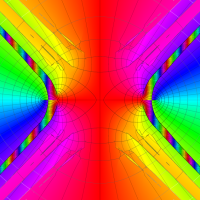
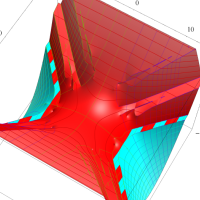
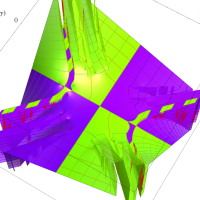
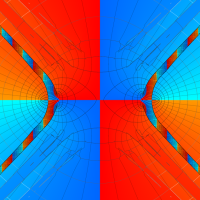
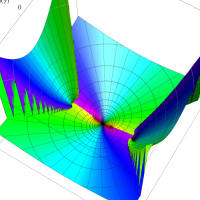
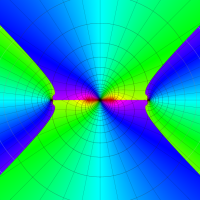
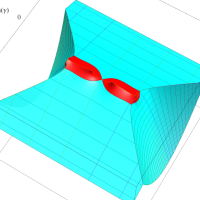
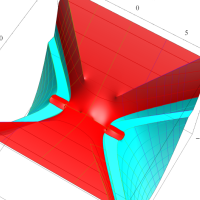
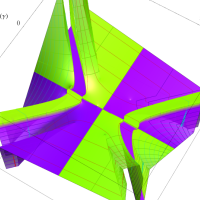
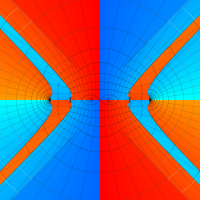
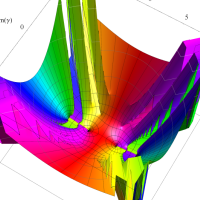
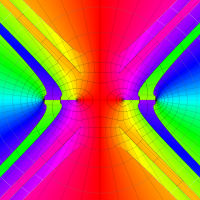
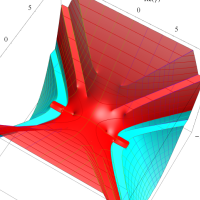
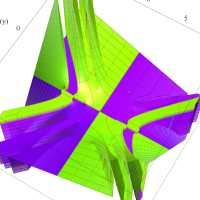
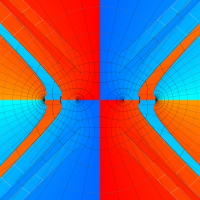
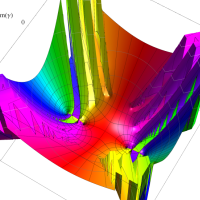
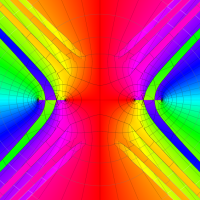
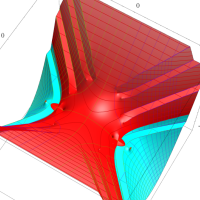
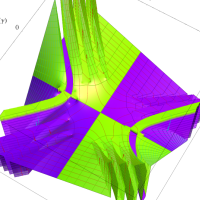
複素変数の第1種扁長回転楕円体波動関数 (角度関数)
複素変数の第1種扁長回転楕円体波動関数 (角度関数)
複素変数の第1種扁長回転楕円体波動関数 (角度関数)
複素変数の第1種扁長回転楕円体波動関数 (角度関数)
複素変数の第1種扁長回転楕円体波動関数 (角度関数)
複素変数の第1種扁長回転楕円体波動関数 (角度関数)
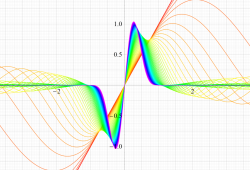
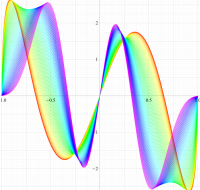
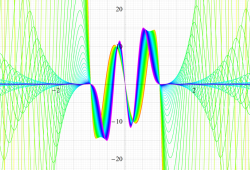
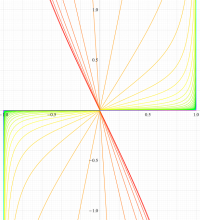
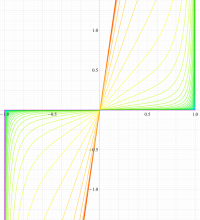
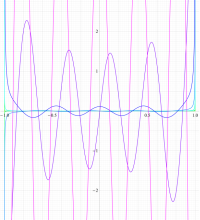
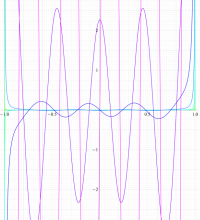
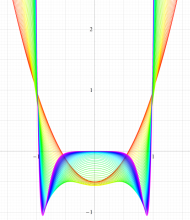
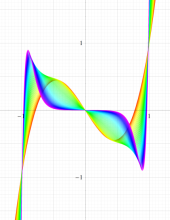
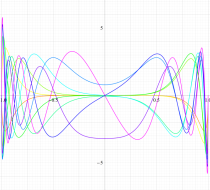
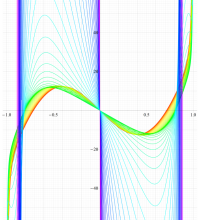
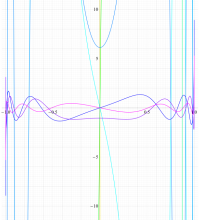
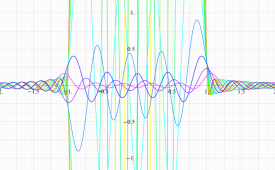
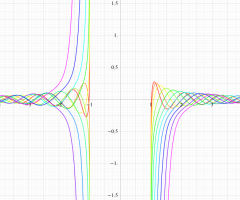
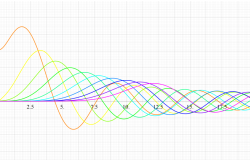
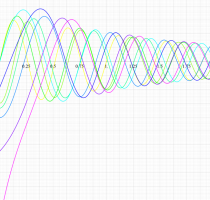
実変数の第2種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
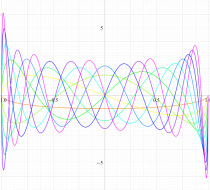
実変数の第2種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
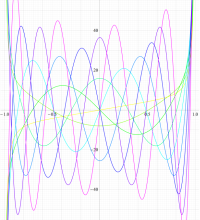
実変数の第2種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第2種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第2種扁長回転楕円体波動関数 (角度関数) のグラフ。 順に、①
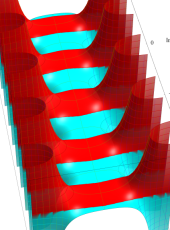
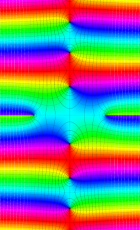
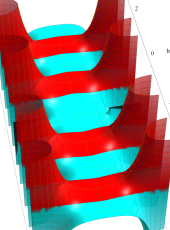
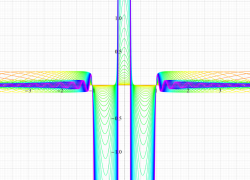
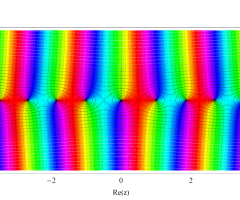
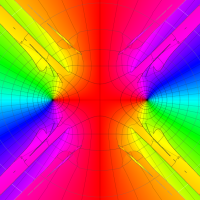
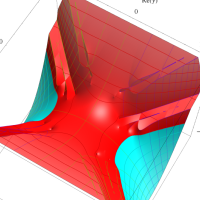
複素変数の第2種扁長回転楕円体波動関数 (角度関数)
複素変数の第2種扁長回転楕円体波動関数 (角度関数)
複素変数の第2種扁長回転楕円体波動関数 (角度関数)
複素変数の第2種扁長回転楕円体波動関数 (角度関数)
複素変数の第2種扁長回転楕円体波動関数 (角度関数)
複素変数の第2種扁長回転楕円体波動関数 (角度関数)
扁平回転楕円体波動関数 (角度関数)
ここで取り扱う扁平回転楕円体波動関数 (角度関数) は、前述の扁長回転楕円体波動関数 (角度関数) において一般に扁平回転楕円体波動関数 (角度関数) は、複素平面上
扁平回転楕円体波動関数は、扁長の場合と同様の応用例がある。
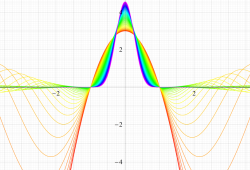
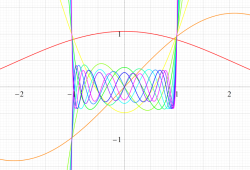
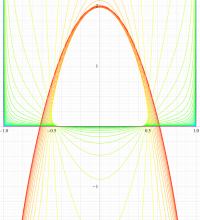
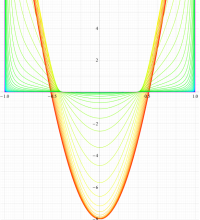
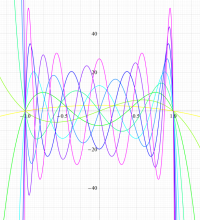
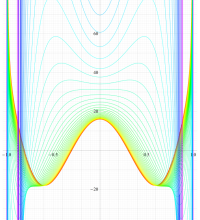
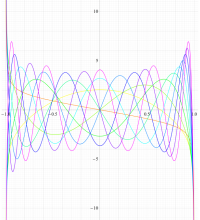
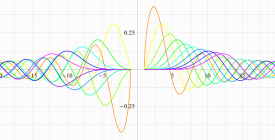
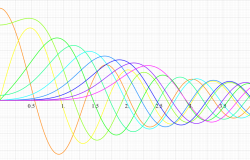
実変数の第1種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第1種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第1種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第1種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第1種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
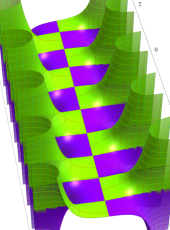
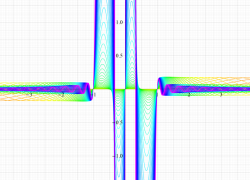
複素変数の第1種扁平回転楕円体波動関数 (角度関数)
複素変数の第1種扁平回転楕円体波動関数 (角度関数)
複素変数の第1種扁平回転楕円体波動関数 (角度関数)
複素変数の第1種扁平回転楕円体波動関数 (角度関数)
複素変数の第1種扁平回転楕円体波動関数 (角度関数)
複素変数の第1種扁平回転楕円体波動関数 (角度関数)
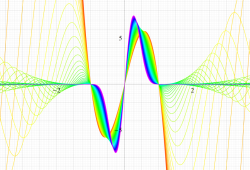
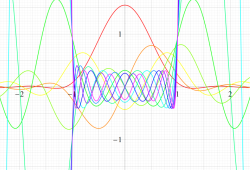
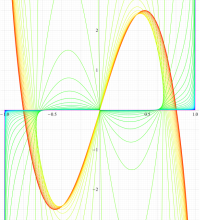
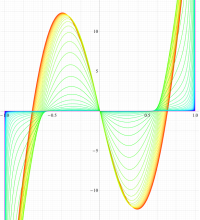
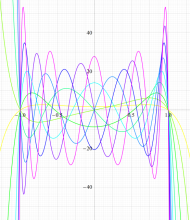
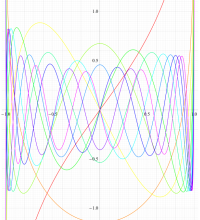
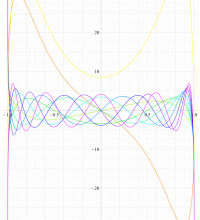
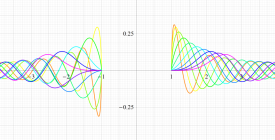
実変数の第2種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第2種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第2種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第2種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
実変数の第2種扁平回転楕円体波動関数 (角度関数) のグラフ。 順に、①
複素変数の第2種扁平回転楕円体波動関数 (角度関数)
複素変数の第2種扁平回転楕円体波動関数 (角度関数)
複素変数の第2種扁平回転楕円体波動関数 (角度関数)
複素変数の第2種扁長回転楕円体波動関数 (角度関数)
複素変数の第2種扁平回転楕円体波動関数 (角度関数)
複素変数の第2種扁平回転楕円体波動関数 (角度関数)
扁長回転楕円体波動関数 (動径関数)
この頁の最初で述べたように、Helmholtz の方程式を扁長回転楕円体座標で変数分離した際の動径成分の満たす微分方程式はとなる。この微分方程式も、
「Meixner - Schäfke の規格化」に基づく二つの回転楕円体波動関数 (動径関数)
このほか、Hankel 関数に倣って第3種と第4種
が定義される。これらの関数は特に、
となり、
回転楕円体波動関数 (動径関数) は、球 Bessel 関数の公式に似た
等を満たす (
初等関数に還元される場合として
となることが知られている。ここに
Meixner - Schäfke によれば、次のように Legendre 陪関数を Hobson 型に変更した関数
も定義される。ここに
のように線形結合となる。すなわち
である。
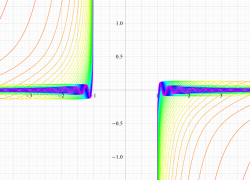
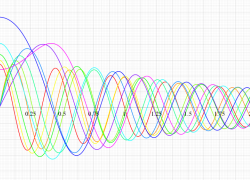
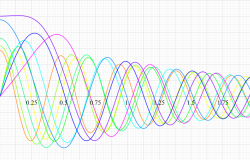
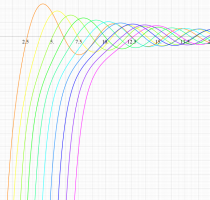
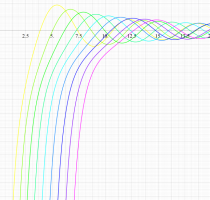
実変数の第1種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第1種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第1種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第1種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第1種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
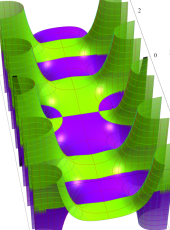
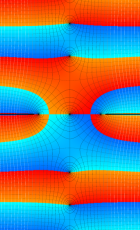
複素変数の第1種扁長回転楕円体波動関数 (動径関数)
複素変数の第1種扁長回転楕円体波動関数 (動径関数)
複素変数の第1種扁長回転楕円体波動関数 (動径関数)
複素変数の第1種扁長回転楕円体波動関数 (動径関数)
複素変数の第1種扁長回転楕円体波動関数 (動径関数)
複素変数の第1種扁長回転楕円体波動関数 (動径関数)
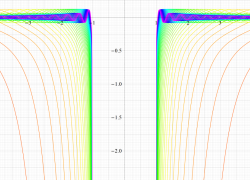
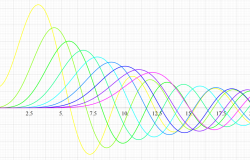
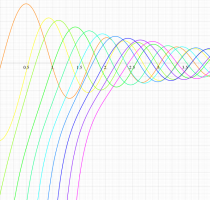
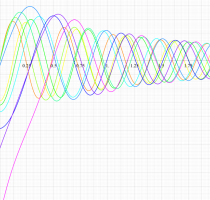
実変数の第2種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第2種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第2種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第2種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第2種扁長回転楕円体波動関数 (動径関数) のグラフ。 順に、①
複素変数の第2種扁長回転楕円体波動関数 (動径関数)
複素変数の第2種扁長回転楕円体波動関数 (動径関数)
複素変数の第2種扁長回転楕円体波動関数 (動径関数)
複素変数の第2種扁長回転楕円体波動関数 (動径関数)
複素変数の第2種扁長回転楕円体波動関数 (動径関数)
複素変数の第2種扁長回転楕円体波動関数 (動径関数)
複素変数の第3種扁長回転楕円体波動関数 (動径関数)
複素変数の第3種扁長回転楕円体波動関数 (動径関数)
複素変数の第3種扁長回転楕円体波動関数 (動径関数)
複素変数の第3種扁長回転楕円体波動関数 (動径関数)
複素変数の第3種扁長回転楕円体波動関数 (動径関数)
複素変数の第3種扁長回転楕円体波動関数 (動径関数)
扁平回転楕円体波動関数 (動径関数)
扁平回転楕円体波動関数 (動径関数) は、前述の扁長回転楕円体波動関数 (動径関数) において一般に扁平回転楕円体波動関数 (動径関数) は、複素平面上
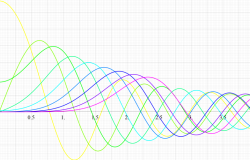
実変数の第1種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第1種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第1種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第1種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第1種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
複素変数の第1種扁平回転楕円体波動関数 (動径関数)
複素変数の第1種扁平回転楕円体波動関数 (動径関数)
複素変数の第1種扁平回転楕円体波動関数 (動径関数)
複素変数の第1種扁平回転楕円体波動関数 (動径関数)
複素変数の第1種扁平回転楕円体波動関数 (動径関数)
複素変数の第1種扁平回転楕円体波動関数 (動径関数)
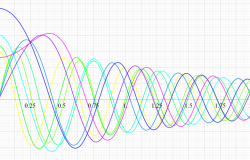
実変数の第2種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第2種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第2種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第2種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
実変数の第2種扁平回転楕円体波動関数 (動径関数) のグラフ。 順に、①
複素変数の第2種扁平回転楕円体波動関数 (動径関数)
複素変数の第2種扁平回転楕円体波動関数 (動径関数)
複素変数の第2種扁平回転楕円体波動関数 (動径関数)
複素変数の第2種扁平回転楕円体波動関数 (動径関数)
複素変数の第2種扁平回転楕円体波動関数 (動径関数)
複素変数の第2種扁平回転楕円体波動関数 (動径関数)
複素変数の第3種扁平回転楕円体波動関数 (動径関数)
複素変数の第3種扁平回転楕円体波動関数 (動径関数)
複素変数の第3種扁平回転楕円体波動関数 (動径関数)
複素変数の第3種扁平回転楕円体波動関数 (動径関数)
複素変数の第3種扁平回転楕円体波動関数 (動径関数)
複素変数の第3種扁平回転楕円体波動関数 (動径関数)
回転楕円体波動固有値関数
回転楕円体微分方程式における固有値
これは、極限
回転楕円体波動固有値関数の数値計算は、Mathieu 固有値関数と同様、無限次連分数方程式や三重対角行列の方程式を用いるのが便利である。三重対角行列法の場合は
とするとき、
となる。ここに
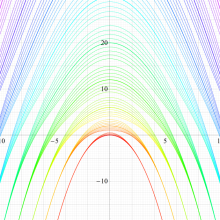
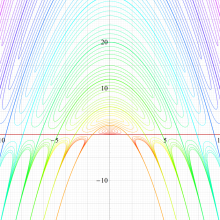
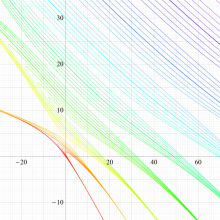
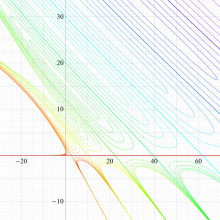
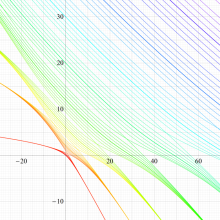
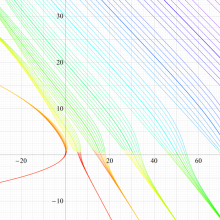
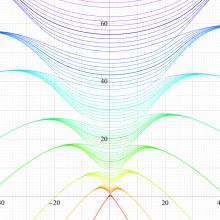
実変数の回転楕円体波動固有値関数のグラフ。 順に、①
回転楕円体波動関数を扱う書籍に挿入されている固有値関数のグラフは、この形であることも多い。
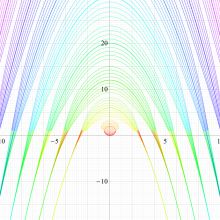
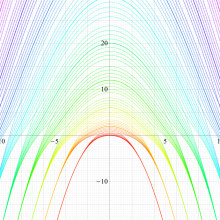
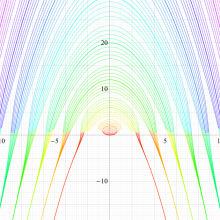
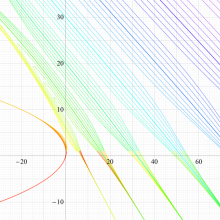
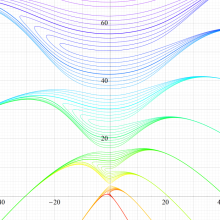
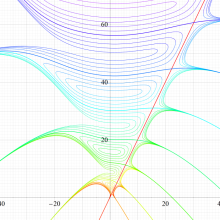
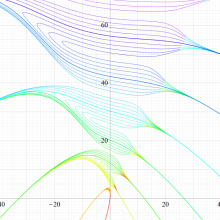
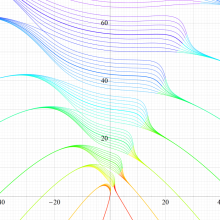
実変数の回転楕円体波動固有値関数のグラフ。 順に、①
この形は、極限によって Mathieu 固有値関数に近づく。
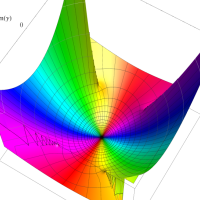
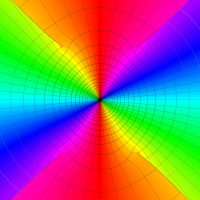
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数
複素変数の回転楕円体波動固有値関数