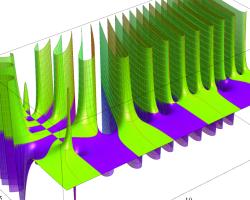
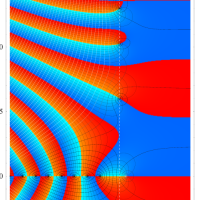
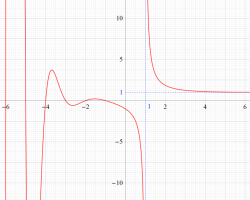
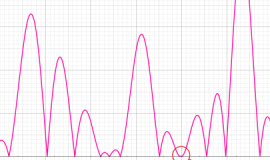
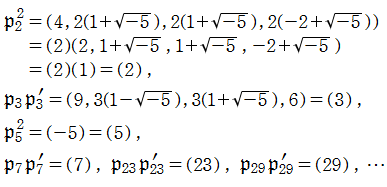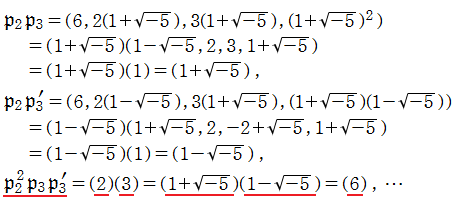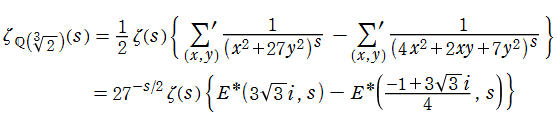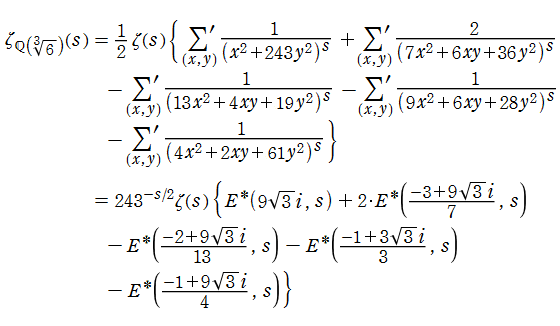特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
ゼータ関数
Riemann のゼータ関数
日:Riemannのゼータ関数,リーマン ζ 関数英:Riemann zeta function,仏:Fonction zêta de Riemann,独:Riemannsche Zetafunktion
元々 「ゼータ関数」 とは、ある特徴を持つ一群の関数を指すが、現在では、発散級数の正規化、作用素等の役割も担う数学的対象物にその意味が拡大されているので、ゼータ関数とは何かを一言で説明するのは難しい。
商を除く四則演算に対して閉じた集合となる可換環は、その要素である元 (必ずしも数とは限らない) が広義の積に関して素元に一意分解されることが多い。このとき、可換環の元全体をわたる和が、同時に素元全体をわたる積にも表わされる例をつくることができる。つまり、素元への一意分解性が解析関数の満たす恒等式に言い換えられる。この解析関数が、対称的な関数等式を満たし複素平面全体に解析接続される等の良い性質を持っている場合、その可換環やこれを包含する体の上で考察される諸問題に対して、関数論的な種々のアプローチがとれるようになる。大雑把な説明であるが、そのような解析関数が (元々の意味での) ゼータ関数である。
具体的な可換環とその素元の例として、整数に対しては素数が、代数体 (代数的数体) の整イデアルに対しては素イデアルがよく知られている。さらに、有限体上における代数関数体が代数体に類似していることに基づいたゼータ関数等、様々な方向からの一般化も考察されているので、これらを総合すると、ゼータ関数の種類は全貌を把握することが難しいほど膨大な数に及ぶ※1。そのうち、整数環に対して定義されるゼータ関数が、よく知られた 「Riemann のゼータ関数」 である。歴史的に最も古くからあり最も基本的なゼータ関数であるため、文脈において単にゼータ関数というとき、それは Riemann のゼータ関数を指す場合が多い。
Riemann のゼータ関数は Dirichlet 級数 (→ Dirichlet のL関数を参照) によって
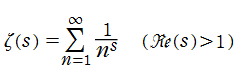
Riemann のゼータ関数についての最初の詳細な研究成果は、L. Euler によってもたらされた。明らかになった事柄として主要なものを列挙すると、
1.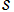 が2以上の偶数のときの
が2以上の偶数のときの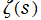 の特殊値、すなわち
の特殊値、すなわち
を求めた。ここに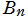 は Bernoulli 数である。特に、
は Bernoulli 数である。特に、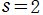 のときの値を求める 「バーゼル問題」 に対する解答が、これに含まれている。(1735年)
のときの値を求める 「バーゼル問題」 に対する解答が、これに含まれている。(1735年)
2.現在では 「Euler の素数積表示式」 または単に 「Euler 積」 等の名称で呼ばれる無限乗積
を発見し、このことから素数の個数は対数的に増大することを推察した。(1737年)
なお、この式が素因数分解の一意性を解析関数の恒等式で表現した例になっている。
3.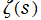 と
と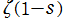 との関係を意味する 「関数等式」 を、数値計算による検証で部分的に求めた※3。
との関係を意味する 「関数等式」 を、数値計算による検証で部分的に求めた※3。
また、以上の結果等を用いて、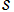 が0または負の奇数のときの
が0または負の奇数のときの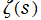 の特殊値と、
の特殊値と、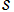 が負の偶数のときの
が負の偶数のときの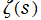 の零点 (自明零点:Trivial zeros と呼ばれる)
の零点 (自明零点:Trivial zeros と呼ばれる)
を求めた。(1749年)
などがある。なお、1.とは異なり、現在でもを求めた。ここに
2.現在では 「Euler の素数積表示式」 または単に 「Euler 積」 等の名称で呼ばれる無限乗積
を発見し、このことから素数の個数は対数的に増大することを推察した。(1737年)
なお、この式が素因数分解の一意性を解析関数の恒等式で表現した例になっている。
3.
また、以上の結果等を用いて、
を求めた。(1749年)
3.はその後、他の数学者達によって厳密な証明が与えられたが、そのうちの G. F. B. Riemann は始めから
1.経路積分を用いて、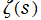 が
が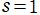 を唯一の特異点 (1位の極) とする有理型関数であることを証明した。
を唯一の特異点 (1位の極) とする有理型関数であることを証明した。
2.関数等式を2通りの方法で厳密に証明するとともに、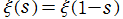 の形で求めた。
の形で求めた。
そのうちの一つは、関数等式の成立が直ちに分かる積分
による。積分の形によって、ゼータ関数と保型形式 (赤線部分) との関係も明らかにした。
3.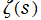 の複素零点
の複素零点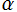 を用いて、ある
を用いて、ある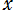 以下の素数の個数を表わす関数
以下の素数の個数を表わす関数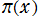 を
を
と求めた。ここに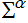 は、複素零点のうち虚部が正であるものを (もし重根があれば重複して) 総和する。また、
は、複素零点のうち虚部が正であるものを (もし重根があれば重複して) 総和する。また、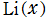 は積分対数関数、
は積分対数関数、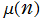 は Möbius 関数である。
は Möbius 関数である。
この公式は現在、「Riemann - von Mangoldt 公式」 と呼ばれる (→ Riemann 素数計数関数を参照)。なお、Riemann の論文の主題はこの公式を求めることであった。
等からなる。記号2.関数等式を2通りの方法で厳密に証明するとともに、
そのうちの一つは、関数等式の成立が直ちに分かる積分
による。積分の形によって、ゼータ関数と保型形式 (赤線部分) との関係も明らかにした。
3.
と求めた。ここに
この公式は現在、「Riemann - von Mangoldt 公式」 と呼ばれる (→ Riemann 素数計数関数を参照)。なお、Riemann の論文の主題はこの公式を求めることであった。
「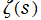 の複素零点
の複素零点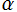 は、すべて1位で
は、すべて1位で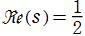 (臨界線) 上のみに存在する。」
(臨界線) 上のみに存在する。」
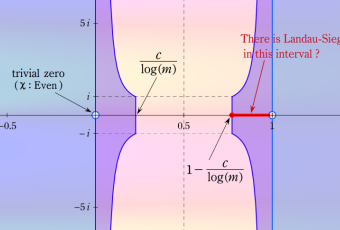
は現在でも証明されず唯一残っている。これが、数学の未解決問題として有名な 「Riemann 予想」 である。またこの複素零点は、前述の自明零点に対比させて 「非自明零点:Non trivial zeros」 と呼ばれる。
なお、臨界線上における非自明零点の間隔が不規則であることも、この関数の神秘的な一面である。これをある無限次元行列式の固有値で説明しようとする試みなど、Riemann 予想の証明を目標に含む様々な研究が行われているが、いずれもまだ解決には至っていない。
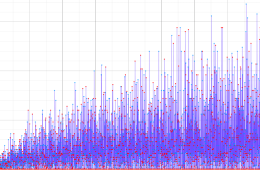
数値計算による Riemann 予想の検証、特に20世紀後半からは電子計算機を用いた検証も行われている。2004年現在、虚部の最も小さいものから順に数えて約10兆個の非自明零点については Riemann 予想の成立が確定しているが、このような検証が、元々は Riemann 予想の反例を見つけるという動機で始められることも多い。非自明零点の探索では、Riemann のゼータ関数そのものよりも便利な、後述の Riemann - Siegel 関数が専ら用いられる。
Riemann のゼータ関数については、各分野から精力的かつ緻密な研究が行われた結果、非常に多くの公式が得られている。簡単な例としては、積分表示式
が有名で、第1の積分は Riemann が前述の論文で1.を証明する際に使用した経路積分の起源でもある。また第2の積分は Euler - Maclaurin 総和公式の応用例であるが、形が簡明で大変美しい。他にも興味深い例として、Hasse の公式
がある。この無限級数は、無限遠点と
【註記】
※1:例えば、「Wikipedia (En.) - List of zeta functions」 には多数のゼータ関数が掲載されている (しかし、それでも全てではない)。
※2:「簡潔」 と書いたが、実際はそれほど簡潔でないことは、引数に対数関数を代入しただけでも分かる。それは、次数が対数列で増加するような "冪級数" である!。
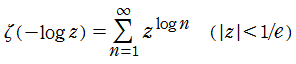
※3:Euler はゼータ関数を無限級数や無限乗積の形で直接扱い、関数記号を特に定めなかった。それでも、Euler は関数等式を個性的で謎めいた記号を用いて表記している。
※4:Riemann の国籍、および戦前の日本がドイツ数学から多くの影響を受けた等の理由で、古い書籍では 「ゼータ」 をドイツ語読みした 「ツェータ関数」 の表記が散見されたが、現在ではほとんど見かけなくなった。
※1:例えば、「Wikipedia (En.) - List of zeta functions」 には多数のゼータ関数が掲載されている (しかし、それでも全てではない)。
※2:「簡潔」 と書いたが、実際はそれほど簡潔でないことは、引数に対数関数を代入しただけでも分かる。それは、次数が対数列で増加するような "冪級数" である!。
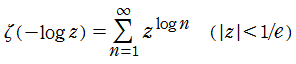
※3:Euler はゼータ関数を無限級数や無限乗積の形で直接扱い、関数記号を特に定めなかった。それでも、Euler は関数等式を個性的で謎めいた記号を用いて表記している。
※4:Riemann の国籍、および戦前の日本がドイツ数学から多くの影響を受けた等の理由で、古い書籍では 「ゼータ」 をドイツ語読みした 「ツェータ関数」 の表記が散見されたが、現在ではほとんど見かけなくなった。
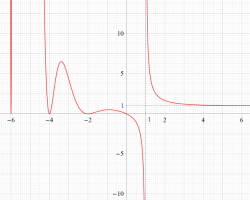
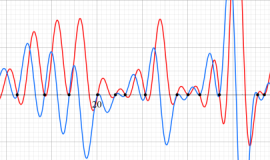
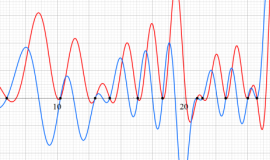
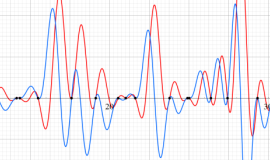
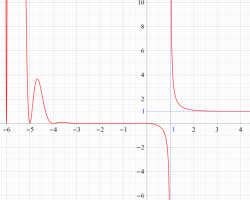
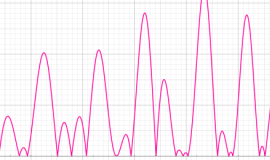
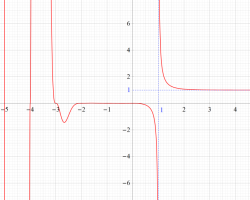
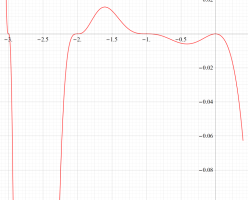
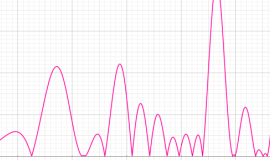
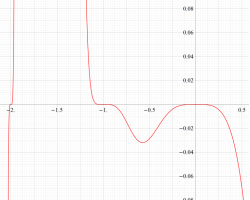
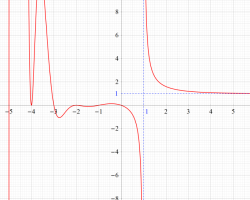
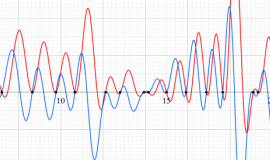
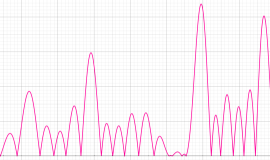
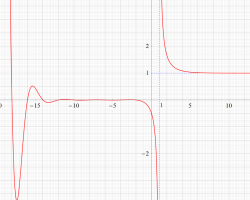
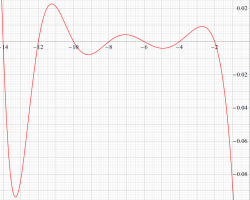
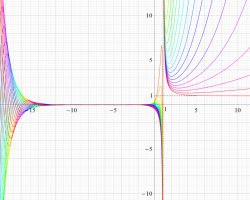
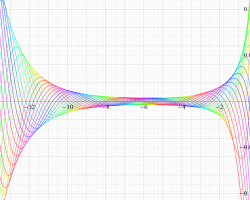
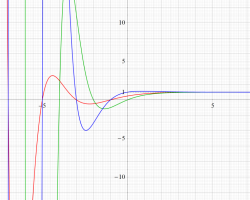
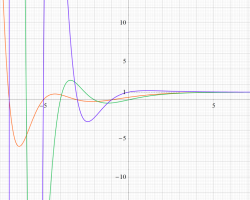
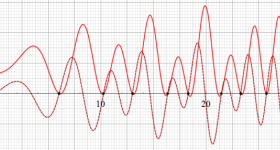
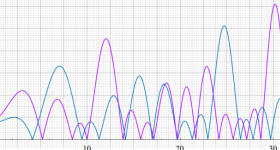
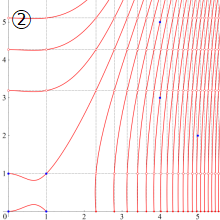
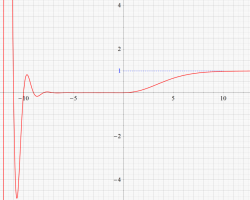
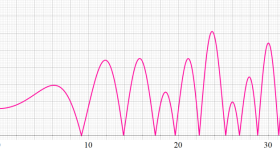
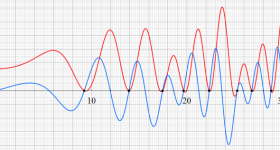
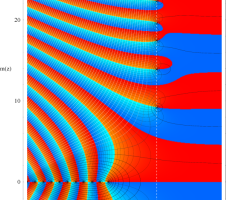
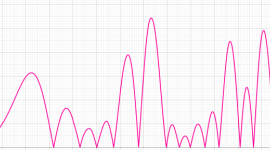
①実軸上。②実軸上のうち、関数値の絶対値が小さいためよく分からない部分を拡大した場合。
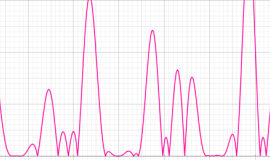
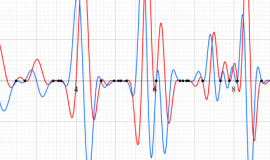
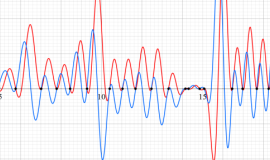
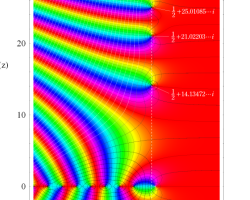
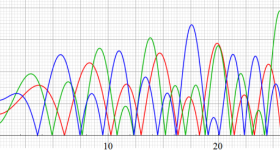
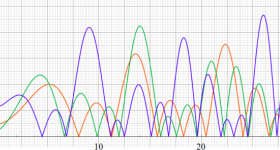
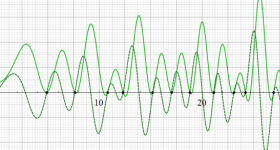
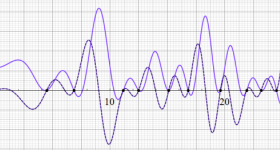
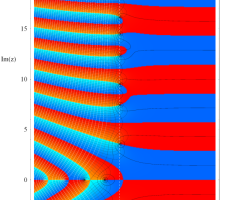
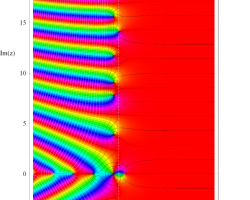
臨界線上の Riemann ゼータ関数のグラフ。
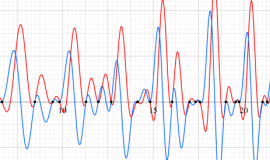
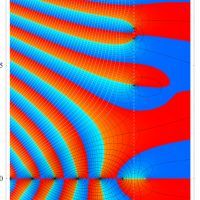
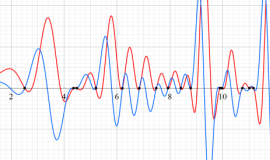
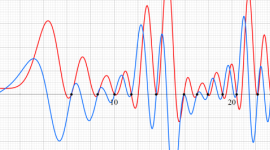
①絶対値のグラフ。高さが0になる所が非自明零点。
②実部と虚部のグラフ。この場合は赤線と青線がともに
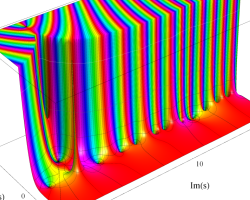
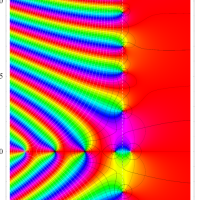
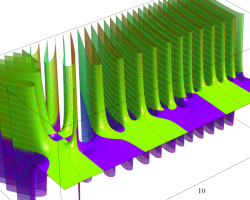
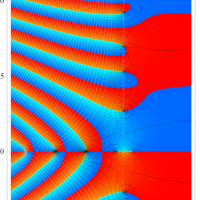
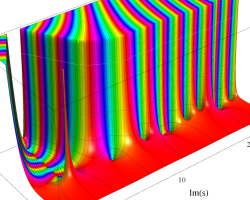
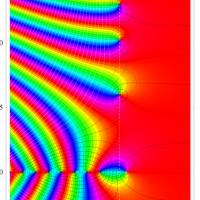
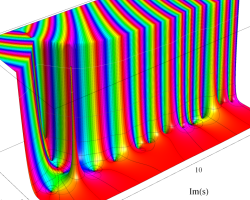
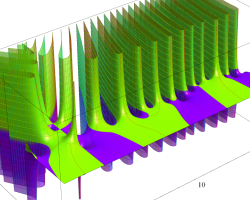
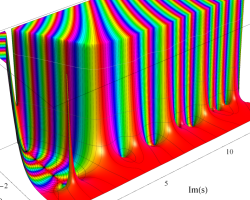
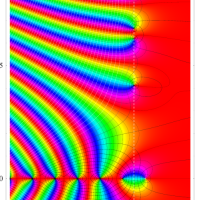
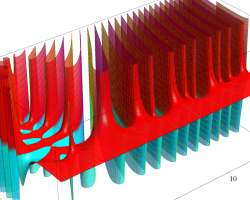
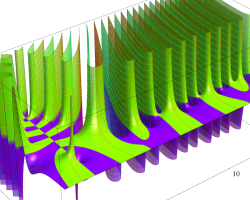
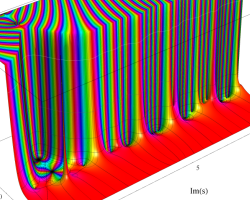
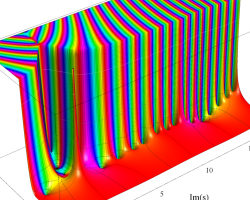
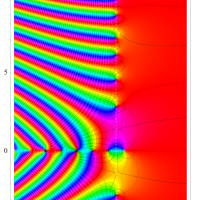
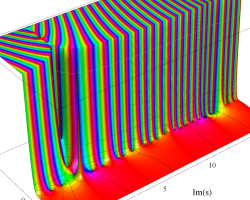
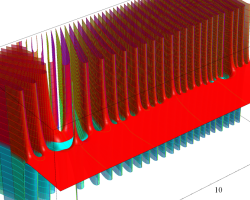
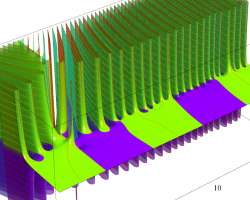
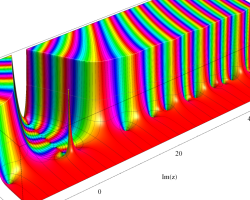
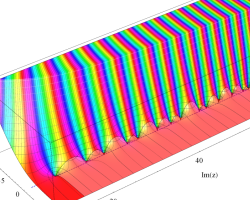
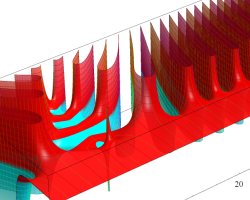
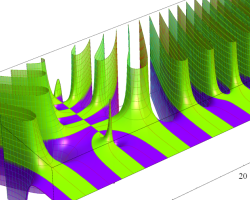
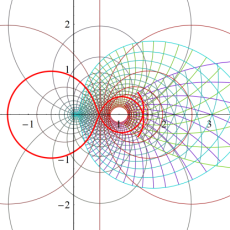
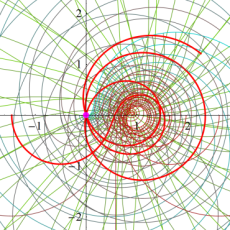
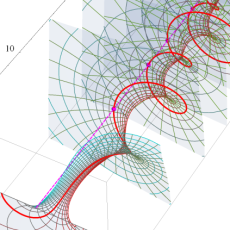
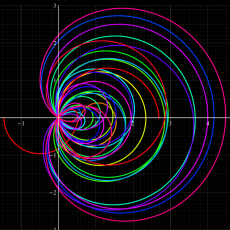
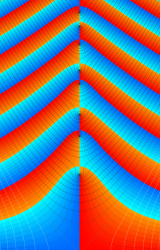
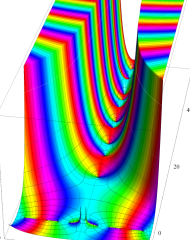
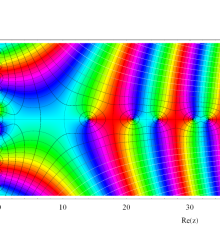
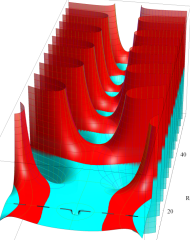
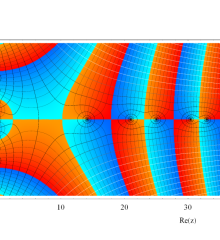
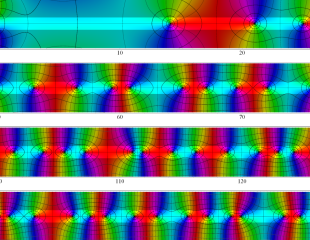
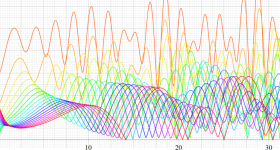
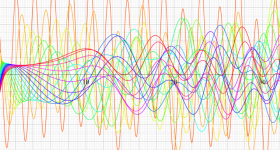
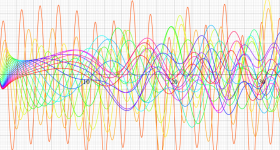
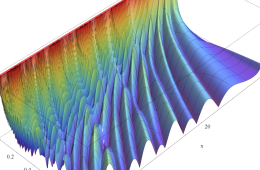
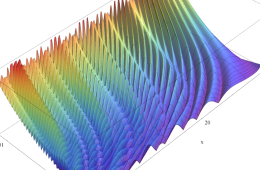
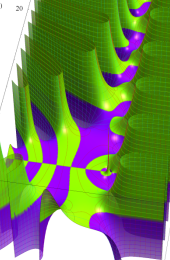
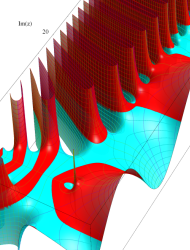
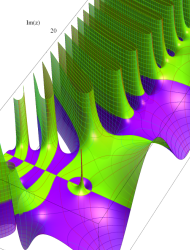
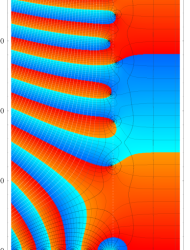
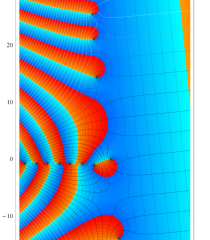
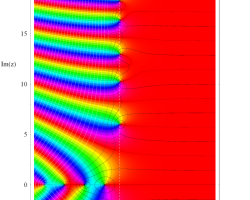
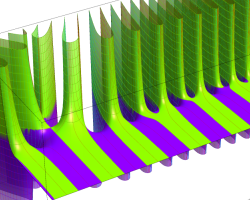
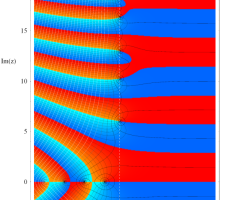
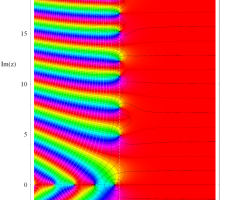
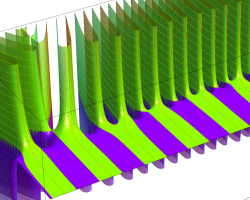
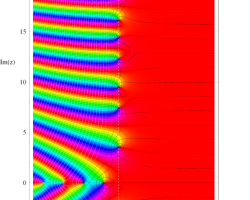
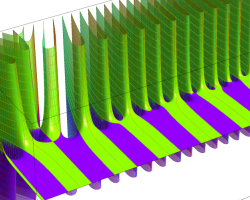
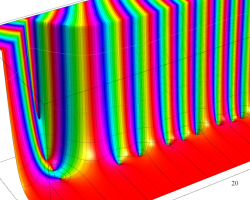
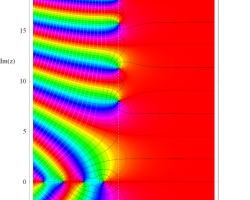
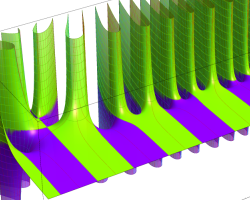
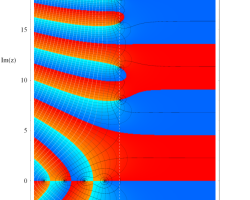
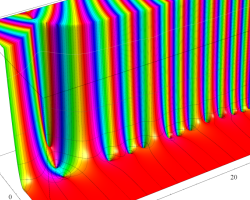
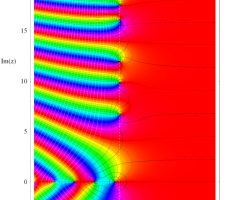
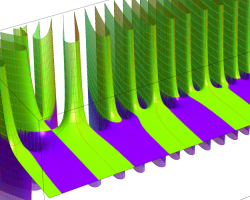
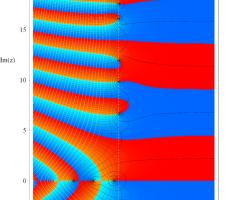
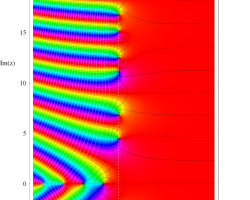
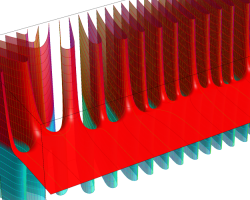
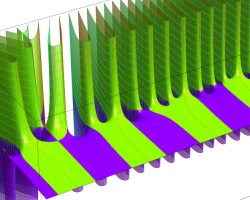
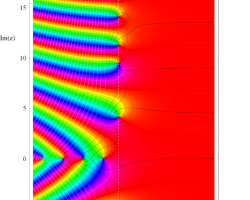
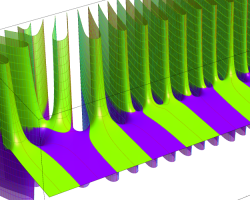
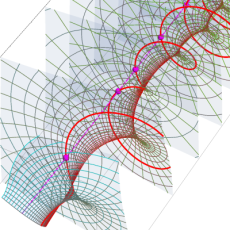
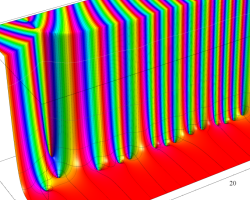
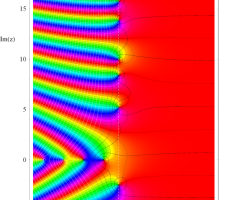
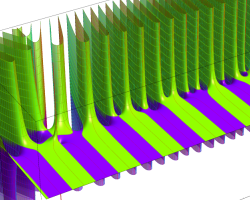
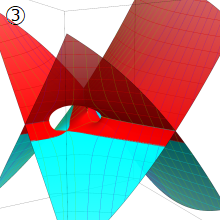
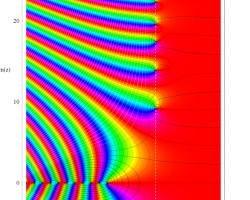
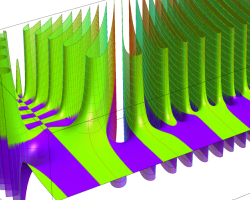
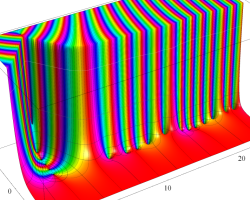
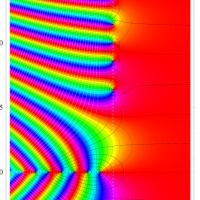
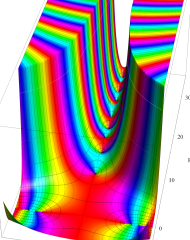
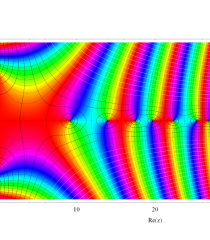
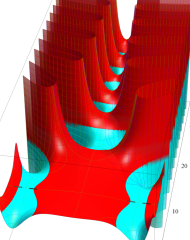
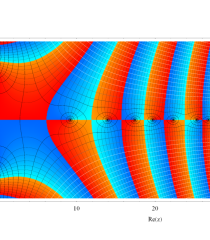
複素変数の Riemann ゼータ関数のグラフ。
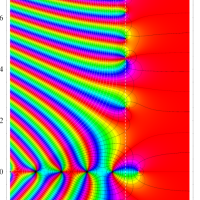
2番目は臨界線をさらに辿った場合で、かつ、値域のスケールを逆双曲線正弦関数的にしている。
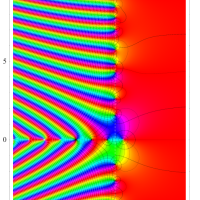
次は、臨界帯と呼ばれる領域 (
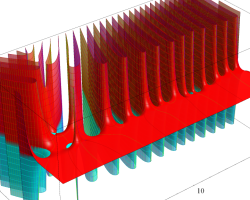
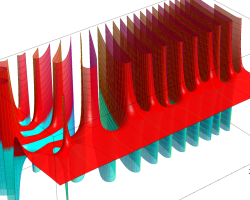
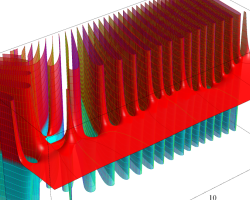
Riemann ゼータ関数
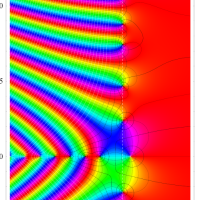
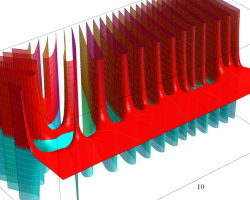
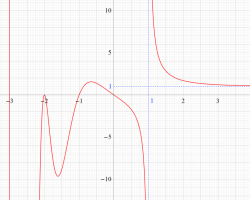
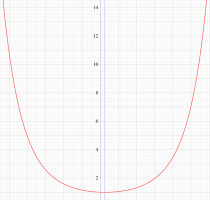
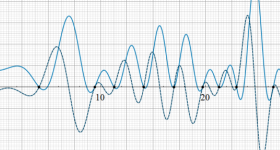
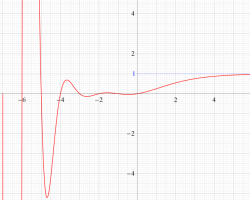
実変数のグラフ。線対称形である。
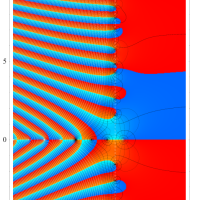
複素変数のグラフ。 Riemann ゼータ関数の本質的な対称性を表わしている。2番目は値域のスケールを対数関数的にした場合。
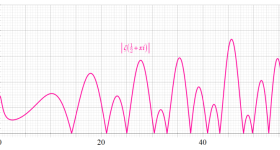
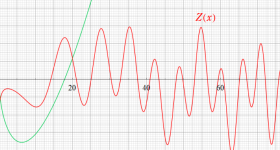
Riemann - Siegel 関数
日:Riemann-Siegel関数,リーマン-ジーゲルZ関数英:Riemann-Siegel function,仏:Fonction de Riemann-Siegel,独:Riemann-Siegelschen Z-funktion
Riemann のゼータ関数のところでも述べたとおり、Riemann 予想における非自明零点の数値計算では、Riemann のゼータ関数そのものよりも、Riemann - Siegel 関数
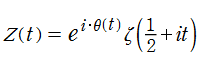
となる。Riemann - Siegel シータ関数は、複素平面上
Riemann は論文 「与えられた数より小さい素数の個数について」 中で、すべての非自明零点が臨界線上にあることを (証明できないが) 「確からしい」 と言及しており、このことから変数を
それは、実質的に
は 「Riemann - Siegel 公式」 と呼ばれるようになった。非自明零点の数値計算において、この公式がいかに有用であるかを Siegel 自身も確認したが、実際、この級数は上記に明示された
20世紀初頭から既に、非自明零点の探索 (数値計算競争) が始まっていたが、初期は主に Euler - Maclaurin 総和公式を用いた。その場合の非自明零点の個数記録は、虚部の最も小さいものから順に数えて約200個が限界であった。しかし、1936年に Riemann - Siegel 公式を併用したとき、初めて飛躍的に1000個を超えた (当時、まだ手計算が主流であったことに留意)。以後、電子計算機による探索が普通となった現在に至るまで、Riemann - Siegel 公式は一貫して使用されている。
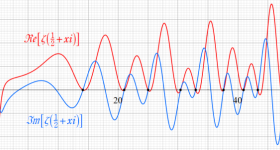
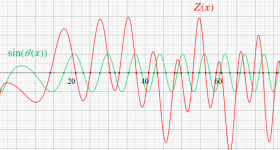
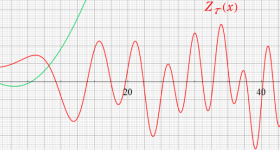
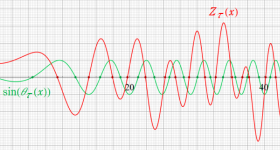
① Riemann - Siegel シータ関数,② Riemann - Siegel シータ関数を正弦関数に代入した関数
である。②は、緑の曲線が複素変数の Riemann - Siegel 関数のグラフ。
Riemann - Siegel 関数における臨界帯に相当する領域は、
Hurwitz のゼータ関数
日:Hurwitzのゼータ関数,フルヴィッツ ζ 関数英:Hurwitz zeta function,仏:Fonction zêta de Hurwitz,独:Hurwitzsche Zetafunktion
Riemann のゼータ関数を一般化した、
は A. Hurwitz による研究に因み、Hurwitz のゼータ関数と呼ばれている。
Hurwitz のゼータ関数は、Riemann のゼータ関数に類似する多くの積分表示式や無限級数表示式を持つが、
のような固有の公式も多い。 Hurwitz のゼータ関数も、
を満たす。しかし、
を除いて、Hurwitz のゼータ関数は Riemann のゼータ関数における Euler の素数積表示に相当する公式を持たず、複素零点も
ところが、次のような Hurwitz のゼータ関数の有限和で表わされる、後述の (原始指標に対する) Dirichlet のL関数
になると、複素零点が
なお、Riemann のゼータ関数から Hurwitz のゼータ関数へ一般化したように、種々ある拡張版のゼータ関数に対しても同様の一般化を行うことは、既に多く試みられている。またこれとは別に、補助変数を設けて他の関数との融合化を図ったものもある。そのような関数の一例として Lerch の超越関数がある。
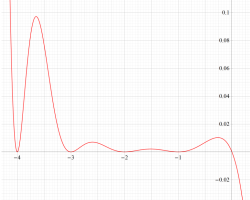
①実軸上。②実軸上のうち、関数値の絶対値が小さいためよく分からない部分を拡大した場合。
臨界線上の Hurwitz ゼータ関数のグラフ。
①
次は、単に美しいという理由で描いた二変数関数としての
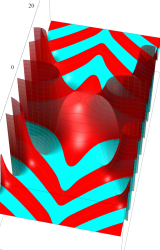
複素変数の Hurwitz ゼータ関数
Hurwitz ゼータ関数
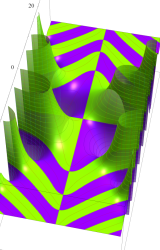
複素変数の Hurwitz ゼータ関数
Hurwitz ゼータ関数
複素変数の Hurwitz ゼータ関数
アニメーション(5.82MB)
複素変数の Hurwitz ゼータ関数
アニメーション(27.3MB)
Hurwitz ゼータ関数
①
② Hurwitz ゼータ関数の第
(ここに第
Dirichlet のL関数
日:DirichletのL関数,ディリクレのL関数,ディリクレのL級数英:Dirichlet L-function,仏:Fonction L de Dirichlet,独:Dirichletsche L-reihen
Euler から始まり現在に至るまで、幾人もの数学者が言わば 「Riemann ゼータ関数の親類」 探しに着手している。そこで発見されたゼータ関数は、しばしばその発見者の名を冠して 「~のゼータ関数」 と呼ばれる。前述の Hurwitz のゼータ関数はその一例である。ここで扱う Dirichlet のL関数も、P. G. L. Dirichlet によって1837年に導入されたゼータ関数であるが※1、「L関数」 と呼ばれる。これは、後述の Dirichlet 指標が付随した級数を考える場合、L関数と称してゼータ関数と区別する習慣が定着したことによる。したがって、「~のL関数」 と呼ばれる一群のゼータ関数も多数存在する。
現在では Dirichlet の業績に因み、一般に
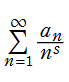
が定義される。ここに
1.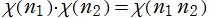 が任意の整数
が任意の整数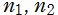 で成立する (乗法性)
で成立する (乗法性)
2.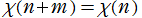 が任意の整数
が任意の整数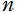 で成立する (周期性)
で成立する (周期性)
3.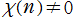 となるのは
となるのは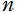 と法
と法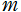 とが互いに素な場合に限る
とが互いに素な場合に限る
Dirichlet 指標は、必ず2.
3.
法が
と表わされるならば、「
は、原始指標
の関係にある。よって Dirichlet のL関数は、原始指標の場合がより本質的であるといえる。
Dirichlet のL関数は、原始指標の場合に限って準対称関数等式
を満たす。ここに、
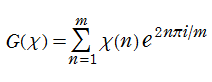
以上のことから、とりわけ実原始指標の場合が重要とされる。実原始指標は、前述とは別方法で定義される Kronecker 指標
1.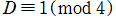 かつ
かつ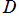 は平方因子を含まない
は平方因子を含まない
2.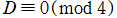 かつ
かつ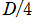 は平方因子を含まず、かつ
は平方因子を含まず、かつ
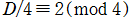 または
または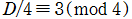
このとき、2.
ここに、
そもそも Dirichlet がこの関数を導入した目的は、
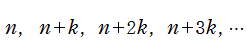
1.Euler の素数積表示式に相当する式を満たす (前述のとおり)。
2.引数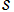 が特定の整数であるときに特殊値を持つ。
が特定の整数であるときに特殊値を持つ。
3.準対称的な関数等式を満たす (前述のとおり)。
4.単位指標のとき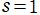 を唯一の極とする有理型関数、その他は超越整関数になる。
を唯一の極とする有理型関数、その他は超越整関数になる。
等が判明した。このような Riemann のゼータ関数との類似性や、数値計算による複素零点の検証結果に基づいて、Dirichlet のL関数に対する 「一般化された Riemann 予想」2.引数
3.準対称的な関数等式を満たす (前述のとおり)。
4.単位指標のとき
「原始指標に対する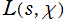 の複素零点は、すべて1位で
の複素零点は、すべて1位で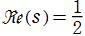 (臨界線) 上のみに存在する。」
(臨界線) 上のみに存在する。」
が立てられているが、いかなる原始指標
すべての Dirichlet のL関数が
Dirichlet のL関数および指標は、二次形式論と呼ばれる数論の一分野でよく現れる。特に、実原始指標に対する Dirichlet のL関数の
は※2、特殊線形群
【註記】
※1:1837年は、Riemann がゼータ関数の研究結果を発表した1859年よりも早いことに注意。なお、(指標の理論は除いて) Dirichlet のL関数のうち特殊な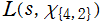 だけは、Euler も研究していた。さらに、15世紀には既に知られていた Madhava - Leibniz 級数
だけは、Euler も研究していた。さらに、15世紀には既に知られていた Madhava - Leibniz 級数
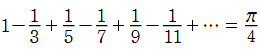 は、
は、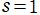 における
における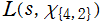 の値と解釈できる。
の値と解釈できる。
※2:より一般的な指標に対する Dirichlet のL関数の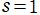 における値は、
における値は、
となる。
※1:1837年は、Riemann がゼータ関数の研究結果を発表した1859年よりも早いことに注意。なお、(指標の理論は除いて) Dirichlet のL関数のうち特殊な
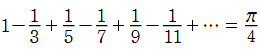
※2:より一般的な指標に対する Dirichlet のL関数の
となる。
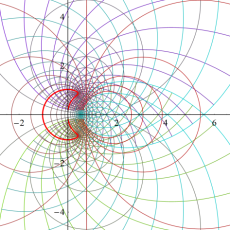
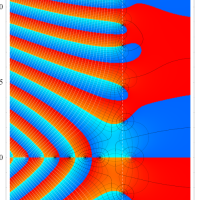
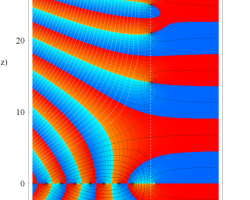
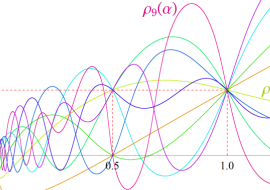
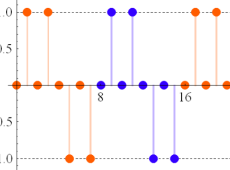
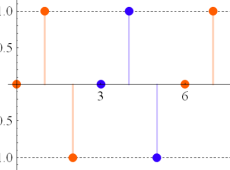
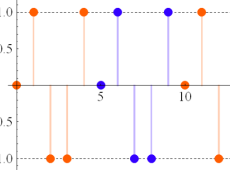
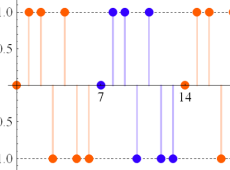
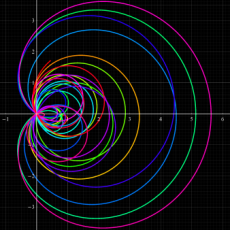
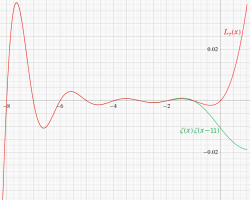
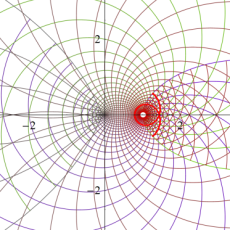
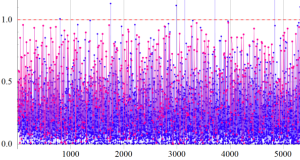
つまり Dirichlet 指標は、各種ゼータ関数の Dirichlet 級数や Euler 積に対して、このグラフが示すような 「ねじれ」 や 「周期的除外」 を起こす。
(なお、単位指標の場合は0と1からなる更に単純なグラフになるので描画しない。)
【実原始指標】
順に、①
順に、①
【複素原始指標】
順に、①
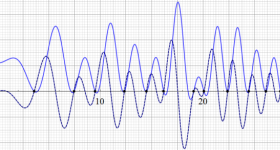
実変数の Dirichlet のL関数のグラフ。
特に
①
②
臨界線上の Dirichlet のL関数のグラフ。
①
②
①
③
①
③
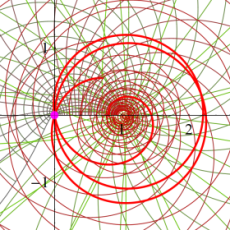
複素変数の Dirichlet のL関数
複素変数の Dirichlet のL関数
複素変数の Dirichlet のL関数
複素変数の Dirichlet のL関数
複素変数の Dirichlet のL関数
複素変数の Dirichlet のL関数
【複素原始指標に対する Dirichlet のL関数】
臨界線上の Dirichlet のL関数のグラフ。(複素指標の場合は、一般に実軸上で実数値をとらない。)
①
複素変数の Dirichlet のL関数
Dirichlet のL関数
複素変数の Dirichlet のL関数
【単位指標に対する Dirichlet のL関数】
実変数および臨界線上の Dirichlet のL関数のグラフ。法が1でない単位指標に対する Dirichlet のL関数は、臨界線上とそうでない複素零点の両方を持つ。(このうち、臨界線上の零点は Riemann ゼータ関数に由来するため、固有の零点ではない。)
①
複素変数の Dirichlet のL関数
Dirichlet のL関数
Ramanujan のゼータ関数
日:Ramanujanのゼータ関数,ラマヌジャンのL関数英:Ramanujan L-function,仏:Fonction L de Ramanujan,独:Ramanujan L-funktion
Dirichlet のL関数が、Dirichlet 指標なる数論的関数からつくられるゼータ関数であるように、ここで扱う Ramanujan のゼータ関数 (または Ramanujan のL関数) は、保型形式の Fourier 係数を指標とするゼータ関数であるといえる。
後述のとおり、保型形式から得られるゼータ関数も多数存在するが、Ramanujan のゼータ関数はその一例を与える最初の関数として、S. Ramanujan によって発見された。具体的に Dirichlet 級数で表示すると、
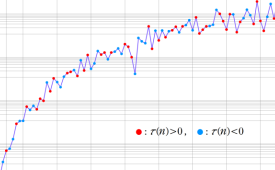
となる。ここに係数
なお Ramanujan のタウ関数の符号 (正負) は、上記のように不規則であり、絶対値も下記のグラフにあるとおり単調増加ではない。Ramanujan は、タウ関数の数論的な性質について二三の予想を立てた。後述の Fourier 係数が満たす不完全形の乗法性は、タウ関数に対する予想の一つを包含している。これらの予想のうち、タウ関数の絶対値に対する上限値評価を表わす 「Ramanujan 予想」
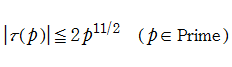
Ramanujan のゼータ関数は、分母が
で表わせるため、「二次のゼータ関数」 と呼ばれることもある。また、対称的な関数等式
を満たし、解析接続によって超越整関数であることが導けるなど、Ramanujan のゼータ関数も Riemann のゼータ関数と同様に良い性質を持っている。そのため、Ramanujan のゼータ関数に対しても 「Riemann 予想」
「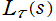 の複素零点は、すべて1位で
の複素零点は、すべて1位で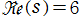 (臨界線) 上のみに存在する。」
(臨界線) 上のみに存在する。」
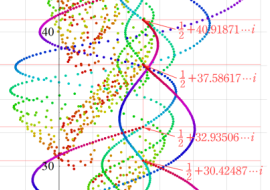
が立てられているものの、現在でも証明されていない。また、Ramanujan のゼータ関数は計算が難しく、特に臨界線上を虚部が大きい方向へ辿るほど評価が難しくなる。最初の数十個の複素零点であっても、実際に臨界線上に存在することを数値計算で確認できるようになったのは1970年代以後のことである※1。
Ramanujan のゼータ関数は、主に保型形式が関係する数論の問題に時々現れる。任意の自然数
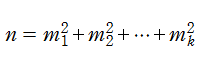
となる※2。
Ramanujan のゼータ関数を含む、より一般的なモジュラー形式から得られるゼータ関数の例は次のようになる。
のように関数等式を満たし、Fourier 級数に展開されるとする。このとき、
を引き起こす作用素
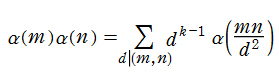
のように Euler 積表示式でも表わせることが分かる。現在このゼータ関数は 「Hecke 作用素によるゼータ関数」 と呼ばれ、関数等式を満たす等の良い性質を持つので
Hecke 作用素によるゼータ関数は、
現在では、上記以外にも保型形式から得られるゼータ関数の様々な例が見出され、数論を始めとする数学の諸問題を解くために応用されている。特に、そのようなゼータ関数の例として、
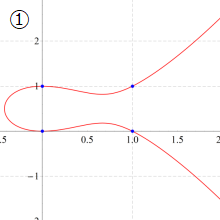
があり、これも Ramanujan によって初めて発見された。なお、付随する保型形式は尖点形式でもある (→ 保型性, グラフは 「Dedekind のエータ関数」 に掲載)。このゼータ関数は超越整関数で、Euler 積表示式や関数等式
を満たし、
にもなっている (ただし上記関係式は、無限遠点となる楕円曲線上の点は個数に含めない場合) ことが挙げられる。これは1954年に M. Eichler が証明した※3。R. P. Langlands はこのようなゼータ関数と保型形式との結び付きをさらに一般化すること、延いては数学の異なる分野の統合を推し進めることを促し、彼が立てた数々の予想や展望は、現在 「Langlands プログラム」 と総称されている。
現在では、一般に楕円曲線の合同式の解の個数から得られる指標を係数とする Dirichlet 級数 (によるゼータ関数) は、同時に重み2の保型形式の Fourier 係数を指標とするゼータ関数でも表わされること (モジュラー性定理) が知られている。A. J. Wiles と R. L. Taylor は、ある特別な場合の楕円曲線に対するモジュラー性定理を証明したが、Fermat の最終定理の代数方程式はこのモジュラー性定理 (が正しいと仮定したとき) に該当しない楕円曲線に由来することが既に知られていたので、その系として Fermat の最終定理も同時に証明された。
Eichler のL関数や Fermat の最終定理の証明手法は、Langlands プログラムの成功例としてよく引き合いに出され、他の未解決問題を考える場合にも指針の一つとなっている。
【註記】
※1:例えば、R. Spira 「Calculation of the Ramanujan τ-Dirichlet Series」 Mathematics of Computation, vol.27, No.122, (1973) p.379-385 等。
※2:J. M. Borwein, K.- K. S. Choi 「On Dirichlet Series for Sums of Squares」 The Ramanujan Journal, vol.7, (2003) p.95-127
※3:この関数の標準名称はないので、以下ではこれを 「Eichler のL関数」 と呼ぶことにする。
なお、この例のように Euler 積表示式に異常な項を発生させる有限個の素数 (この場合は11) は、しばしば通称で 「悪い素数」 と呼ばれる。正式には 「導手 (Conductor)」 といい、数論のほか様々な場面で不思議な現象を起こす。
※1:例えば、R. Spira 「Calculation of the Ramanujan τ-Dirichlet Series」 Mathematics of Computation, vol.27, No.122, (1973) p.379-385 等。
※2:J. M. Borwein, K.- K. S. Choi 「On Dirichlet Series for Sums of Squares」 The Ramanujan Journal, vol.7, (2003) p.95-127
※3:この関数の標準名称はないので、以下ではこれを 「Eichler のL関数」 と呼ぶことにする。
なお、この例のように Euler 積表示式に異常な項を発生させる有限個の素数 (この場合は11) は、しばしば通称で 「悪い素数」 と呼ばれる。正式には 「導手 (Conductor)」 といい、数論のほか様々な場面で不思議な現象を起こす。
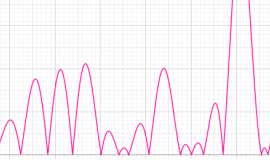
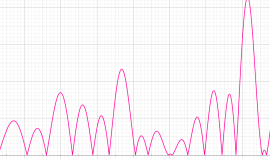
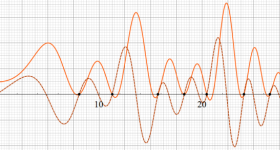
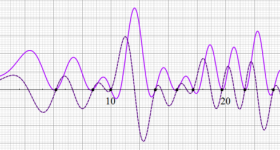
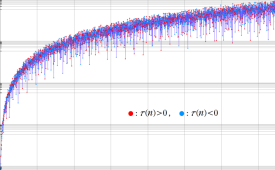
①実軸上。②実軸上のうち、関数値の絶対値が小さい部分を拡大した場合。
臨界線上の Ramanujan ゼータ関数のグラフ。①絶対値のグラフ。②実部と虚部のグラフ。
複素変数の Ramanujan ゼータ関数のグラフ。
Ramanujan ゼータ関数の臨界帯は、領域
Ramanujan ゼータ関数
Deligne が証明した Ramanujan 予想を
臨界線上の Eichler のL関数のグラフ。①絶対値のグラフ。②実部と虚部のグラフ。
複素変数の Eichler のL関数のグラフ。
Ramanujan - Siegel 関数
この関数は、Riemann のゼータ関数に対する非自明零点の数値計算を目的とした、前述の Riemann - Siegel 関数と同様に、Ramanujan のゼータ関数に対しても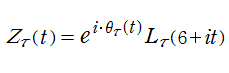
である。上記の定義から、Ramanujan - Siegel 関数は
なお、Ramanujan - Siegel という関数名は仮称であって、Ramanujan や Siegel が定義したという意味ではない。
①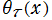 ,②
,②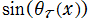
である。②において緑の曲線が複素変数の Ramanujan - Siegel 関数のグラフ。
Dedekind のゼータ関数
日:Dedekind のゼータ関数,デーデキント ζ 関数英:Dedekind zeta function,仏:Fonction zêta de Dedekind,独:Dedekindsche Zetafunktion
Dedekind のゼータ関数とは、代数体における代数的整数は素因数分解の一意性を持たないが、代数的整数環のイデアルは素イデアル分解の一意性を持つという事実に基づいて定義されるゼータ関数で、1877年に J. W. R. Dedekind が初めて導入した。したがって、代数的整数論における様々な問題の証明や理論の表現に Dedekind のゼータ関数が用いられている。
なお、この関数の説明にはイデアル等の前準備が必要なので、以下では始めにそれらの概要について触れ、その後に Dedekind のゼータ関数を説明するという順を踏む。
【準備1:代数体とその整数環】
有理数係数の
の解 (代数的数:有理数の拡張) の一つを
と書ける数の集合
の解 (代数的整数:整数の拡張) にもなっている元で構成される部分集合
【準備2:代数体の共役体と判別式】
まず共役数が必要となる。共役数とは、代数的数
このとき、
さらに
と書けるとき、各
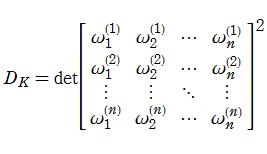
【準備3:イデアルの概要】
可換環
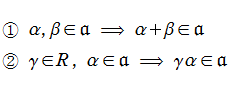
の形にも書けて、しばしば
である。つまりイデアルとは、
で定められる。また、イデアル
となる。さらに、単位元を持つ

なお、環
以下では、ほとんどの場合
【準備4:イデアルのノルム】
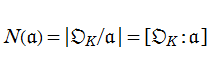
同様に、
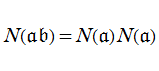
のように一意分解されるならば、
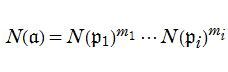
【Dedekind のゼータ関数】
以上の準備を経て、一般の
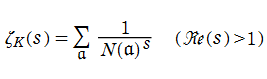
が導かれる。ここに、積は
を満たす。以上のことから、
「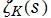 の複素零点は、すべて1位で
の複素零点は、すべて1位で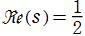 (臨界線) 上のみに存在する。」
(臨界線) 上のみに存在する。」
が立てられているが、いかなる代数体
【Dedekind のゼータ関数:二次体の場合】
平方因子を含まない整数を
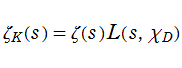
となり、これは二次体の基本数
【Dedekind のゼータ関数:円分体の場合】
1の
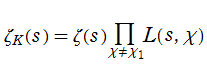
判別式は
【Dedekind のゼータ関数:純三次体の場合】
虚二次体や特殊な三次体 (純三次体など) の Dedekind ゼータ関数は、二元二次形式をわたる Dirichlet 級数によっても表わせる。(以降、二元二次形式を単に 「二次形式」 と記す。)
虚二次体を
となる。ここに、
となる。
純三次体
となる。具体的な表示式は、下記のグラフとともに掲載している※5。
【註記】
※1:剰余環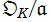 とは、
とは、
と表わされる有限集合である。つまり、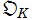 の元を
の元を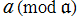 の違いで分割した有限個の部分集合から成る集合のことである。
の違いで分割した有限個の部分集合から成る集合のことである。
また、拡大体記号の分かりやすい例としては、実数体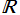 の拡大体である複素数体
の拡大体である複素数体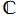 に対して
に対して![[C:R]=2](siki_spec020/zeta26100.png) 、有理数体
、有理数体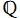 の拡大体である
の拡大体である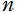 次体
次体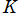 に対して
に対して![[K:Q]=n](siki_spec020/zeta26300.png) などが挙げられる。
などが挙げられる。
※2:イデアル等のイメージが掴みやすくなるよう、以下では具体的に二次体![K=Q(Sqrt[-5])](siki_spec020/zeta26400.png) の場合を例にとって説明する。
の場合を例にとって説明する。
![Sqrt[-5]](siki_spec020/zeta26500.png) は最小多項式
は最小多項式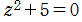 の解の一つとなるので、共役数は
の解の一つとなるので、共役数は![Sqrt[-5], -Sqrt[-5]](siki_spec020/zeta26700.png) の2個であるが、
の2個であるが、![Conlugate[-Sqrt[-5]]=Sqrt[-5]](siki_spec020/zeta26800.png) なので
なので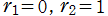 となる。
となる。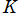 の元は
の元は![a+b*Sqrt[-5] (a, b∈Q)](siki_spec020/zeta27000.png) の形に書けるから、
の形に書けるから、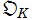 の基底は
の基底は![1, Sqrt[-5]](siki_spec020/zeta27100.png) 、その共役数は
、その共役数は![1, -Sqrt[-5]](siki_spec020/zeta27200.png) となり、判別式は
となり、判別式は
![Q(Sqrt[-5])の判別式](siki_spec020/zeta27300.png) となる。
となる。
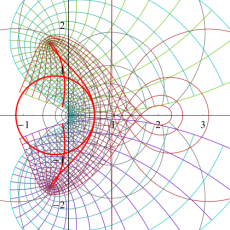
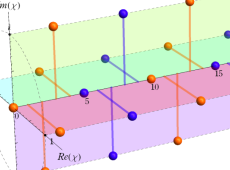
以下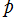 は素数とする。
は素数とする。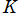 の素イデアル
の素イデアル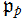 をいくつか列挙すれば、
をいくつか列挙すれば、
となる (これの求め方は、例えば 「数学セミナー増刊号:入門|現代の数学[5]数論への出発 (1980)」 にある)。一方、単項イデアル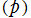 は
は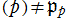 ならば素イデアルではないので、次のように素イデアルの積に一意分解される。
ならば素イデアルではないので、次のように素イデアルの積に一意分解される。
(なお、以下の演算では、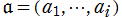 の基底
の基底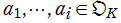 が公倍数
が公倍数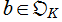 を持つときは
を持つときは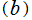 を括り出して良く、また、
を括り出して良く、また、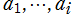 のうち最低でも2数が
のうち最低でも2数が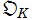 の互いに素な既約元 (この場合は
の互いに素な既約元 (この場合は![2, 3, 1+Sqrt[-5], 1-Sqrt[-5]](siki_spec020/zeta28200.png) のうち異なる2数) になれば
のうち異なる2数) になれば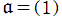 として良いことを用いている。これは 「Euclid の互除法」 に基づくが、この事の分かりやすい説明が、辻 順平氏 「tsujimotter
のノートブック」 (http://tsujimotter.hatenablog.com/entry/ideal-z5) にあるので参照して欲しい。)
として良いことを用いている。これは 「Euclid の互除法」 に基づくが、この事の分かりやすい説明が、辻 順平氏 「tsujimotter
のノートブック」 (http://tsujimotter.hatenablog.com/entry/ideal-z5) にあるので参照して欲しい。)
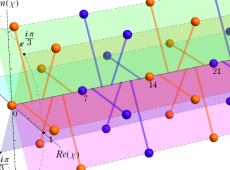
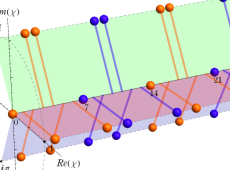
同様の演算により、合成数による単項イデアルも、次のように素イデアルの積に一意分解される。(赤線部分のように、![Q(Sqrt[-5])](siki_spec020/zeta28700.png) を数の世界で考える限り、6の分解方法は2通り存在してしまう。しかしイデアルで考えれば、その分解は一意となっている。)
を数の世界で考える限り、6の分解方法は2通り存在してしまう。しかしイデアルで考えれば、その分解は一意となっている。)
なお、一般に二次体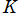 での単項イデアル
での単項イデアル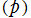 の分解型は、次の3種類に限られる。
の分解型は、次の3種類に限られる。
二次体の Dedekind ゼータ関数が、より簡単なゼータ関数の積に還元できるのは、この分解型の違いを用いて、Euler 積表示式を変形できるからである。もっと複雑な形であるが、円分体や一部の3次体でも分解型が知られており、同様のことが可能となる。一般的な場合はそのように上手くいくとは限らないため、計算は非常に難しくなる。
なお、二次体![Q(Sqrt[-5])](siki_spec020/zeta28700.png) の整イデアルに対するノルムも、以上の結果から容易に求められることが分かる。
の整イデアルに対するノルムも、以上の結果から容易に求められることが分かる。
※3:より一般的な代数体に対する Dedekind ゼータ関数の計算方法については、Emmanuel Tollis の論文 「Zeros of Dedekind zeta functions in the Critical strip. (Mathematics of computation, Vol.66, No.219,(1997), p.1295-1321)」 等があるが、その式は大変複雑である。
※4:ここでは、「類数」 や 「イデアル類」 についての説明は省略する。詳細は、鹿野 健 (共著) 「リーマン予想」 等を参照願います。
※5:純三次体の場合の具体的な表示式の例については、Daniel Shanks の論文 「Calculation and Applications of Epstein zeta functions. (Mathematics of Computation, Vol.29, No.129, (1975), p.271-287)」 に多数掲載されている。
※1:剰余環
と表わされる有限集合である。つまり、
また、拡大体記号の分かりやすい例としては、実数体
※2:イデアル等のイメージが掴みやすくなるよう、以下では具体的に二次体
![Q(Sqrt[-5])の判別式](siki_spec020/zeta27300.png)
以下
となる (これの求め方は、例えば 「数学セミナー増刊号:入門|現代の数学[5]数論への出発 (1980)」 にある)。一方、単項イデアル
(なお、以下の演算では、
同様の演算により、合成数による単項イデアルも、次のように素イデアルの積に一意分解される。(赤線部分のように、
なお、一般に二次体
二次体の Dedekind ゼータ関数が、より簡単なゼータ関数の積に還元できるのは、この分解型の違いを用いて、Euler 積表示式を変形できるからである。もっと複雑な形であるが、円分体や一部の3次体でも分解型が知られており、同様のことが可能となる。一般的な場合はそのように上手くいくとは限らないため、計算は非常に難しくなる。
なお、二次体
※3:より一般的な代数体に対する Dedekind ゼータ関数の計算方法については、Emmanuel Tollis の論文 「Zeros of Dedekind zeta functions in the Critical strip. (Mathematics of computation, Vol.66, No.219,(1997), p.1295-1321)」 等があるが、その式は大変複雑である。
※4:ここでは、「類数」 や 「イデアル類」 についての説明は省略する。詳細は、鹿野 健 (共著) 「リーマン予想」 等を参照願います。
※5:純三次体の場合の具体的な表示式の例については、Daniel Shanks の論文 「Calculation and Applications of Epstein zeta functions. (Mathematics of Computation, Vol.29, No.129, (1975), p.271-287)」 に多数掲載されている。
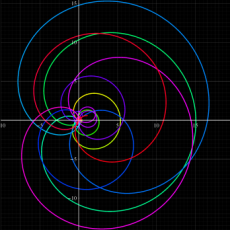
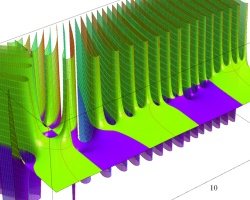
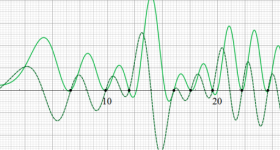
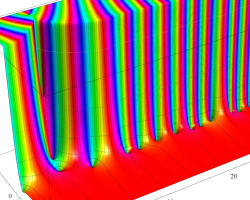
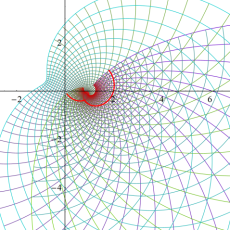
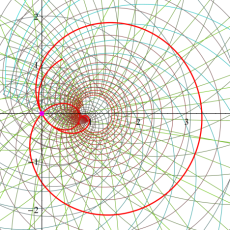
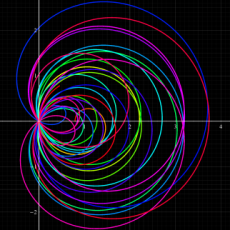
複素変数の Dedekind のゼータ関数のグラフ。
Dedekind のゼータ関数
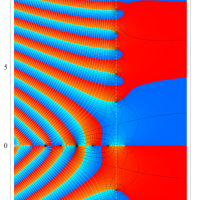
①実変数、および②,③臨界線上の Dedekind のゼータ関数のグラフ。
複素変数の Dedekind のゼータ関数のグラフ。
①実変数、および②,③臨界線上の Dedekind のゼータ関数のグラフ。
複素変数の Dedekind のゼータ関数のグラフ。
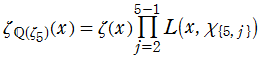
複素変数の Dedekind のゼータ関数のグラフ。
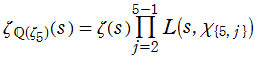
①,②実変数、および③,④臨界線上の Dedekind のゼータ関数のグラフ。②は、①の一部分を拡大したグラフ。
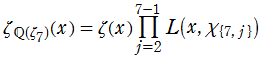
複素変数の Dedekind のゼータ関数のグラフ。
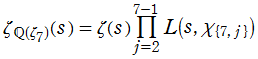
Dedekind のゼータ関数
①,②実変数、および③,④臨界線上の Dedekind のゼータ関数のグラフ。②は、①の一部分を拡大したグラフ。
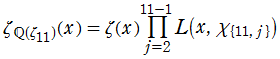
複素変数の Dedekind のゼータ関数のグラフ。
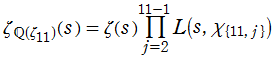
Dedekind のゼータ関数
①実変数、および②,③臨界線上の Dedekind のゼータ関数
複素変数の Dedekind のゼータ関数
純三次体
①実変数、および②,③臨界線上の Dedekind のゼータ関数
複素変数の Dedekind のゼータ関数
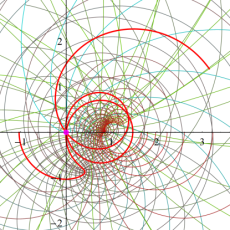
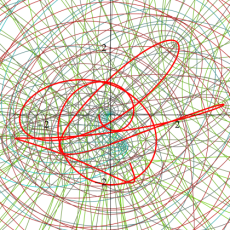
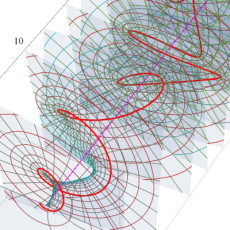
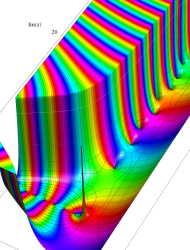
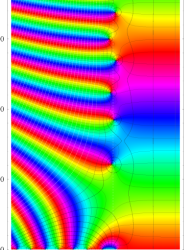
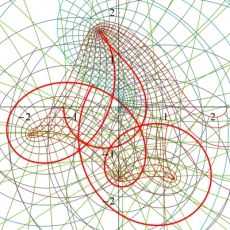
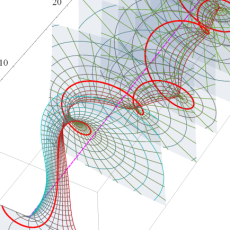
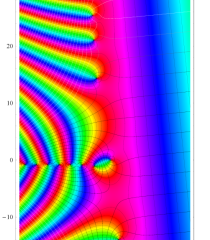
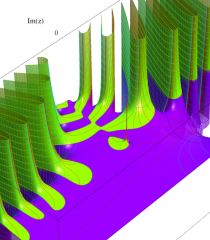
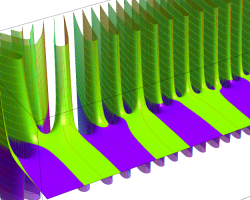
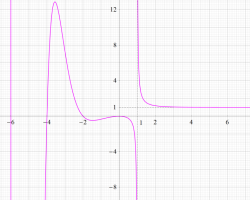
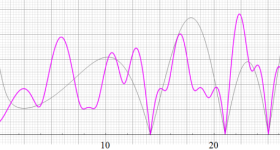
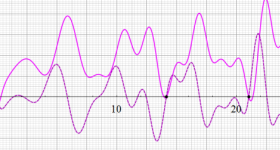
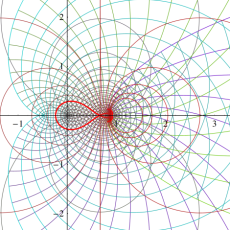
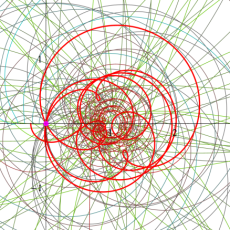
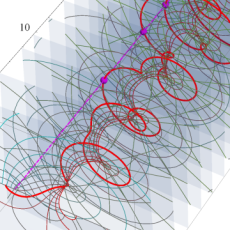
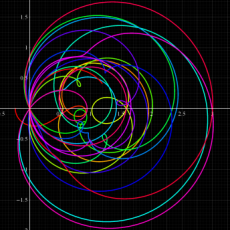
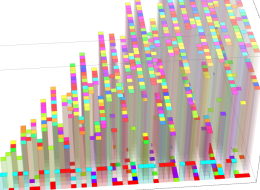
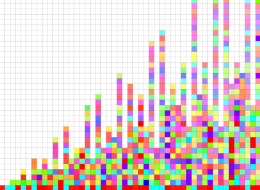
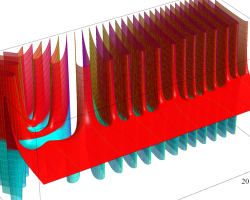
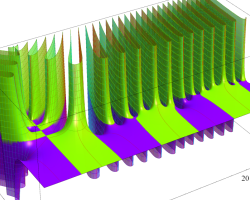
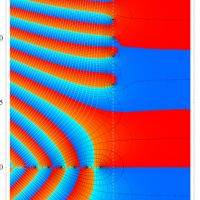
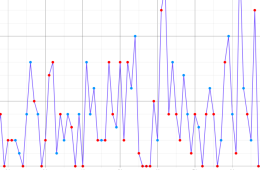
【 Petite Galerie 】
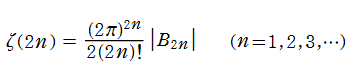
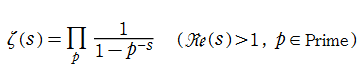
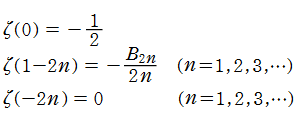
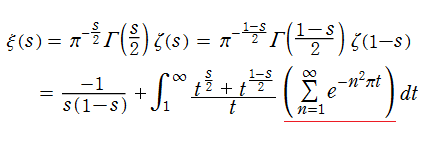
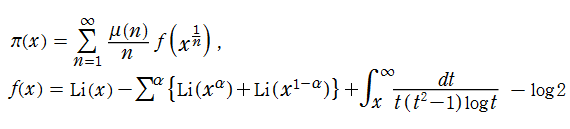
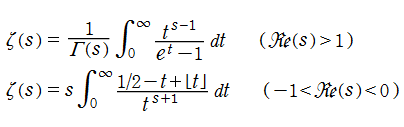
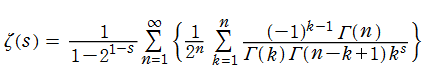
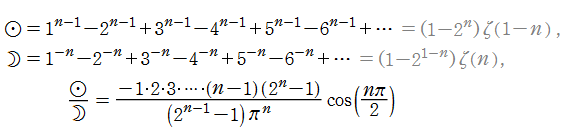




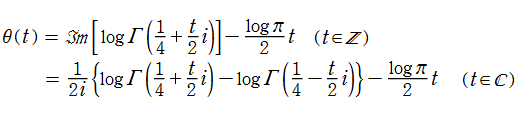
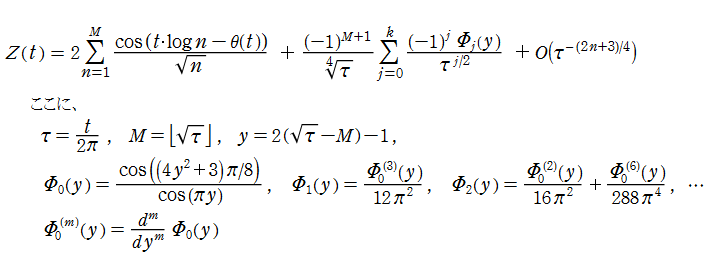

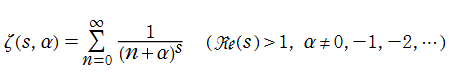
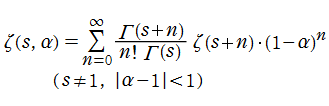
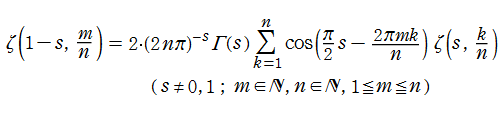
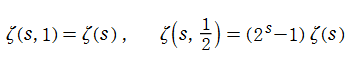
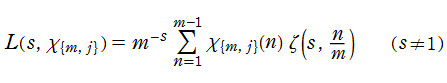












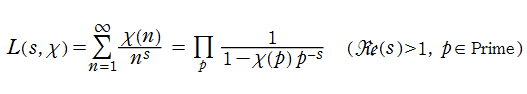
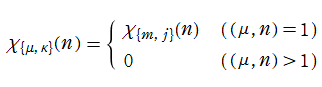
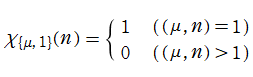
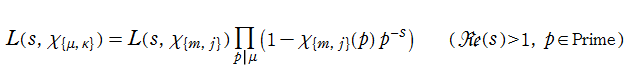
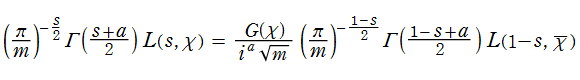

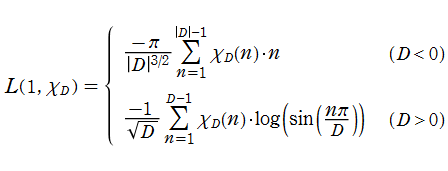



















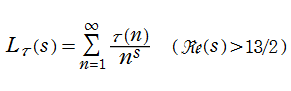
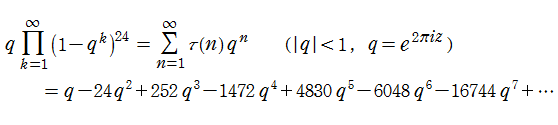
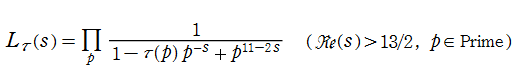
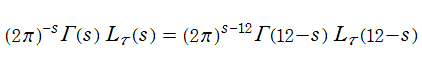
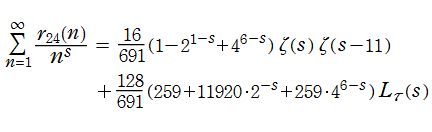
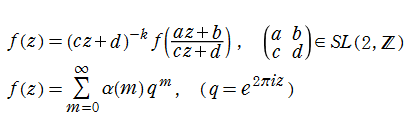
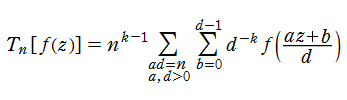
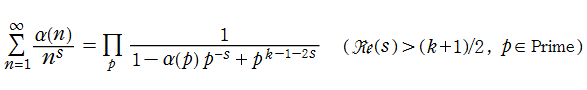
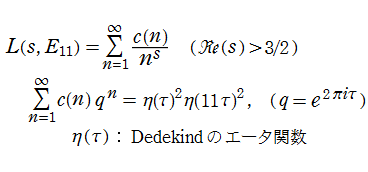
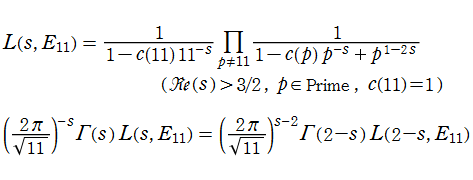




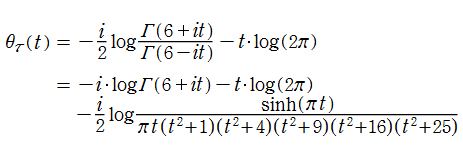

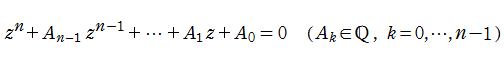
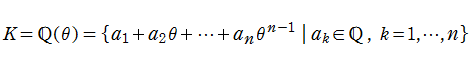
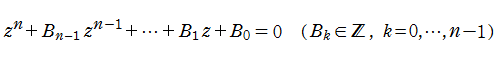
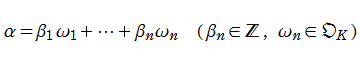
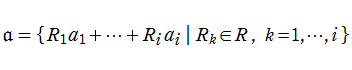
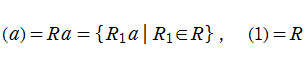
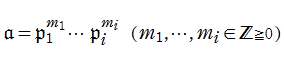
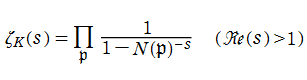

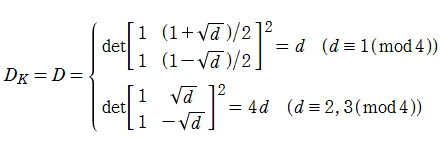
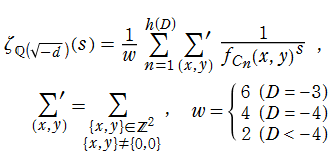
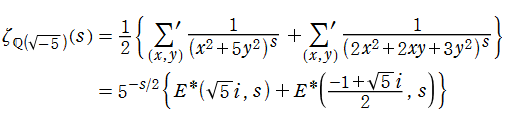
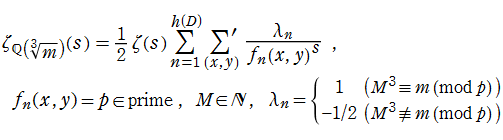
![Q(Sqrt[-5])の素イデアル](siki_spec020/zeta27600.png)