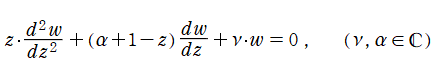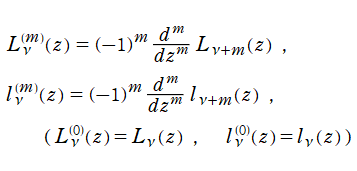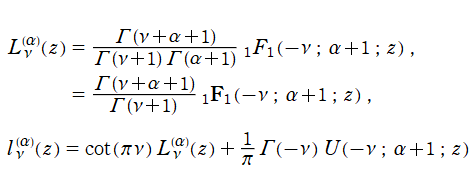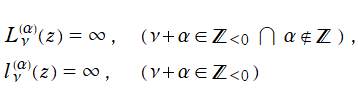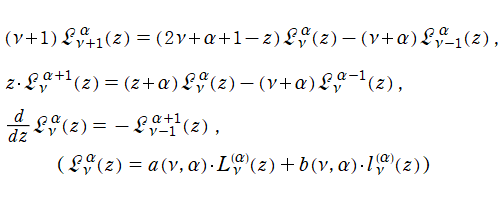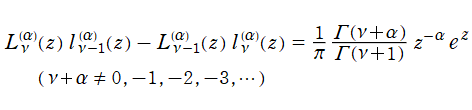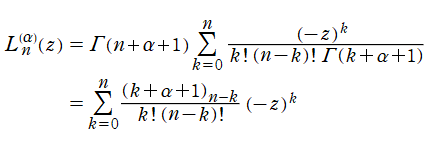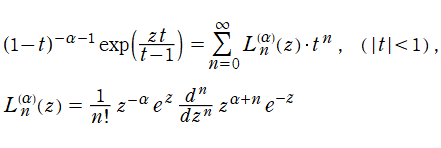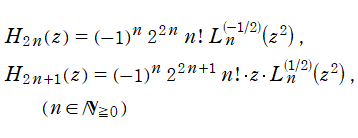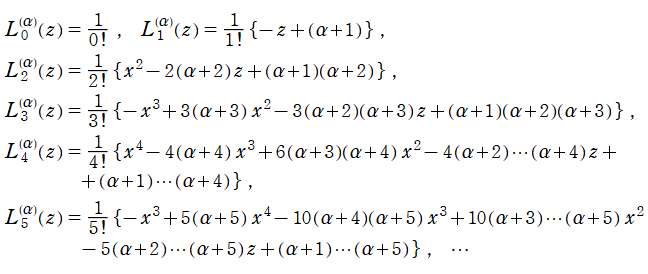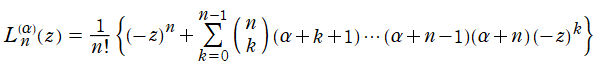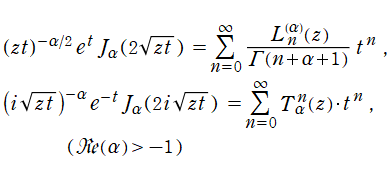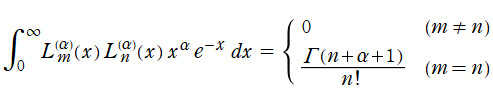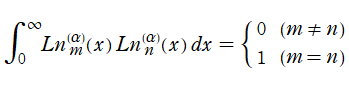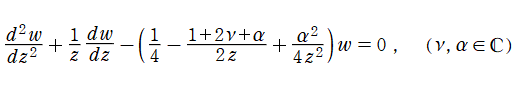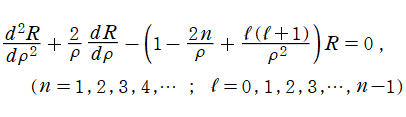Laguerre 関数
日:
Laguerre関数,
ラゲール関数
英:
Laguerre function,仏:
Fonction de Laguerre,独:
Laguerre-funktion
二階の線形常微分方程式
は Laguerre の陪微分方程式と呼ばれ、
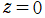
を確定特異点、
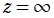
を1級の不確定特異点とする。その解の基本系
+b・l[ν,α](z)](siki_spec190/laguerre00400.png)
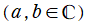
を成す二つの関数
, l[ν,α](z)](siki_spec190/laguerre00600.png)
を、第1種および第2種 Laguerre 陪関数と言う※1。特に、
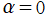
の場合は Laguerre 関数と呼ばれ、第1種を
](siki_spec190/laguerre00800.png)
で略記する習慣が定着している※2。Laguerre 陪関数の定義は、Laguerre 関数の逐次微分
に由来するが、Laguerre の陪微分方程式とその解によって、階数
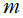
は複素数
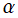
にまで拡張される。
解の具体的表示として、
合流型超幾何関数で表わされた、
を採用する※3。この表示式から、Laguerre 陪関数は本質的に合流型超幾何関数と同じで、その別表現に過ぎないことが分かる。なお、ガンマ関数係数の影響等によって不定値となる場合は、上記の式に l'Hôpital の定理を適用する等の極限を取る。ただし、下記
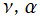
の場合では関数自体が存在しない。
第1種および第2種 Laguerre 陪関数は、一般に
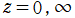
を特異点とする無限多価関数であるが、
](siki_spec190/laguerre01400.png)
は

の特別な値によって
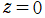
での様相が異なる。両者とも
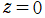
が対数分岐点となる場合は、分枝切断線を実軸上の区間
![(-∞, 0]](siki_spec190/laguerre01500.png)
に置くのが普通とされる。
Laguerre 陪関数は、
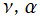
に関する整数差の線形漸化式 (隣接関係式)、および導関数の公式
を満たす。ここに
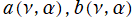
は、
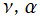
の二変数について1を周期とする任意の周期関数である。また、第1種と第2種は関係式
で結ばれる。
第1種 Laguerre 関数に限り、次数と変数の反転性
が成り立つ。
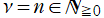
である第1種 Laguerre 陪関数は、多項式
に還元される。しかし、専らこの場合が応用上は重要であるため、Laguerre 陪多項式 (
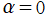
の場合は Laguerre 多項式) と呼ばれる。Laguerre 陪多項式の上記以外の表現方法としては、母関数表示式および 「Rodrigues の公式」
がよく知られている。尤も、
=1](siki_spec190/laguerre02300.png)
および
=α+1-z](siki_spec190/laguerre02400.png)
を初期関数として漸化式を用いても容易に得られる※4。一般に Laguerre 陪多項式は、偶関数または奇関数にならない。
Hermite 多項式は、Laguerre 陪多項式の特別な場合
で表わせる。
Laguerre 陪多項式は、積分区間が
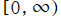
に変更された Gauss 数値積分法、統計学における二つの相関する乱数を変数とする確率密度関数にも応用されるが、大半は量子力学での事例が占め、とりわけ
水素原子周辺の電子の存在確率を表わす波動関数が著しい。それらの応用事例では、Laguerre 陪多項式の直交多項式としての性質が重要になるが 、これは
末尾の節で触れる。
また、Laguerre 陪関数の歴史等については、
次節に譲る※1。
【註記】
※1:当サイトでは、Laguerre 関数と Laguerre 陪関数とを別々の節としたが、数式等の説明文では両者を一括して扱い、そのほとんどを第1節に掲載する。
※2:第2種 Laguerre 陪関数の記号
](siki_spec190/laguerre02700.png)
は当サイトが独自に定めたものであり、同様に
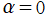
の場合は
](siki_spec190/laguerre02800.png)
で略記することとする。
※3:第2種 Laguerre 陪関数の標準的な定義は存在しない。当サイトでは、
](siki_spec190/laguerre01400.png)
が余弦関数に相当していると見たとき、正弦関数に相当した振る舞いとなるよう
](siki_spec190/laguerre02700.png)
を定義している。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針を、別頁
Questions にも掲載している。)
※4:Laguerre 陪多項式を具体的に表示すると、若干長大な式になる。
係数等のパターンを把握する目的ならば、むしろ次の表示式の方が良い。
](siki_spec190/laguerre03700.png)
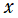
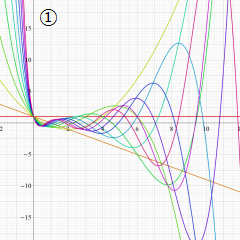
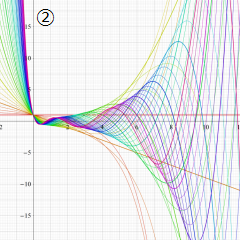
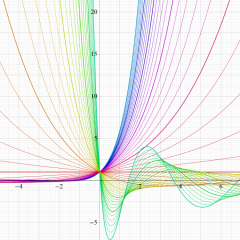
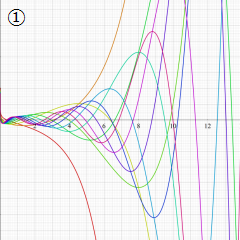
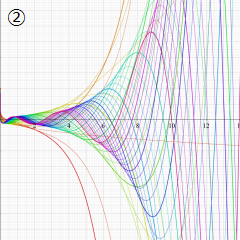
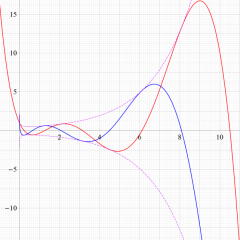
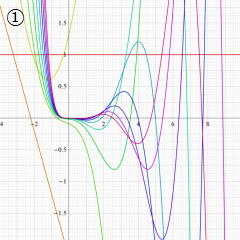
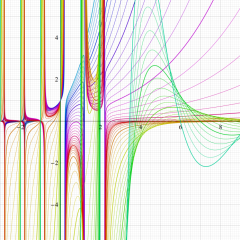
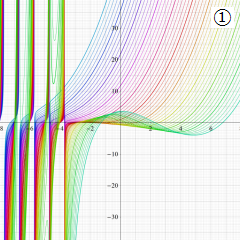
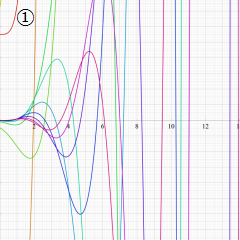
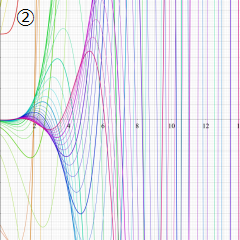
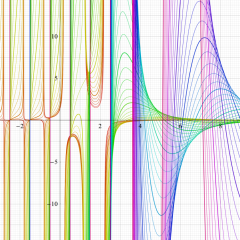
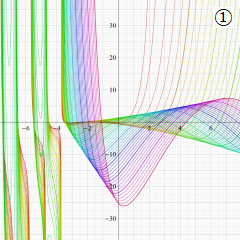
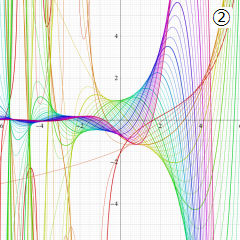
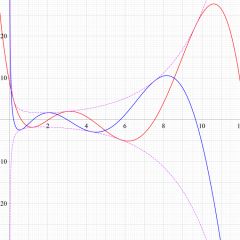
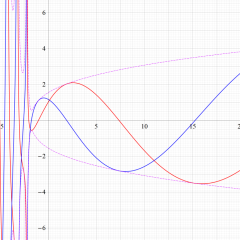
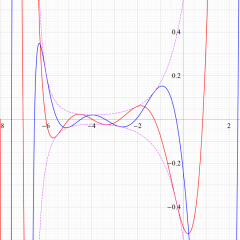
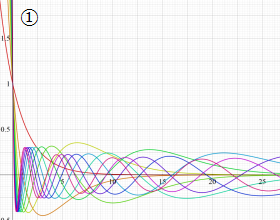
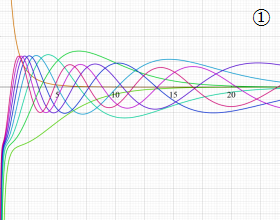
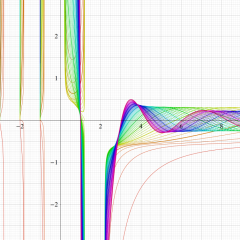
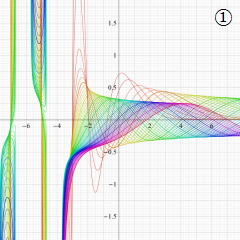
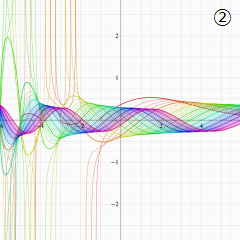
を実変数とする、第1種 Laguerre 関数のグラフ。
①整数次 (Laguerre 多項式)
](siki_spec190/laguerre03100.png)
,
②実数次
](siki_spec190/laguerre03200.png)
。
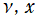
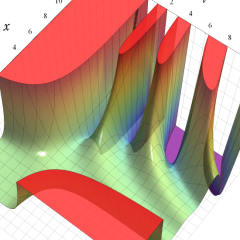
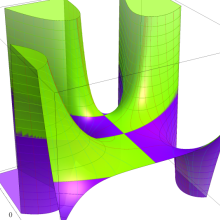
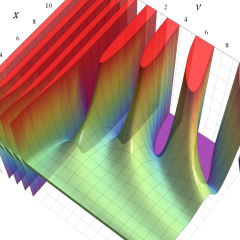
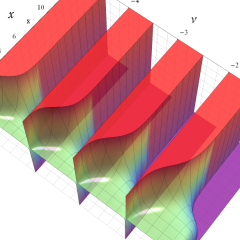
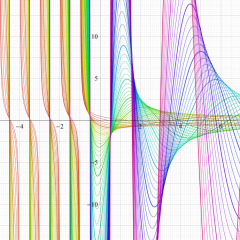
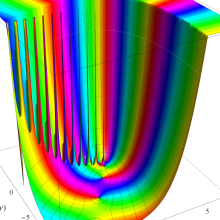
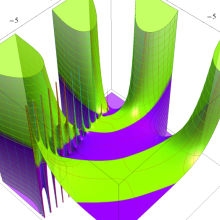
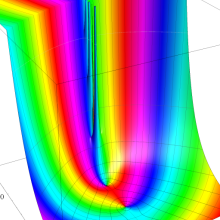
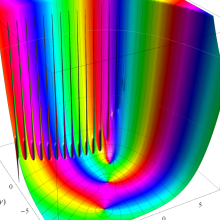
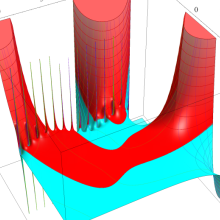
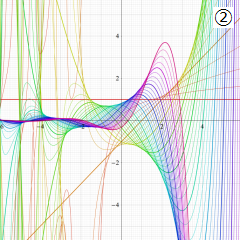
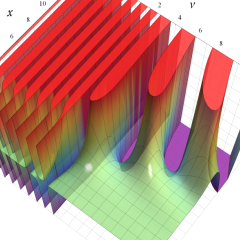
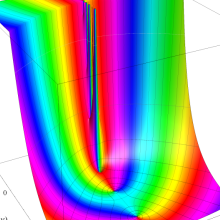
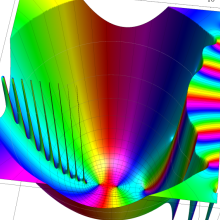
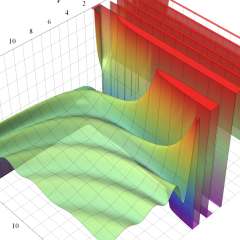
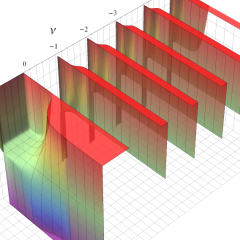
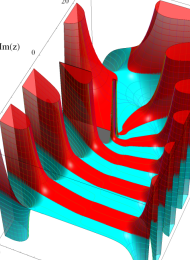
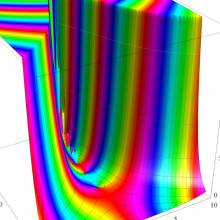
を実2変数とする、第1種 Laguerre 関数
](siki_spec190/laguerre03200.png)
のグラフ。

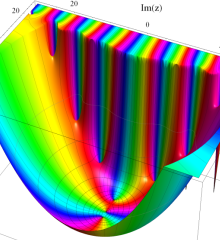
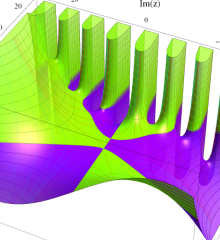
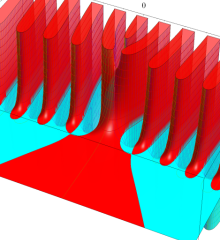
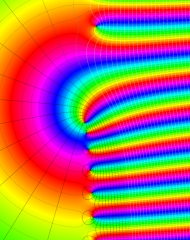
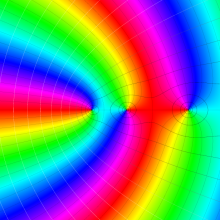
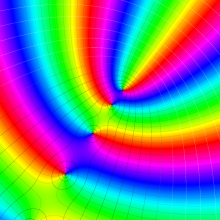
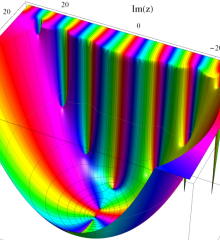
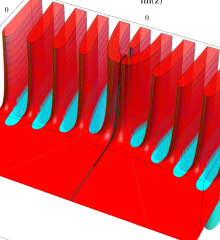
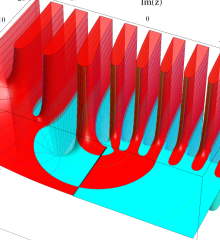
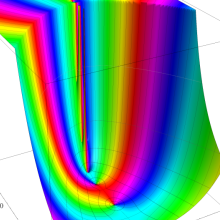
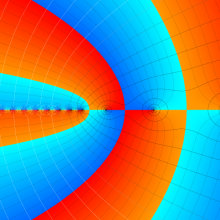
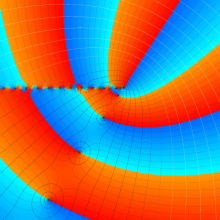
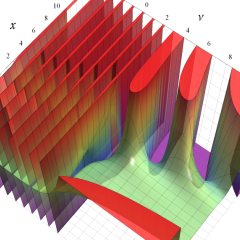
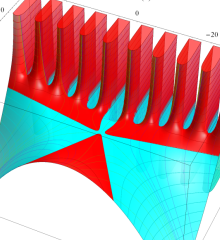
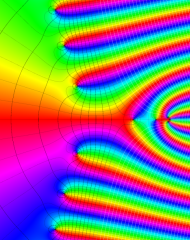
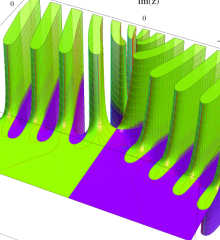
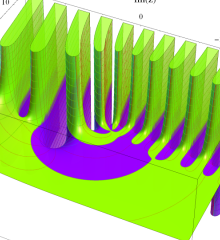
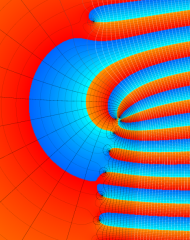
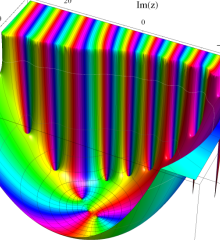
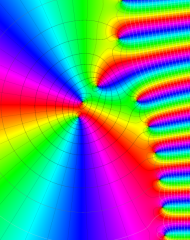
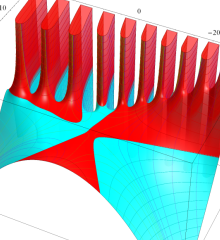
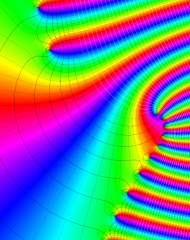
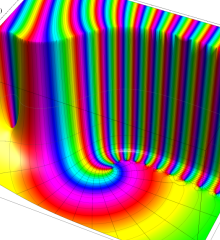
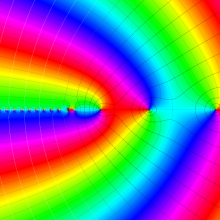
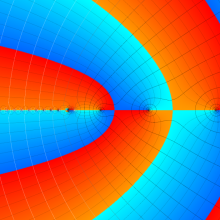
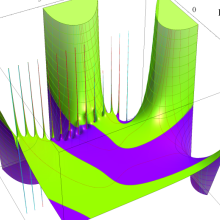
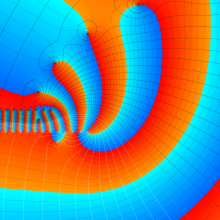
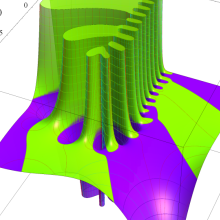
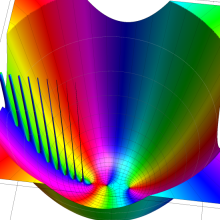
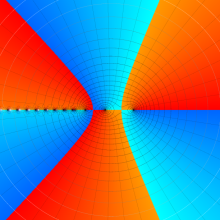
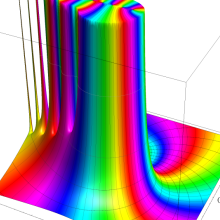
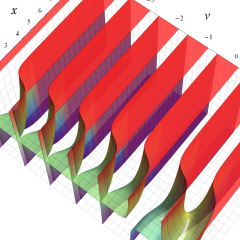
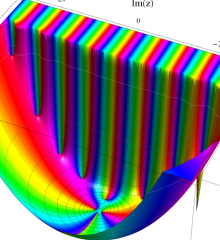
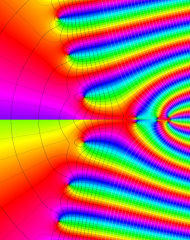
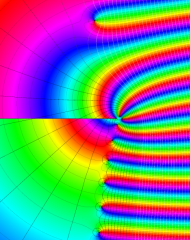
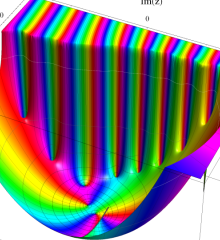
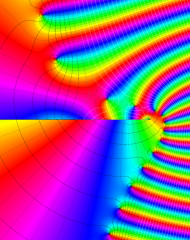
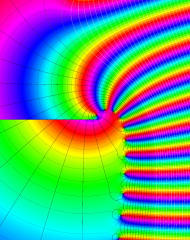
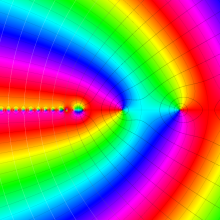
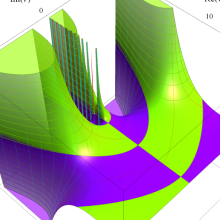
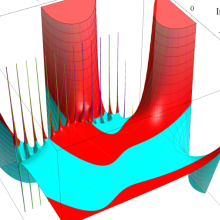
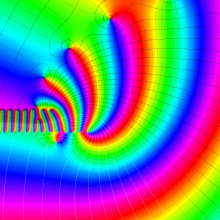
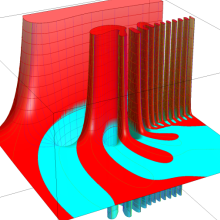
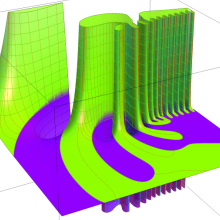
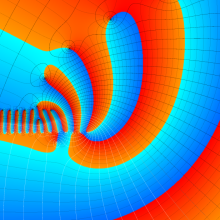
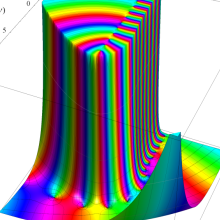
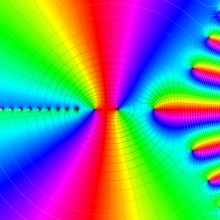
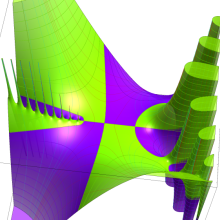
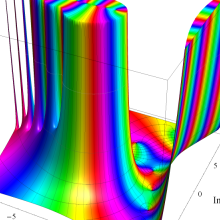
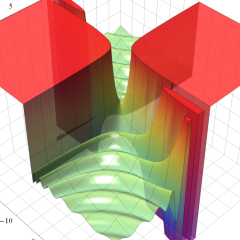
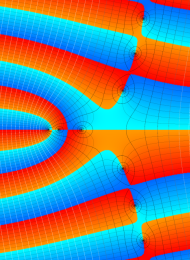
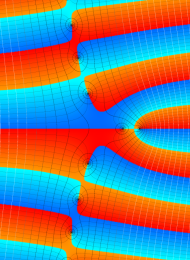
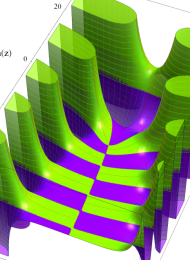
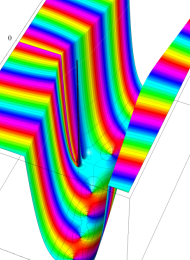
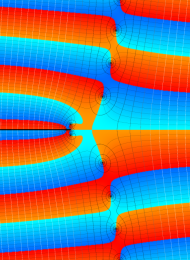
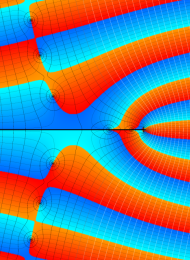
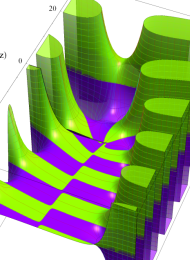
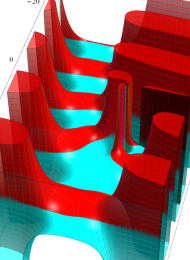
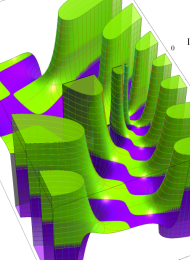
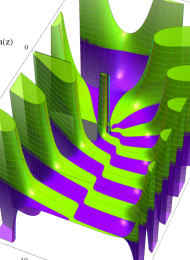
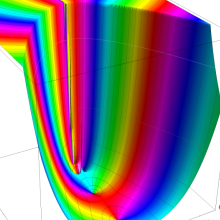
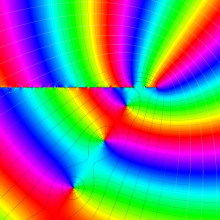
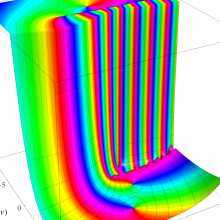
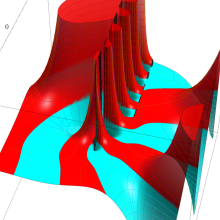
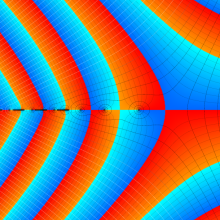
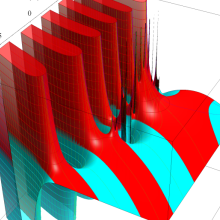
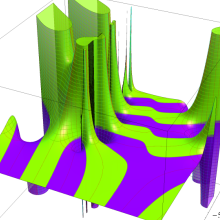
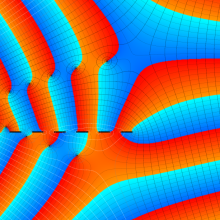
を複素変数とする、第1種 Laguerre 関数
](siki_spec190/laguerre03400.png)
のグラフ。

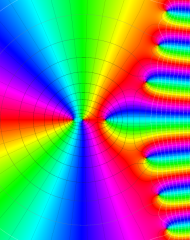
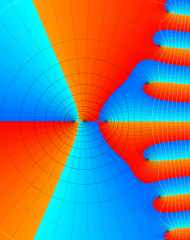
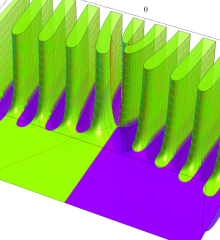
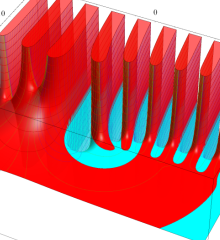
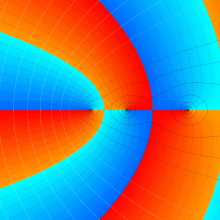
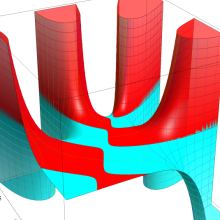
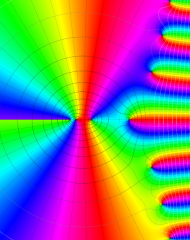
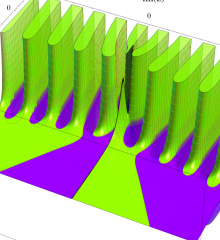
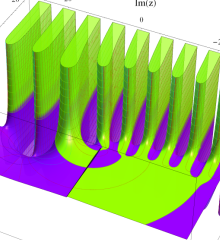
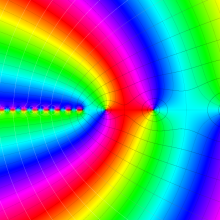
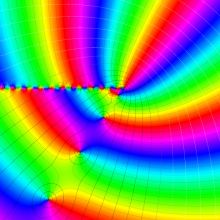
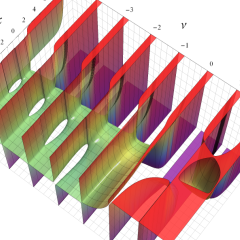
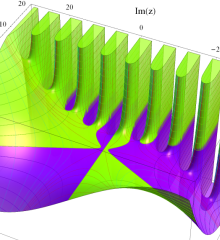
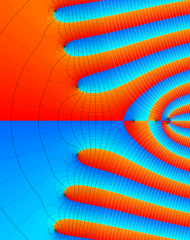
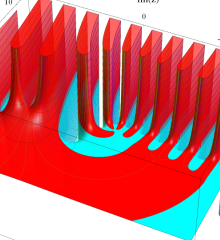
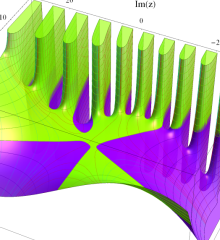
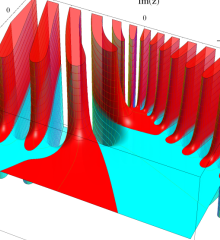
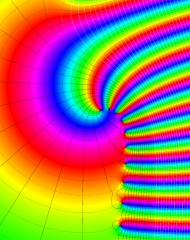
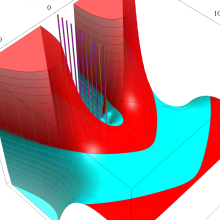
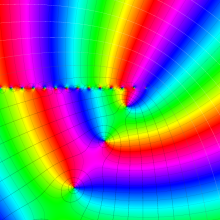
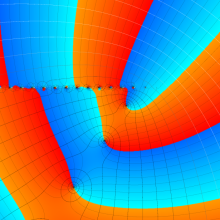
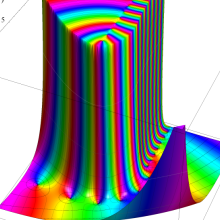
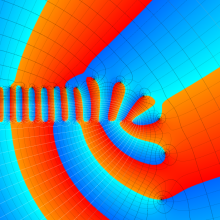
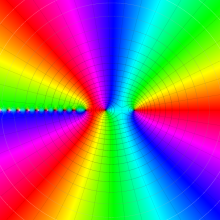
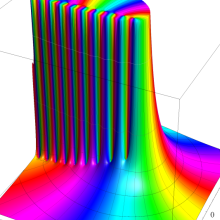
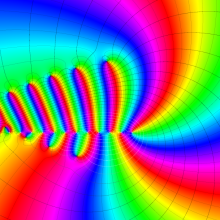
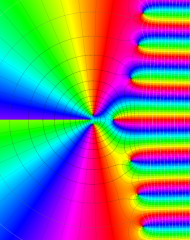
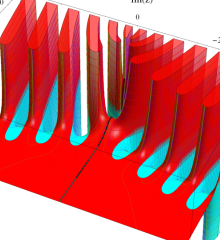
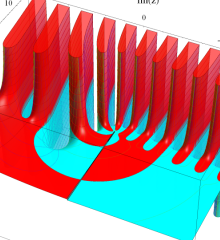
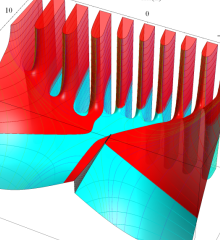
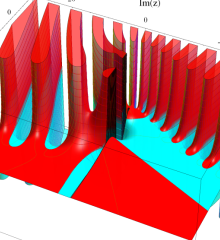
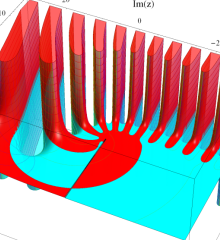
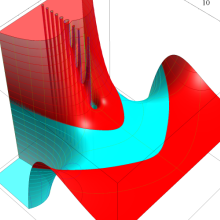
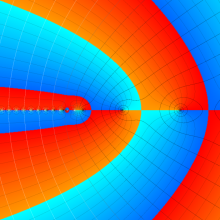
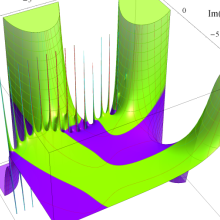
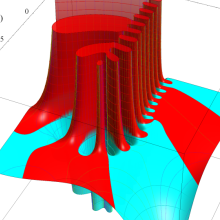
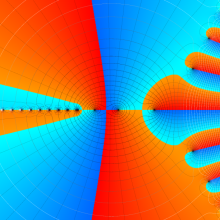
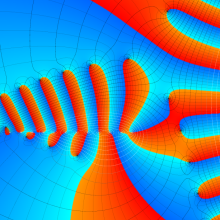
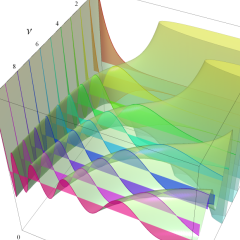
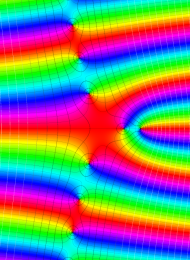
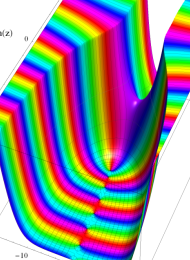
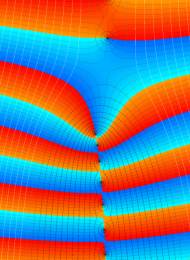
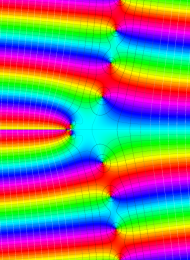
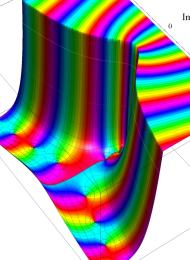
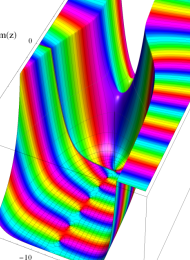
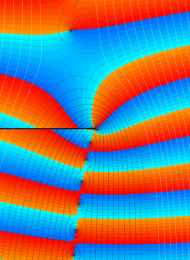
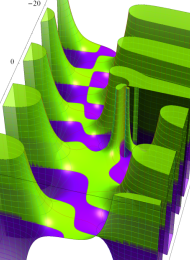
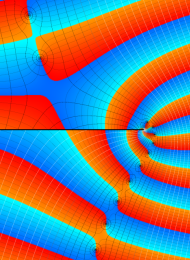
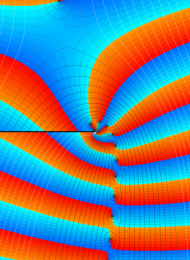
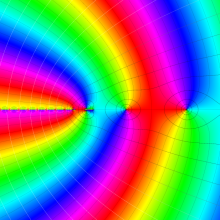
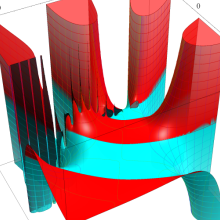
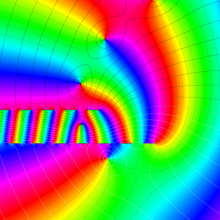
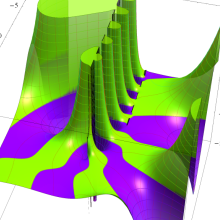
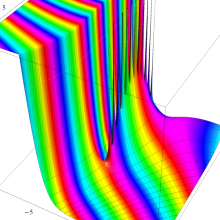
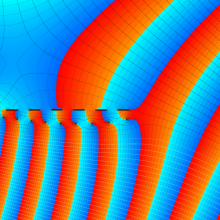
を複素変数とする、第1種 Laguerre 関数
](siki_spec190/laguerre03500.png)
のグラフ。

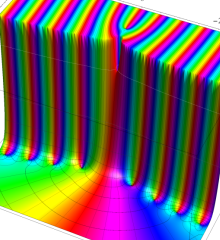
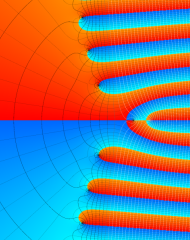
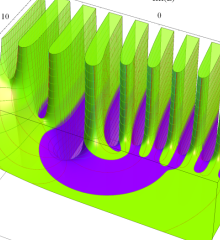
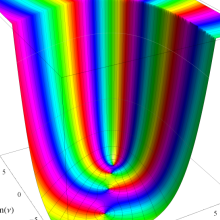
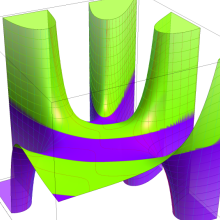
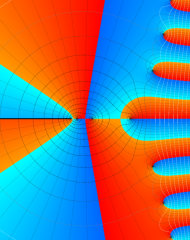
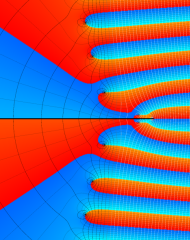
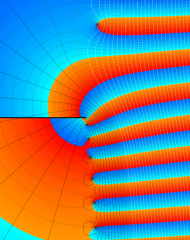
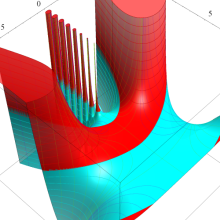
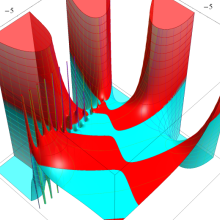
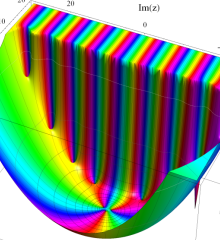
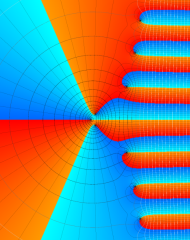
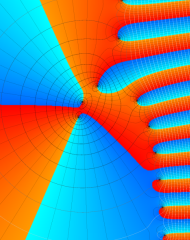
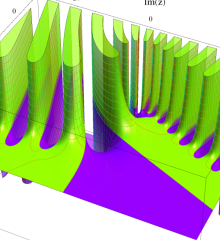
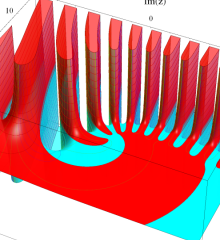
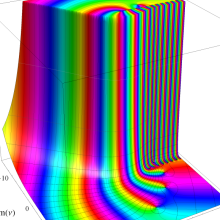
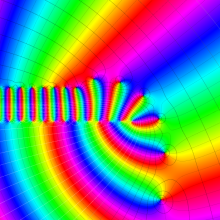
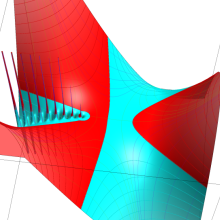
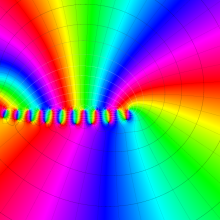
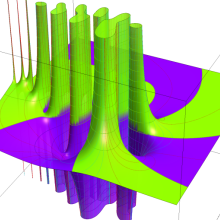
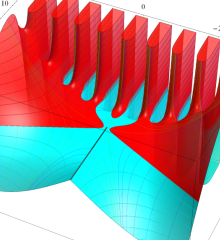
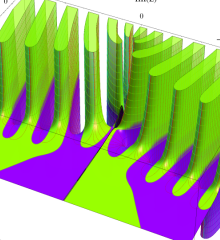
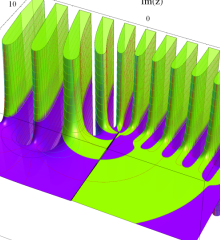
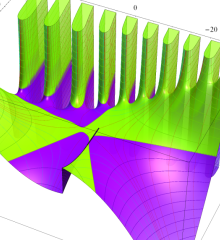
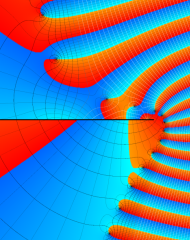
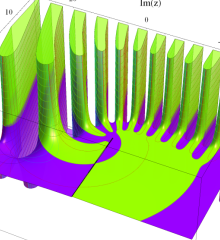
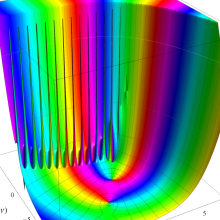
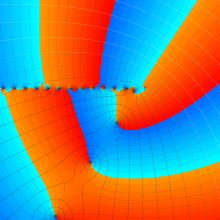
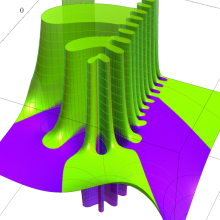
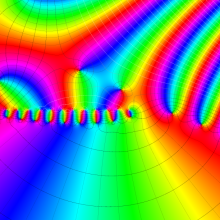
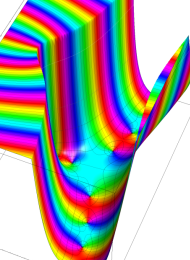
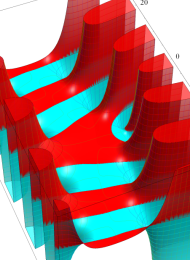
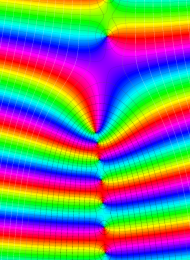
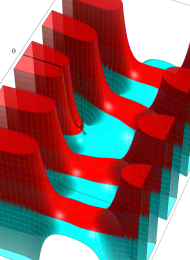
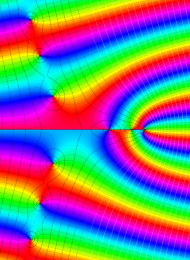
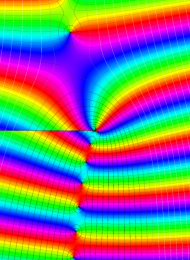
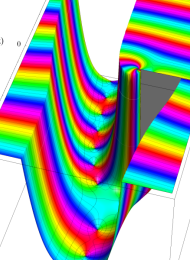
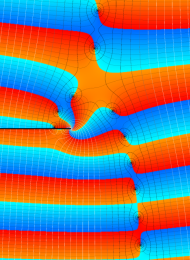
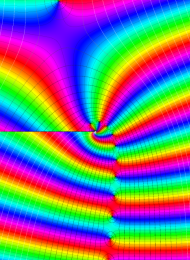
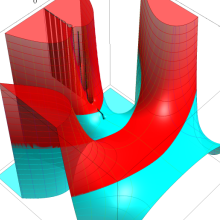
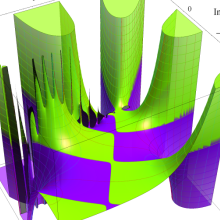
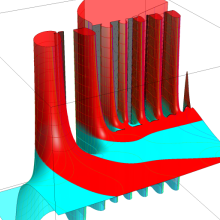
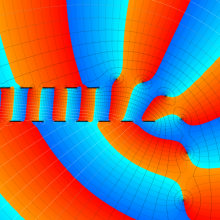
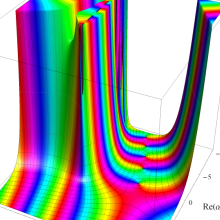
を複素変数とする、第1種 Laguerre 関数
](siki_spec190/laguerre03600.png)
のグラフ。
アニメーション
(11.5MB)

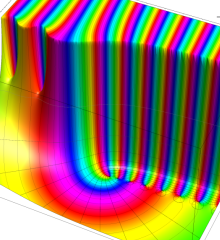
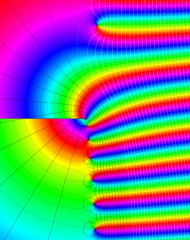
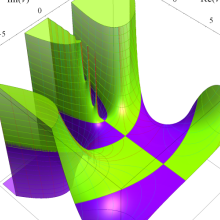
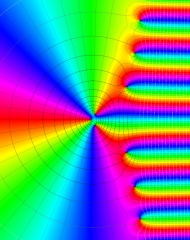
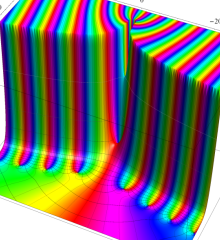
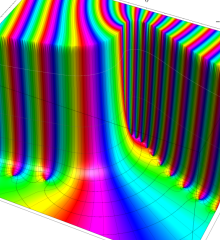
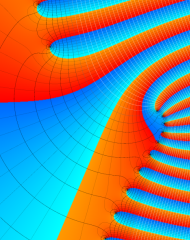
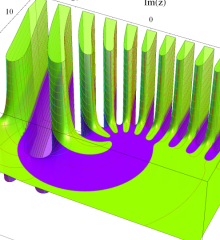
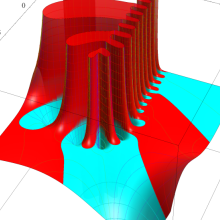
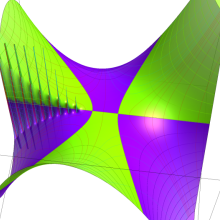
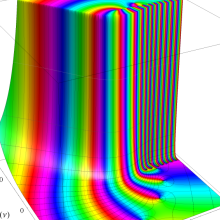
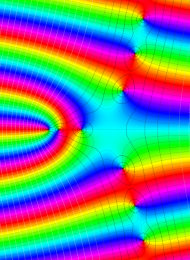
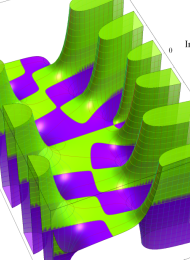
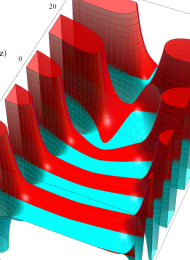
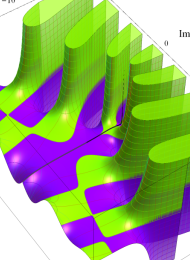
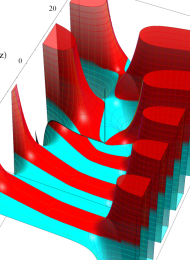
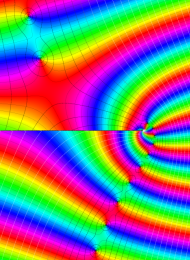
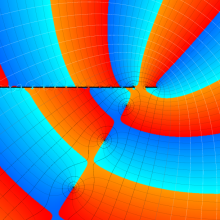
を複素変数とする、第1種 Laguerre 関数
](siki_spec190/laguerre00800.png)
のグラフ。
 (変数ν)](siki_spec190/laguerre04000.png)

を実変数とする、第1種 Laguerre 関数
](siki_spec190/laguerre03200.png)
のグラフ。

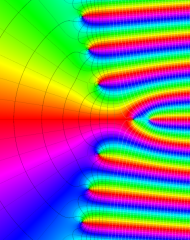
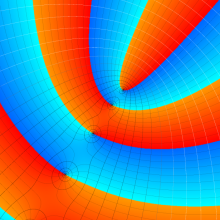
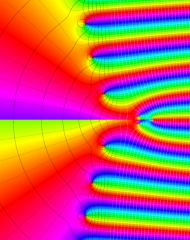
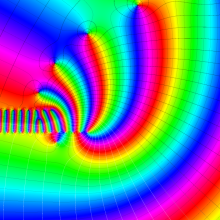
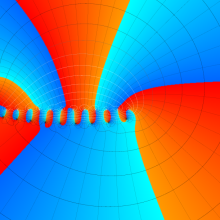
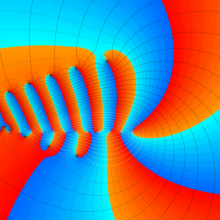
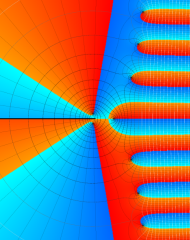
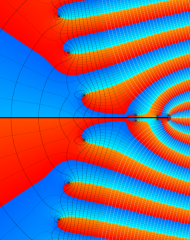
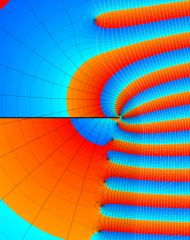
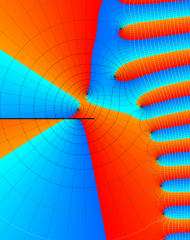
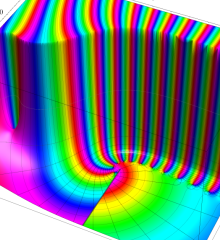
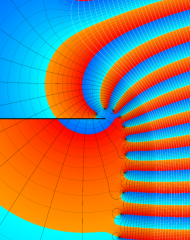
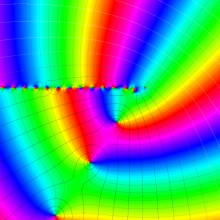
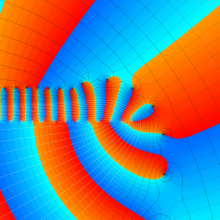
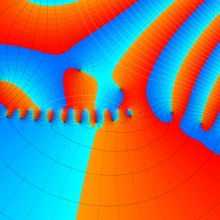
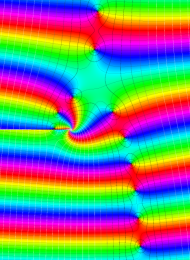
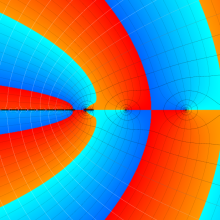
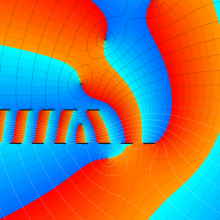
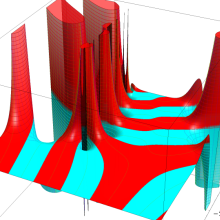
を複素変数とする、第1種 Laguerre 関数
](siki_spec190/laguerre03800.png)
のグラフ。

を複素変数とする、第1種 Laguerre 関数
](siki_spec190/laguerre03900.png)
のグラフ。
](siki_spec190/laguerre04800.png)
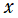
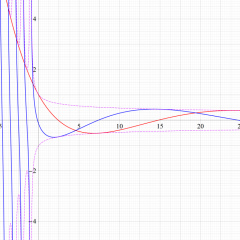
を実変数とする、第2種 Laguerre 関数のグラフ。
①整数次
](siki_spec190/laguerre04100.png)
,
②実数次
](siki_spec190/laguerre04200.png)
。
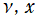
を実2変数とする、第2種 Laguerre 関数
](siki_spec190/laguerre04200.png)
のグラフ。
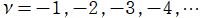
では関数が定義されない。
2番目は、
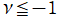
の範囲を拡大した場合。

を複素変数とする、第2種 Laguerre 関数
](siki_spec190/laguerre04500.png)
のグラフ。

を複素変数とする、第2種 Laguerre 関数
](siki_spec190/laguerre04600.png)
のグラフ。

を複素変数とする、第2種 Laguerre 関数
](siki_spec190/laguerre04700.png)
のグラフ。
アニメーション
(10.9MB)

を複素変数とする、第2種 Laguerre 関数
](siki_spec190/laguerre02800.png)
のグラフ。
 (変数ν)](siki_spec190/laguerre05200.png)

を実変数とする、第2種 Laguerre 関数
](siki_spec190/laguerre04200.png)
のグラフ。
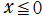
では実数値を取らない。

を複素変数とする、第2種 Laguerre 関数
](siki_spec190/laguerre05000.png)
のグラフ。

を複素変数とする、第2種 Laguerre 関数
](siki_spec190/laguerre05100.png)
のグラフ。
とl[ν](z)の関係](siki_spec190/laguerre05400.png)
余弦・正弦関数に類似した、
](siki_spec190/laguerre03200.png)
と
](siki_spec190/laguerre04200.png)
の関係。このとき、両者の包絡線は
^2+l[ν](z)^2)](siki_spec190/laguerre05300.png)
となる。
日:
Laguerre陪関数,
ラゲール陪関数
英:
Associated Laguerre function,
Generalized Laguerre function
仏:
Fonction associée de Laguerre,独:
Assoziierten Laguerre-funktion
Laguerre 陪関数の数学的な性質については、一部を除いて概ね最初の節で触れたので、ここでは二三の追加と歴史的な話題に留める。
Laguerre 多項式 (つまり、
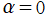
の場合のみ) の萌芽は、J. L. Lagrange, R. Murphy (1833年) 等が手掛けた研究に現れる。19世紀中葉になると、P. L. Chebyshev (1859年) がやや一般的な多項式論を展開し、その中で Laguerre 多項式が再び取り上げられた。E. N. Laguerre (1879年) は
不完全ガンマ関数を論じる過程で Laguerre 多項式を導き、これを個別の研究対象とした。
一方、Laguerre 陪多項式は N. Y. Sonin (1880年) が初めて論文で扱い、程なく Laguerre も1879年以来の研究を発展させる中で独立にこれを見出した。現在では、後者の名を冠して Laguerre 陪多項式と呼ばれることが多いが、Sonin 多項式と呼ぶこともある。ただし、
](siki_spec190/laguerre05450.png)
と若干形が異なる、
等を Sonin 多項式と定義する場合も多く、しかも著者によって甚だしく一定していない※1。
Sonin は関心分野としていた
Bessel 関数の研究から、最初の節に掲載したそれとは異なる形の母関数表示式
を発見した。また、Sonin はこの派生として 「古典的直交多項式」 のある一般的性質も導いた。Sonin の研究内容は、同邦人であった Chebyshev から大きな影響を受けている。
なお、多項式になる場合を超えた Laguerre 陪関数についても、19世紀以降に種々の結果が得られたが、応用事例がほとんど存在しなかったこともあって、重要視されていない※2。
【註記】
※1:このうち、Sonin による本来の定義は
](siki_spec190/laguerre05700.png)
である (添字が上下逆になっているが、誤りではない)。しばしば、名をフランス語風に転記して 「Sonine 多項式」 とも表記される。
※2:むしろ (多項式でない) Laguerre 陪関数の役割は、代わりに合流型超幾何関数または
Coulomb 波動関数が担うようになった。現在、特殊関数の総合事典の多くでは、直交多項式で一つの章を設け、それが非整数次に拡張された場合を、超幾何関数または合流型超幾何関数の章に (相互関係式として) 掲載するというスタイルを採用している。
](siki_spec190/laguerre06900.png)
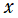
を実変数とする、第1種 Laguerre 陪関数のグラフ。
①整数次 (Laguerre 陪多項式)
](siki_spec190/laguerre05800.png)
,
②実数次
](siki_spec190/laguerre05900.png)
。
アニメーション
(44.7MB)
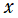
を実変数とし
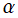
が動くときの、第1種 Laguerre 陪関数
](siki_spec190/laguerre10200.png)
のグラフ。
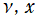
を実2変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre05900.png)
のグラフ。
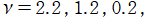
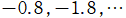
では関数が定義されない。
2番目は、
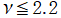
の範囲を拡大した場合。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre06200.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre06300.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre06400.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre06500.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre06600.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre06700.png)
のグラフ。
アニメーション
(11.2MB)

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre06800.png)
のグラフ。
 (変数ν)](siki_spec190/laguerre07400.png)

を実変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre05900.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre07000.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre07100.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre07200.png)
のグラフ。

を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre07300.png)
のグラフ。
 (変数α)](siki_spec190/laguerre08000.png)
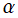
を実変数とする、第1種 Laguerre 陪関数のグラフ。
①](siki_spec190/laguerre07500.png)
,
②](siki_spec190/laguerre07600.png)
。
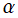
を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre07700.png)
のグラフ。
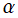
を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre07800.png)
のグラフ。
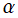
を複素変数とする、第1種 Laguerre 陪関数
](siki_spec190/laguerre07900.png)
のグラフ。
](siki_spec190/laguerre09000.png)
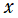
を実変数とする、第2種 Laguerre 陪関数のグラフ。
①整数次
](siki_spec190/laguerre08100.png)
,
②実数次
](siki_spec190/laguerre08200.png)
。
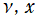
を実2変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08200.png)
のグラフ。
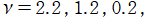
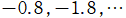
では関数が定義されない。
2番目は、
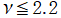
の範囲を拡大した場合。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08300.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08400.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08500.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08600.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08700.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08800.png)
のグラフ。
アニメーション
(10.8MB)

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08900.png)
のグラフ。
 (変数ν)](siki_spec190/laguerre09500.png)

を実変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre08200.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre09100.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre09200.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre09300.png)
のグラフ。

を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre09400.png)
のグラフ。
 (変数α)](siki_spec190/laguerre10100.png)
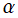
を実変数とする、第2種 Laguerre 陪関数のグラフ。
①](siki_spec190/laguerre09600.png)
,
②](siki_spec190/laguerre09700.png)
。
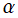
を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre09800.png)
のグラフ。
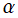
を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre09900.png)
のグラフ。
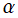
を複素変数とする、第2種 Laguerre 陪関数
](siki_spec190/laguerre10000.png)
のグラフ。
とl[ν,α](z)の関係](siki_spec190/laguerre10500.png)
余弦・正弦関数に類似した、
](siki_spec190/laguerre10200.png)
と
](siki_spec190/laguerre10300.png)
の関係。このとき、両者の包絡線は
^2+l[ν,α](z)^2)](siki_spec190/laguerre10400.png)
となる。
Laguerre 陪多項式
](siki_spec190/laguerre10600.png)
は、
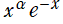
を重み関数とし、直交区間を
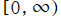
とする直交多項式であり、具体的に
なる直交性を持っている。
そこで、当サイトでは独自に
を導入し、これを 「正規化 Laguerre 陪関数」 と呼ぶ※1。よって、
}](siki_spec190/laguerre11000.png)
は
正規直交関数系を成すとともに、重み関数が現れない直交性
を満たす。
同様に、
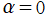
の場合を 「正規化 Laguerre 関数」 と呼び、記号
](siki_spec190/laguerre11200.png)
を用いることにするが、特に、
が成り立つ。
](siki_spec190/laguerre11400.png)
は、微分方程式
の第1種の基本解になる。
水素原子中の電子の波動関数における動径部分
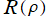
は、本質的に
の形の微分方程式を満たし※2、解を Laguerre 陪多項式で表わすのが普通であるが、代わりに正規化 Laguerre 陪関数を用いて
](siki_spec190/laguerre11800.png)
とした方が若干簡明な形になる。
【註記】
※1:関数記号は正規化 (Normalization) に基づく。また、当サイトでは
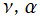
を非整数、

を複素変数として
](siki_spec190/laguerre11900.png)
のグラフの多くを描画するが、このような事例は応用でほとんど現れない。
※2:この微分方程式の形は、Coulomb 波動方程式に近い。
](siki_spec190/laguerre14300.png)
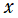
を実変数とする、正規化 Laguerre 関数のグラフ。
①整数次
](siki_spec190/laguerre12000.png)
,
②実数次
](siki_spec190/laguerre12100.png)
。
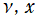
を実2変数とする、正規化 Laguerre 関数
](siki_spec190/laguerre12100.png)
のグラフ。

を複素変数とする、正規化 Laguerre 関数
](siki_spec190/laguerre12200.png)
のグラフ。

を複素変数とする、正規化 Laguerre 関数
=Ln[1.7](-z)](siki_spec190/laguerre12300.png)
のグラフ。

を複素変数とする、正規化 Laguerre 関数
](siki_spec190/laguerre12400.png)
のグラフ。
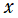
を実変数とする、正規化 Laguerre 陪関数のグラフ。
①整数次
](siki_spec190/laguerre12500.png)
は、
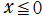
で実数値を取らない。また、
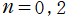
のときも実数値を取らない。
②実数次
](siki_spec190/laguerre12700.png)
は、
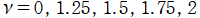
のときに実数値を取らず、グラフが描かれない。
アニメーション
(24.0MB)
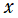
を実変数とし
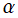
が動くときの、正規化 Laguerre 陪関数
](siki_spec190/laguerre12900.png)
のグラフ。
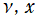
を実2変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre12700.png)
のグラフ。
](siki_spec190/laguerre12900.png)
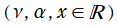
は、
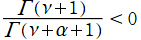
となる場合に実数値を取らない。具体的に
](siki_spec190/laguerre12700.png)
ならば、
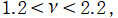
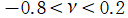
並びに
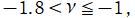
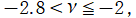
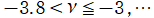
で実数値を取らない。
2番目は、
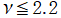
の範囲を拡大した場合。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre13700.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre13800.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre13900.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre14000.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre14100.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre14200.png)
のグラフ。
 (変数ν)](siki_spec190/laguerre14800.png)

が変数ならば、
](siki_spec190/laguerre11200.png)
は
](siki_spec190/laguerre00800.png)
と定数倍の違いしかない。よって、
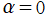
の場合は全て省略する。

を実変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre12700.png)
のグラフ。
アニメーション
(28.4MB)

を実変数とし
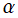
が動くときの、正規化 Laguerre 陪関数
](siki_spec190/laguerre12900.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre14400.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre14500.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre14600.png)
のグラフ。

を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre14700.png)
のグラフ。
 (変数α)](siki_spec190/laguerre15400.png)
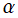
を実変数とする、正規化 Laguerre 陪関数のグラフ。
①](siki_spec190/laguerre14900.png)
,
②](siki_spec190/laguerre15000.png)
。
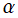
を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre15100.png)
のグラフ。
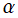
を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre15200.png)
のグラフ。
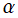
を複素変数とする、正規化 Laguerre 陪関数
](siki_spec190/laguerre15300.png)
のグラフ。
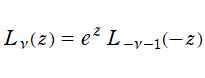
](siki_spec190/laguerre02700.png) は当サイトが独自に定めたものであり、同様に
は当サイトが独自に定めたものであり、同様に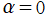 の場合は
の場合は](siki_spec190/laguerre02800.png) で略記することとする。
で略記することとする。](siki_spec190/laguerre01400.png) が余弦関数に相当していると見たとき、正弦関数に相当した振る舞いとなるよう
が余弦関数に相当していると見たとき、正弦関数に相当した振る舞いとなるよう](siki_spec190/laguerre02700.png) を定義している。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針を、別頁 Questions にも掲載している。)
を定義している。(この事は、後にグラフでも確認する。また、第2種関数の定義に対する当サイトの方針を、別頁 Questions にも掲載している。)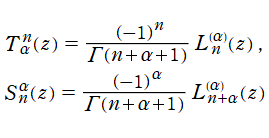
](siki_spec190/laguerre05700.png) である (添字が上下逆になっているが、誤りではない)。しばしば、名をフランス語風に転記して 「Sonine 多項式」 とも表記される。
である (添字が上下逆になっているが、誤りではない)。しばしば、名をフランス語風に転記して 「Sonine 多項式」 とも表記される。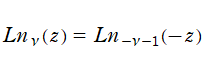
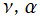 を非整数、
を非整数、 を複素変数として
を複素変数として](siki_spec190/laguerre11900.png) のグラフの多くを描画するが、このような事例は応用でほとんど現れない。
のグラフの多くを描画するが、このような事例は応用でほとんど現れない。