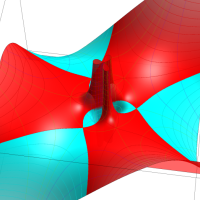
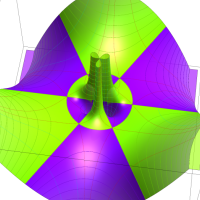
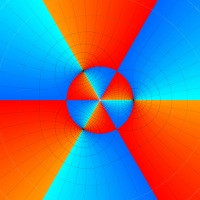
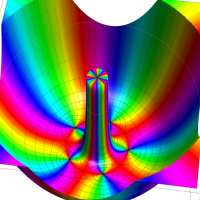
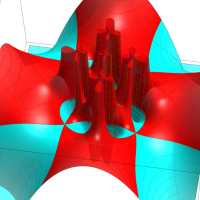
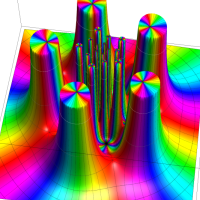
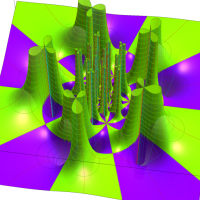
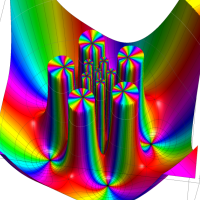
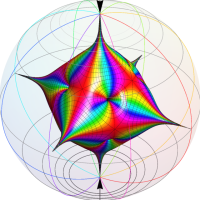
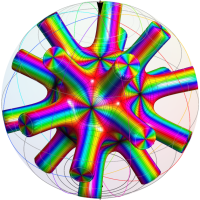
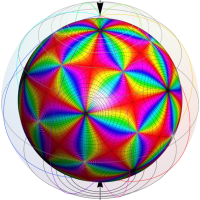
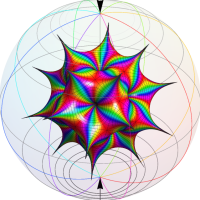
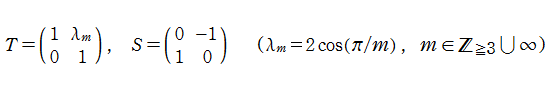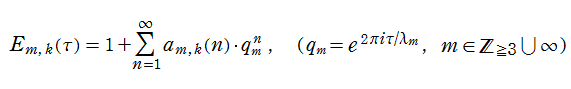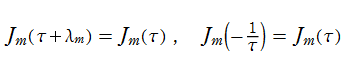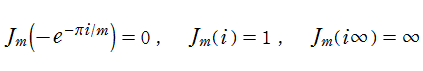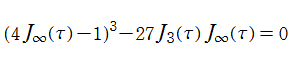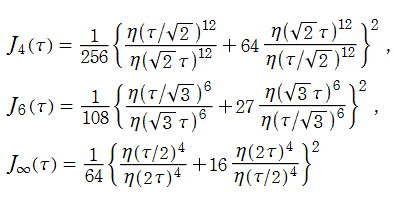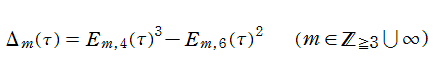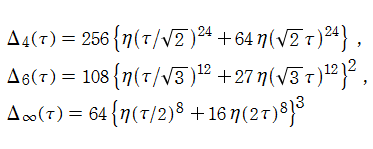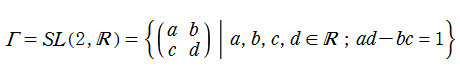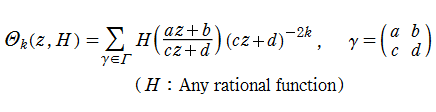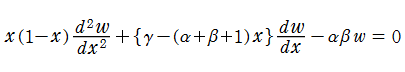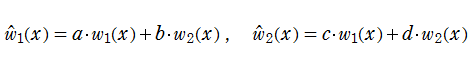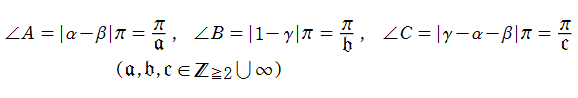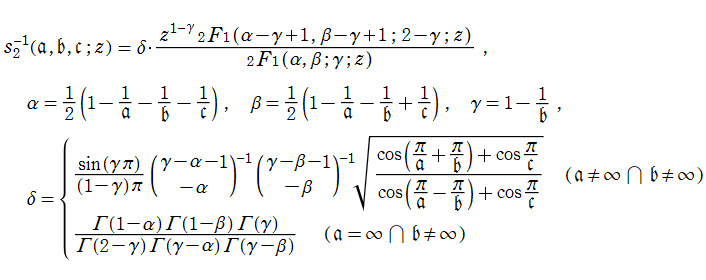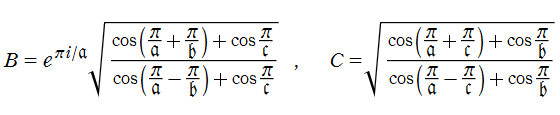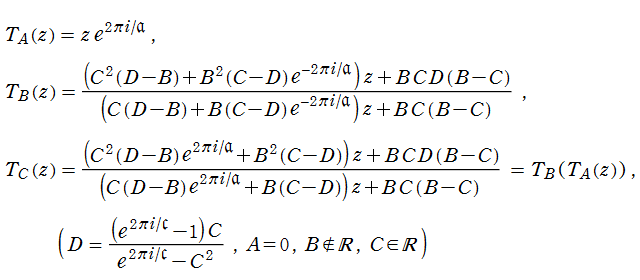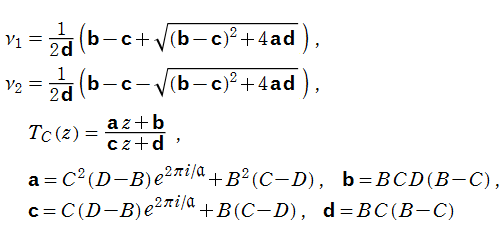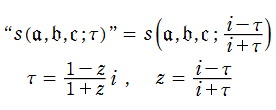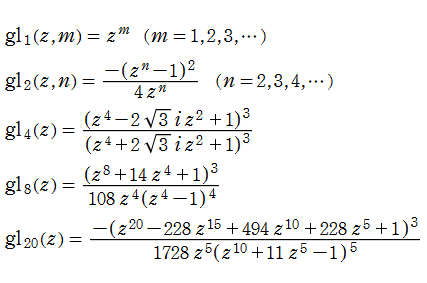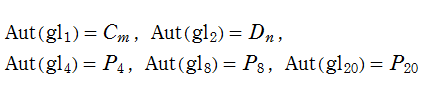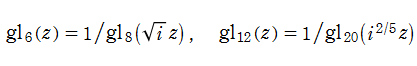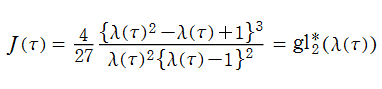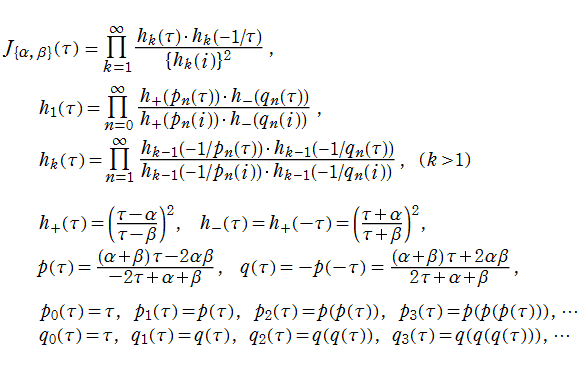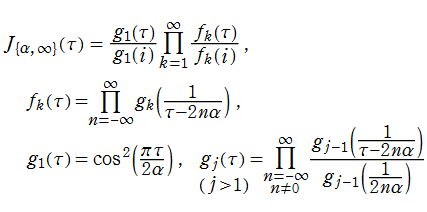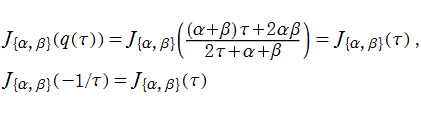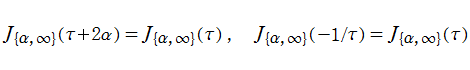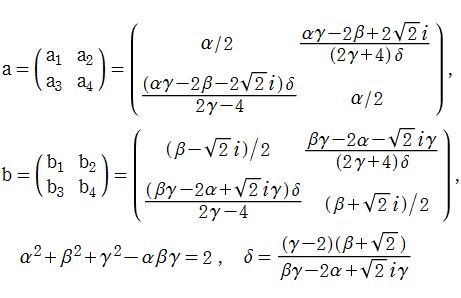特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
保型関数
数論的保型関数
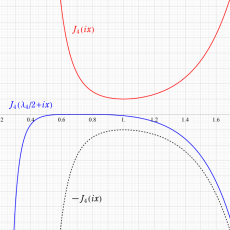
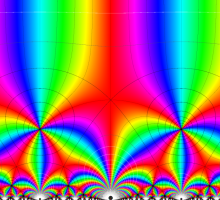
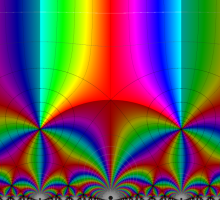
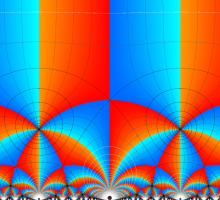
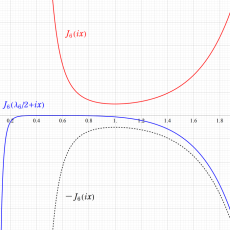
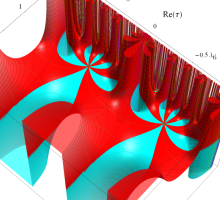
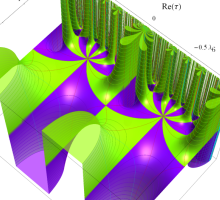
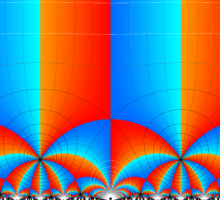
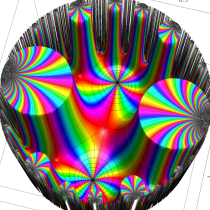
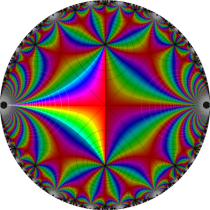
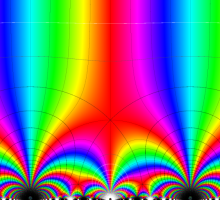
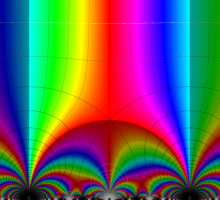
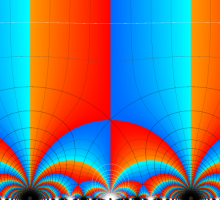
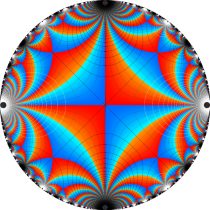
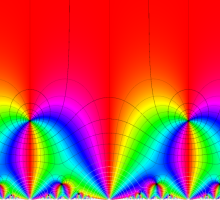
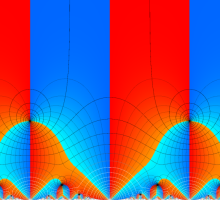
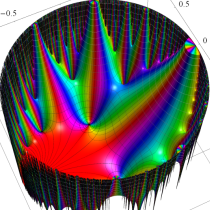
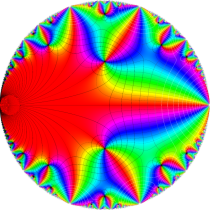
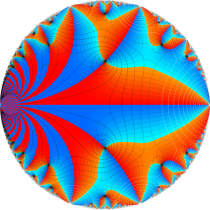
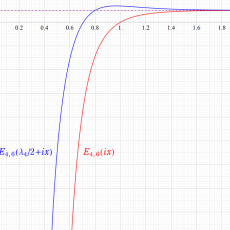
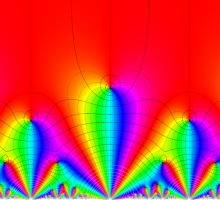
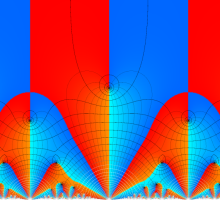
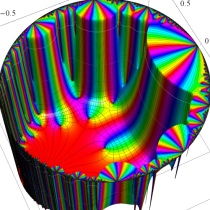
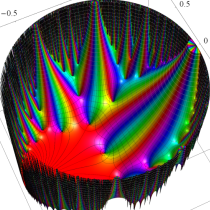
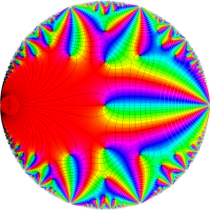
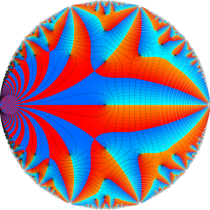
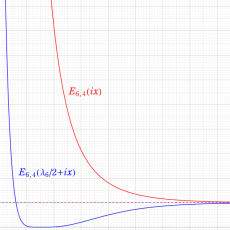
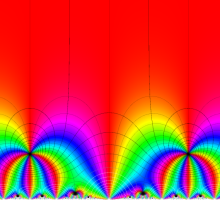
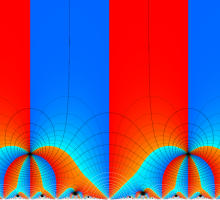
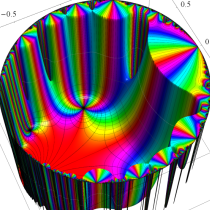
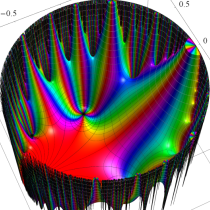
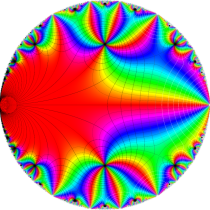
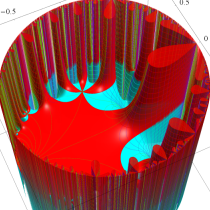
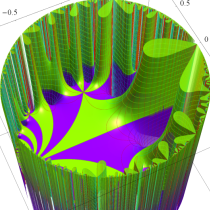
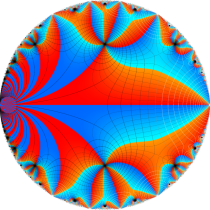
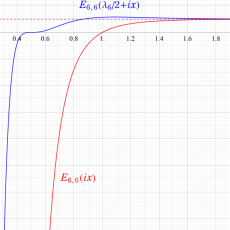
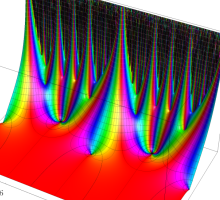
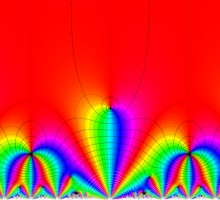
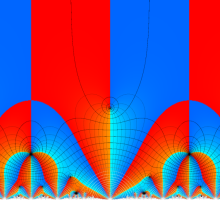
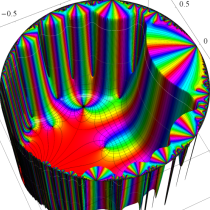
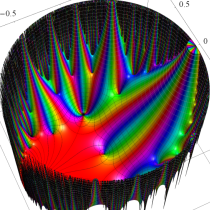
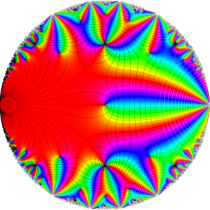
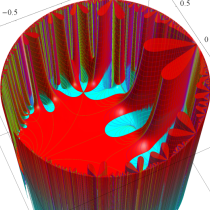
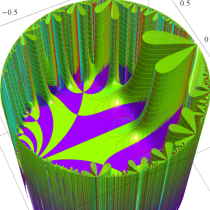
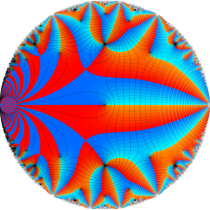
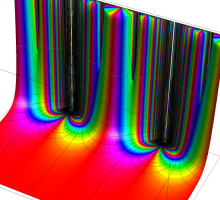
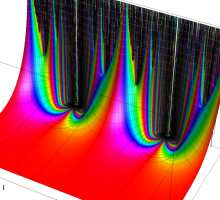
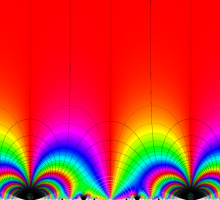
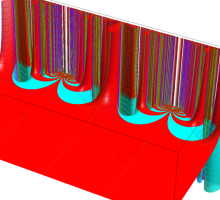
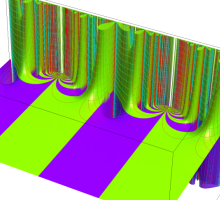
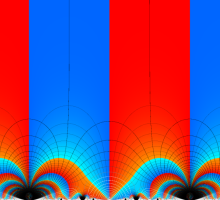
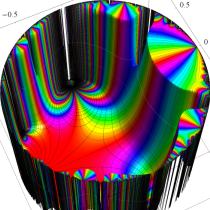
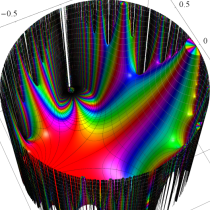
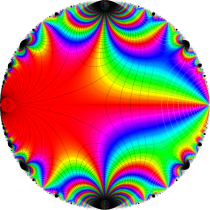
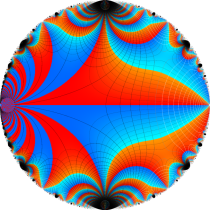
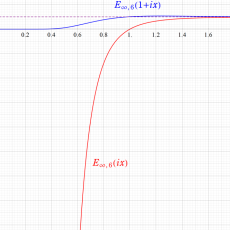
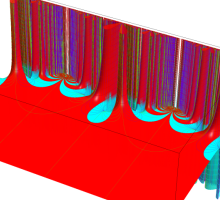
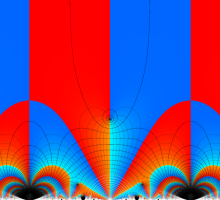
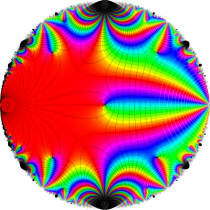
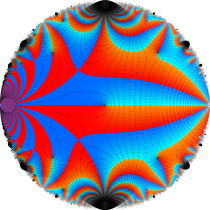
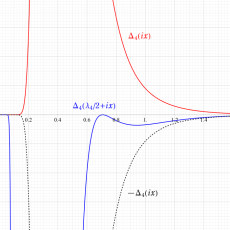
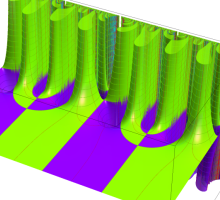
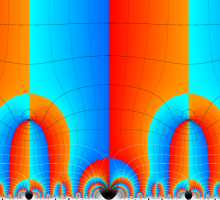
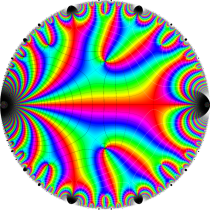
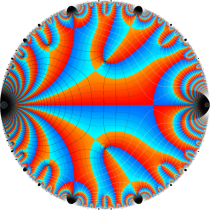
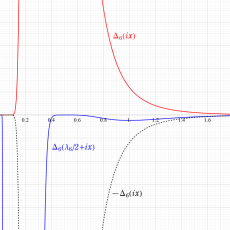
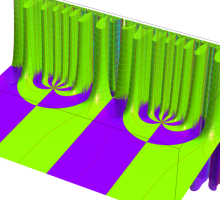
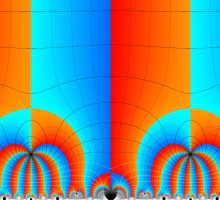
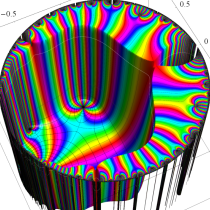
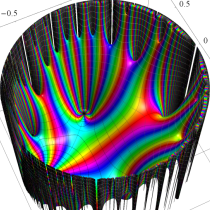
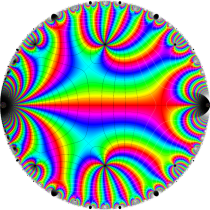
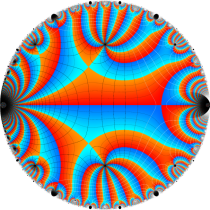
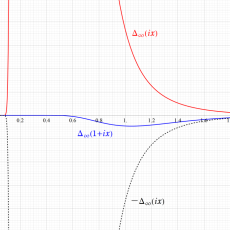
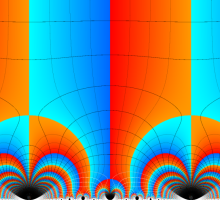
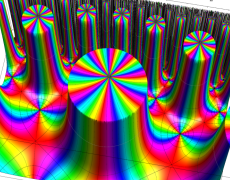
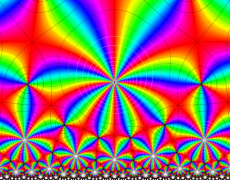
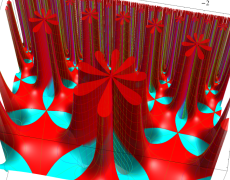
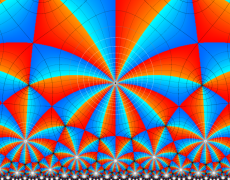
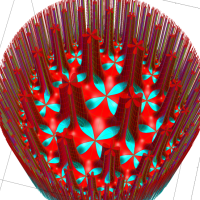
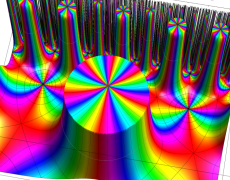
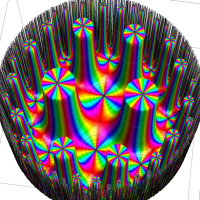
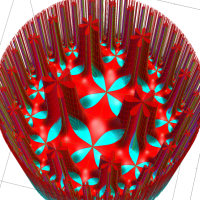
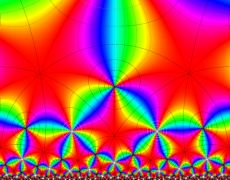
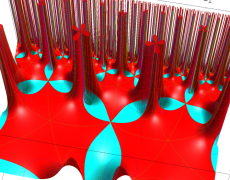
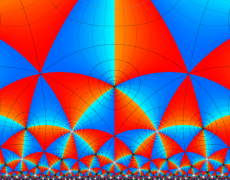
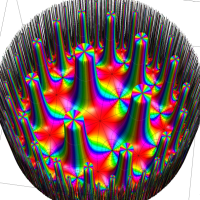
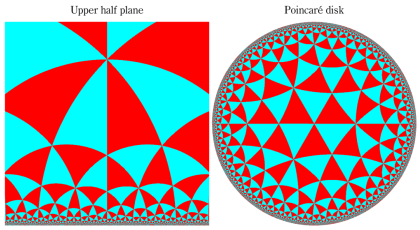
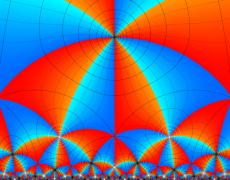
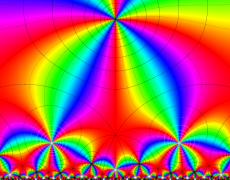
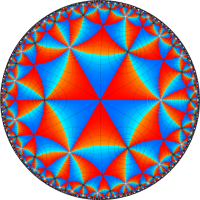
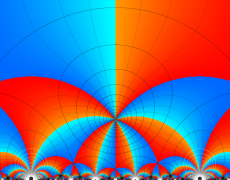
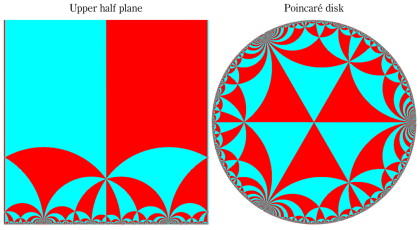
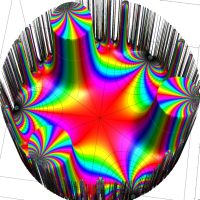
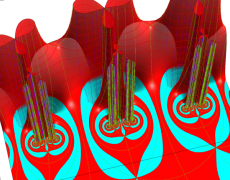
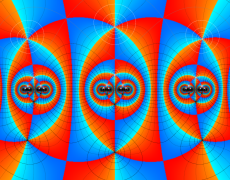
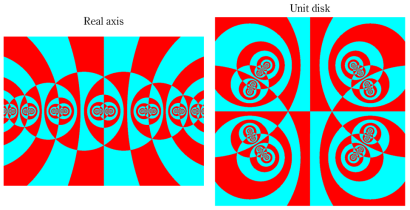
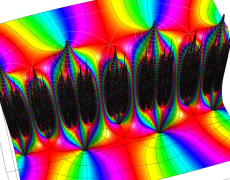
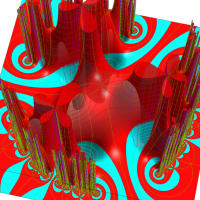
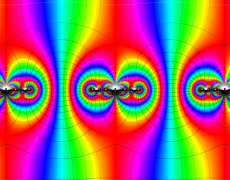
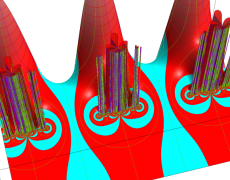
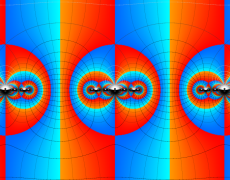
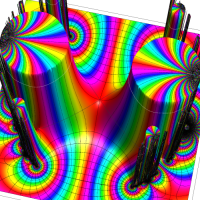
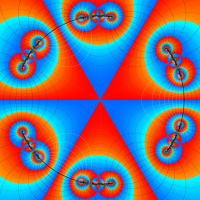
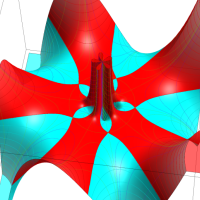
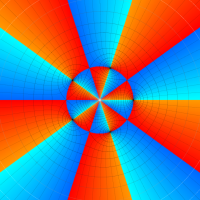
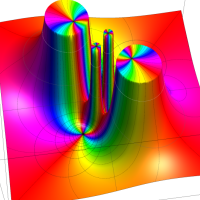
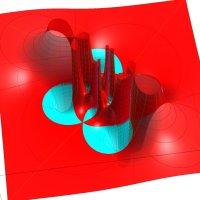
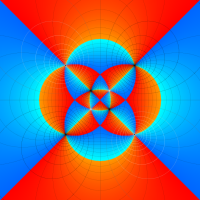
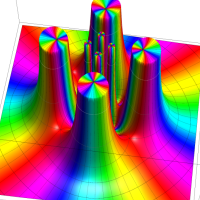
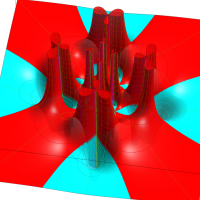
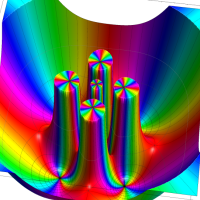
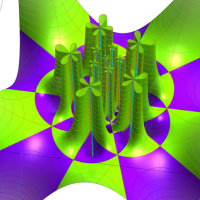
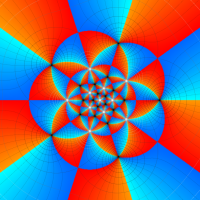
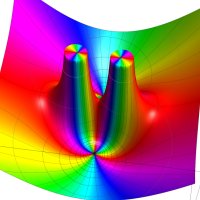
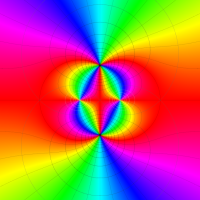
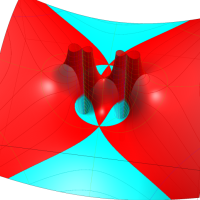
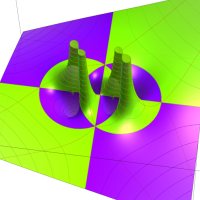
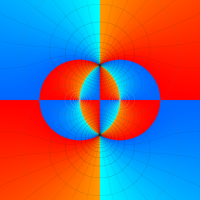
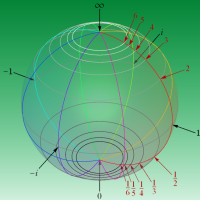
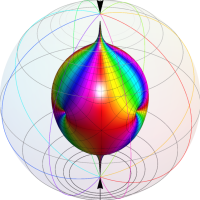
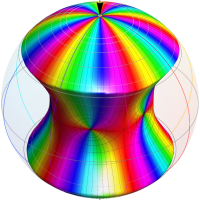
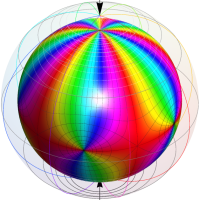
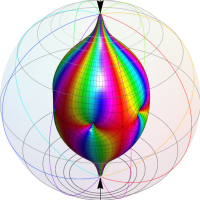
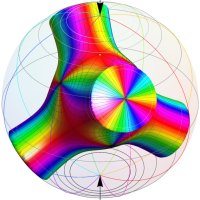
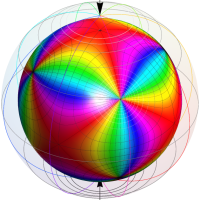
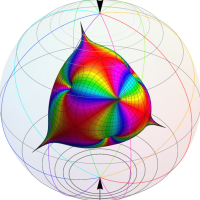
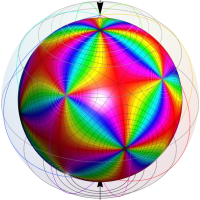
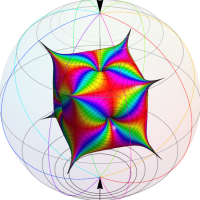
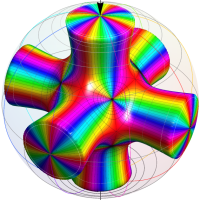
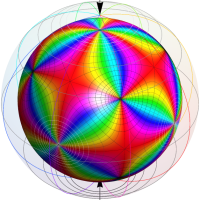
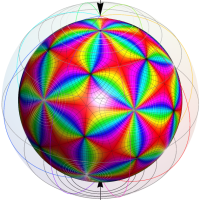
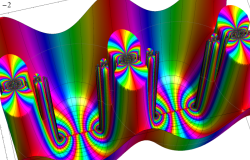
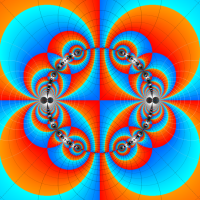
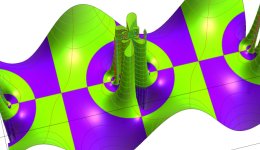
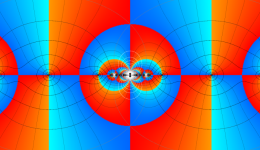
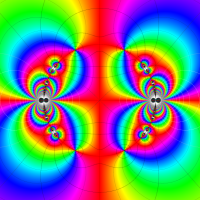
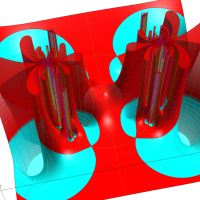
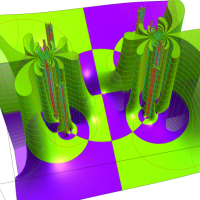
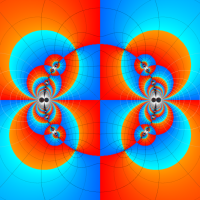
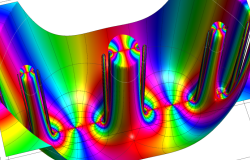
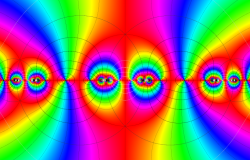
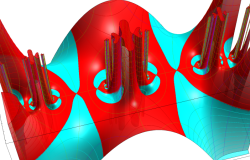
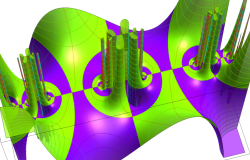
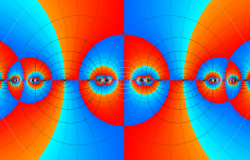
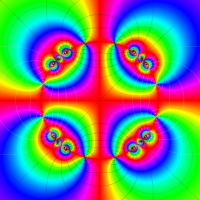
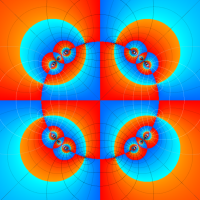
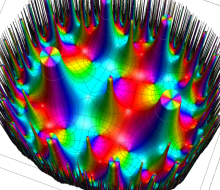
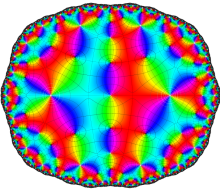
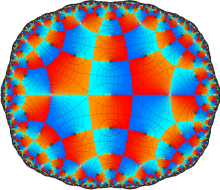
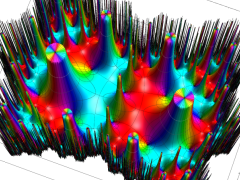
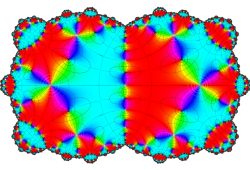
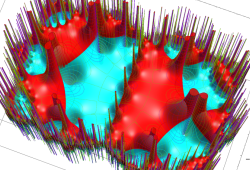
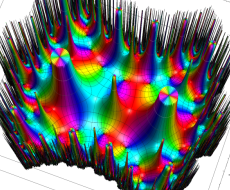
Klein の楕円モジュラー関数John Garrett Leo の論文「Fourier Coefficients of Triangle Functions」(2008, Univ. of California, Los Angeles) によると、
の合成変換全体に対して不変な保型関数
の形に級数展開されるとするとき※2、もし
で表わされる。ここに、
数論的保型関数は、
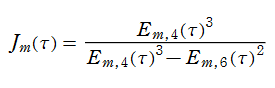
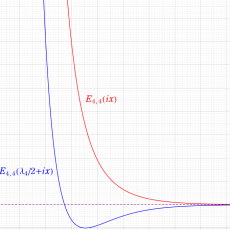
を満たす。また、基本領域の半分である円弧三角形の各頂点において、次の特殊値をとる。
の関係にある。
と表わすことができる。
【註記】
※1:基本領域が "コンパクト" な数論的保型関数まで含めれば全部で85種類あり、それらは全て Schwarz の保型関数で表わせる。なお、"数論的" の意味を説明することは省略する。詳細は、志賀 弘典 著 「保型関数:古典理論とその現代的応用 (共立出版 2017年)」 の第8章等を参照。また分野が若干異なるが、![SL(2, Z[2*cos(π/m)])](siki_spec120/autom00300.png) に対する実解析的保型形式との関連が、数学セミナー Vol.37, No.8 (1998年8月号) の記事 「セルバーグ予想」 で触れられている。
に対する実解析的保型形式との関連が、数学セミナー Vol.37, No.8 (1998年8月号) の記事 「セルバーグ予想」 で触れられている。
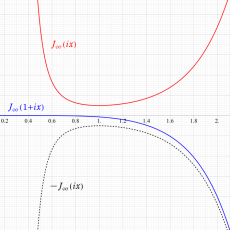
※2:J. G. Leo の論文では、この Eisenstein 級数を](siki_spec120/autom02000.png) と表記しているが、当サイトでは、むしろ正規化 Eisenstein 級数に相当すると考えて
と表記しているが、当サイトでは、むしろ正規化 Eisenstein 級数に相当すると考えて](siki_spec120/autom02100.png) と表記する。実際、
と表記する。実際、=E3(τ)](siki_spec120/autom02120.png) となっている。
となっている。
※1:基本領域が "コンパクト" な数論的保型関数まで含めれば全部で85種類あり、それらは全て Schwarz の保型関数で表わせる。なお、"数論的" の意味を説明することは省略する。詳細は、志賀 弘典 著 「保型関数:古典理論とその現代的応用 (共立出版 2017年)」 の第8章等を参照。また分野が若干異なるが、
※2:J. G. Leo の論文では、この Eisenstein 級数を
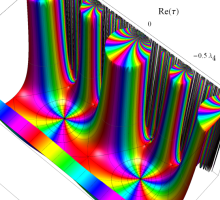
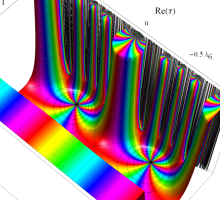
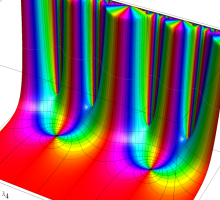
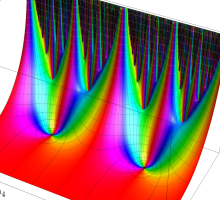
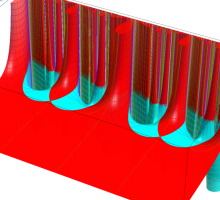
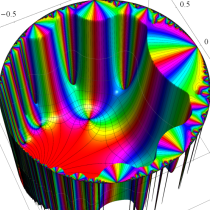
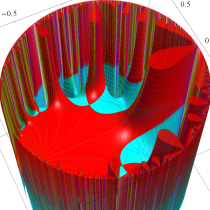
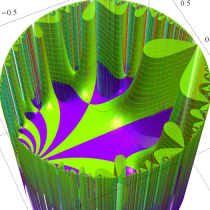
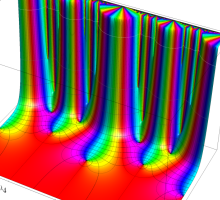
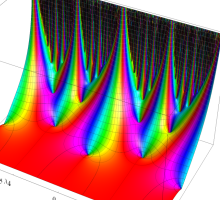
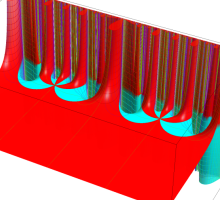
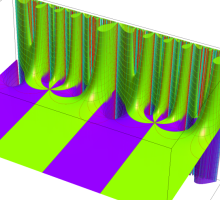
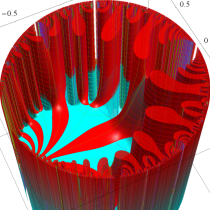
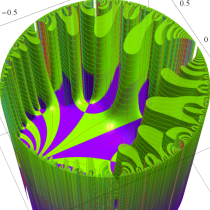
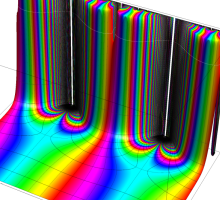
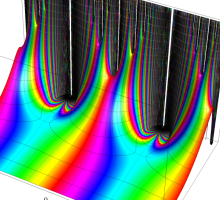
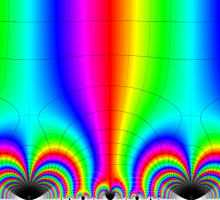
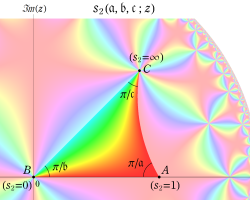
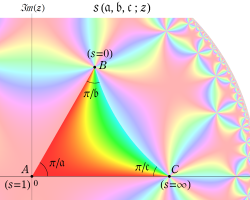
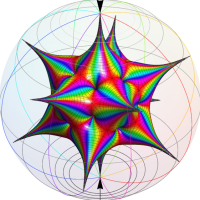
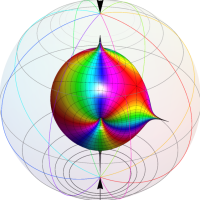
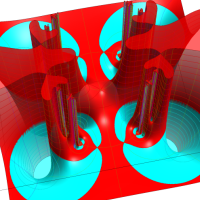
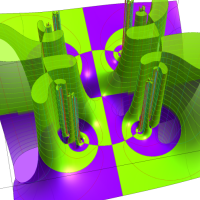
この関数の基本領域が、円弧多角形であることを示したグラフ。
この関数の基本領域が、円弧多角形であることを示したグラフ。
この関数の基本領域が、円弧多角形であることを示したグラフ。
数論的保型形式
と表わされる関数を解析接続したものと一致する。
数論的尖点形式は、数論的保型関数の定義式における分母、すなわち
で定義される。これは、基本領域に附随する全ての尖点で値0をとる。
特に、
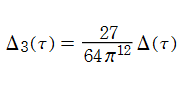
と表わすことができる。
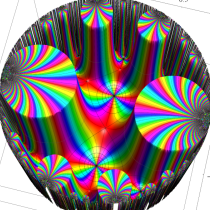
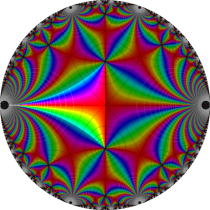
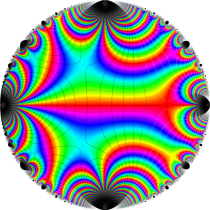
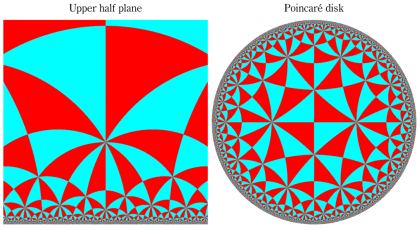
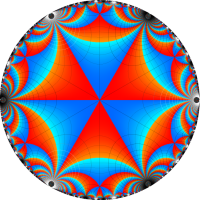
Schwarz の保型関数
日:保型関数英:Automorphic function,仏:Fonction automorphe,独:Automorphe funktion
【一般的な保型関数とPoincaré 級数】
楕円モジュラー関数の所での説明と重複するが、保型関数とは、特殊線形群の離散部分群
と表わされるとき、二つの条件
*すべての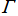 に対して、
に対して、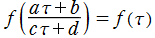 を満たす。
を満たす。
*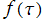 は、任意の尖点の周りで一般に有理型である。
は、任意の尖点の周りで一般に有理型である。
*
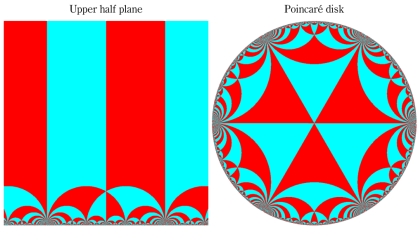
を満たす、上半平面
この他にも、作用する領域が
上記の最も広い意味での保型関数は、「Poincaré 級数」※1
の二つの商によって表わされる (ただし、Poincaré 級数の総和対象としての
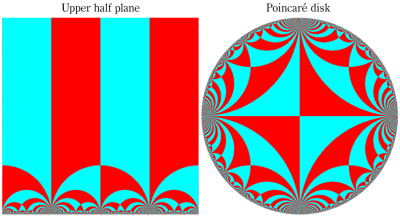
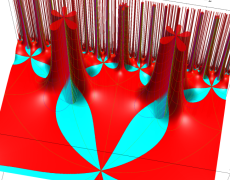
下図では、広義の保型関数が持つ基本領域の形状を例示する。
Klein 群の保型関数が持つ基本領域の形状は、3次元双曲型非 Euclid 空間を埋め尽くした (球面で囲まれた多面体から成る) 基本領域達の、Riemann 球面による断面上の図形として捉えることができる。この考え方は Poincaré (1881年, 1883年) が先鞭を付け、以後の Klein 群の研究は、一変数の保型関数論と若干異なる方向に発展することとなる。
【Gauss - Schwarz 理論:整数パラメーターの場合】
Gauss の超幾何微分方程式
の線形独立な二つの解を
の形に変わることが、線形微分方程式論から保証される。よって、二つの解の比
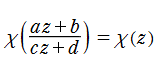
として超幾何微分方程式の
①: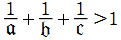 →
→ 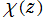 は初等有理関数 (Galois 的有理関数)、定義域は楕円型非 Euclid 平面。
は初等有理関数 (Galois 的有理関数)、定義域は楕円型非 Euclid 平面。
②: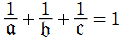 →
→ 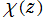 は楕円関数 (の特別な例)、定義域は Euclid 平面。
は楕円関数 (の特別な例)、定義域は Euclid 平面。
③: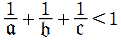 →
→ 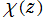 は保型関数、定義域は双曲型非 Euclid 平面 (円の内部)。
は保型関数、定義域は双曲型非 Euclid 平面 (円の内部)。
②:
③:
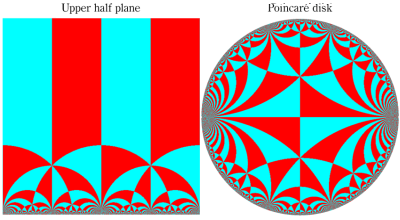
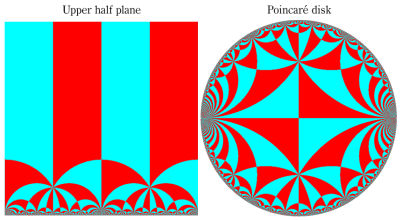
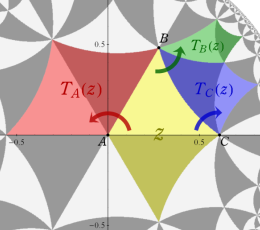
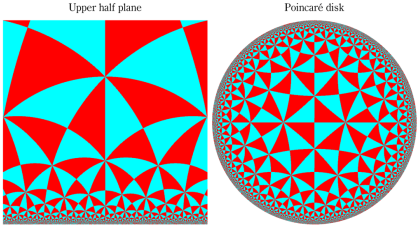
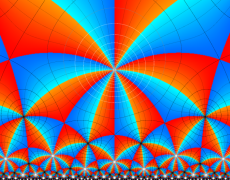
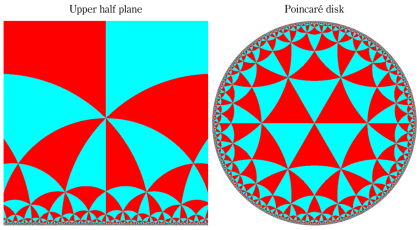
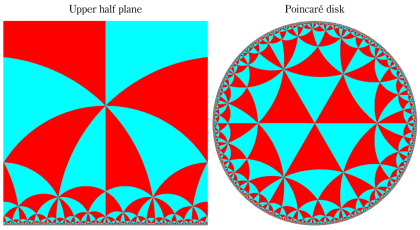
となる。①, ②の場合は有限種類しかないが、③は無数にある。③は Fuchs 関数のさらに特別な例になっており、Schwarz の保型関数あるいは三角形関数と呼ばれ、円の内部を存在領域とする有理型関数となる。これは、楕円モジュラー関数と本質的に異なる保型関数を構成した、最初の理論体系の例であり、現在ではそれを 「Gauss - Schwarz 理論」 と呼ぶ※2。
ただし、Schwarz の研究は①を解明することに主軸が置かれ、未知の超越関数③については具体的な定義・構成をしなかった (円弧三角形から成る基本領域が円の内部を一重に覆うことは証明した)。程なく、F. Klein,H. Poincaré 等によって③の全貌が解明され、保型関数に新たな種類が加わることになった。(なお、前述のとおり保型関数は③以外の種類もある。③のように基本領域の半分が円弧三角形の場合では、Klein 群のようなフラクタル形状の自然境界は生じない。)
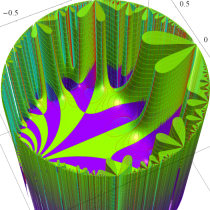
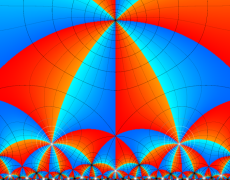
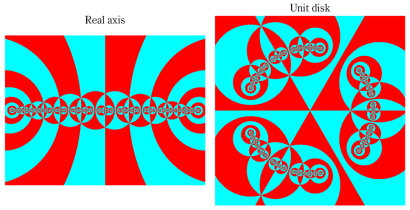
単位円内部における Schwarz の保型関数の一つを
で表わされる。ここに
となる。また、その場合の頂点
となる。すなわち
で表わされる。
なお、単位円内部における Schwarz の保型関数
を用いる。
Schwarz の保型関数は、特別な場合として Klein の楕円モジュラー関数になる場合
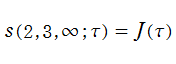
Schwarz の保型関数における円弧三角形の変換群は、三角形群 (triangle group) と呼ばれる。特に、(2,3,7)-triangle group や (2,3,8)-triangle group は、Klein、A. Hurwitz 等が群論的アプローチで代数曲面や位相幾何学を論じた際に用いられた。また、20世紀になると志村 五郎, 谷山 豊, A. Weil 等によって高次元虚数乗法論, 志村多様体論が構築され、それらの主要目的である類体論の一般化が試みられる中で、Schwarz の保型関数が現れている。
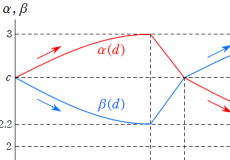
【Gauss - Schwarz 理論:一部が純虚数パラメーターの場合】
Schwarz の保型関数における3個のパラメーター
このような純虚数パラメーターの
純虚数パラメーターの場合に拡張された Gauss - Schwarz 理論は、佐々木武, 吉田正章, 市川尚志によって論じられている (ただし、超幾何微分方程式の形やパラメーターの取り方は当サイトと異なる)※4。
【註記】
※1:Poincaré 級数は保型形式の一例で、(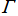 が Fuchs 群ならば) 「テータ Fuchs 関数」 とも呼ばれる。後者の名称は、この級数が保型関数版のテータ関数に相当すると考えた Poincaré が使い始めた。(Fuchs 群なる名称等も同様に) "Fuchs" が付く理由は、Fuchs 型の線形常微分方程式を解く逆関数を求めること ― 楕円積分がその逆関数である楕円関数で解かれることの類似 ― を、Poincaré が保型関数研究の主題と捉えていたからである。
が Fuchs 群ならば) 「テータ Fuchs 関数」 とも呼ばれる。後者の名称は、この級数が保型関数版のテータ関数に相当すると考えた Poincaré が使い始めた。(Fuchs 群なる名称等も同様に) "Fuchs" が付く理由は、Fuchs 型の線形常微分方程式を解く逆関数を求めること ― 楕円積分がその逆関数である楕円関数で解かれることの類似 ― を、Poincaré が保型関数研究の主題と捉えていたからである。
同時期、群論的・位相幾何学的な方向から保型関数を研究していた Klein は、度々 Poincaré と意見が衝突した。特に "Fuchs" を含むこれらの名称を Klein は、「verfrüht (時期尚早)」 と評し、誰の名も冠しない 「Automorphe funktion (保型関数)」 を使うべきであると主張した。
両者の論争は、数学史でも割合触れられることが多い。どのような言葉が交わされたかについては、
・斎藤利弥 著 「線形微分方程式とフックス関数 (Ⅰ)」 p.276~279
・J. J. Gray 著 「リーマンからポアンカレにいたる 線型微分方程式と群論」 p.256~268
等に詳しい。
※2:Gauss - Schwarz 理論 に基づいて保型関数のプログラムを開発した経過を、「Mathematica Code」 の頁 で公開しています。(ただし、純虚数パラメーターに対応していない古い世代のコード。)
で公開しています。(ただし、純虚数パラメーターに対応していない古い世代のコード。)
※3:面倒なので当サイトは従わなかったが、Schwarz 以来、第1~3変数は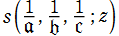 と表示するのが本来の記法である (しかも、実際には逆保型関数に対する記号である)。因みに、Klein によれば、関数記号
と表示するのが本来の記法である (しかも、実際には逆保型関数に対する記号である)。因みに、Klein によれば、関数記号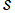 は Schwarz の名ではなく球面 (sphära) に由来する ― (本質的に
は Schwarz の名ではなく球面 (sphära) に由来する ― (本質的に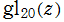 と同じ)
と同じ)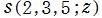 は、Riemann 球面上に移すと理解しやすくなるから ― とのことらしい。
は、Riemann 球面上に移すと理解しやすくなるから ― とのことらしい。
※4:吉田正章 「私は超幾何関数:於北大早春学校」 (2006年3月 北海道大学での講演論文) 等を参照。(ただし、外来語を独自の訳語で記述しており、少々読みづらい。末尾の参考文献に挙がっている他2者との共著論文の方が、(英文であるが) 人によっては馴染めるかもしれない。)
※1:Poincaré 級数は保型形式の一例で、(
同時期、群論的・位相幾何学的な方向から保型関数を研究していた Klein は、度々 Poincaré と意見が衝突した。特に "Fuchs" を含むこれらの名称を Klein は、「verfrüht (時期尚早)」 と評し、誰の名も冠しない 「Automorphe funktion (保型関数)」 を使うべきであると主張した。
両者の論争は、数学史でも割合触れられることが多い。どのような言葉が交わされたかについては、
・斎藤利弥 著 「線形微分方程式とフックス関数 (Ⅰ)」 p.276~279
・J. J. Gray 著 「リーマンからポアンカレにいたる 線型微分方程式と群論」 p.256~268
等に詳しい。
※2:Gauss - Schwarz 理論 に基づいて保型関数のプログラムを開発した経過を、「Mathematica Code」 の頁
※3:面倒なので当サイトは従わなかったが、Schwarz 以来、第1~3変数は
※4:吉田正章 「私は超幾何関数:於北大早春学校」 (2006年3月 北海道大学での講演論文) 等を参照。(ただし、外来語を独自の訳語で記述しており、少々読みづらい。末尾の参考文献に挙がっている他2者との共著論文の方が、(英文であるが) 人によっては馴染めるかもしれない。)
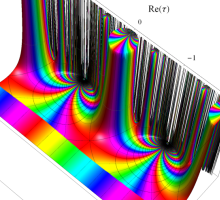
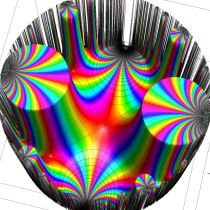
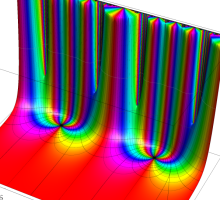
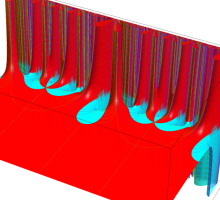
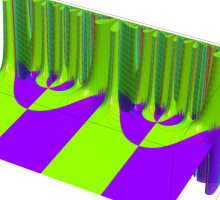
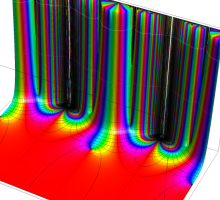
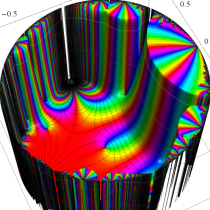
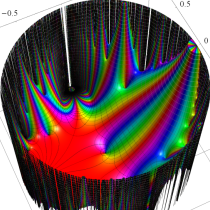
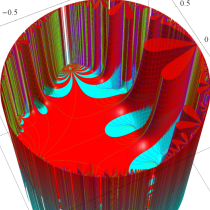
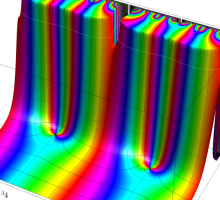
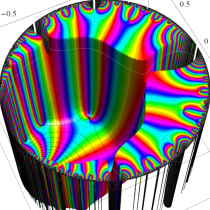
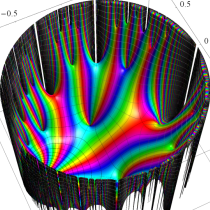
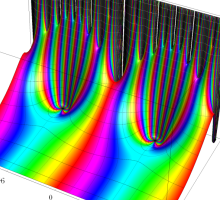
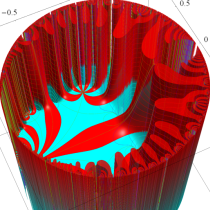
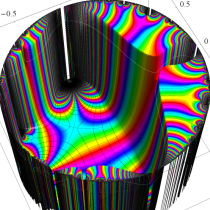
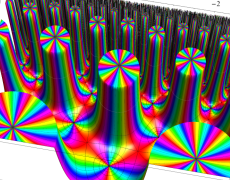
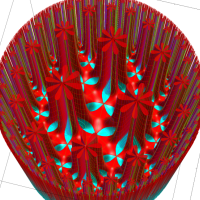
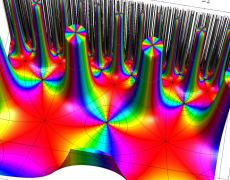
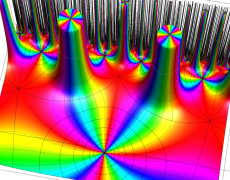
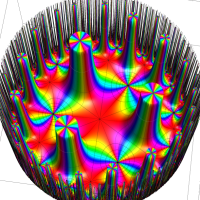
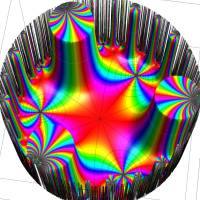
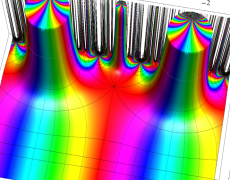
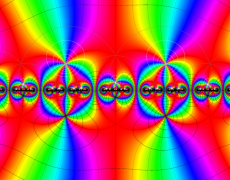
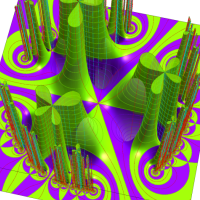
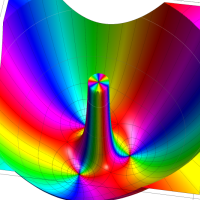
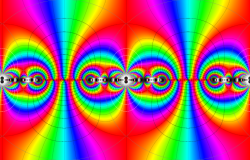
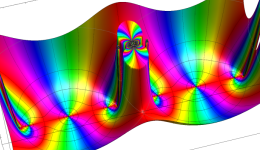
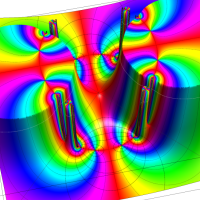
複素変数の Schwarz の保型関数
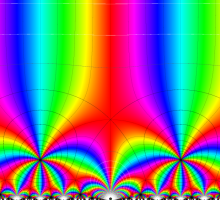
この関数の基本領域が、円弧多角形であることを示したグラフ。
アニメーション(10.40MB)
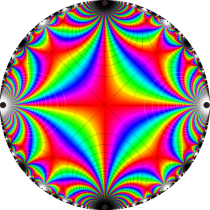
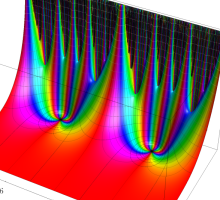
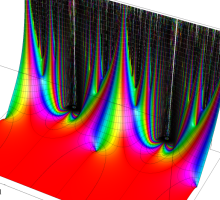
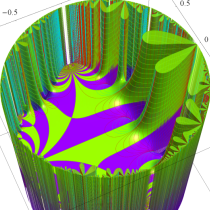
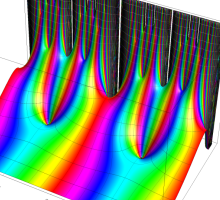
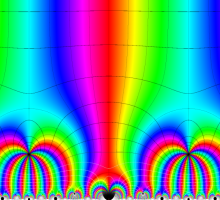
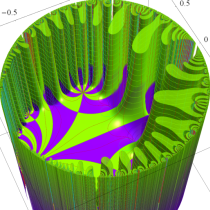
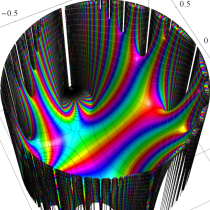
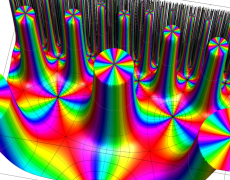
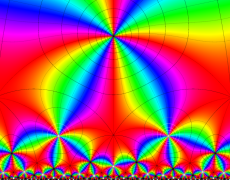
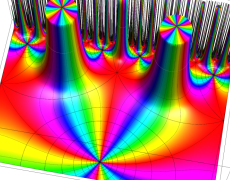
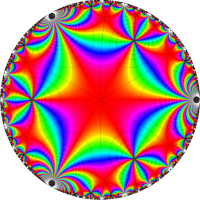
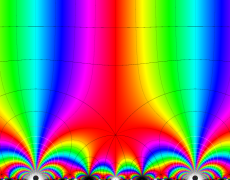
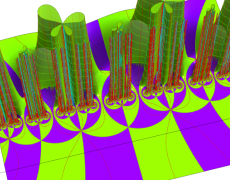
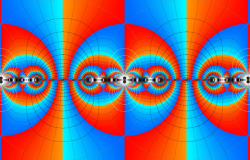
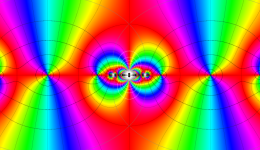
複素変数の Schwarz の保型関数
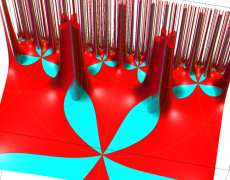
複素変数の Schwarz の保型関数
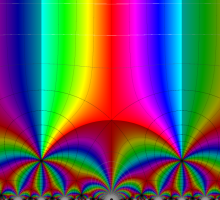
この関数の基本領域が、円弧多角形であることを示したグラフ。
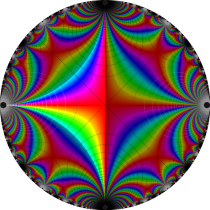
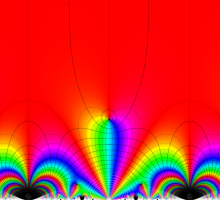
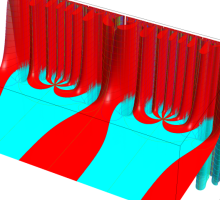
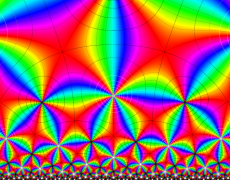
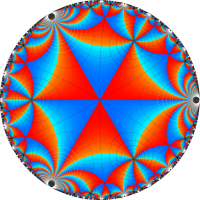
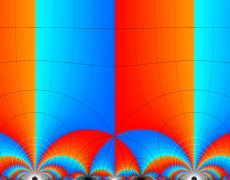
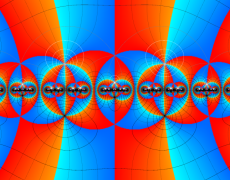
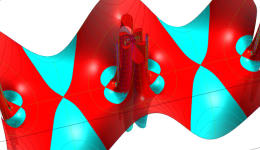
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
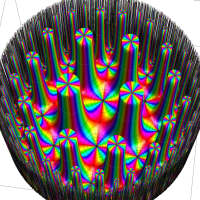
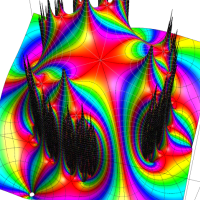
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
複素変数の Schwarz の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
アニメーション(16.80MB, 5.09MB)
複素変数の Schwarz の保型関数
次の関数
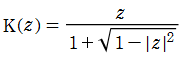
因みに、双曲的非 Euclid 幾何学の平面モデルである Klein 円板、Poincaré 円板、および上半平面を最も早く発見したのは E. Beltrami (1868年) である。他にも曲面モデルとして擬球、(二葉)回転双曲面があり、各モデルの相互関係等についても前掲のサイトに詳しい説明がある。
Galois 的有理関数
前述のように、保型関数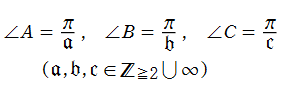
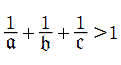
Schwarz, Klein 等の研究を経て、具体的な Galois 的有理関数の式が次のように求められている。
Galois 的有理関数は、三次元特殊直交群の有限部分群である巡回群
となる。
なお、正6面体、正12面体に対応する Galois 的有理関数は、
である。(以下のグラフにおいて、
特に、ある一次分数変換によって
の定義](siki_spec120/autom14600.png)
の有理関数部分として現れる。
【註記】
※1:これはあまり一般的な名称ではないが、例えば 難波 誠 著 「複素関数 三幕劇 (朝倉書店 1990年)」 で使用されている。ここでの記述もこの書籍に基づく。ただし、記号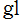 は独自に設定したものである。
は独自に設定したものである。
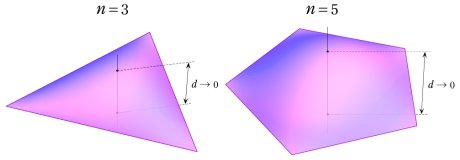
※2:正2面体とは、2枚の正多角形の対応する辺どうしを貼り合わせて、厚みを0とした "正多面体" を言う (下図を参照)。
これは、正多面体群を研究していた Klein によって、(少なくとも群論では) 正多面体に追加すべきであることが発見された。
※1:これはあまり一般的な名称ではないが、例えば 難波 誠 著 「複素関数 三幕劇 (朝倉書店 1990年)」 で使用されている。ここでの記述もこの書籍に基づく。ただし、記号
※2:正2面体とは、2枚の正多角形の対応する辺どうしを貼り合わせて、厚みを0とした "正多面体" を言う (下図を参照)。
これは、正多面体群を研究していた Klein によって、(少なくとも群論では) 正多面体に追加すべきであることが発見された。
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
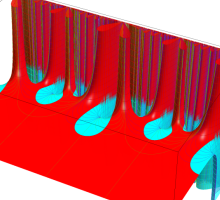
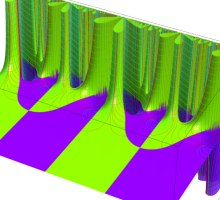
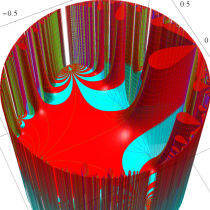
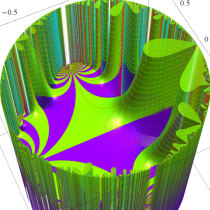
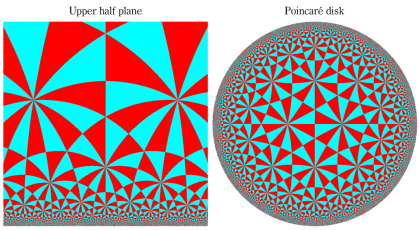
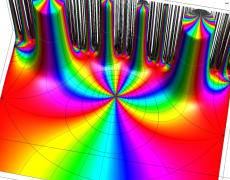
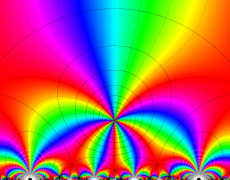
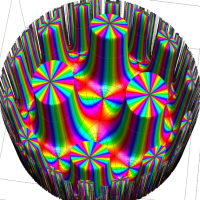
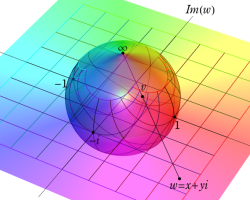
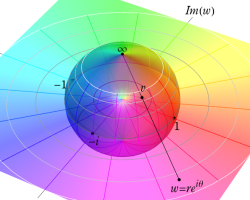
Riemann 球面にはいくつかの流儀があるが、ここでは、複素平面上の単位円を共有する半径1の球を Riemann 球面とし、(この球を地球に喩えれば) 複素平面から Riemann 球面への写像は、無限遠点を北極点に、原点を南極点に、単位円を赤道に移すものを採用している。換言すれば、北極点からの極射影によって Riemann 球面上の点を複素平面上に射影した点が、写像元の点となる (下図 ①,②)。
なお、以降のグラフでは、視覚補助用の球面を重ねて描画しているが、その凡例は ③ のとおりとする。
さらに、見やすい形状の曲面になるよう、以降のグラフでは関数値に任意定数を足して Riemann 球面の中心から離れるようにしている。例えば、各々1番目のグラフは、球の中心から関数の零点がある位置までの距離が、この定数に相当する。(この処理をしないと、零点はすべて球の中心付近に集まり、曲面の起伏が激しくなるため非常に見づらくなる。)
*******
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
複素変数の Galois 的有理関数
【 Petite Galerie 】
臨時ニュース:超新星爆発が発生!!
一般の保型関数
前述のとおり、一般に保型関数は Poincaré 級数で表わせる。しかし、 Poincaré 級数は理論的に収束することが分かっていても、実際の数値計算では、膨大な総和項数や高精度の数値を使用しなければ、充分な精度で結果が得られないことが多い。ここに掲載するグラフは、代替方法があるか、または条件が良いため例外的に描画が成功した事例である。以降の説明は、主にその計算方法について行う。なお、関数記号はいずれも独自に導入したものである。
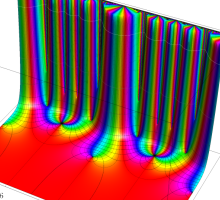
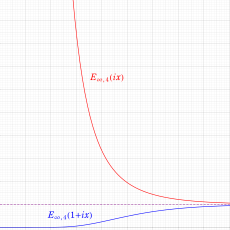
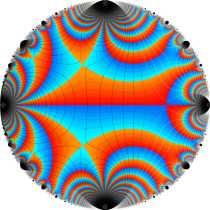
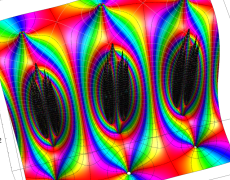
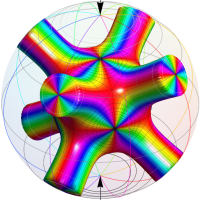
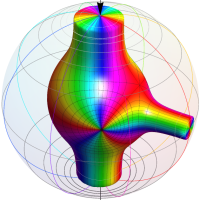
【Schottky 群に関する保型関数】
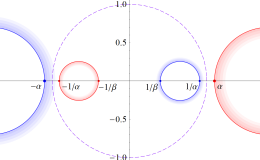
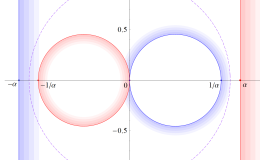
基本領域の半分が円弧4辺形になる保型関数 (Fuchs 関数) であるが、その一部の辺が実軸や単位円周を共有する (Poincaré は、これを 「第2種の辺」 と呼んだ) ので自然境界を持たない。特異点 (極・真性特異点) は実軸上または単位円周上にあり、Cantor 集合状の極限集合を形成する。
具体的には Fig.1 のように、実軸上に中心を持ち実数区間
なお、
のように、初期関数が三角関数となる※1。
を満たす。特に、
となり、これは数論的保型関数と類似している。実際、
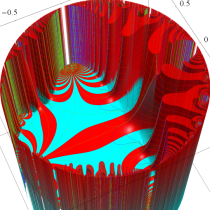
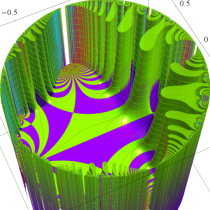
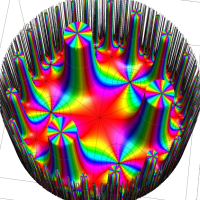
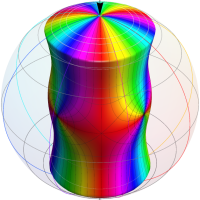
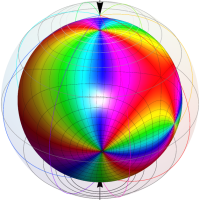
【Klein 群に関する保型関数:4辺形の内角がいずれも45°】
この保型関数は、基本領域の半分が円弧4辺形で各頂点の内角はいずれも45°、その各辺に対する鏡映は Klein 群が作用する一次分数変換で表わされる例である。極限集合はフラクタル形状の閉曲線で、それが関数の自然境界となり、その内部 (原点を含む側) が関数の存在領域となる。(この保型関数は、偏角の正負による区分線が基本領域の辺と一致しない普遍的な事例 ― 例えば楕円関数でも同様の事例が無数にある ― となっている。)
Poincaré 級数で計算できた数少ない事例で、D. Mumford,C. Series,D. J. Wright 著 「インドラの真珠」 に負う所が大きい。より詳しい内容は同著を参照して頂きたいが、概略は次のとおりである。
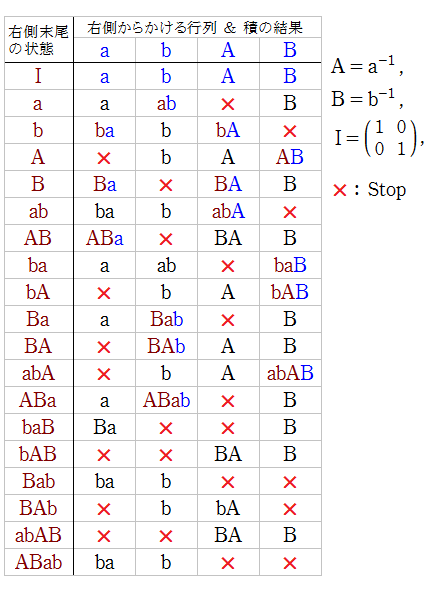
この関数を独自の記号
さらに、行列
上記の制約のもとで生成される、すべての合成行列からなる集合を
と表記すると、
と定義される。すなわち、
を満たす。
【註記】
※1:定義上の項数・反復回数は無限大であるが、数値計算ではかなり少ない有限値に設定しないと、すぐにメモリーオーバーを起こすか途方もない時間がかかる。因みに、誤差が約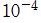 の精度で良ければ、20項・4回反復程度で求められる。
の精度で良ければ、20項・4回反復程度で求められる。
※2:もっと一般的に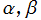 を複素数とすることもできるが、一部のパラメータ指定値で計算不能になる等の問題が生じる。詳細は 「インドラの真珠」 を参照。
を複素数とすることもできるが、一部のパラメータ指定値で計算不能になる等の問題が生じる。詳細は 「インドラの真珠」 を参照。
※1:定義上の項数・反復回数は無限大であるが、数値計算ではかなり少ない有限値に設定しないと、すぐにメモリーオーバーを起こすか途方もない時間がかかる。因みに、誤差が約
※2:もっと一般的に
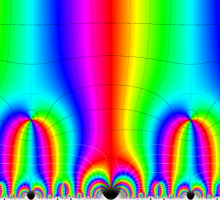
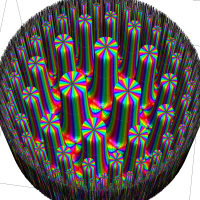
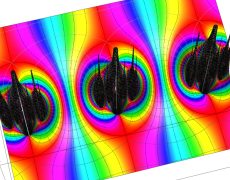
単位円周上に極限集合を持つ Schottky 群の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
実軸上に極限集合を持つ Schottky 群の保型関数
単位円周上に極限集合を持つ Schottky 群の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
実軸上に極限集合を持つ Schottky 群の保型関数
単位円周上に極限集合を持つ Schottky 群の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
この関数の基本領域が、円弧多角形であることを示したグラフ。
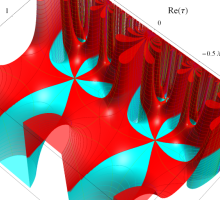
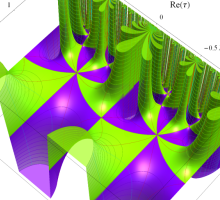
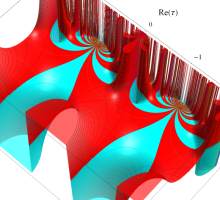
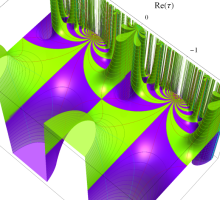
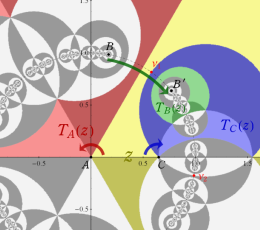
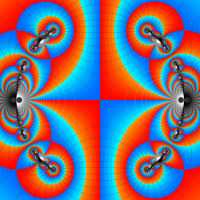
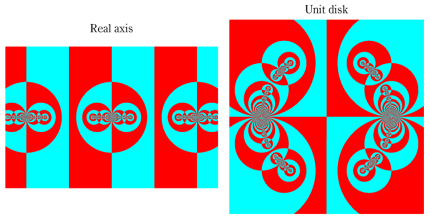
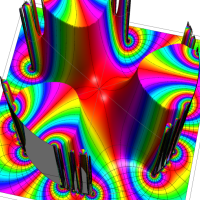
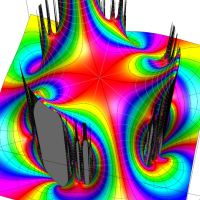
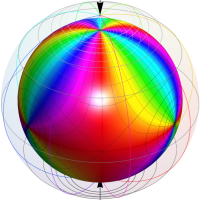
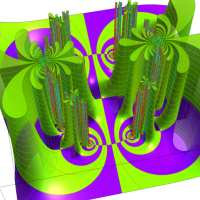
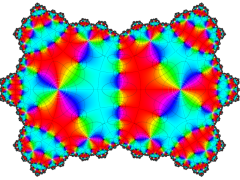
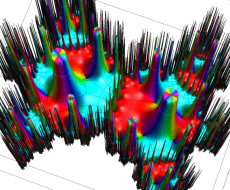
Klein 群の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
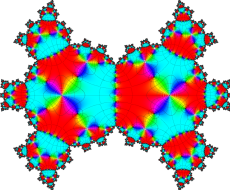
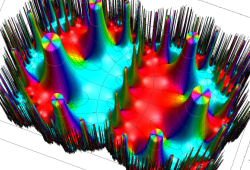
Klein 群の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
Klein 群の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
Klein 群の保型関数
この関数の基本領域が、円弧多角形であることを示したグラフ。
アニメーション(12.30MB)
Klein 群の保型関数の基本領域。存在領域の外部 (暗く表示している部分) にも4辺形の円弧を延長している。ここに、パラメータ
【 Petite Galerie 】
Charm'd magic casements,opening on the foam / Of perilous seas, in faery lands forlorn.
もの寂しき妖精の国の、険しく泡立つ海に開ける、魅惑の魔法の窓。
(John Keats 「ナイチンゲールに寄せる叙情詩 (Ode to a Nightingale)」 の一節より)
もの寂しき妖精の国の、険しく泡立つ海に開ける、魅惑の魔法の窓。
(John Keats 「ナイチンゲールに寄せる叙情詩 (Ode to a Nightingale)」 の一節より)