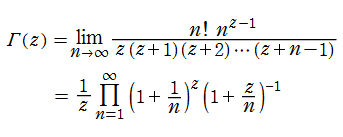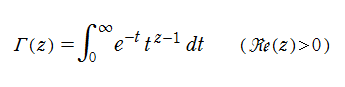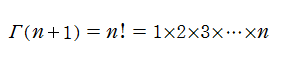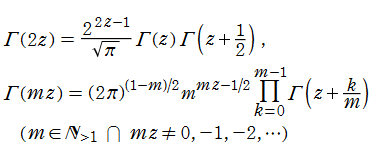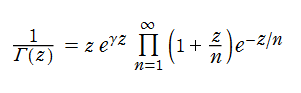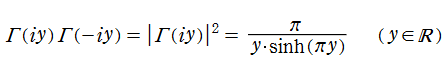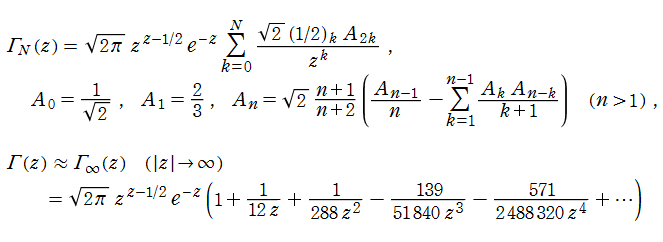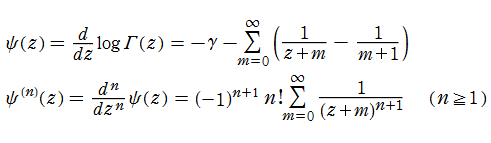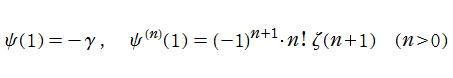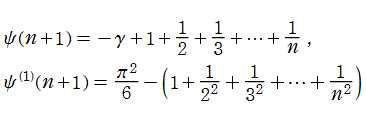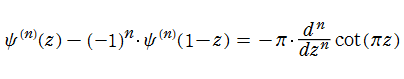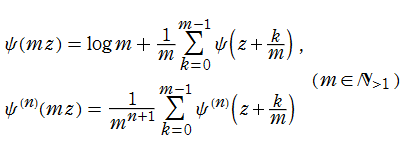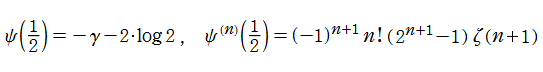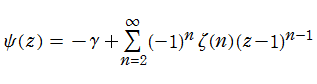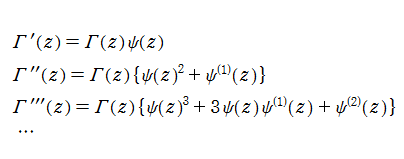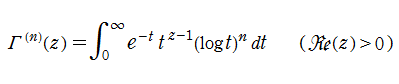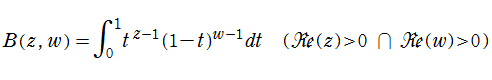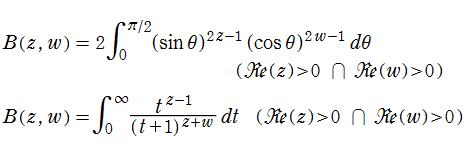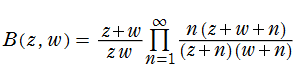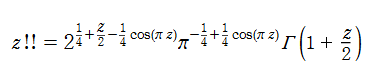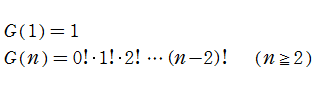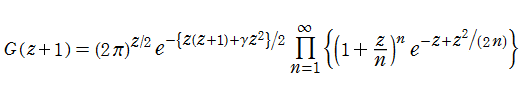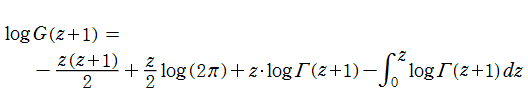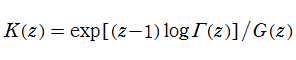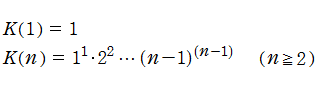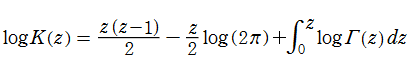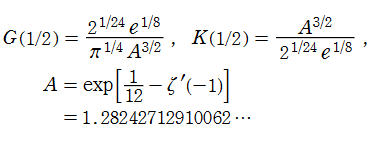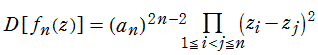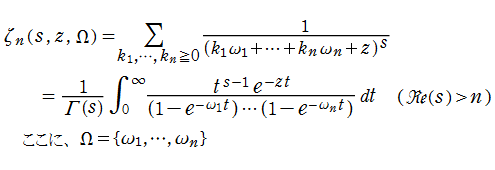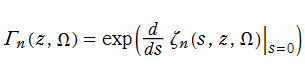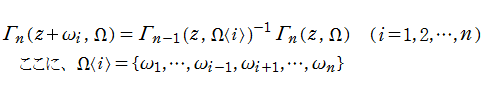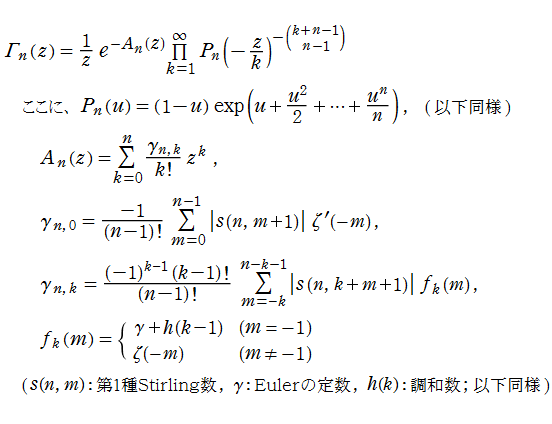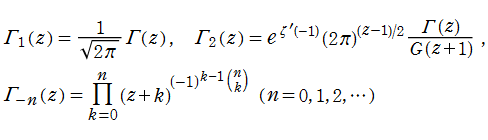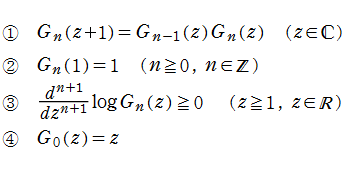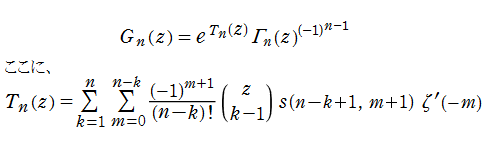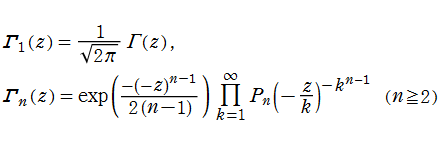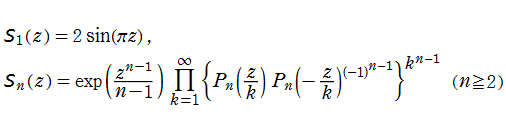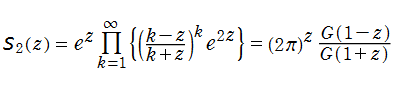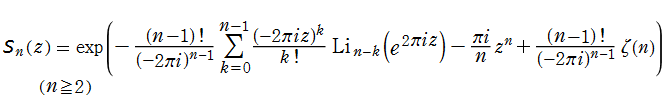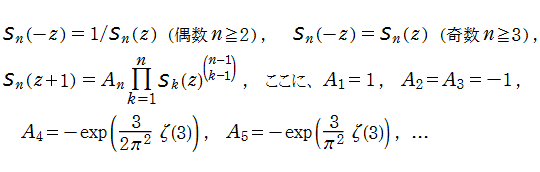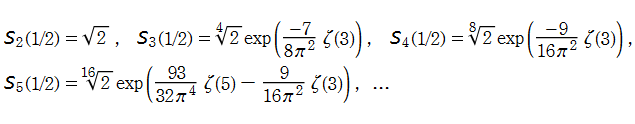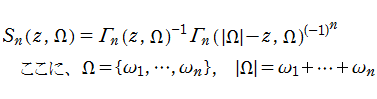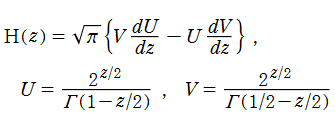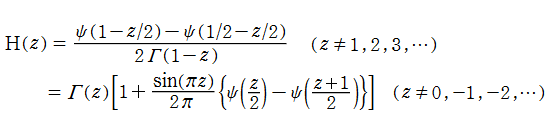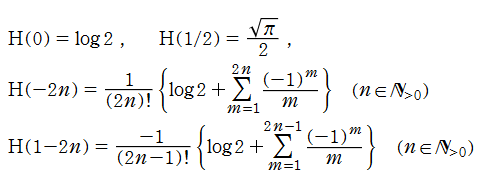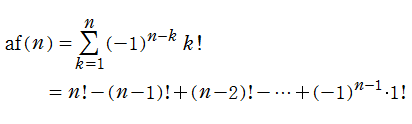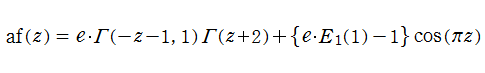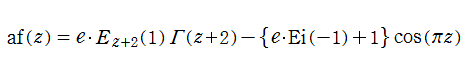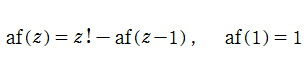特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
ガンマ関数(階乗関数)
ガンマ関数
日:ガンマ関数,Γ関数英:Gamma function,仏:Fonction gamma,独:Gammafunktion
日:階乗関数
英:Factorial function,仏:Fonction factorielle,独:Fakultätsfunktion
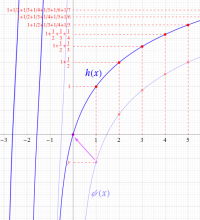
ガンマ関数は、L. Euler によって1729年に発見された。その動機は、通常は自然数
Euler は、まず極限表示式、およびこれを式変形して得られる無限乗積
によってガンマ関数を定義し、後年、それが次の積分表示式にも一致することを示した。
現在、この定積分は「第2種 Euler 積分」と呼ばれ、ガンマ関数の定義と言えばまずこれを挙げる人が多い。(この他に「第1種 Euler 積分」という定積分もあって、これは後述のベータ関数のことを指す。)
ガンマ関数は、関数等式
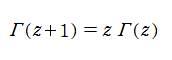
が従うので、階乗の連続化になっている※1。この他にも、「相補公式」 (または 「相反公式」 等) と呼ばれる関数等式
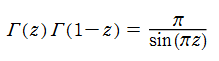
など、ガンマ関数は様々な関係式を満たす。特に、相補公式または倍数公式から、
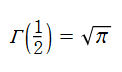
現在では、A. M. Legendre が初めて用いた記号
複素解析関数としてのガンマ関数は、引数が正でない整数のときに1位の極をもつ有理型関数で、零点を持っていない。よって、ガンマ関数の逆数は超越整関数である。このことから、Weierstrassの標準形と呼ばれる表示
が可能である。ここに現れた
一方で、前述の相補公式およびそれを式変形すると得られる公式
は、ガンマ関数が初等関数に近いことを示している。実際、(日本に以前あった) 大学教養課程で最初に現れる特殊関数がガンマ関数であったことも、それが基礎的な関数と見なされていた証である。用途から見ても、ガンマ関数は直接単独で用いられる事例よりも、むしろ三角関数や指数関数のように間接的に用いられることが多い。例えば、超幾何関数を冪級数展開したときの係数はガンマ関数で表わされる他、ゼータ関数の対称的な関数等式における関与などが挙げられる。しかし、確率・統計学や差分法など、ガンマ関数が単独で多用される応用分野もいくつかある。
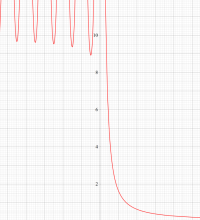
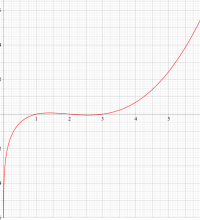
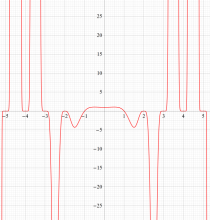
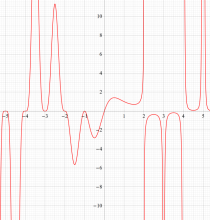
それらの応用分野では、大きな正数に対する階乗・ガンマ関数値がしばしば必要となり、数値計算法の発達に寄与することとなった。漸近級数展開式
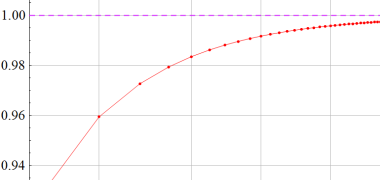
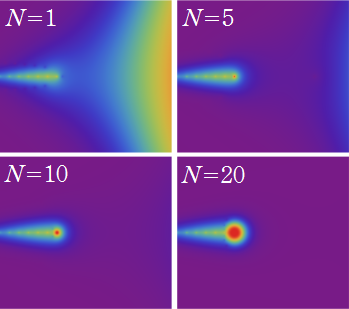
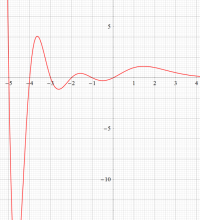
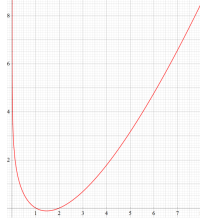
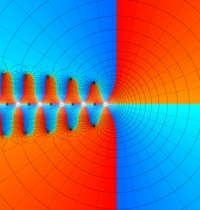
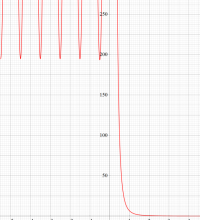
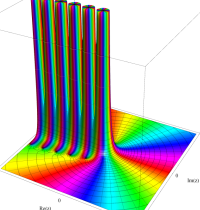
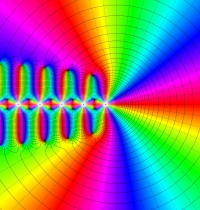
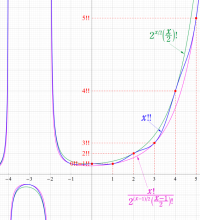
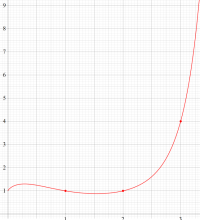
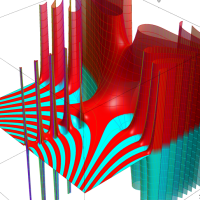
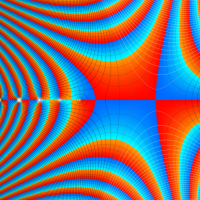
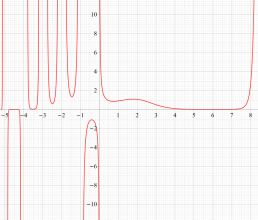
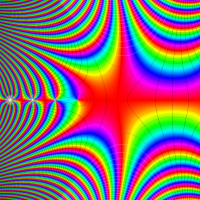
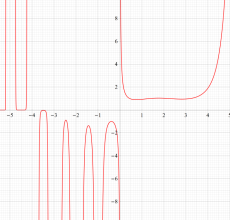
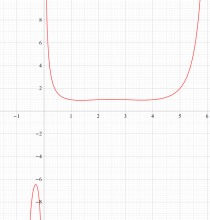
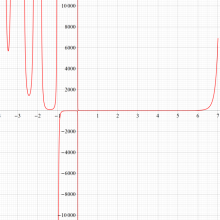
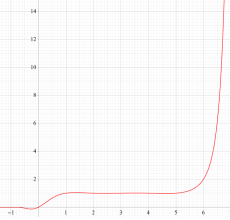
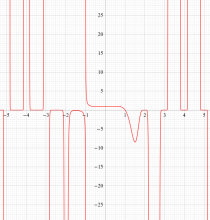
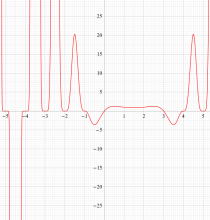
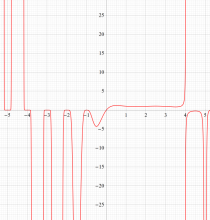
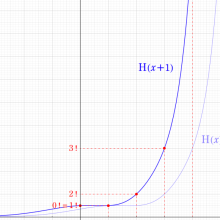
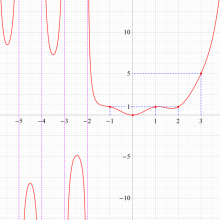
もその一例であって、これは絶対値が大きい複素変数のガンマ関数を計算する際にも重宝する※2。歴史的に前後するが、J. Stirling によって1730年に求められた 「Stirling の公式」
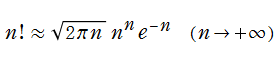
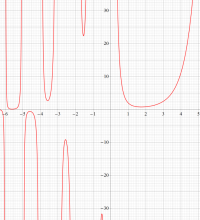
図:Stirling の公式と階乗との比
【註記】
※1:厳密には、さらに第3の条件
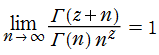 を課せば、この関数等式を満たす (階乗の連続化に相応しい) 関数が、ガンマ関数に限定される。実解析学の立場から見た (実変数
を課せば、この関数等式を満たす (階乗の連続化に相応しい) 関数が、ガンマ関数に限定される。実解析学の立場から見た (実変数 の) ガンマ関数の限定条件としては、
の) ガンマ関数の限定条件としては、
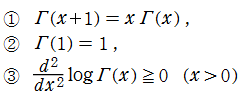 がある。これは現在「Bohr - Mollerup の定理」と呼ばれている。
がある。これは現在「Bohr - Mollerup の定理」と呼ばれている。
なお、Bohr - Mollerup の定理③を満たさない "階乗の連続化" の例を、独自研究の頁に掲載しています。
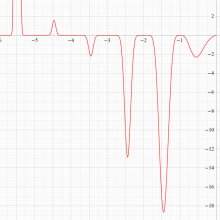
※2:理論上この漸近級数は、無限遠点でしか収束しない。実際、加算項数が増えるにしたがって、原点中心の円形発散領域が次第に大きくなる。しかし、加算項数を適当な有限個で止めると、(実用上は許容できる程度に) 良い近似が得られる (次図を参照)。このような発散級数は 「Poincaré 型の級数展開式」 と呼ばれる。
※1:厳密には、さらに第3の条件
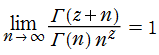
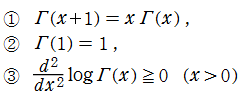
なお、Bohr - Mollerup の定理③を満たさない "階乗の連続化" の例を、独自研究の頁に掲載しています。
※2:理論上この漸近級数は、無限遠点でしか収束しない。実際、加算項数が増えるにしたがって、原点中心の円形発散領域が次第に大きくなる。しかし、加算項数を適当な有限個で止めると、(実用上は許容できる程度に) 良い近似が得られる (次図を参照)。このような発散級数は 「Poincaré 型の級数展開式」 と呼ばれる。
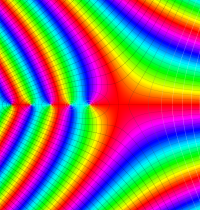
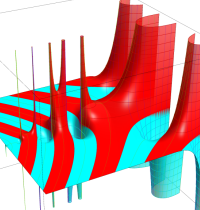
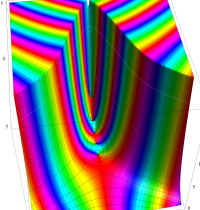
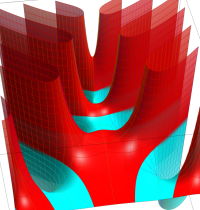
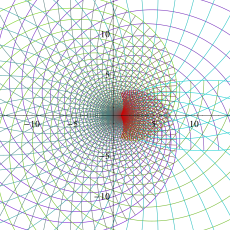
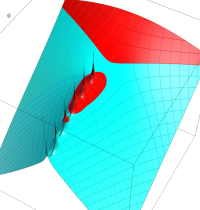
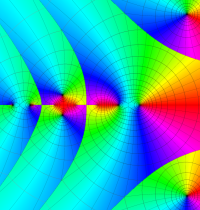
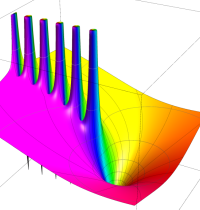
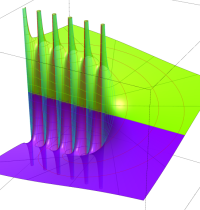
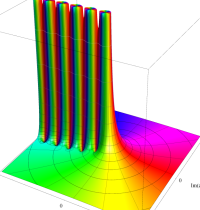
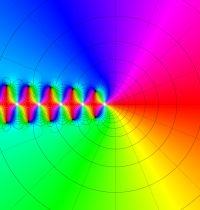
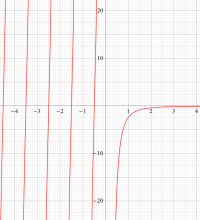
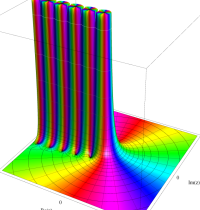
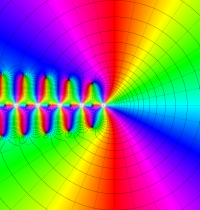
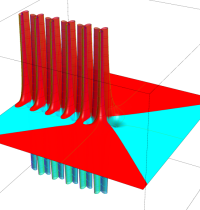
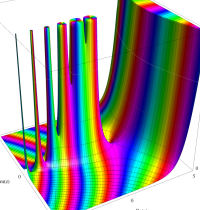
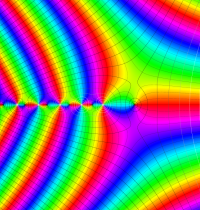
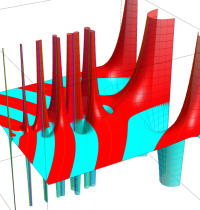
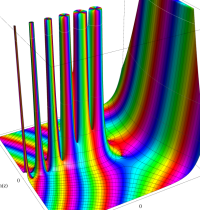
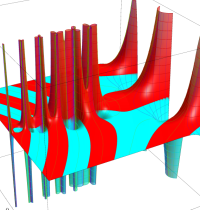
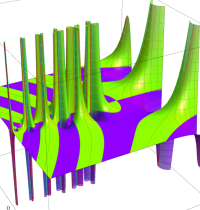
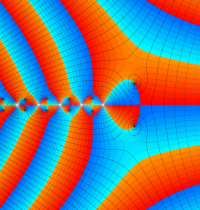
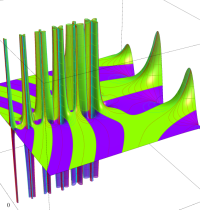
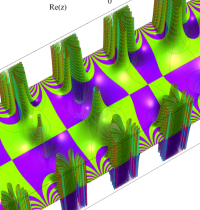
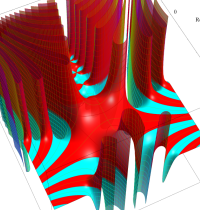
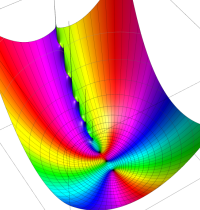
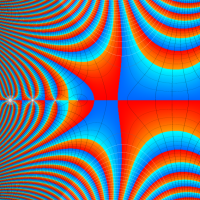
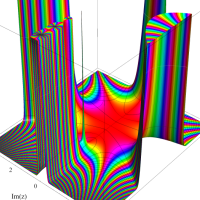
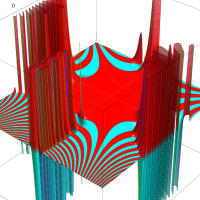
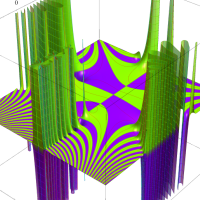
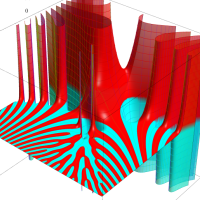
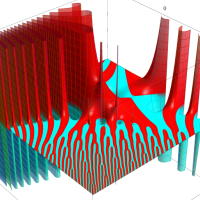
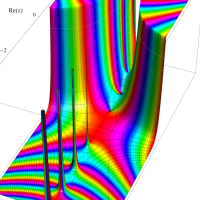
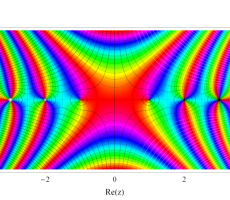
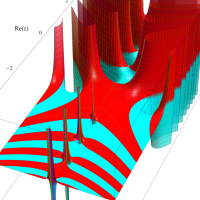
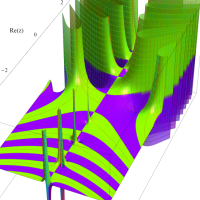
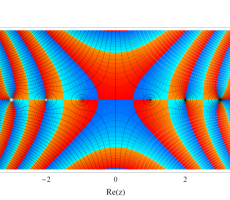
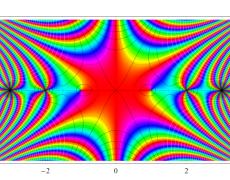
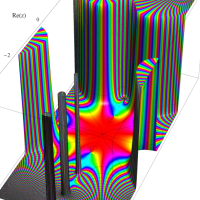
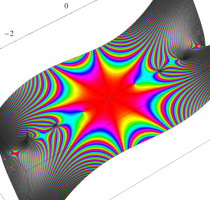
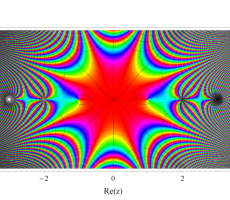
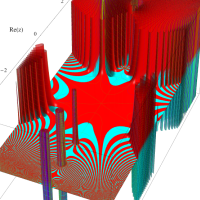
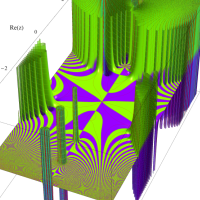
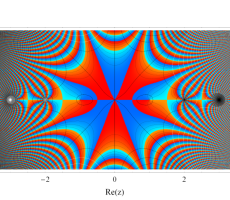
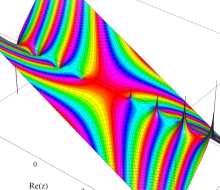
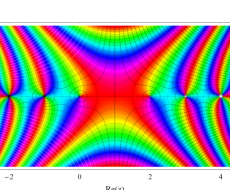
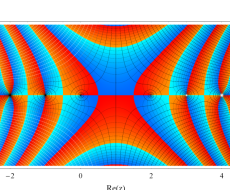
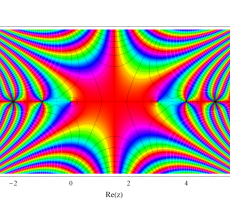
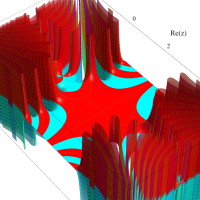
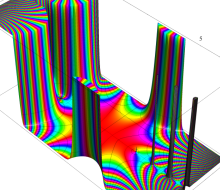
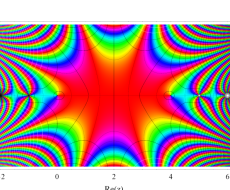
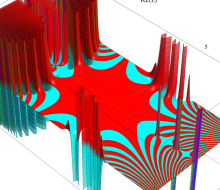
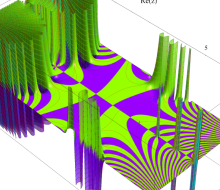
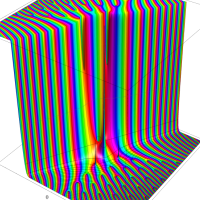
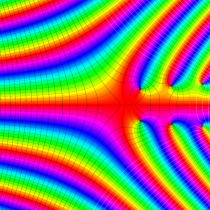
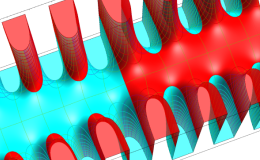
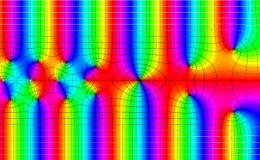
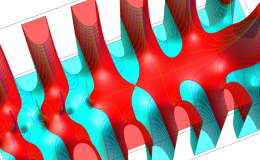
複素変数のガンマ関数のグラフ。6番目は、鞍点で絶対値の等高線が結節点 (自己交差する点) になることを示したグラフである。これと同等のグラフが、柴垣 和三雄 著 「ガンマ函数の理論と応用 (附表, 小数第6位まで有効な複素変数のガンマ函数表)」 (1952年 岩波書店) の99~100頁にある。
ガンマ関数
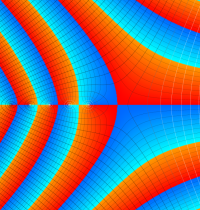
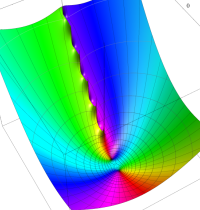
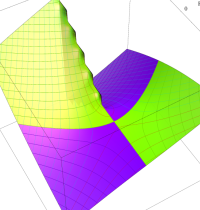
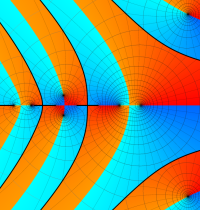
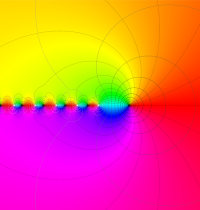
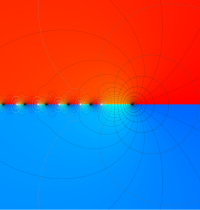
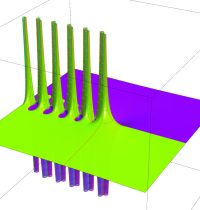
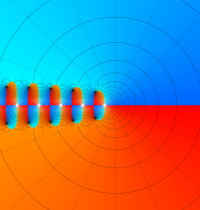
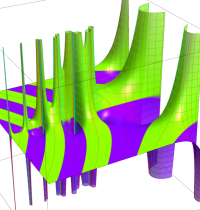
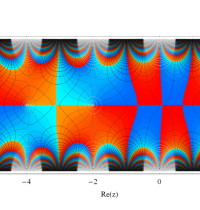
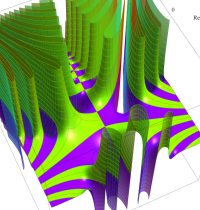
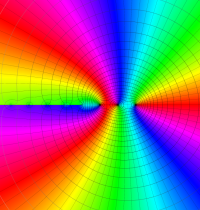
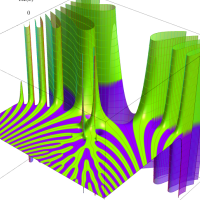
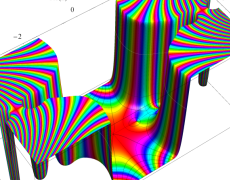
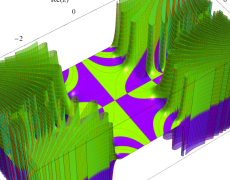
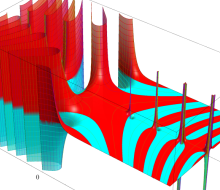
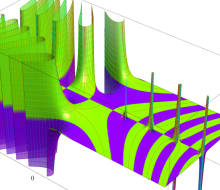
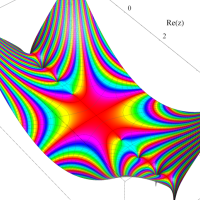
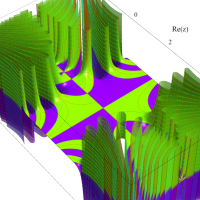
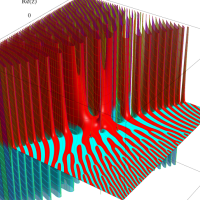
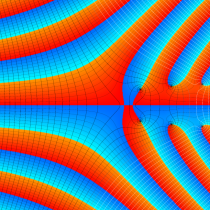
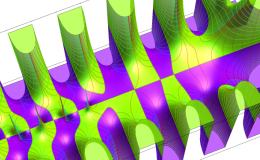
複素変数のガンマ関数の逆数のグラフ。これは、無限遠点を除く複素平面上で特異点を持たない。つまり超越整関数である。
ガンマ関数の逆数
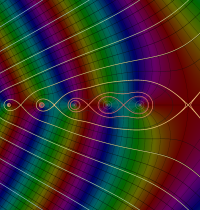
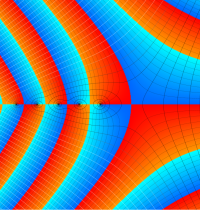
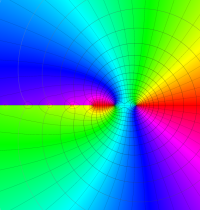
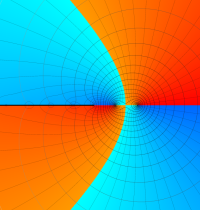
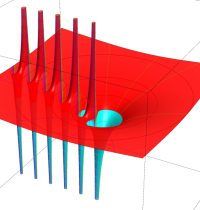
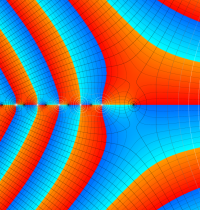
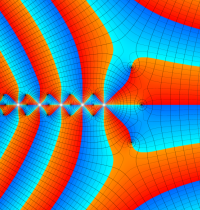
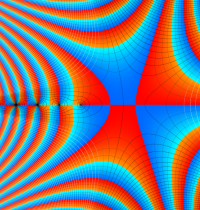
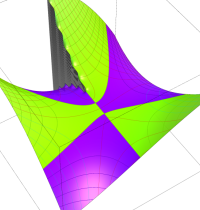
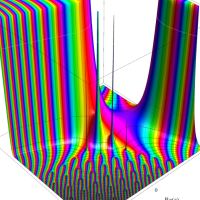
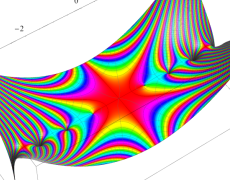
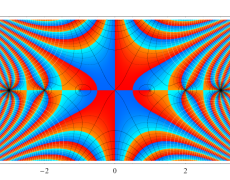
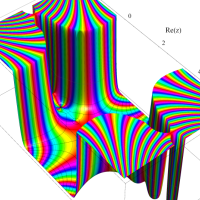
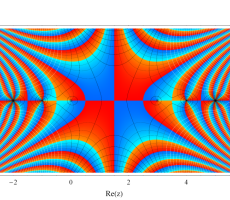
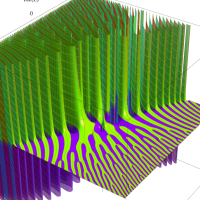
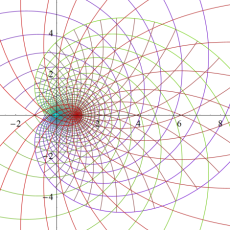
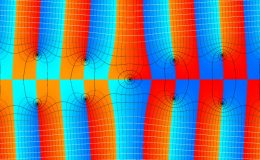
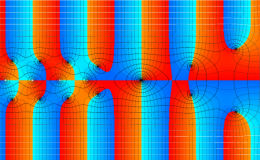
複素変数のガンマ関数の対数のグラフ。複素平面上では、対数に由来する多価性を持つ。ここでは、単純にガンマ関数の対数をとるだけではなく、合理的な解析接続が施された関数を採用している。この定義は、Barnes のG関数、K関数などで有用になる。
もし、単純に
ポリガンマ関数
日:ポリガンマ関数,多Γ関数英:Polygamma function,仏:Fonction polygamma,独:Polygammafunktion
ディガンマ関数は、ガンマ関数を対数微分したものであって、このディガンマ関数を逐次微分したものを習慣上ギリシャ数詞を冠して、トリガンマ関数、テトラガンマ関数、ペンタガンマ関数…のように呼ぶ。これらを総称してポリガンマ関数と呼び、
と定義する。Legendre (1809年), C. F. Gauss (1810年) 等、多くの数学者がこの関数の研究を手掛けた。
ポリガンマ関数は関数等式
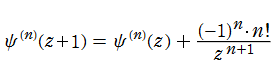
が従うので、調和数の連続化になっている。例えば、
となる。またこの事から、ポリガンマ関数は対数関数や分数関数の差分化に相当するものと捉えられる。
明らかに、ポリガンマ関数の基本的な性質は、ガンマ関数のそれを対数微分および逐次微分すれば得られる。例えば、相補公式は
となり、多倍数公式は
となることが分かる。ここで
なる非自明な結果が導かれる。ポリガンマ関数の数値計算でも、ガンマ関数の漸近級数展開式を項別に対数・逐次微分して得られる級数が便利である。
複素解析関数としてのポリガンマ関数は、定義域が正でない整数のときに極をもつ有理型関数で、その極の位数はディ、トリ、テトラとなるに従い、1位、2位、3位…となる。またこのほか零点も持っている。ガンマ関数同様、いかなる代数的微分方程式の解にもならない。
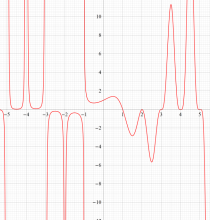
ディガンマ関数は Riemann ゼータ関数
ポリガンマ関数は、応用上ガンマ関数と似た目的で用いられるほか、特に各種の分数の無限和を評価する際に用いられる。
なお、ディガンマ関数は
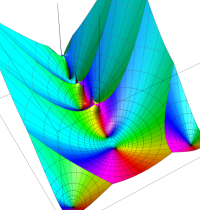
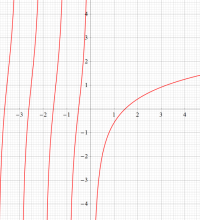
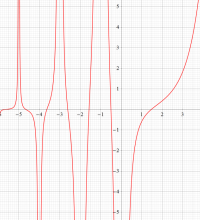
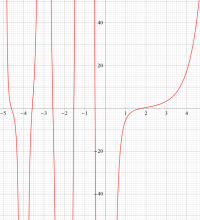
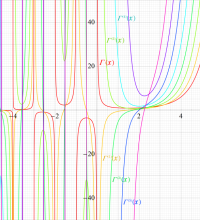
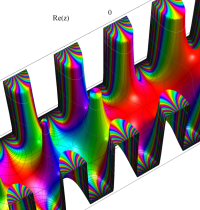
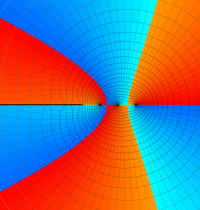
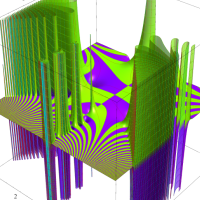
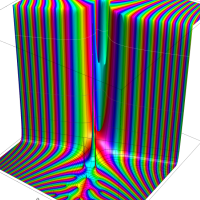
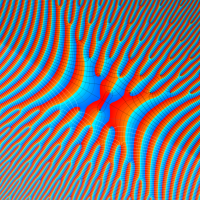
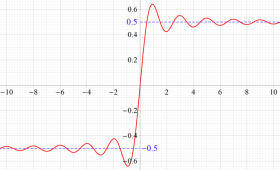
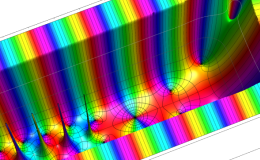
複素変数のディガンマ関数のグラフ。
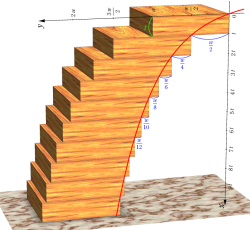
積木を最大の迫り出し幅で重ねる方法。調和級数は無限大に発散するので、迫り出し幅は理論上いくらでも大きくできる。
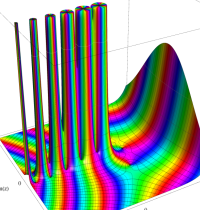
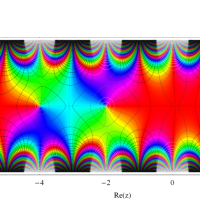
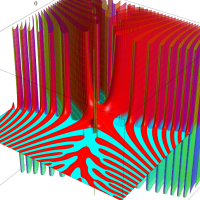
複素変数のトリガンマ関数のグラフ。
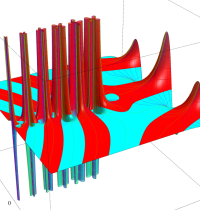
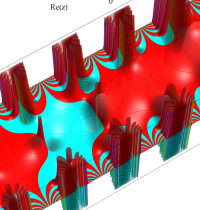
複素変数のテトラガンマ関数のグラフ。
複素変数のペンタガンマ関数のグラフ。
ガンマ関数の導関数
ガンマ関数の導関数は、ポリガンマ関数を用いて次のように表わされる。また、ガンマ関数の導関数は、積分表示式
によっても表わすことができる。
複素解析関数としてのガンマ関数の
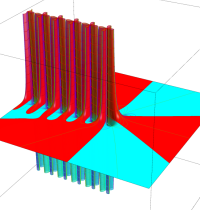
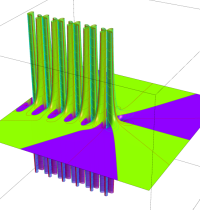
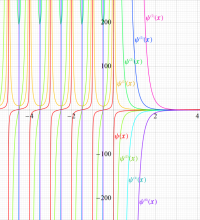
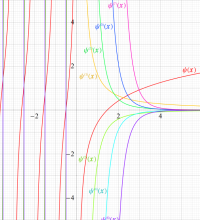
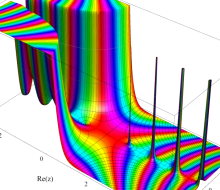
複素変数のガンマ関数の導関数のグラフ。
複素変数のガンマ関数の2位導関数のグラフ。
複素変数のガンマ関数の3位導関数のグラフ。
ベータ関数
日:ベータ関数英:Beta function,仏:Fonction bêta,独:Betafunktion
ベータ関数は二変数関数であって、二つのガンマ関数の積を一つの積分として表わそうとすると自然に出てくる。この定積分は、しばしば 「第1種 Euler 積分」 とも呼ばれ、
と表わされる。ベータ関数は Euler (1730年),Legendre (1826年) 等の研究を経て、現在に至っている。第1種 Euler 積分の名称は Legendre によるが、ベータ関数の名称は J. Binet (1839年) に始まる。
置換積分を施して、上記とは異なるベータ関数の積分表示式が多数得られている。特に、
などがよく知られている。
ベータ関数はガンマ関数との間に、
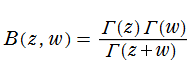
は、ガンマ関数の無限積表示式から容易に導ける。
また、ベータ関数は無限級数
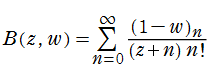
二項係数の連続化は、ベータ関数の逆数によって表わすことができる。(次のグラフを参照。)
ベータ関数はその積分表示式の形から、初等代数関数の積分値を評価する際によく現れる。それらの積分は、種々の図形の面積や体積を計算するときにも重宝する。なお同じ理由により、和算の 「円理」 と呼ばれる分野でも、ベータ関数に相当する値の数表が作成されていた※1。(ただし、和算には関数という概念は無い。)
ガンマ関数と同様に、ベータ関数は確率論や統計学での応用事例が多い。また、物理学者 G. Veneziano は、核子内部の「強い力」の性質がベータ関数で表現できることを発見したが、その式は同時に弦(String)の構造を記述していることにも気付いた。ここに弦理論が創始され、後年これは超弦理論へと発展することとなる。
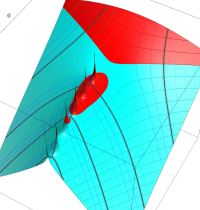
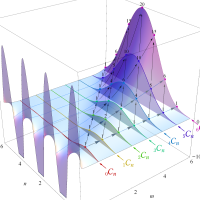
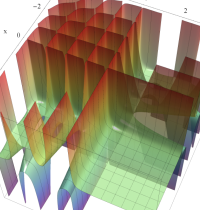
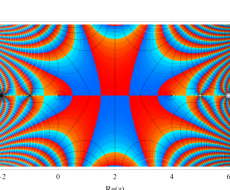
実2変数のベータ関数のグラフ。(値域の座標を逆双曲線正弦関数で圧縮した場合。)
二重階乗関数
日:二重階乗関数英:Double factorial function,仏:Fonction double factorielle,独:Doppel fakultätsfunktion
自然数
を二重階乗関数という。複素変数のときは、ガンマ関数を用いて
と表わされる。
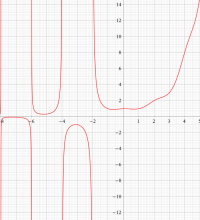
複素解析関数としての二重階乗関数は、負の偶数点において1位の極を持つが、全体的なグラフ形状は、ガンマ関数とかなり異なる。
純粋数学、物理学等での二重階乗関数の応用は、専ら変数が自然数のときである。冪級数の係数によく現れる。
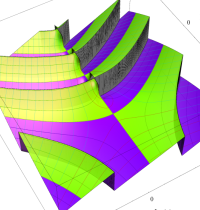
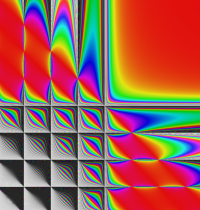
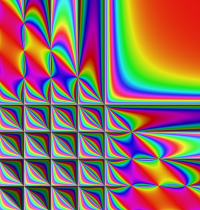
複素変数の二重階乗関数のグラフ。定義式に含まれる指数関数と余弦関数の合成関数が、ガンマ関数のグラフとの違いを生む原因となっている。
Barnes のG関数
日:BarnesのG関数,バーンズのG関数英:Barnes G-function,仏:Fonction G de Barnes,独:Barnessche G-funktion
Barnes のG関数はガンマ関数を拡張したもので、E. W. Barnes によって定義された。なお、この関数は多重ガンマ関数と呼ばれることもあるが、当サイトではこの名称を、後述するさらに広い意味の関数に対して用いることとする。
Barnes のG関数は、関数等式
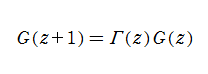
となる。このため、正の実軸上において Barnes のG関数の値はガンマ関数よりも急激に増大する。
複素関数としての Barnes のG関数は超越整関数であり、無限積表示式
で表わされる。この式から、正でない整数点
Barnes のG関数は、積分表示式
を持つ (ここに、
物理学等での Barnes のG関数の応用は、ガンマ関数に比べると少ない。一方、純粋数学では Barnes のG関数のみならず、さらにこれを一般化した関数が数多く定義され、ガンマ関数系の拡張理論が展開されている。後述の多重ガンマ関数はその代表的な例である。
この他に、Barnes のG関数を用いて、K関数
が定義されている。この関数は、関数等式
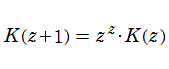
となる。このことから、
K関数も、積分表示式
を持ち、その類似性から Barnes のG関数と同クラスであることが分かる。
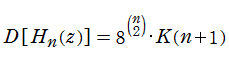
Barnes のG関数、並びにK関数の特殊値として、
が知られている。ここに、
【註記】
※1:この公式は、http://reference.wolfram.com/language/ref/Hyperfactorial.html に掲載がある。
なお、多項式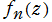 の
の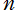 次 (最高次) 定係数を
次 (最高次) 定係数を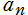 、
、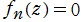 の解を
の解を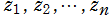 とするとき、判別式
とするとき、判別式![D[f n (z)]](siki_spec010/gamma4411.png) は次のようになる。
は次のようになる。
※1:この公式は、http://reference.wolfram.com/language/ref/Hyperfactorial.html に掲載がある。
なお、多項式
複素変数の Barnes のG関数のグラフ。これは、無限遠点を除く複素平面上で特異点を持たない。つまり超越整関数である。
Barnes のG関数
複素変数の Barnes のG関数の対数のグラフ。ガンマ関数と同様の分枝切断線を採用する。
複素変数のK関数のグラフ。
多重ガンマ関数
日:多重ガンマ関数英:Multiple gamma function,仏: Multiple fonction gamma,独:Vielfach-Gammafunktion
多重ガンマ関数の研究は19世紀後半から現れ始め、H. Kinkelin (1860年), O. Hölder (1886年) 等が先駆者として知られている※1。Barnes も独立に、前述のG関数の導入とその拡張を研究 (1900~1904年) したが、現在では Barnes によって得られた結果が一般に定着している。
Barnes は始めに、現在 「Barnes の多重ゼータ関数 (多重 Hurwitz ゼータ関数)」 と呼ばれている関数
を導入し、これを用いて 「Barnes の多重ガンマ関数」 を
と定義した (単純に、前掲の多重ゼータ関数の Dirichlet 級数を代入するだけでは収束しない無限乗積になる。この定義式の意味は、例えば前掲の積分表示式や、Euler - Maclaurin 和公式を適用した多重ゼータ関数を代入する等の方法によって、解析接続が成されていると解釈する) 。
Barnes の多重ガンマ関数は、複素平面全体において一価有理型関数で種々の公式を満たす。例えば、
が成り立つ。また後述のように、Barnes の多重ガンマ関数に対する相補公式から 「Barnes の多重三角関数」 が定義される。
Barnes の多重ガンマ関数
また、整数
多重ガンマ関数は、上記の Barnes による定義の他にもいくつかの異なる定義がある。Vignéras の多重ガンマ関数
つまり、Vignéras の多重ガンマ関数は
Vignéras の多重ガンマ関数は、Barnes の多重ガンマ関数
また、黒川信重は1991年に、後述の多重三角関数
を定義した (同氏はこれを 「素朴な定義」 と称している。以下ではこの関数を 「黒川の多重ガンマ関数」 と呼ぶが、残念ながら現在ではほとんど扱われることがない。よって、ここでもグラフの描画は省略する) 。
多重ガンマ関数は、各種のゼータ関数やその導関数の特殊値および Stirling 数の表示、モジュラー形式との関連等で近年注目されており、多重ゼータ関数・多重三角関数とともに、数論や組合わせ論での重要度が増しつつある。また、これらの関数は既に多変数化や q-類似などにも拡張されていて、全貌が掴めないほど種類が多くなっているため、21世紀初頭における特殊関数の新しい鉱脈のような趣を呈している。
【註記】
※1 : 特に Kinkelin は、多重ガンマ関数の主要な性質のほとんどを導き出していたが、現在では何故かこの業績が忘れ去られている。この点は、黒川信重 著 「現代三角関数論 (岩波書店 2013年)」 で指摘されている。なお、同著は多重ガンマ関数・多重三角関数の詳細な情報源として欠かせない書籍である。
※2 : この公式は、小野寺 一浩の論文「Weierstrass product representations of multiple gamma and sine functions, Kodai Mathematical Journal 32 (2009) p.77-90」に基づいています。より詳しい情報はこれを参照願います。
※1 : 特に Kinkelin は、多重ガンマ関数の主要な性質のほとんどを導き出していたが、現在では何故かこの業績が忘れ去られている。この点は、黒川信重 著 「現代三角関数論 (岩波書店 2013年)」 で指摘されている。なお、同著は多重ガンマ関数・多重三角関数の詳細な情報源として欠かせない書籍である。
※2 : この公式は、小野寺 一浩の論文「Weierstrass product representations of multiple gamma and sine functions, Kodai Mathematical Journal 32 (2009) p.77-90」に基づいています。より詳しい情報はこれを参照願います。
複素変数の Barnes の多重ガンマ関数
実変数の Barnes の多重ガンマ関数
複素変数の Barnes の多重ガンマ関数
実変数の Barnes の多重ガンマ関数
複素変数の Barnes の多重ガンマ関数
実変数の Vignéras の多重ガンマ関数
複素変数の Vignéras の多重ガンマ関数
実変数の Vignéras の多重ガンマ関数
複素変数の Vignéras の多重ガンマ関数
複素変数の Barnes の二重ガンマ関数
多重三角関数
日:多重三角関数(多重正弦関数)英:Multiple sine function,仏: Multiple fonction sinus,独:Vielfach-Sinusfunktion
ガンマ関数の相補公式から三角関数が生じるように、各種の多重ガンマ関数に対しても類似の手順を踏むと、三角関数の拡張版が得られる。現在これらは多重三角関数と呼ばれており、いくつかの定義が知られている。1991年に黒川信重は、前述の 「黒川の多重ガンマ関数」 に対してこれを考えて、「黒川の多重三角関数」
を導入した。これは、Hölder によって1886年に導入されていた 「Hölder の二重三角関数」
を特別な場合として含み、積分表示式
でも定義される。また
と表わすこともできる。
黒川の多重三角関数は、対称性や擬周期性
を満たし、
と表わされる。
複素関数としての黒川の多重三角関数は、
さらに一般的な場合として、Barnes の多重ガンマ関数に対しても 「Barnes の多重三角関数」
が定義される。この関数は Barnes 以来、多くの数学者が同等の定義を行うが、特に新谷卓郎によるモジュラー形式との関係の研究、黒川信重による Selberg ゼータ関数のガンマ関数因子に関する研究など、数論への応用を経て次第に注目されるようになり、現在では多重三角関数と言えば大抵この関数を指すようになっている。
このうち、周期が
複素変数の黒川の多重三角関数
実変数の黒川の多重三角関数
複素変数の黒川の多重三角関数
実変数の黒川の多重三角関数
複素変数の黒川の多重三角関数
複素変数の Barnes の多重三角関数
実変数の Barnes の多重三角関数
複素変数の Barnes の多重三角関数
実変数の Barnes の多重三角関数
複素変数の Barnes の多重三角関数
複素変数の Barnes の二重三角関数
アニメーション(13.00MB)
複素変数の Barnes の二重三角関数
ガンマ関数に関連する関数
ここでは、やや出現頻度が低いけれども、ガンマ関数の拡張や亜種としてよく知られている関数をいくつか取り挙げる。【Hadamard のガンマ関数】
ガンマ関数が階乗の連続化に最も相応しいことは、種々の理由から了承される。例えば、Bohr - Mollerup の定理③は、ガンマ関数のグラフが階乗の補間曲線として滑らかである (対数凸である) ことを示しているし、超幾何関数系の理論に度々現れる階乗が即座にガンマ関数に置き換えられるのは、それが関数等式
しかしながら、非整数に対する階乗も、整数に対するそれと同じ関数等式に従うであろうという推測は、逆に、論理的な必然性が無いと見ることもできる※1。J. S. Hadamard はその観点に立って、具体的な関数
を1894年に定義した。現在、これは 「Hadamard のガンマ関数」 と呼ばれている※2。不定値を避けるため、
を使い分ける定義を採用した方が、数値計算等で便利である。
Hadamard のガンマ関数は、関数等式および階乗との関係式
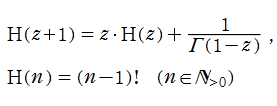
Hadamard のガンマ関数に対する相補公式は、
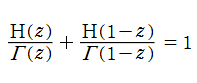
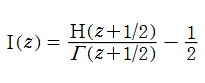
Hadamard のガンマ関数は、特殊値
を持っている。
【交互階乗関数】
自然数
は、ガンマ関数, 不完全ガンマ関数, 積分指数関数等を用いた、
によって連続化できる。複素変数
等である。ここに、
交互階乗関数は、関数等式
を満たす。これは、元々の交互階乗が満たす漸化式と全く同じ形である。また、特殊値
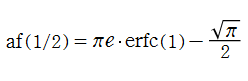
定義式に含まれる
【註記】
※1:それゆえ慎重を期して、階乗の連続化関数は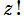 で表記されることが少なかったのかもしれない。
で表記されることが少なかったのかもしれない。
※2:Hadamard が用いた関数記号は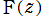 であったが、現在では主流となっていない。
であったが、現在では主流となっていない。
※1:それゆえ慎重を期して、階乗の連続化関数は
※2:Hadamard が用いた関数記号は
複素変数の Hadamard のガンマ関数
Hadamard のガンマ関数
アニメーション(11.20MB)
Eisenstein 級数に現れるガンマ関数因子を Hadamard のガンマ関数に置き換えて、
とした関数のグラフ。Eisenstein 級数の頁にあるアニメーションとの違いを確認する。
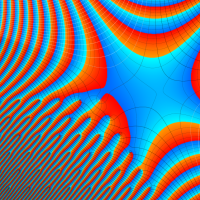
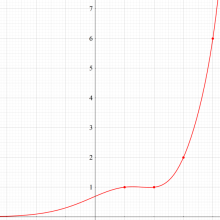
複素変数の関数
複素変数の交互階乗関数