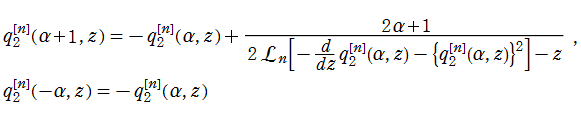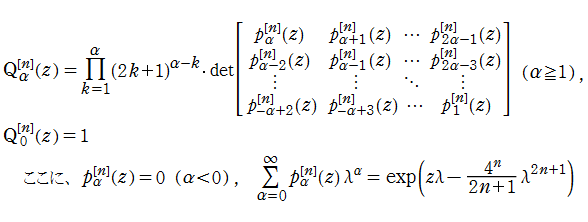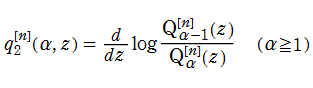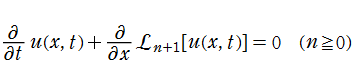特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
高階微分方程式の Painlevé 超越関数
第1a種 Chazy 超越関数
P. Painlevé 等が2階の代数的な非線形常微分方程式に対して得た成果、すなわち、その方程式の解が動く特異点として極のみを持つ(Painlevé 性を持つ)場合を具体的に特定・分類したことを、に拡張することは、既に Painlevé の時代から着手されていたが、現在でも解決されていない。C. É. Picard は、2階以上の一般的な代数的非線形常微分方程式に対する分類を試みていたが、Painlevé 性を持たない場合をも含めて考察したため困難を極め、達成できなかった。
3階の場合で Painlevé 性を持つような方程式のいくつかを、1910~1911年に J. Chazy が例示している※1。特にそのうち、第3種,第12種 Chazy 方程式の解は自然境界を持ち、複素平面の一部分を存在領域とする保型関数を含み、しかもその自然境界自体が動くことを示した。これは2階以下の場合には見られない現象で、このことが3階以上の分類を難しくしている一因とも考えられている。第9種,第10種 Chazy 方程式の解は、種数2の Abel 関数と楕円関数を合成した関数で表わされるとの指摘がある。Chazy 方程式の中では、保型関数との絡みもあって第3種,第12種に関する研究が多いようである。
Chazy の例示した方程式のいくつかは、係数関数として任意の楕円関数,Lamé 関数等を含むものがあり、これらの解の計算は非常に困難と思われる。そこで、ここではこのような例は扱わず、第3種,第9種,第10種,および第12種も前述の理由から扱わない。さらに実際に計算を試みて、その結果が二重周期関数となる第7種も扱わない※2。第1f 種は、簡単な式変形によって解が楕円関数または第1種 Painlevé 超越関数となることが明らかなので、これも扱わない。結局、ここで取り扱う Chazy 方程式の解である「Chazy 超越関数」は、第1a種,第1b種,第1c種,第1d種,第1e種,第8種,第13a種,および第13b種である。
ここではさらに他の例として、U. Muğan & F. Jrad 「Non-polynomial third order equations which pass the Painlevé test」(Zeitschrift für Naturforschung 59A (2004) p.163-180) の165頁および166頁にある3例を、独自に「第1種,第2種,および第3種 Muğan - Jrad 超越関数」と称して取り扱う (このような研究はまだ新しく、微分方程式自体に標準的な名称がない)。
このように、現在まで世界中の数学者によって Painlevé 性を持つ非線形常微分方程式の例が多数発見されているが、3階以上の場合についての分類は完成しておらず、各階の方程式の最小個数は知られていない。
第1a種 Chazy 方程式
の解を、ここでは具体的に
である。なお、統一的な関数記号はまだ存在していないため、この頁での記号はすべて独自に設定したものである。
また、この頁の関数は主に、W. Fair と Y. L. Luke による連分数近似法を拡張した方法によって計算した。
【註記】
※1 J. Chazy の原論文の他、比較的新しい下記論文で Chazy 方程式の種類を確認することができる。
Y. Y. Bagderina 「Equivalence of Third-Order Ordinary Differential Equations to Chazy Equations I –XIII」, Studies in Applied Mathematics, No.120 (2008) p.293-332.
※2 「Mathematica 関連」に掲載しているコード「Chazy.m」は、第3種,第7種,第9種,第10種,および第12種についても搭載しています。(ただし、第3種,第12種の自然境界近傍は不正確です。)
※1 J. Chazy の原論文の他、比較的新しい下記論文で Chazy 方程式の種類を確認することができる。
Y. Y. Bagderina 「Equivalence of Third-Order Ordinary Differential Equations to Chazy Equations I –XIII」, Studies in Applied Mathematics, No.120 (2008) p.293-332.
※2 「Mathematica 関連」に掲載しているコード「Chazy.m」は、第3種,第7種,第9種,第10種,および第12種についても搭載しています。(ただし、第3種,第12種の自然境界近傍は不正確です。)
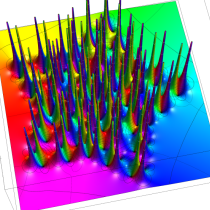
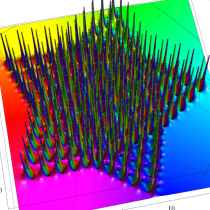
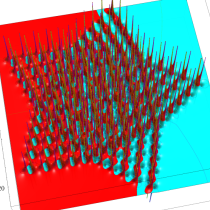
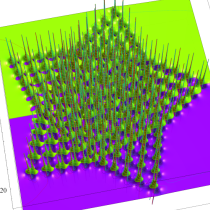
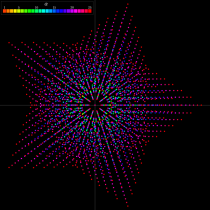
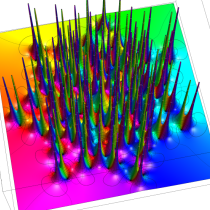
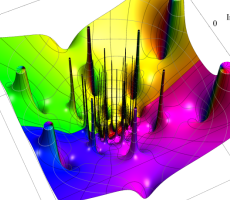
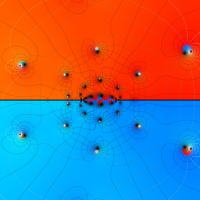
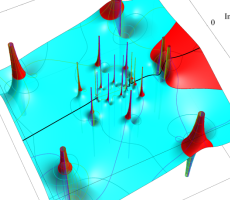
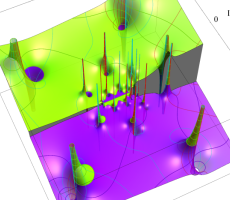
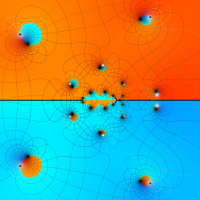
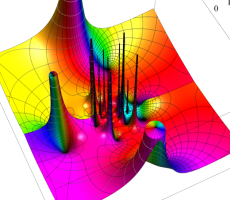
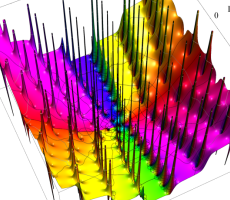
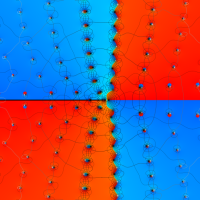
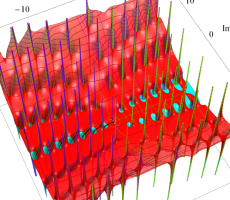
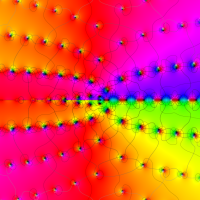
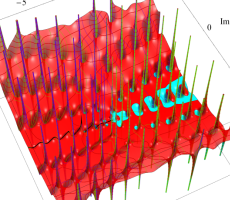
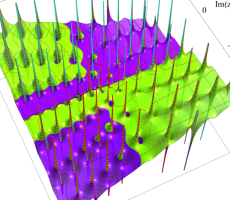
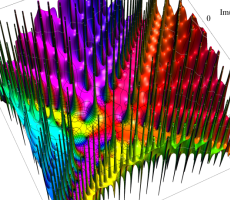
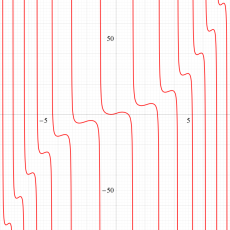
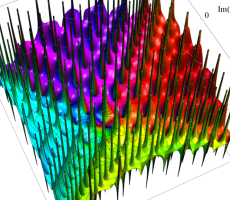
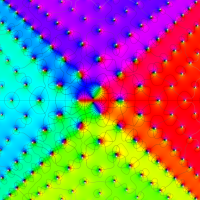
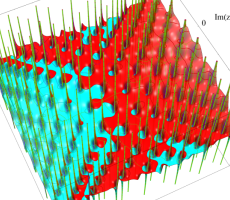
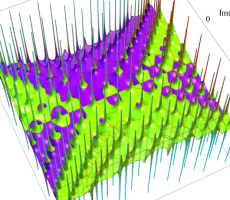
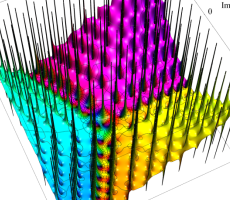
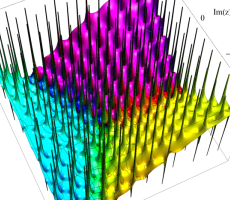
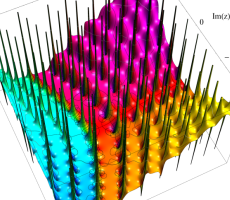
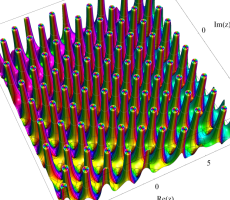
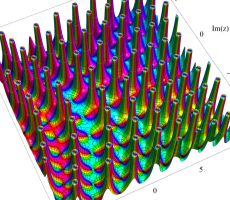
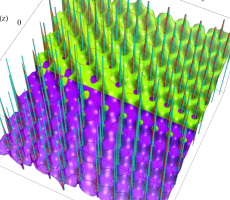
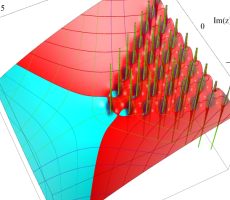
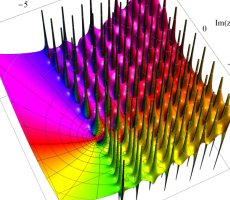
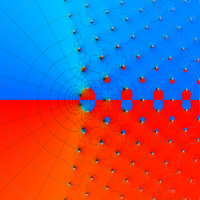
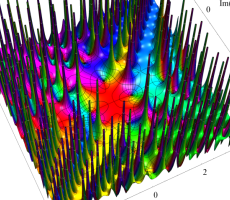
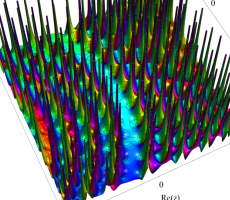
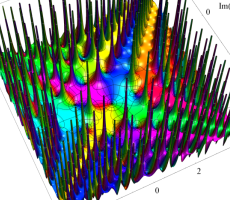
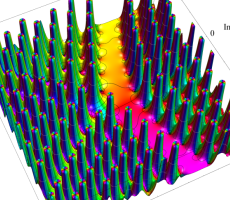
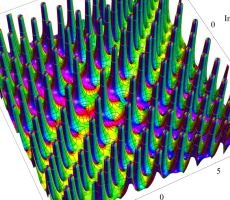
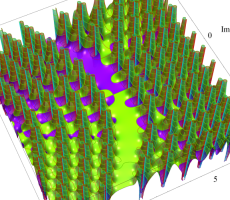
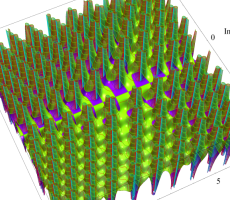
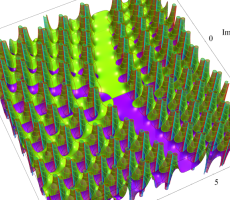
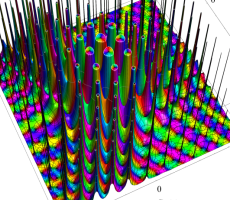
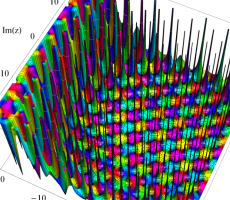
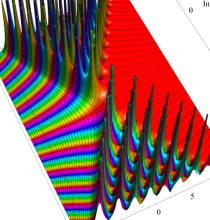
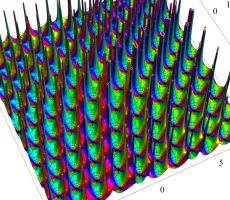
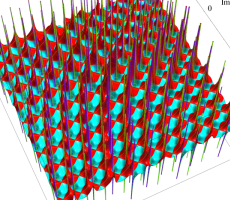
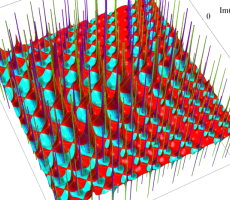
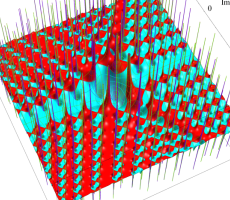
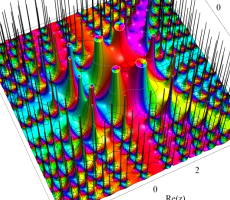
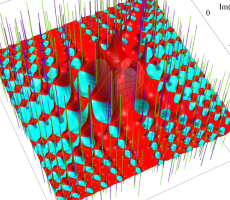
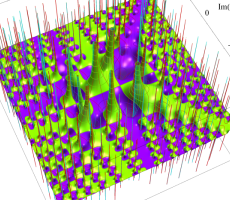
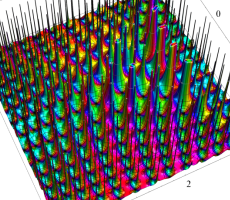
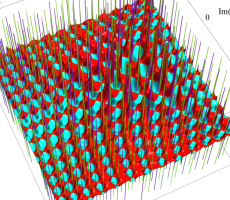
複素変数の第1a種 Chazy 超越関数
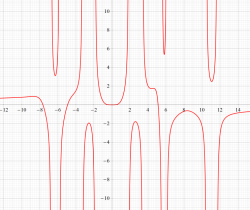
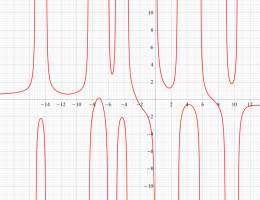
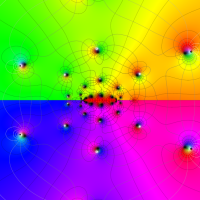
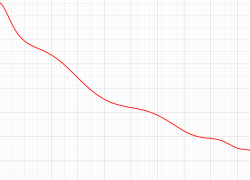
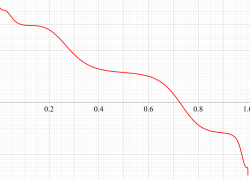
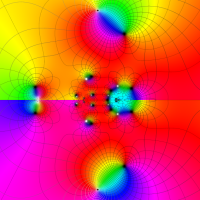
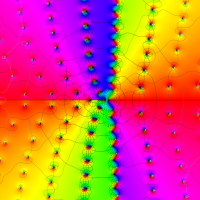
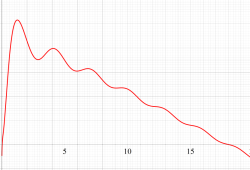
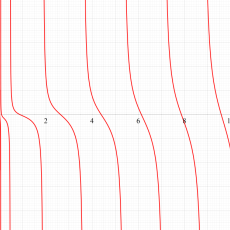
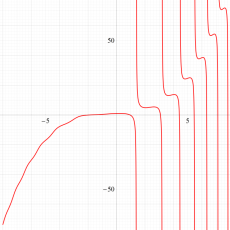
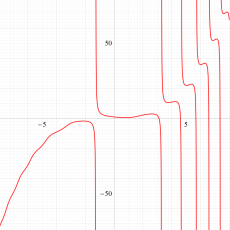
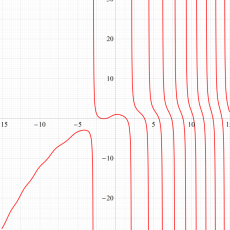
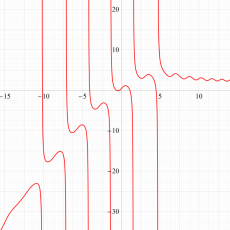
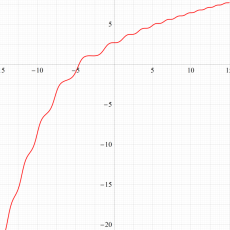
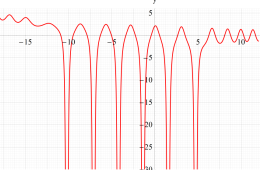
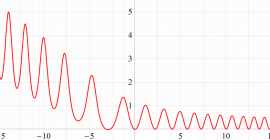
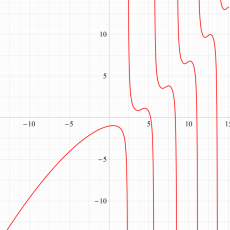
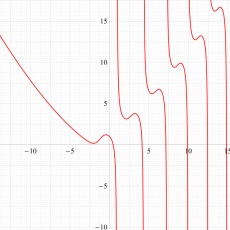
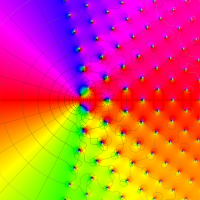
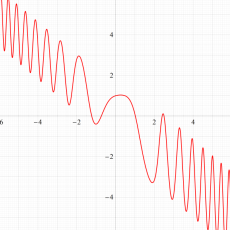
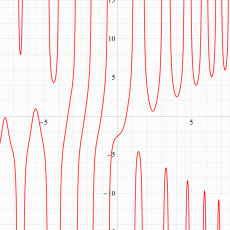
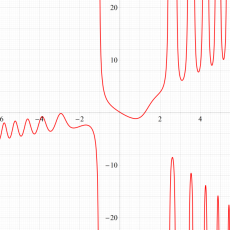
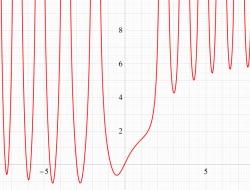
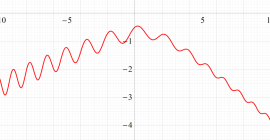
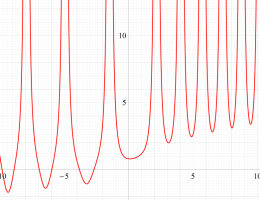
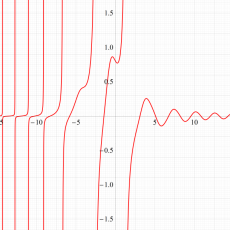
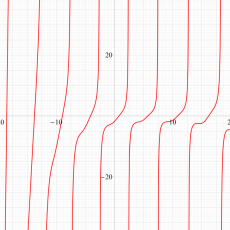
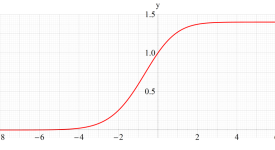
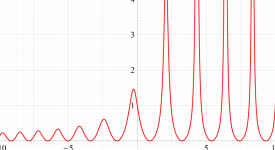
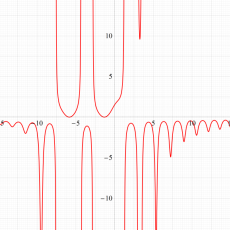
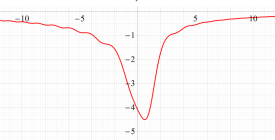
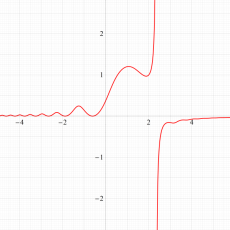
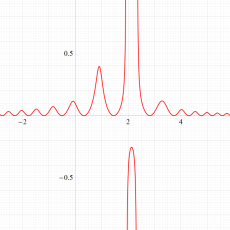
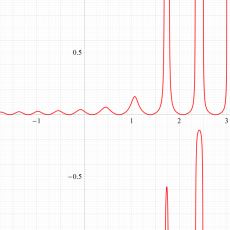
実変数の第1a種 Chazy 超越関数
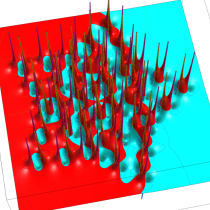
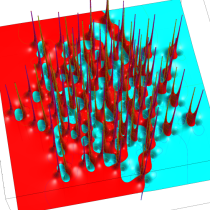
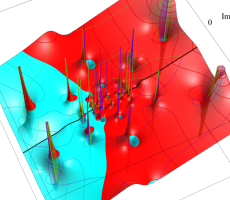
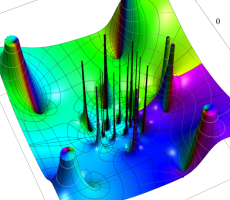
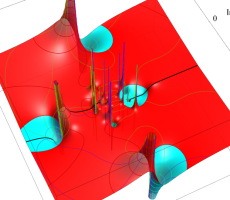
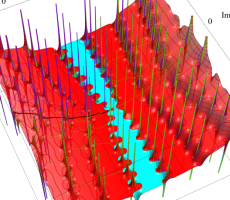
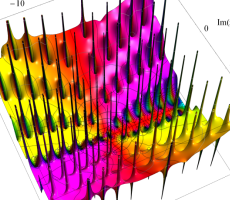
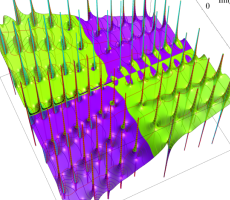
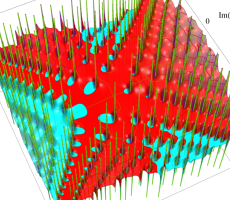
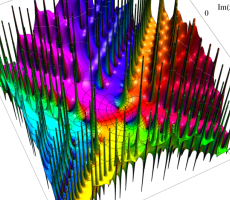
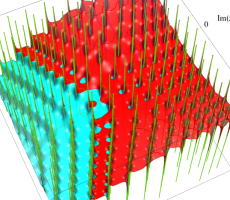
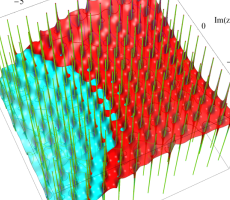
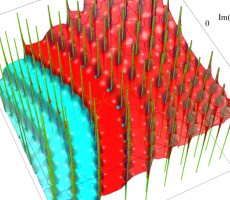
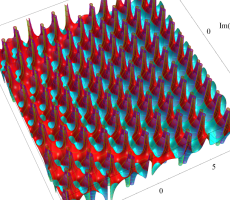
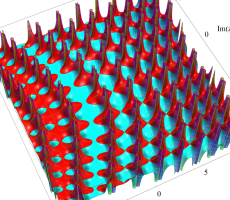
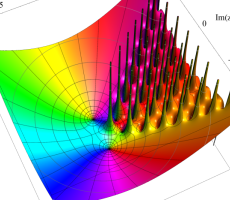
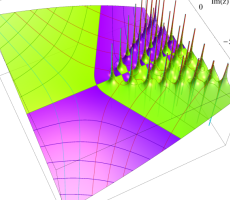
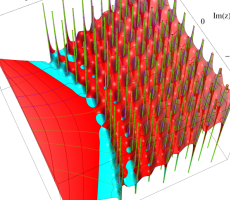
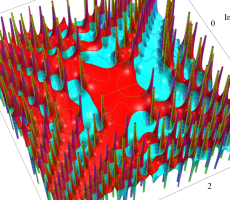
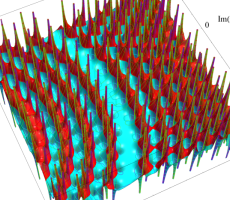
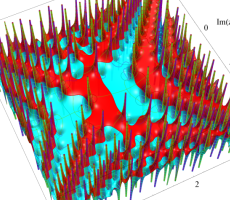
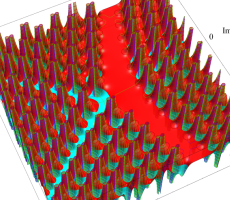
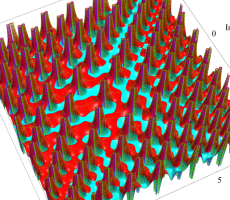
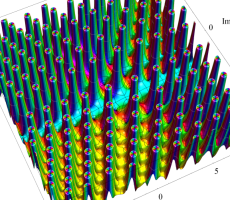
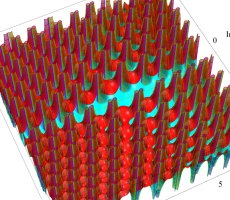
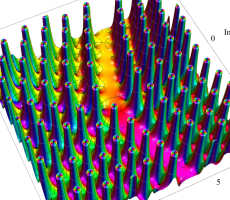
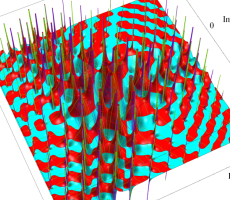
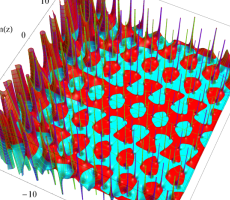
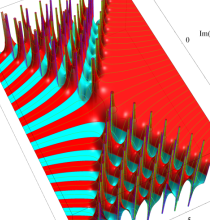
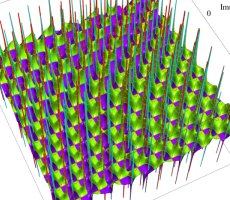
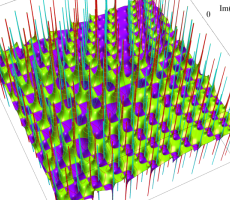
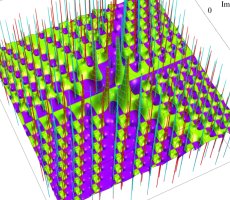
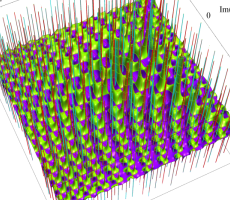
複素変数の第1a種 Chazy 超越関数
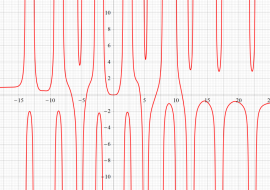
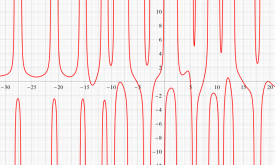
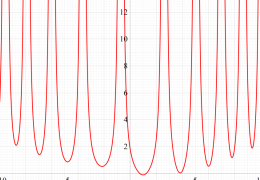
実変数の第1a種 Chazy 超越関数
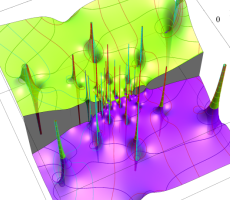
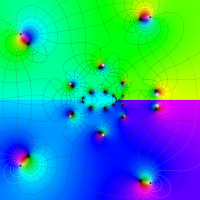
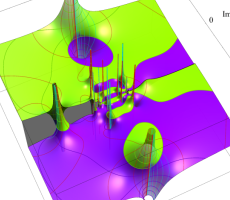
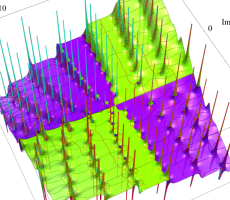
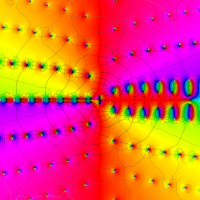
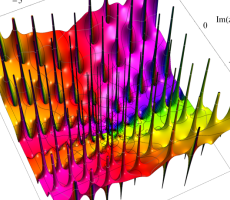
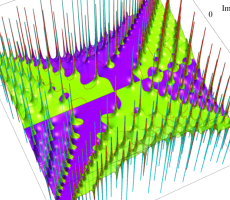
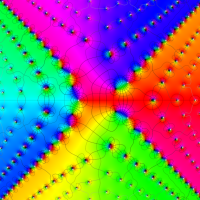
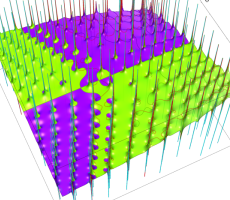
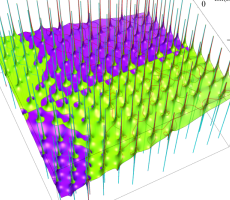
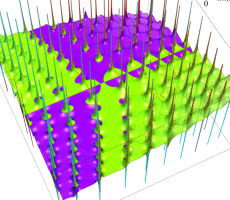
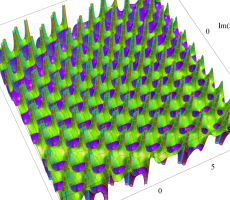
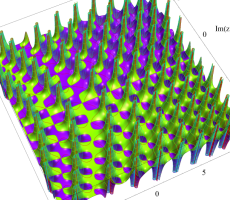
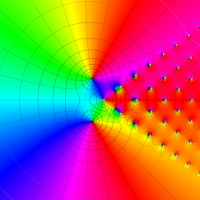
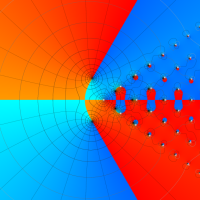
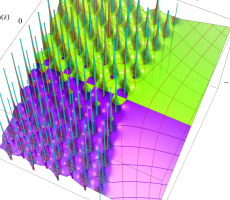
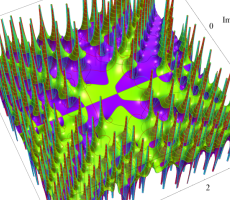
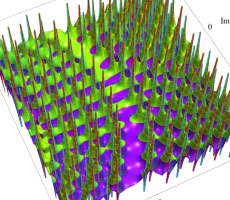
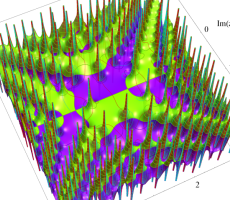
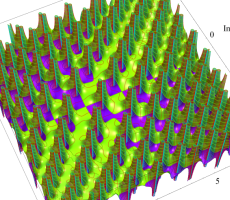
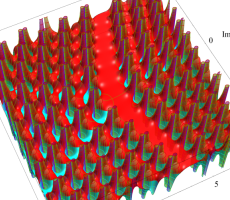
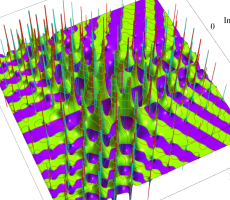
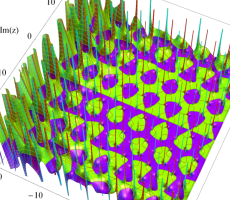
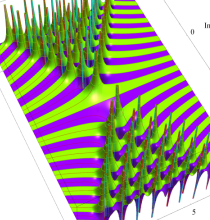
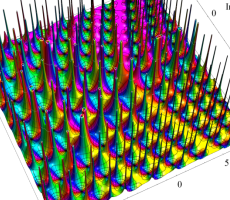
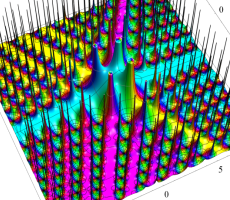
複素変数の第1a種 Chazy 超越関数
第1b種 Chazy 超越関数
第1b種 Chazy 方程式の解を、ここでは具体的に
である。
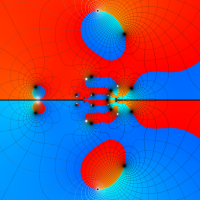
複素変数の第1b種 Chazy 超越関数
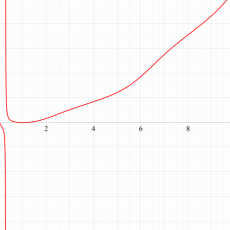
実変数の第1b種 Chazy 超越関数
複素変数の第1b種 Chazy 超越関数
実変数の第1b種 Chazy 超越関数
複素変数の第1b種 Chazy 超越関数
第1c種 Chazy 超越関数
第1c種 Chazy 方程式の解を、ここでは具体的に
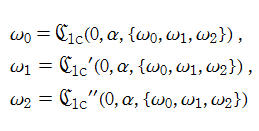
複素変数の第1c種 Chazy 超越関数
実変数の第1c種 Chazy 超越関数
複素変数の第1c種 Chazy 超越関数
実変数の第1c種 Chazy 超越関数
複素変数の第1c種 Chazy 超越関数
第1d種 Chazy 超越関数
第1d種 Chazy 方程式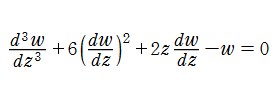
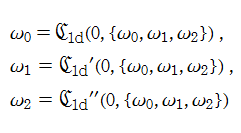
また、第1d種 Chazy 方程式において両辺を微分したのち、変換
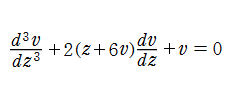
となる。
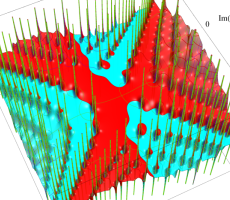
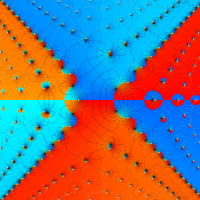
複素変数の第1d種 Chazy 超越関数
実変数の第1d種 Chazy 超越関数
複素変数の第1d種 Chazy 超越関数
実変数の第1d種 Chazy 超越関数
複素変数の第1d種 Chazy 超越関数
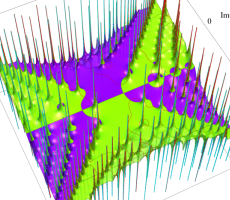
複素変数の第1d種 Chazy 超越関数の導関数
実変数の第1d種 Chazy 超越関数の導関数
複素変数の第1d種 Chazy 超越関数の導関数
第1e種 Chazy 超越関数
第1e種 Chazy 方程式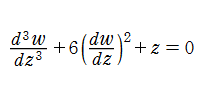
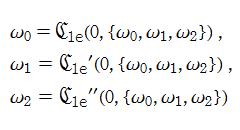
の関係にある。
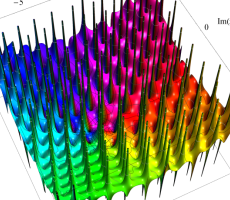
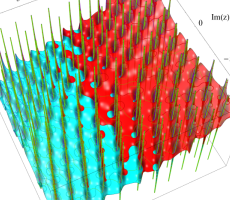
複素変数の第1e種 Chazy 超越関数
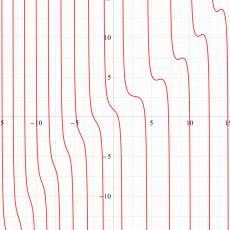
実変数の第1e種 Chazy 超越関数
複素変数の第1e種 Chazy 超越関数
実変数の第1e種 Chazy 超越関数
複素変数の第1e種 Chazy 超越関数
第8種 Chazy 超越関数
第8種 Chazy 方程式の解を、ここでは具体的に
である。
複素変数の第8種 Chazy 超越関数
実変数の第8種 Chazy 超越関数
複素変数の第8種 Chazy 超越関数
実変数の第8種 Chazy 超越関数
複素変数の第8種 Chazy 超越関数
第13a種 Chazy 超越関数
第13a種 Chazy 方程式の解を、ここでは具体的に
である。
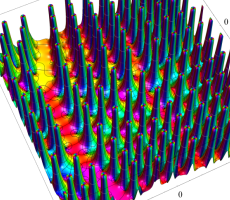
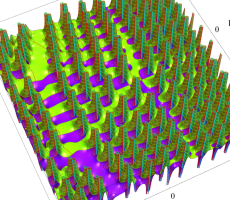
複素変数の第13a種 Chazy 超越関数
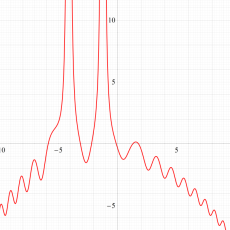
実変数の第13a種 Chazy 超越関数
複素変数の第13a種 Chazy 超越関数
実変数の第13a種 Chazy 超越関数
複素変数の第13a種 Chazy 超越関数
第13b種 Chazy 超越関数
第13b種 Chazy 方程式の解を、ここでは具体的に
である。
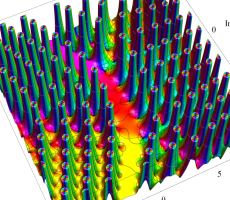
複素変数の第13b種 Chazy 超越関数
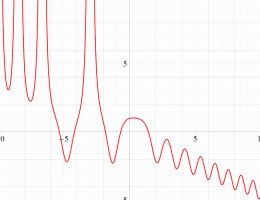
実変数の第13b種 Chazy 超越関数
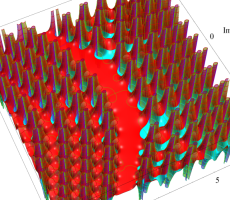
複素変数の第13b種 Chazy 超越関数
実変数の第13b種 Chazy 超越関数
複素変数の第13b種 Chazy 超越関数
第1種 Muğan - Jrad 超越関数
U. Muğan と F. Jrad による非線形常微分方程式の解を、ここでは具体的に
である。特別な場合の第1種 Muğan - Jrad 超越関数は、対数微分すると第2種 Painlevé 超越関数になる。すなわち
の関係にある。
複素変数の第1種 Muğan - Jrad 超越関数
実変数の第1種 Muğan - Jrad 超越関数
複素変数の第1種 Muğan - Jrad 超越関数
実変数の第1種 Muğan - Jrad 超越関数
複素変数の第1種 Muğan - Jrad 超越関数
第2種 Muğan - Jrad 超越関数
U. Muğan と F. Jrad による非線形常微分方程式の解を、ここでは具体的に
である。
複素変数の第2種 Muğan - Jrad 超越関数
実変数の第2種 Muğan - Jrad 超越関数
複素変数の第2種 Muğan - Jrad 超越関数
実変数の第2種 Muğan - Jrad 超越関数
複素変数の第2種 Muğan - Jrad 超越関数
第3種 Muğan - Jrad 超越関数
U. Muğan と F. Jrad による非線形常微分方程式の解を、ここでは具体的に
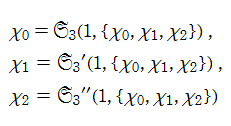
複素変数の第3種 Muğan - Jrad 超越関数
実変数の第3種 Muğan - Jrad 超越関数
複素変数の第3種 Muğan - Jrad 超越関数
実変数の第3種 Muğan - Jrad 超越関数
複素変数の第3種 Muğan - Jrad 超越関数
高階 Painlevé 方程式の古典関数解
第2種 Painlevé 方程式に相当する、より高階の代数的な非線形常微分方程式で、その解が Painlevé 性を持つものとして、
が知られている。ここに、任意関数
で定義される。
によって求めることができる。特に
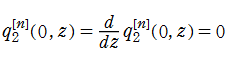
の対数微分
としても表わすことができる。これらの関数も、Yablonskii - Vorob'ev 多項式の場合と同様に、組合わせ論等での応用が知られている。
以上の結果はすべて、
の系列は、Korteweg - de Vries 方程式の階層 (KdV hierarchy) となっている。
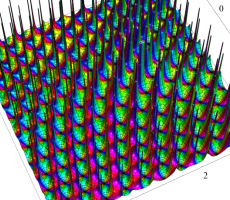
4階第2種 Painlevé 方程式の有理関数解
4階第2種 Painlevé 方程式の有理関数解
4階第2種 Painlevé 方程式の有理関数解
4階第2種 Painlevé 方程式の有理関数解
(前述の対数微分形から、有理関数解の分母は必ず2個の4階 Yablonskii - Vorob'ev 多項式の積になる。以下同様。)
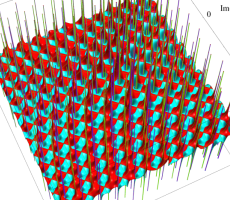
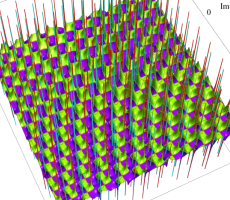
6階第2種 Painlevé 方程式の有理関数解
6階第2種 Painlevé 方程式の有理関数解
6階第2種 Painlevé 方程式の有理関数解
6階第2種 Painlevé 方程式の有理関数解

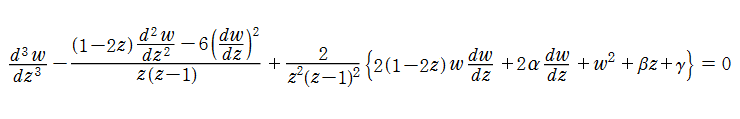
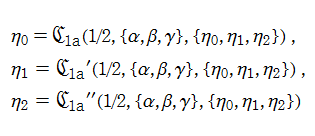
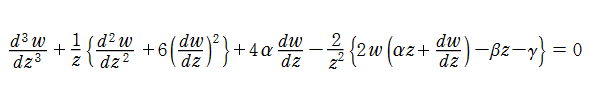
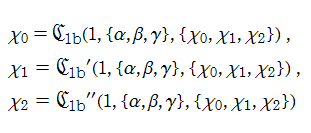


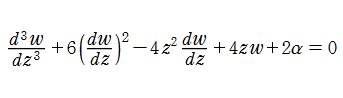



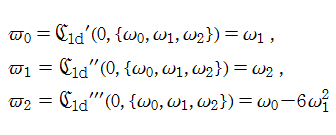










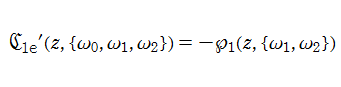


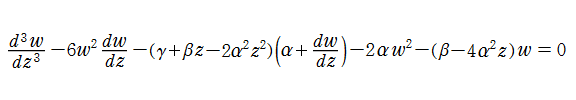
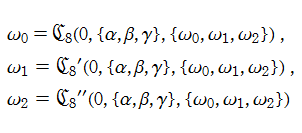






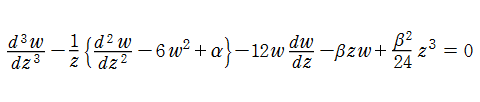
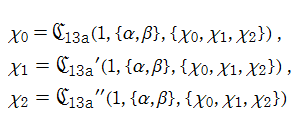








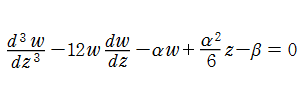
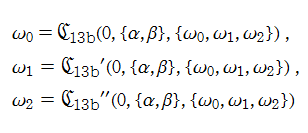






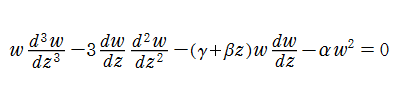
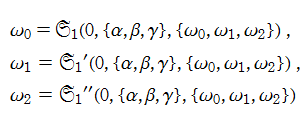
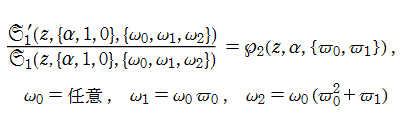






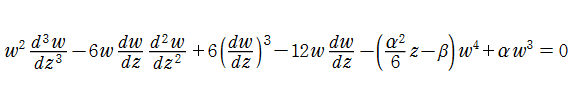
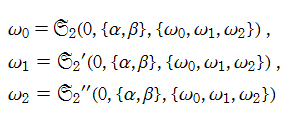






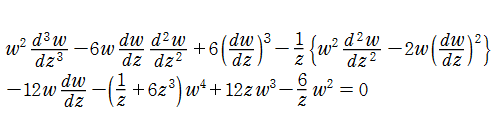






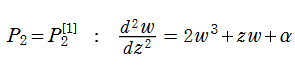
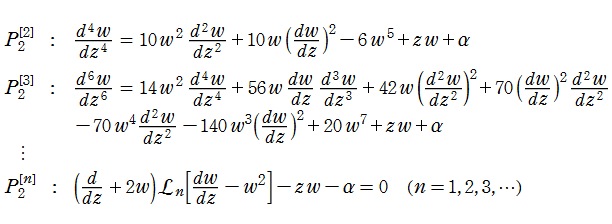
![微分演算子Ln[u]の定義](siki_spec330/3painleve1280.png)