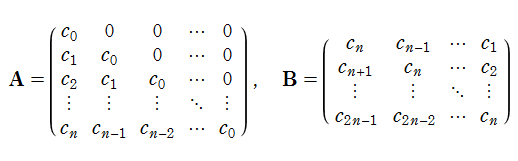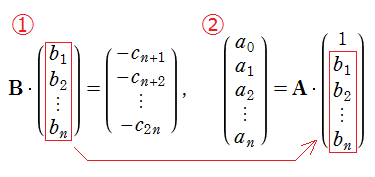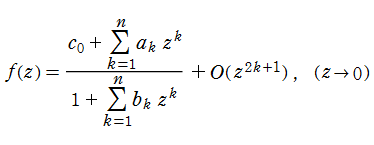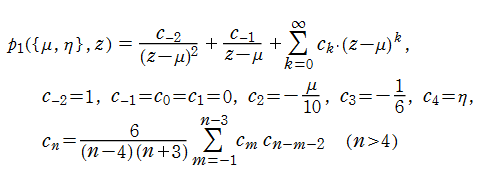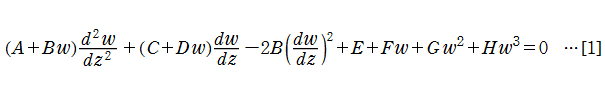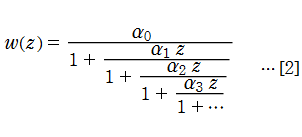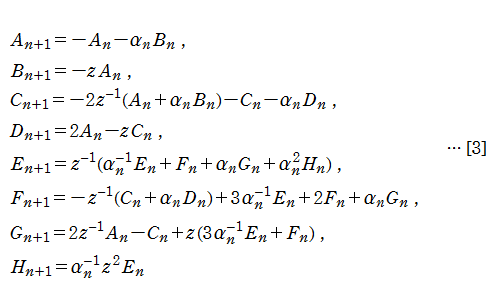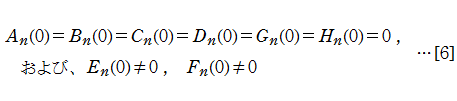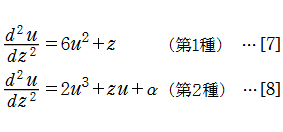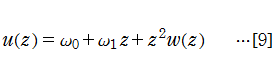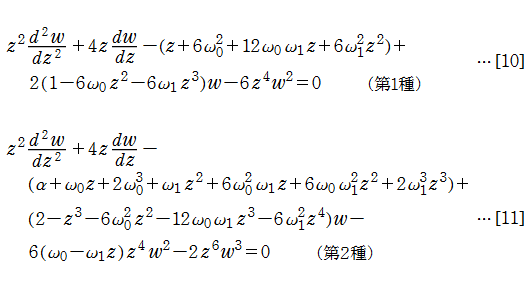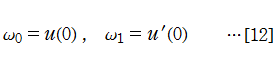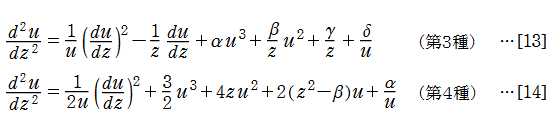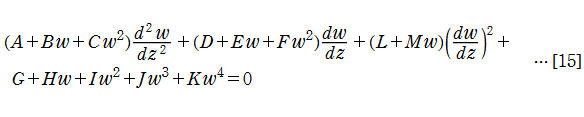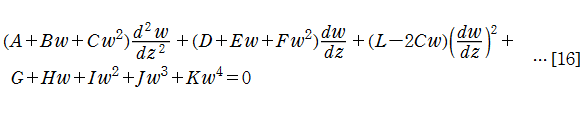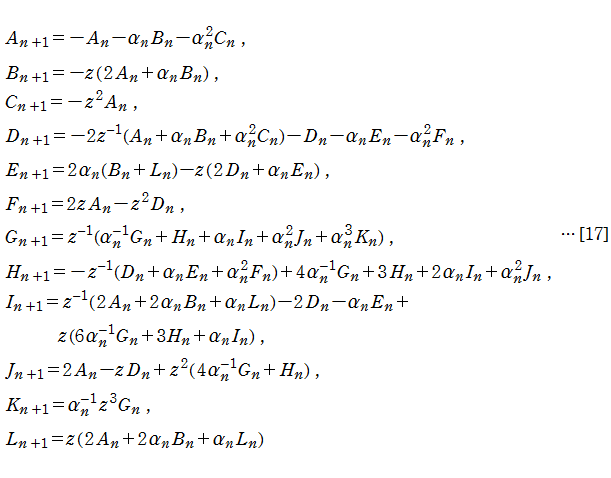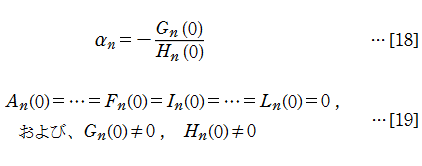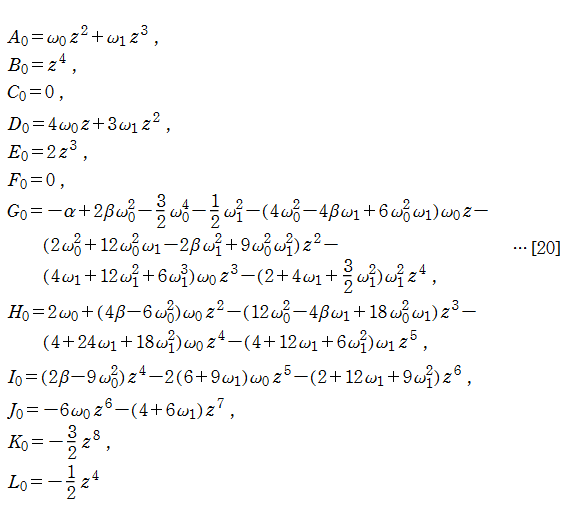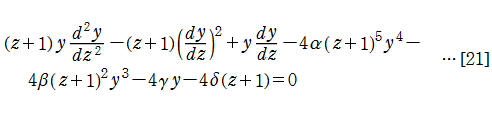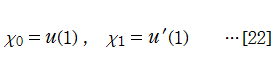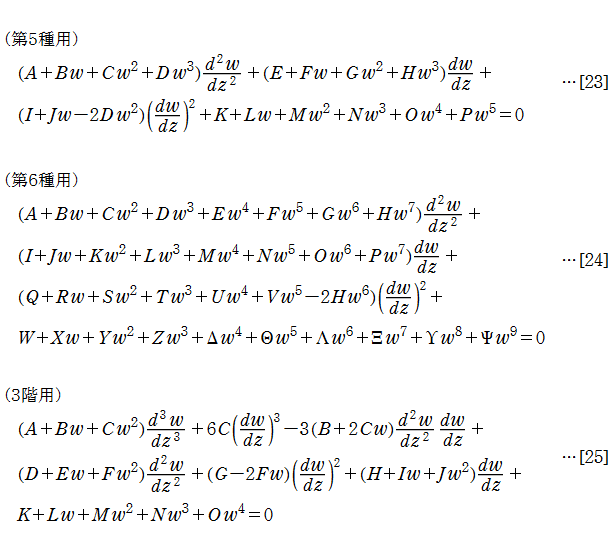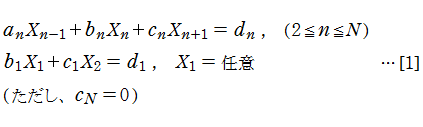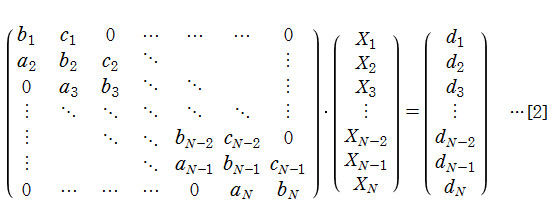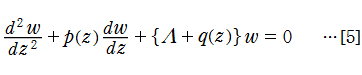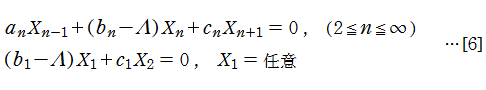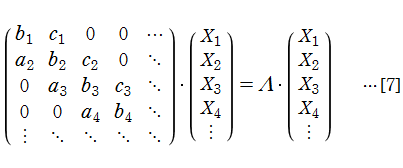特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
Home Menu
いくつかの数値計算法
関数計算に用いた数値計算法のうち、比較的珍しい方法や独自の方法を中心に説明します※1。
なお、詳細やコード実装例は、別頁 Mathematica関連 にある個別のファイルを参照して下さい。
なお、詳細やコード実装例は、別頁 Mathematica関連 にある個別のファイルを参照して下さい。
※1:このほか Euler - Maclaurin 総和法などを使用していますが、これらはより詳しい説明が他にも多数あるので省略します。なお、独自の方法に対して当サイトは種々の知的財産権を保有しています。注意事項 (Notes)!の内容に留意願います。
Padé 近似法
H. Padé が1890年頃に開発・発展させた関数近似法であるが、その発想は合理的な級数近似法を模索した F. G. Frobenius の研究にまで遡れる。冪級数近似では、級数展開の中心点から最も近い所にある極などの特異点を超えた範囲では収束しない (有限の収束半径が存在する)。しかし、多項式ではなく有理関数で近似し、しかも両者が共に収束する有界な範囲で結果が一致していれば、有理関数近似は特異点を超えて収束すると期待できる。
Padé 近似は、多項式と多項式の有理関数で上記の効果が実現されるような近似法であって、その定係数を具体的に求める際に正方行列を用いる。行列の形にはいくつかの種類がある。
当サイトでは、極を持つ関数のみならず、級数の収束が遅いだけの関数等にも使用している。
計算法の説明
Padé 近似を適用しようとする関数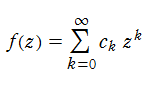
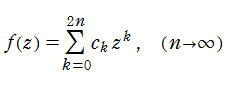
を作り、①線形代数方程式を解いて
これらの結果を用いて、関数
で近似する。
簡単な計算比較の例
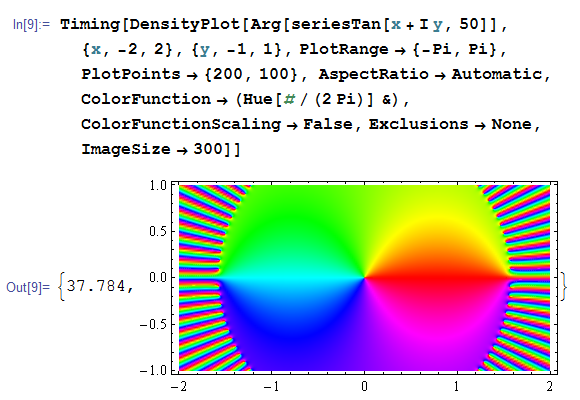
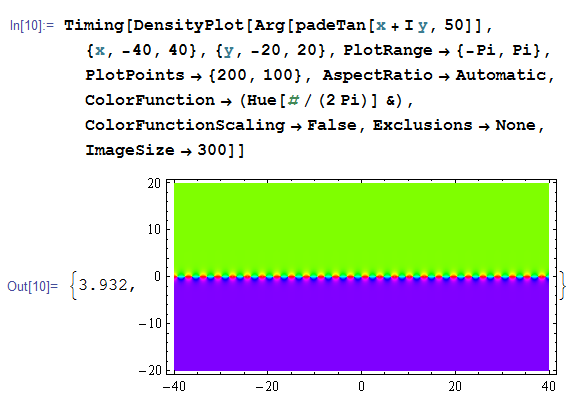
正接関数 (タンジェント) を、Mathematica実装関数、冪級数近似 (50項)、Padé 近似 (50項/50項) で計算する。特異点よりも絶対値が小さい範囲内ならば、3種類とも同じ結果になる。しかし、冪級数近似の収束範囲は
Padé 近似は、(冪級数と同じ50項使用でも) はるかに広い範囲で収束する。(しかも、約4秒しかかからない。これは、前のような非収束域の描画に時間を要しないため。)
適用例 ~ 第1種 Painlevé 超越関数
近似しようとする関数が分岐点を持たず、収束半径が0でない冪級数に展開できて、その係数を具体的に求められる場合であれば、Padé 近似を適用できる。そのような例は非常に多いため、極めて有用な数値計算法といえる※1。例えば、
に展開できる。よって、有理関数項を除いた (冪級数の) 部分にPadé 近似を適用できる。
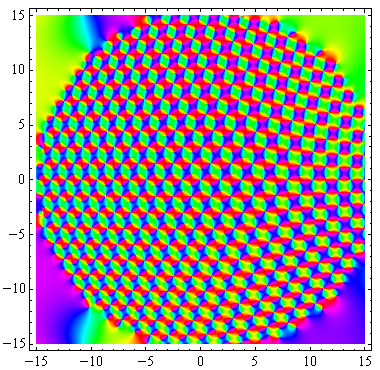
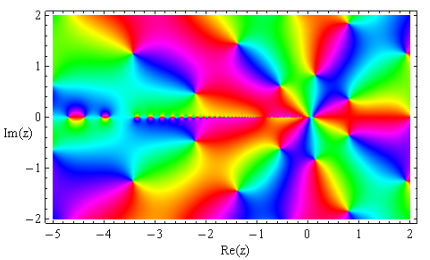
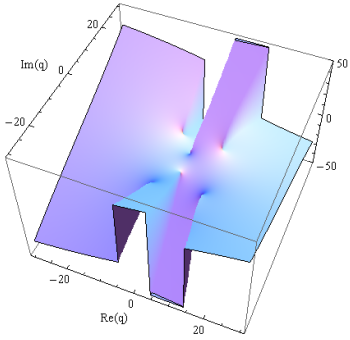
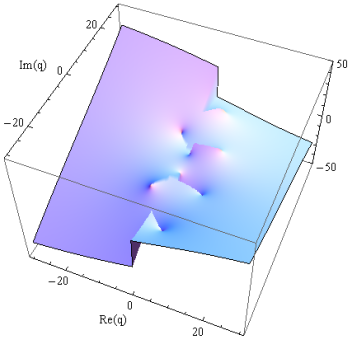
次のグラフは、この方法によって
(
【註記】
※1 ただし欠点もある。この方法や後述の Fair - Luke 法,および三重対角行列法は、いずれも要素数の多い行列計算が伴うが、大抵の数値・数式処理システムでは負荷の掛かる計算になる。
また、上記の描画事例に見られるような収束の限界をもっと遠方に広げる場合は、行列の要素数を大幅に増やす必要がある。(本来は漸近級数の併用が理想的だが、無数の特異点が散在する上記のような事例では、複素数値計算に適した漸近級数展開が確立されていないことも多い。)
* * *※1 ただし欠点もある。この方法や後述の Fair - Luke 法,および三重対角行列法は、いずれも要素数の多い行列計算が伴うが、大抵の数値・数式処理システムでは負荷の掛かる計算になる。
また、上記の描画事例に見られるような収束の限界をもっと遠方に広げる場合は、行列の要素数を大幅に増やす必要がある。(本来は漸近級数の併用が理想的だが、無数の特異点が散在する上記のような事例では、複素数値計算に適した漸近級数展開が確立されていないことも多い。)
Fair - Luke 法
ある特定の形に限られるが、代数的非線形微分方程式の解に対してPadé 近似が適用できるよう、W. Fair と Y. L. Luke が開発した方法。近似に使う有理関数は、Padé 近似と同じく多項式の有理関数が選択できる他、連分数も選択できる。当サイトでは専ら後者を用いているので、それを説明する。また、私はこの方法が適用できる代数的非線形微分方程式の種類を若干広げた、「拡張された Fair - Luke 法」を開発したので、併せてこれも説明する。
当サイトでは Painlevé 超越関数、および3階の Painlevé 超越関数に使用している。
「Fair - Luke 法」の説明
2階非線形常微分方程式、の解
と表わされるとき、係数
によって求められる係数を用いて
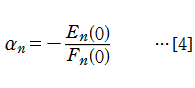
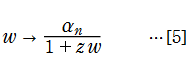
ゆえに、[2]によって解
が課せられる。W. Fair と Y. L. Luke は論文※1において、第1種、第2種 Painlevé 方程式
は、この方法が適用できる方程式であることを指摘している。また V. Novokshenov は、実際にこのことを数値計算で検証し、複素領域における第1種、第2種 Painlevé 超越関数の動く特異点の詳細を明らかにした※2。具体的には、[7],[8]に
を代入し、それぞれ
に変形したのち、 Fair - Luke 法を適用する。明らかに、
で定義される。
【註記】
※1 W. Fair and Y. L. Luke,
「Rational Approximations to the Solution of the Second Order Riccati Equation」
Mathematics of Computation, 20 (1968), pp.602-605.
※2 V. Yu. Novokshenov,
「Padé approximations for Painlevé I and II transcendents」
Theoretical and Mathematical Physics, 159 (No.3) (2009), pp.853-862.
※1 W. Fair and Y. L. Luke,
「Rational Approximations to the Solution of the Second Order Riccati Equation」
Mathematics of Computation, 20 (1968), pp.602-605.
※2 V. Yu. Novokshenov,
「Padé approximations for Painlevé I and II transcendents」
Theoretical and Mathematical Physics, 159 (No.3) (2009), pp.853-862.
「拡張された Fair - Luke 法」の説明
(2013年9月17日 掲載記事)微分方程式[1]を拡張したもので、その解が、連分数[2]によって表わされるような、 Fair - Luke 法の拡張を考える。
始めに、第3種、および第4種 Painlevé 方程式
が取り扱えるような微分方程式の形を決定する。この場合、非線形な項で最高次のものは
が候補となることが分かる。さらに検証によって、実際に条件を満たすためには
が得られた。微分方程式[16]に変換[5]を施して得られる漸化式は
となり、連分数[2]の係数はこの場合
と定義される。これを「拡張された Fair - Luke 法」と呼ぶこととする。
第3種 Painlevé 方程式[13]の場合は、原点に動かない分岐点を持つため若干テクニックが必要となる。よってこれは後述し、先に第4種 Painlevé 方程式[14]の場合を述べる。[14]も[9]を代入すれば、拡張された Fair - Luke 法における漸化式の初期値として
を採用できることが分かる。
第4種の場合は、第1種、第2種の場合に比べて漸化式とその初期値が複雑であるため、計算可能な複素領域は狭くなる。
第3種 Painlevé 方程式[13]の場合は、原点が動かない分岐点なので[12]のような指定値は使えない。また、分枝切断線が生じるが、そのままの Fair - Luke 法ではこれが 「極が密集したもの」 となるため、その近傍で値が不正確になる※1。さらに、[13]は分数形の項があるため、これも両辺にかけることで解消する必要がある。
そこで[13]の解を
に対して、拡張された Fair - Luke 法を適用する。これにより
を採用することとなる。
以後、漸化式の初期値は、前述の要領で求められるので省略するが、さらに複雑な結果になる。第5種、第6種 Painlevé 方程式も動かない分岐点を持つので、同様のテクニックが必要になる。
第5種、第6種 Painlevé 方程式、および特定の3階非線形常微分方程式に適用できる[16]相当の微分方程式型はそれぞれ
となるが、漸化式や初期値は極めて長大な式となるため、ここに表記できない。別頁 Mathematica関連 にあるコード「Painleve.m」および「Chazy.m」をダウンロードのうえ、ご確認下さい。
* * *
無限次元三重対角行列の固有値
元々は、線形代数における三重対角行列法 (または L. Thomas 法) を基礎とする数値計算法である。三重対角行列法とは、三項間の漸化式の
を解く方法をいう。これはさらに、Gauss の消去法が元になっている。(→ Wikipedia「Tridiagonal matrix algorithm」を参照。)
この三重対角行列法において行列を無限次元にし、2階線形常微分方程式の固有値を求める場合に適用したものが、標題の数値計算法である。
計算法の説明
三重対角行列法において、漸化式の項が正負両方向に無限個で、この漸化式[3]と線形代数方程式[4]は、2階線形常微分方程式
の固有値
なお、漸化式が[1]と同様に、
のように途中から開始されるときの線形代数方程式は、[2]において
となる。整数次の Mathieu 固有値関数を求める場合などが、この具体例となっている。
【註記】
※1:例えば、
宮崎佳典、浅井信吉、蔡東生、池辺八洲彦
「Mathieu微分方程式の逆固有値問題」
日本応用数理学会論文誌 Vol.8, No.2, (1998), p199-222
P. E. Falloon
「Theory and Computation of Spheroidal Harmonics with General Arguments」
Australia: University of Western Australia, (2001)
P. Abbott
「Tricks of the Trade (Legendre Functions and Spheroial Harmonics)」
The Mathematica Journal Vol.7, Issue1, (1997), p18-22
※1:例えば、
宮崎佳典、浅井信吉、蔡東生、池辺八洲彦
「Mathieu微分方程式の逆固有値問題」
日本応用数理学会論文誌 Vol.8, No.2, (1998), p199-222
P. E. Falloon
「Theory and Computation of Spheroidal Harmonics with General Arguments」
Australia: University of Western Australia, (2001)
P. Abbott
「Tricks of the Trade (Legendre Functions and Spheroial Harmonics)」
The Mathematica Journal Vol.7, Issue1, (1997), p18-22
計算比較(Mathematicaと異なる分枝切断線)
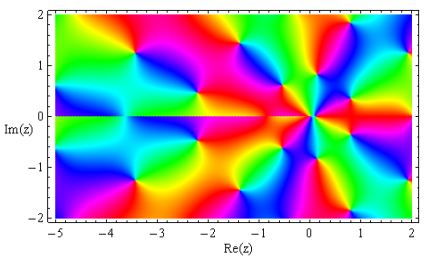
無限次元三重対角行列による固有値計算法を用いた場合の Mathieu 固有値関数は、Mathematica の実装関数とは異なる分枝切断線となる。(どちらが望ましいということではなく、単に好みの問題である。本来、分枝切断線の形状は任意に決めることができる。)因みに Mathematica は、「Newton 法の一般化形式」 を使用しているとのことらしい。
Mathieu 固有値関数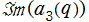 (無限次元三重対角行列による固有値計算法)
(無限次元三重対角行列による固有値計算法)
Mathieu 固有値関数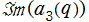 (Mathematica)
(Mathematica)