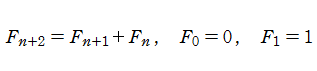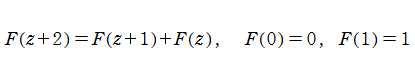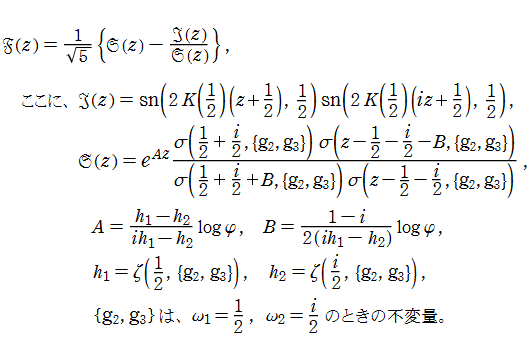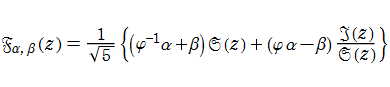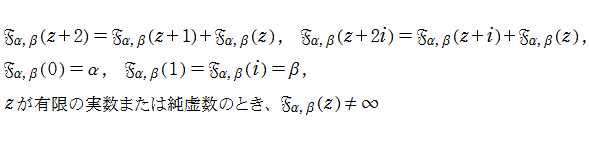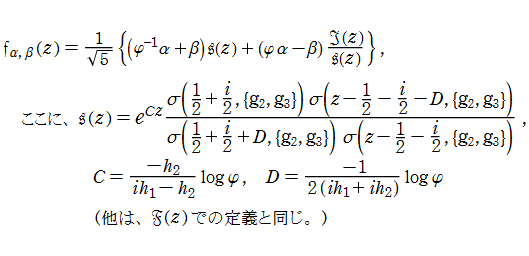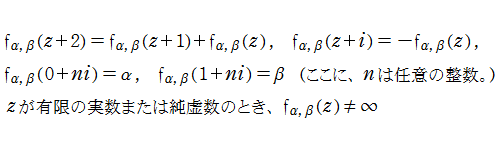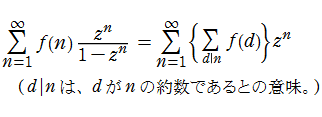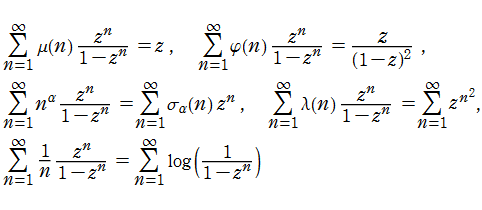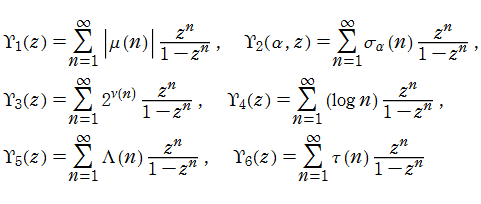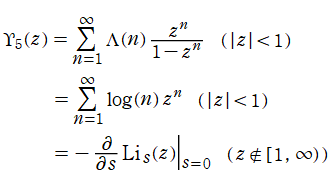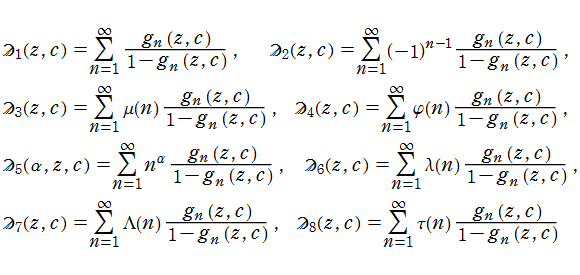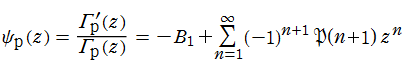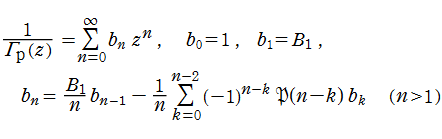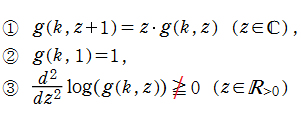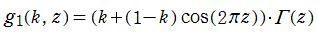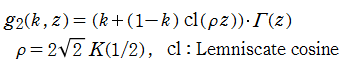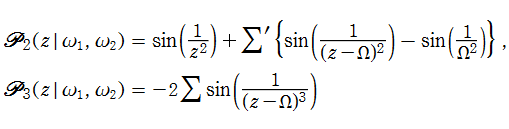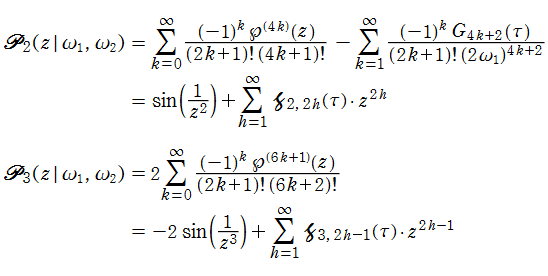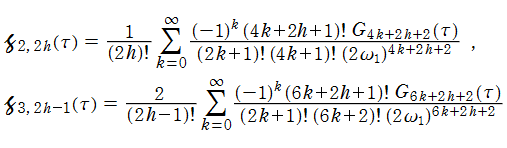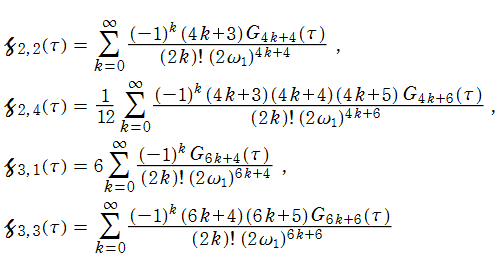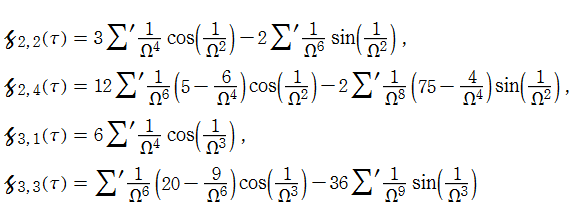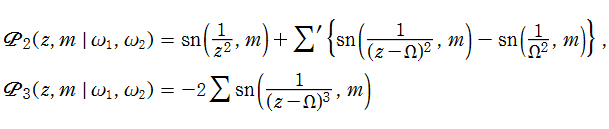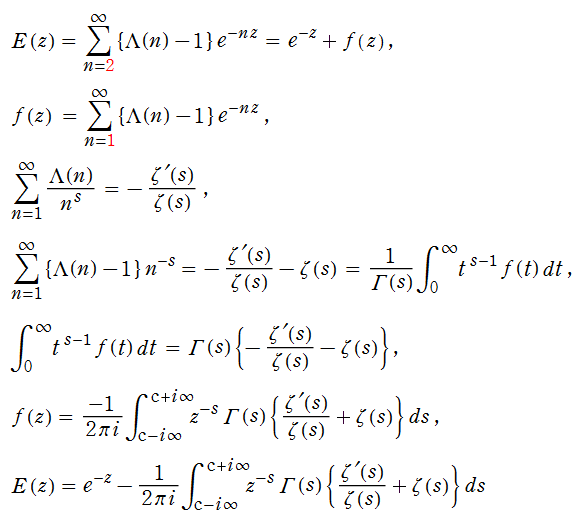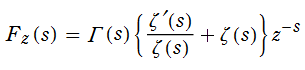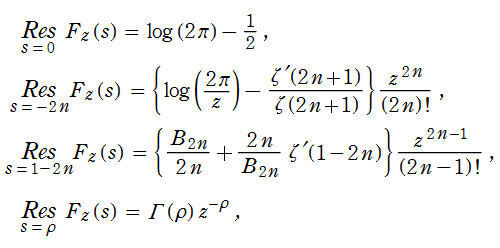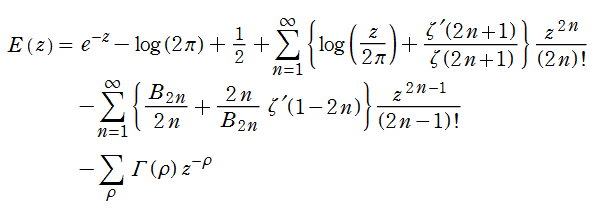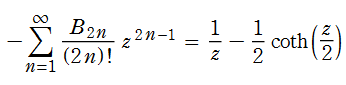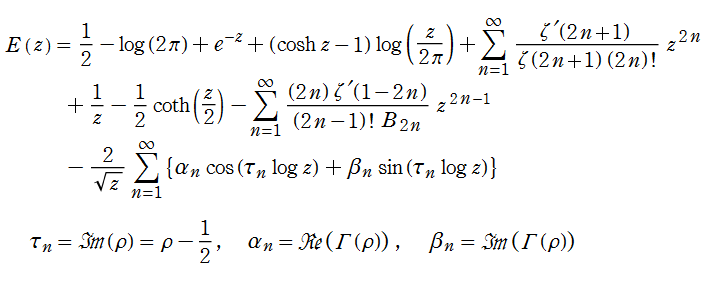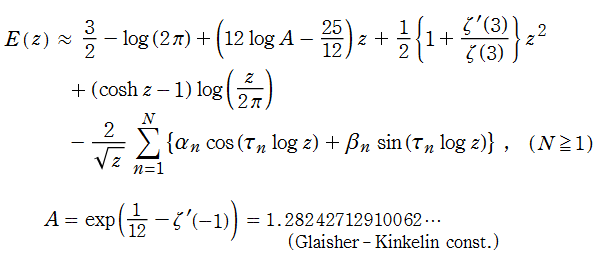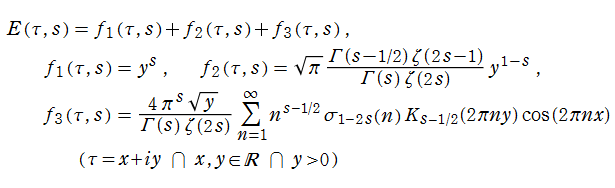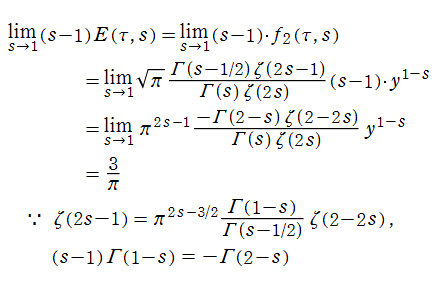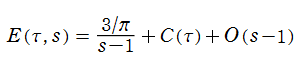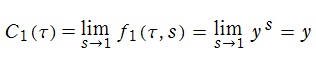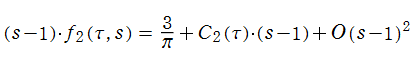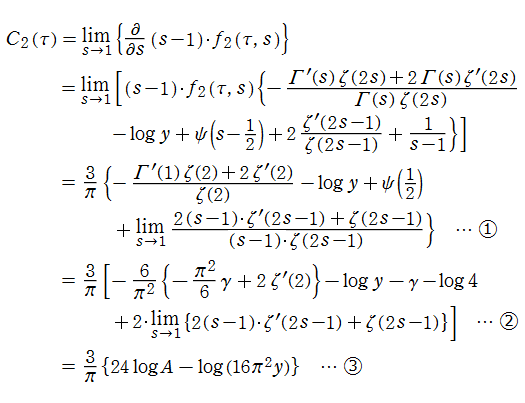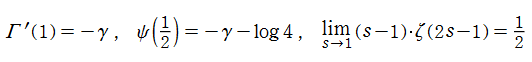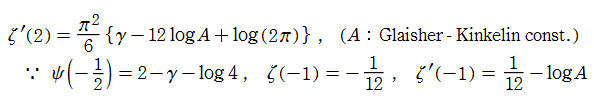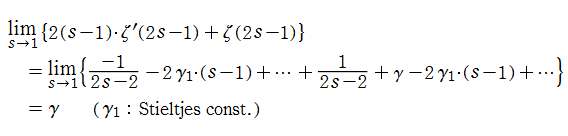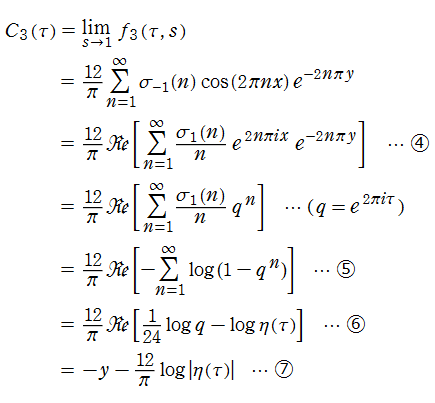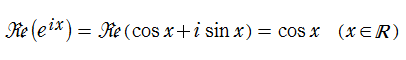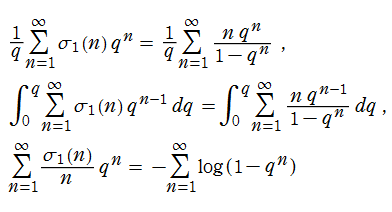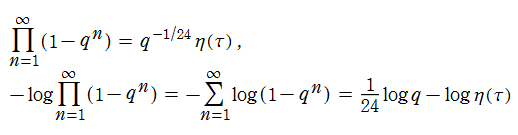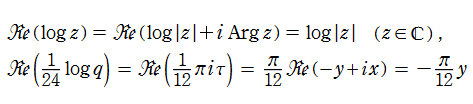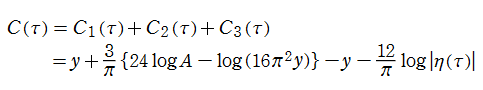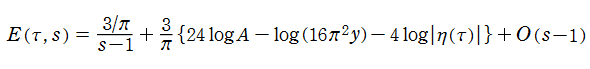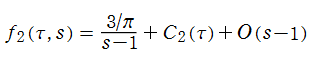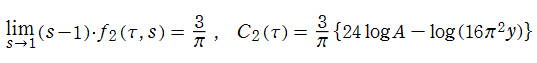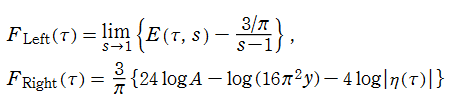独自研究：特殊関数グラフィックスライブラリー Special Functions

Ｈｏｍｅ Menu

独自研究

　　｢当て推量数学｣で探索する｢新しい特殊関数｣。

楕円 Fibonacci 関数

(2013年9月17日掲載記事)
　Fibonacci 数

は、漸化式

で定義される数列で、数学のみならず、自然界の様々な事象に広く見られる。
　この数列に対して、

を複素数に拡張した「Fibonacci 関数」

を定義できることが既に知られており、関数等式

を満たす。なお参考までに、実変数および複素変数の Fibonacci 関数のグラフは次のとおり。

　以下では、これを楕円関数化することを考えた。

楕円 Fibonacci 関数

　実数方向では Fibonacci 関数の関数等式を満たし、同時に、虚数方向でも類似する関数等式を満たすような関数を

で定義し、これを「楕円 Fibonacci 関数」と呼ぶこととした。
　楕円 Fibonacci 関数は、次の関数等式や性質を満たす。

　次のグラフからも分かるように、楕円 Fibonacci 関数は実軸に対して鏡映対称とならない。このため、非整数の実数上で楕円 Fibonacci 関数は一般に複素数値となる。
　実変数の楕円 Fibonacci 関数

と、複素変数の楕円 Fibonacci 関数

のグラフ。(実変数のグラフの赤線は実部、青線は虚部。)

　楕円 Fibonacci 関数は、次のように一般化できる。

　一般化楕円 Fibonacci 関数は、次の関数等式や性質を満たす。

特に、

である。また、

は Lucas 数に対する「楕円 Lucas 関数」となる。
　実変数の楕円 Lucas 関数

と、複素変数の楕円 Lucas 関数

のグラフ。(実変数のグラフの赤線は実部、青線は虚部。)

虚数方向に周期的な Fibonacci 関数

　前の結果を応用して、実数方向では Fibonacci 関数の関数等式を満たし、同時に、虚数方向では周期関数となる「周期的 Fibonacci 関数」

が定義できる。
　周期的 Fibonacci 関数は、次の関数等式や性質を満たす。

　次のグラフからも分かるように、周期的 Fibonacci 関数は実軸に対して鏡映対称となる。このため、実軸上で周期的 Fibonacci 関数は常に実数値となる。
　実変数の周期的 Fibonacci 関数

と、複素変数の周期的 Fibonacci 関数

のグラフ。

　（

楕円 Fibonacci 関数のコードを、｢Mathematica Code｣の頁に掲載しています。）

未知の Lambert 級数

　Lambert 級数はｑ-級数の一種と見ることができ、保型関数論や数論との繋がりもある。Lambert 級数の母関数は、

で表わされる。特に、

となることが知られている。ここに、

は Möbius 関数、

は Euler のトーシェント関数、

は約数関数、および

は Liouville 関数である。このうち、３番目と４番目の関係式は、楕円モジュラー関数と関連がある。
　以下では、上記と異なる係数の Lambert 級数や、Lambert 級数そのものの拡張について考える。

他の数論的関数が係数の場合

　前述とは異なる数論的関数を係数とする Lambert 級数として、

を考える。ここに、

は素因数分解に含まれる異なる素数の個数 (素数ニュー関数)、

は Von Mangoldt のラムダ関数、および

は Ramanujan のタウ関数である。これらの母関数は果たして何であろうか？…。
　各関数の複素変数でのグラフ。順に、①

, ②

, ③

, ④

, ⑤

, ⑥

。

　グラフから推測すれば、①,③,④は互いに似ており、重み２の Eisenstein 級数との類似を感じさせる。②は重み６の Eisenstein 級数と類似している。⑤は何となく初等関数に還元できそうな気がする。⑥は尖点形式 (モジュラー判別式) に似ている。

(2021年9月12日追加記事)
　次のとおり⑤は、ポリ対数関数を変数

で微分したのち、極限を取ると得られる関数に一致することが判明した。(前述の｢初等関数に還元できる｣との予想は誤りでした。)

　なお、このポリ対数(導)関数の極限は単位円の外部でも存在する。グラフで確認すると、次のようになっている。

「Mandelbrot - Lambert 級数」

　Lambert 級数の各項

をグラフで見ると、次のようになる。

　Mandelbrot 集合の反復力学系関数を

で定義する (

の関数のとき Mandelbrot 集合、

の関数のとき Julia 集合)。
　このとき、

をグラフで見ると、次のようになる。

　これらの結果は、あたかも Lambert 級数の「Mandelbrot 集合版」のようになっている。そこで、次の関数を考える。

　各関数の複素変数でのグラフ。順に、①

, ②

, ③

, ④

, ⑤

, ⑥

, ⑦

, ⑧

。

素数正弦関数・素数ガンマ関数

　古い (恐らく1990年代前半の) ノートを見ていて、当時から下記の独自関数を考えていた事を思い出しました。再度検証してみたところ新たな結果も得られたので、今回ここで取り上げることにしました。(いずれも、やや自明な結果かもしれない。)

素数正弦関数

　正負の素数に１位の零点を持つ超越整関数

を、素数正弦関数と呼ぶことにする。その対数微分は、素数ゼータ関数

の偶数での特殊値を用いて

と表わされる。よって、素数正弦関数自体の冪級数展開式は

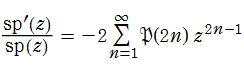
となる。
　素数正弦関数と正弦関数の商

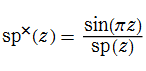
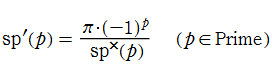
は、0, ±1, 正負の合成数に１位の零点を持つ超越整関数となる。この関数を用いれば、素数正弦関数の素数における微係数 (傾き) は

で表わされる。
　素数正弦関数のグラフは次のようになる。

素数ガンマ関数

　負の素数に１位の極を持ち、零点を持たない有理型関数

を、素数ガンマ関数と呼ぶことにする。ここに、

は Meissel - Mertens 定数とする (以下同様)。
　素数ガンマ関数の対数微分は、素数ゼータ関数

の特殊値を用いて

と表わされる。よって、素数ガンマ関数の逆数の冪級数展開式は

となる。
　また、素数ガンマ関数の対数微分の冪級数展開式、および Meissel - Mertens 定数の定義式から

となることが分かる。ここに、

は Euler の定数である。
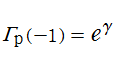
　素数ガンマ関数は、素数正弦関数と

の関係にある。しかし、ガンマ関数が満たす差分関数等式に相当するような、素数ガンマ関数の関係式は見つかっていない (恐らくそのような関係式は持っていない。よって｢ガンマ関数｣を含む名称で呼ぶのは適切でないかもしれない)。
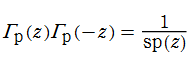
　素数ガンマ関数のグラフは次のようになる。

非 Bohr - Mollerup 型ガンマ関数

を実数パラメータ、

を複素変数とする関数

は、

を満たす任意の周期関数とする。
　このとき、関数

は、Bohr - Mollerup の定理①,②を満たすが、定理③は満たさない。すなわち、

となり、階乗の "擬似的な" 連続化に相当する。
　しかし、実変数のグラフは周期関数の影響から振動し、正の定義域で一般に単調増加にならない。この結果は、｢１より大きい階乗 (の連続化) は単調増加になるはずだ｣という私達の理性にも反している。

周期関数因子が三角関数の例

　この関数の実変数グラフ、および複素変数グラフ (アニメーション：6.27MB)

周期関数因子が楕円関数の例

　この関数の実変数グラフ、および複素変数グラフ (アニメーション：7.82MB)

真性特異点を持つ二重周期関数

(2017年11月11日掲載記事)
　Weierstrass の楕円関数およびその導関数の部分分数展開式を、次のように変形した関数を定義する。ただし、周期を

とし、総和記号は Weierstrass の楕円関数に準じる。

　関数

は二重周期関数であるが、格子状に並ぶ真性特異点を持ち、その周囲に無数の零点がある。したがって、(有理型関数ではないので) 本来は楕円関数ではないが、さしずめ｢位数が

の楕円関数｣とも言える状況になっている。

複素変数の

のグラフ。

複素変数の

のグラフ。

とし、その

階導関数を

と表記する。また、Eisenstein 級数を

とするとき、関数

は、Weierstrass の楕円関数の無限級数、および Laurent 級数に展開できる。(ただし、後者は有限の収束半径を持つ。)

ここに、Laurent 級数展開の係数は、

である。特に、

が小さい場合の係数

を、逆数変数の三角関数級数で表わすと、

となる。(私はこれらを用いた楕円モジュラー関数の類似をいくつか試みたが、特筆するような結果は得られなかった。)

複素変数の ①

, ②

, ③

, ④

のグラフ。(ただし、

とする。)

　さらに、部分分数展開式を Jacobi の楕円関数によって変形した関数

を定義する。関数

も格子状に並ぶ真性特異点を持つ二重周期関数であるが、その格子点の周囲に無数の (1位の) 極がある。

複素変数の

のグラフ。

複素変数の

のグラフ。

　（

真性特異点を持つ二重周期関数等のコードを、｢Mathematica Code｣の頁に掲載しています。）

von Mangoldt 指数級数の漸近公式

(2018年06月23日掲載記事)
　英語版 Wikipedia の Von Mangoldt function を見ると、｢Exponential series｣という項目があり、関数

のグラフを掲載するとともに、この関数を von Mangoldt 指数級数 (von Mangoldt exponential series) と称している。グラフの詳細説明 (More detailes) を見ると、描画に必要な級数の加算は 20億項以上 (!) との説明がある。
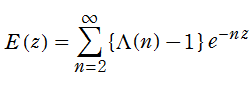
　今回、この関数を非常に少ない項数で近似できる漸近公式が得られた (2018年6月) ので、ここでその概要を示すことにする。因みに、(管理人の力量不足もあって) これに辿り着くまで５～６年間は様々な方法を試行錯誤したように記憶している。
　(実は、この方法を思い付いた直後、念のため G. H. Hardy & J. E. Littlewood の原論文｢Contributions to the Theory of the Riemann Zeta-Function and the Theory of the Distribution of Primes, Acta Mathematica. 41, p.119–196｣を確認したところ、ほとんど同じ方法による考察が既にあることが分かった。ただし、

に対して適用している点が異なる。また、その論文の目的は、より重要な｢素数定理の誤差項の下限評価を求める｣ことにあった。)

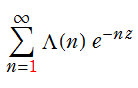
【漸近公式を求める方法】
　この方法の要点は、逆 Mellin 変換と留数定理を用いることであるが、複素関数論では割合よく見られる方法なので、以降ではその道筋だけを簡単に示す。
　まず、逆 Mellin 変換までの手順を一気に記すと、

となる。この逆 Mellin 変換の積分経路は、被積分関数

のすべての極を左側に見ながら (正の向きに) 囲う留数定理にもなっている。(次の図を参照。本来は、まず有界で閉じた矩形の積分経路を設定し、次に矩形の辺の長さを無限大にする極限を取らなければならない。)

　Riemann ゼータ関数の非自明零点を

と表記するとき、各々の極における留数は、

となる。したがって、留数定理から

を得る。分子に Bernoulli 数がある級数の収束半径は有界であるが、幸いこの級数部分は

と解釈できるので分離し、さらに、Riemann 予想が正しいと仮定して

とするならば、最終的に目標の漸近公式

が得られる。

【原点近傍での漸近近似式】
　

のもとでは、漸近公式における高次 (ここでは3次以上) の冪項、および絶対値が大きい非自明零点の項は無視できる。対数因子を持つ項も消えるがここでは残すことにした。よって、漸近近似式

が得られる。次のコードは、絶対値が小さい最初の3個まで非自明零点を加算するとした漸近近似式による。

　Wikipedia にあるものと同じ範囲でグラフを描画する。(たった0.873秒で計算できることに注目して下さい。)

　直前のグラフと Wikipedia のグラフとを (一方の画像を半透明にして) 重ねてみる。→ 一致している。

　先の More detailes では、｢０に近付くにつれて振動が増大するが、－0.337877の切片を持つ直線のように見える｣との記述もある。この事は、漸近近似式をさらに定数項と1次の項のみに簡略化すると、一層明らかになる。前とは異なる描画範囲のグラフでそれを確認する。

　実際、この1次関数の定数項は

となる。

【複素領域ではどうなっている？】
　残念ながら、この漸近公式は引数の偏角が虚軸に近付くほど収束が遅くなり、虚軸上で発散する (ただし、虚軸は von Mangoldt 指数級数の自然境界と思われる)。原因は、非自明零点に由来する級数部分にある。偏角が実軸から離れると三角関数は指数関数的に増大するようになり、次第にガンマ関数が０に近付く速さと拮抗し始めるからである。また、

の漸近公式ゆえ、引数の絶対値が大きい領域では誤差が大きくなる。したがって複素変数のときは、実変数の場合のような少ない加算項数では無理である (以降の計算では、非自明零点級数での加算項数を10,000にしている)。
　次のグラフは、漸近公式と冒頭の定義級数との誤差を、その絶対値の大きさで色分けしたものである。(分量の理由から、以降ではコードの掲載を省略します。詳細は Mathematica Code の頁にあるファイルを参照願います。)

　この結果に基づき、領域によって計算方法を使い分けるようにしたコードを用いて、von Mangoldt 指数級数を複素領域で描画する。1番目は虚数方向の半周期分、2番目は原点に近い領域、3番目はさらに原点に近い領域である。(ただし、偏角が虚軸にかなり近い領域での概形は不正確かもしれない。また、2・3番目のグラフは約37時間も掛かっている。)

　（

von Mangoldt 指数級数のコードを、｢Mathematica Code｣の頁に掲載しています。）

Kronecker の極限公式の導出方法

(2019年3月6日掲載記事)
　実解析的 Eisenstein 級数の頁に掲載した第1 Kronecker の極限公式 (以降｢第1｣を省略する) は、Glaisher - Kinkelin 定数が現れる等、形が大抵の文献にあるそれとは随分異なっている。そこで念のため、ここに導出過程を掲載し、後半では Mathematica による検証結果も掲載する。

【手計算による Kronecker の極限公式の導出】
　実解析的 Eisenstein 級数の頁にある

の Fourier 級数展開式を再掲すると次のようになるが、以降では、説明の都合上これを３項に分けて

と表記する。

　当然ながら、当サイトの定義と異なる

に対する Kronecker の極限公式は、ここでの結果と相違することがある。因みに、

における

は、

に置き換えても結果は変わらない。なぜならば、約数関数は

を満たすからである。

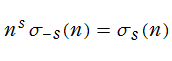
【手順１：

における留数を求める】
　

にある１位の極は

のみに由来する。よって、その留数を求めると、

となる。すなわち、

を

に依存しない

の関数とすれば、Kronecker の極限公式は

の形になることが分かる。

は、

に対する極限から生じる

の関数の和になる。そこで、それぞれを

と表記しよう。すなわち、

である。

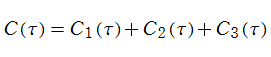
【手順２：

を求める】
　単に、極限をとれば次のように求められる。

（しかし、これは

から生じる

と相殺されることになる。）

【手順３：

を求める】
　実はここに、Glaisher - Kinkelin 定数が現れる原因がある。

とは、

を冪級数展開したときの１次の項の係数である。つまり、｢手順１｣の結果から、

となるはずである。すなわち、

は具体的に

となる。ここに、①は｢手順１｣の結果を援用、②では

を使用、③では、Riemann ゼータ関数の対称関数等式の両辺を対数微分して得られる式

並びに、Riemann ゼータ関数の Laurent 級数展開式とその導関数から得られる式

を使用している。

【手順４：

を求める】
　これも｢手順２｣と同様、単に極限をとれば求められるが、計算はやや複雑である。このとき、第2種変形 Bessel 関数が初等関数

に還元されることに留意すれば、目的の結果

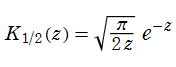
が得られる。ここに、④～⑦では以下の事実を使用している。
　まず④は、冒頭で述べた約数関数の性質、および

　⑤は、NISTにある公式：27.7.5において

とし、その両辺を

で割って区間

で積分する。

ゆえ級数は一様収束で、積分と総和記号の交換が可能。積分定数も生じない。つまり、次の等式が成り立つ。

　⑥は、Dedekind のエータ関数の無限乗積表示式から得られる。すなわち、

　⑦は、⑥に対する計算をさらに進めて得られるところの

を使用する。

【手順５：Kronecker の極限公式を得る】
　｢手順２｣～｢手順４｣の結果から、

となる。よって、

に対する Kronecker の極限公式

が証明された。
　なお、

に対する Kronecker の極限公式も、同様の方法で求められる (導出過程は省略する) が、

に相当する項の分母に

が無いため Glaisher - Kinkelin 定数が現れず、代わりに Euler 定数が (相殺されないため) 現れる。また、その場合の

における留数は

になる。

【Mathematicaによる検証】
　得られた公式の信頼性を補強 (および手計算を検算) する目的から、以降では Mathematica を用いた二つの検証を行う。

【検証１】
　｢手順１｣と｢手順３｣の検証、すなわち

の Laurent 級数展開が

となるか検証する。幸い、Mathematica では容易に Laurent 級数展開式を求められる。

　よって、この結果は

を意味し、手順１と手順３の正当性が確認された。

【検証２】
　Kronecker の極限公式自体の検証。次のように左辺 (極限をとる) と右辺とに分けて、両者の一致、並びに両者の差が (ほとんど) ０になることを確認する。

　この検証では、実解析的 Eisenstein 級数のコードが必要になるので、併せてそれも掲載する。因みに、この Fourier 級数は

が０に近くなければ速く収束する。また、

の近傍では充分な精度で収束する。(なお、このコードは高精度数値を使用するので遅く、グラフの描画には不向きである。)

　第2列目が

、第3列目が

、第4列目 (最右列) が両者の差である。差が０の近似数となるので、この Kronecker 極限公式の信頼性は高い。

s＝4 および 3 における Fibonacci ゼータ関数の特殊値

(2024年6月22日掲載記事)
　自然数における Fibonacci ゼータ関数の特殊値の超越性については、Eisenstein 級数や Lambert 級数による表示式で論じられることが多い。一方、

はテータ零値と q -ポリガンマ関数の値、

はテータ零値のみで表示できる閉形式が知られている。
　そこで、

及び

についても同様 (なるべく楕円テータ関数) の閉形式で表示することを考える。

【Fibonacciゼータ関数から派生した関数】
　Fibonacci ゼータ関数

の一般 Dirichlet 級数表示において、奇数番目の項のみを加算した｢奇数項 Fibonacci ゼータ関数｣の公式

は、例えば D. Lowry-Duda の論文｢The Fibonacci zeta function and modular forms｣に載っている。二つの関数から直ちに、偶数番目の項のみを加算した｢偶数項 Fibonacci ゼータ関数｣

が得られる。さらに同様の方法で、｢交代 Fibonacci ゼータ関数｣

も得られる。（コードは Zeta.m に搭載済み。）
　後に、

の値を

から求める事例等を見るが、その前に (Fibonacci ゼータ関数を除く) それぞれの関数のグラフを確認しよう。

　奇数項 Fibonacci ゼータ関数

のグラフ。

　偶数項 Fibonacci ゼータ関数

のグラフ。

　交代 Fibonacci ゼータ関数

のグラフ。

　1および2の累乗をインデックスとする Fibonacci 数から成る無限級数

は、Millin の級数と呼ばれる。そこで、これを一般 Dirichlet 級数にした

を、このサイトでは｢Millin - Fibonacci ゼータ関数｣と呼ぶことにする。これの計算可能な式を、Fibonacci ゼータ関数の Lambert 級数表示式を求める場合と同じ方法で求めよう。

　Millin - Fibonacci ゼータ関数は、虚軸を自然境界とする右半平面が存在領域となる。これは、

が単位円を自然境界とし、その内部 (原点を含む側) を存在領域とすることに由来する。したがって、Millin - Fibonacci ゼータ関数のグラフは、

および

と大きく異なる。
　因みに

は、1929年の K. Mahler による超越数論で要となった関数であって、

なる代数的数について

は超越数であることが証明されている。

　Millin - Fibonacci ゼータ関数

のグラフ。

【註記：Millin について】
　この級数は、1974年にアメリカのペンシルベニア州の高校生であった D. A. Millin が証明したのでその名が冠せられているが、これは誤植が定着した名であって、正しくは D. A. Miller である。詳細は、History of Science and Mathematics の記事｢Who was D. A. Millin, the eponym of the Millin Series ?｣に掲載されているが、併せて Miller 本人からと思われる投稿もあって、その中で誤植名 Millin を "気に入っているので誰も変えないで欲しい" と発言している。
　現在、D. A. Miller は計算理論を専門とするアメリカの数学者となっている。

【s＝4におけるFibonacciゼータ関数の特殊値】
　以降では、サイト管理人が作成した Mathematica コード｢Zeta.m｣の事前読込が必要になる。
　（

このコードは、Mathematica Codeの頁にあります。）

　始めに、

の閉形式を求める。

　1番目の Lambert 級数は、Mathematica (Ver.8時点。以下同様) で明示的に求められない。

　しかし、Lambert 級数を q-級数に書き換えれば、Mathematica で明示的に求められるようになる。

　2番目の Lambert 級数は、直接または q-級数のどちらであっても、Mathematica で明示的に求められない。
　これは、岩波数学公式Ⅲの49頁にある公式と、NISTの公式23.6.8を等号で結ぶと、容易に得られる。(これらの Lambert 級数は Eisenstein 級数の主要部分でもある。)