特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
参考資料 Menu
関数の特異点一覧
特異点は大別すると、分岐を伴う特異点 (分岐点) と、分岐を伴わない特異点とに分けられる。複素球面上の関数が孤立した点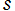 に特異点を持つとき、その関数は特異点
に特異点を持つとき、その関数は特異点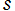 を中心に級数展開すると、大抵次のような関数項が現れる。
を中心に級数展開すると、大抵次のような関数項が現れる。
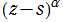
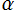 が負の整数 :
が負の整数 : 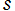 は (位数
は (位数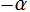 の) 極
の) 極
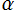 が有理数
が有理数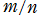 (
(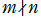 ) :
) : 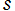 は巻数
は巻数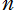 の代数分岐点
の代数分岐点
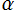 が無理数 :
が無理数 : 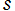 は対数分岐点
は対数分岐点
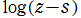 :
: 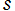 は対数分岐点
は対数分岐点
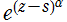
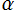 が負の整数 :
が負の整数 : 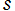 は真性特異点
は真性特異点
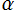 が非整数 :
が非整数 : 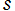 は超越分岐点
は超越分岐点
これらの関数はまた、特異点の近傍での振る舞いを決定する典型的な関数と言うことができる。
以下では、これらの関数を具体的なグラフで見ることとする。なお、簡単のため、特異点が原点の場合 (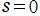 ) で考える。色は、関数値の偏角に 「グラフの凡例」 で説明しているカラーリングを適用する。
) で考える。色は、関数値の偏角に 「グラフの凡例」 で説明しているカラーリングを適用する。
以下では、これらの関数を具体的なグラフで見ることとする。なお、簡単のため、特異点が原点の場合 (
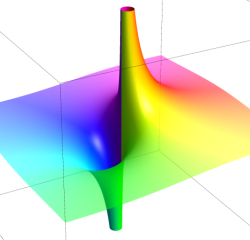
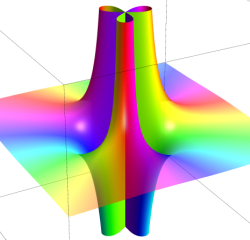
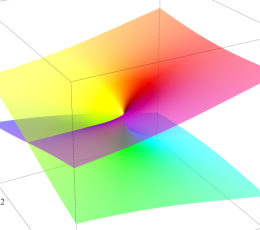
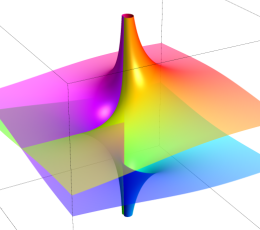
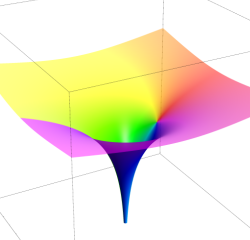
極(Pole)
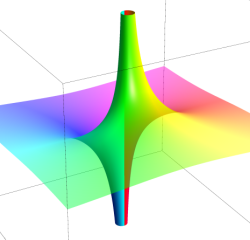
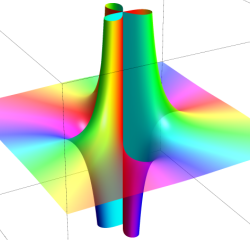
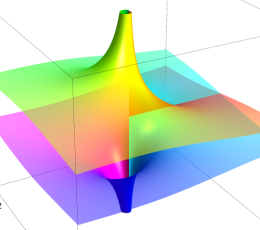
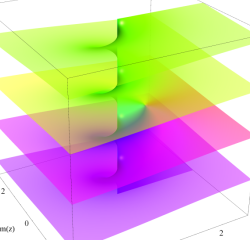
真性特異点
原点を中心に (負数次の項が無限個の) Laurent 級数に展開される。
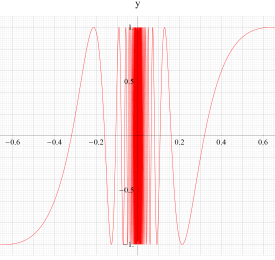
実軸上での断面は実解析学でよく知られた曲線である。
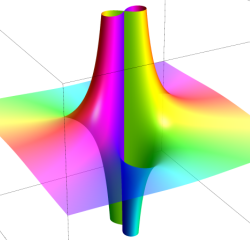
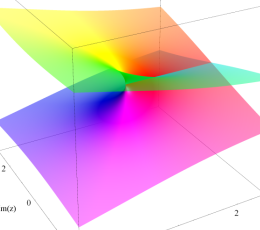
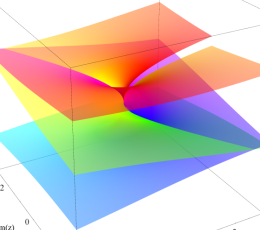
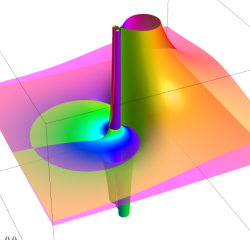
代数分岐点
特異点の周囲での2回転が偏角1回転分に相当する。
ただし負数次なので、近傍の形状は極のようになる。
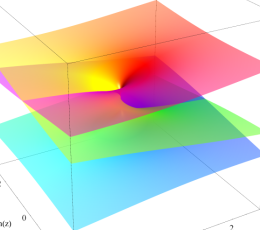
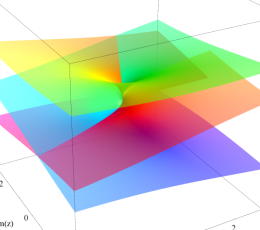
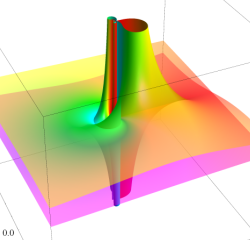
対数分岐点
巻数は
巻数が
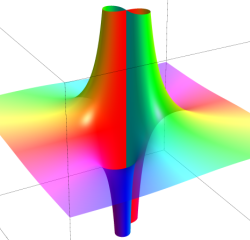
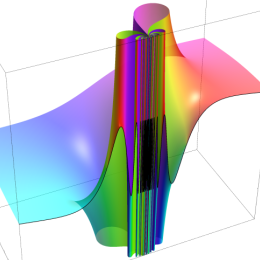
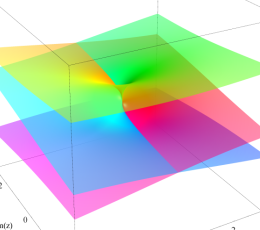
超越分岐点
特にこの例では、原点を中心に Puiseux 級数に展開される。
【 Petite Galerie 】
アニメーション(12.00MB)「会議は踊る:特異点のウィンナ・ワルツ」
(背景画像は、Wilhelm Gause作「ホーフブルクの宮中舞踏会」(1900年)。Wikipedia上のパブリックドメイン画像を使用。)
(背景画像は、Wilhelm Gause作「ホーフブルクの宮中舞踏会」(1900年)。Wikipedia上のパブリックドメイン画像を使用。)