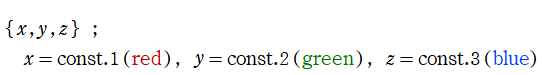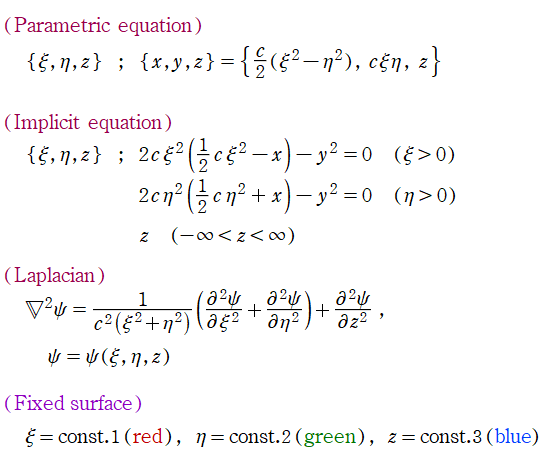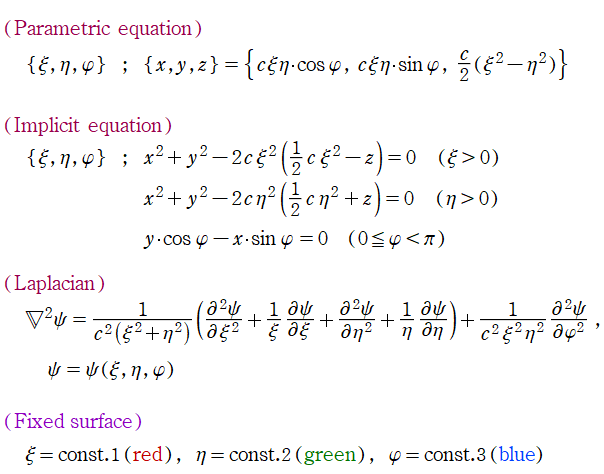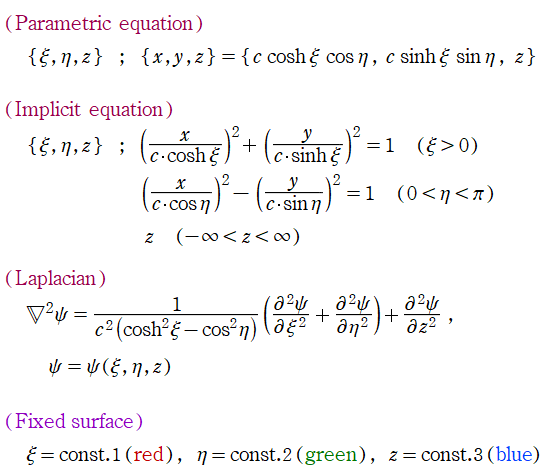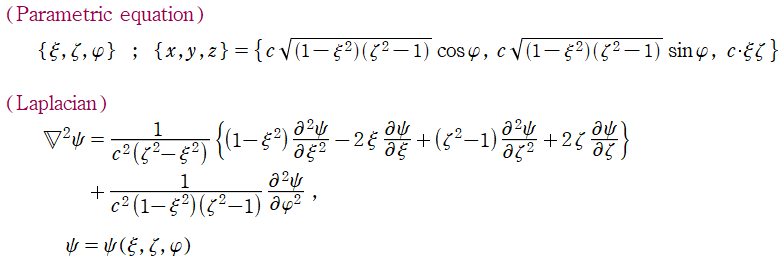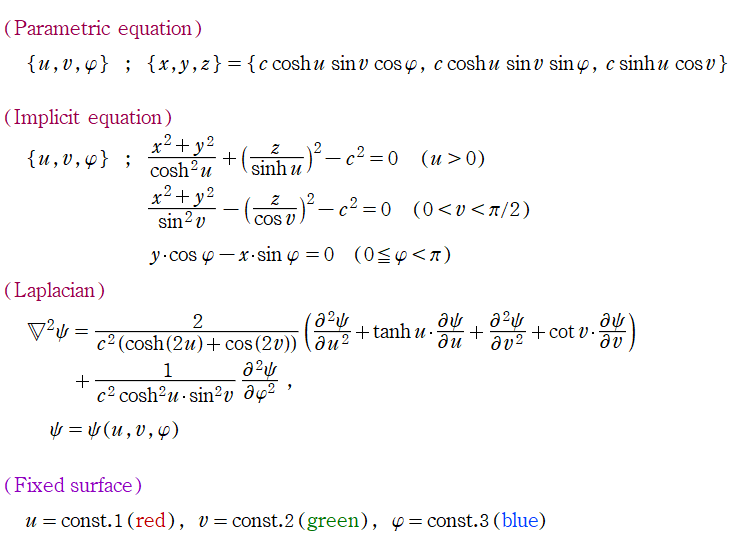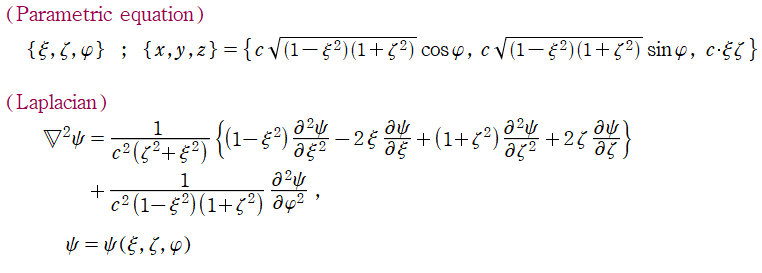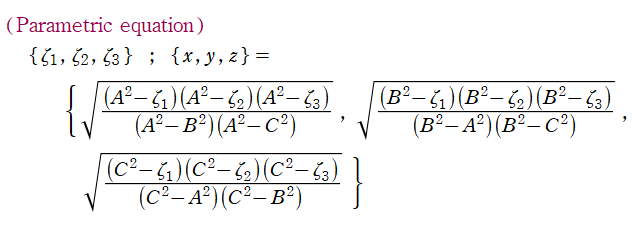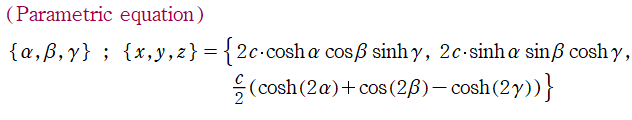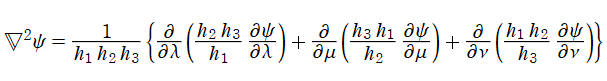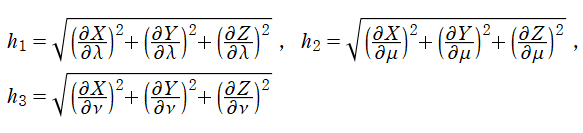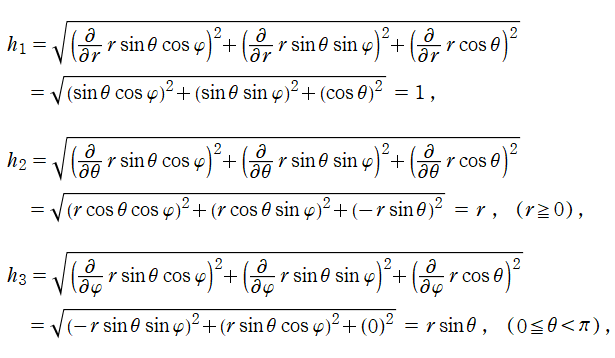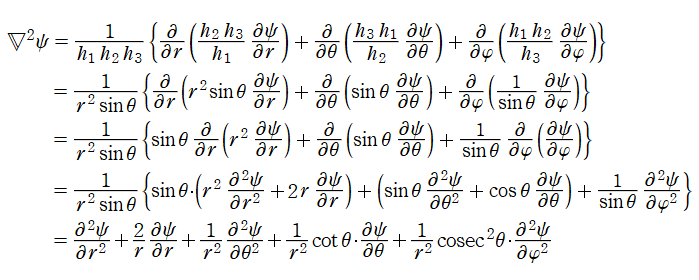参考資料 Menu

三次元座標系一覧

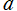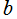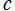　三次元 Euclid 空間における Laplace の方程式や Helmholtz の方程式を変数分離形に持ち込む際に用いる、種々の座標系の定義式とその図についての一覧。数式中のa, bおよびcは任意定数とする。
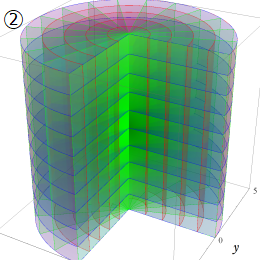
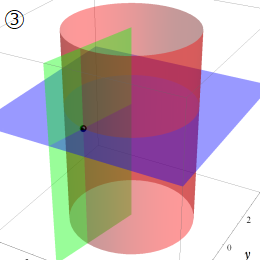
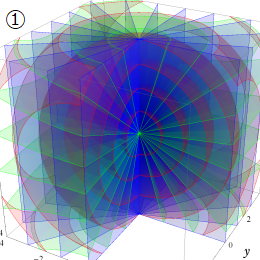
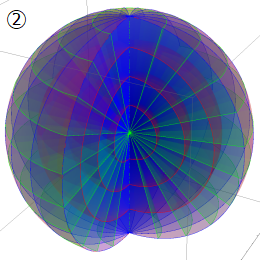
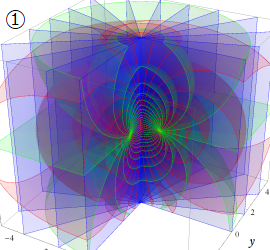
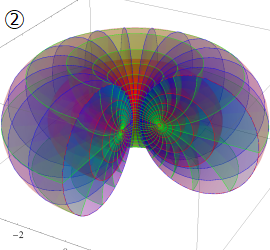
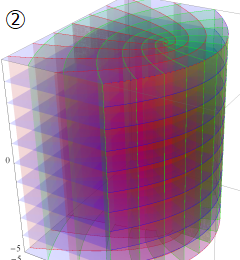
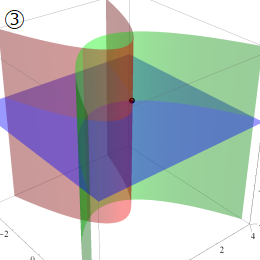
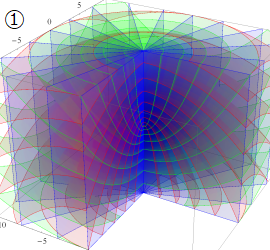
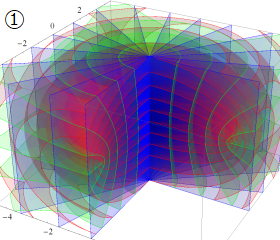
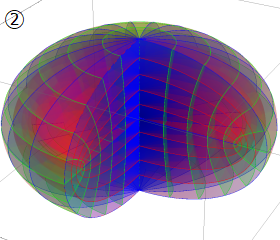
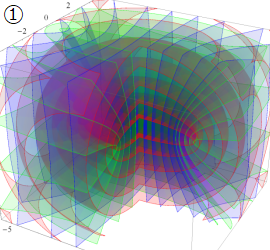
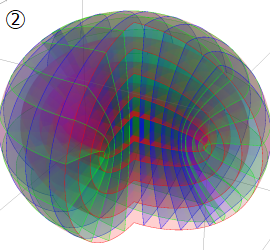
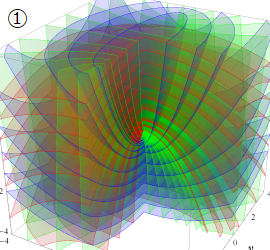
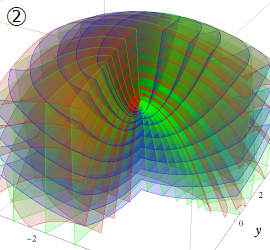
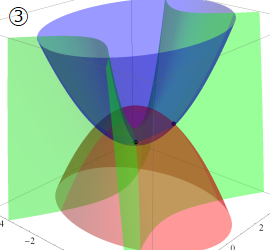
　グラフに付した番号は、①：描画範囲全体, ②：○○座標の "○○" 内に限定した描画, ③：各座標方向の定曲面のみを描画 ― を示す。放物柱座標以外の①と②は、内部の状況が分かるよう前方の直角領域を取り除いている。
　（Mathematica Code ここに掲載している図のコードは、｢Mathematica Code｣ の頁にあります。）

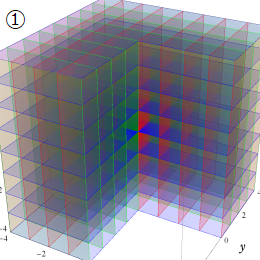
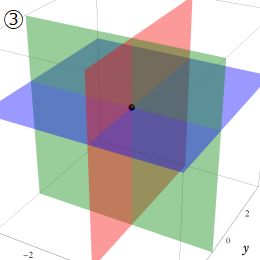
直交直線座標（直角直線座標）

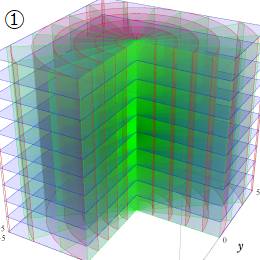
　通常の三次元座標系。Laplace, Helmholtz 方程式の解はいずれも (純虚) 指数関数のみで構成され、特殊関数は現れない。
  • 直角座標の定義式

  • 直角座標の図1
  • 直角座標の図3

円柱座標

　Laplace 方程式の解：Bessel 関数が現れる。
　Helmholtz 方程式の解：Bessel 関数が現れる。
  • 円柱座標の定義式

  • 円柱座標の図1
  • 円柱座標の図2
  • 円柱座標の図3

球座標（極座標）

　Laplace 方程式の解：Legendre 陪関数 (Legendre 関数を含む) が現れる。
　Helmholtz 方程式の解：Legendre 陪関数 (Legendre 関数を含む), 球 Bessel 関数が現れる。
　特に球座標では、θを天頂角、φを方位角と呼ぶ習慣がある。
  • 球座標の定義式

  • 球座標の図1
  • 球座標の図2
  • 球座標の図3

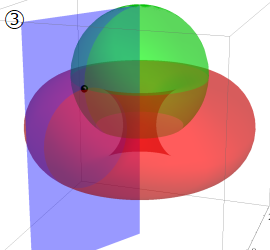
円環座標

　Laplace 方程式の解：円環関数が現れる。
　Helmholtz 方程式の解：円環座標では変数分離できない。
  • 円環座標の定義式

  • 円環座標の図1
  • 円環座標の図2
  • 円環座標の図3

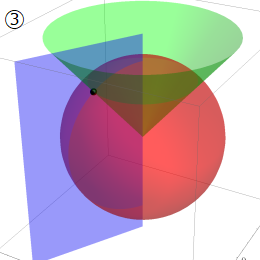
双極座標

　Laplace 方程式の解：Legendre 陪関数が現れる。(分離定数の取り方によっては円錐関数が現れる。)
　Helmholtz 方程式の解：双極座標では変数分離できない。
  • 双極座標の定義式

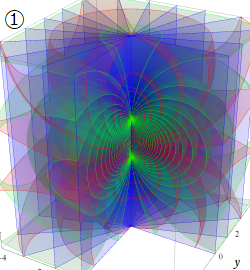
  • 双極座標の図1
  • 双極座標の図2
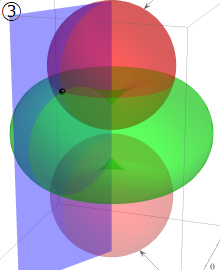
  • 双極座標の図3

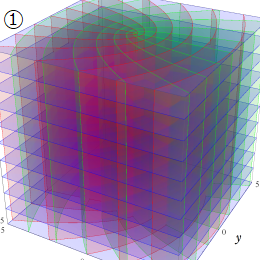
放物柱座標

　Laplace 方程式の解：放物柱関数が現れる。
　Helmholtz 方程式の解：放物柱関数が現れる。
  • 放物柱座標の定義式

  • 放物柱座標の図1
  • 放物柱座標の図2
  • 放物柱座標の図3

回転放物体座標

　Laplace 方程式の解：Bessel 関数, 変形 Bessel 関数が現れる。
　Helmholtz 方程式の解：回転放物体関数 (Coulomb 波動関数) が現れる。
  • 回転放物体座標の定義式

  • 回転放物体座標の図1
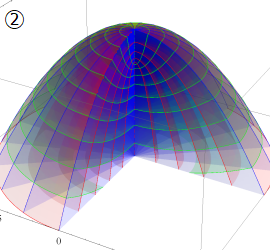
  • 回転放物体座標の図2
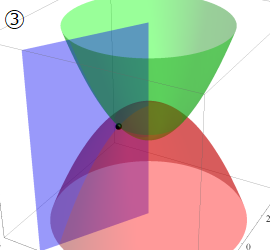
  • 回転放物体座標の図3

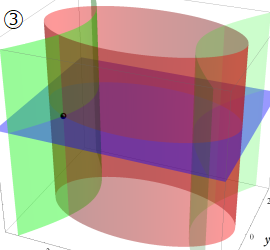
楕円柱座標

　Laplace 方程式の解：Mathieu 関数, 変形 Mathieu 関数が現れる。
　Helmholtz 方程式の解：Mathieu 関数, 変形 Mathieu 関数が現れる。
  • 楕円柱座標の定義式

  • 楕円柱座標の図1
  • 楕円柱座標の図2
  • 楕円柱座標の図3

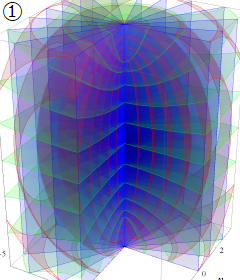
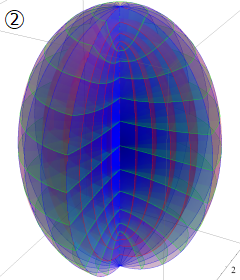
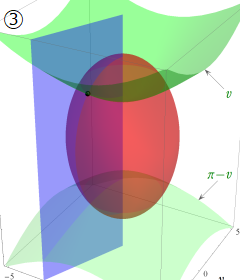
回転楕円体座標

　Laplace 方程式の解：Legendre 陪関数 (Legendre 関数を含む) が現れる。
　Helmholtz 方程式の解：回転楕円体波動関数 (角度関数, 動径関数) が現れる。

扁長回転楕円体座標の場合

  • 扁長回転楕円体座標の定義式

  • 扁長回転楕円体座標の図1
  • 扁長回転楕円体座標の図2
  • 扁長回転楕円体座標の図3

　この他、扁長回転楕円体座標として次の定義を採用することも多い。
  • 扁長回転楕円体座標の他の定義式

扁平回転楕円体座標の場合

  • 扁平回転楕円体座標の定義式

  • 扁平回転楕円体座標の図1
  • 扁平回転楕円体座標の図2
  • 扁平回転楕円体座標の図3

　この他、扁平回転楕円体座標として次の定義を採用することも多い。
  • 扁平回転楕円体座標の他の定義式

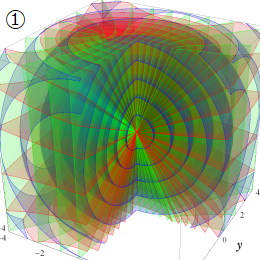
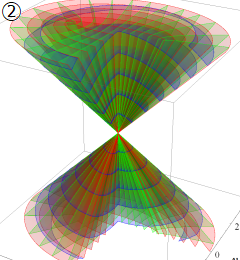
楕円体座標

　Laplace 方程式の解：Lamé 関数が現れる。
　Helmholtz 方程式の解：Lamé 波動関数 (当サイト未掲載) が現れる。
　なお、楕円体座標は "共焦点楕円体座標" と呼ばれることもある。
  • 楕円体座標の定義式

  • 楕円体座標の図1
  • 楕円体座標の図2
  • 楕円体座標の図3

　楕円体座標の定義は他にも二三ある。前述の媒介変数表示式に対して、変換b^2=A^2-B^2, c^2=A^2-C^2、およびη[k]^2=A^2-ζ[k]を施すと、
  • 楕円体座標の他の定義式(1)

が得られる。これは、書籍等で最も多く採用されている表示式であるが、ラプラシアンは前述よりも複雑になるので省略する。
　また、次のJacobi の楕円関数を用いる表示式が採用されていることもある。(lは任意定数とする。)
  • 楕円体座標の他の定義式(2)

円錐座標

　Laplace 方程式の解：Lamé 関数が現れる。
　Helmholtz 方程式の解：Lamé 波動関数 (当サイト未掲載) が現れる。
　円錐の名を冠するが、実際は二つの座標方向が "楕円錐" になる座標系である。
  • 円錐座標の定義式

  • 円錐座標の図1
  • 円錐座標の図2
  • 円錐座標の図3

共焦点放物体座標

　Laplace 方程式の解：Baer 関数 (当サイト未掲載) が現れる※1。
　Helmholtz 方程式の解：Baer 波動関数 (当サイト未掲載) が現れる※1。
  • 共焦点放物体座標の定義式

  • 共焦点放物体座標の図1
  • 共焦点放物体座標の図2
  • 共焦点放物体座標の図3

　もしa^2=-b^2=cに限れば、各方程式の解および座標系の式は次のようになる。
　Laplace 方程式の解：Mathieu 関数, 変形 Mathieu 関数が現れる。
　Helmholtz 方程式の解：Whittaker - Hill 関数 (グラフ未掲載･説明文のみ) が現れる。
  • 特別な場合の共焦点放物体座標の定義式

【註記】
　※1：Baer 関数および Baer 波動関数の詳細については、
　(1) MathWorld：Baer differential equation
　(2) Wikipedia：Baer function
　(3) Wikipedia：Paraboloidal coordinates
等を参照。ただし、基礎になっている座標系の定義式は、当サイトと異なる場合がある。
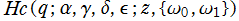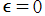　Baer 関数は、合流型 Heun 関数合流型Heun関数(Hc)でε=0とした関数と同クラスである。

曲線座標系におけるラプラシアンを求める方法

　曲線座標系が、媒介変数表示式{x, y, z}={X(λ,μ,ν),Y(λ,μ,ν), Z(λ,μ,ν)}で与えられているとき、曲線座標上の関数ψ(λ,μ,ν)のラプラシアンは、
  • ψ(λ,μ,ν)のラプラシアン

で求められる。ここに、
  • h1, h2, h3

は、座標スケール因子 (Scale factor) と呼ばれる。
　(この公式自体はベクトル解析を用いて導かれるが、その過程は省略する。長谷川 正之・稲岡 毅 ｢ベクトル解析の基礎 (第1版)｣ (1990年 森北出版) の118～127頁に分かりやすい解説がある。)

【例：球座標の場合】
　媒介変数表示式は球座標の媒介変数表示式(1)球座標の媒介変数表示式(2)であるから、座標スケール因子は
  • 球座標の h1, h2, h3

となり、球座標上の関数ψ(r,θ,φ)のラプラシアンが、

  • 球座標のラプラシアン
と求められる。

参考資料 Menu