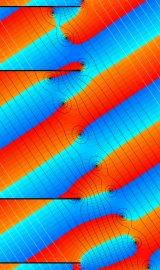
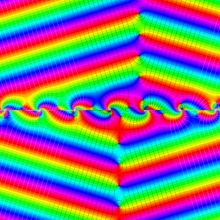
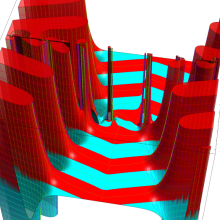
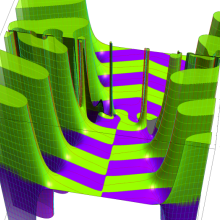
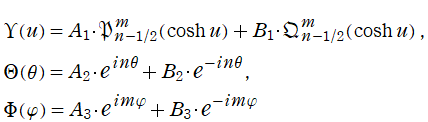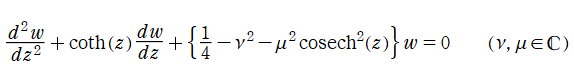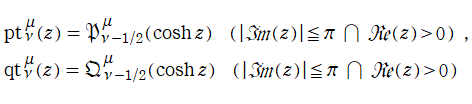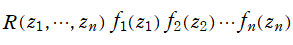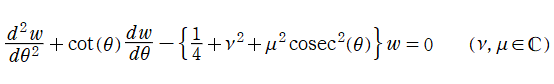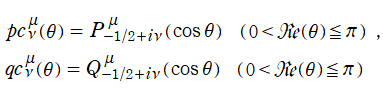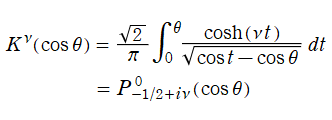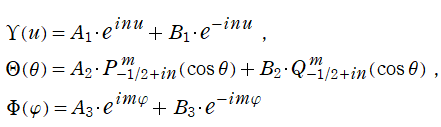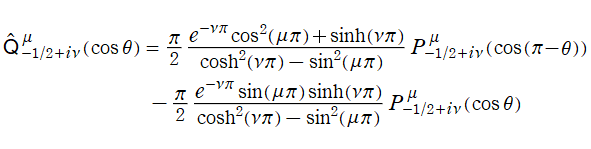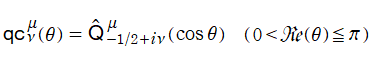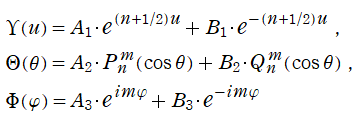特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
Legendre 関数に関連する関数
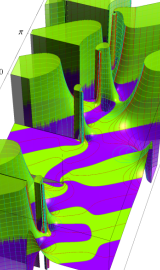
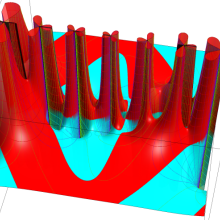
円環関数
日:円環関数,英:Toroidal function,仏:Fonction toroïdal,独:Toroidale funktion
円環座標
となる。
以降では、二階の線形常微分方程式
の解の基本系
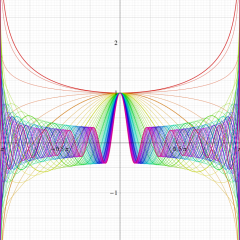
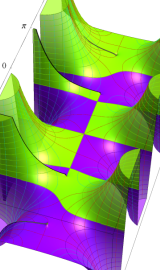
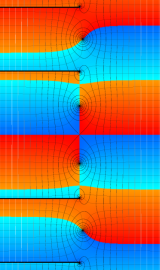
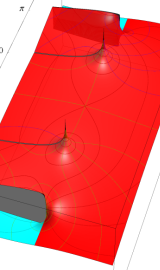
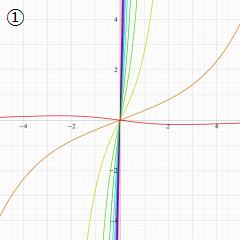
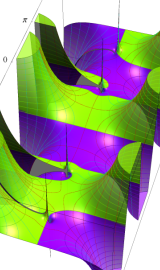
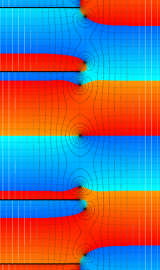
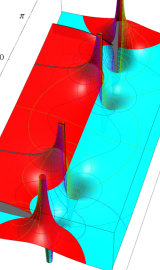
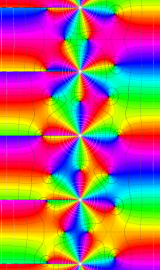
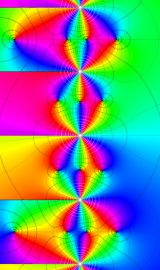
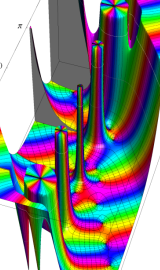
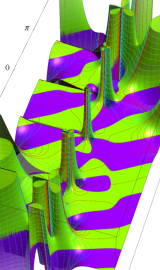
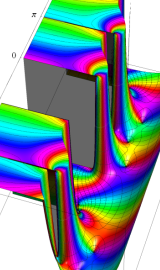
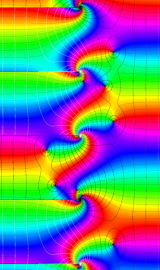
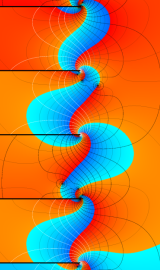
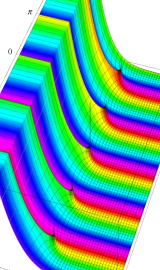
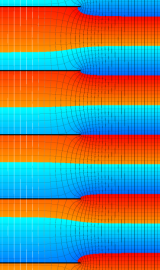
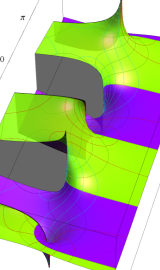
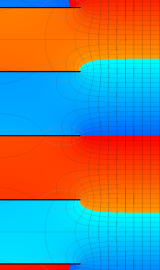
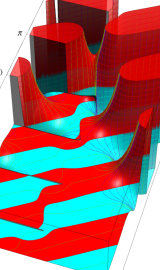
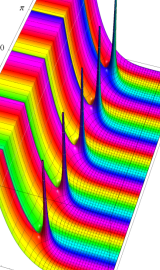
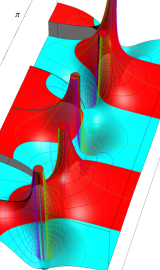
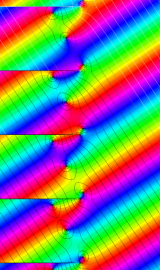
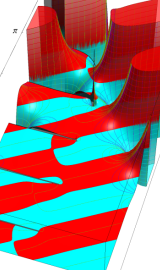
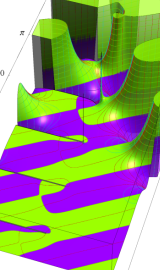
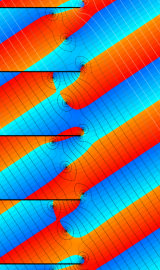
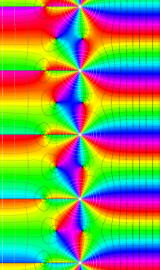
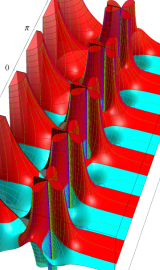
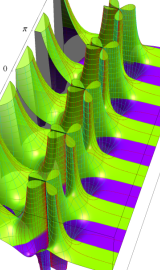
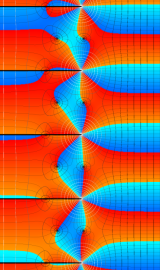
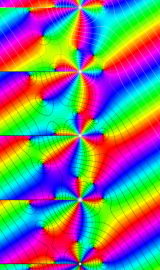
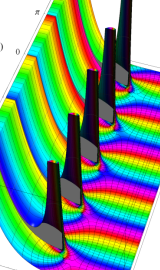
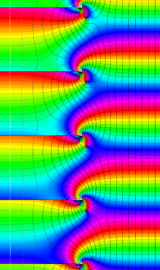
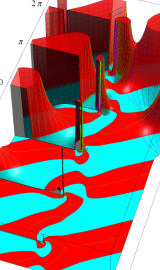
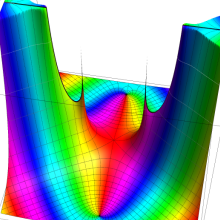
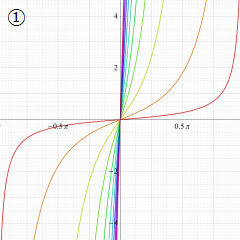
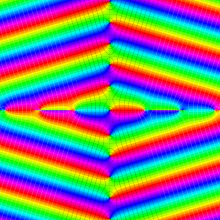
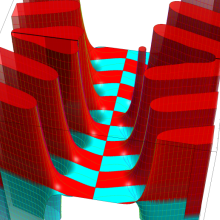
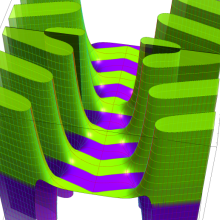
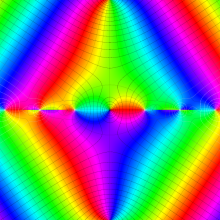
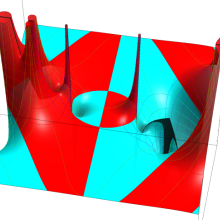
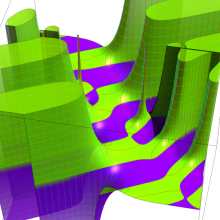
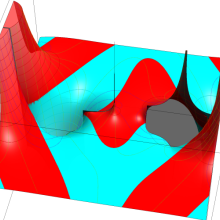
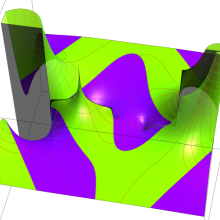
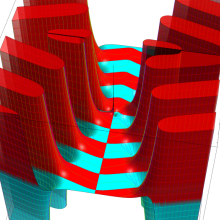
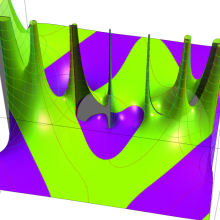
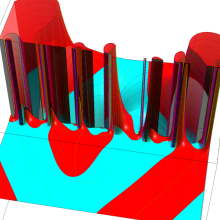
円環関数
この関数は、前述の Laplace 方程式で専ら必要となる実変数
となるが、一般に他の領域では一致せず、周期関数にもならない。この解析接続では、主に Hobson 型の頁に掲載している解析接続公式および Ferrers 型との分枝関係式を用いる※2。
【註記】
※1:偏微分方程式の解が、変数分離できない関数因子![R(z[1],…, z[n])≠ρ[1](z[1])…ρ[n](z[n])](siki_spec170/legendrerel02300.png) を伴った、
を伴った、
の形にならば分離できる場合を、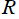 - 分離可能 (
- 分離可能 (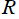 - Separable) という。
- Separable) という。
※2:Mathematica のコード 「GaussHypergeometric.m」 では、Ferrers 型または Hobson 型の Legendre 陪関数に、余弦関数または双曲線余弦関数を代入した関数の、様々な解析接続を実装した。これを用いれば、当サイトとは異なる分枝切断線を持つ円環関数 (または後述の円錐関数) も計算できる。
※1:偏微分方程式の解が、変数分離できない関数因子
の形にならば分離できる場合を、
※2:Mathematica のコード 「GaussHypergeometric.m」 では、Ferrers 型または Hobson 型の Legendre 陪関数に、余弦関数または双曲線余弦関数を代入した関数の、様々な解析接続を実装した。これを用いれば、当サイトとは異なる分枝切断線を持つ円環関数 (または後述の円錐関数) も計算できる。
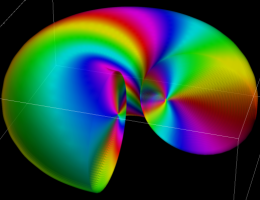
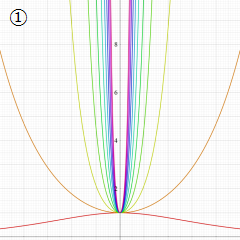
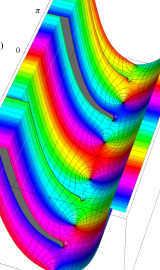
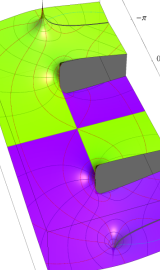
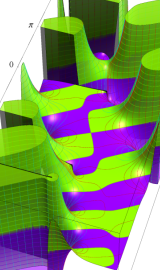
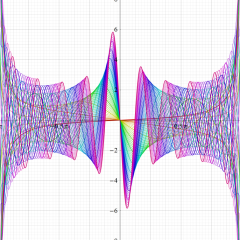
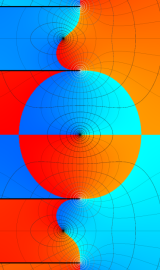
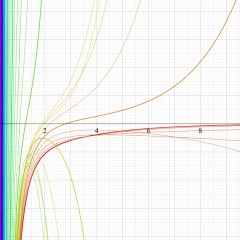
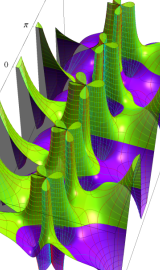
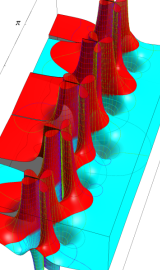
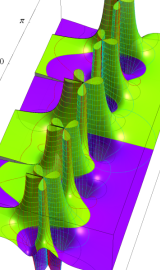
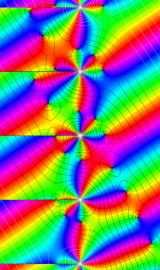
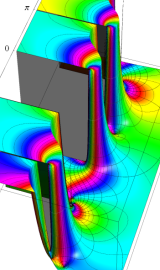
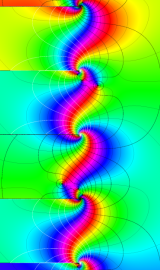
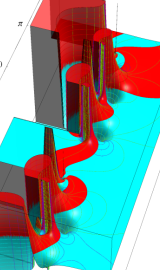
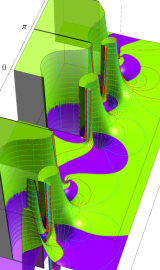
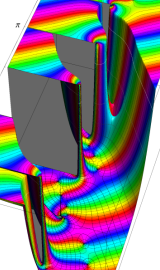
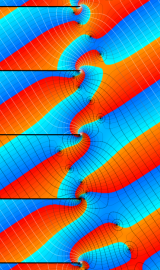
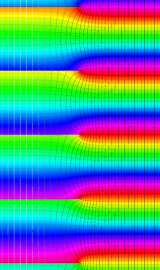
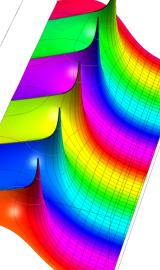
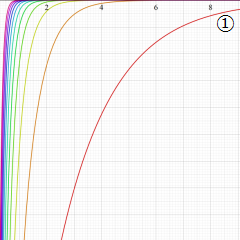
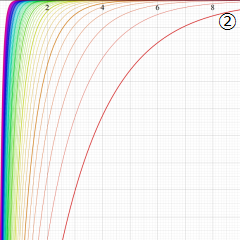
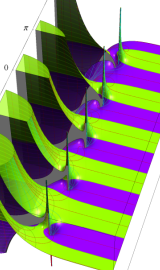
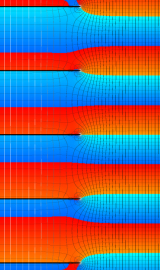
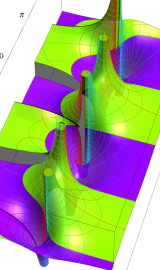
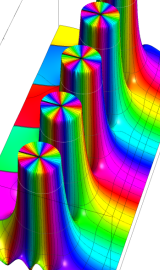
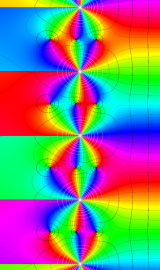
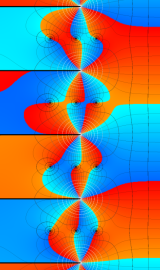
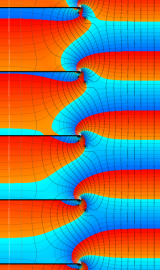
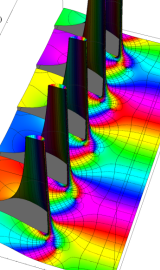
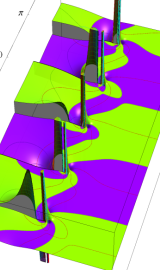
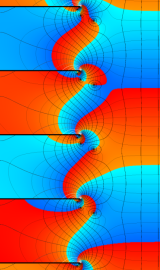
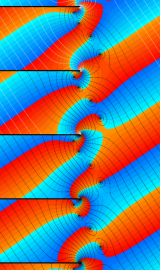
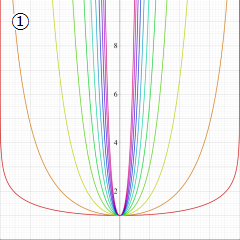
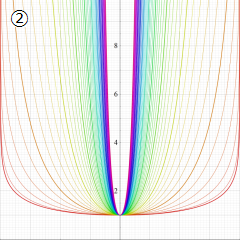
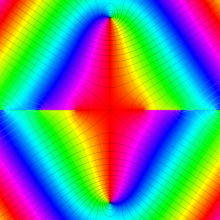
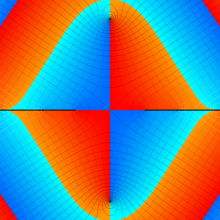
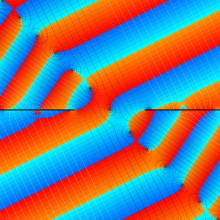
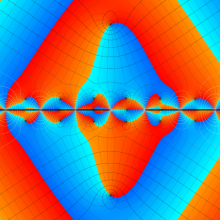
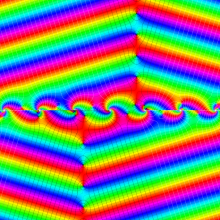
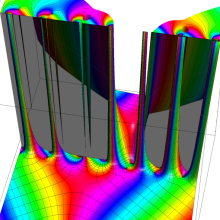
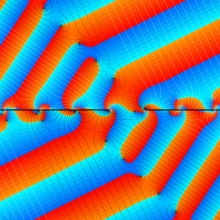
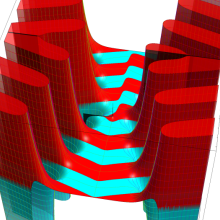
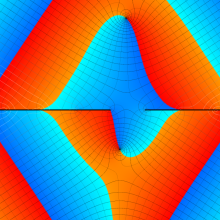
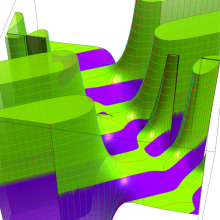
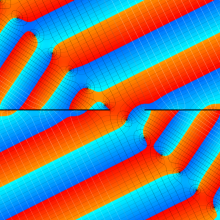
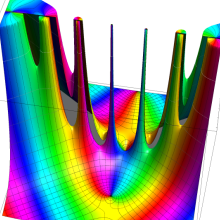
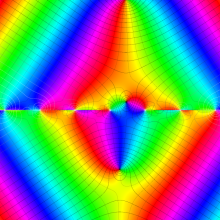
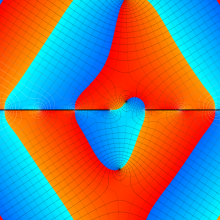
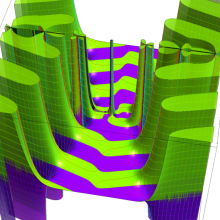
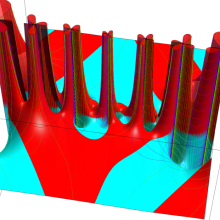
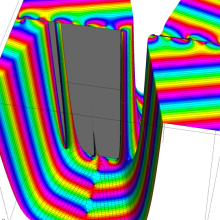
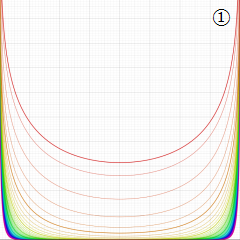
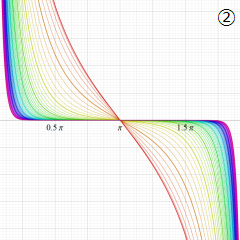
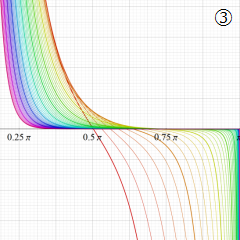
虚軸上での第1種円環関数
虚軸上での第1種円環関数
(
虚軸上での第1種円環関数
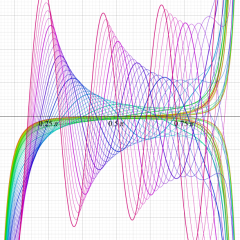
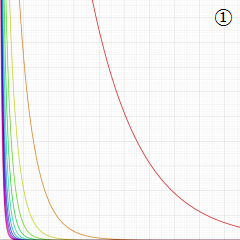
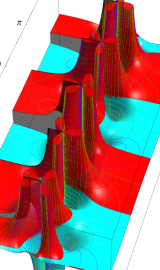
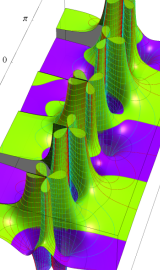
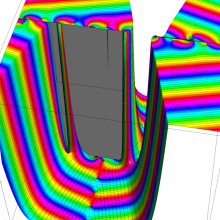
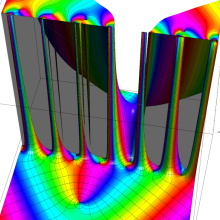
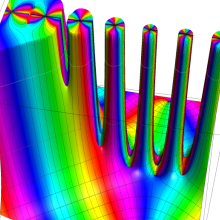
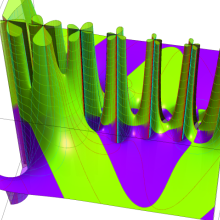
円錐関数
日:円錐関数,英:Conical function,仏:Fonction conique,独:Kegelfunktion
二階の線形常微分方程式
の解の基本系
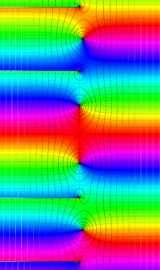
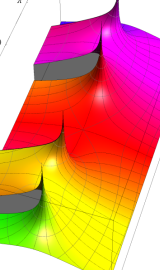
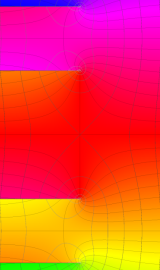
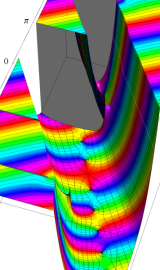
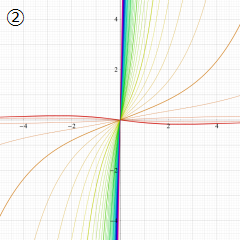
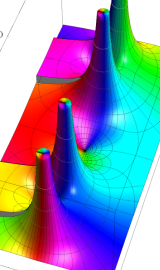
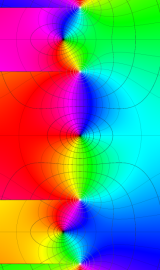
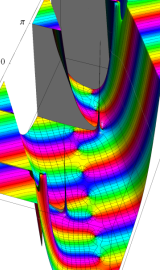
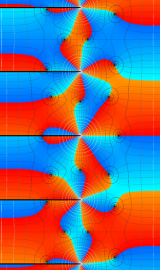
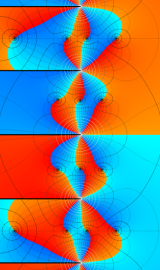
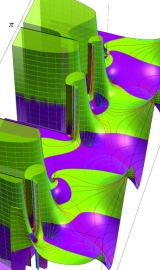
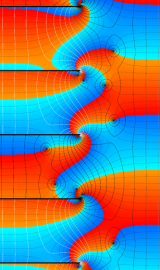
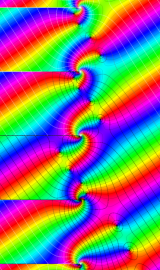
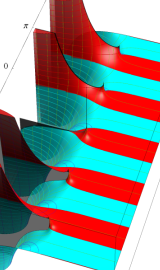
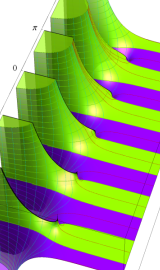
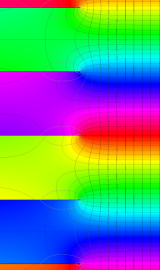
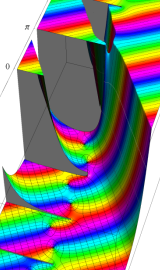
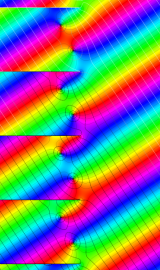
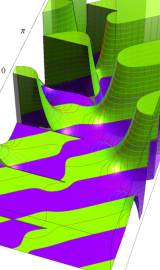
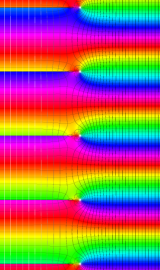
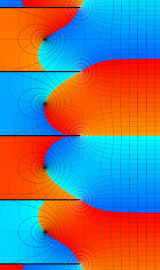
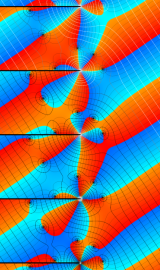
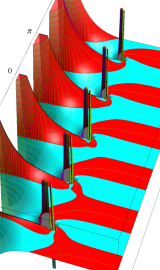
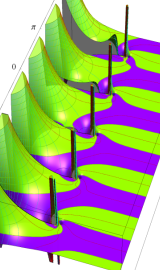
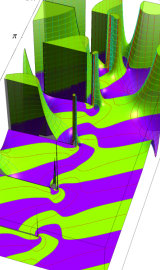
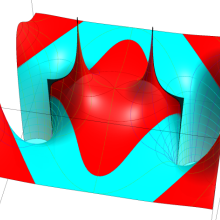
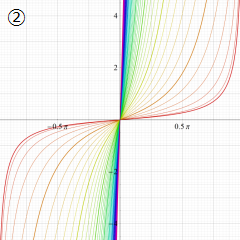
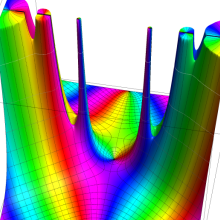
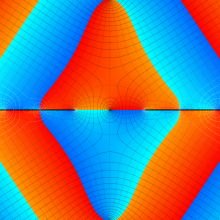
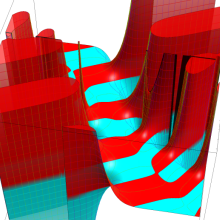
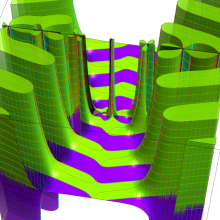
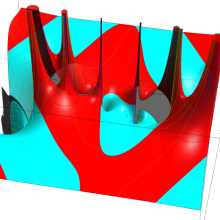
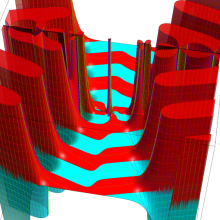
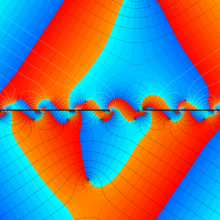
円錐関数
この関数は、元々の円錐関数で専ら必要となる実変数
となるが、一般に他の領域では一致せず、周期関数にもならない。この解析接続も、主に Hobson 型の頁に掲載している解析接続公式および Ferrers 型との分枝関係式を用いる。
この関数が名称に "円錐" を冠する理由は、やや複雑である。G. F. Mehler は1881年の論文※2で、球座標 (ただし
以上のことを踏まえて、Mehler は論文中で度々用いた積分関数
を "円錐関数" と呼んでおり、恐らくこれが名称の起源になっていると思われる。また、円錐関数はしばしば 「Mehler の関数」 と呼ばれる。
Laplace 方程式の解として円錐関数が現れるような変数分離の座標系は円錐座標※3ではなく、強いて言えば双極座標である。C. Neumann は1881年の論文※4で紡錘形※5の周囲に生じる電界を論じた際、双極座標を用いて "Mehler の円錐関数" を導き、これを詳しく考察している。
実際、双極座標
となり、
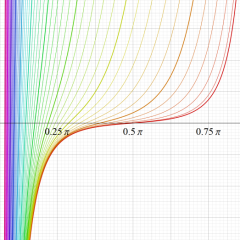
NISTの14.20で定義されている円錐関数は、
となっている (ただし、NISTでは引数に余弦関数を代入しない)。この関数に対しても、分枝が単連結となるよう前述と同様の解析接続を施して、
を満たすようにした関数
【註記】
※1:引数に余弦関数を代入しない定義、さらに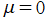 の場合を、円錐関数と呼ぶことも多い。
の場合を、円錐関数と呼ぶことも多い。
なお、](siki_spec170/legendrerel08700.png) ,
, ](siki_spec170/legendrerel08800.png)
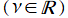 のグラフは、既に Legendre 関数の頁に多数掲載している。
のグラフは、既に Legendre 関数の頁に多数掲載している。
※2:Ueber eine mit den Kugel- und Cylinderfunctionen verwandte Function und ihre Anwendung in der Theorie der Elektricitatsvertheilung. Mathematische Annalen 18 (1881) p.161-194
※3:円錐座標ならば、3方向の解のうち2方向は (代数的) Lamé 関数、1方向は冪関数が基底関数になる。円錐座標における円錐面は実際には楕円錐面であるため、双極座標よりもはるかに複雑になる。
※4:Ueber die Mehler'schen Kegelfunctionen und deren Anwendung auf elektrostatische Probleme. Mathematische Annalen 18 (1881) p.195-236
※5:Neumann は、この紡錘形をコノイド (Conoid) と称しているが、現在通用しているコノイドは一般的な線織面のことを言うので、意味が異なる。
※6:本来、双極座標における Laplace 方程式の解は、位相の 1/2 ずれを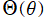 に寄せず、
に寄せず、
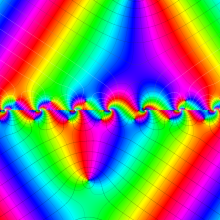
とするのが標準的な表示である。その場合、固有関数の図は次のようになる。
※1:引数に余弦関数を代入しない定義、さらに
なお、
※2:Ueber eine mit den Kugel- und Cylinderfunctionen verwandte Function und ihre Anwendung in der Theorie der Elektricitatsvertheilung. Mathematische Annalen 18 (1881) p.161-194
※3:円錐座標ならば、3方向の解のうち2方向は (代数的) Lamé 関数、1方向は冪関数が基底関数になる。円錐座標における円錐面は実際には楕円錐面であるため、双極座標よりもはるかに複雑になる。
※4:Ueber die Mehler'schen Kegelfunctionen und deren Anwendung auf elektrostatische Probleme. Mathematische Annalen 18 (1881) p.195-236
※5:Neumann は、この紡錘形をコノイド (Conoid) と称しているが、現在通用しているコノイドは一般的な線織面のことを言うので、意味が異なる。
※6:本来、双極座標における Laplace 方程式の解は、位相の 1/2 ずれを
とするのが標準的な表示である。その場合、固有関数の図は次のようになる。
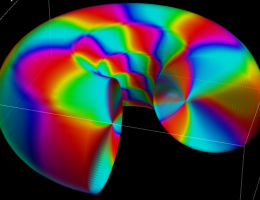
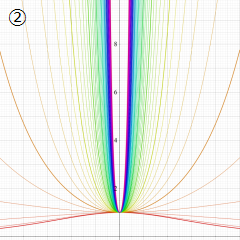
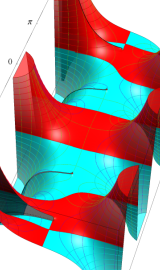
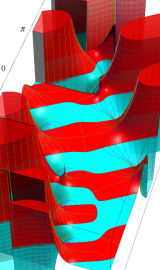
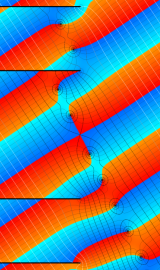
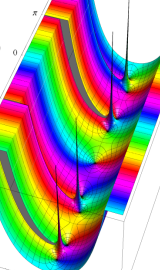
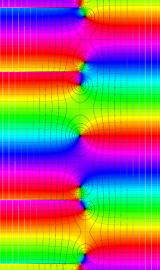
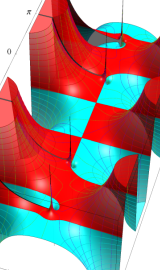
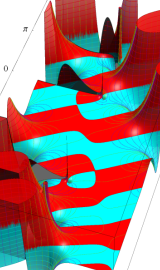
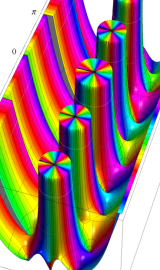
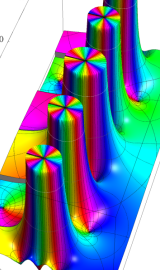
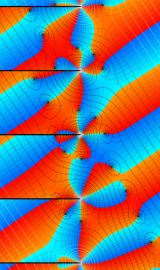
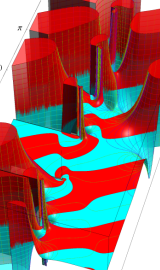
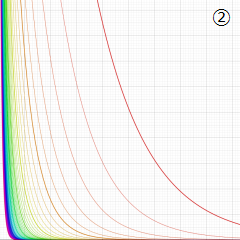
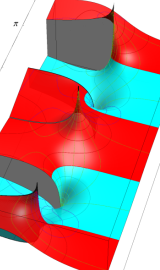
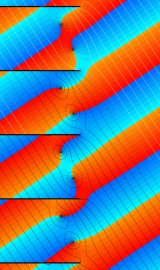
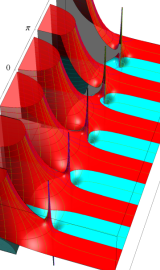
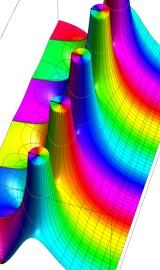
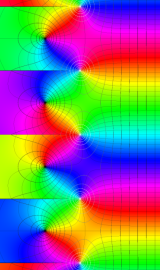
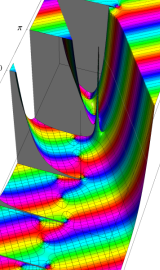
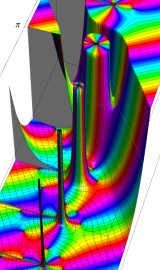
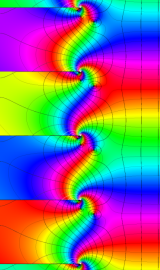
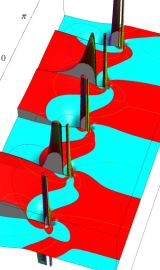
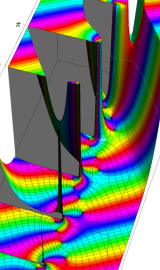
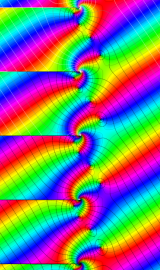
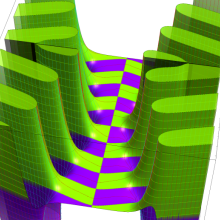
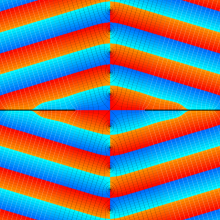
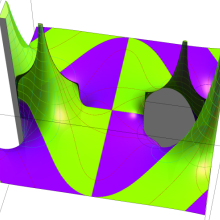
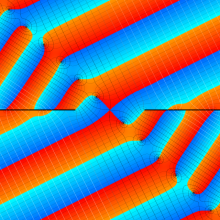
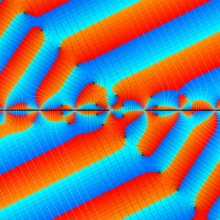
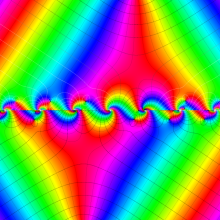
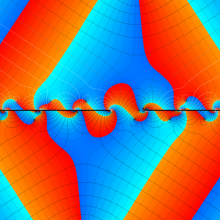
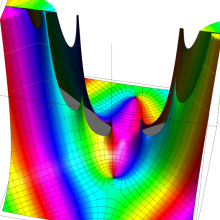
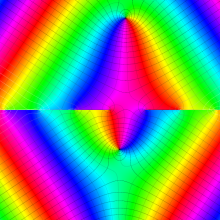
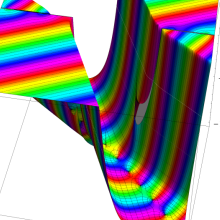
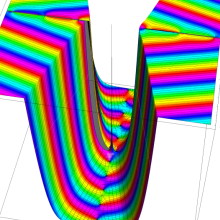
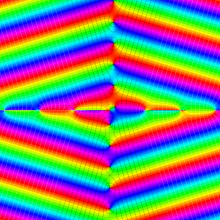
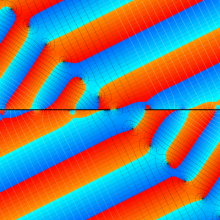
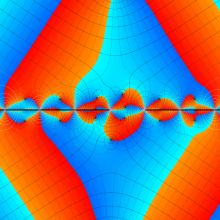
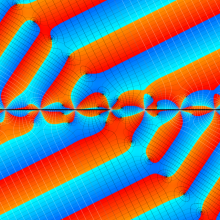
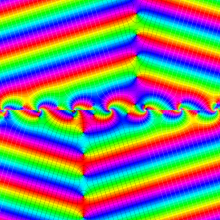
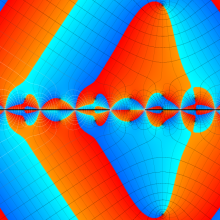
複素変数の第2種円錐関数