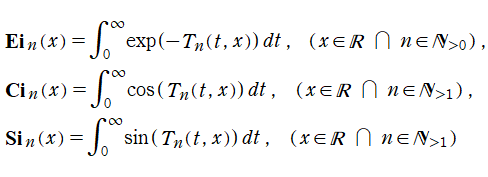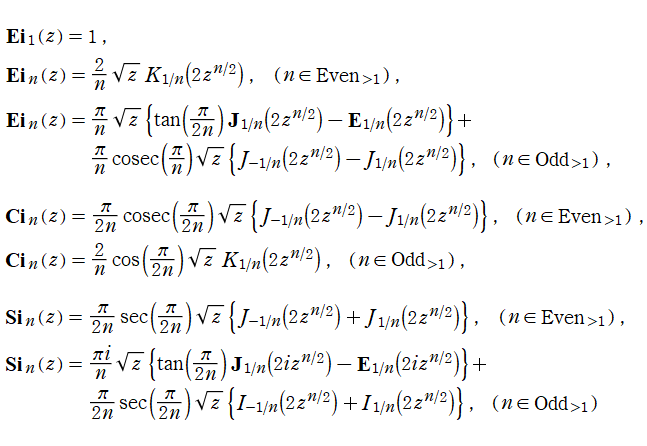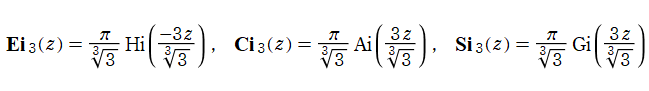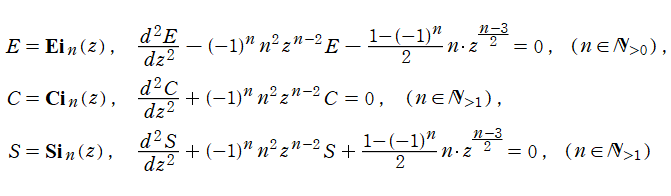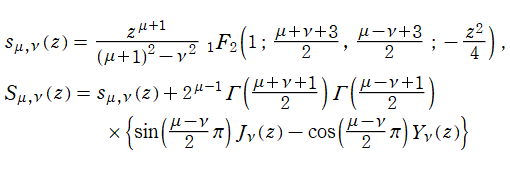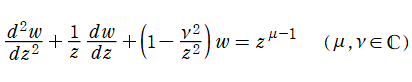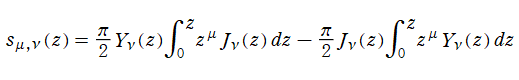特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
Bessel 関数に関連する関数
Struve 関数
日:Struve関数,ストルーヴェ関数英:Struve function,仏:Fonction de Struve,独:Struvesche funktion
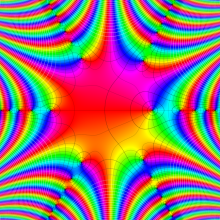
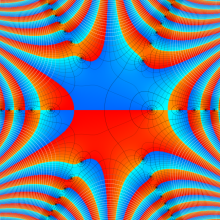
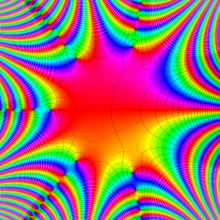
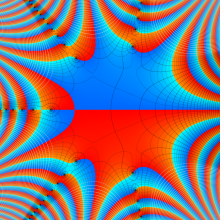
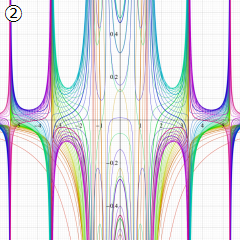
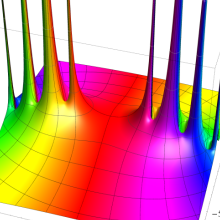
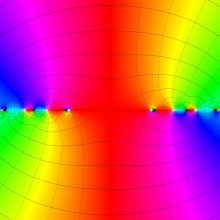
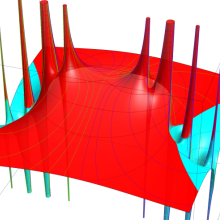
Struve 関数
の一般解として、
で定義される。
を満たす。希に、
一方、変形 Struve 関数
の一般解として、
で定義される。
を満たす。希に、
Struve 関数および変形 Struve 関数は、正規化された一般超幾何関数の特別な場合
として表わせる。また、両者は次数
となる。
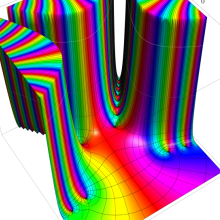
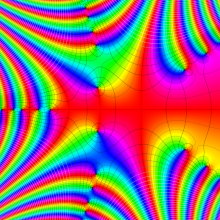
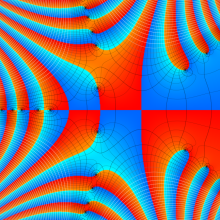
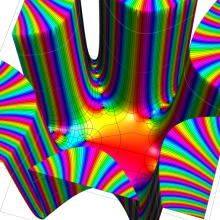
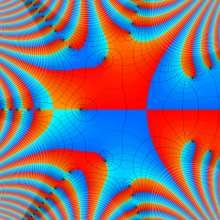
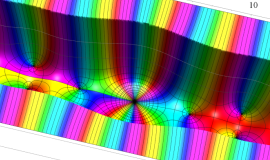
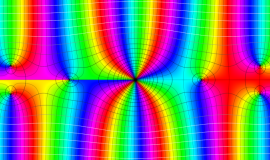
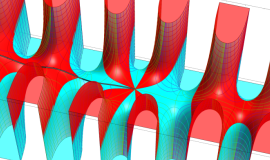
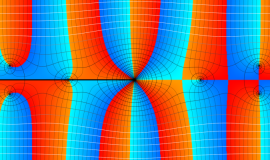
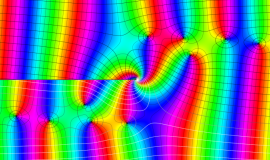
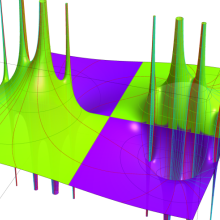
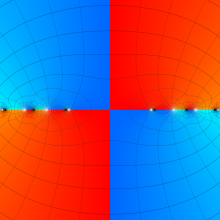
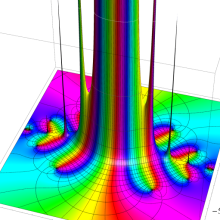
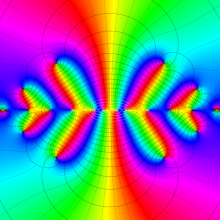
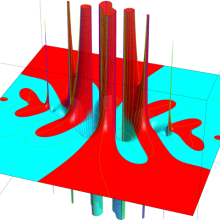
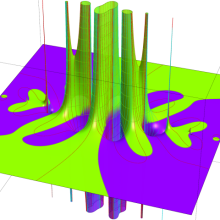
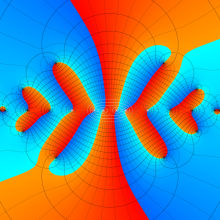
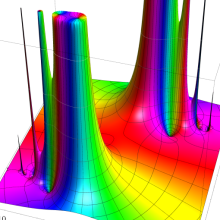
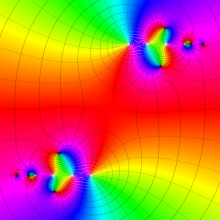
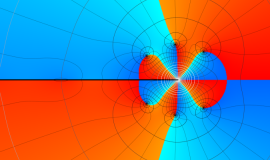
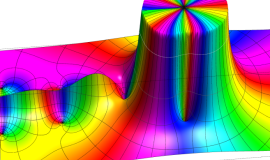
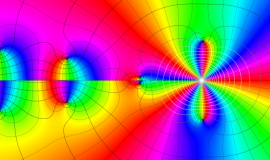
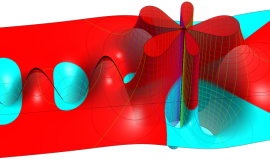
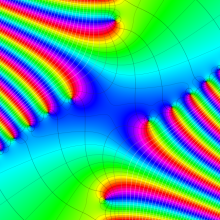
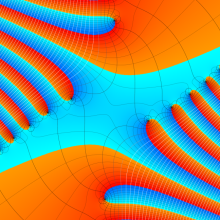
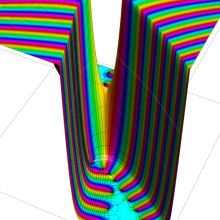
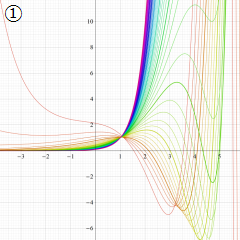
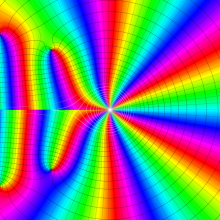
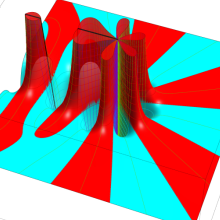
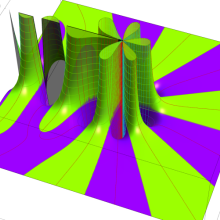
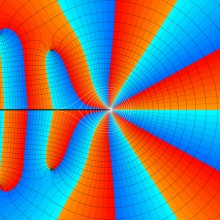
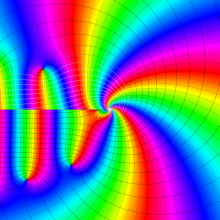
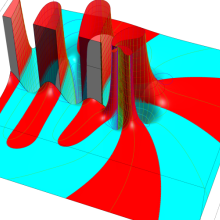
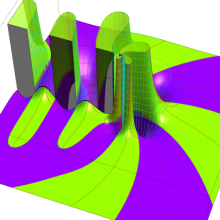
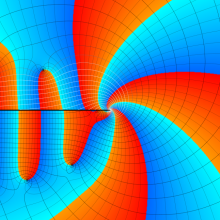
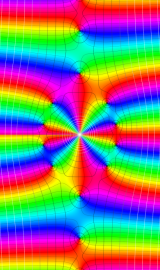
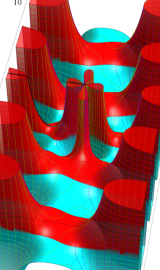
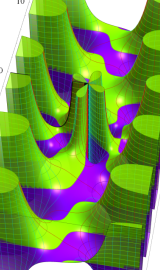
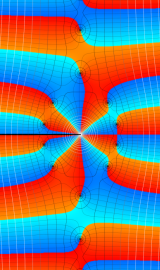
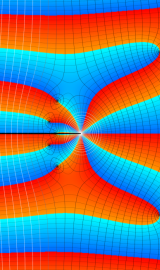
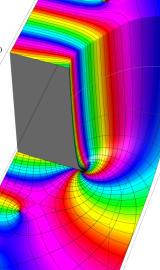
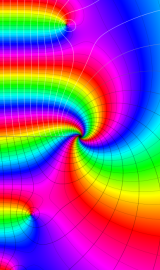
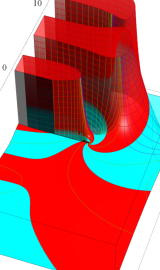
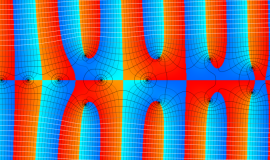
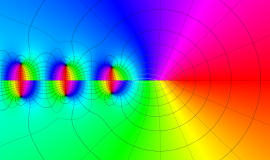
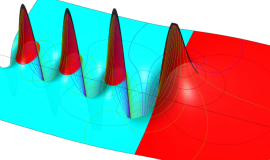
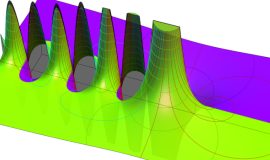
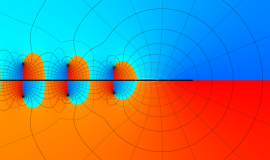
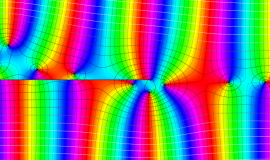
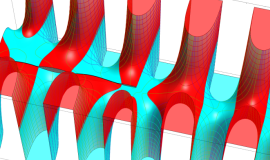
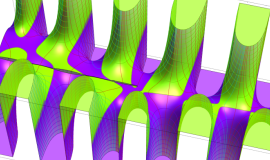
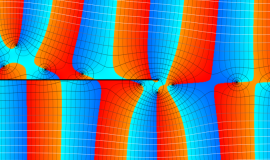
一般に Struve 関数および変形 Struve 関数は、複素平面上
Struve 関数は、光学望遠鏡の改良に関連して K. H. Struve が1882年に導入した。また変形 Struve 関数は、J. W. Nicholson が1911年に導入した。Struve 関数の応用事例は徐々に増えつつあり、流体力学 (非定常空気力学、流体中の物体の振動など)、光の回折現象、電磁気学、量子力学 (デコヒーレンス、ナノチューブ) 等が知られている。
【註記】
E. Jahnke,F. Emde 著 「Tables of Functions with formulae and curves」 では、次の優雅な記号で Struve 関数を表記している。(フォント 「INOVATOR」 で表示した S。)
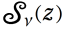
E. Jahnke,F. Emde 著 「Tables of Functions with formulae and curves」 では、次の優雅な記号で Struve 関数を表記している。(フォント 「INOVATOR」 で表示した S。)
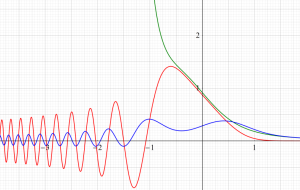
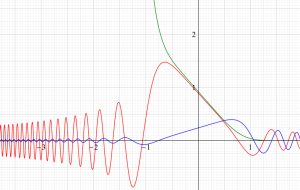
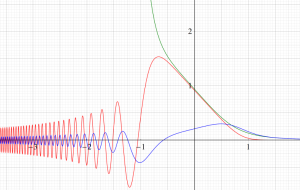
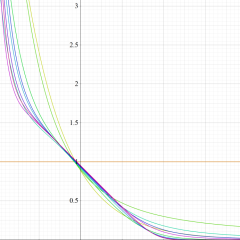
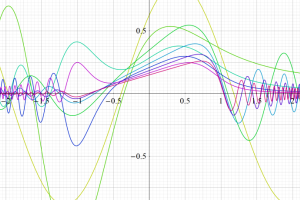
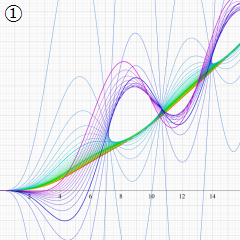
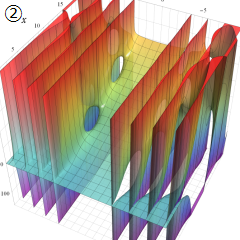
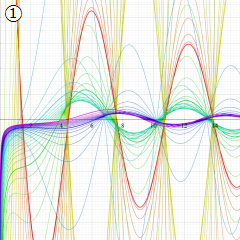
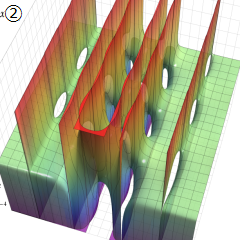
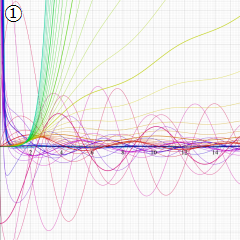
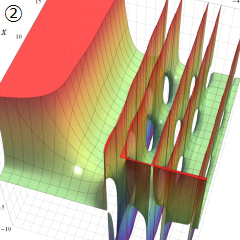
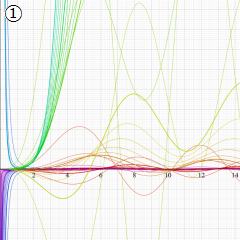
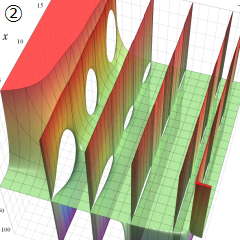
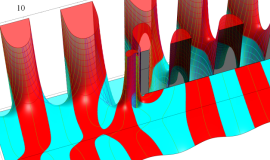
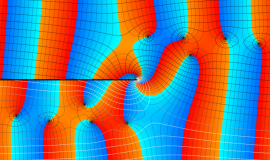
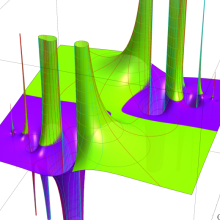
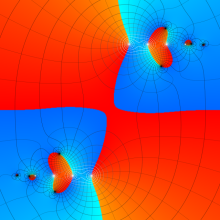
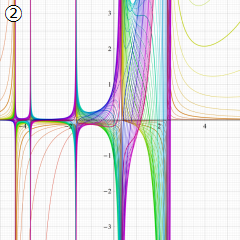
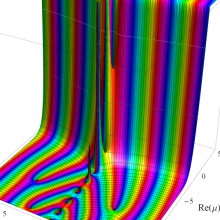
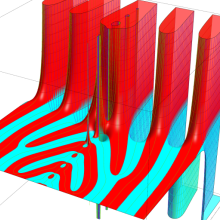
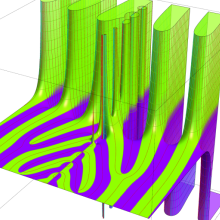
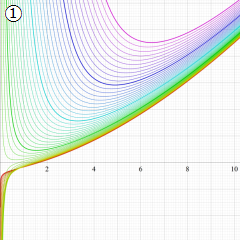
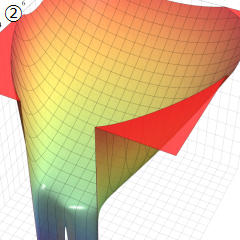
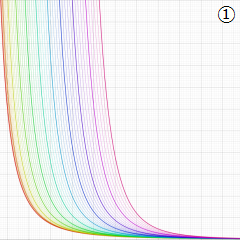
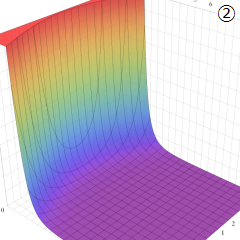
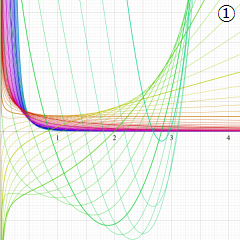
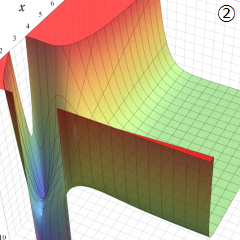
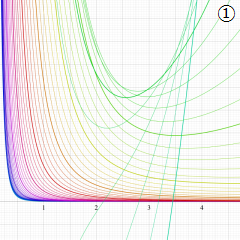
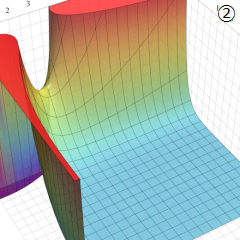
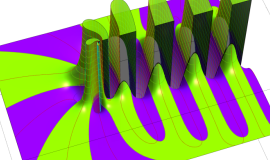
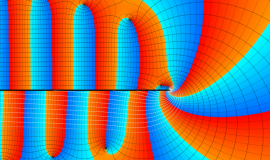
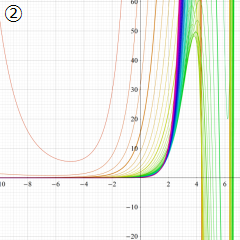
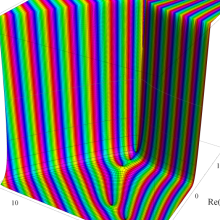
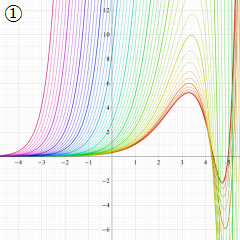
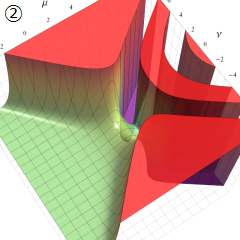
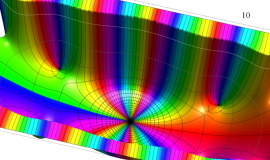
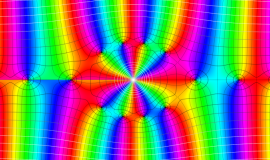
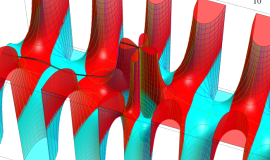
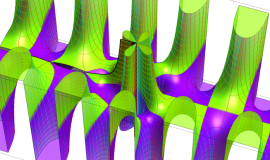
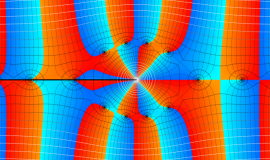
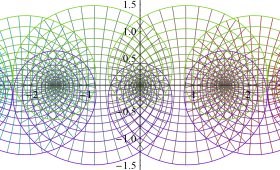
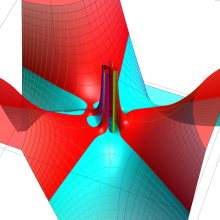
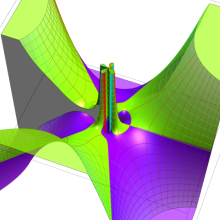
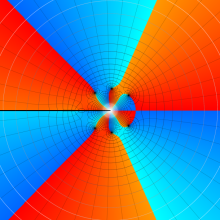
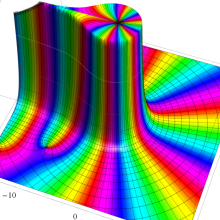
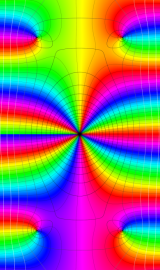
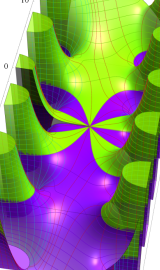
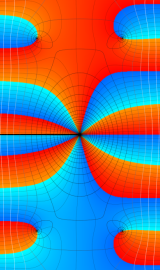
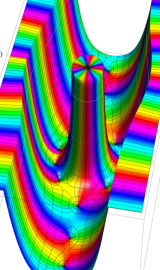
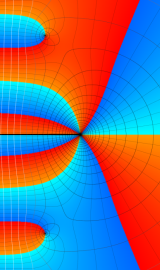
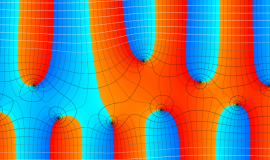
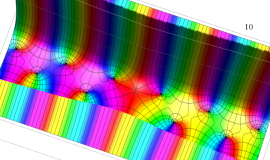
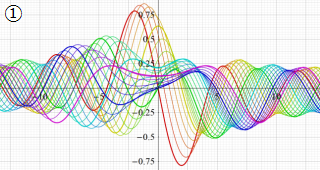
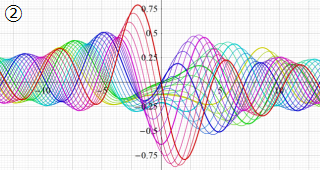
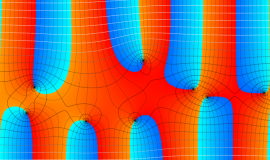
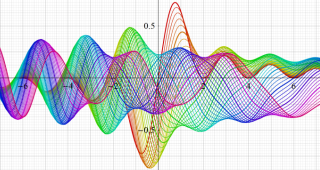
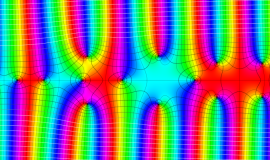
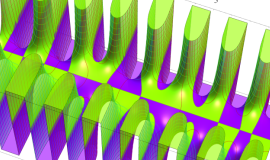
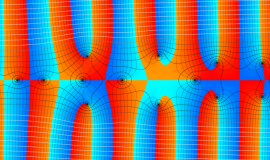
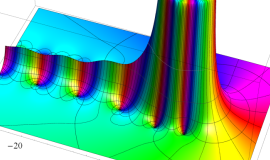
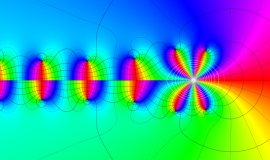
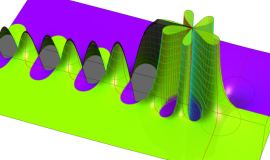
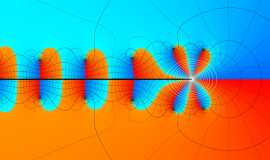
Struve 関数
Struve 関数
アニメーション(11.4MB)
アニメーション(7.24MB)
Anger - Weber 関数
日:Anger関数,アンガー関数英:Anger function,仏:Fonction d'Anger,独:Angersche funktion
日:Weber関数,ウェーバー関数
英:Weber function,仏:Fonction de Weber,独:Webersche funktion
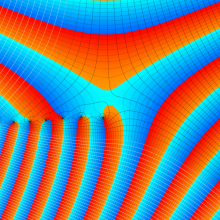
Anger 関数
で定義され※1、非斉次の Bessel の微分方程式
を満たす。希に、Anger - Weber 同伴関数
が導入されることもある (「NIST-Handbook of Mathematical Functions」 の Chapter11:p.287~)。ただし、2番目の式は l'Hôpital の定理を適用して極限をとれば、
それぞれの関数は互いに、
等の関係にある。また、非斉次の線形漸化式 (隣接関係式)
を満たす。
特に、
のように Bessel 関数、Struve 関数で表わされる。
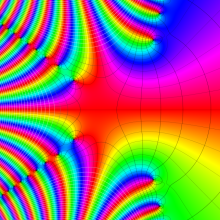
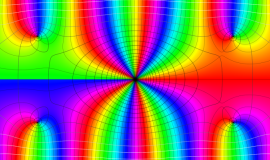
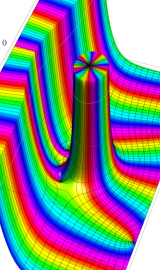
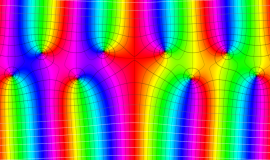
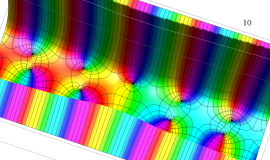
Anger 関数
上記の公式等からも推察されるように、応用上は Struve 関数とともに用いられることが多い。Anger 関数の名称は C. T. Anger (1855年)、Weber 関数の名称は H. F. Weber (1879年) の研究結果に因む。Weber 関数は、Weber - Lommel 関数と呼ばれることもある。
【註記】
※1:特に](siki_spec140/besselrel06000.png) の積分表示式は、整数次の第1種 Bessel 関数のそれと全く同じ形であり、その次数を非整数次に読み替えただけであることに注目して欲しい。
の積分表示式は、整数次の第1種 Bessel 関数のそれと全く同じ形であり、その次数を非整数次に読み替えただけであることに注目して欲しい。
※1:特に
以降では、
以降では、
アニメーション(10.8MB)
Whittaker 積分関数
日:Whittaker積分関数,ホイッタカーの積分英:Whittaker's integral,仏:Intégrale de Whittaker,独:Whittakersche Integrale
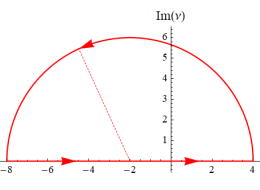
Whittaker 積分関数は、積分表示式
で定義される。ここに、
また、Whittaker 積分関数は正規化された一般超幾何関数、およびその部分を冪級数に展開した式
でも表わされる。冪級数展開式のガンマ関数係数が
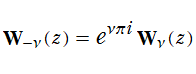
を満たす。特に、
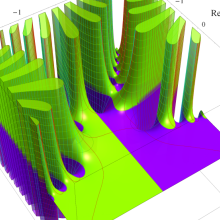
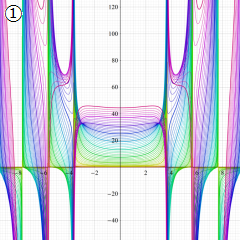
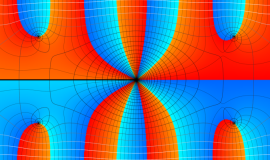
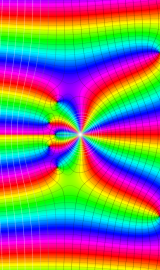
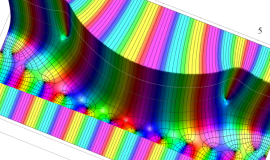
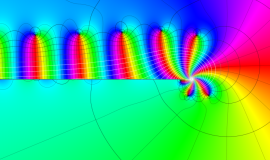
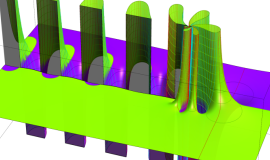
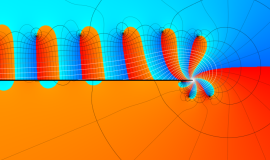
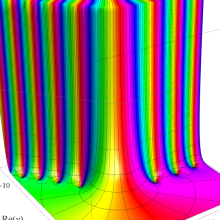
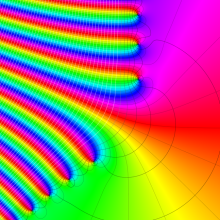
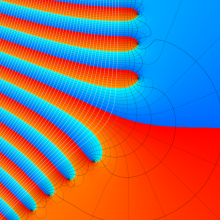
Whittaker 積分関数は複素平面上
Whittaker 積分関数は、E. T. Whittaker が Bessel 関数と Legendre 関数の関係を論じた1902年の論文で初めて導入した関数であって※1、合流型超幾何微分方程式の一般解として有名な Whittaker 関数とは異なる。
【註記】
※1:E. T. Whittaker 「On a New Connexion of Bessel Functions with Legendre Functions」 Proceedings of the London Mathematical Society, Vol.s1-35, Issue 1, (1902年), p.198-206
なお、この関数に言及している (管理人が知る限りの) 他の書籍とその掲載頁として、
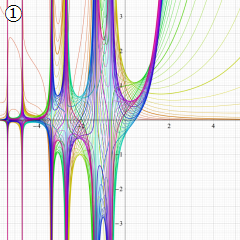
① G. N. Watson 「A Treatise on the Theory of Bessel Functions」 (1922年) の p.339,
② 森口繁一,宇田川銈久,一松 信 「岩波 数学公式Ⅲ 特殊関数」 (1960年) の p.231
がある。②はその記述内容から、恐らく①を情報源にしていると思われる。一方、比較的新しい書籍では、この関数をほとんど見かけない。
※1:E. T. Whittaker 「On a New Connexion of Bessel Functions with Legendre Functions」 Proceedings of the London Mathematical Society, Vol.s1-35, Issue 1, (1902年), p.198-206
なお、この関数に言及している (管理人が知る限りの) 他の書籍とその掲載頁として、
① G. N. Watson 「A Treatise on the Theory of Bessel Functions」 (1922年) の p.339,
② 森口繁一,宇田川銈久,一松 信 「岩波 数学公式Ⅲ 特殊関数」 (1960年) の p.231
がある。②はその記述内容から、恐らく①を情報源にしていると思われる。一方、比較的新しい書籍では、この関数をほとんど見かけない。
アニメーション(17.2MB, 8.89MB)
Airy - Hardy 積分関数
日:Airy-Hardy積分関数,エアリー・ハーディー積分英:Airy-Hardy integral,仏:Intégrale d'Airy-Hardy,独:Airy-Hardy Integrale
多項式
と表わされるとき、積分
を Airy - Hardy 積分関数という。これは、Airy 関数 (の積分表示式) の拡張を意図して、G. H. Hardy が1910年に導入した※1。
Airy - Hardy 積分関数は、次のとおり Bessel 関数, 変形 Bessel 関数, Anger 関数, および Weber 関数で表わされる。
ただし、冪関数が代入された Bessel 関数と変形 Bessel 関数は解析接続されているとし、そのとき上記の関数は全て超越整関数になる。
に還元される。
Airy - Hardy 積分関数は、斉次または非斉次の線形常微分方程式
を満たす。特に、
【註記】
※1:G. H. Hardy 「On certain definite integrals considered by Airy and Stokes」 Quarterly Journal 41 (1910年) p.226 - 240
なお、この関数も、
① 「A Treatise on the Theory of Bessel Functions」 の p.320-324,
② 「岩波 数学公式Ⅲ 特殊関数」 の p.231-232
に詳細な記述があるが、②にある微分方程式は一部が誤っている。また、②ではこの関数の名称を 「一般 Airy 積分」 としている。
※2:もし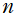 を非自然数に拡張できれば、さらに高等な関数が現れると思われるが、これを論じている文献等は今のところ見当たらない。(微分方程式の係数に
を非自然数に拡張できれば、さらに高等な関数が現れると思われるが、これを論じている文献等は今のところ見当たらない。(微分方程式の係数に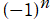 が現れるので、恐らく難しい。)
が現れるので、恐らく難しい。)
※1:G. H. Hardy 「On certain definite integrals considered by Airy and Stokes」 Quarterly Journal 41 (1910年) p.226 - 240
なお、この関数も、
① 「A Treatise on the Theory of Bessel Functions」 の p.320-324,
② 「岩波 数学公式Ⅲ 特殊関数」 の p.231-232
に詳細な記述があるが、②にある微分方程式は一部が誤っている。また、②ではこの関数の名称を 「一般 Airy 積分」 としている。
※2:もし
Lommel 関数
日:Lommel関数,ロンメル関数英:Lommel function,仏:Fonction de Lommel,独:Lommelsche funktion
Lommel 関数
と定義され、非斉次の Bessel の微分方程式
を満たす、第1種・第2種 Bessel 関数とは線形独立な解である。ただし、
特に、
によっても定義できる。また、Lommel 関数は第1種 Bessel 関数項の無限級数
によっても表わせる。
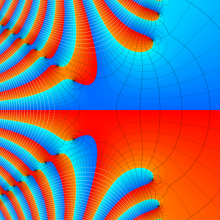
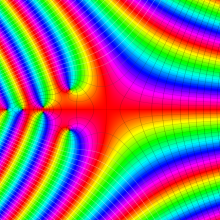
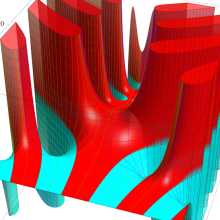
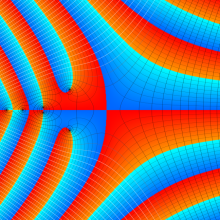
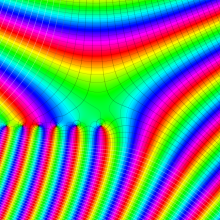
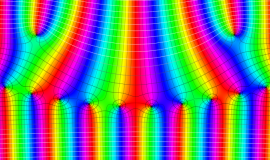
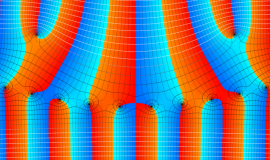
一般に Lommel 関数は、複素平面上
Lommel 関数は、Bessel 関数の詳細な研究をおこなった E. von Lommel によって1880年に導入された。現在、Bessel 関数系の公式には Lommel の名を冠するものが多く、その影響の大きさを窺わせる。
【註記】
※1:関数記号は, S[μ,ν](z)](siki_spec140/besselrel13800.png) が一般的であるが、これを
が一般的であるが、これを, S2[μ,ν](z)](siki_spec140/besselrel14700.png) で表記することもある (例えば 「Wolfram Math World」 は後者を採用している)。
で表記することもある (例えば 「Wolfram Math World」 は後者を採用している)。
※1:関数記号は
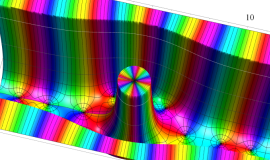
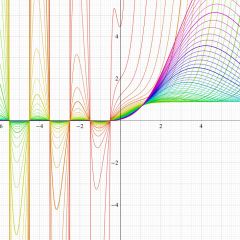
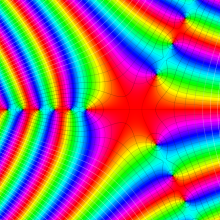
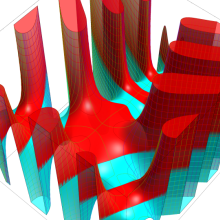
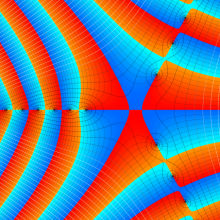
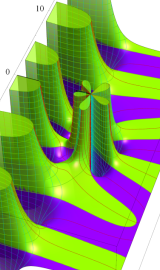
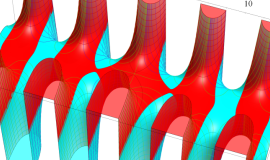
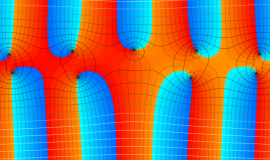
Lommel 関数
Lommel 関数
Lommel 関数
Lommel 関数
Lommel 関数
Lommel 関数
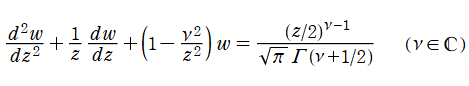
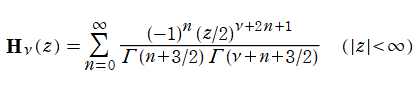
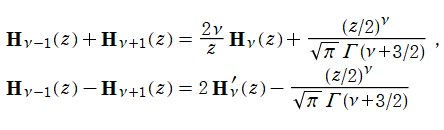

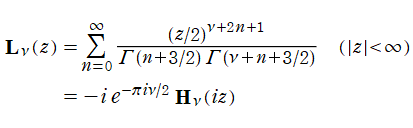
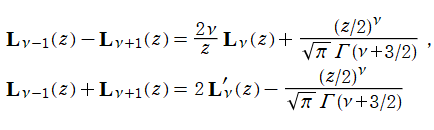
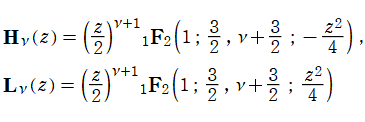
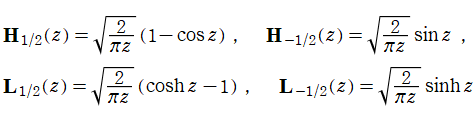













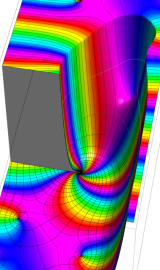
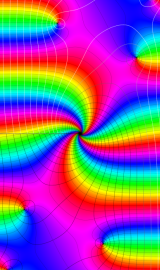

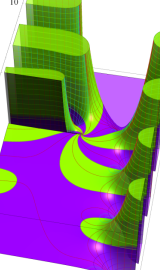
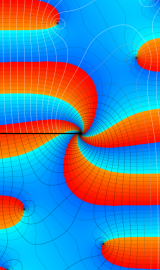














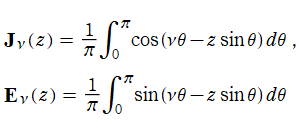
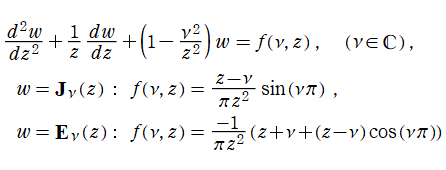
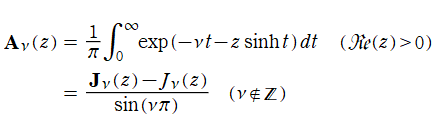
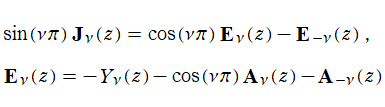
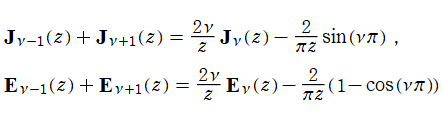
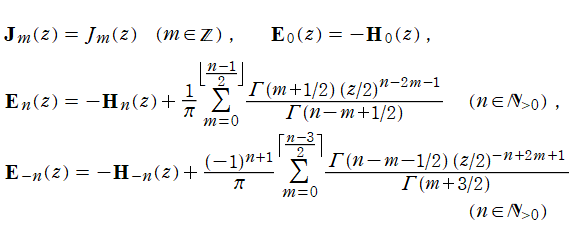


















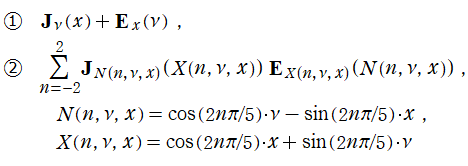








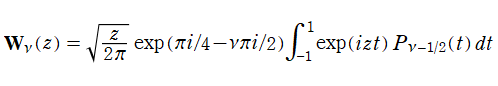
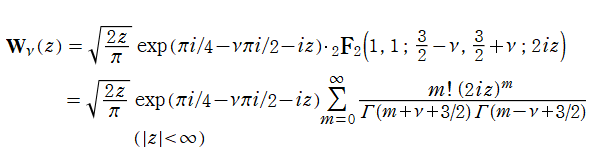
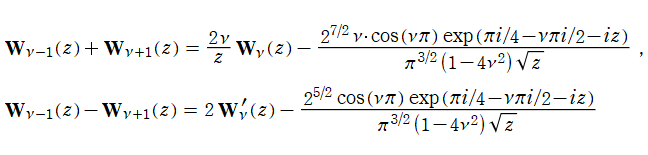





の定義式](siki_spec140/besselrel11300.png)