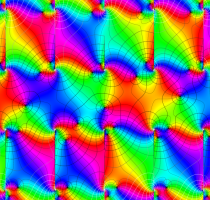
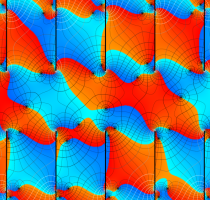
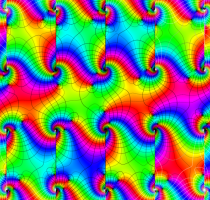
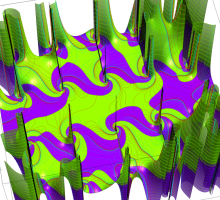
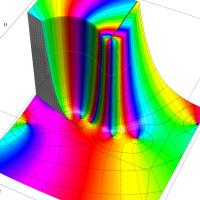
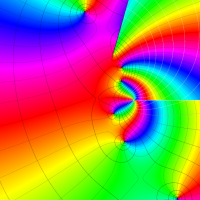
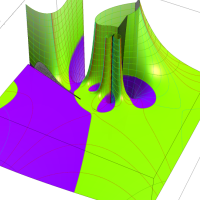
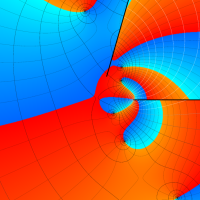
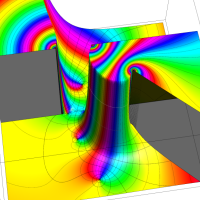
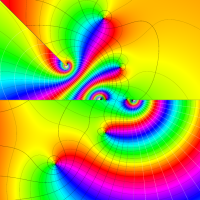
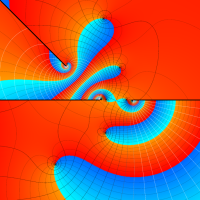
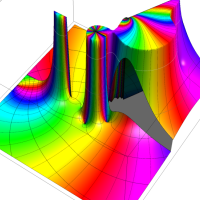
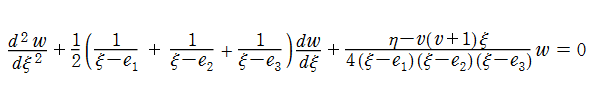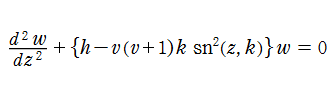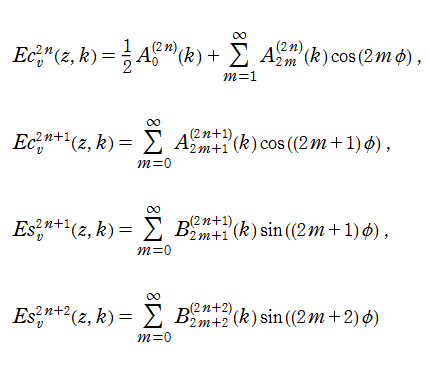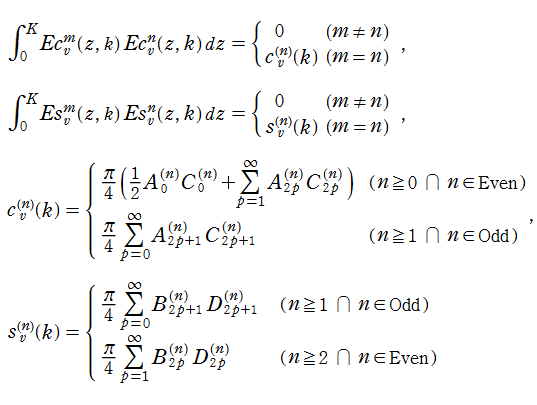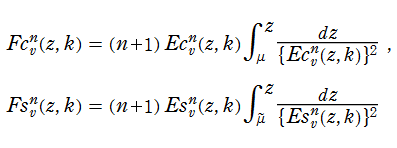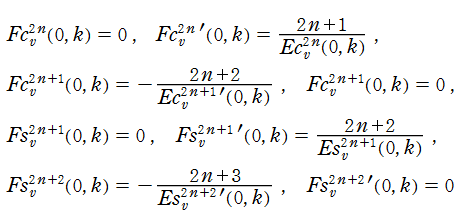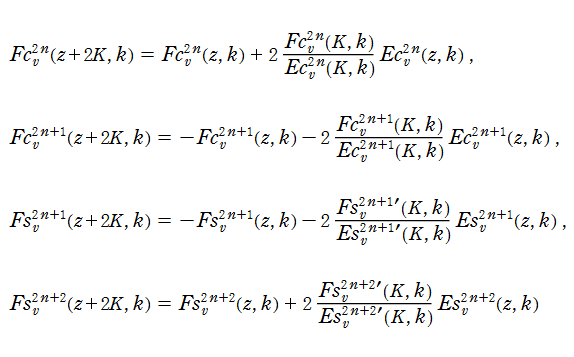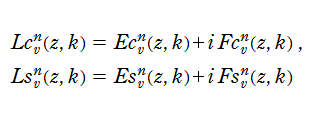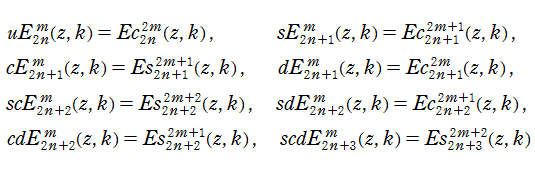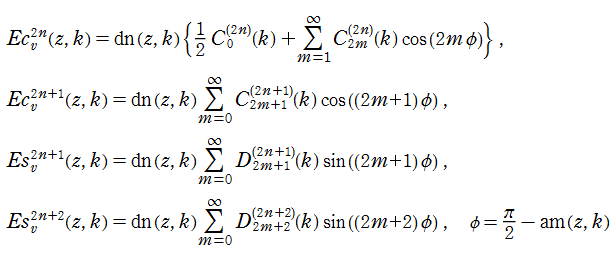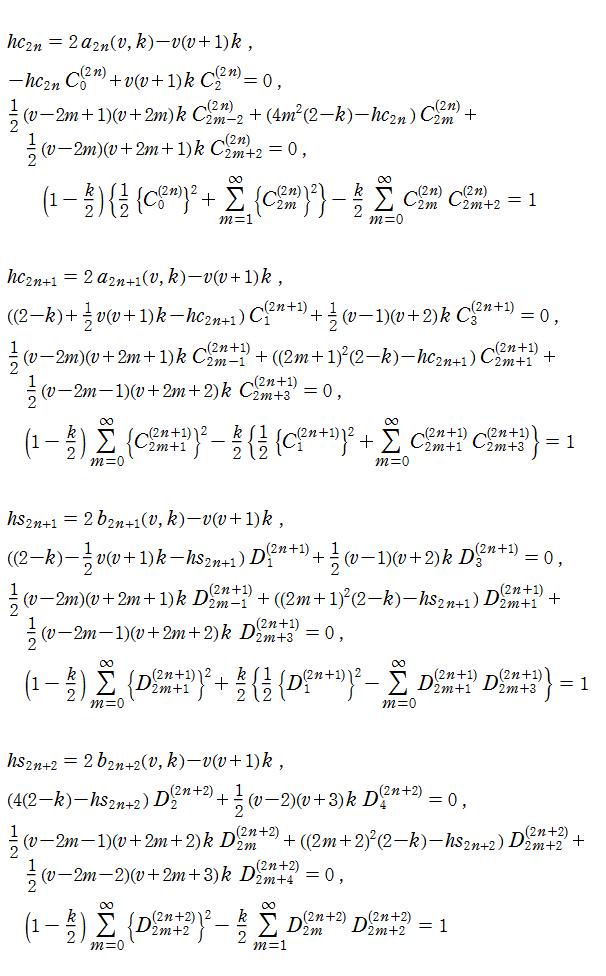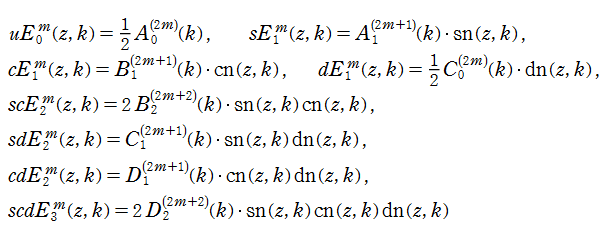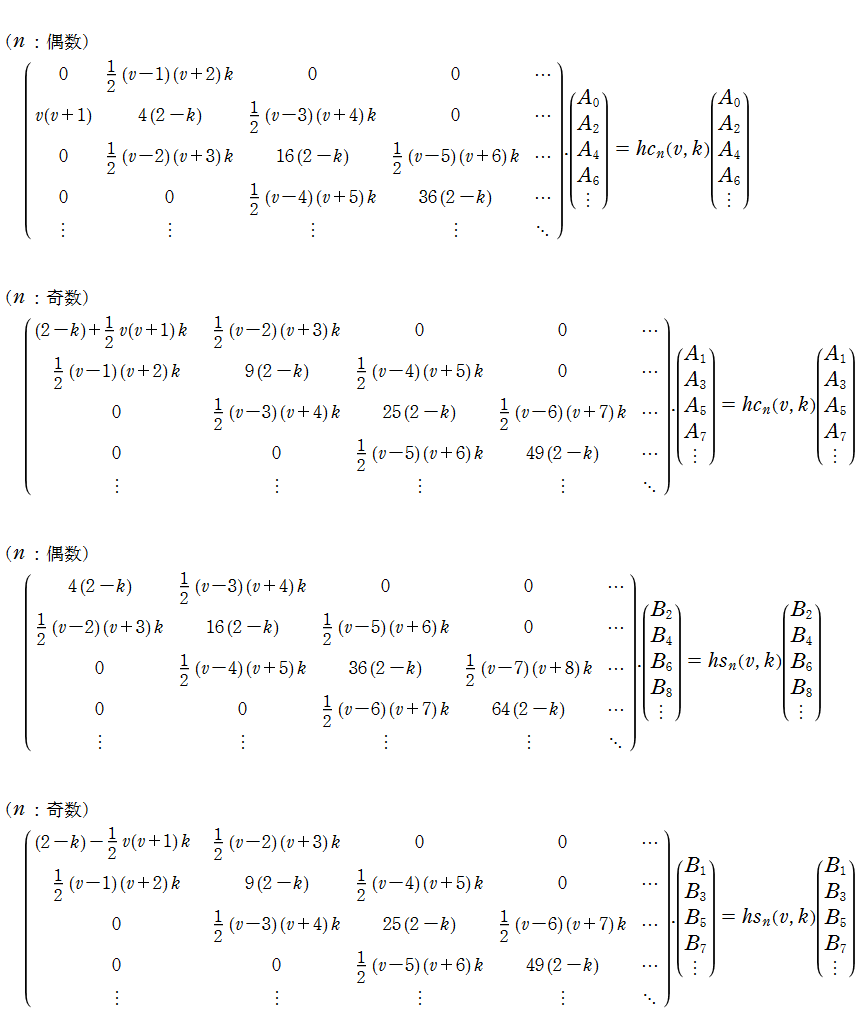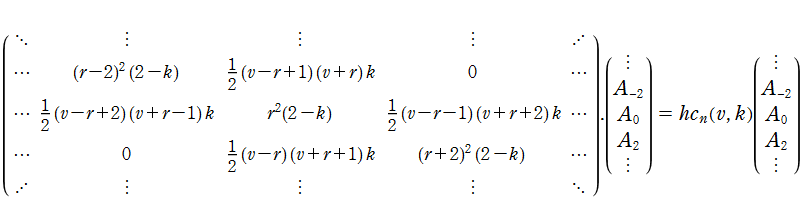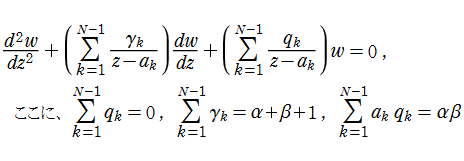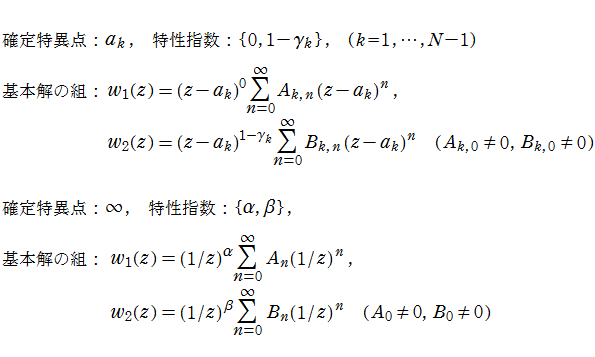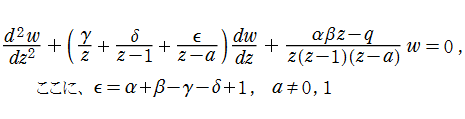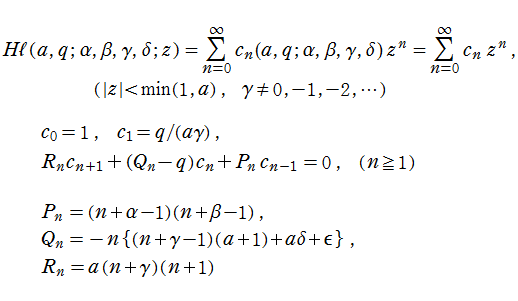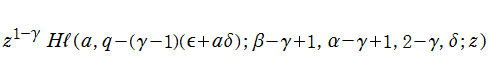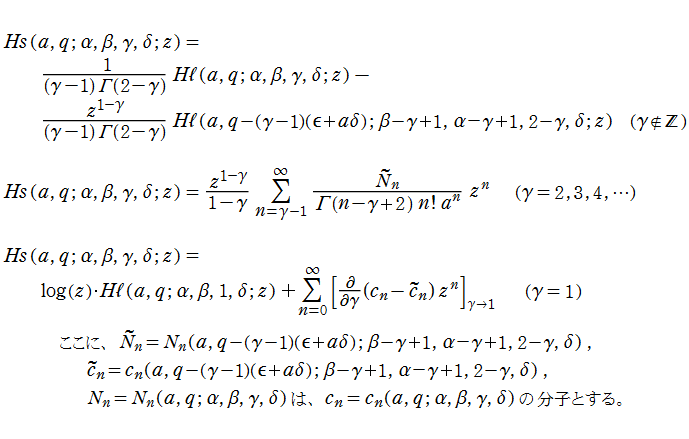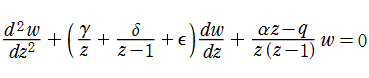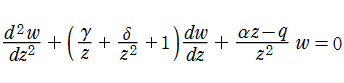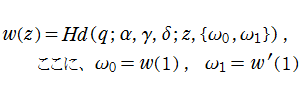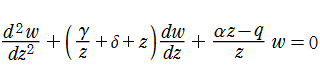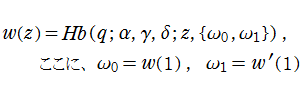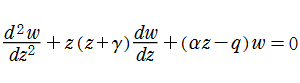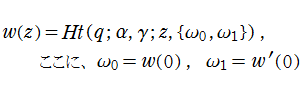特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
Lamé 関数
Lamé 関数
日:Lamé関数,ラーメ関数(ラメ関数)英:Lamé function,仏:Fonction de Lamé,独:Lamésche funktion
Laplace の方程式を楕円体座標で変数分離すると、その各成分の満たす微分方程式は、いずれも
の形に帰着できる。これを、代数的な Lamé の微分方程式といい、その解を 代数的 Lamé 関数という※1。代数的な Lamé の微分方程式は、1837年に G. Lamé によって初めて導入された。
代数的な Lamé の微分方程式は、
代数的な Lamé の微分方程式は、Jacobi の楕円関数を用いた変換
によって
なる形に帰着できる※2。通常はこれを Lamé の微分方程式、その解を Lamé 関数という場合が多い (ここでもこれを扱う)。
Lamé の微分方程式は、より一般的な Hill の微分方程式の特別な場合である。したがって Floquet の定理により、Lamé の微分方程式の固有値
第1種 Lamé 関数は周期関数であるため、次のように Fourier 級数に展開できる (ただし、
ここに、Fourier 係数
第1種 Lamé 関数は、直交性
を有する。ただし、
また、第1種 Lamé 関数とは反対の偶奇性を持ち、非周期的な第2の基本解
を、第2種 Lamé 関数という。ここに、
を満たすように選んだ任意定数であるとする。
第2種 Lamé 関数は、周期性の代わりに次の関数等式を満たす。
このほか、第3種 Lamé 関数として
を独自に定義する。これは指数関数や Hankel 関数の類似である。
一般に Lamé 関数は、複素平面上で Jacobi の楕円関数が
Lamé の微分方程式は、19世紀中頃から超幾何微分方程式に次いで注目された線形常微分方程式の具体例である。楕円関数に対する興味も背景にあって、G. Lamé を始め、C. Hermite、J. Liouville、H. E. Heine 等、多くの数学者が Lamé の微分方程式を研究した。さらに、1881年に G. H. Halphen は、楕円関数を係数とする一般的な線形常微分方程式に関する論文を発表した。
しかし、Lamé の微分方程式のように固有値 (アクセサリーパラメーター) を持つ線形常微分方程式の理論は、超幾何微分方程式のそれに比べて格段に難しい。例えば、「Gauss - Schwarz 理論」 の拡張 ― 基本領域の半分が円弧四角形である保型関数を、Lamé (または後述の Heun) 微分方程式の2基本解の比の逆関数で表わす理論 ― は、可能であることが分かっていても、実際に具体的な係数を決定するのは大変困難である。このように、不明な点も多いため現在でも研究が続けられている。
Lamé 関数の古典的応用事例としては、楕円体の平衡形状論のように境界条件が楕円体である場合の物理問題や、惑星の温度分布などが知られるが、計算が複雑で取り扱いも難しいため限られていた。しかし、電子計算機の性能がかなり向上した現在では、Lamé 関数に対する抵抗感も薄まる傾向にあり、後述の Heun 関数とともに応用事例の数は増えつつある (楕円体関数系の特殊関数は、21世紀になってようやく Bessel 関数並に駆使できる時代が到来したと言えるのかもしれない)。
【註記】
※1 : Laplace の方程式を円錐座標で変数分離したときも、座標の2方向で代数的な Lamé の微分方程式が現れる。なお、代数的 Lamé 関数のグラフの概形は、より標準的な Heun 関数のそれに似ていると思われる。
※2 : 他にも、Weierstrass の楕円関数や三角関数を用いた変換によって得られる形など、Lamé の微分方程式は二三の異なる形が存在する。
※3 : ここに記述した第1種 Lamé 関数、後述の Lamé 多項式、Lamé 固有値関数の公式、およびグラフの結果は、「NIST - Handbook of Mathematical Functions」 に基づいているので、さらに詳細な情報が必要な場合は同著 (Web 版のほうがより詳しい) を併せて参照して下さい。(ただし、「NIST」 での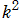 を、ここでは
を、ここでは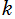 と表記している。)
と表記している。)
※1 : Laplace の方程式を円錐座標で変数分離したときも、座標の2方向で代数的な Lamé の微分方程式が現れる。なお、代数的 Lamé 関数のグラフの概形は、より標準的な Heun 関数のそれに似ていると思われる。
※2 : 他にも、Weierstrass の楕円関数や三角関数を用いた変換によって得られる形など、Lamé の微分方程式は二三の異なる形が存在する。
※3 : ここに記述した第1種 Lamé 関数、後述の Lamé 多項式、Lamé 固有値関数の公式、およびグラフの結果は、「NIST - Handbook of Mathematical Functions」 に基づいているので、さらに詳細な情報が必要な場合は同著 (Web 版のほうがより詳しい) を併せて参照して下さい。(ただし、「NIST」 での
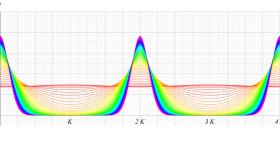
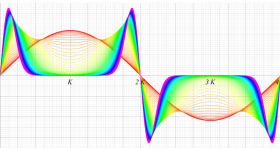
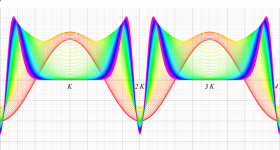
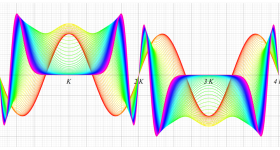
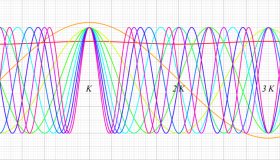
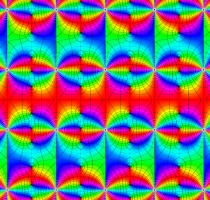
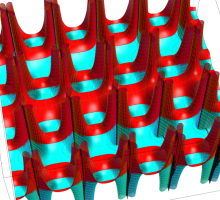
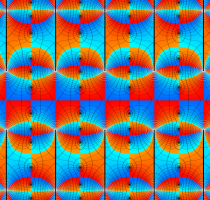
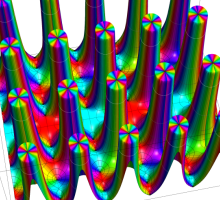
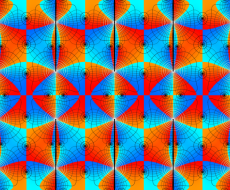
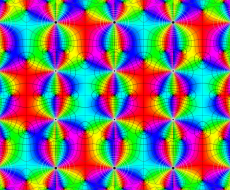
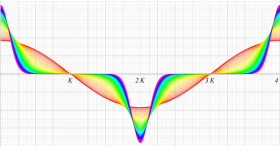
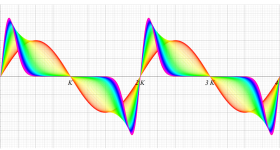
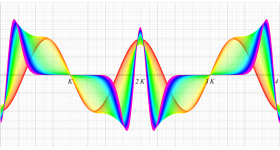
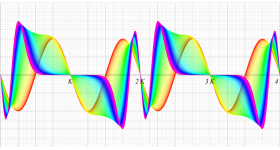
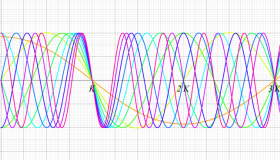
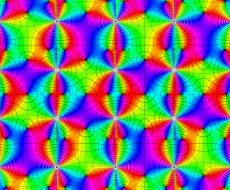
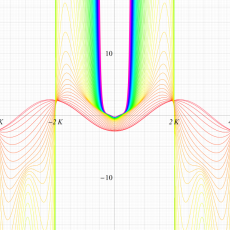
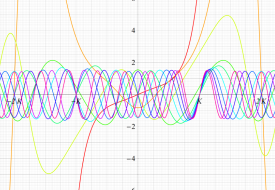
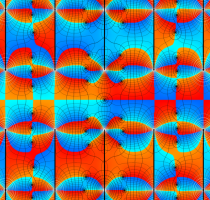
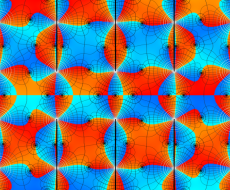
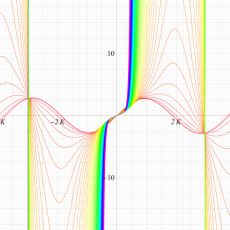
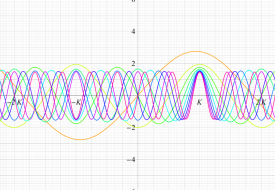
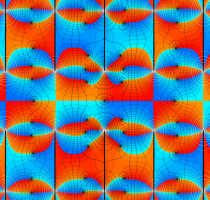
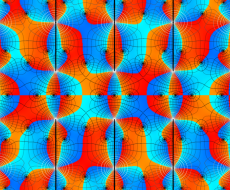
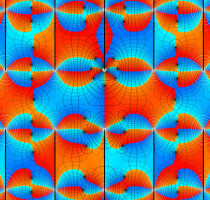
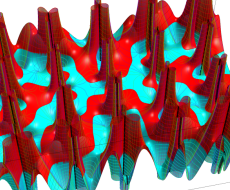
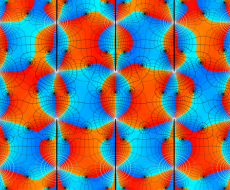
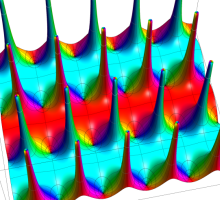
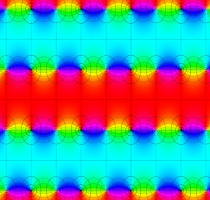
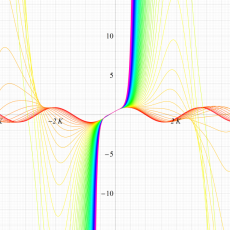
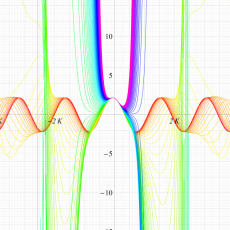
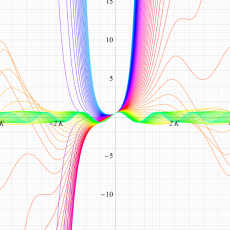
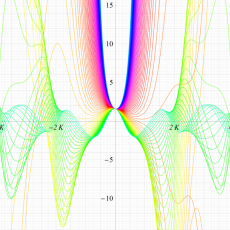
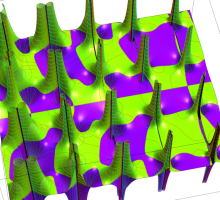
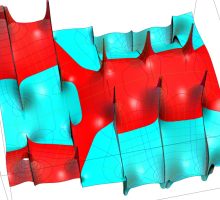
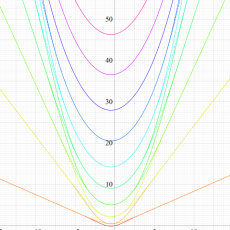
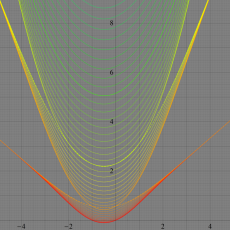
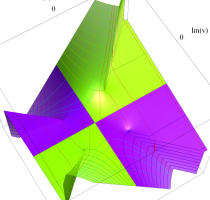
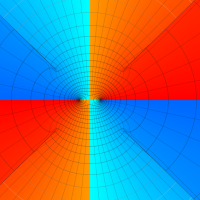
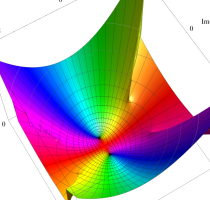
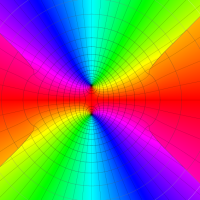
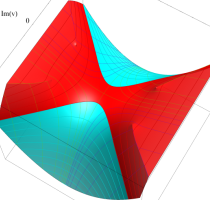
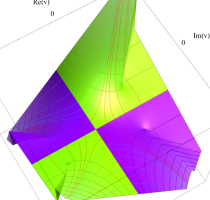
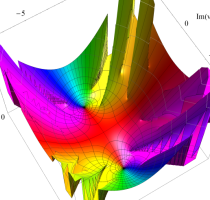
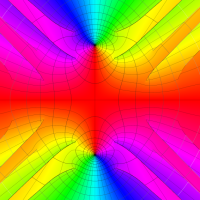
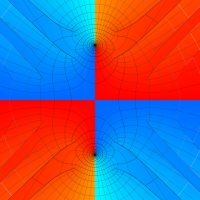
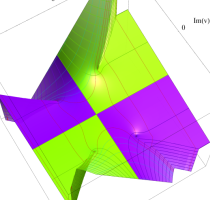
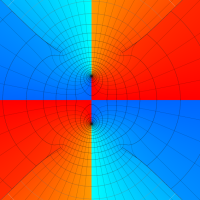
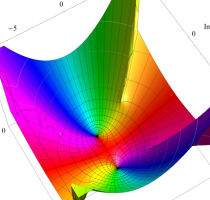
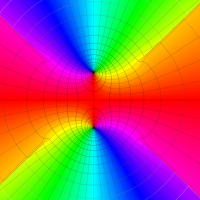
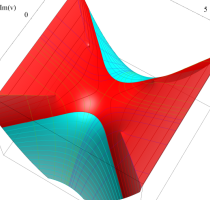
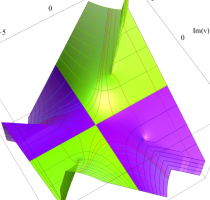
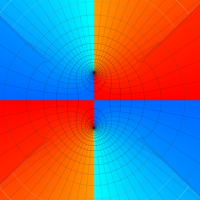
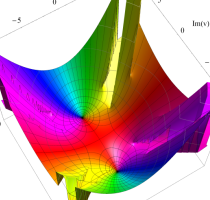
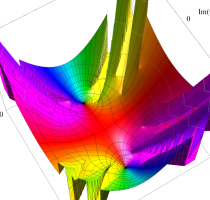
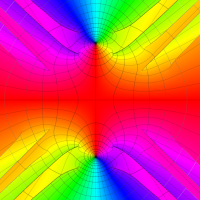
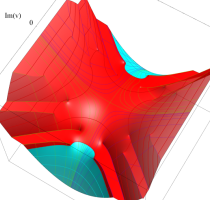
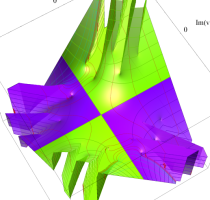
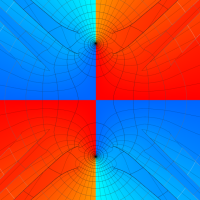
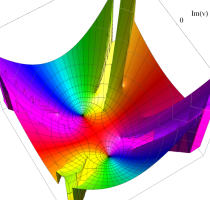
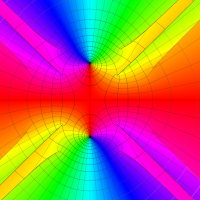
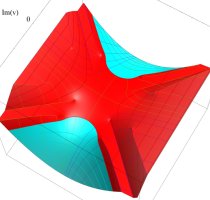
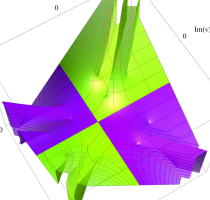
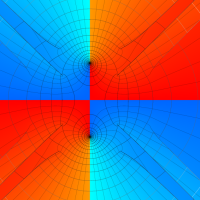
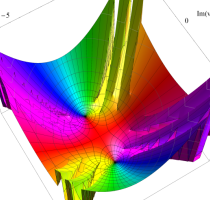
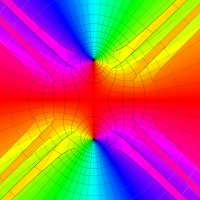
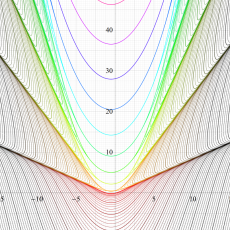
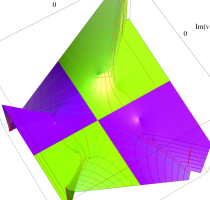
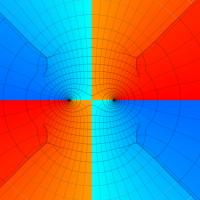
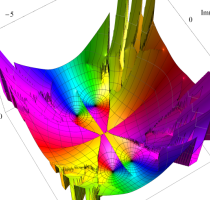
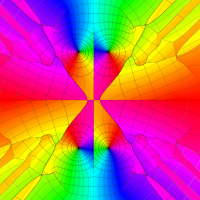
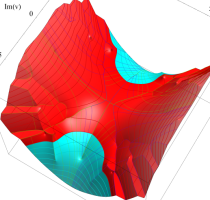
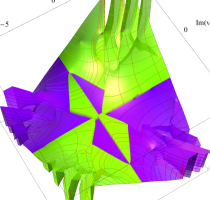
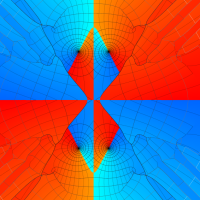
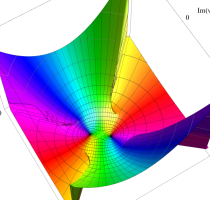
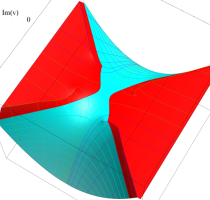
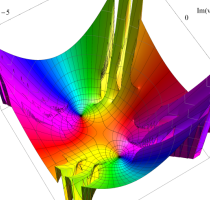
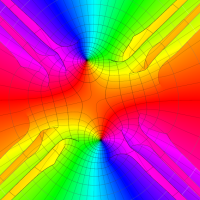
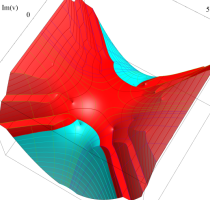
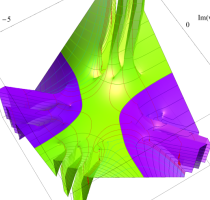
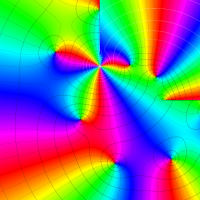
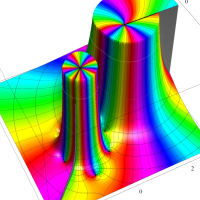
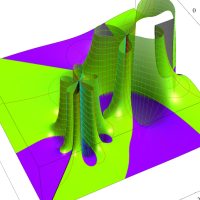
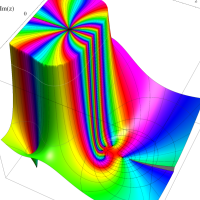
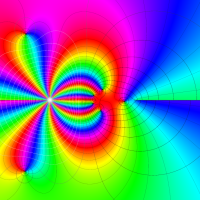
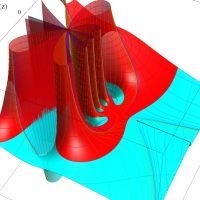
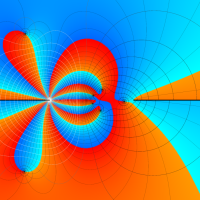
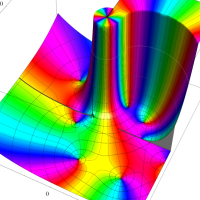
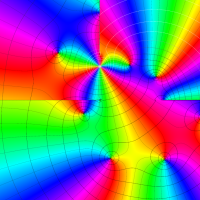
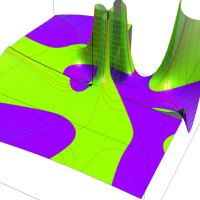
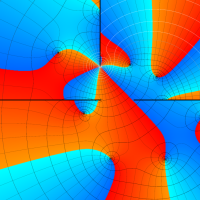
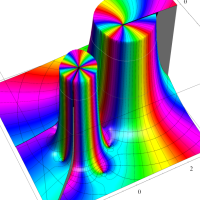
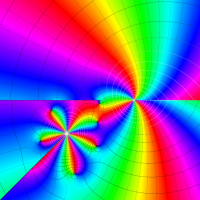
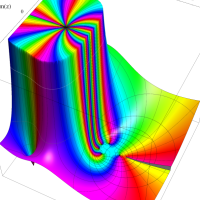
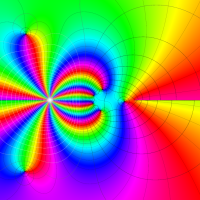
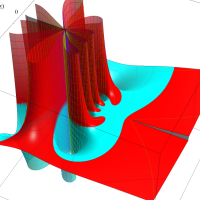
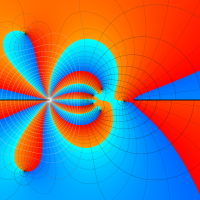
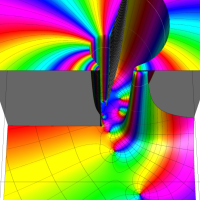
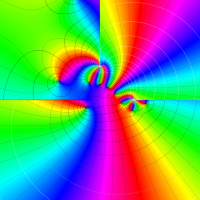
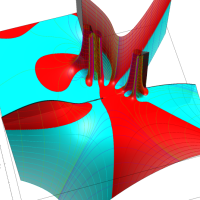
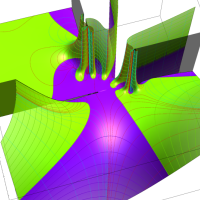
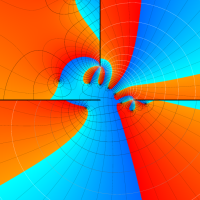
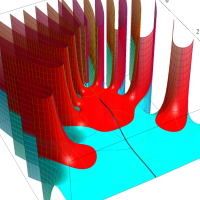
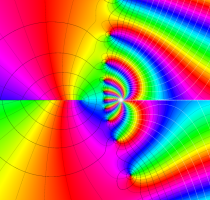
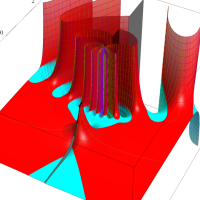
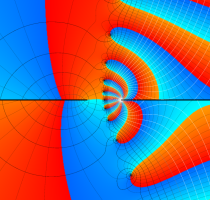
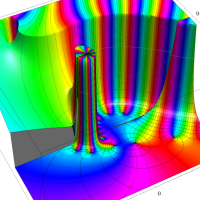
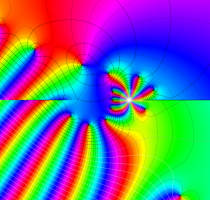
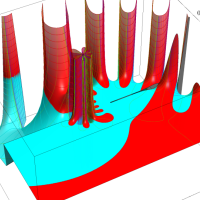
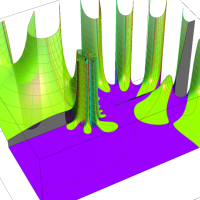
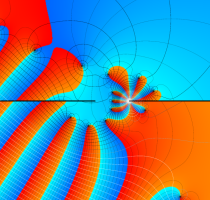
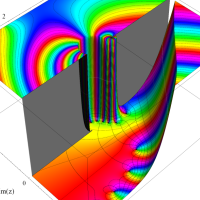
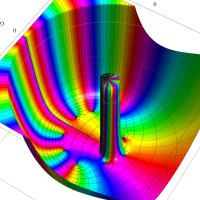
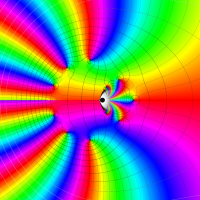
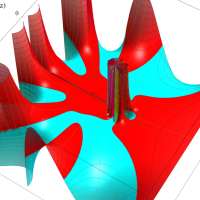
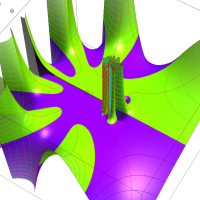
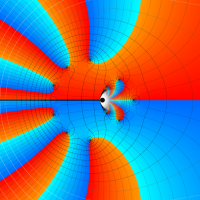
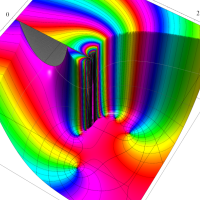
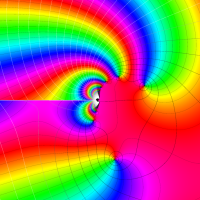
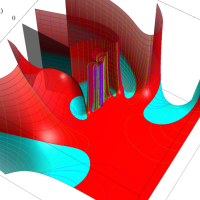
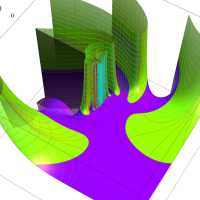
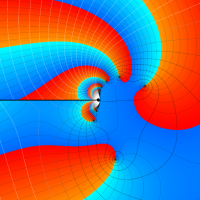
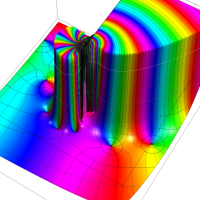
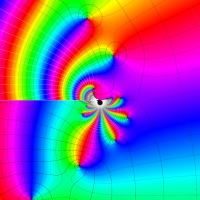
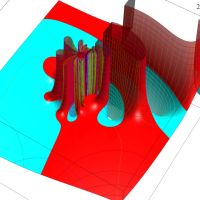
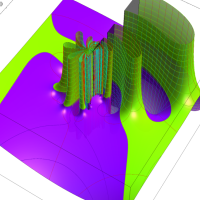
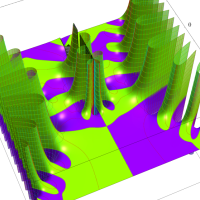
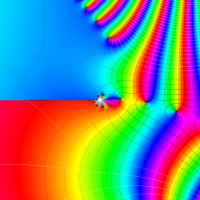
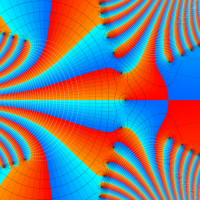
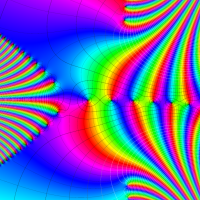
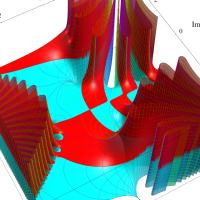
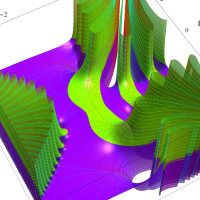
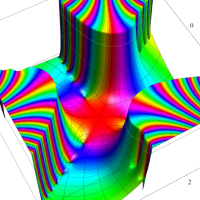
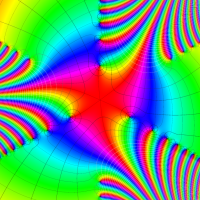
実変数の第1種 Lamé 関数のグラフ。順に、①
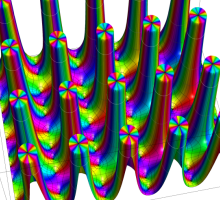
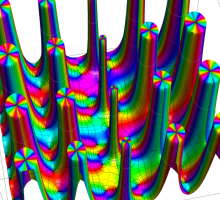
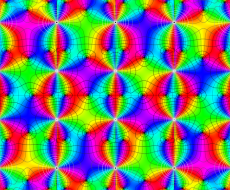
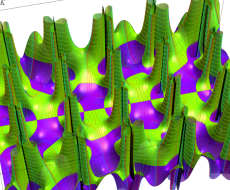
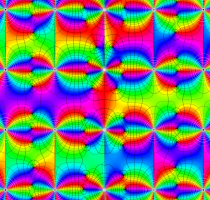
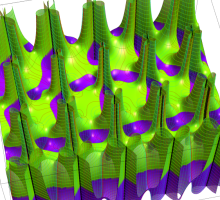
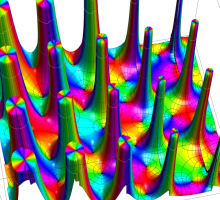
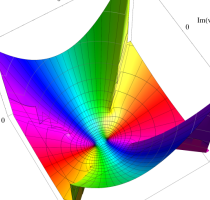
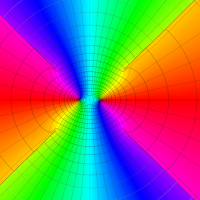
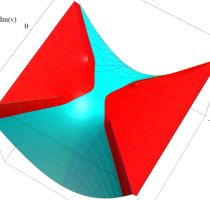
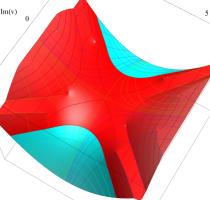
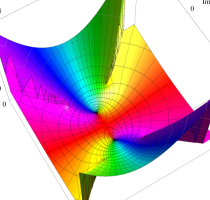
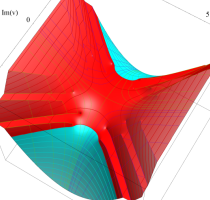
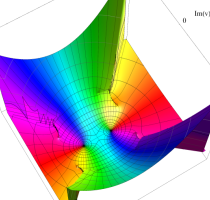
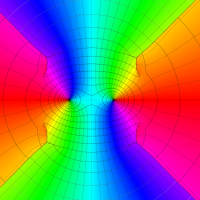
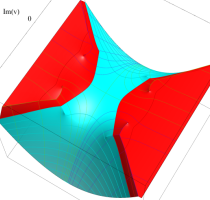
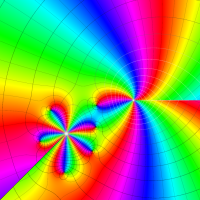
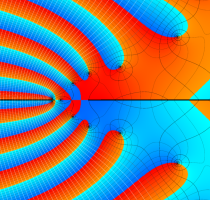
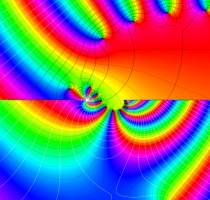
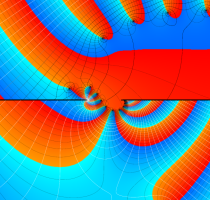
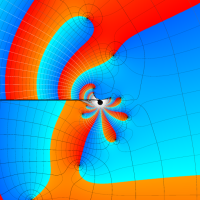
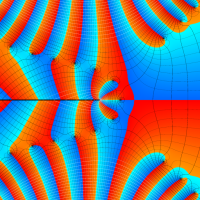
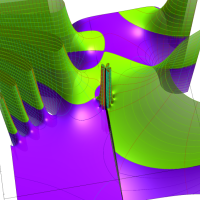
複素変数の第1種 Lamé 関数
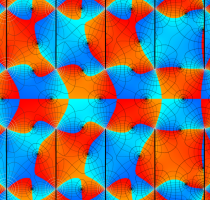
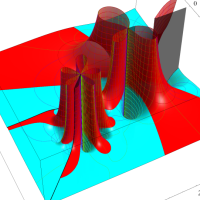
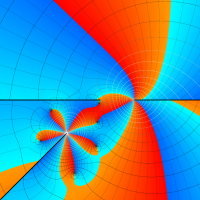
複素変数の第1種 Lamé 関数
複素変数の第1種 Lamé 関数
複素変数の第1種 Lamé 関数
アニメーション(5.20MB)
複素変数の第1種 Lamé 関数
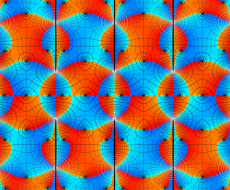
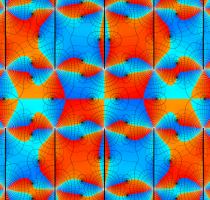
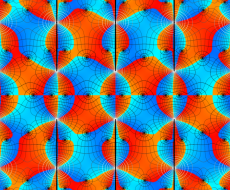
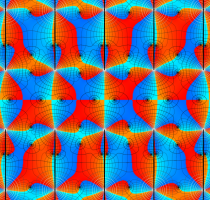
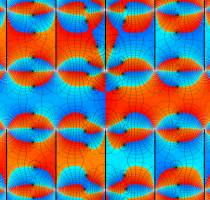
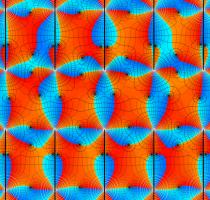
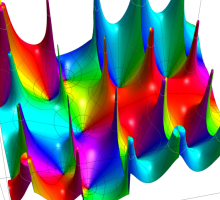
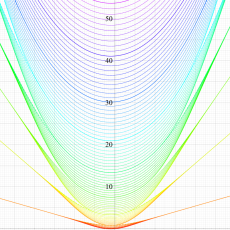
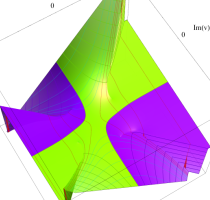
実変数の第1種 Lamé 関数のグラフ。順に、①
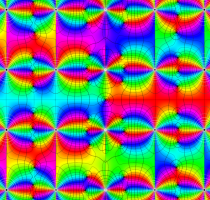
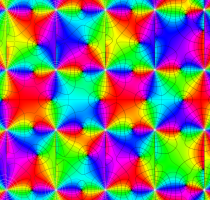
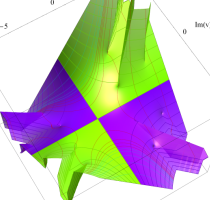
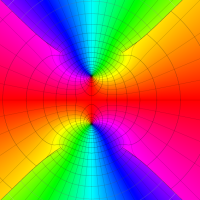
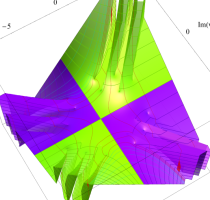
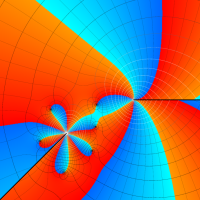
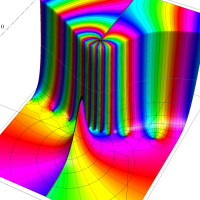
複素変数の第1種 Lamé 関数
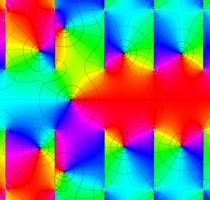
複素変数の第1種 Lamé 関数
複素変数の第1種 Lamé 関数
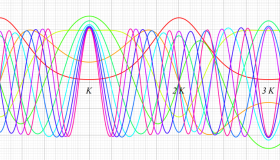
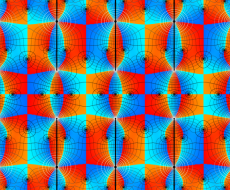
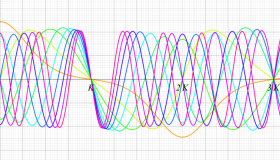
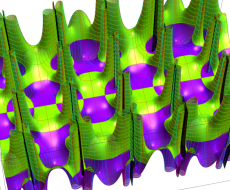
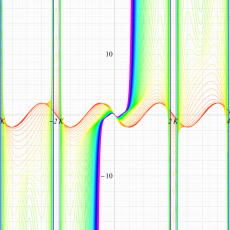
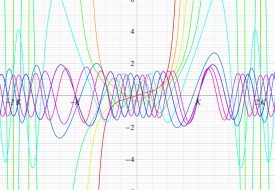
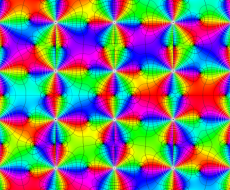
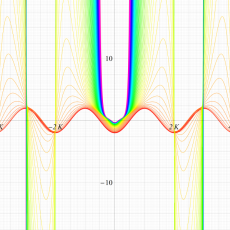
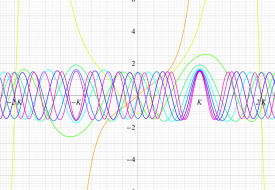
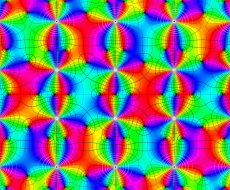
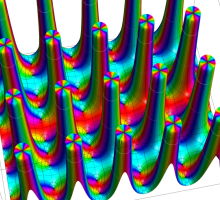
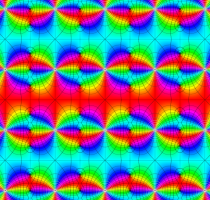
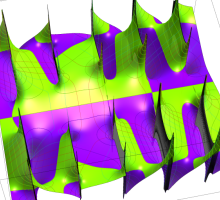
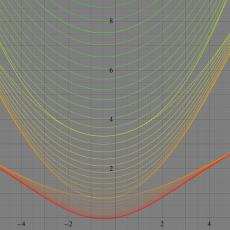
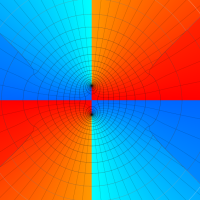
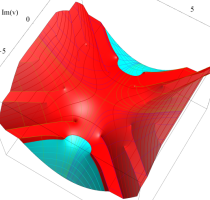
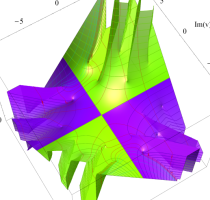
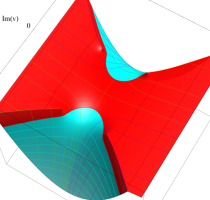
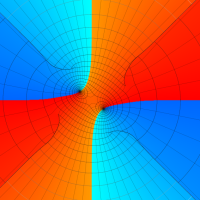
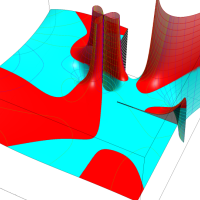
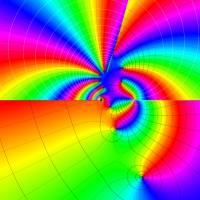
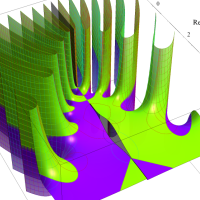
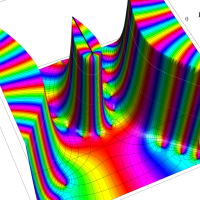
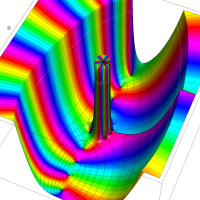
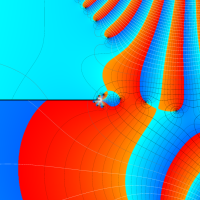
実変数の第2種 Lamé 関数のグラフ。順に、①
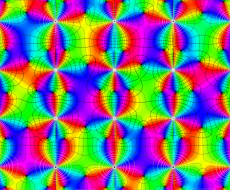
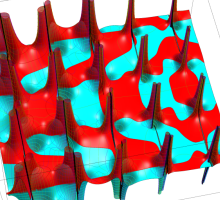
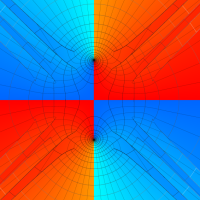
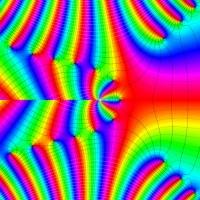
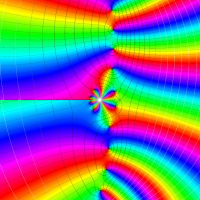
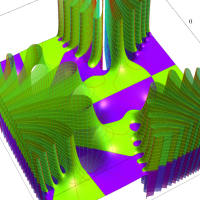
複素変数の第2種 Lamé 関数
複素変数の第2種 Lamé 関数
複素変数の第2種 Lamé 関数
複素変数の第2種 Lamé 関数
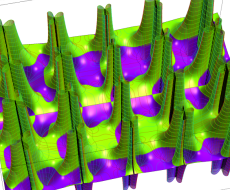
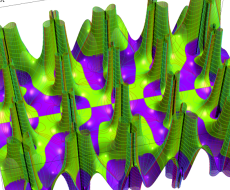
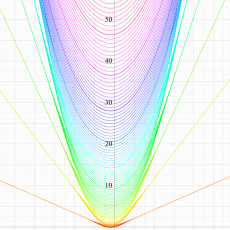
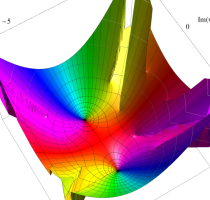
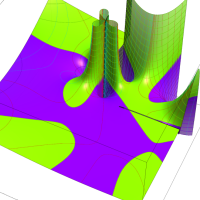
実変数の第2種 Lamé 関数のグラフ。順に、①
複素変数の第2種 Lamé 関数
複素変数の第2種 Lamé 関数
複素変数の第2種 Lamé 関数
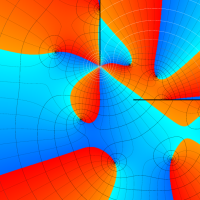
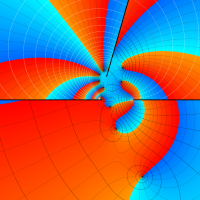
複素変数の第3種 Lamé 関数
複素変数の第3種 Lamé 関数
複素変数の第3種 Lamé 関数
複素変数の第3種 Lamé 関数
複素変数の第3種 Lamé 関数
Lamé 多項式
日:Lamé多項式,ラーメ多項式(ラメ多項式)英:Lamé polynomials,仏:Polynôme de Lamé,独:Laméschen Polynom
第1種 Lamé 関数
現在、Lamé 多項式は無理関数因子の型に基づいて8種類に分類されている。それらを一般に通用している関数記号とともに、第1種 Lamé 関数との関係式で表わすと、次のようになる。
したがって、Lamé 多項式が満たす公式等は第1種 Lamé 関数のそれと同じである。特に、数値計算に便利な Fourier 級数は全く同じものが使用できる。しかし実際は、このうちの
を用いることができる。ここに、係数
つまり、第1種 Lamé 関数の場合も、係数を求める過程で不定形が出現するために
となる。ここに現れた形の楕円関数は、それぞれの Lamé 多項式において常に発生する因子であり、代数的な Lamé の微分方程式の解では無理関数因子に相当する。また、Lamé 多項式の関数記号の由来でもある。
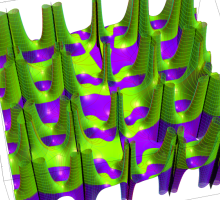
なお、実変数のグラフは、前項で掲示した第1種 Lamé 関数のそれに部分的に含まれているので省略する。また、複素変数のグラフは、Lamé 多項式が初等代数関数に Jacobi の楕円関数を代入した関数であることを踏まえて、各々2種類のグラフ (3次元絶対値グラフ、およびその平面グラフ) に留める。
(
複素変数の Lamé 多項式
複素変数の Lamé 多項式
複素変数の Lamé 多項式
複素変数の Lamé 多項式
複素変数の Lamé 多項式
複素変数の Lamé 多項式
複素変数の Lamé 多項式
複素変数の Lamé 多項式
一般 Lamé 関数
を直接解いて得られる、次の初期条件を満たす解
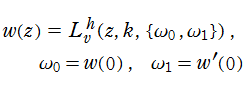
特に、
で表わされる。すなわち、第1種~第3種 Lamé 関数はこの特殊型である。
一般 Lamé 関数も、複素平面上で Jacobi の楕円関数が
いずれも
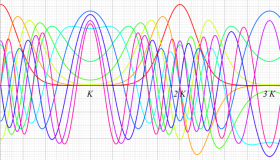
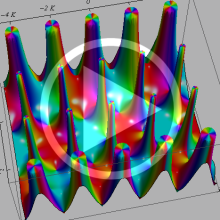
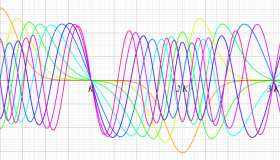
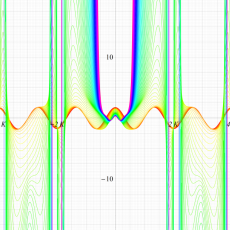
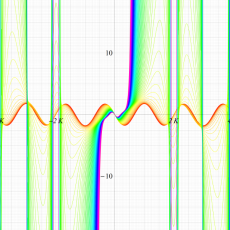
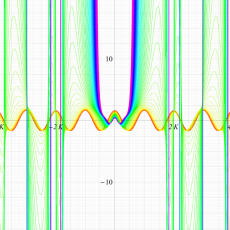
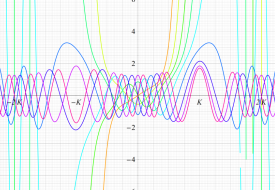
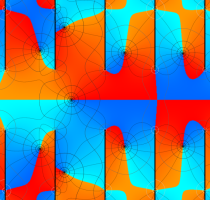
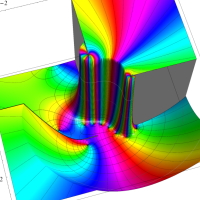
実変数の一般 Lamé 関数のグラフ。順に、①
いずれも
複素変数の一般 Lamé 関数
複素変数の一般 Lamé 関数
複素変数の一般 Lamé 関数
複素変数の一般 Lamé 関数
複素変数の一般 Lamé 関数
アニメーション(7.74MB)
複素変数の一般 Lamé 関数
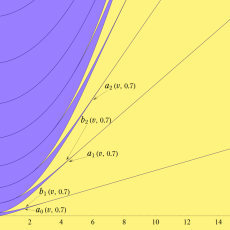
Lamé 固有値関数
Lamé の微分方程式についても、Mathieu 関数と同様に Floquet の定理が適用できて、二つの基本解
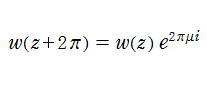
固有値
特に
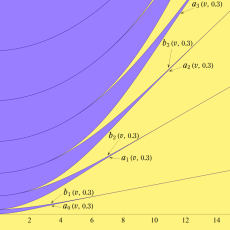
Lamé 固有値関数の数値計算は、Mathieu 固有値関数と同様に、無限次連分数方程式や三重対角行列の固有値に基づく方程式を用いると便利である。補助的な固有値関数
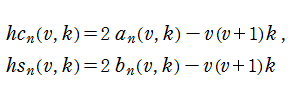
となる。ここに
なお、
によって求められる。ここに
①:
①:
(実線は
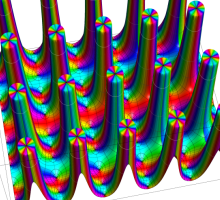
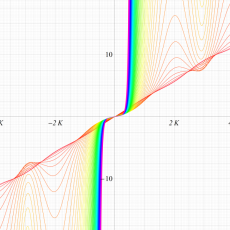
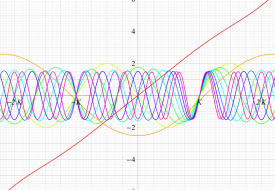
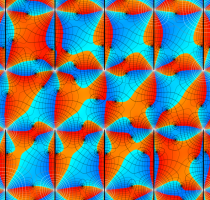
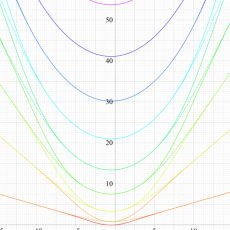
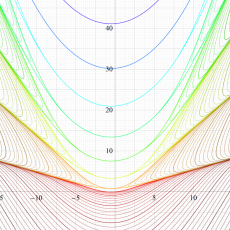
実変数の Lamé 固有値関数のグラフ。
実変数の Lamé 固有値関数のグラフ。
①:
実変数の Lamé 固有値関数のグラフ。
①:
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
実変数の Lamé 固有値関数
実変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
複素変数の Lamé 固有値関数
Heun 関数
日:Heun関数,ホイン関数英:Heun function,仏:Fonction de Heun,独:Heun funktion
一般に 「Fuchs 型」 と称される二階線形常微分方程式
は、微分方程式の特異点として
となる。ここに、
このように、線形常微分方程式の解の局所的な振る舞いは、微分方程式の特異点の位置と特性指数の値によってほぼ決定される※1。この理論の基礎は、L. Fuchs (1865年), F. G. Frobenius (1873年) 等によって整備されたが、先駆的には G. F. Riemann がP関数の研究をとおして重要な例を与えている。実際、
一方、19世紀後半は Lamé の微分方程式にも関心が集まり始めた時期であった。これは
を Heun の微分方程式、その解
を、局所 Heun 関数 (Local Heun function) という※2。このとき、第2種の解は
となり、
上記の第2種関数は
を、具体的な第2種局所 Heun 関数として独自に定義する※2。これは、
より一般的な Heun 関数は、Riemann のP関数の無限級数で表わされる (記載例:「NIST」の716頁にある公式31.11.(ii)等) が、ここでは独自定義の関数として、Heun の微分方程式を直接数値的に解いて得られる関数
を、「一般 Heun 関数」 と称して扱う※2。
超幾何関数に対して合流型超幾何関数があるように、Heun の微分方程式についても、確定特異点のいくつかを合流させて不確定特異点に変えた各種の 「合流型 Heun の微分方程式」 と、その解となる 「合流型 Heun 関数」 が詳しく研究されている。当サイトでは、上記の一般 Heun 関数に準ずる方法で定義された合流型 Heun 関数を採用するが、詳細は別項目として後述する。
合流型も含めた Heun 関数の応用例としては、ブラックホールの各種計量における特殊解への摂動問題、ヘリウムなど複数個のポテンシャル中心点を持つ調和振動子に関する量子力学等が知られている。
【註記】
※1 : 「ほぼ」 ではなく、アクセサリーパラメーターを持たないため完全に決定できる場合、その線形常微分方程式は 「rigid (リジッド)」 であると呼ばれる。超幾何微分方程式や一般超幾何関数の微分方程式は、rigid な例である。
※2 : ここで描画する Heun 関数のグラフは、次のような形状の分枝切断線を採用する。
 のときに
のときに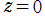 で対数分岐点を持つ第2種局所 Heun 関数が定義されている。記号
で対数分岐点を持つ第2種局所 Heun 関数が定義されている。記号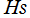 はその記述箇所からの拝借である (ただし、線形結合式の係数は当サイトと異なる定義) 。
はその記述箇所からの拝借である (ただし、線形結合式の係数は当サイトと異なる定義) 。
※3 : 具体的な192個の解の表示式は、Robert S. Maierの論文 「The 192 Solutions of the Heun equation」 (Mathematics of Computation, Vol.76, No.258 (2007), p.811-843) で確認できる。
※4 : Heun 関数のプログラミング着手時から、無限次元三重対角行列法による固有値計算を試みているが、現在も上記の問題等が解決できていない。
※1 : 「ほぼ」 ではなく、アクセサリーパラメーターを持たないため完全に決定できる場合、その線形常微分方程式は 「rigid (リジッド)」 であると呼ばれる。超幾何微分方程式や一般超幾何関数の微分方程式は、rigid な例である。
※2 : ここで描画する Heun 関数のグラフは、次のような形状の分枝切断線を採用する。
① 実軸上の、区間![(-∞, 0]](siki_spec300/lame1800.png) および
および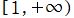 の半直線。
の半直線。
② 中心が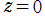 で偏角が
で偏角が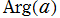 である動径上の、区間
である動径上の、区間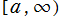 の半直線。
の半直線。
この分枝切断線は、例えば Oleg V. Motygin の論文 「On evaluation of the Heun functions」 (arXiv:1506.03848.) でも採用されている。因みにこの論文では、② 中心が
※3 : 具体的な192個の解の表示式は、Robert S. Maierの論文 「The 192 Solutions of the Heun equation」 (Mathematics of Computation, Vol.76, No.258 (2007), p.811-843) で確認できる。
※4 : Heun 関数のプログラミング着手時から、無限次元三重対角行列法による固有値計算を試みているが、現在も上記の問題等が解決できていない。
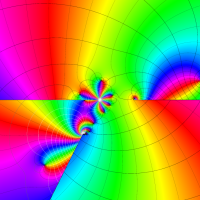
複素変数の第1種局所 Heun 関数
複素変数の第1種局所 Heun 関数
複素変数の第1種局所 Heun 関数
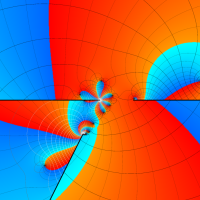
複素変数の第2種局所 Heun 関数
複素変数の第2種局所 Heun 関数
複素変数の第2種局所 Heun 関数
複素変数の一般 Heun 関数
複素変数の一般 Heun 関数
合流型 Heun 関数
日:合流型Heun関数,合流型ホイン関数英:Confluent Heun function,仏:Fonction de Heun confluente,独:Konfluente Heun funktion
Heun の微分方程式が有する4個の確定特異点
現在では、合流させる確定特異点の選択方法に応じて、4種類の典型的な合流型 Heun の微分方程式が次のように定義されている。
【Confluent Heun equation】
これは、
ここでは、この微分方程式の解を
と表記することにする (標準的な関数記号がまだ存在しないため※1:以下同様) 。また、分枝切断線は実軸上の区間
【Doubly-confluent Heun equation】
これは、
ここでは、この微分方程式の解を
と表記することにする。また、分枝切断線は実軸上の区間
【Biconfluent Heun equation】
これは、
ここでは、この微分方程式の解を
と表記することにする。また、分枝切断線は実軸上の区間
【Triconfluent Heun equation】
これは、
ここでは、この微分方程式の解を
と表記することにする。この関数は超越整関数である。
*******
なお、確定特異点の合流が段階的な順序を経て成されると見るならば、Heun の微分方程式と4種類の合流型 Heun の微分方程式は、次のような階層構造になっていると考えることもできる。
【註記】
※1 : Maple および Mathematica では、両者ともに局所 Heun 関数が HeunG、合流型 Heun 関数が HeunC, HeunD, HeunB, および HeunT なるコマンド名で実装されているが、パラメーターおよび初期値の取り方は当サイトと異なる。
※1 : Maple および Mathematica では、両者ともに局所 Heun 関数が HeunG、合流型 Heun 関数が HeunC, HeunD, HeunB, および HeunT なるコマンド名で実装されているが、パラメーターおよび初期値の取り方は当サイトと異なる。
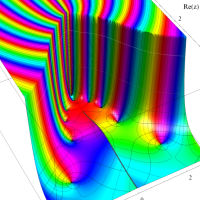
複素変数の合流型 Heun 関数
複素変数の合流型 Heun 関数
複素変数の合流型 Heun 関数
複素変数の合流型 Heun 関数
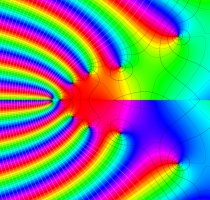
複素変数の合流型 Heun 関数
複素変数の合流型 Heun 関数
複素変数の合流型 Heun 関数
複素変数の合流型 Heun 関数
複素変数の合流型 Heun 関数
合流型 Heun 関数