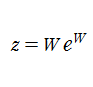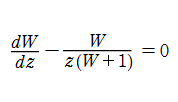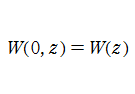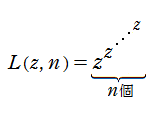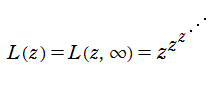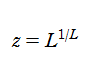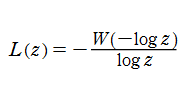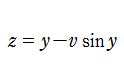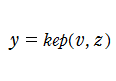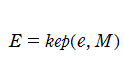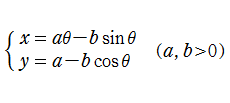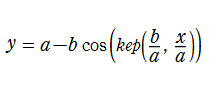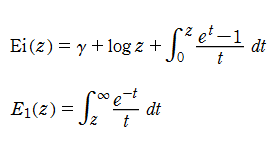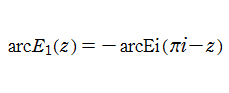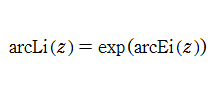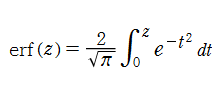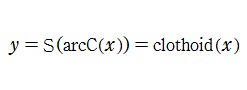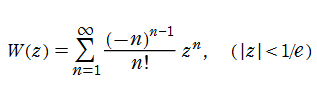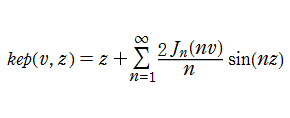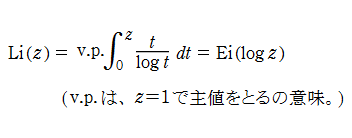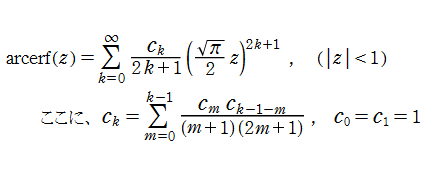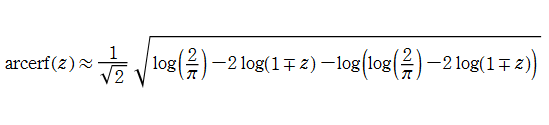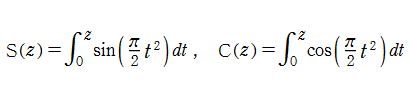種々の逆関数
日:
乗積対数関数,英:
Product logarithm
日:
LambertのW関数,
ランベルトのW関数
英:
Lambert's W function,仏:
Fonction W de Lambert,独:
Lambertsche W-funktion
初等関数の逆関数は、必ずしも初等関数とは限らない。例えば、5次以上の多項式関数の逆関数は一般に初等関数のみでは表わせない(Abel - Ruffini
の定理)。ただし5次の場合、
楕円モジュラー関数の使用を許容すれば具体的に表わせる。6次以上は一般的にそれでも表わせない。
ここでは、初等関数の逆関数が初等関数にならない他の例を、幾つか扱う。
乗積対数関数
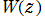
は、方程式
を
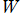
について解くと得られる逆関数で、対数関数の一般化とみなされるのでその名がある。したがって、乗積対数関数は各種の超越方程式の解を表現できる。しばしば、乗積対数関数は Lambert のW関数とも呼ばれる。
乗積対数関数は、複素平面上
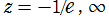
に特異点を持つ無限多価関数であるが、そのうちの主値は、対数関数と同様に実軸上で実数値をとる一分枝であるとされ、冪級数展開式
を解析接続すると得られる。通常それは、実軸上の区間
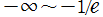
に分枝切断線が置かれる。
乗積対数関数は、代数的な非線形常微分方程式
を満たす(ただしこの微分方程式は、乗積対数関数を複素平面上で平行移動した関数も解になるので Painlevé 性を持たない)。
なお、無限個ある乗積対数関数の各分枝は、虚数部分の順で数え上げて第
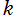
分枝と呼び、
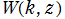
と表記される。特に
である。
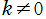
である第
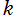
分枝の乗積対数関数は、実軸上の区間
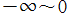
に分枝切断線が置かれる。
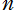
個の累乗が入れ子構造になった
は、初等関数である。しかし入れ子が無限個ならば、それは初等関数で表わせない。
ここでは、これを無限累乗関数と呼ぶこととする(標準的な名称はまだ存在しない)。ただし複素変数の場合は、無限個の累乗を表記どおりに計算しても発散するので、この関数が方程式
を
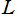
について解いた逆関数であると解釈する。そのとき、乗積対数関数
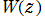
によって
と表わされる。
無限累乗関数は、複素平面上
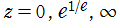
に特異点を持つ無限多価関数であって、通常は
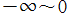
および
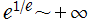
に分枝切断線を置く。
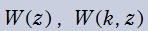
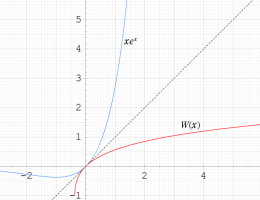
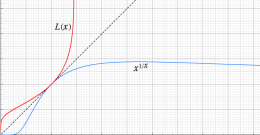
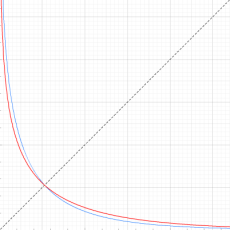
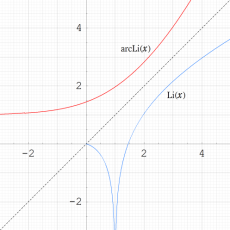
実変数の乗積対数関数
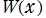
のグラフ。逆関数関係を確認するため、
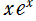
とともに描画する。
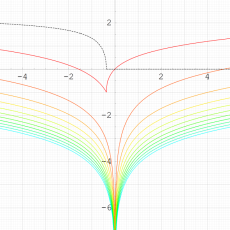
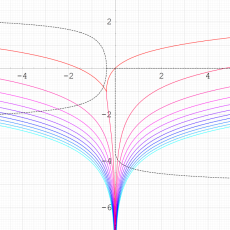
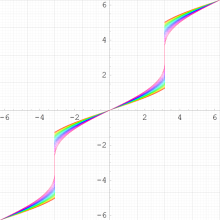
実変数の乗積対数関数
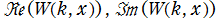
のグラフ。①:
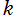
=0~10 (+1),②:
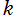
=-10~0 (+1)。
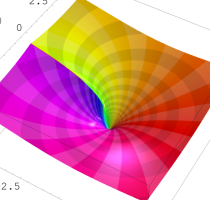
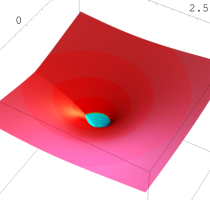
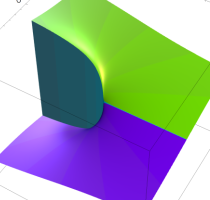
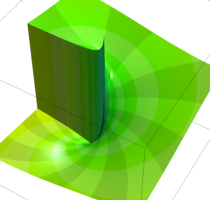
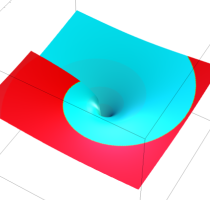
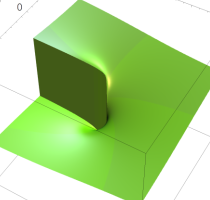
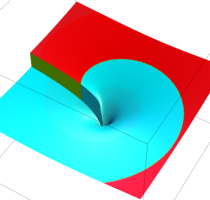
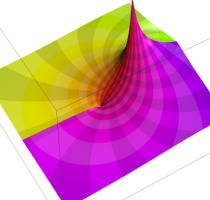
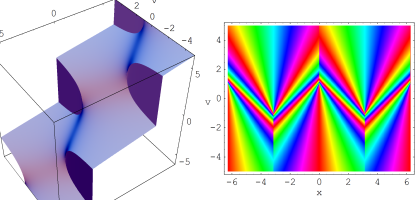
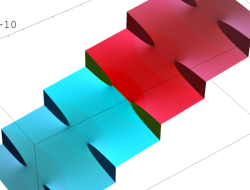
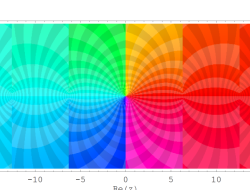
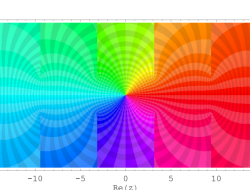
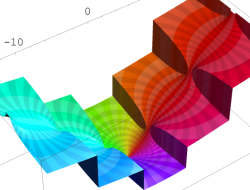
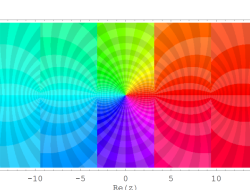
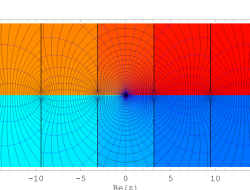
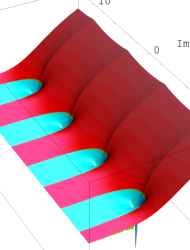
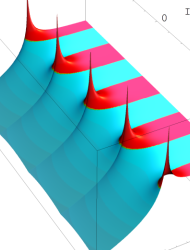
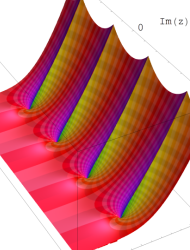
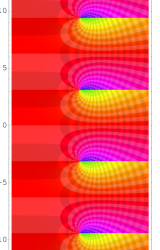
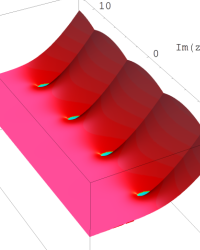
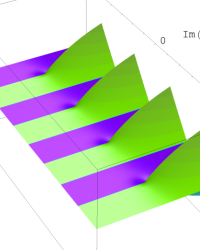
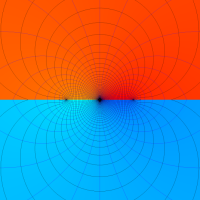
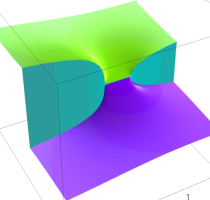
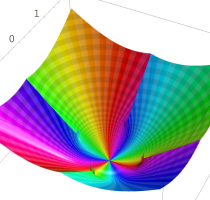
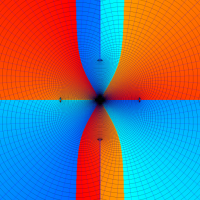
複素変数の乗積対数関数
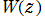
のグラフ。
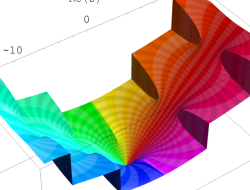
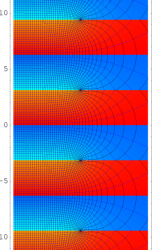
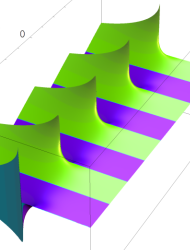
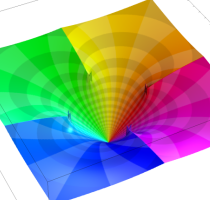
複素変数の乗積対数関数
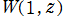
のグラフ。
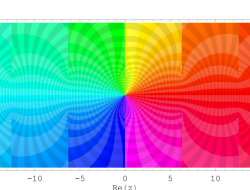
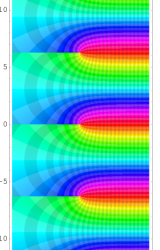
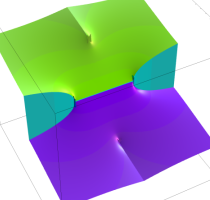
複素変数の乗積対数関数
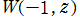
のグラフ。
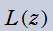
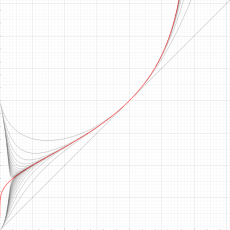
実変数の無限累乗関数
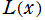
のグラフ。逆関数関係を確認するため、
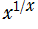
とともに描画する。
実変数の無限累乗関数
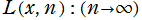
(有限回の累乗関数が無限累乗関数に収束する様子)のグラフ。
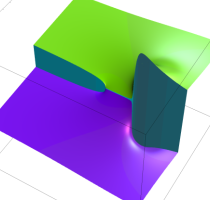
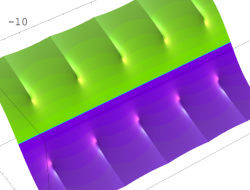
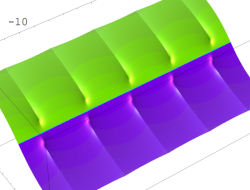
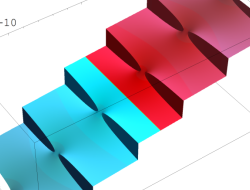
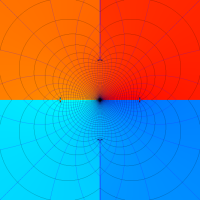
複素変数の無限累乗関数
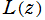
のグラフ。
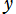
を変数とする初等関数(Kepler の方程式)
を
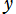
について解いて得られる
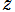
の関数を、Kepler の逆関数という。この関数に対する標準的な記号は存在しないので、ここでは
なる記号を使用する。
Kepler の逆関数は、
Bessel 関数を係数とする Fourier 級数
で表わされるが、
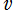
が0に近くないときは収束が極めて遅いため、実際は、Kepler の方程式を直接数値計算で解くことが多い。惑星の運動問題に関連して F. W. Bessel がこの Fourier 級数に興味を抱き、ここから Bessel 関数の組織的研究に導かれた。
Kepler の逆関数は前述のとおり、専ら天体の軌道論で用いられる。すなわち、天体が楕円軌道を描くときの離心近点離角
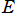
は、平均近点離角
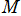
、離心率
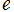
を用いて
と表わされる。
なお、トロコイド(余擺線)と呼ばれる曲線は、
なるパラメータ表示で定義されるが、これからパラメータ変数
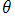
を消去し、
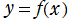
の型にすると得られる
は、トロコイドの一部分を表わす。
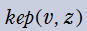
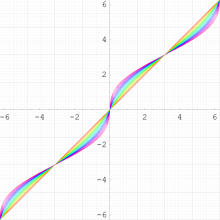
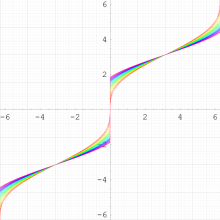
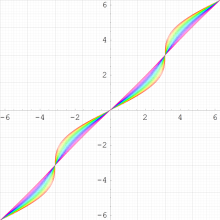
実変数の Kepler の逆関数
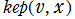
のグラフ。順に、①:
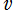
=0~0.95 (+0.05),②:
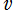
=1~1.95 (+0.05),③:
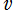
=-1~-0.05 (+0.05),④:
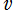
=-2~-1.05 (+0.05)。
実2変数の Kepler の逆関数
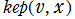
のグラフ。
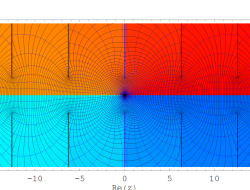
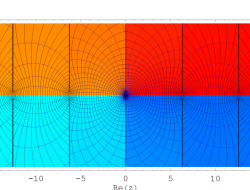
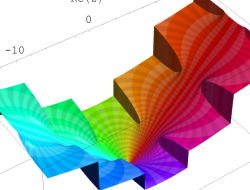
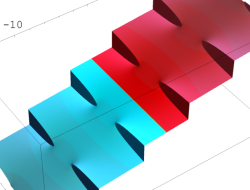
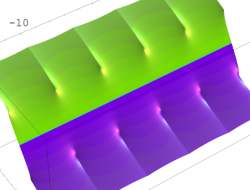
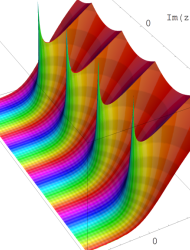
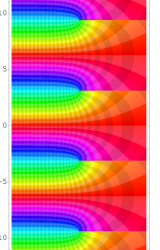
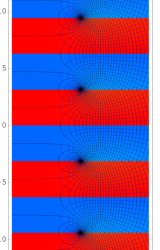
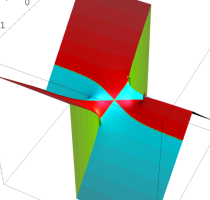
複素変数の Kepler の逆関数
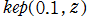
のグラフ。
複素変数の Kepler の逆関数
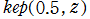
のグラフ。
複素変数の Kepler の逆関数
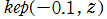
のグラフ。
複素変数の Kepler の逆関数
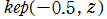
のグラフ。
以降では、特殊関数の逆関数について幾つかの例を扱う。
二つの
積分指数関数
の逆関数を逆積分指数関数と呼び、それぞれを
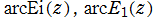
と表記する(標準的な関数記号は存在しない)。
二つの逆積分指数関数は、ともに
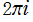
を周期とする周期関数であって、互いに
の関係にある。つまり、二つの積分指数関数は本質的に同じ関数(の異なった分枝)であるといえる。
また
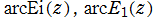
はそれぞれ、複素平面上
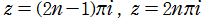
(
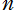
は整数)に特異点を持つ無限多価関数であって、通常は
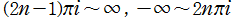
に分枝切断線を置く。
逆積分指数関数は、実変数の場合に限って希に統計学で用いられる。
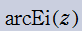
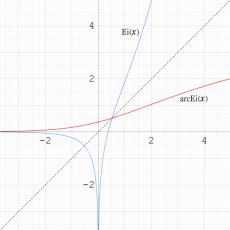
実変数の逆積分指数関数
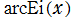
のグラフ。逆関数関係を確認するため、積分指数関数とともに描画する。
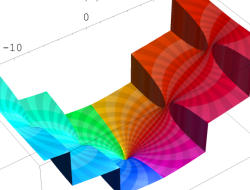
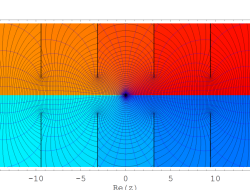
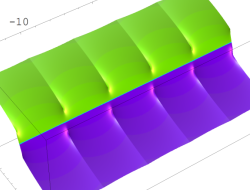
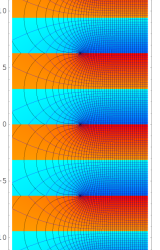
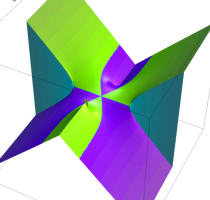
複素変数の逆積分指数関数
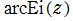
のグラフ。
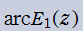
実変数の逆積分指数関数
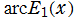
のグラフ。逆関数関係を確認するため、積分指数関数とともに描画する。
複素変数の逆積分指数関数
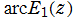
のグラフ。
積分対数関数
の逆関数を逆積分対数関数と呼び、
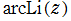
で表わす(標準的な関数記号は存在しない)。
逆積分対数関数は、
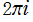
を周期とする周期関数であって、逆積分指数関数と
の関係にある。また逆積分対数関数は、複素平面上
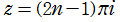
(
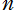
は整数)に特異点を持つ無限多価関数であって、通常は
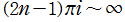
に分枝切断線を置く。
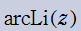
実変数の逆積分対数関数
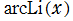
のグラフ。逆関数関係を確認するため、積分対数関数とともに描画する。
複素変数の逆積分対数関数
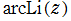
のグラフ。
日:
逆誤差関数
英:
Inverse error function,仏:
Fonction d'erreur inverse,独:
Inverse Fehlerfunktion
誤差関数
の逆関数を逆誤差関数と呼び、
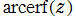
で表わす(標準的な関数記号は存在しない)。
逆誤差関数は、複素平面上
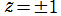
に特異点を持つ無限多価関数であって、通常は
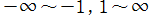
に分枝切断線を置く。その概形は、逆双曲線正接関数に似ている※1。
逆誤差関数を
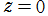
中心に冪級数展開すると
となる。また、
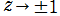
のとき
で近似できる。
逆誤差関数は、実変数の場合に限って統計学や確率論で希に用いられる。
【註記】
※1 : Mathematica にも逆誤差関数が実装されているが、なぜか複素変数の場合はサポートされていない。

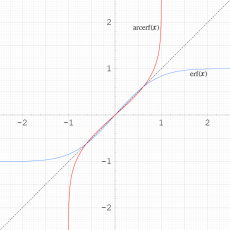
実変数の逆誤差関数
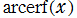
のグラフ。逆関数関係を確認するため、誤差関数とともに描画する。
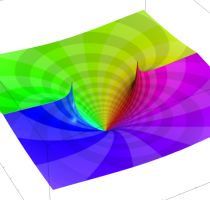
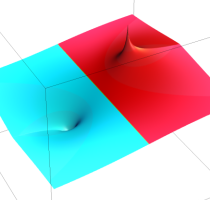
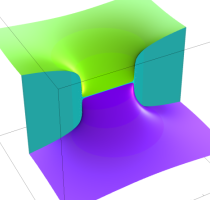
複素変数の逆誤差関数
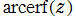
のグラフ。
Fresnel 関数
の逆関数を逆 Fresnel 関数と呼び、
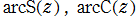
で表わす(標準的な関数記号は存在しない)。
複素平面上において逆 Fresnel 関数は、
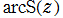
が
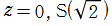
、
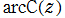
が
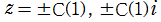
に分岐点を持つ無限多価関数である。
クロソイド曲線を定義する連立方程式から、パラメータを消去すれば
がクロソイド曲線(の一部分)を表わす関数となる。
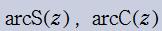
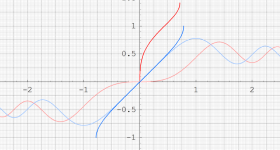
実変数の逆 Fresnel 関数
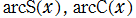
のグラフ。逆関数関係を確認するため、Fresnel 関数とともに描画する。
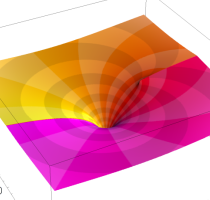
複素変数の逆 Fresnel 関数
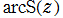
のグラフ。
複素変数の逆 Fresnel 関数
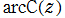
のグラフ。

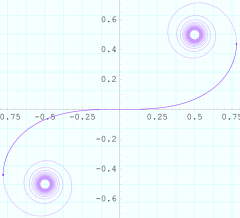
実変数のクロソイド関数
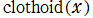
のグラフ。確認のため、クロソイド曲線とともに描画する。
複素変数のクロソイド関数
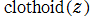
のグラフ。