特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
参考資料 Menu
数学記号一覧
ただし、特殊関数以外の記号は、当サイトで使用した一部の記号のみを掲載しています。
| 特殊関数 | 一般的な関数 | 数学記号 |
特殊関数の記号
当サイトで使用した特殊関数の記号。(独自に定めた記号も含まれています。)| 英文字 | ギリシャ文字 | その他 |
は英文字の 英文字
| A, a | B, b | C, c | D, d | E, e | F, f | G, g |
| H, h | I, i | J, j | K, k | L, l | M,m | N, n |
| O, o | P, p | Q, q | R, r | S, s | T, t | U, u |
| V, v | W,w | X, x | Y, y | Z, z |
[A，a]
Klein 群の保型関数
Anger - Weber 同伴関数
Mathieu 固有値関数
Lamé 固有値関数
位数２のモックテータ関数
原点対称の Airy 関数
交互階乗関数
算術幾何平均
第1種 Airy 関数
第1種一般 Airy 関数
積分 Airy 関数
積分 Airy 関数
積分 Airy 関数
Airy - Fresnel 関数
Abel 関数
楕円振幅関数
逆積分指数関数
逆積分指数関数
逆誤差関数
逆 Fresnel 関数
逆 Fresnel 関数
逆積分対数関数
原点対称の Airy 関数
[B，b]
Blasius 関数
Blasius 導関数
Blasius 2位導関数
Mathieu 固有値関数
Lamé 固有値関数
Bailey Mod９恒等式
Bailey Mod９恒等式
Bailey Mod９恒等式
位数２のモックテータ関数
第1種 Kelvin 関数
第1種 Kelvin 関数
第2種 Airy 関数
第2種一般 Airy 関数
q-二項展開
積分 Airy 関数
積分 Airy 関数
Airy - Fresnel 関数
[C，c]
一般 Clausen 関数
一般 Clausen 関数 (解析接続型)
Fresnel (余弦) 関数
超 Fresnel (余弦) 関数
第1種 Gegenbauer 関数
第1種 Gegenbauer 関数 (繰込形式)
Coulomb 正規化因子
Mittag - Leffler 三角関数
Rogers - Ramanujan 連分数（→Rogers - Ramanujan 恒等式）
第1a種 Chazy 超越関数
第1b種 Chazy 超越関数
第1c種 Chazy 超越関数
第1d種 Chazy 超越関数
第1e種 Chazy 超越関数
第8種 Chazy 超越関数
第13a種 Chazy 超越関数
第13b種 Chazy 超越関数
Glasser 積分関数
Glasser 積分関数
Jacobi の楕円関数 (Glaisher 表記)
Jacobi の楕円関数 (Glaisher 表記)
第1種 Mathieu (偶) 関数
第1種変形 Mathieu (偶) 関数
Lamé 多項式
Lamé 多項式
正則化不完全ガンマ関数（冪級数の連続化）
積分双曲線関数
積分双曲線関数
積分三角関数
積分三角関数
一般積分三角関数
一般積分三角関数
Airy - Hardy 積分関数
Clausen 関数
Clausen 関数 (解析接続型)
クロソイド関数（→逆 Fresnel 関数）
Gauss の楕円関数（レムニスケート余弦関数）
Jackson の楕円関数（→ Gauss の楕円関数）
正規化された Gegenbauer 関数
Jacobi の楕円関数
q-三角関数
q-三角関数～第2の定義
q-三角関数
q-三角関数
Squigonometric 関数
Squigonometric 関数
[D，d]
第1種 Debye 関数
第2種 Debye 関数
第2種楕円積分
第2種楕円積分
第2種完全楕円積分
放物柱関数
第2種 Gegenbauer 関数
Wigner のD関数
Wigner のd関数
Duffing 関数
非強制振動型 Duffing 関数
Dyson Mod27恒等式
Dyson Mod27恒等式
Dyson Mod27恒等式
Dyson Mod27恒等式
Lamé 多項式
Jacobi の楕円関数
Jacobi の楕円関数 (Glaisher 表記)
Jacobi の楕円関数 (Glaisher 表記)
[E，e]
第2種完全楕円積分
第2種楕円積分
第2種楕円積分
第1種楕円積分
第2種楕円積分
第3種楕円積分
正規化 Eisenstein 級数
実解析的 Eisenstein 級数
実解析的 Eisenstein 級数
数論的保型形式
積分指数関数
積分指数関数
相補積分指数関数
一般積分指数関数
Airy - Hardy 積分関数
Mittag - Leffler 関数
Weber 関数
Glasser 積分関数
Glasser 積分関数
正則化不完全ガンマ関数（冪級数の連続化）
第1種 Lamé 関数
第1種 Lamé 関数
誤差関数
相補誤差関数（→誤差関数）
虚部誤差関数（→誤差関数）
超誤差関数
超虚部誤差関数（→超誤差関数）
q-指数関数
[F，f]
Dawson 関数
Fresnel 補助関数
Fresnel interference pattern 関数
Abramowitz 積分関数
第1種合流型超幾何関数
正規化された合流型超幾何関数
第1種Coulomb波動関数
第1種楕円積分
第1種楕円積分
Ramanujan のテータ関数
Weber の楕円モジュラー関数
第1種超幾何関数
正規化された超幾何関数
一般超幾何関数
正規化された一般超幾何関数
位数３のモックテータ関数
位数５のモックテータ関数
位数５のモックテータ関数
位数５のモックテータ関数
位数５のモックテータ関数
位数７のモックテータ関数
位数７のモックテータ関数
位数７のモックテータ関数
第2種 Lamé 関数
第2種 Lamé 関数
第2種 Mathieu (奇) 関数
第3種変形 Mathieu 関数
第2種変形 Mathieu 関数
[G，g]
Goodwin - Staton 関数
Fresnel 補助関数
Barnes のＧ関数
Vignéras の多重ガンマ関数
Gauss の和（→ Dirichlet のＬ関数）
第1種 Grüneisen 関数
第2種 Grüneisen 関数
第1種 Jacobi 関数
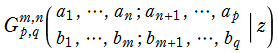
Meijer のＧ関数
第2種合流型超幾何関数
第2種 Coulomb 波動関数
Eisenstein 級数
Glaisher - Ramanujan 関数
Göllnitz - Gordon 恒等式
Göllnitz - Gordon 恒等式
第2種超幾何関数
楕円モジュラー形式（不変量）
楕円モジュラー形式（不変量）
第2種 Mathieu (偶) 関数
第3種変形 Mathieu 関数
第2種変形 Mathieu 関数
Glasser 積分関数
Glasser 積分関数
Glasser 積分関数
Glasser 積分関数
Glasser 積分関数
Glasser 積分関数
Scorer 関数（→ Airy 関数）
Galois 的有理関数
Galois 的有理関数
[H，h]
Hadamard のガンマ関数
Euler 和
一般 Euler 和
第1種 Hankel 関数（第3種 Bessel 関数）
第2種 Hankel 関数（第4種 Bessel 関数）
第1種球 Hankel 関数（第3種球 Bessel 関数）
第2種球 Hankel 関数（第4種球 Bessel 関数）
第1種 Hermite 関数
第2種 Hermite 関数
第1種 Hermite 関数
第2種 Hermite 関数
第1種 Hankel - Coulomb 波動関数
第2種 Hankel - Coulomb 波動関数
Hill 関数
第1種 q-Hermite 関数
第2種 q-Hermite 関数
Struve 関数
Scorer 関数（→ Airy 関数）
Hardy - Littlewood 関数（→ Riesz 関数）
正規化された Hermite 関数
(一般) Hermite 多項式
第1種局所 Heun 関数
第2種局所 Heun 関数
一般 Heun 関数
合流型 Heun 関数
合流型 Heun 関数 (Doubly-confluent type)
合流型 Heun 関数 (Biconfluent type)
合流型 Heun 関数 (Triconfluent type)
[I，i]
第1種変形 Bessel 関数
正則化不完全ベータ関数
積分変形 Bessel 関数
変形 Bessel - Fresnel 関数
[J，j]
Anger 関数
第1種 Bessel 関数
Jackson - Slater 恒等式
Klein の楕円モジュラー関数
Klein の楕円モジュラー関数の平方根
一般の楕円モジュラー関数
数論的保型関数
Schottky 群の保型関数
第1種 q-Bessel 関数
第1種 q-Bessel 関数～第2の定義
第1種球 Bessel 関数
積分 Bessel 関数
積分 Bessel 関数
一般積分 Bessel 関数
Bessel - Fresnel 関数
Bessel - Fresnel 関数
[K，k]
Ｋ関数 (超階乗関数)
第1種完全楕円積分
第2種変形 Bessel 関数
Struve 関数
第2種 Kelvin 関数
第2種 Kelvin 関数
Kepler の逆関数
積分変形 Bessel 関数
Bickley - Naylor 関数
変形 Bessel - Fresnel 関数
[L，l]
Dirichlet のＬ関数
Eichler のＬ関数
第1種 Laguerre 関数
第2種 Laguerre 関数
第1種 Laguerre 陪関数
第2種 Laguerre 陪関数
弁別係数（→ 楕円有理関数）
Lambert の無限累乗関数
第1種 q-Laguerre 陪関数
第2種 q-Laguerre 陪関数
Rogers の二重対数関数
変形 Struve 関数
Lotka - Volterra 関数
Lotka - Volterra 関数
一般 Lamé 関数
第3種 Lamé 関数
第3種 Lamé 関数
ポリ対数関数
積分対数関数
積分対数関数～別定義
正規化された Laguerre 陪関数
q-対数関数
Ramanujan のゼータ関数
[M，m]
変形 Struve 関数
第1種 Whittaker 関数
第3種 Mathieu 関数
第3種変形 Mathieu 関数
第3種変形 Mathieu 関数
[N，n]
第2種 Bessel 関数（Neumann 関数）
第2種 Whittaker 関数～別定義
Jacobi の楕円関数 (Glaisher 表記)
Jacobi の楕円関数 (Glaisher 表記)
Jacobi の楕円関数 (Glaisher 表記)
第3種 Mathieu 関数
第3種変形 Mathieu 関数
第3種変形 Mathieu 関数
[O，o]
（現在、該当なし。）
[P，p]
正則化不完全ガンマ関数
第1種 Legendre 関数
第1種 Legendre 陪関数（Ferrers 型）
第1種 Legendre 陪関数（Hobson 型）
第1種 Jacobi 関数
Pearcey 積分関数
素数ゼータ関数
第1種 q-Legendre 陪関数（Ferrers 型）
第1種 q-Legendre 陪関数（Hobson 型）
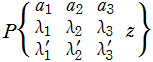
Riemann のＰ関数
第1種円錐関数
正規化された Jacobi 関数
第1種回転楕円体波動関数（動径関数)
第1種回転楕円体波動関数（角度関数）
第1種円環関数
Weierstrass の楕円関数
第1種 Painlevé 超越関数
第2種 Painlevé 超越関数
第2種変形 Painlevé 超越関数
第3種 Painlevé 超越関数
第4種 Painlevé 超越関数
第5種 Painlevé 超越関数
第6種 Painlevé 超越関数
[Q，q]
正則化不完全ガンマ関数
第2種 Legendre 関数
第2種 Legendre 陪関数（Ferrers 型）
第2種 Legendre 陪関数（Hobson 型）
第2種 Jacobi 関数
第2種 Jacobi 関数
第2種 Jacobi 関数
Marcum のＱ関数
ノーム関数（→完全楕円積分）
Yablonskii - Vorob'ev 多項式
第2種 Painlevé 方程式の有理関数解
第2種 Painlevé 方程式の Airy 関数解
(一般) 岡本多項式
第4種 Painlevé 方程式の有理関数解
第4種 Painlevé 方程式の Hermite 関数解
高階 Yablonskii - Vorob'ev 多項式
高階第2種 Painlevé 方程式の有理関数解
第2種 q-Legendre 陪関数（Ferrers 型）
第2種 q-Legendre 陪関数（Hobson 型）
第2種円錐関数
第2種円錐関数 (NIST型)
第2種回転楕円体波動関数（動径関数）
第2種回転楕円体波動関数（角度関数）
第2種円環関数
[R，r]
Riemann 素数計数関数
Riemann 素数計数指数関数
楕円有理関数
Romanovski 関数
Zernike 関数
Rogers - Ramanujan 恒等式
Rogers - Ramanujan 恒等式
Rogers Mod14恒等式
Rogers Mod14恒等式
Rogers Mod14恒等式
(Bessel 型) Riccati 関数
(Hankel 型) Riccati 関数
Riesz 関数
[S，s]
一般 Clausen 関数
一般 Clausen 関数 (解析接続型)
Fresnel (正弦) 関数
超 Fresnel (正弦) 関数
黒川の多重三角関数
Barnes の多重三角関数
Barnes の多重三角関数 (単位周期)
Lommel 関数
Lommel 関数
第2種 Gegenbauer 関数
Mittag - Leffler 三角関数
Rogers - Selberg 恒等式
Rogers - Selberg 恒等式
Rogers - Selberg 恒等式
Dedekind の和
Schwarz の保型関数
Schwarz の保型関数～補助定義
Sievert 積分関数
第1種回転楕円体波動関数（動径関数）
第2種回転楕円体波動関数（動径関数）
第3種回転楕円体波動関数（動径関数）
第4種回転楕円体波動関数（動径関数）
燕尾点正準積分関数（Swallowteil canonical integral function）
第1種 Muğan - Jrad 超越関数
第2種 Muğan - Jrad 超越関数
第3種 Muğan - Jrad 超越関数
Glasser 積分関数
Glasser 積分関数
Jacobi の楕円関数 (Glaisher 表記)
Jacobi の楕円関数 (Glaisher 表記)
第1種 Mathieu (奇) 関数
第1種変形 Mathieu (奇) 関数
Lamé 多項式
Lamé 多項式
Lamé 多項式
Lamé 多項式
q-三角関数
q-三角関数
q-三角関数～第2の定義
正則化不完全ガンマ関数（冪級数の連続化）
積分双曲線関数
積分三角関数
一般積分三角関数
一般積分三角関数
Airy - Hardy 積分関数
Gauss の楕円関数（レムニスケート正弦関数）
超レムニスケート関数
超対数関数
Jackson の楕円関数（→ Gauss の楕円関数）
Jacobi の楕円関数
Squigonometric 関数
Squigonometric 関数
[T，t]
第1種 Chebyshev 関数
Owen のＴ関数
q-三角関数
積分逆正接関数
一般積分逆正接関数
正規化された第1種 Chebyshev 関数
第1種楕円 Chebyshev 関数
[U，u]
Voigt 関数
第2種 Chebyshev 関数
第2種合流型超幾何関数
第1種放物柱関数
Lamé 多項式
正規化された第2種 Chebyshev 関数
[V，v]
Voigt 関数
第2種 Chebyshev 関数
NISTの Chebyshev 関数
第2種放物柱関数
Van der Pol 関数
強制振動型 Van der Pol 関数
第2種楕円 Chebyshev 関数
[W，w]
乗積対数関数
分枝
の乗積対数関数
Whittaker 積分関数
NISTの Chebyshev 関数
放物柱関数
第1種放物柱関数
第2種放物柱関数
第1種放物柱関数
第2種放物柱関数
第3種放物柱関数
第4種放物柱関数
第2種 Whittaker 関数
Wright 関数
[X，x]
Lorenz 関数
[Y，y]
第2種 Bessel 関数
第2種 q-Bessel 関数
第2種 q-Bessel 関数～第2の定義
第2種球 Bessel 関数
球面調和関数
超球面調和関数
積分 Bessel 関数
一般積分 Bessel 関数
Bessel - Fresnel 関数
Lorenz 関数
[Z，z]
非自明零点に関する Dirichlet 級数
非自明零点に関する Dirichlet 級数
円板上の Zernike 関数
Kelvin's ship - wave pattern
Lorenz 関数
ギリシャ文字
| Α, α | Β, β | Γ, γ | Δ, δ | Ε, ε | Ζ, ζ |
| Η, η | Θ, θ | Ι, ι | Κ, κ | Λ, λ | Μ, μ |
| Ν, ν | Ξ, ξ | Ο, ο | Π, π | Ρ, ρ | Σ, σ |
| Τ, τ | Υ, υ | Φ, φ | Χ, χ | Ψ, ψ | Ω, ω |
[Α，α]
（現在、該当なし。）
[Β，β]
ベータ関数
不完全ベータ関数
一般化不完全ベータ関数
q-ベータ関数
[Γ，γ]
ガンマ関数
Barnes の多重ガンマ関数
Barnes の多重ガンマ関数 (単位周期)
黒川の多重ガンマ関数
不完全ガンマ関数
不完全ガンマ関数
正則化不完全ガンマ関数
Stieltjes 関数
q-ガンマ関数
q-Euler 定数
q-Euler 定数
位数６のモックテータ関数
楕円ガンマ関数
第2種 q-超幾何関数
[Δ，δ]
楕円モジュラー形式（判別式）
Sitaramachandrarao 関数
数論的尖点形式
[Ε，ε]
Jacobi の第2種楕円関数
Dedekind エータ関数の24乗根因子（→Dedekind のエータ関数）
[Ζ，ζ]
Riemann のゼータ関数
Hurwitz のゼータ関数
Riemann - Siegel 関数
Weierstrass の楕円ゼータ関数
Jacobi のゼータ関数（→楕円積分）
Jacobi の第2種楕円関数
Dedekind のゼータ関数
q-ゼータ関数
q-ゼータ関数～別定義
q-Hurwitz ゼータ関数
q-Hurwitz ゼータ関数～別定義
Fibonacci ゼータ関数
Ramanujan - Siegel 関数
[Η，η]
Dedekind のエータ関数
Conway - Norton の楕円モジュラー関数
[Θ，θ]
Riemann - Siegel シータ関数
Ramanujan - Siegel シータ関数
楕円テータ関数
Neville のテータ関数
Riemann テータ関数
指標付き Riemann テータ関数
Scaled - Riemann テータ関数
Coulomb 波動関数の位相
Lane - Emden 関数
[Ι，ι]
（現在、該当なし。）
[Κ，κ]
（現在、該当なし。）
[Λ，λ]
Heuman のラムダ関数
楕円モジュラー・ラムダ関数
正4面体方程式に付随する楕円モジュラー関数
正8面体方程式に付随する楕円モジュラー関数
正20面体方程式に付随する楕円モジュラー関数
回転楕円体波動固有値関数
位数６のモックテータ関数
[Μ，μ]
位数２のモックテータ関数
位数６のモックテータ関数
Appell - Lerch 級数
変形 Appell - Lerch 級数
[Ν，ν]
位数３のモックテータ関数
[Ξ，ξ]
Riemann のゼータ関数（クシー関数）
Riemann のゼータ関数（クシー関数）
[Ο，ο]
（現在、該当なし。）
[Π，π]
第3種楕円積分
第3種楕円積分
第3種完全楕円積分
Jacobi の第3種楕円関数
q-円周率
[Ρ，ρ]
位数３のモックテータ関数
位数６のモックテータ関数
[Σ，σ]
Weierstrass の楕円シグマ関数
Coulomb 位相シフト
位数６のモックテータ関数
[Τ，τ]
Ramanujan のタウ関数（→ Ramanujan のゼータ関数）
[Υ，υ]
第2種 q-合流型超幾何関数
[Φ，φ]
Lerch の超越関数
Lerch の超越関数～別定義
第1種 Strömgren 関数
第2種 Strömgren 関数
第1種 q-合流型超幾何関数
第1種 q-合流型超幾何関数～別定義
第1種 q-超幾何関数
Julia 集合の Böttcher 関数
Mandelbrot 集合の Böttcher 関数
位数３のモックテータ関数
位数５のモックテータ関数
位数５のモックテータ関数
位数６のモックテータ関数
[Χ，χ]
Dirichlet 指標（→ Dirichlet のＬ関数）
Kronecker 指標（→ Dirichlet のＬ関数）
位数３のモックテータ関数
位数５のモックテータ関数
位数５のモックテータ関数
[Ψ，ψ]
ディガンマ関数（→ポリガンマ関数）
ポリガンマ関数
楕円的臍点正準積分関数（Elliptic umbilic canonical integral function）
双曲的臍点正準積分関数（Hyperbolic umbilic canonical integral function）
余次元 K の尖点正準積分関数
q-ディガンマ関数（→ q-ポリガンマ関数）
q-ポリガンマ関数
Ramanujan の1ψ1関数
位数３のモックテータ関数
位数５のモックテータ関数
位数５のモックテータ関数
位数６のモックテータ関数
[Ω，ω]
位数３のモックテータ関数
その他
Lobachevsky 関数
超指数関数（テトレーション）
q-階乗
q-シフト因子（q-Pochhammer 記号）
楕円シフト因子（楕円 Pochhammer 記号）
Wigner の 3-j 記号
一般的な関数の記号
当サイトで使用した特殊関数以外の関数記号のうち、特に説明を要する記号のみを掲載しています。数論的関数
Möbius 関数
（
の素因数分解が、偶数個の相異なる素数の積のとき１、奇数個の相異なる素数の積のとき－1、平方因子を含むとき０。）
Euler のファイ関数 または Euler のトーシェント関数
（
と互いに素な、以下の自然数の個数。）
素数ニュー(ν)関数
（
の素因数分解における相異なる素数の個数。）
約数関数
（
の約数をそれぞれ乗した数の総和。）
Liouville のラムダ関数
（
の素因数分解を
とするとき、
の値。）
Von Mangoldt のラムダ関数
（
の素因数分解が、単一の素数の冪乗となる場合はその素数の自然対数、異なる素数からなる場合は０。）
Legendre の記号 (平方剰余記号)
を素数とするとき、
Jacobi の記号 (Kronecker の記号)
の素因数分解をとするとき、Legendre の記号によって
となる (Legendre の記号の一般化に相当する)。特に、
素数階段関数
（正の実数
以下の素数の個数。）
分割数
（正整数
を、それ以下の正整数の和で表わす方法の個数。ただし、和の順序の入れ替えはカウントしない。）その他
自然対数の底数
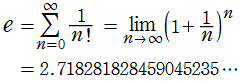
指数関数
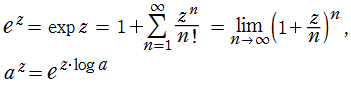
対数関数。指数関数の逆関数。(当サイトでは、底数を明示しない場合は自然対数とする。)
三角関数
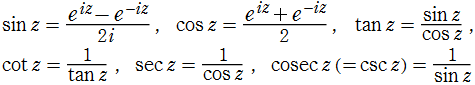
逆三角関数。三角関数の逆関数。
双曲線関数
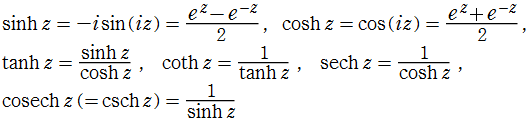
逆双曲線関数。双曲線関数の逆関数。
Gudermann 関数 (注意：下記の場合分け方法は、分枝切断線の形状によって異なる。)
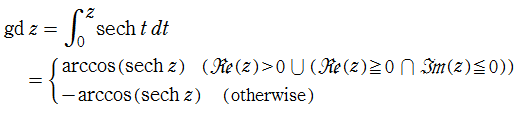
符号関数
（
が正数のとき１、負数のとき－1、０のとき０となる。）
Bernoulli 数
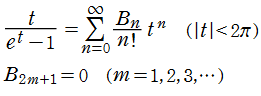
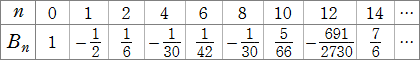
Bernoulli 多項式
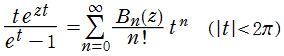
Fibonacci 数
二項係数
Pochhammer 記号
第1種 Stirling 数
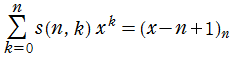
Euler の定数 (Euler - Mascheroni 定数)
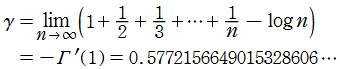
調和数
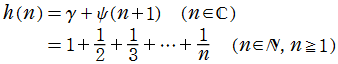
床関数
（実数
以下の最大の整数。複素数
のときは
とする。）
天井関数
（実数
以上の最小の整数。複素数のときは
とする。）
Kronecker のデルタ
（全ての引数が等しいときは1、そうでないときは0。）
数学記号
当サイトで使用した数学記号のうち、特に説明を要する記号のみを掲載しています。
自然数全体の集合 (０の扱いは文脈による)。
整数全体の集合。
有理数全体の集合。
代数的数
を最小基底とする代数的数体 (代数体)。
実数全体の集合。
複素数全体の集合。
集合に対する元の属性。
は集合
の元である。
和集合 (集合
と集合
の合併集合)。つまり、または。
積集合 (集合
と集合の共通部分集合)。つまり、かつ。
差集合 (集合
から集合を除いた集合)。
集合の位数または長さ (集合
の元の個数)。
は
の約数。
はの約数ではない。
合同式。
をで割った剰余がに等しい。
, 
のうちの最大の値。
, のうちの最小の値。
実数
の区間
。(ただし、交換子積
の意味で用いることもある。)
実数
の区間
。この場合は
も可。
実数
の区間
。この場合は
も可。
実数
の区間
。この場合は，も可。ただし、この記号は他の意味に用いることもある。例えば、
を ｢との最大公約数｣ の意味として、
：とは互いに素
：とは互いに素でないのようにも用いる。
の絶対値。(グラフの座標インデックスとしての
も同じ意味。)
の偏角。
の実部。(グラフの座標インデックスとしての
も同じ意味。)
の虚部。(グラフの座標インデックスとしての
も同じ意味。)
の共役複素数。
漸近的に等しい。
極限
のとき、表記
は、
の意味。
Landau の記号。
極限
のとき、表記
は、
の意味。
多項式
の次数。 
Cauchy の主値。
, 間の線積分経路上に極などの特異点
があるとき、次の極限をとることの意味。
ラプラシアン (ナブラ２乗)。
次元 (直交直線座標) 空間内の関数
に対して、次のように作用する偏微分演算子。
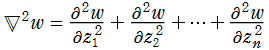
(ただし文献等では、
を
と表記することも多い。)
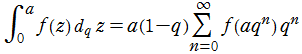
Thomae 積分 (q-積分)。
【 Petite Galerie 】
三角関数：高校数学の難所の一つ (私も苦心しました…。)