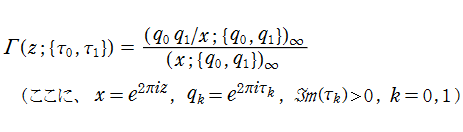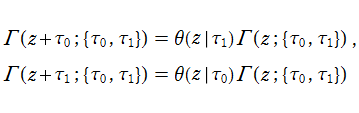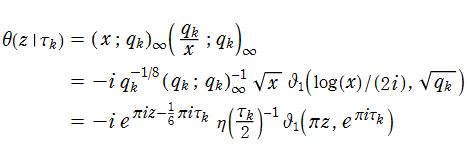特殊関数 グラフィックスライブラリー
Graphics Library of Special functions

楕円ガンマ関数 (楕円階乗関数)

楕円ガンマ関数

　S. Ruijsenaars の楕円ガンマ関数は、q-ガンマ関数の楕円関数化に相当し、楕円シフト因子を用いて

• 

と表わされる。
　楕円ガンマ関数は二重関数等式、

• 

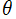
を満たす。ここに、は本質的に楕円テータ関数

• 

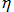
であり、は Dedekind のエータ関数である。
　また、楕円ガンマ関数は１を周期とする周期関数である。

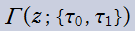
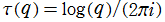
　以降、とする。
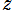
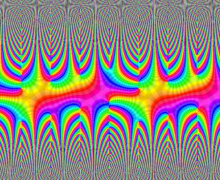
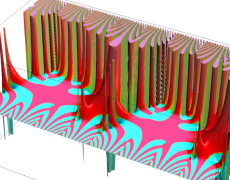
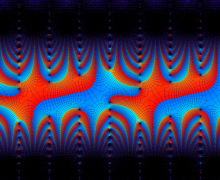
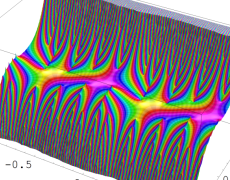
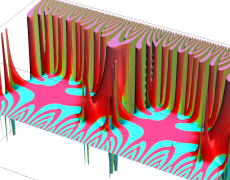
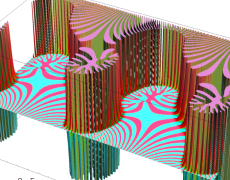
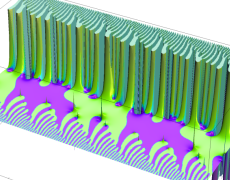
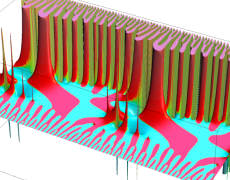
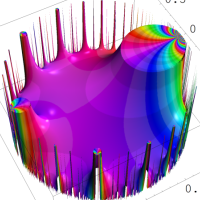
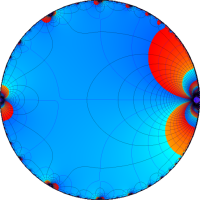
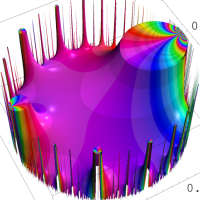
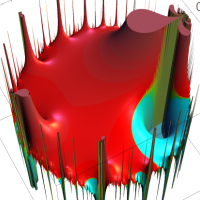
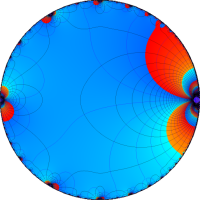
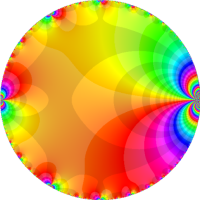
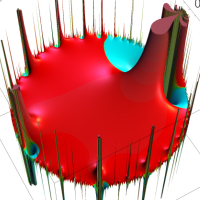
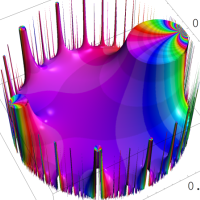
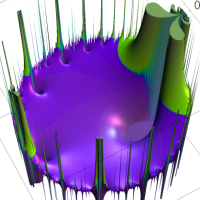
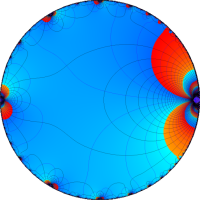
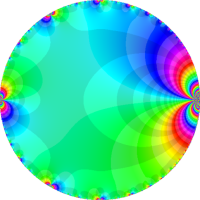
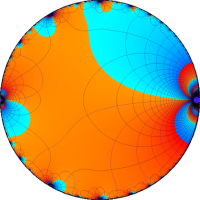
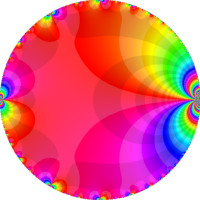
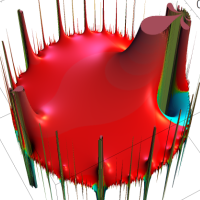
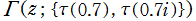
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

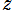
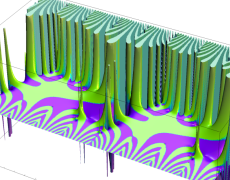
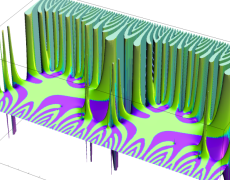
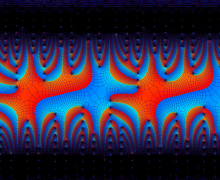
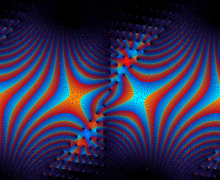
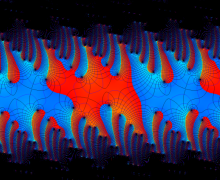
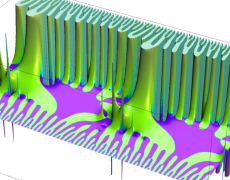
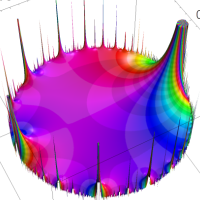
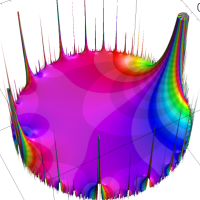
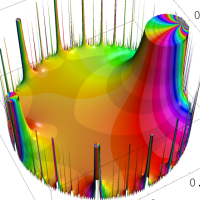
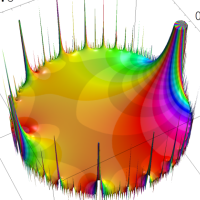
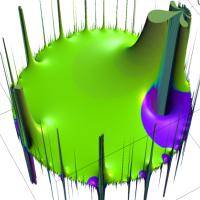
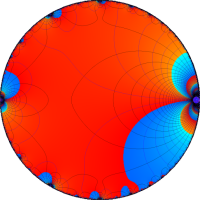
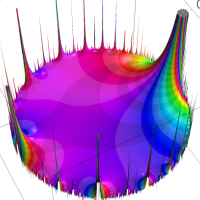
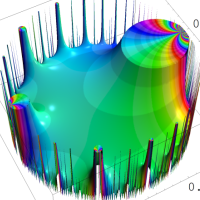
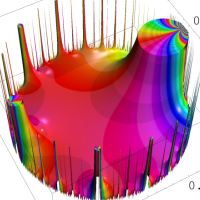
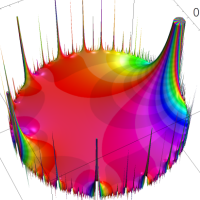
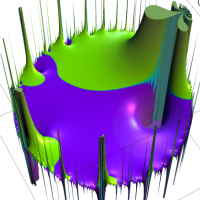
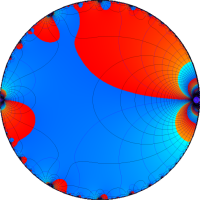
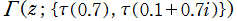
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

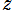
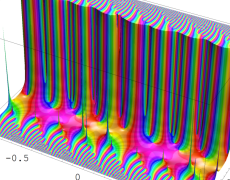
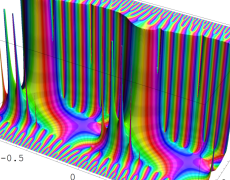
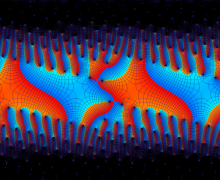
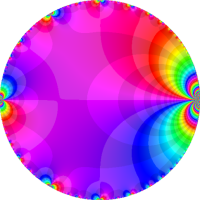
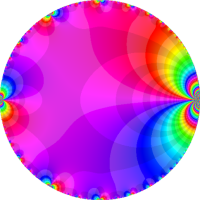
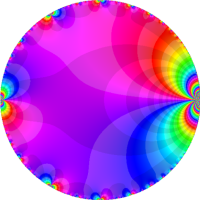
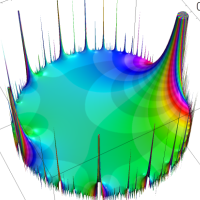
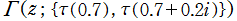
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

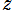
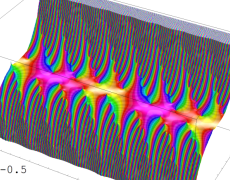
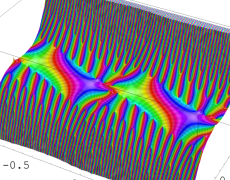
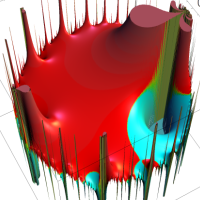
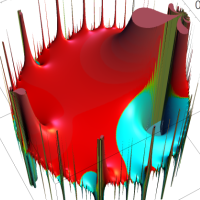
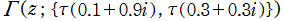
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

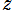
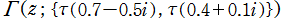
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

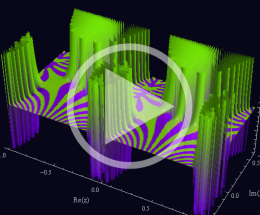
　アニメーション（6.11MB）
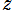
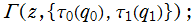
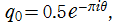
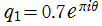
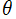
　を複素変数とする 楕円ガンマ関数のグラフ。＝1/26～2 (+1/26) 。

• 

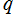
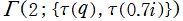
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

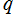
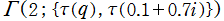
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

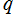
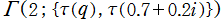
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

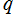
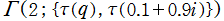
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

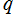
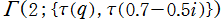
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
• 

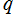
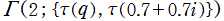
　を複素変数とする楕円ガンマ関数のグラフ。２番目は、１番目のグラフの垂直軸を常用対数目盛にした場合。

• 
• 
• 
• 
• 
•