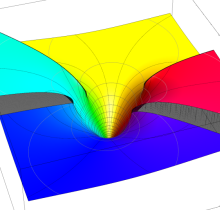
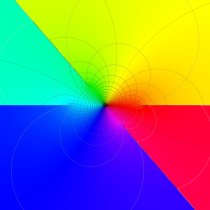
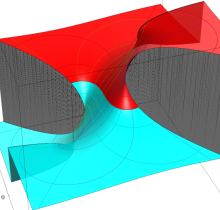
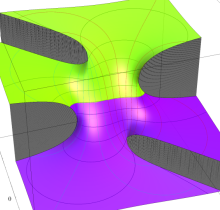
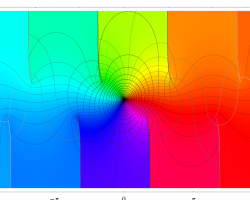
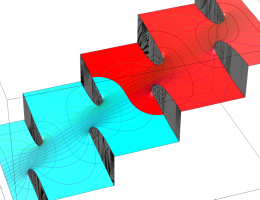
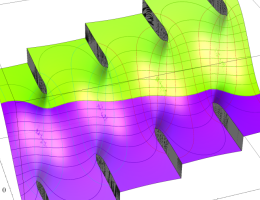
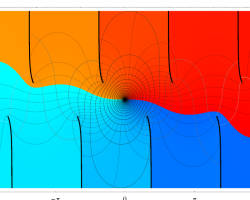
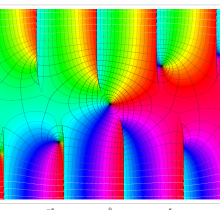
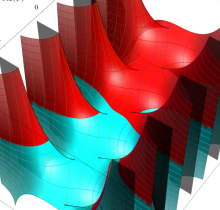
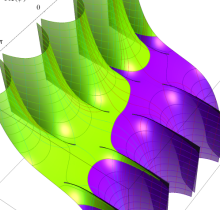
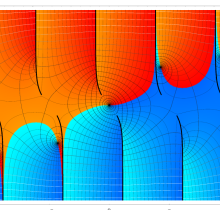
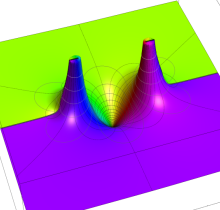
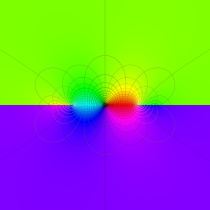
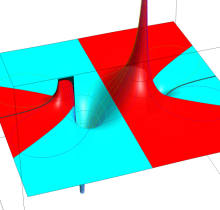
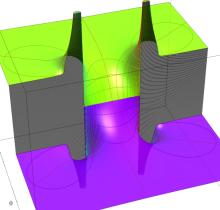
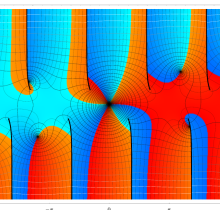
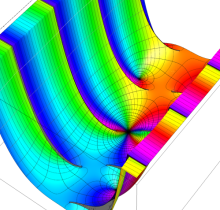
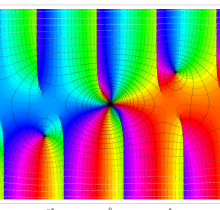
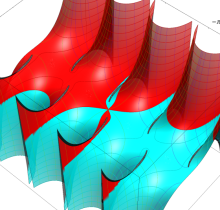
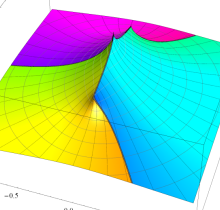
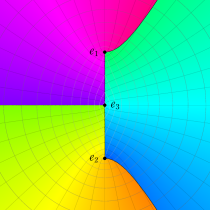
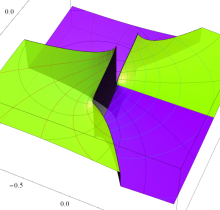
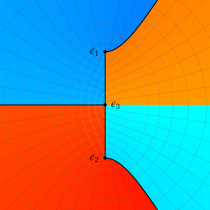
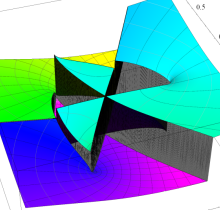
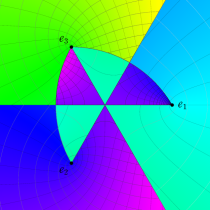
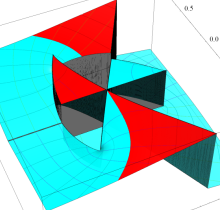
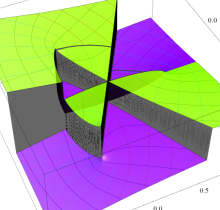
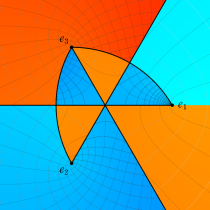
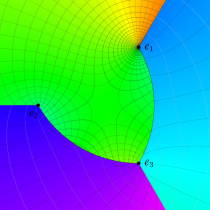
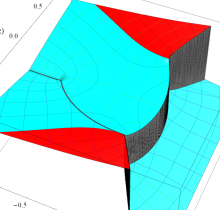
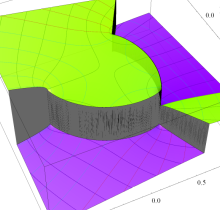
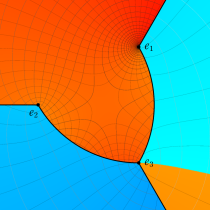
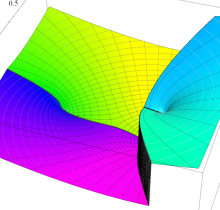
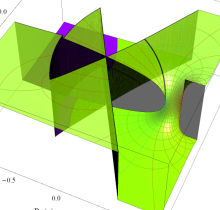
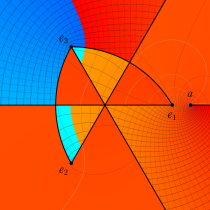
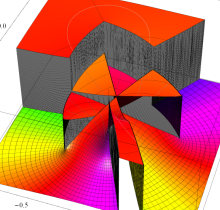
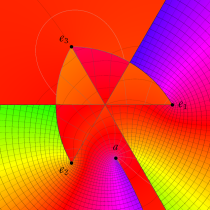
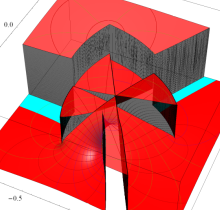
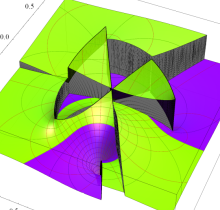
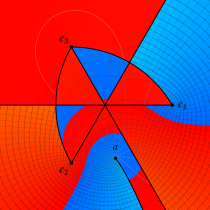
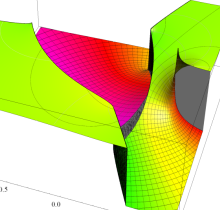
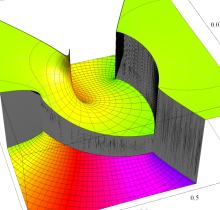
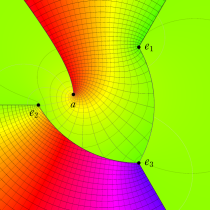
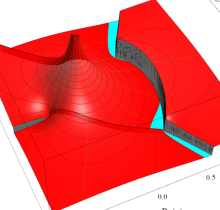
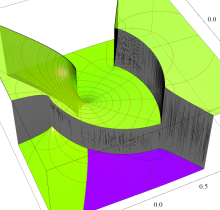
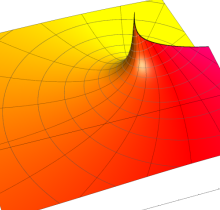
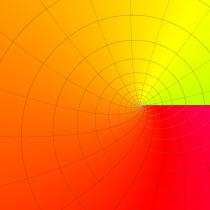
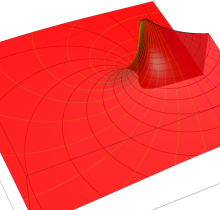
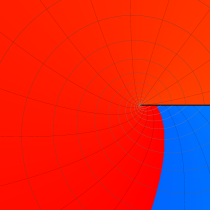
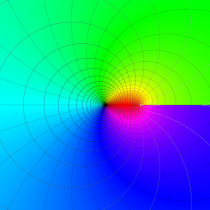
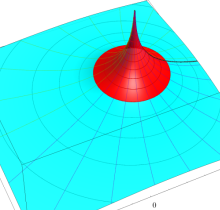
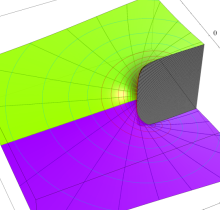
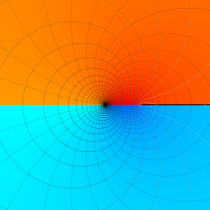
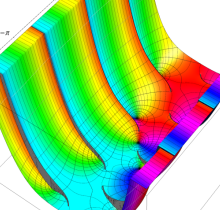
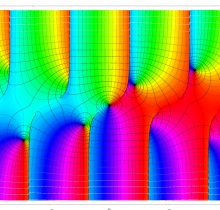
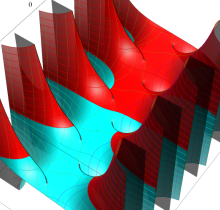
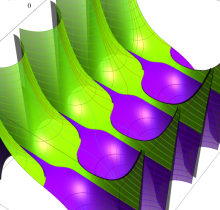
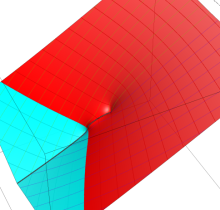
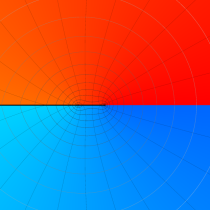
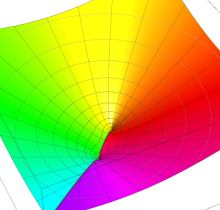
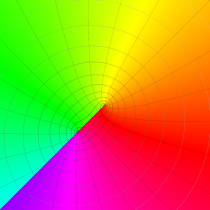
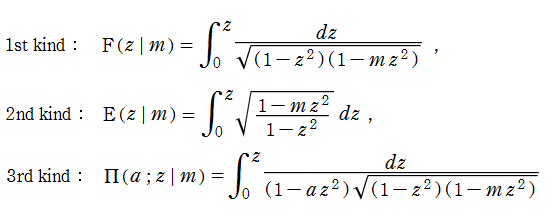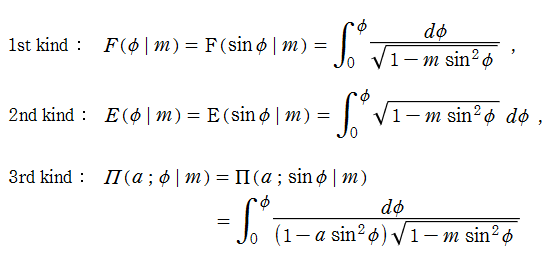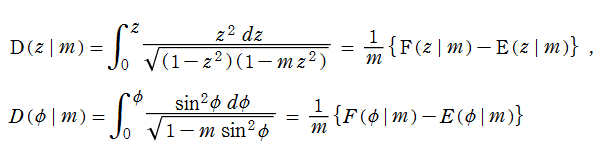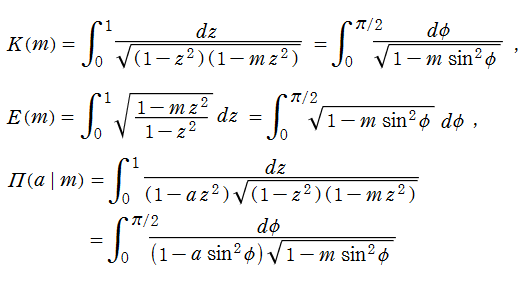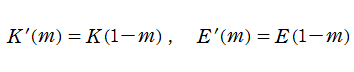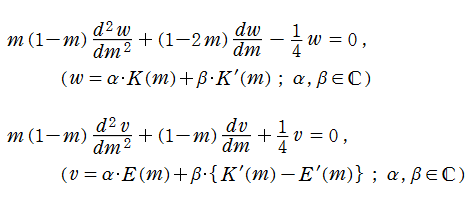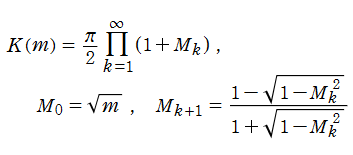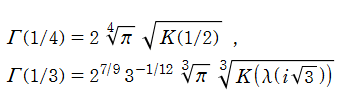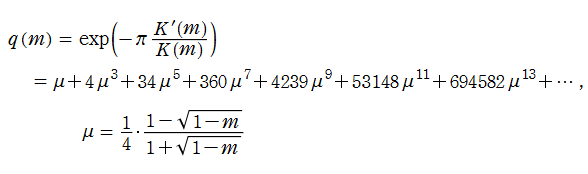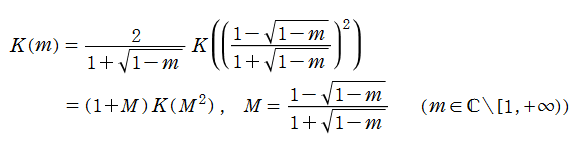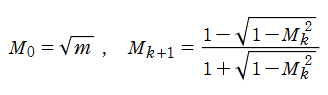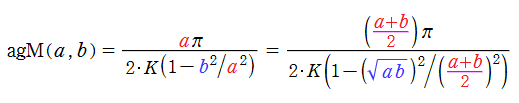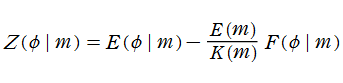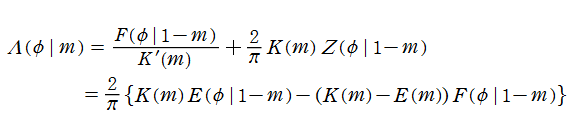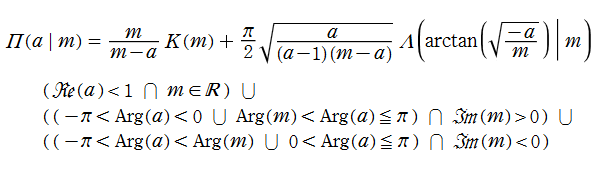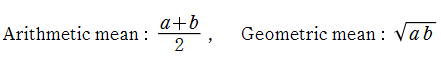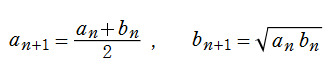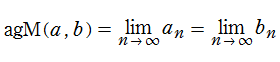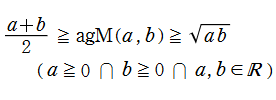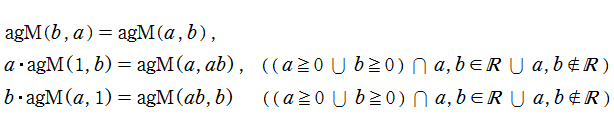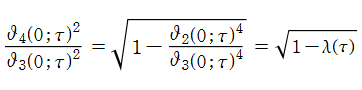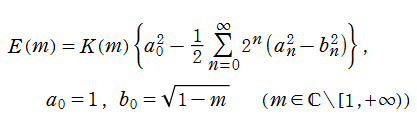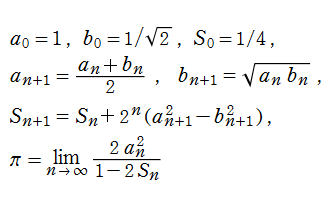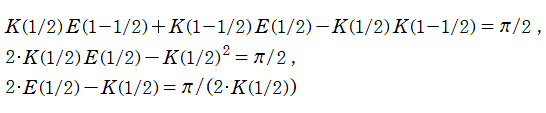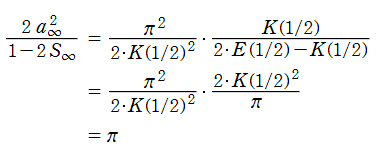特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
楕円積分
楕円積分
日:楕円積分英:Elliptic integral,仏:Intégrale elliptique,独:Elliptische Integrale
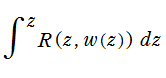
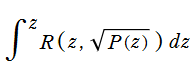
狭義には、前述の楕円積分から初等関数に還元できる積分項を取り除いたものを 「楕円積分」 と言い、楕円無理関数
【第1種楕円積分】
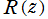 の特異点が、前述の代数分岐点のみである場合。
の特異点が、前述の代数分岐点のみである場合。
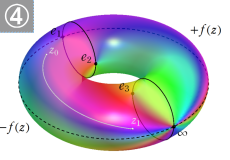
第1種楕円積分の多価性は、トーラス上での積分経路の周回数のみに由来し※3、その逆関数は1価有理型関数たる楕円関数になる。
【第2種楕円積分】
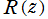 の特異点が、前述の代数分岐点の他は、留数が0の極のみである場合。
の特異点が、前述の代数分岐点の他は、留数が0の極のみである場合。
第2種楕円積分の多価性も、トーラス上での積分経路の周回数のみに由来するが、その逆関数は1価関数にならない。
【第3種楕円積分】
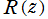 の特異点が、前述の代数分岐点の他に、留数が0でない極を持つ場合。
の特異点が、前述の代数分岐点の他に、留数が0でない極を持つ場合。
第3種楕円積分の多価性は、トーラス上での積分経路の周回数のみならず留数にも由来する。逆関数は1価関数にならない。
第1種楕円積分の多価性は、トーラス上での積分経路の周回数のみに由来し※3、その逆関数は1価有理型関数たる楕円関数になる。
【第2種楕円積分】
第2種楕円積分の多価性も、トーラス上での積分経路の周回数のみに由来するが、その逆関数は1価関数にならない。
【第3種楕円積分】
第3種楕円積分の多価性は、トーラス上での積分経路の周回数のみならず留数にも由来する。逆関数は1価関数にならない。
現在では、歴史的な理由あるいは用途に応じて、楕円積分の具体的な表示式が 「標準形」 として定着している。以降、その主な標準形を列挙するとともに、それぞれの満たす公式や応用事例等にも触れる。
【Legendre - Jacobi の標準形】※4
最も古くから考察されてきた標準形で、A. M. Legendre 等が一般の楕円積分から初等関数に還元できない部分として、この3種類の形を抽出した。このうち、第1種の逆関数が Jacobi の楕円関数になるので、C. G. J. Jacobi の名も冠せられている。
Legendre - Jacobi の標準形は、物理学等との接点を持ちつつ研究されてきた経緯もあって、実用的な事例と絡めて論じられることが多い。例えば、この標準形は長方形の内部や外部へ等角写像する際に都合が良いため、帯電物体が長方形であるときの電場と磁場の解析などに応用される。
なお、これらに
も、しばしば Legendre - Jacobi の標準形と呼ばれ、単振り子の運動など、この形での応用事例も多数ある。
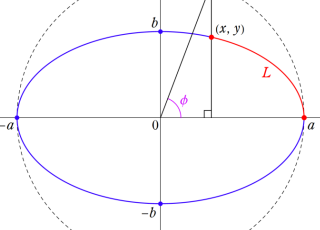
歴史的に、曲線や曲面の計測で生じた積分の形からも、Legendre - Jacobi の標準形は示唆されていた。特に、楕円の周の長さが第2種によって
第1種と第2種は、
に還元され、ここで更に
なお、冗長ではあるが第1種と第2種の差、つまり
を定義することがある (例えば、NISTの §19 - 2)。弾性板が歪曲してできるエラスティカなる曲線は、
【Weierstrass の標準形】
複素解析学が整備された後、主に不変式論からの影響で導入された標準形であり、そのため純粋数学的な用途が多い。名称の直接的な由来は、第1種の逆関数が Weierstrass の楕円関数になるからである。(関数記号は、当サイトで独自に定めたものである。)
ここに、楕円関数論に準拠して多項式部分を
第2種・第3種は、第1種を用いて、
と表わせる。(逆に、第1種~第3種が互いに大きく異なる原因が、Weierstrass の楕円ゼータ関数・シグマ関数にあると見ることもできる。)
【Riemann の標準形】
状況・用途等は Weierstrass の標準形と同じで、その多項式部分
【註記】
※1:Abel 積分の基本対称式の逆関数は、多変数の多重周期有理型関数すなわち Abel 関数となる。Abel 積分・Abel 関数論は、複素解析学がもたらした最高到達点の一つとされ、「19世紀数学の華」 と称される。
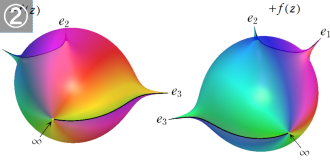
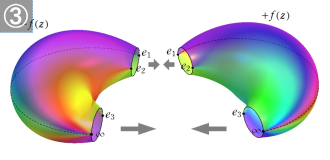
※2:通常は、分岐点を Riemann 面上に写した点でも正則性が使えるように、局所座標変換を併せて導入する。なお、Abel 積分や超楕円積分における被積分関数の Riemann 面は、2個以上のトーラスを接合した (穴が2個以上ある) 曲面と同相になる。
※3:その積分経路は、トーラスの穴を潜って緯度線に沿う経路と、穴を潜らずに経度線に沿う経路との線形結合になる。それぞれの1周回が、第1種の逆関数である楕円関数では二つの基本周期になる。
※4:当サイトでは、母数の一般的な表記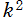 ではなく、
ではなく、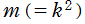 を一貫して使用する。また、
を一貫して使用する。また、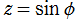 と変換した方の関数記号を斜体とし、そうでない方を立体 (正体) とする独自の区別を使用する。
と変換した方の関数記号を斜体とし、そうでない方を立体 (正体) とする独自の区別を使用する。
その他:当サイトで採用している楕円積分 (Legendre - Jacobi の標準形),後述の Heuman のラムダ関数の分枝切断線は、Mathematica で採用されているそれとは異なる、独自の形状である。しかし、Weierstrass の標準形の分枝切断線は、Mathematica のそれを踏襲する。(当サイト管理人は、Mathematica がどのような方法で分枝切断線の形状 ― 特に Weierstrass 標準形の場合 ― を定めているか調べたが、完全には解明できなかった。)
※1:Abel 積分の基本対称式の逆関数は、多変数の多重周期有理型関数すなわち Abel 関数となる。Abel 積分・Abel 関数論は、複素解析学がもたらした最高到達点の一つとされ、「19世紀数学の華」 と称される。
※2:通常は、分岐点を Riemann 面上に写した点でも正則性が使えるように、局所座標変換を併せて導入する。なお、Abel 積分や超楕円積分における被積分関数の Riemann 面は、2個以上のトーラスを接合した (穴が2個以上ある) 曲面と同相になる。
※3:その積分経路は、トーラスの穴を潜って緯度線に沿う経路と、穴を潜らずに経度線に沿う経路との線形結合になる。それぞれの1周回が、第1種の逆関数である楕円関数では二つの基本周期になる。
※4:当サイトでは、母数の一般的な表記
その他:当サイトで採用している楕円積分 (Legendre - Jacobi の標準形),後述の Heuman のラムダ関数の分枝切断線は、Mathematica で採用されているそれとは異なる、独自の形状である。しかし、Weierstrass の標準形の分枝切断線は、Mathematica のそれを踏襲する。(当サイト管理人は、Mathematica がどのような方法で分枝切断線の形状 ― 特に Weierstrass 標準形の場合 ― を定めているか調べたが、完全には解明できなかった。)
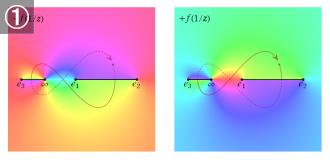
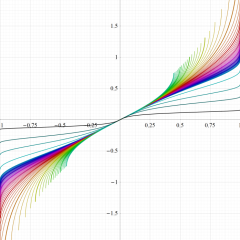
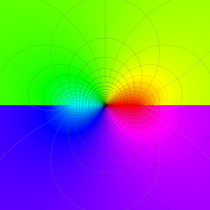
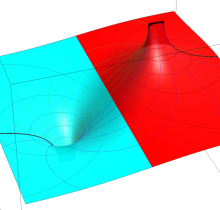
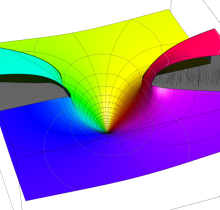
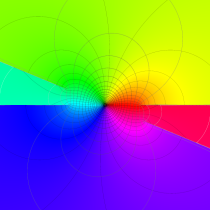
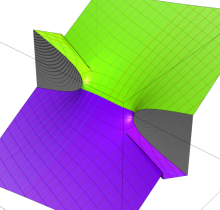
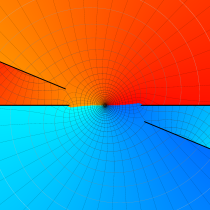
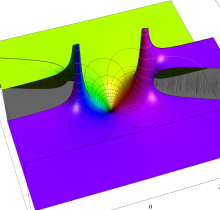
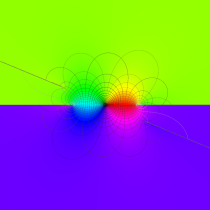
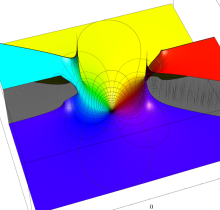
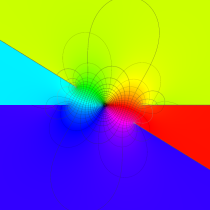
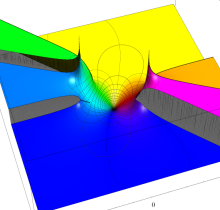
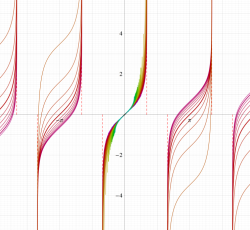
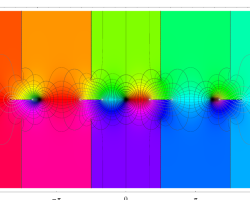
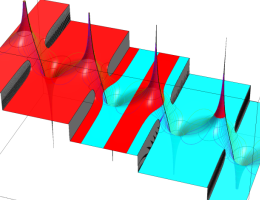
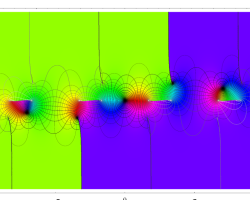
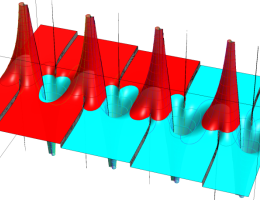
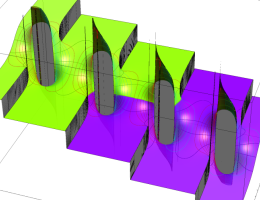
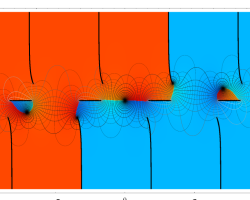
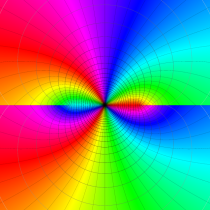
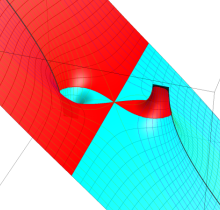
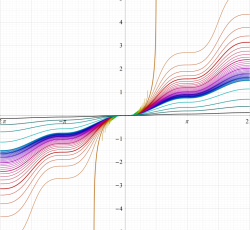
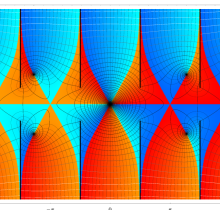
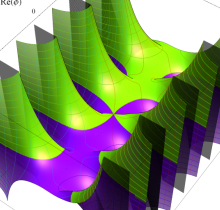
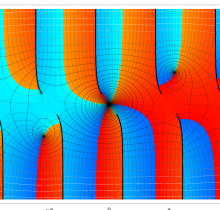
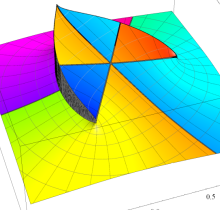
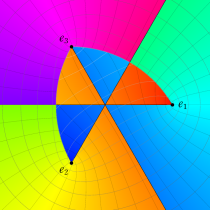
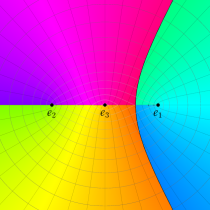
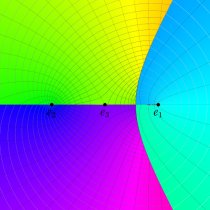
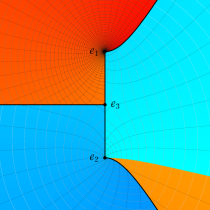
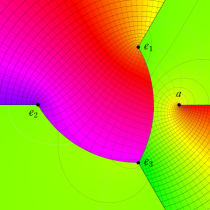
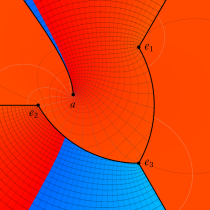
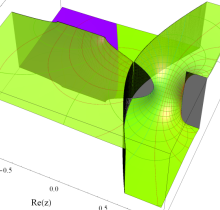
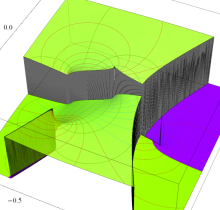
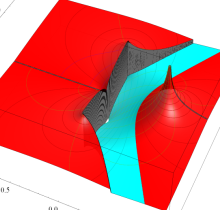
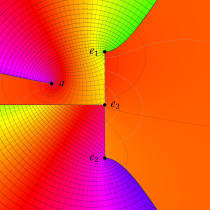
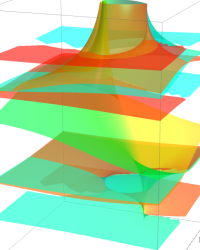
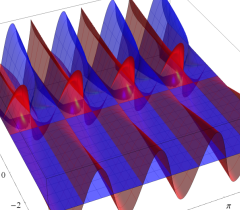
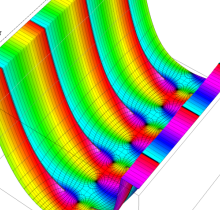
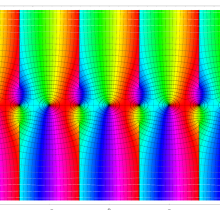
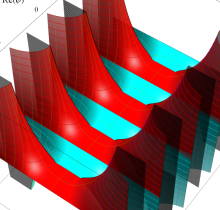
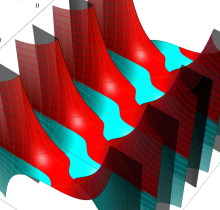
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
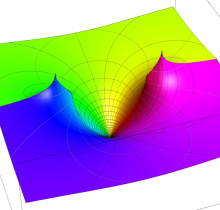
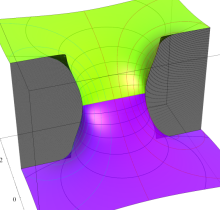
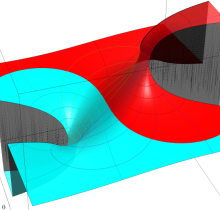
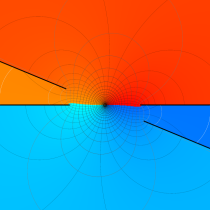
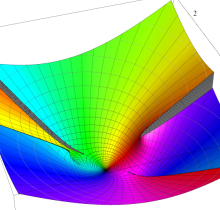
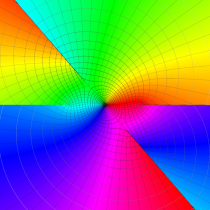
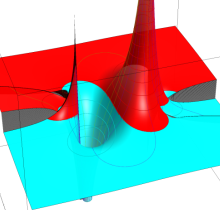
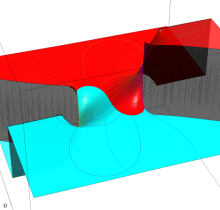
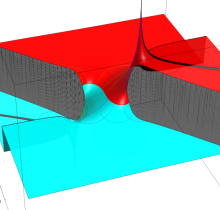
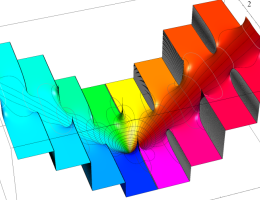
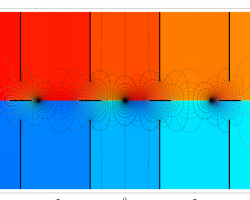
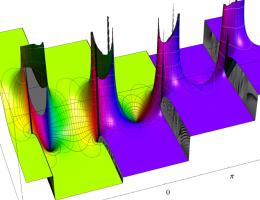
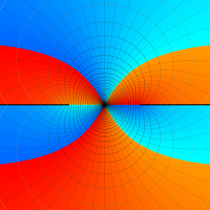
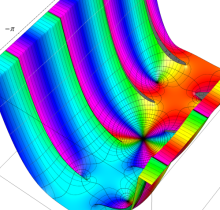
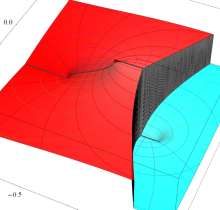
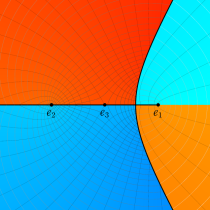
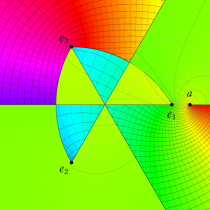
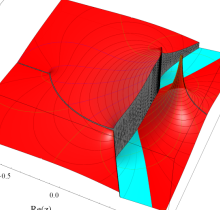
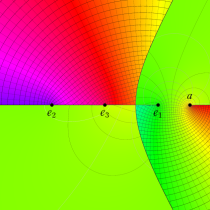
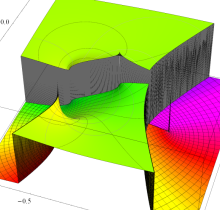
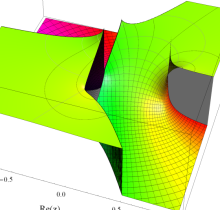
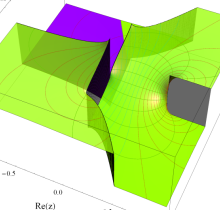
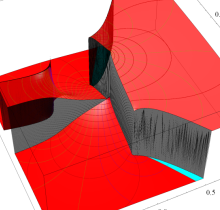
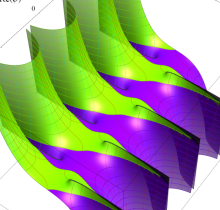
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
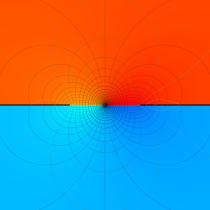
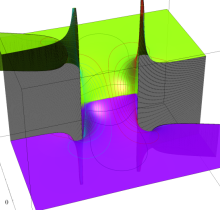
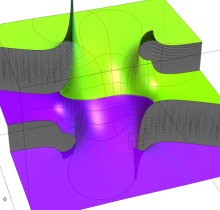
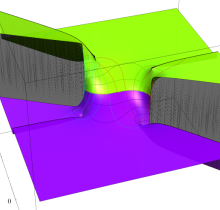
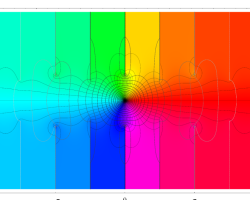
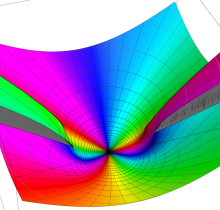
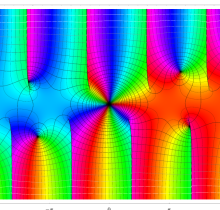
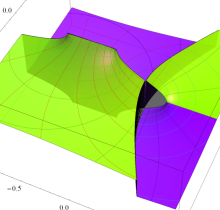
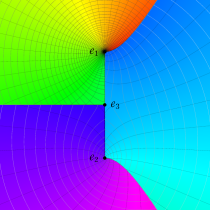
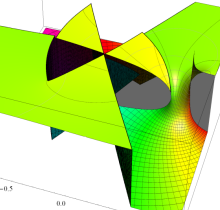
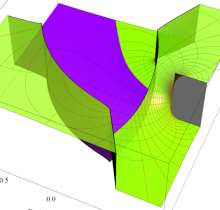
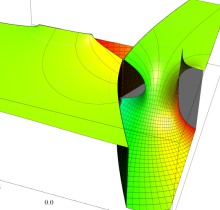
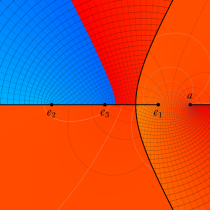
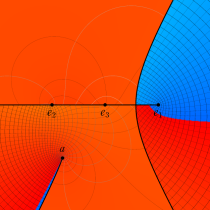
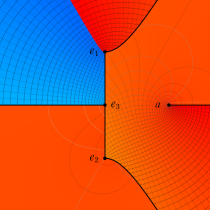
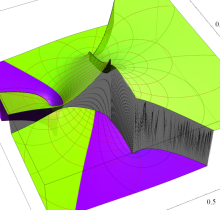
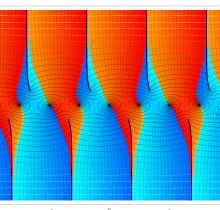
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
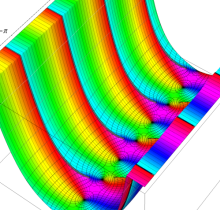
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
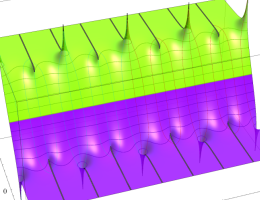
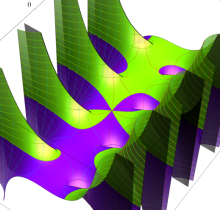
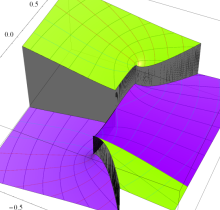
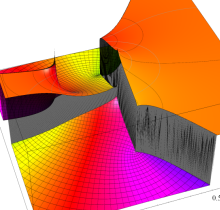
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
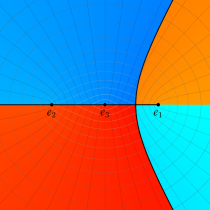
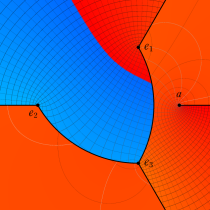
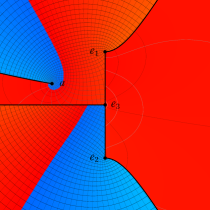
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第1種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
複素変数の第2種楕円積分
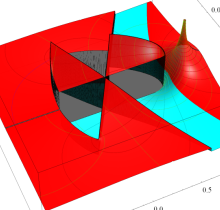
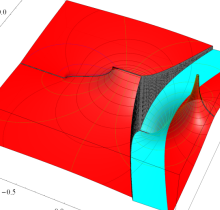
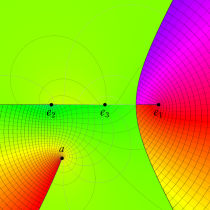
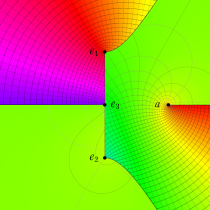
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
複素変数の第3種楕円積分
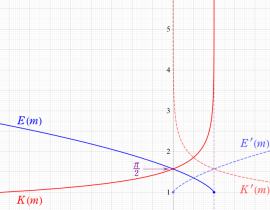
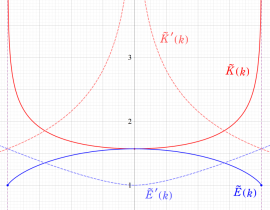
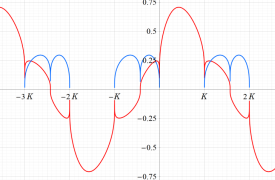
完全楕円積分
日:完全楕円積分英:Complete elliptic integral,仏:Complète intégrale elliptique,独:Vollständigen elliptische Integrale
Legendre - Jacobi の標準形で
を完全楕円積分と言い、順に、第1種、第2種、第3種の名を冠して呼ばれる (これに対比させて、不定積分の (普通の) 楕円積分を 「不完全楕円積分」 と呼ぶことがある)。ここで
なる関数記号で表記する習慣が定着している (
同様に
第1種と第2種完全楕円積分は、「Legendre の関係式」
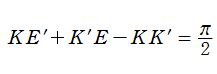
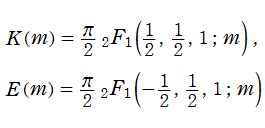
超幾何関数表示から冪級数展開式も得られるが、収束が遅いので数値計算に向かない。それよりも、後述する算術幾何平均の反復計算を介する方が、はるかに収束が速く便利である。このほか、Landen 変換 (後述のコラムを参照) に基づく無限乗積表示式
も収束が速いので数値計算に適している。
特定の有理数に対するガンマ関数値は、第1種完全楕円積分によって表わせる。例えば、
となる。ここに、
第1種~第2種完全楕円積分はいずれも、複素平面上
結局のところ、完全楕円積分は楕円積分の特殊値であり、楕円関数や保型関数とともに論じられることが多いので、応用分野もそれらと共通ないしは関連する。すなわち、種々の図形の計量や積分計算、数論、電磁気学、統計力学、測地学などで出現する。
楕円関数論では、「ノーム (Nome)」 と呼ばれる特別な変数
でもある。q-解析学で用いられる
ノーム関数は、楕円モジュラー・ラムダ関数
【コラム:Landen 変換と算術幾何平均】
次の関数等式における母数の変換を、(第1種完全楕円積分に対する) Landen 変換という。
ここで、反復すると急速に0に近付く漸化式
を用意し、関数等式に適用すれば、![K(M[∞]^2) = π/2](siki_spec080/ellipticinteg12800.png) であるから前述の無限乗積表示式が導かれる。
であるから前述の無限乗積表示式が導かれる。
一方、関数等式において![Sqrt[1-m] = b/a](siki_spec080/ellipticinteg12900.png) と置けば、
と置けば、
となるので、Landen 変換は算術幾何平均の別表現になっている。
次の関数等式における母数の変換を、(第1種完全楕円積分に対する) Landen 変換という。
ここで、反復すると急速に0に近付く漸化式
を用意し、関数等式に適用すれば、
一方、関数等式において
となるので、Landen 変換は算術幾何平均の別表現になっている。
② Mathematica の表記法ではなく、もっと通用している母数の表記法に従えば、
複素変数の第1種完全楕円積分
複素変数の第2種完全楕円積分
複素変数の第3種完全楕円積分
複素変数の第3種完全楕円積分
複素変数の第3種完全楕円積分
複素変数の第3種完全楕円積分
複素変数の第2種完全楕円積分
複素変数のノーム関数
複素変数のノーム関数
複素変数のノーム関数
Jacobi のゼータ関数
日:Jacobiのゼータ関数,ヤコビのゼータ関数英:Jacobi's zeta function,仏:Fonction zêta de Jacobi,独:Jacobische Zetafunktion
Jacobi のゼータ関数とは、楕円積分と完全楕円積分を用いて
と表わされる関数であり、第2種楕円関数
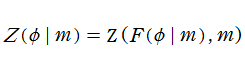
Jacobi のゼータ関数は奇関数であり、周期性
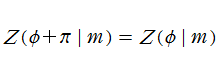
【註記】
※1:むしろ、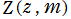 を Jacobi のゼータ関数と呼ぶほうが一般的であるが、Mathematica では
を Jacobi のゼータ関数と呼ぶほうが一般的であるが、Mathematica では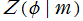 にこの名称を与えているので、当サイトも後者に従うこととする。なお、これらは関数名称に 「ゼータ」 を含むが、勿論、Riemann ゼータ関数など Dirichlet 級数の一種ではない。
にこの名称を与えているので、当サイトも後者に従うこととする。なお、これらは関数名称に 「ゼータ」 を含むが、勿論、Riemann ゼータ関数など Dirichlet 級数の一種ではない。
※1:むしろ、
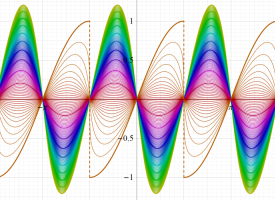
① 実2変数の Jacobi のゼータ関数
②
複素変数の Jacobi のゼータ関数
複素変数の Jacobi のゼータ関数
複素変数の Jacobi のゼータ関数
Heuman のラムダ関数
日:Heuman のラムダ関数,ホイマンのラムダ関数英:Heuman's lambda function,仏:Fonction lambda de Heuman,独:Heumansche Lambda-funktion
Heuman のラムダ関数とは、楕円積分と完全楕円積分、および前述の Jacobi のゼータ関数を用いて
と表わされる関数である。1941年に C. Heuman が第3種完全楕円積分の数表を作成する過程で、公式
を使用したので、その名が冠せられている。
しかし、その他でこの関数が現れる分野はほとんどない。M. Abramowitz & I. A. Stegun 著 「Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables」 も、p.595 で簡単に触れているのみである。
Heuman のラムダ関数は奇関数であり、擬周期性
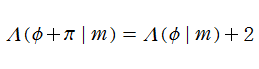
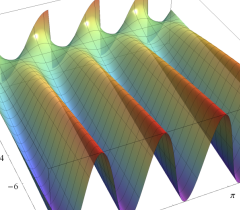
① 実2変数の Heuman のラムダ関数
②
複素変数の Heuman のラムダ関数
複素変数の Heuman のラムダ関数
複素変数の Heuman のラムダ関数
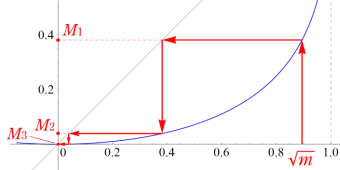
算術幾何平均
日:算術幾何平均英:Arithmetic-geometric mean,仏:Moyenne arithmético-géométrique,独:Arithmetisch-geometrisches Mittel
2つの数
が広く知られているが、現在では両者を統合した 「算術幾何平均 (Arithmetic - geometric mean) 」 が定義されている。
は、極限
と表記される。
算術幾何平均の値は、算術平均と幾何平均の間
になる。また、算術幾何平均は、
等の変換式を満たす。
算術幾何平均は、第1種完全楕円積分と
の関係にある。算術幾何平均の収束が極めて速いため、これは第1種完全楕円積分の数値計算で大変重宝する。
算術幾何平均、およびその楕円積分との関係は、J. L. Lagrange (1784年) が発見している。また、算術幾何平均そのものではないが同等の結果が導ける 「Landen 変換」 を、J. Landen (1775年) が発見した。C. F. Gauss (1800年) は Lagrange とは独立に算術幾何平均の再発見を行い、超幾何関数および下記に説明するモジュラー関数との関係も明らかにした。
算術幾何平均の理論は、次のように楕円テータ関数が満たす恒等式を、漸化式と捉えて反復適用した極限が、
となる事実に基づいている。これを、規格化された算術幾何平均
との反復に基づくこととなり、ここに楕円モジュラー・ラムダ関数が現れる。楕円テータ関数の漸化式から分かるように、算術幾何平均は楕円関数の周期比を2倍する変換 (「位数2の変換」という) である。さらに Legendre は位数3の変換、Gauss は位数5および位数7の変換も求めた。
第2種・第3種完全楕円積分も、算術幾何平均と同じ漸化式の値を用いる無限級数によって計算できる。例えば前者は
となる※2。これは、円周率の高精度数値計算法である 「Gauss - Legendre のアルゴリズム」
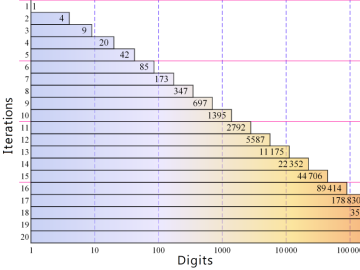
の根拠公式でもある※3、このことから、円周率の桁数記録とともに算術幾何平均も話題になることがある。
(Gauss - Legendre アルゴリズムの反復回数と一致桁数との関係。桁数 (横軸) は常用対数目盛。)
【註記】
※1:実際の計算技法では、後者の漸化式を![b(n+1)=Sqrt[a(n)]*Sqrt[b(n)]](siki_spec080/ellipticinteg18800.png) と解釈した方が、より広い
と解釈した方が、より広い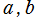 の範囲で求められる。
の範囲で求められる。
※2:第3種の場合は、「NIST Handbook of Mathematical Functions」の p.493 にある公式 19.8.7~19.8.10 を参照。
※3:なぜ円周率になるかを説明する。Gauss - Legendre のアルゴリズムの反復子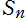 は、母数を
は、母数を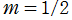 と置いた第2種の無限級数から得られる
と置いた第2種の無限級数から得られる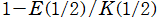 に収束することが、漸化式の形から分かる。また、反復子
に収束することが、漸化式の形から分かる。また、反復子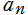 は、算術幾何平均と第1種完全楕円積分の関係から
は、算術幾何平均と第1種完全楕円積分の関係から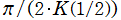 に収束する。
に収束する。
完全楕円積分の所で触れた 「Legendre の関係式」 から、
が得られるので、
となることが分かる。
※1:実際の計算技法では、後者の漸化式を
※2:第3種の場合は、「NIST Handbook of Mathematical Functions」の p.493 にある公式 19.8.7~19.8.10 を参照。
※3:なぜ円周率になるかを説明する。Gauss - Legendre のアルゴリズムの反復子
完全楕円積分の所で触れた 「Legendre の関係式」 から、
が得られるので、
となることが分かる。
① 実2変数の算術幾何平均
②
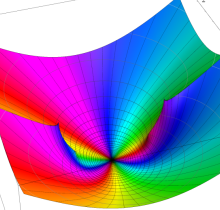
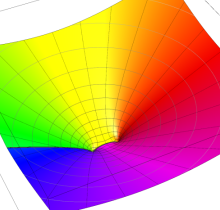
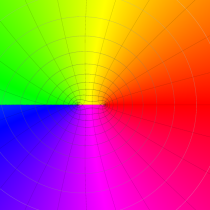
複素変数の算術幾何平均
複素変数の算術幾何平均
複素変数の算術幾何平均
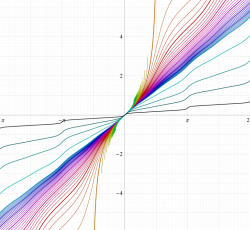
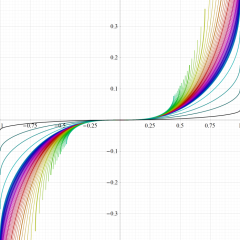
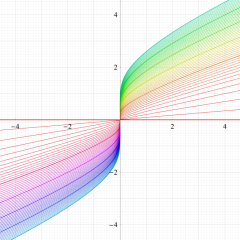
実変数の算術幾何平均
複素変数の算術幾何平均