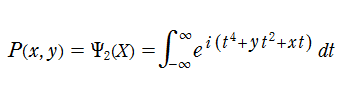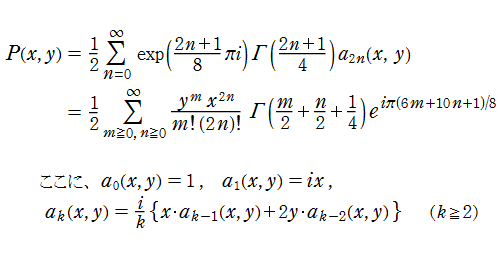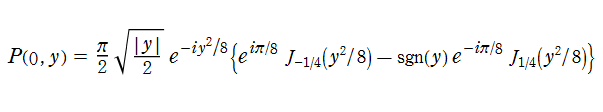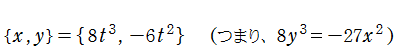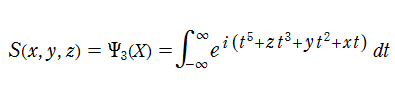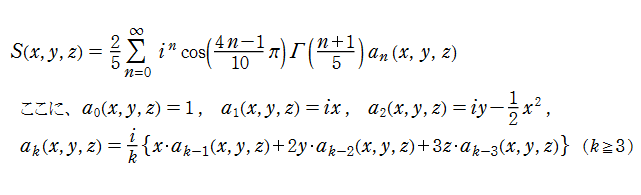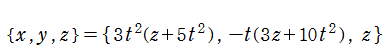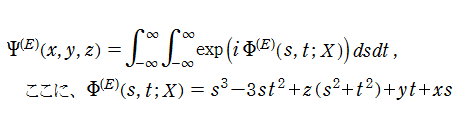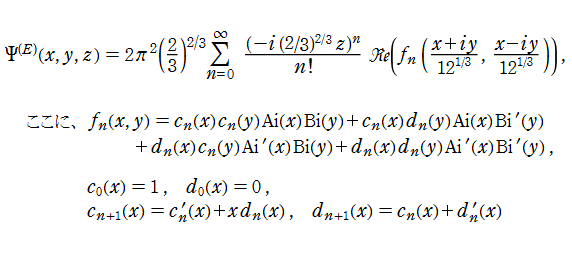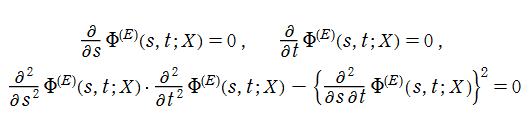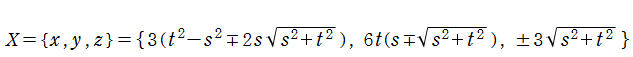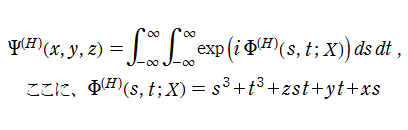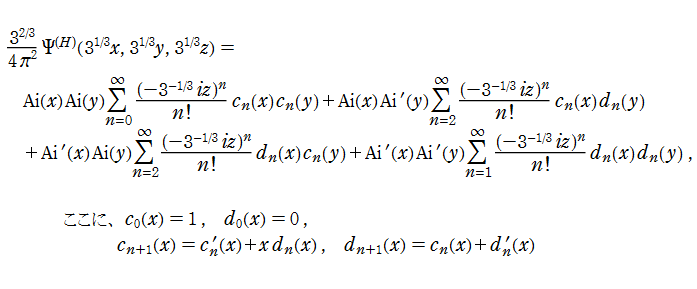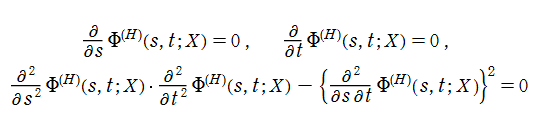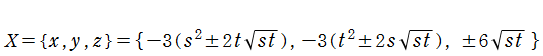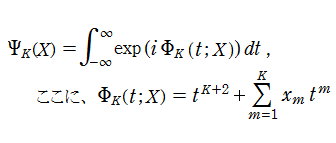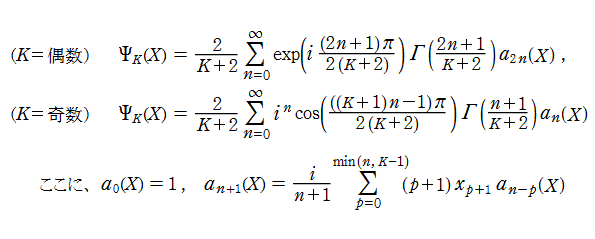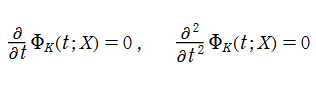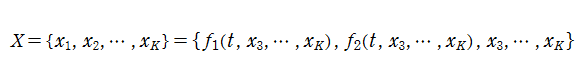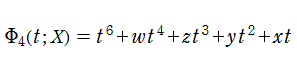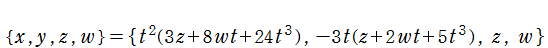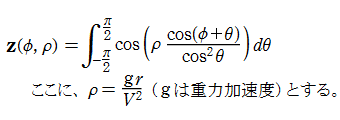特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
カタストロフィー理論の特殊関数
Pearcey 積分関数
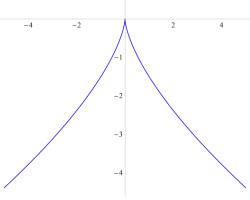
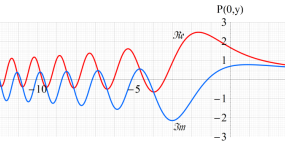
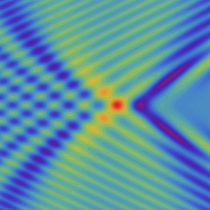
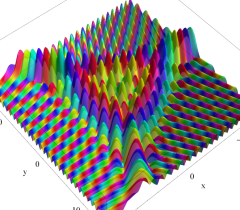
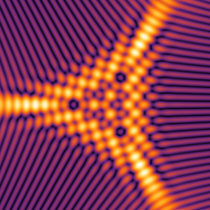
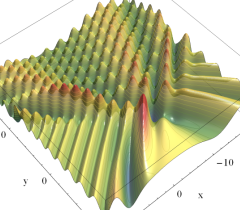
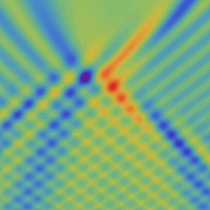
2変数は、1946年に T. Pearcey が屈折によって交差した光の干渉を説明するために初めて考察したので、現在は、Pearcey 積分関数 (または、Pearcey 積分) と呼ばれる。ここに、関数
Pearcey 積分関数を
となる。また、
のように Bessel 関数に還元される。
Pearcey 積分関数は
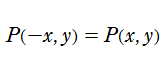
Pearcey 積分関数は、カタストロフィー理論における尖点 (Cusp catastrophe) と呼ばれる分岐現象に関連する※1。これは、後述の 「余次元
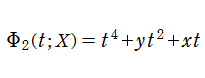
の形状で説明される。またこの場合は、
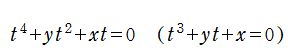
を用いて、このカタストロフィーが説明されることもある※2。
カタストロフィー理論自体は、微分方程式や差分方程式などによって記述される力学系が、パラメーターの連続変化に応じて定性的に異なる複数の解空間へ分岐する現象を説明するために、R. F. Thom によって導入された。Thom は、このような分岐を生ずる曲面構造をカタストロフィーと呼び、(「初等カタストロフィー」 の場合は) 7種類の分岐点形状 「折り目,尖点,燕尾点,蝶点,楕円的臍点,双曲的臍点,放物的臍点」 に分類できることを示した。
【註記】
※1 取りあえず、この頁で扱う関数を 「カタストロフィー理論の~」 としたが、実際にカタストロフィー理論でどのように用いられるかの詳細はここでは触れない (恐らく、以降に掲載した各図は光の干渉が起きる領域を表わしており、その境界が初等カタストロフィーの7種類の分岐点形状に対応していると思われる)。
内容は、「NIST Handbook of Mathematical Functions」 を参考にしているので、正確な意味はそちらを参照願います。また、Pearcey 積分関数を別にすれば、ここでの各関数の英語名は恐らく通称ではなく (「NIST」 にも、標準的な命名法は無い旨の記述がある)、日本語名もまだ存在しないため、さらにこれを意訳したものである。
※2 この場合視覚的には、構造安定性が 「破綻」 する分岐点が、原点になることが分かる。
※1 取りあえず、この頁で扱う関数を 「カタストロフィー理論の~」 としたが、実際にカタストロフィー理論でどのように用いられるかの詳細はここでは触れない (恐らく、以降に掲載した各図は光の干渉が起きる領域を表わしており、その境界が初等カタストロフィーの7種類の分岐点形状に対応していると思われる)。
内容は、「NIST Handbook of Mathematical Functions」 を参考にしているので、正確な意味はそちらを参照願います。また、Pearcey 積分関数を別にすれば、ここでの各関数の英語名は恐らく通称ではなく (「NIST」 にも、標準的な命名法は無い旨の記述がある)、日本語名もまだ存在しないため、さらにこれを意訳したものである。
※2 この場合視覚的には、構造安定性が 「破綻」 する分岐点が、原点になることが分かる。
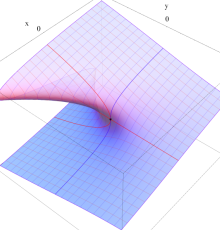
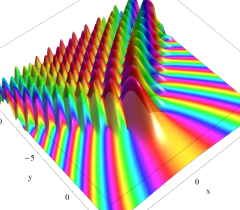
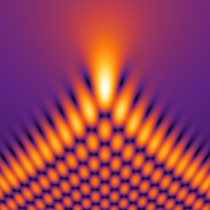
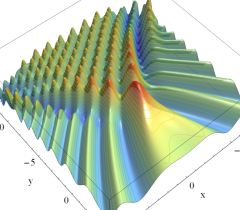
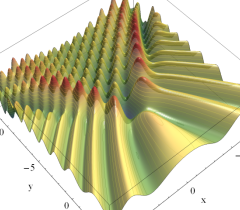
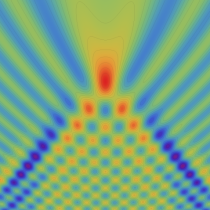
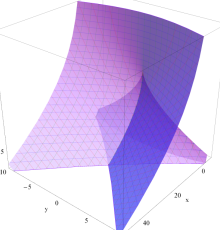
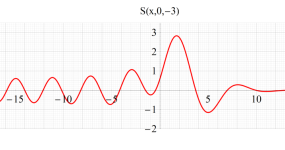
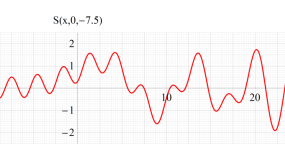
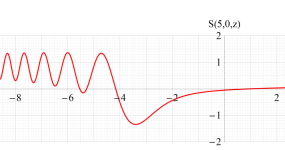
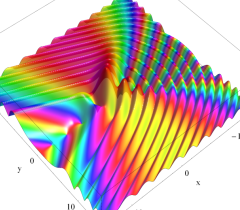
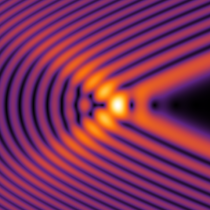
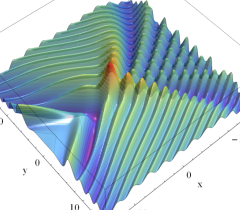
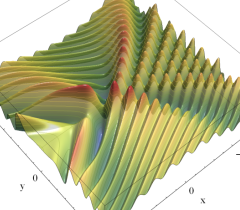
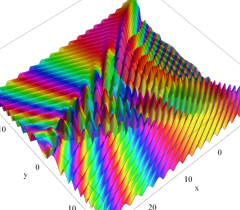
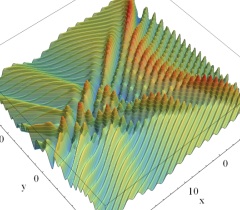
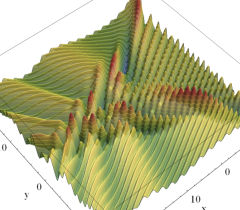
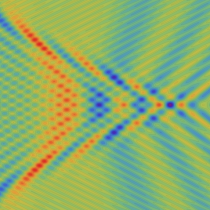
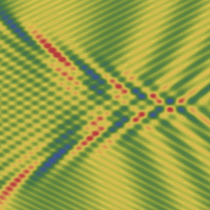
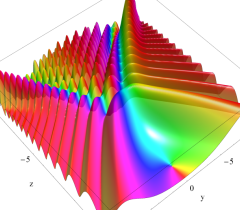
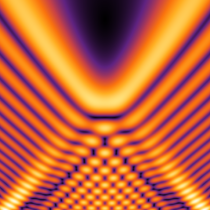
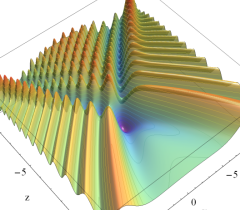
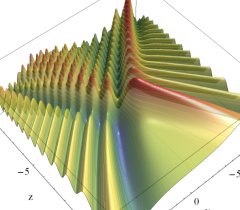
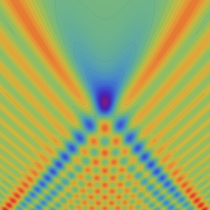
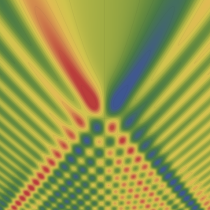
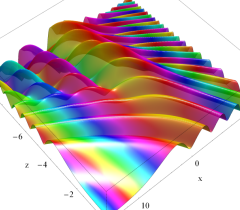
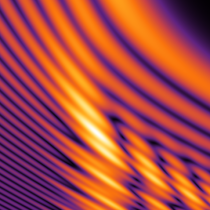
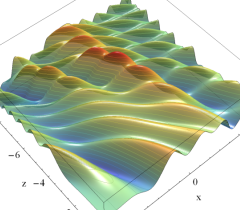
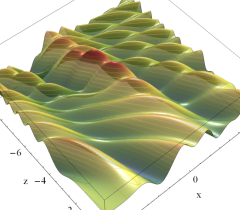
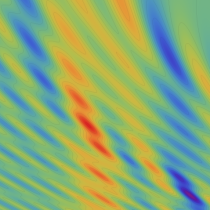
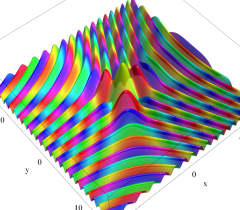
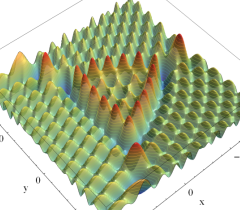
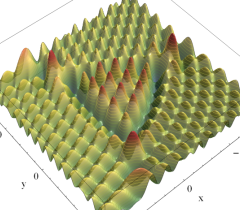
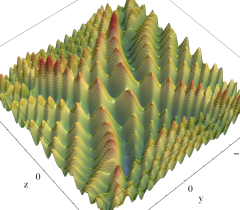
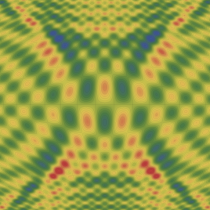
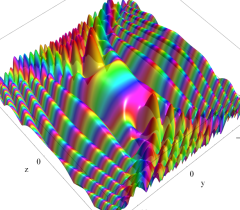
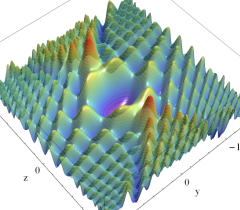
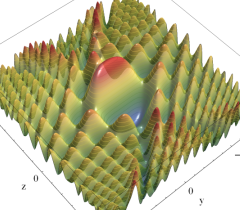
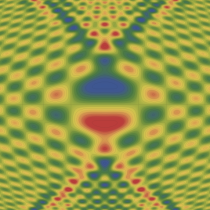
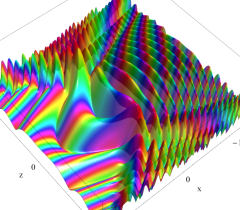
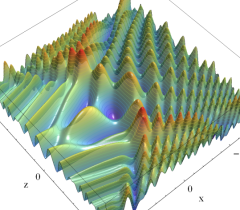
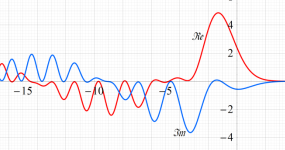
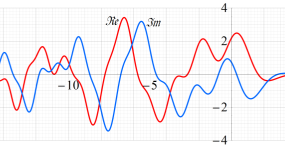
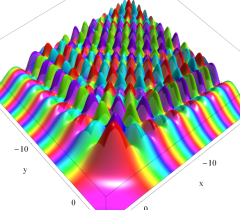
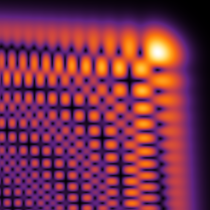
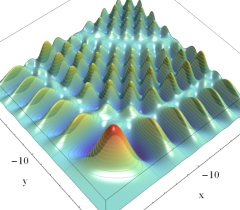
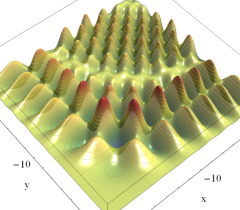
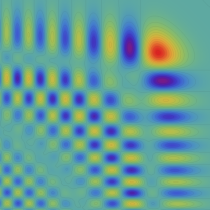
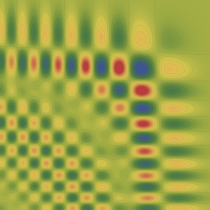
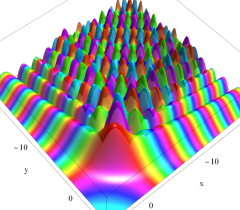
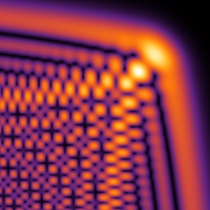
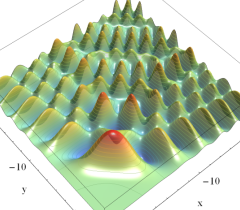
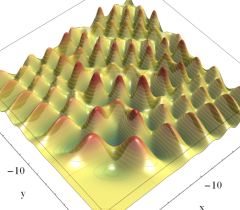
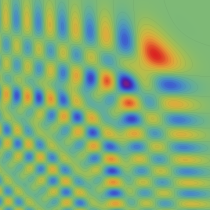
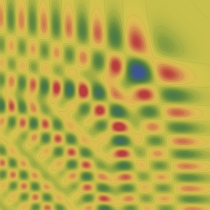
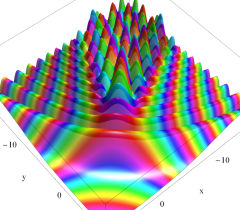
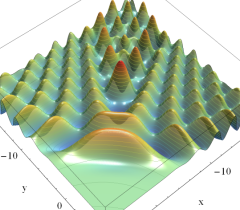
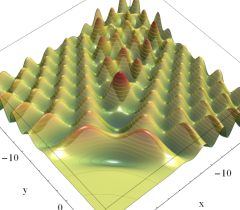
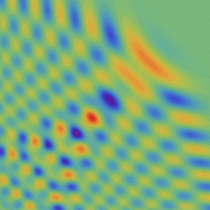
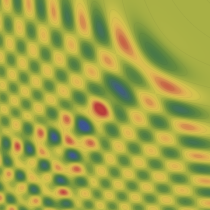
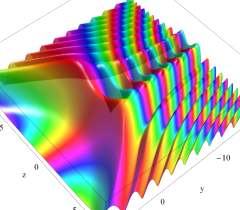
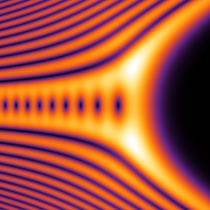
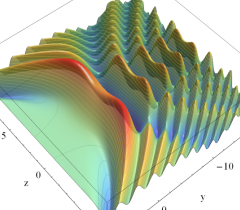
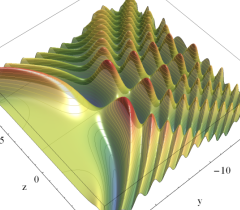
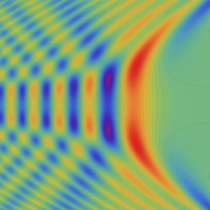
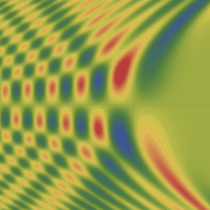
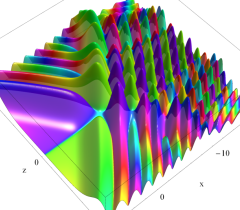
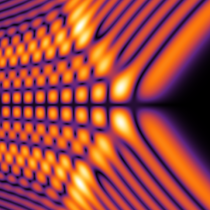
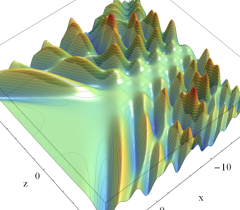
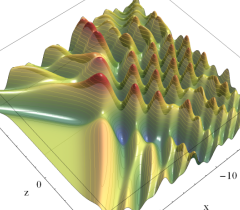
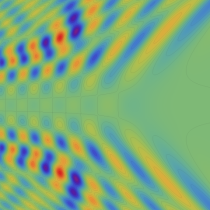
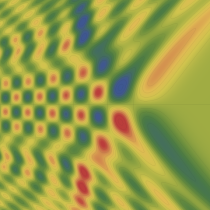
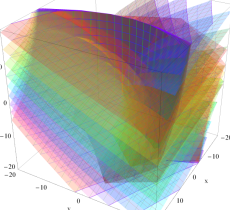
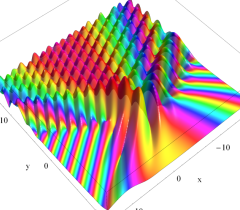
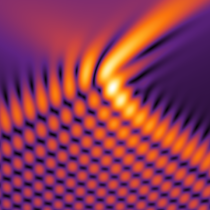
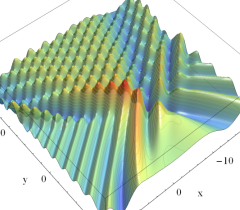
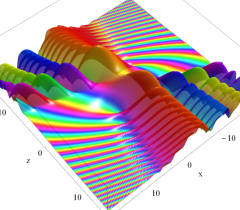
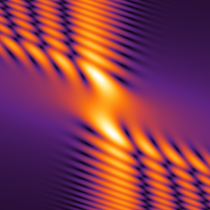
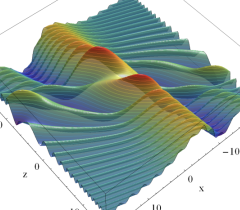
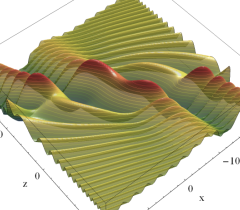
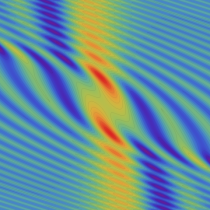
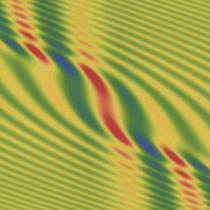
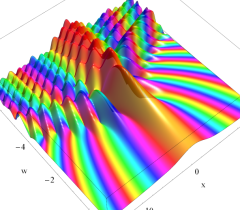
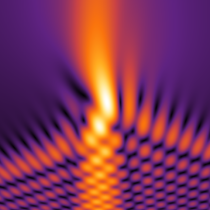
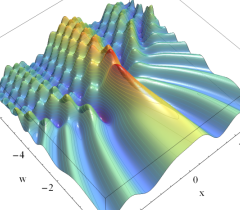
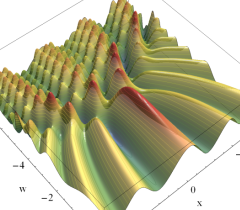
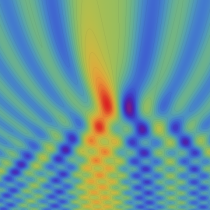
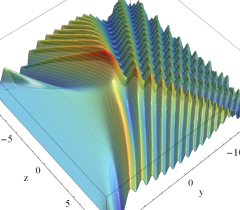
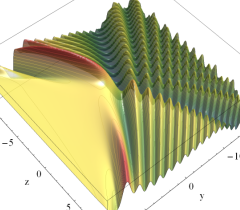
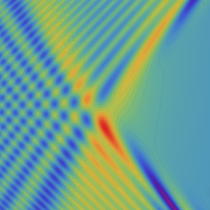
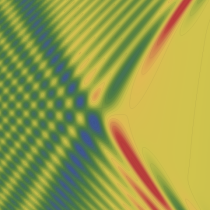
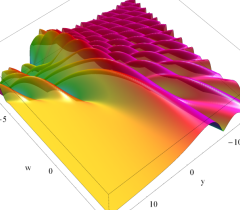
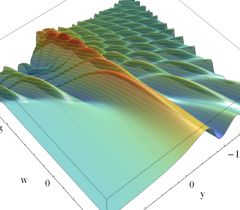
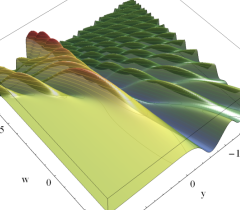
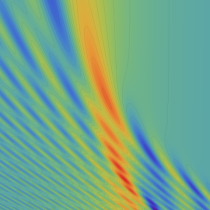
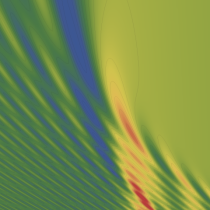
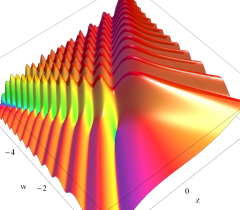
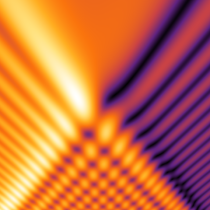
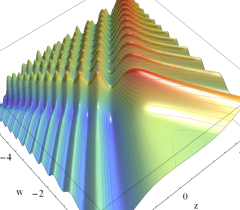
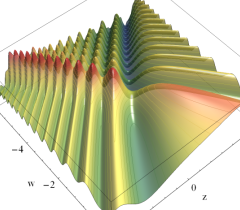
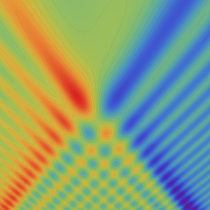
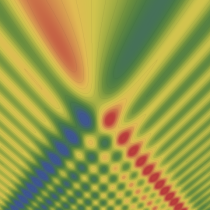
実2変数の Pearcey 積分関数
燕尾点正準積分関数
3変数を、燕尾点正準積分関数 (Swallowteil canonical integral function) という。(関数
この関数は、
となる。
燕尾点正準積分関数は
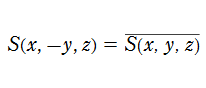
燕尾点正準積分関数は、カタストロフィー理論における燕尾点 (Swallowteil catastrophe) と呼ばれる分岐現象に関連する。これは、後述の 「余次元
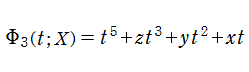
の形状で説明される。
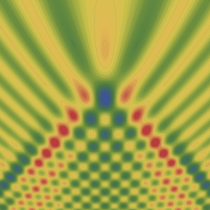
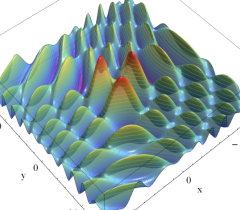
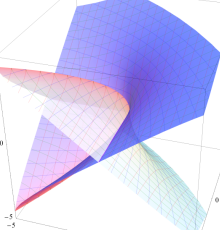
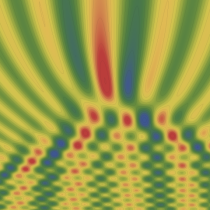
実2変数の燕尾点正準積分関数
実2変数の燕尾点正準積分関数
実2変数の燕尾点正準積分関数
実2変数の燕尾点正準積分関数
アニメーション(8.23MB)
実2変数の燕尾点正準積分関数
楕円的臍点正準積分関数
3変数を、楕円的臍点正準積分関数 (Elliptic umbilic canonical integral function) という。
この関数を、
となる。
楕円的臍点正準積分関数は
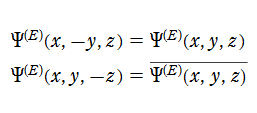
楕円的臍点正準積分関数は、カタストロフィー理論において楕円的臍点 (Elliptic umbilic catastrophe) と呼ばれる分岐現象に関連する。その形状を説明する3次元代数曲面は、代数方程式
によって得られるパラメータ表示式
で表わされる。
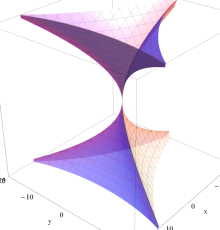
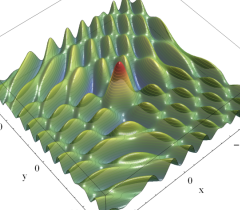
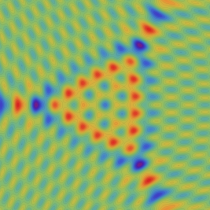
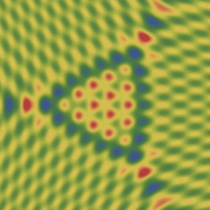
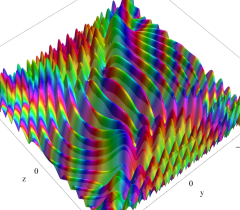
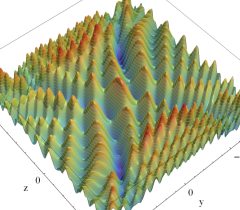
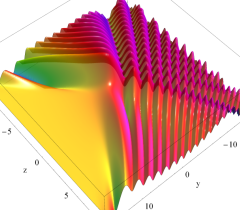
実2変数の楕円的臍点正準積分関数
実2変数の楕円的臍点正準積分関数
実2変数の楕円的臍点正準積分関数
実2変数の楕円的臍点正準積分関数
実2変数の楕円的臍点正準積分関数
双曲的臍点正準積分関数
3変数を、双曲的臍点正準積分関数 (Hyperbolic umbilic canonical integral function) という。
この関数を、
となる。
双曲的臍点正準積分関数は
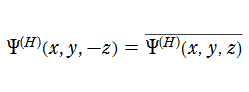
双曲的臍点正準積分関数は、カタストロフィー理論において双曲的臍点 (Hyperbolic umbilic catastrophe) と呼ばれる分岐現象に関連する。その形状を説明する3次元代数曲面は、代数方程式
によって得られるパラメータ表示式
で表わされる。
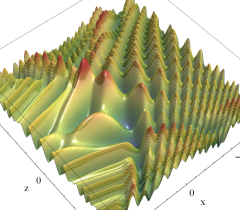
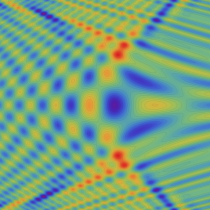
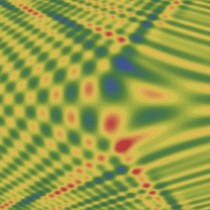
実2変数の双曲的臍点正準積分関数
実2変数の双曲的臍点正準積分関数
実2変数の双曲的臍点正準積分関数
実2変数の双曲的臍点正準積分関数
実2変数の双曲的臍点正準積分関数
余次元4の尖点正準積分関数
余次元 (Codimension ※1) をを、余次元
この関数は、
となる。
余次元
によって得られるパラメータ表示式
で表わされる。
特に、
である場合 (Butterfly catastrophe と呼ばれる) を扱う。このとき、先のパラメータ表示式は具体的に
となる。
【註記】
※1 「NIST Handbook of Mathematical Functions」 にある用語を使用。 同著の Chapter36 「Integrals with Coalescing Saddles」 を参照。
※1 「NIST Handbook of Mathematical Functions」 にある用語を使用。 同著の Chapter36 「Integrals with Coalescing Saddles」 を参照。
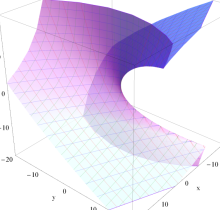
実2変数の余次元4尖点正準積分関数
実2変数の余次元4尖点正準積分関数
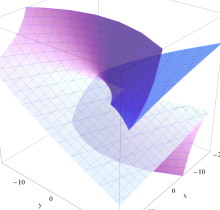
実2変数の余次元4尖点正準積分関数
実2変数の余次元4尖点正準積分関数
実2変数の余次元4尖点正準積分関数
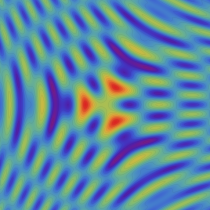
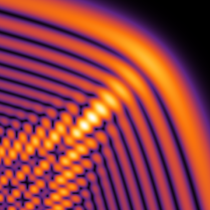
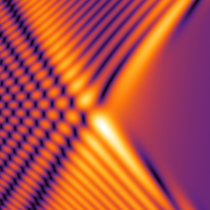
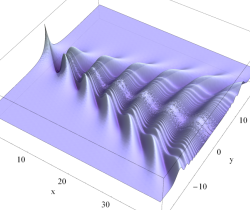
Kelvin's ship-wave pattern
充分な水深のある水面上を一定速度極座標
この積分は変数を実数に限れば、中点法等による数値計算が可能である※1。なお、変換
Kelvin's ship - wave pattern の積分は、余次元
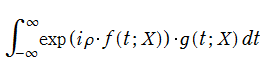
Kelvin's ship - wave pattern は船舶と水面との相互作用以外にも、例えば、対流圏において山頂等が擾乱点となる場合に形成される雲の模様にも現れることで知られている。(そのような事例は、Google等で画像検索すると見ることができる。)
【註記】
※1 : この積分は、被積分関数が積分端点に近付くほど激しく振動する (真性特異点を持つ) ので、若干計算が難しい。ここでの計算は、改良された中点法に基づいて Kay Herbert が作成した Mathematica コード (http://demonstrations.wolfram.com/KelvinShipWavePattern/) を用いた。
※1 : この積分は、被積分関数が積分端点に近付くほど激しく振動する (真性特異点を持つ) ので、若干計算が難しい。ここでの計算は、改良された中点法に基づいて Kay Herbert が作成した Mathematica コード (http://demonstrations.wolfram.com/KelvinShipWavePattern/) を用いた。
Kelvin's ship - wave pattern を用いて、夕刻 (または夜明?) の海上の風景を構成する。