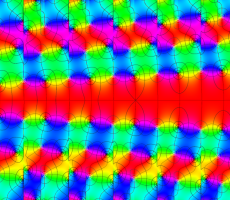
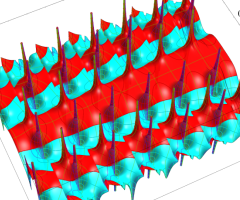
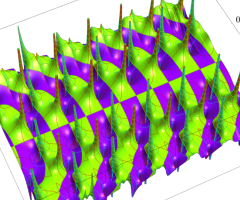
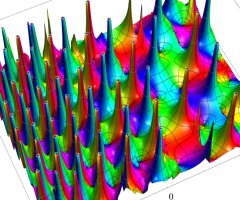
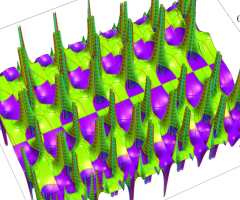
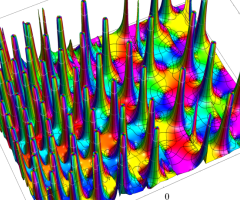
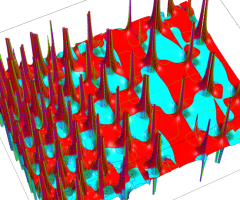
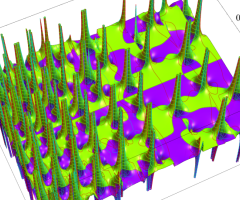
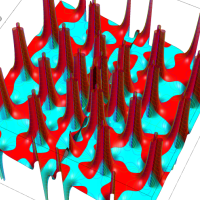
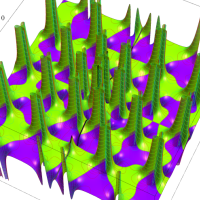
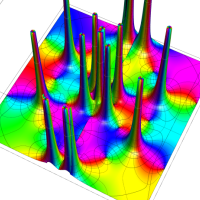
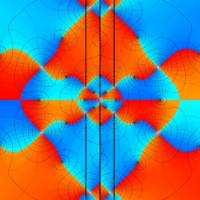
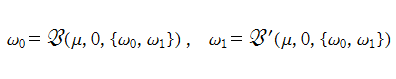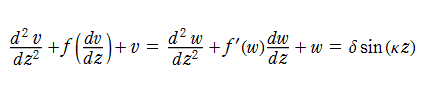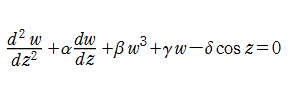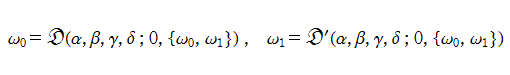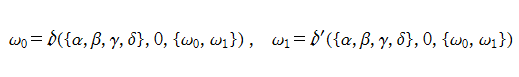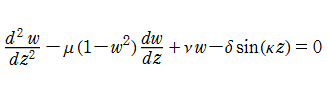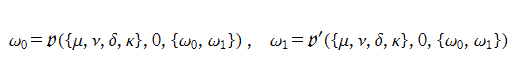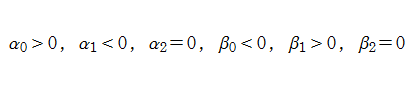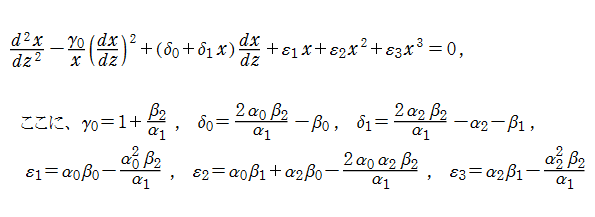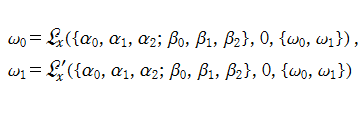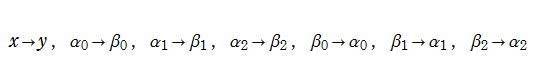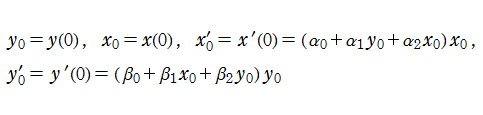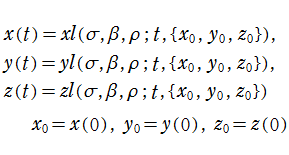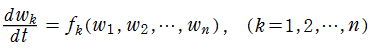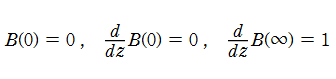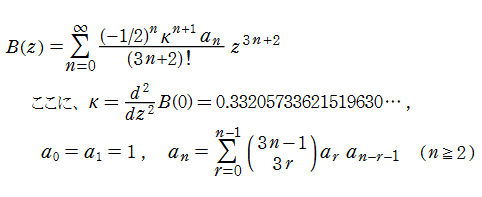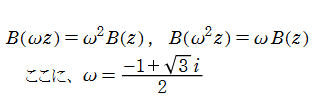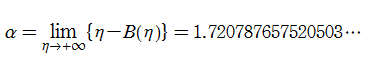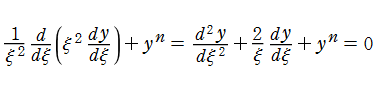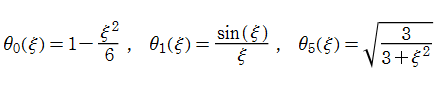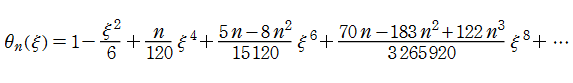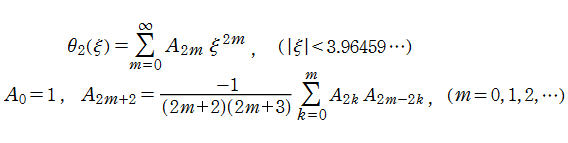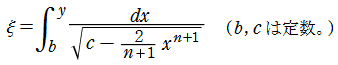特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
非線形微分方程式の解となる関数
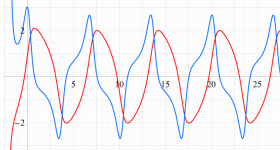
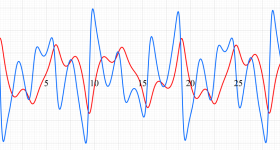
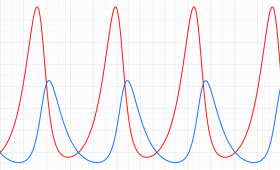
Van der Pol 関数 (Van der Pol の微分方程式の解)
日:Van der Polの微分方程式,ファン・デル・ポール方程式英:Van der Pol equation,仏:Équation différentielle de Van der Pol,独:Van der Pol-Differentialgleichung
2階の非線形常微分方程式
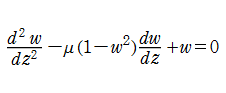
は初期値である。
B. Van der Pol は、この微分方程式および後述の強制振動型 Van der Pol の微分方程式を理論的に研究するとともに、アナログ真空管回路を用いたシミュレーションによっても詳しく研究した。強制振動型 Van der Pol の微分方程式は、Van der Pol の微分方程式において強制振動項
Van der Pol の微分方程式は、楽器などの弦の振動モデルとして Rayleigh (J. W. Strutt)が導いた、非線形減衰関数
の特別な場合である。つまり、Van der Pol の微分方程式は、3極管に由来する非線形特性として関数
この場合のように、
一般に、非線形常微分方程式
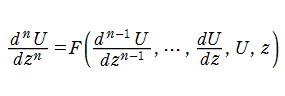
例えば、解の唯一性から、初期値の異なる軌道は互いに交わらないことが判明する。特に、軌道が極限時間経過後に安定運動に到達する場合、この吸引集合(アトラクターと呼ばれる)の形状が一目瞭然となる。このような解の軌道に着目する方法は、H. Poincaré によって始められた※1。
アトラクターはその形状に応じていくつかの種類がある。2次元位相空間であれば、不動点となる「ポイントアトラクター」、閉曲線となる「リミットサイクル」、非整数次元の形状やフラクタル形状となる「ストレンジアトラクター」があり、前2者は複数個出現することも珍しくない(微分方程式の非線形性の原因が超越関数による場合は、無限個出現することもある)。
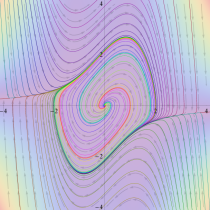
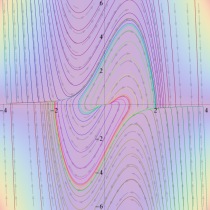
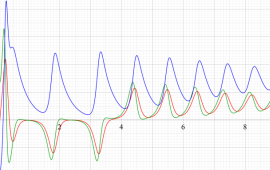
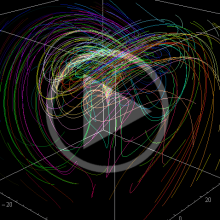
Van der Pol の微分方程式のアトラクターは、原点を中心とする1個のリミットサイクルとなり、すべての軌道は初期値に応じてリミットサイクルの内部または外部に巻き付くように漸近する。
【註記】
※1:しかしながら、以後この頁では、Poincaré の方法からは逸れた 単体の振る舞いも考える。
単体の振る舞いも考える。
そもそも、この頁で扱う微分方程式の解は、(Blasius 関数を除いて) いずれも複素関数として考察すること自体が希であり、したがって関数記号も (Lane - Emden 関数以外は) やむを得ず独自に導入したものである。
Poincaré が上記の方法を導入した動機は、天体力学における多体問題にあった。任意の時刻を変数とする関数としてこの解を求めることは極めて困難なので、代わりに、解が常に有界な範囲に留まるかどうか(=天体が周回し続けるか、または途中で離脱するか?)に問題の視点を移したのである。
※1:しかしながら、以後この頁では、Poincaré の方法からは逸れた
そもそも、この頁で扱う微分方程式の解は、(Blasius 関数を除いて) いずれも複素関数として考察すること自体が希であり、したがって関数記号も (Lane - Emden 関数以外は) やむを得ず独自に導入したものである。
Poincaré が上記の方法を導入した動機は、天体力学における多体問題にあった。任意の時刻を変数とする関数としてこの解を求めることは極めて困難なので、代わりに、解が常に有界な範囲に留まるかどうか(=天体が周回し続けるか、または途中で離脱するか?)に問題の視点を移したのである。
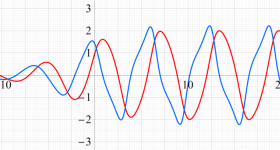
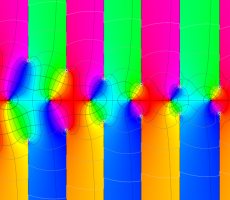
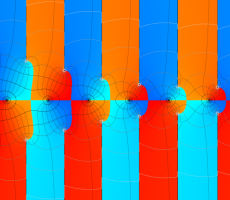
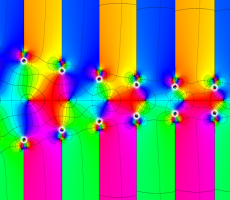
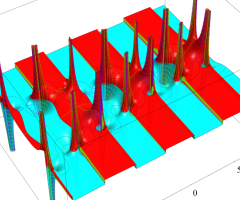
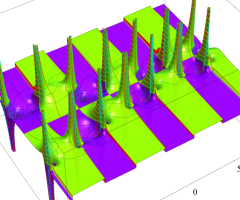
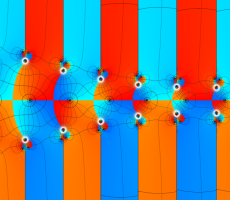
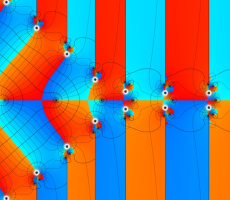
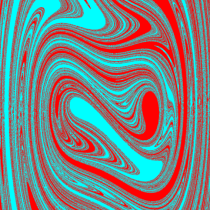
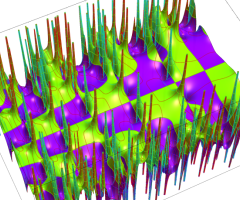
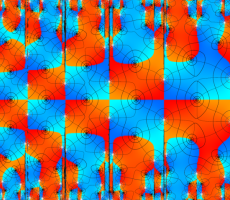
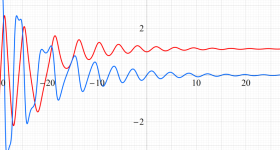
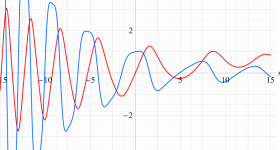
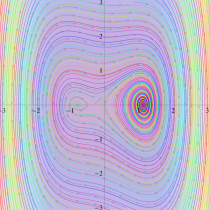
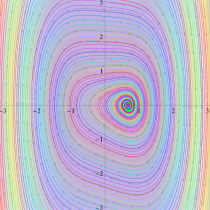
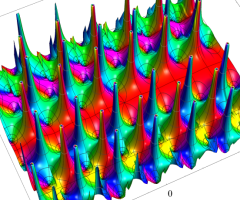
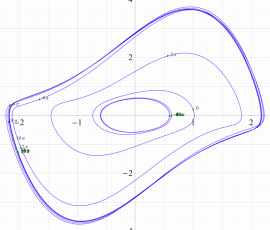
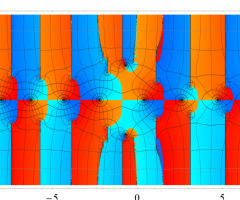
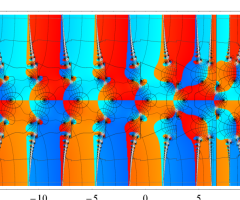
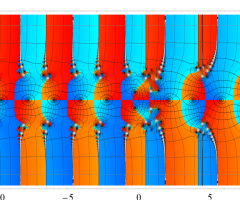
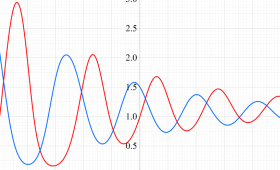
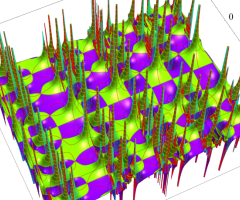
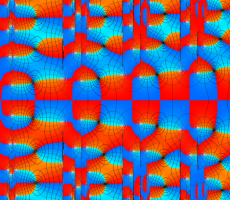
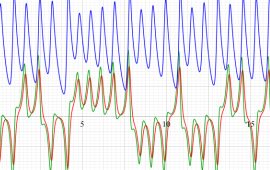
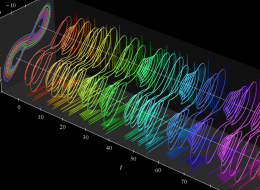
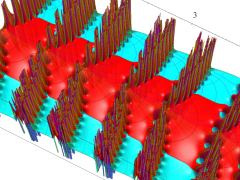
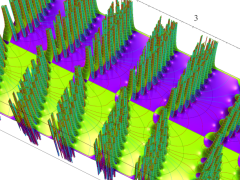
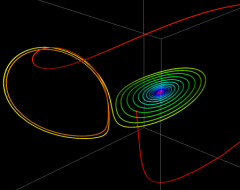
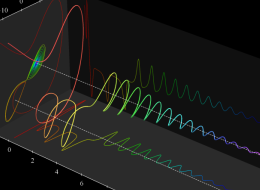
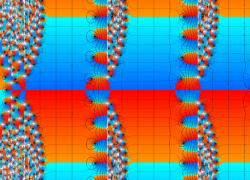
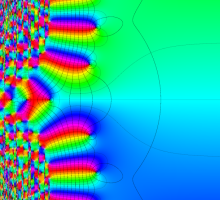
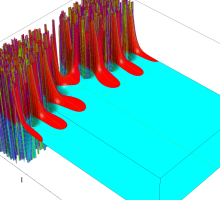
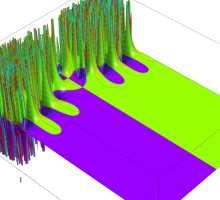
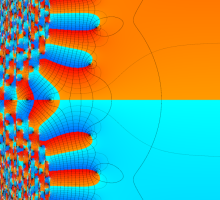
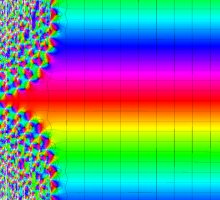
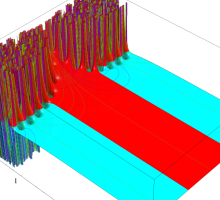
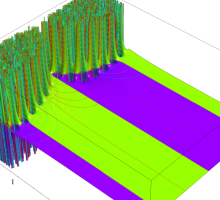
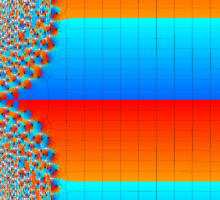
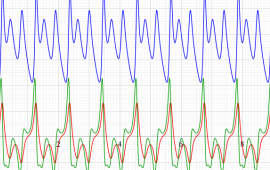
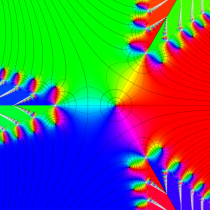
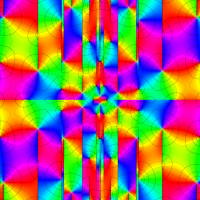
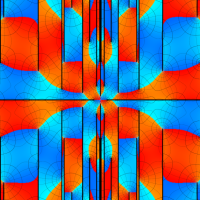
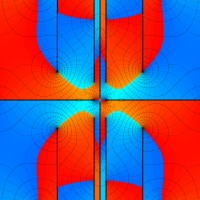
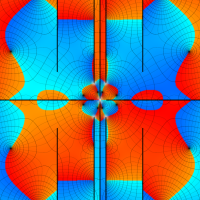
位相平面上での Van der Pol 関数。様々な初期値からの軌道を重ね描きした図。背景色はスカラー場の強度に基づく。
①:
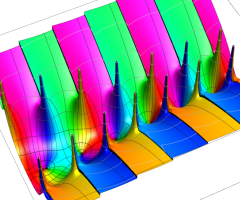
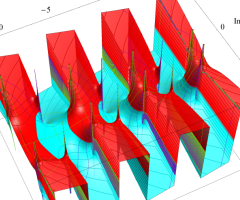
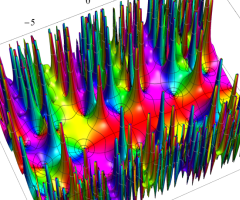
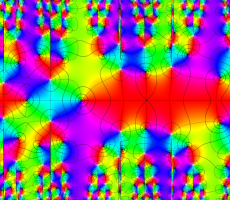
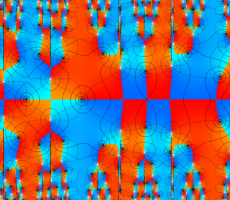
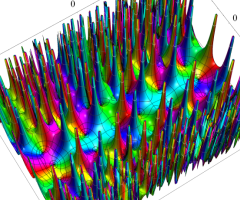
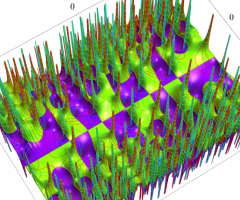
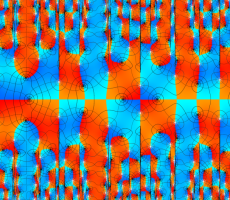
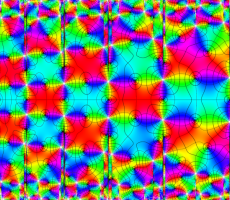
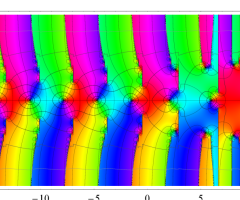
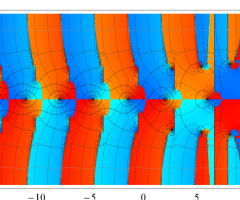
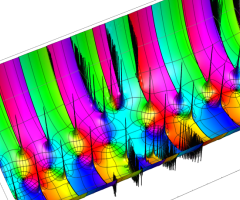
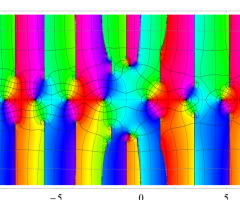
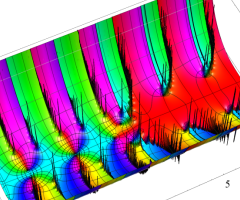
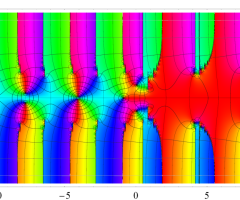
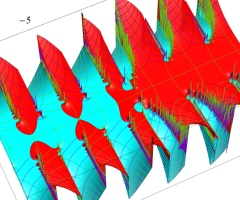
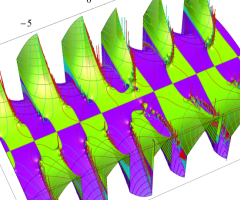
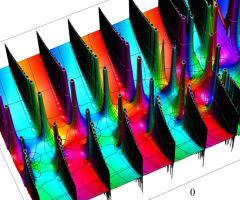
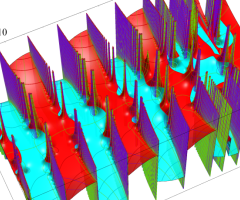
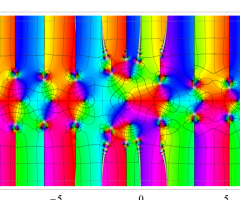
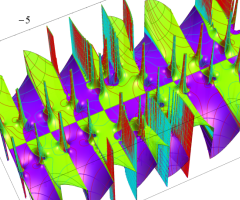
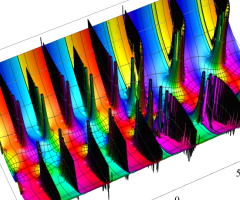
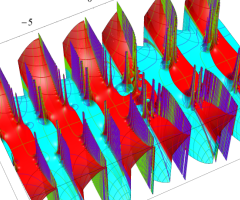
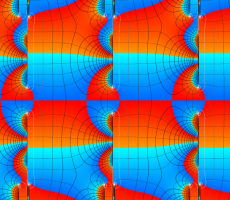
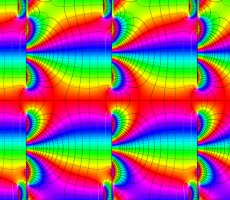
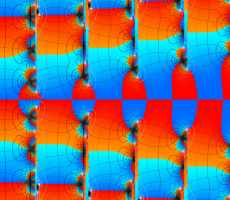
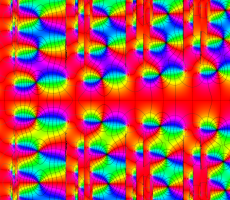
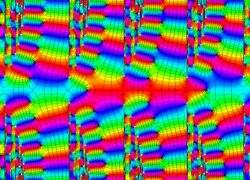
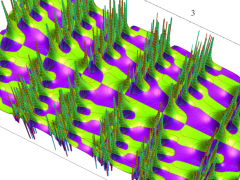
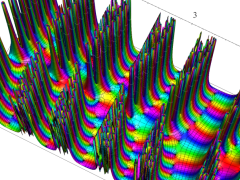
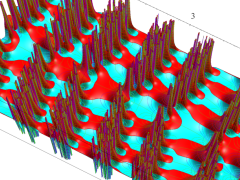
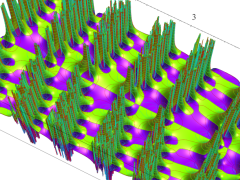
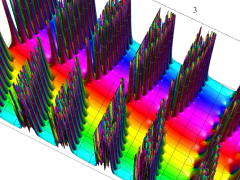
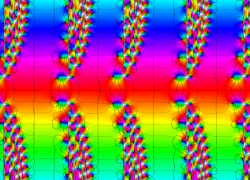
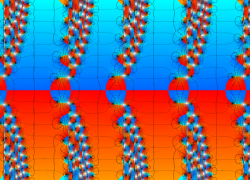
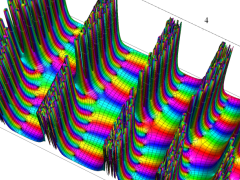
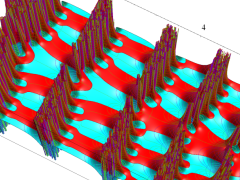
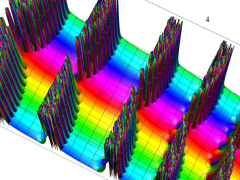
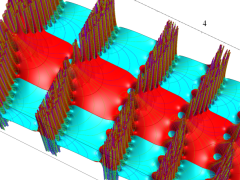
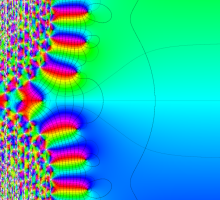
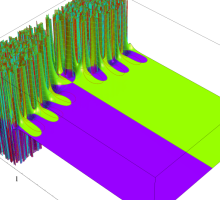
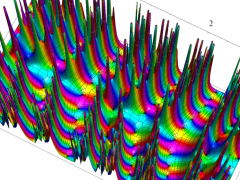
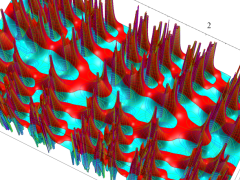
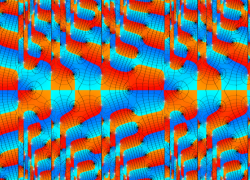
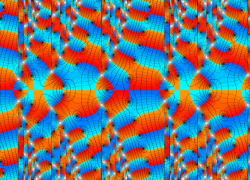
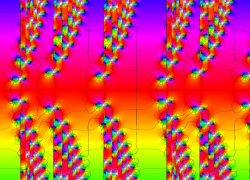
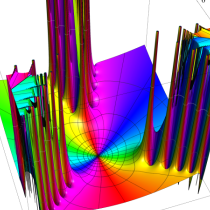
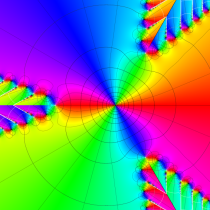
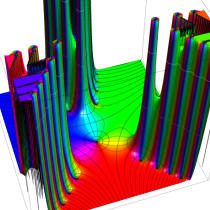
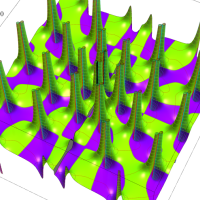
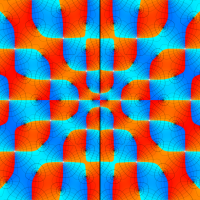
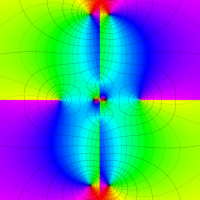
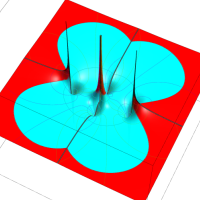
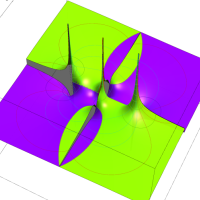
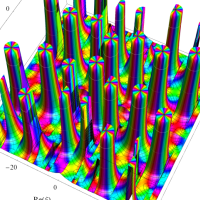
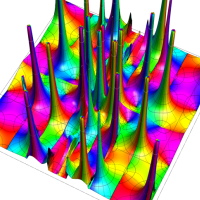
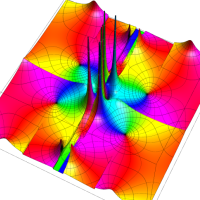
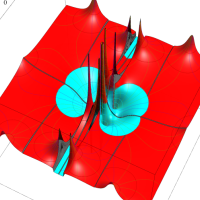
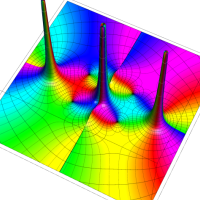
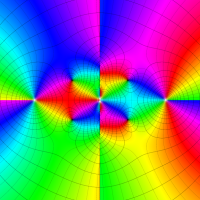
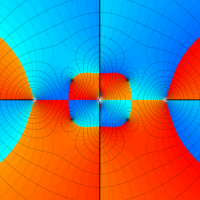
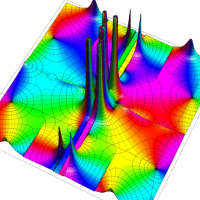
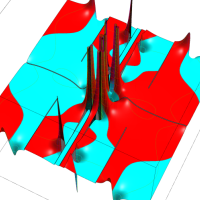
複素変数の Van der Pol 関数
複素変数の Van der Pol 関数
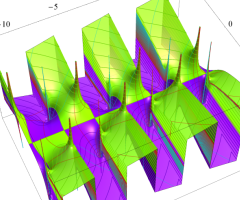
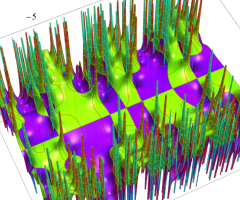
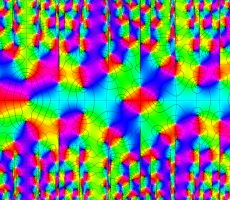
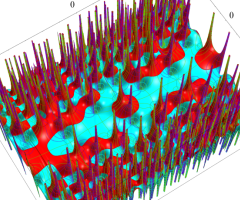
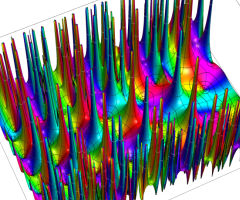
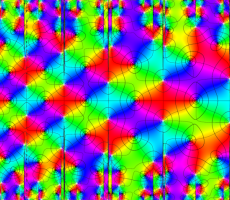
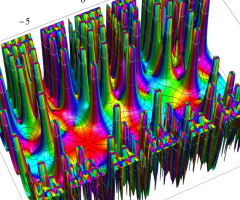
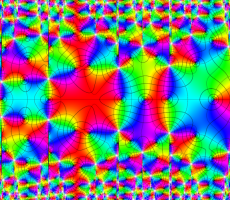
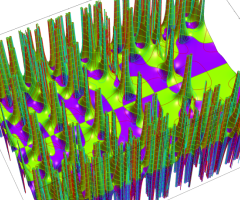
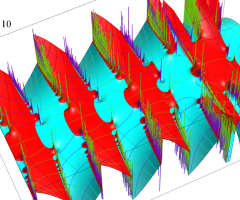
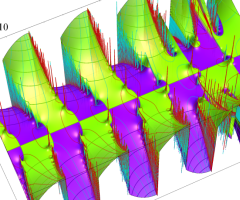
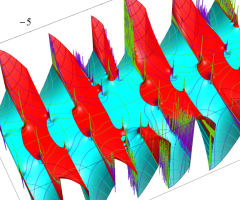
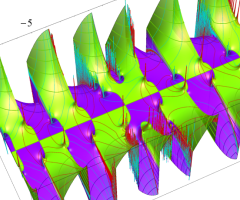
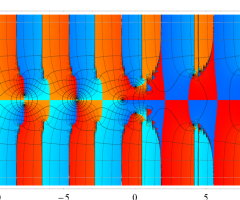
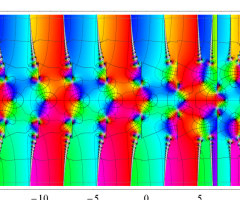
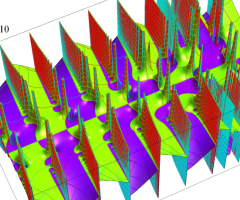
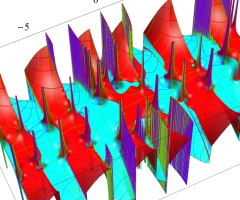
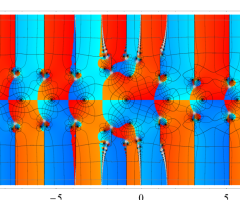
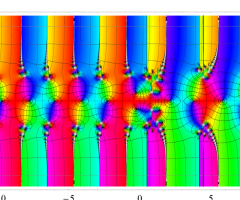
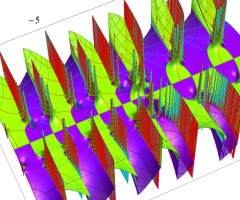
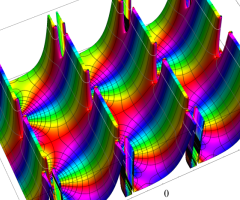
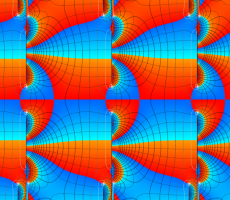
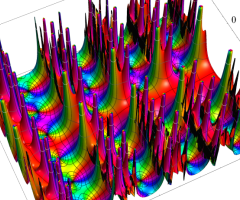
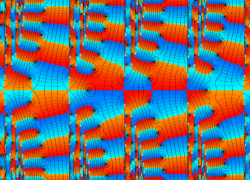
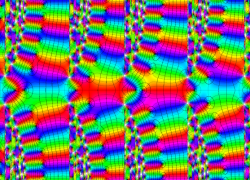
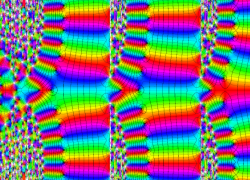
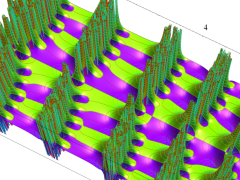
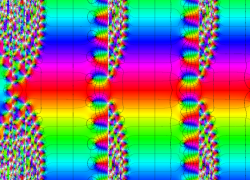
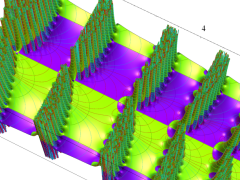
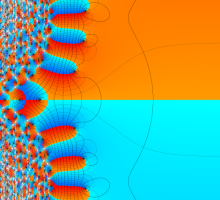
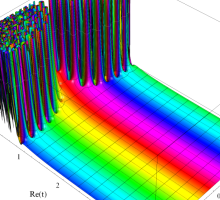
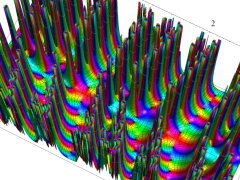
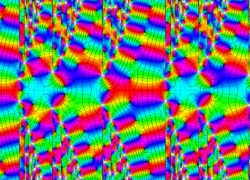
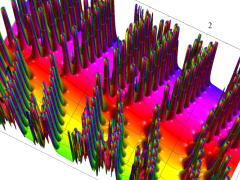
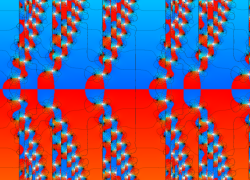
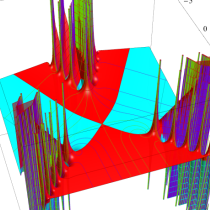
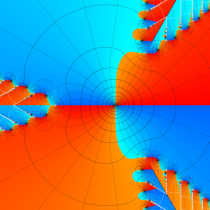
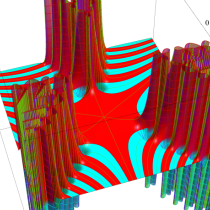
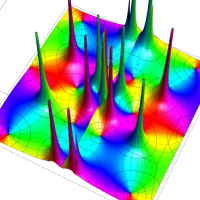
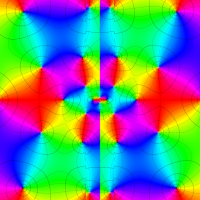
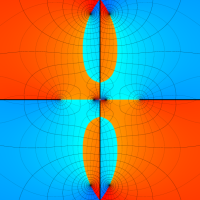
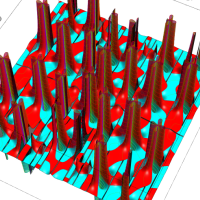
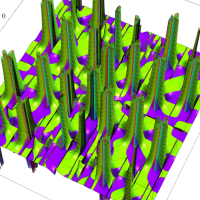
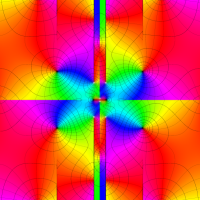
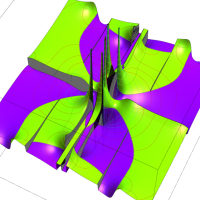
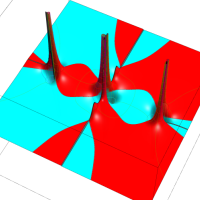
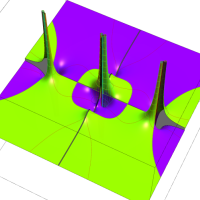
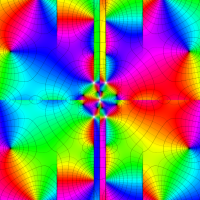
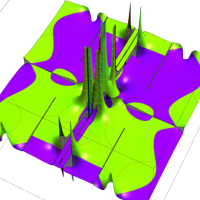
複素変数の Van der Pol 関数の導関数
複素変数の Van der Pol 関数の導関数
Duffing 関数 (Duffing の微分方程式の解)
日:Duffingの微分方程式,ダフィン方程式英:Duffing equation,仏:Équation différentielle de Duffing,独:Duffing-Differentialgleichung
2階の非線形常微分方程式
を、Duffing の微分方程式といい、解
は初期値である。Duffing の微分方程式はその表示から、2井戸形ポテンシャル中にある質点が周期的外力を受け続けるときの運動を表わすものとされ、1918年に G. Duffing によって詳しい研究が始まった。
強制振動項
さらに、Duffing の微分方程式は係数
なお、アトラクターの形状は、
ストレンジアトラクターが生成される過程を説明しようとして S. Smale らは、折りたたんで馬蹄形にしたパイ生地全体をさらに折りたたんで馬蹄形にするという無限操作との相似性から、「馬蹄形力学」と呼ばれる変換写像を導入した。
①:
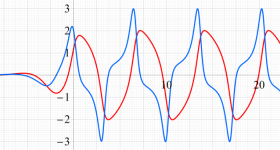
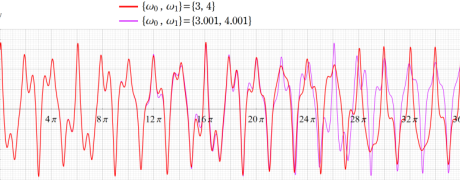
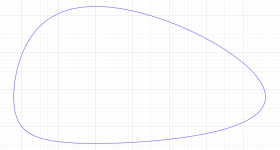
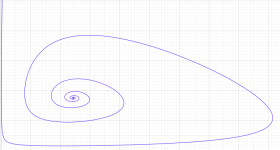
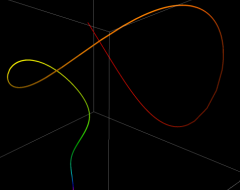
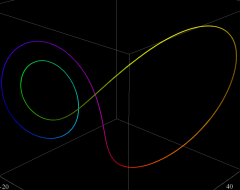
②:ストレンジアトラクターを持つ「上田の解」
上田の解をより広い範囲で見るとともに、初期値がわずかに異なる解
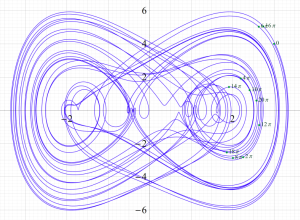
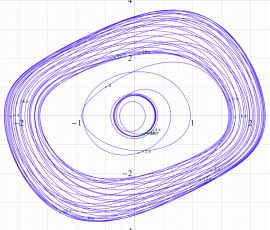
上田の解の位相平面上での軌道
100万までの
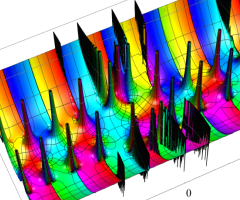
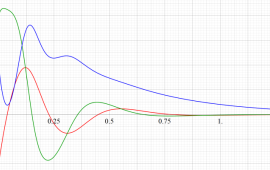
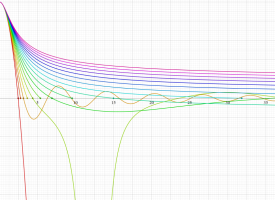
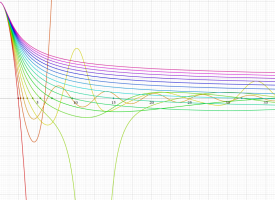
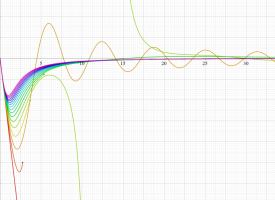
実変数の Duffing 関数
これは、減衰項の係数
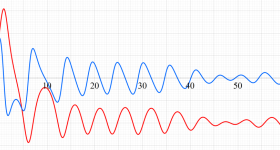
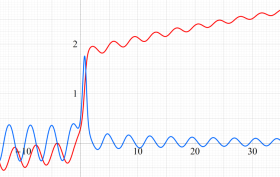
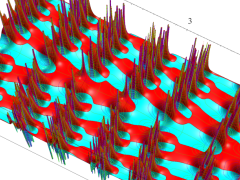
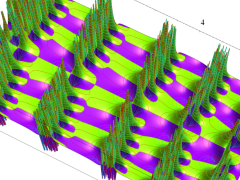
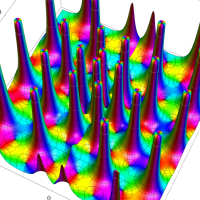
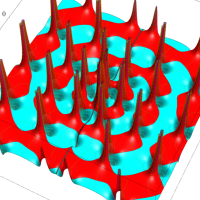
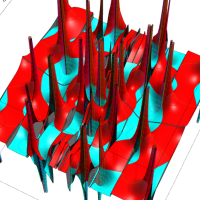
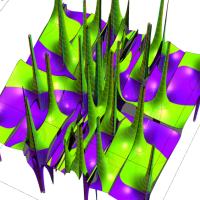
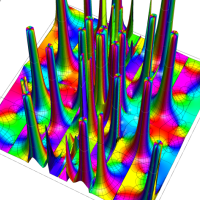
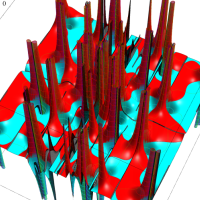
2個のポイントアトラクターを持つ Duffing 関数が、有限時間後にそのどちらに吸引されるかを表わした初期値関数の図。
①:吸引が強い場合
②:吸引が弱い場合
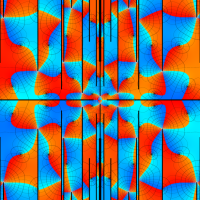
複素変数の Duffing 関数
複素変数の Duffing 関数
複素変数の Duffing 関数
複素変数の Duffing 関数の導関数
複素変数の Duffing 関数の導関数
複素変数の Duffing 関数の導関数
非強制振動型 Duffing 関数 (非強制振動型 Duffing の微分方程式の解)
2階の非線形常微分方程式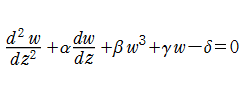
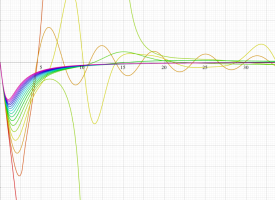
は初期値である。微分方程式の形から非強制振動型 Duffing 関数は、さしずめ減衰振動化した楕円関数といった様相になる。事実、
ポテンシャルエネルギーが関数
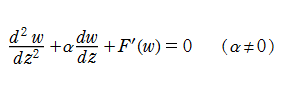
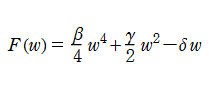
①:
②:
位相平面上での非強制振動型 Duffing 関数。様々な初期値からの軌道を重ね描きした図。背景色はスカラー場の強度。
①:
②:
2個のポイントアトラクターを持つ非強制振動型 Duffing 関数が、有限時間後にそのどちらに吸引されるかを表わした初期値関数の図。
①:
複素変数の非強制振動型 Duffing 関数
複素変数の非強制振動型 Duffing 関数
複素変数の非強制振動型 Duffing 関数の導関数
複素変数の非強制振動型 Duffing 関数の導関数
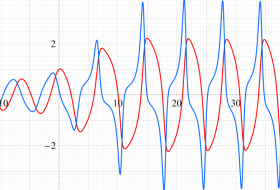
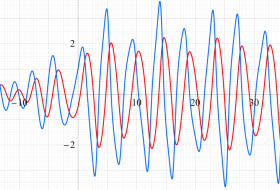
強制振動型 Van der Pol 関数 (強制振動型 Van der Pol の微分方程式の解)
Van der Pol の微分方程式において強制振動項を考慮した、2階の非線形常微分方程式を、強制振動型 Van der Pol の微分方程式といい、解
は初期値である。強制振動型 Van der Pol 関数は、
Van der Pol は1927年にアナログ真空管回路を用いて、この微分方程式の解が定数
強制振動型 Van der Pol の微分方程式が、ストレンジアトラクターの解を含む方程式かどうかは不明である。
①:
②:
位相平面上の軌道とともに、
①:
②:
-1000から100万までの
実変数の強制振動型 Van der Pol 関数
複素変数の強制振動型 Van der Pol 関数
複素変数の強制振動型 Van der Pol 関数
複素変数の強制振動型 Van der Pol 関数
複素変数の強制振動型 Van der Pol 関数の導関数
複素変数の強制振動型 Van der Pol 関数の導関数
複素変数の強制振動型 Van der Pol 関数の導関数
Lotka - Volterra 関数 (Lotka - Volterra の微分方程式の解)
日:Lotka-Volterraの微分方程式,ロトカ-ヴォルテラ方程式英:Lotka-Volterra equation,仏:Équation de Lotka-Volterra,独:Lotka-Volterra-Gleichungen
連立の1階非線形微分方程式
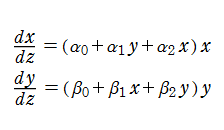
となる場合を言う。このとき解
連立1階非線形微分方程式を
となる。この解
は初期値である。
なる変換を施したものになる。また、2種個体数の初期値の関係は
をもとに決めることができる。
狭義の Lotka - Volterra の微分方程式は、常に周期解となるためポイントアトラクターを持たない。しかし一般の場合において係数が
を満たすときは減衰振動解、すなわちポイントアトラクターを持つ。さらに、係数がもっと一般的な場合には、解が有界でないこともある。なお、一般の Lotka-Volterra の微分方程式が Painlevé 性を持つのは、係数が
となる場合(楕円関数に還元される場合)のみで、これは狭義の Lotka-Volterra の微分方程式に含まれない。
S. V. Volterra は、第1次世界大戦前後での漁獲量変動の説明としてこの微分方程式を用いたが、すでに A. J. Lotka によって同形の微分方程式が研究されていることが後年に判明したため、Lotka - Volterra の微分方程式と呼ばれるようになった。
一般に、このような連立非線形微分方程式で表わされる系は、生物学や化学など学術の広範囲で現れる (例えば、ブリュセレーター(ブリュッセル学派)方程式など)。また、それらの系では3連あるいは4連以上となることも珍しくない。後述の Lorenz 方程式は、3連非線形微分方程式の例として有名である。
①:周期解
②:減衰振動解
位相平面上の Lotka - Volterra 関数の軌道図。
①:周期解
②:減衰振動解
複素変数の Lotka - Volterra 関数
複素変数の Lotka - Volterra 関数
複素変数の Lotka - Volterra 関数
以降は、パラメータが通常の Lotka - Volterra 関数の範囲を超える場合である。
実変数の Lotka - Volterra 関数
複素変数の Lotka - Volterra 関数
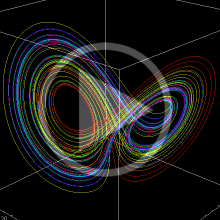
Lorenz 関数 (Lorenz の微分方程式の解)
日:Lorenzの微分方程式,ローレンツ方程式英:Lorenz equation,仏:Équation de Lorenz,独:Lorenz-Gleichungen
” バタフライ効果 - 蝶の羽ばたき程度の擾乱は、気象の劇的な変化を起こしうるか? ”
前述の Lotka - Volterra の微分方程式のように、複数個の時間的変動量が相互依存の関係にある系は、自然な方法で連立非線形微分方程式に表わすことができ、その解の組は多次元の位相空間内で軌道を描くことをこれまで見てきたが、専ら2次元の場合であった。ここでは3次元になる例として Lorenz の微分方程式を扱う。
1963年に気象学者の E. N. Lorenz は、大気圏の上層と下層の温度差が空気の対流を生む現象を数学的に論じるため、これを単純化したモデル、例えば、水を張った鍋を底面から加熱した時に生じる流体の運動や熱の移動について定式化した。それでも方程式は非常に複雑になるので、実際には更なる単純化によって、流速関数および温度の線形成分からの相異関数の満たす微分方程式に帰着させ、各関数を Fourier 級数に展開したときの時刻
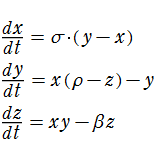
Lorenz の微分方程式は、解の位相空間を
ここに、
特に
先の物理的な意味では、
物理的意味からは逸れるが、
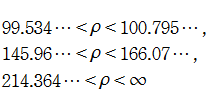
以降では、Lorenz の微分方程式の解についても複素関数的な扱いを試みる。このとき、直接数値的に求めた解を 「Lorenz 関数」 と称し、初期条件を明示した関数記号
で表記することにする (独自の記号である)。
【註記】
※1:時刻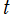 を明示的に含まない形 (自律系) の連立微分方程式
を明示的に含まない形 (自律系) の連立微分方程式
における 「不動点」 とは、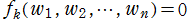 となるような位相空間内の点
となるような位相空間内の点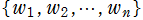 のことである。その名称は、不動点を初期値とする解が時刻
のことである。その名称は、不動点を初期値とする解が時刻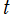 に係わらず恒等的に一定値となることに因む。
に係わらず恒等的に一定値となることに因む。
不動点の 「安定」・「不安定」 とは、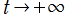 としたときに不動点近傍の軌道がどのように挙動するかを区別する名称で、すべての軌道が吸引される場合を安定、一部の例外を除いて反発する場合を不安定という。そのとき軌道は、不動点を結節点や渦状点、鞍状点とするように振る舞う。
としたときに不動点近傍の軌道がどのように挙動するかを区別する名称で、すべての軌道が吸引される場合を安定、一部の例外を除いて反発する場合を不安定という。そのとき軌道は、不動点を結節点や渦状点、鞍状点とするように振る舞う。
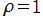 のように安定・不安定の境界線上になる場合、不動点は退化し (退化不動点となり)、異なる定常状態の解への分岐点となる。
のように安定・不安定の境界線上になる場合、不動点は退化し (退化不動点となり)、異なる定常状態の解への分岐点となる。
不動点の安定性のみではなく、不動点周りの軌道の振る舞いまで含めて考えれば、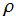 の場合分けは上記よりも細かくなる。それを、軌道の反復運動を生じるセパレータの変形や Lorenz アトラクターが発生するメカニズム等と比較しながら論じた詳しい説明が、J. M. T. Tompson & H. B. Stewart 著 「非線形力学とカオス」 の第11章 「Lorenz 系」 にある。
の場合分けは上記よりも細かくなる。それを、軌道の反復運動を生じるセパレータの変形や Lorenz アトラクターが発生するメカニズム等と比較しながら論じた詳しい説明が、J. M. T. Tompson & H. B. Stewart 著 「非線形力学とカオス」 の第11章 「Lorenz 系」 にある。
※1:時刻
における 「不動点」 とは、
不動点の 「安定」・「不安定」 とは、
不動点の安定性のみではなく、不動点周りの軌道の振る舞いまで含めて考えれば、
位相空間内の
複素変数の Lorenz 関数
複素変数の Lorenz 関数
複素変数の Lorenz 関数
実変数の Lorenz 関数
位相空間内の
複素変数の Lorenz 関数
複素変数の Lorenz 関数
複素変数の Lorenz 関数
実変数の Lorenz 関数
位相空間内の
複素変数の Lorenz 関数
複素変数の Lorenz 関数
複素変数の Lorenz 関数
実変数の Lorenz 関数
位相空間内の
複素変数の Lorenz 関数
複素変数の Lorenz 関数
複素変数の Lorenz 関数
アニメーション①(3.54MB)
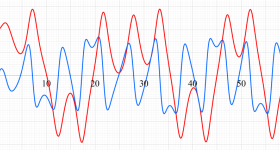
Lorenz 方程式の解の軌道が変形する様子。
アニメーション②(1.48MB)
Lorenz 方程式の解が漸近的に周期軌道となる 「窓」 区間の周辺。
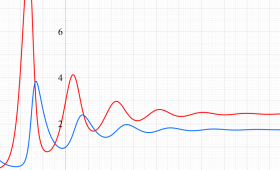
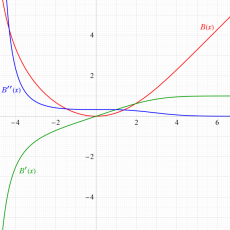
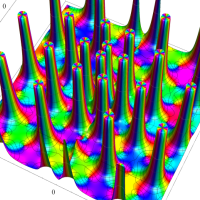
Blasius 関数
日:Blasius関数,ブラジウス関数英:Blasius function,仏:Fonction de Blasius,独:Blasius-funktion
3階の非線形常微分方程式である、Blasius の微分方程式
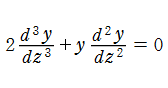
となるものを、Blasius 関数という※1。
Blasius の微分方程式、および Blasius 関数は、流体力学における Blasius 境界層(Blasius boundary layer:一方向かつ一定速度の粘性流体に対して平行に保持された半無限板上に形成される、理想化された安定的な二次元境界層。板によって剪断された流体は、板の表面に近いほど粘性に由来する減速が生じ、一定速度である領域と区別される層を形成する※2。)内部での粘性流体の速度分布を記述するために、1908年に P. R. H. Blasius によって導入された。
具体的には、流体の元々の一定速度を
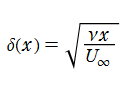
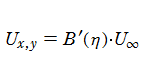
Blasius 関数は、冪級数によって
と表わされる。冪級数展開式から、原点中心の3数性
を満たすことが分かる。
Blasius 関数の複素平面上における特異点は、閉じた式で表わされない複雑な位置に存在するが、特異点の一つを
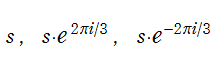
【註記】
※1:標準的な関数記号は存在しない。文献等では、単に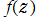 と表記することが多いようである。
と表記することが多いようである。
※2:これは理想化された条件下での現象であるため、自然界では限られた場合にしか見られない。大抵は些細な原因で擾乱が生じるため、整った層流にはならない。すなわち「乱流」が起きる。
※3:複素領域における Blasius 関数については、例えば次の論文が詳しい。
J. P. Boyd 「The Blasius Function in the Complex Plane」 Experimental Mathematics, Vol.8, No.4 (1999)
※1:標準的な関数記号は存在しない。文献等では、単に
※2:これは理想化された条件下での現象であるため、自然界では限られた場合にしか見られない。大抵は些細な原因で擾乱が生じるため、整った層流にはならない。すなわち「乱流」が起きる。
※3:複素領域における Blasius 関数については、例えば次の論文が詳しい。
J. P. Boyd 「The Blasius Function in the Complex Plane」 Experimental Mathematics, Vol.8, No.4 (1999)
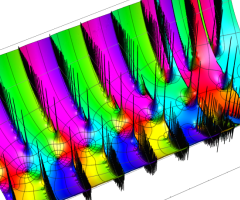
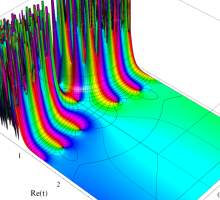
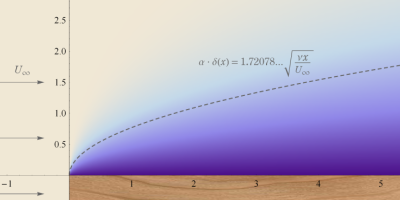
Blasius 導関数を用いて、Blasius 境界層を視覚化する(
なお、
となる。次のグラフでは、排除厚さで見積られる境界層の厚さを、併せて破線で表示している。
複素変数の Blasius 関数
複素変数の Blasius 関数の導関数
複素変数の Blasius 関数の2位導関数
Lane - Emden 関数
日:Lane-Emden関数,レーン-エムデン関数英:Lane-Emden function,仏:Fonction de Lane-Emden,独:Lane-Emden-funktion
進化の様々な段階における恒星の内部で、温度や圧力,気体の密度が中心からの距離に応じてどのように分布しているかについては、1870年に J. H. Lane が初めて考察した。また、1907年に J. R. Emden は、それまでに他の科学者によって得られていた結果も踏まえて、自身の研究成果をまとめた。このような歴史的経緯に基づき、この問題で考察されるようになった非線形常微分方程式
は現在、Lane - Emden の微分方程式と呼ばれる。このとき、
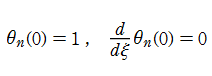
Lane - Emden の微分方程式は導出の際、圧力
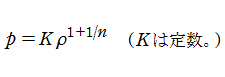
に還元されるが、その他の場合は、既知の関数で明示的に表わせないので数値的に求めるしかない※1。一般的な指数の Lane - Emden 関数は、原点を中心に冪級数展開すると
となる。特に
によって係数を具体的に求めることができる。
複素変数の Lane - Emden 関数は、指数
【註記】
※1:以下のグラフでは、指数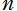 が非負整数または半奇数である場合のみを描画する。(なお、NDSolveComplexDomain.m を用いて複素変数のグラフが描画できるのは、
が非負整数または半奇数である場合のみを描画する。(なお、NDSolveComplexDomain.m を用いて複素変数のグラフが描画できるのは、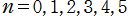 並びに
並びに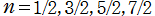 に限る。)
に限る。)
※2:この現象は、Lane - Emden の微分方程式が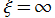 の近傍で、
の近傍で、
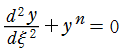
に摂動することから分かる。つまり、Lane - Emden 関数は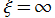 の近傍で超楕円積分
の近傍で超楕円積分
の逆関数に近付く。
※1:以下のグラフでは、指数
※2:この現象は、Lane - Emden の微分方程式が
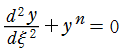
の逆関数に近付く。
複素変数の Lane - Emden 関数
複素変数の Lane - Emden 関数
複素変数の Lane - Emden 関数
複素変数の Lane - Emden 関数
複素変数の Lane - Emden 関数
複素変数の Lane - Emden 関数
複素変数の Lane - Emden 導関数
複素変数の Lane - Emden 導関数
複素変数の Lane - Emden 導関数
複素変数の Lane - Emden 導関数
複素変数の Lane - Emden 導関数
複素変数の Lane - Emden 導関数